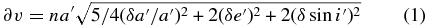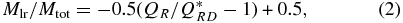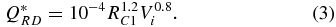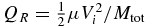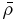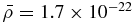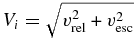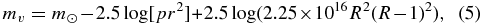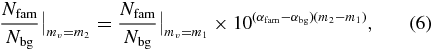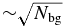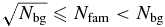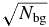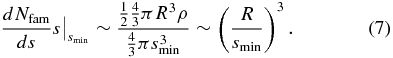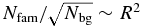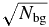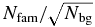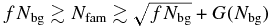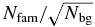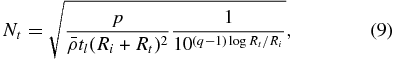IDENTIFYING COLLISIONAL FAMILIES IN THE KUIPER BELT

Families are identified by linking a set of objects that likely originated from very similar heliocentric positions and velocities and thus had nearly the same (osculating) heliocentric orbital elements at some point in the past. Some differences in the osculating elements between family members are expected because the collision that forms the family gives each member an independent velocity kick relative to the center-of-mass orbit of the two colliding bodies. The initial collision does not generally change the orbital angles—ω, the argument of periapse, Ω, the longitude of the ascending node, and M, the mean anomaly—by more than ∼10°, depending on the velocity of impact and the orbit. Over time, since each family member has a slightly different semimajor axis, they have different periods and the orbital phases (given by the mean anomalies) are quickly randomized (several orbital periods). On secular timescales, the differing semimajor axes impart to each family member a slightly different apsidal and nodal precession rate, causing the orbital angles ω and Ω to also randomize. The information in these angles is eventually lost, except in the case of very young families, e.g., the ∼500 kyr old Datura family (Nesvorny et al. 2006).

For objects which are on stable orbits, the so-called proper or free orbital elements, e_proper and i_proper, are roughly conserved, along with the mean semimajor axis, a. Proper elements are calculated by removing the time-dependent perturbations by the major planets. The value of the proper elements depends on the positions of the planets and all the orbital elements; however, since the original family started at the same time, with somewhat similar orbital elements, they have a similar spread in proper orbital elements as in the initial osculating elements. Thus, groups of objects with similar proper elements may have shared very similar orbits in the past, potentially due to a common origin in a particular collision. We have found that current observations of KBOs allow for a quite accurate measurement of proper orbital elements; in general, clustering in these orbital elements will not be hindered by observational uncertainty.

Hirayama (1918) first identified clusters of main belt asteroids that were likely of a common origin. Roughly half of all known asteroids are associated with identified families, including about 60% of asteroids with an H magnitude fainter than 13, up to the SDSS completeness limit of H ∼ 15 in the outer belt and H ∼ 17 in the inner belt (Parker et al. 2008). Such families are now known to have formed from collisions between asteroids. Asteroid collisional families are identified dynamically by clustering in proper orbital elements and spectroscopically by the distinct color differences between different families and between family members and background objects.

While rough calculations of the proper orbital elements can in some cases be carried out analytically, accurate family member identification of asteroids today involves numerical orbit integration coupled to frequency filtering to remove the periodic perturbations from the planets (e.g., Knežević & Milani 2000). Likewise, identification of family members has advanced beyond visual inspection of proper eccentricity and proper inclination versus semimajor axis plots to include clustering algorithms, with a metric given by, e.g.,

$$\begin{equation} \partial v = n a^{\prime } \sqrt{5/4(\delta a^{\prime }/a^{\prime })^{2}+2(\delta e^{\prime })^{2} + 2(\delta \sin i^{\prime })^{2}} \end{equation} \tag{ 1 }$$

with the coefficients fine-tuned to produce accurate results (Zappala et al. 1990). Here, ∂v is a distance in proper element space with dimensions of velocity, while n, a', e', and i', are the proper mean motion, semimajor axis, eccentricity, and inclination of the particles, respectively. Note that the commonly employed Hierarchical Clustering Method, which links family members together through a friends-of-friends technique, assumes that the family is tightly clumped relative to the background, a criterion that is usually not satisfied in the Kuiper Belt, as will be shown in Section 5.

The Haumea family was initially identified by the discovery of a class of objects with unusually deep water ice spectra and was later shown to be tightly clustered dynamically, with a velocity dispersion of only ∼140 m s⁻¹ (Brown et al. 2007; Barkume et al. 2008; Ragozzine & Brown 2007). This is much smaller than the escape velocity from Haumea (∼900 m s⁻¹). Brown et al. (2007) proposed a collisional origin for the family members, with a high-velocity (∼3 km s⁻¹) impact stripping the proto-Haumea (with an initial density of 2.0 g cm⁻³, consistent with other large KBOs) of some of its icy mantle and leaving behind the ∼2.6 g cm⁻³, rapidly rotating dwarf planet, along with its two satellites and associated family members.

A collisional scenario like that proposed by Brown et al. (2007) is only probable early in the solar system in the thin pre-excitation planetesimal disk, but subsequent scattering by Neptune into the current Kuiper Belt would have destroyed the dynamical coherence of the family. Levison et al. (2008b) proposed a collisional scenario in which two scattered disk objects collided after the Kuiper Belt was already excited, resulting in the formation of the Haumea family in the excited classical region. Such a scenario renders plausible a collision between two large KBOs and preserves the dynamical coherence of the family, but it does not explain the low velocity dispersion between family members. Schlichting & Sari (2009) later proposed a scenario in which a giant impact creates a rapidly rotating, high-density Haumea with a large satellite. In this model, a subsequent impact onto the satellite (after Haumea is on its current orbit) forms the family with a low velocity dispersion. However, detailed numerical simulations of the collisional scenarios of Brown et al. (2007) and Schlichting & Sari (2009) show that such collisions are unlikely to explain the near-breakup spin rate of Haumea (Leinhardt et al. 2010). Instead, Leinhardt et al. (2010) suggest a scenario in which the family formed directly by a single low-speed "graze and merge" impact event, as also recommended by Toth & Lisse (2010). This impact event is able to explain the low velocity dispersion of the family, the presence of both satellites and unbound family members, and the near-breakup rotation and enhanced density (relative to other large KBOs) of Haumea. It is still unclear, however, how such an impact scenario would arise, as any collision with Haumea in the current Kuiper Belt environment would be a high-speed event, with a possible exception arising from a "late" instability of a large binary.

The asteroid belt includes identified collisional families that have formed by cratering impacts as well as those formed by catastrophic disruption (e.g., Durda et al. 2007). One feature of those families formed in cratering events is that the largest impact fragment is considerably smaller in size than the target body. This size difference can be an order of magnitude in radius or larger (i.e., ∼5 mag fainter). While such family-forming collisions likely occur in the Kuiper Belt, these are not the most likely families to be found, particularly around parent bodies of radius ≲ 500 km, due to the extreme faintness of nearly all the family members. Similarly, super-catastrophic impacts are also unlikely to result in identifiable families in the Kuiper Belt because all the fragments would be considerably smaller than the parent body.

Catastrophic collisions, in which the target body is entirely broken up, but roughly half the mass re-accretes due to gravity, are then the most likely source of any asteroid belt family analogs that will be identifiable in the Kuiper Belt. In such collisions, roughly half the total colliding mass ends in the largest fragment. The differential size distribution of the remaining fragments is well described by a power law, N(⩾ r)∝r^{1 − q}, with index q ranging at least from ∼3 to 6, that conserves the total mass and geometric volume prior to the collision and cuts off at some non-zero minimum size (Z. M. Leinhardt & S. T. Stewart 2011, in preparation). The velocity distribution of the fragments spans the range with some velocities larger than the escape velocity and some smaller than the escape velocity with respect to the largest remnant (Z. M. Leinhardt & S. T. Stewart 2011, in preparation), with a significant number (of order 50%) of the fragments having a velocity ≲ v_esc.

The type of impact necessary for catastrophic disruption of a parent body can be calculated using the catastrophic disruption criteria of Stewart & Leinhardt (2009), where the mass of the largest remnant (M_lr) is given by

$$\begin{equation} M_{{\rm lr}}/M_{{\rm tot}} = -0.5(Q_{R}/Q^{*}_{RD} -1) + 0.5, \end{equation} \tag{ 2 }$$

and the catastrophic disruption threshold Q*_RD is (in cgs units)

$$\begin{equation} Q^{*}_{RD} = 10^{-4} R_{C1}^{1.2} V_{i}^{0.8}. \end{equation} \tag{ 3 }$$

Here, R_C1 is the radius of a spherical body containing the entire colliding mass (M_tot) at a density of 1 g cm⁻³, V_i is the impact velocity, and $Q_{R}=\frac{1}{2}\mu V_{i}^{2}/M_{{\rm tot}}$ is the reduced mass (μ) kinetic energy, scaled to the total colliding mass. These scaling laws have been shown to hold for large icy bodies to within a factor of two (Marcus et al. 2010). Q*_RD is defined such that half the mass remains in the largest remnant when Q_R/Q*_RD = 1. At typical relative velocities in the cold classical belt of ev_orb ≈ 0.1 × 5 km s⁻¹ ≈ 500 m s⁻¹, catastrophic disruption is very unlikely to occur for target bodies larger than ∼100 km in radius. However, at the higher inclinations and eccentricities of the dynamically excited classical belt, typical relative velocities of $v_{\rm {imp}} \approx \sqrt{e^2+i^2}v_{\rm {orb}} \approx \sqrt{0.1^2 + 0.3^2}v_{\rm {orb}} \approx 1.6$ km s⁻¹ can lead to impacts that disrupt even 500 km radius target bodies (assuming a 350 km radius projectile in Equations (2) and (3)).

The probability, p, of a collision between two bodies of sizes R_i and R_t in a time t_l is (Levison et al. 2008b)

$$\begin{equation} p = N_{i}N_{t}t_{l}(R_{i}+R_{t})^{2}\bar{\rho }, \end{equation} \tag{ 4 }$$

where N is the number of objects and $\bar{\rho }$ is the mean intrinsic impact rate. Adopting the value $\bar{\rho }=1.7 \times 10^{-22}$ km⁻² yr⁻¹ as a reasonable mean impact rate for the entire Kuiper Belt assuming it has always existed as it is today (as in Levison et al. 2008b), the probability of a collision between a 500 km radius target and a 350 km radius projectile in the age of the solar system is ∼4 × 10⁻³, assuming a differential size distribution with q = 4.8. The probability reaches ∼1 for a single collision between a 250 km radius target and a 100 km radius projectile since the Kuiper Belt attained its current form. Note that the above projectile sizes of 350 km and 100 km are the smallest objects that yield Q_R/Q*_RD = 1 at typical impact velocities $V_{i} = \sqrt{v_{\rm {rel}}^{2} + v_{\rm {esc}}^{2}}$, with v_rel = 1.6 km s⁻¹. Note that these probabilities may be increased by considering enhancements of the Kuiper Belt populations in the past as discussed in Section 3.2.

Because of the steep slope in the size distribution for KBOs, collision probabilities significantly increase with decreasing size of the target and projectile; families are more likely to exist around smaller parent bodies. In addition, the differential size distribution of collisional families may often have a steeper slope, q ≈ 4–5.5 (Z. M. Leinhardt & S. T. Stewart 2011, in preparation), than the background population below the break in the size distribution, where q ≈ 1.5–2.5 (Fuentes et al. 2009; Fraser & Kavelaars 2009). From these two facts, one would conclude that collisional families are more likely to be found as the largest remnants of smaller parent bodies, a topic that we will return to in Section 7 with more information.

Following Levison et al. (2008b), there are three major stages in the history of the Kuiper Belt as found in virtually all successful models of the formation and evolution of the outer solar system (see, e.g., recent reviews by Chiang et al. 2007; Levison et al. 2008a; Morbidelli et al. 2008). In Stage I, KBOs were in an environment where they could grow, which implies a large quiescent planetesimal disk where collisions were common, but gentle enough to lead to accretion (Kenyon et al. 2008). A dense thin planetesimal disk is also required for the formation of observed KBO binaries (Schlichting & Sari 2008). The Kuiper Belt that we see today is neither massive nor dynamically quiescent: 100–1000 times more mass is needed to grow the observed objects. Thus, there must have been some sort of dynamical event (Stage II) that significantly excited the orbits of the KBOs. This event was either violent enough to perturb ∼99% of the primordial objects onto planet-crossing orbits, thereby dynamically producing the Kuiper Belt's small mass, or excited the Kuiper Belt enough that collisions became erosional, removing the extra mass by pulverizing objects to dust, or some combination of the two. It was during this violent period that most of the structure of the observed Kuiper Belt was established. Note that this initial mass estimate assumes that KBOs formed by two-body coagulation. If instead KBOs formed by gravitational instability (e.g., Chiang & Youdin 2010), the dense thin planetesimal disk is no longer necessary, nor is the additional mass. In this case, the dynamical sculpting during Stage II would not have to remove most of the mass of the early Kuiper Belt. Regardless, since the dramatic period that led to its present structure, the Kuiper Belt has been relatively quiet (Stage III). The only significant dynamical changes may have resulted from the continuing collisions among the smaller bodies and the gradual decay of intrinsically unstable populations. This stage corresponds to the last ∼4 billion years of solar system history.

Collisions in the Stage I planetesimal disk may have produced families, but the subsequent excitation of the disk removes all signatures of these families (no orbital properties are conserved) and they cannot be studied at the present day with dynamics alone. Only toward the end of Stage II, when the remaining dynamical evolution of Neptune is small, can one hope to conserve orbital properties that are observable today (though Levison et al. 2008b do find that smooth low-eccentricity Neptune migration is not efficient at capturing Haumea-family members and that the shape of this family would be preserved). These "primordial" families are particularly valuable probes of Kuiper Belt formation, since they were created in an environment that cannot be observed today, but which varies between different outer solar system formation models. For example, if the age of a currently coherent collision family in the excited population (perhaps the Haumea family) could be securely measured to be more than ∼4.1 Gyr ago, then a connection between the formation of the Kuiper Belt and the late heavy bombardment (∼3.8–4.1 Gyr ago), as proposed by the Nice model (Gomes et al. 2005), could potentially be ruled out.

During Stage II, the mass of the Kuiper Belt is being eroded and the dynamical sculpting of the currently observed KBO orbits is accomplished. How these two, potentially separate, processes were completed affects where we would find KBO families today. If objects were on their final orbits before most of the mass was removed by collisional grinding, then the frequency of families will be high, since the appropriate number density to assume for collision probabilities is much higher than seen today. On the other hand, if mass was removed dynamically, then there would presumably be a somewhat enhanced number of collisional families only after orbits have mostly settled down, so that the number of coherent families remaining today would be much less.

This concept has a specific application to the Kuiper Belt in the as yet unclear origin of the cold classical population. One model proposes an in situ formation, with collisional grinding doing most of the work of removing mass from this region (e.g., Kenyon et al. 2008), while another, inspired by the Nice model, proposes that Neptune scattered with large eccentricity to an orbit near its current location, and the cold classical population was emplaced as Neptune's eccentricity damped (Levison et al. 2008a).

We can estimate the differences in the number of families produced by two core accretion models: where the classical population is formed in situ and where the classical population is dynamically emplaced. When the cold classical population forms in situ, the quiescent phase of evolution that produces observable families comes after the dynamical perturbation that imparted the small observed eccentricities and inclinations to the Stage I planetesimal disk. For this case, assuming that dynamical perturbation removed 50% of the original mass, the Stage III collisional cascade starts with basically the observed cold classical belt with 50–500 times as many objects as are currently present (Kenyon et al. 2008).

The size distribution would not necessarily be the same as observed today and one could expect, following Pan & Sari (2005), that it was mostly objects below the currently observed break that participated in the mass loss via collisional cascade (Kenyon et al. 2008). This significantly increases the number of objects at sizes below the break. As in Levison et al. (2008b), we should also account for the falloff of this number enhancement as a function of time in determining the number of families formed in this early dense stage. From their work, we estimate that the time-averaged enhancement is a factor of ∼20 lower than the initial enhancement in the number of bodies. If both target and impactor populations are enhanced, the number of families increases as the square of the number of bodies (Equation (4)), leading to a potential increase in the number of families in the cold classical belt by a factor of ∼5–100 times over what would be predicted based on the currently observed belt. A more precise estimate of the expected number of families depends on the detailed collisional grinding history.

On the other hand, in a model that predicts dynamical emplacement of the cold classical population (like the Nice model), the number of expected families is far fewer. In this formation scenario, the Stage I pre-excitation planetesimal disk extends to only ∼30 AU, and a major instability among the giant planets puts Neptune on an eccentric orbit. While Neptune's orbit is eccentric, the cold classical region is dynamically unstable, allowing objects scattering off Neptune to fill this region (Levison et al. 2008a). Though there are collisional families formed in the cold classical region during this time, they cannot remain dynamically coherent until Neptune's orbit circularizes. At this point, formerly unstable objects in the cold classical region are stranded in the stable orbits observed today. In this model, the cold classical population starts out much smaller than in the in situ formation model. Thus, a Nice-model-like emplacement of the cold classical population would have far fewer families than in the collisional grinding model.

Whatever the formation model, families continue to form throughout Stage III. These formation events can involve collisions between objects in stable and/or unstable populations. Unstable populations, such as the scattered disk, must have been much larger in the past, significantly increasing the number of collisions expected in the early outer solar system, as discussed in detail by Levison et al. (2008b). The scattered disk population must have been 100 times bigger in the past, with a relatively rapid decay constant, leading to an increase in the number of expected families by a factor of ∼25, which is needed to increase the probability of a putative Haumea collision.

Not all of these collisions produce families that are dynamically stable. Levison et al. (2008b) looked at the "collision orbits" of combinations of impactors in three model scattered disk populations assuming a fixed mass ratio of 5 between impactor and target and found that 10%–30% of such collisions would emplace families in the stable region of the Kuiper Belt, mostly with high perihelia and a large range of inclinations (see their Figure 2). It is beyond the scope of this paper to reassess their model for different mass ratios, but a mass ratio of 5 is generally reasonable, and we adopt the result that roughly 10%–30% of SDO–SDO families are emplaced in the Kuiper Belt, where they are stable and observable today. This leads to an increase in the number of families by about a factor of ∼2–8, over what would be assumed based on the currently observed population. The size of the largest progenitor family thus created is that due to the Haumea family, presumably, and the next largest would be ∼400 km in radius. In any case, the number and distribution of KBO families is a key observational parameter that has significant power to improve theories of the formation and evolution of the outer solar system. To understand the observational constraints on families, we must investigate their detectability as a function of size and orbit.

Using the criterion of the ratio of family members to background objects close to the largest remnant for whether or not a family is readily identifiable, it is clear that families like those in the asteroid belt, with most of the mass having Δv ∼ v_esc, will be very difficult to identify around families with progenitors in the size (radius) range 100–500 km. Figure 2 (panels 1 and 2) shows a histogram and a cumulative number plot versus log Δv_min for one of the few families with k = 1 that had a family member to background KBO ratio greater than one anywhere in the orbital element volume defined by Δv_min ⩽ v_esc and up to any limiting magnitude. Note that this family occurs in the hot classical belt at very high inclination (32°) with a progenitor of radius 470 km. As discussed in Section 3.1, it is unlikely that such a large KBO has undergone a potentially family-forming collision in the age of the solar system (p ∼ 4 × 10⁻³), unless the collision probability has been greatly enhanced by the presence of scattered disk objects (Levison et al. 2008b; see Section 3.2 of this paper).

Zoom In Zoom Out Reset image size

Figure 2 (panels 3 and 4) shows a plot of the density of KBOs in proper orbital element space. This plot includes both the background synthetic KBO population (Figure 1) and the "base case" collisional family. The family stands out visually throughout much of the classical belt region, particularly in inclinations.

Figure 2 includes the ratio of family members to background objects at all sizes. However, the size distribution for collisional families has a larger slope than the background KBO population below the break in the size distribution, so the degree to which family members outnumber background objects will depend on size. Figure 3 (panels 1 and 2) shows histograms and cumulative number distributions versus log Δv_min for the same family shown in Figure 2, now including only bodies with m_v ⩽ 28. The magnitude dependence of the observability of the family is clear; the family members are outnumbered by the background objects by a factor of nearly 10. The issue is greater at even brighter magnitude limits. Panels 3 and 4 of Figure 3 again show this family plotted against the background in density, but with a magnitude limit of m_v ⩽ 28. Note that clumping of the family members is still clear to the eye in inclination-semimajor axis space, though this is partly due to our choice of a single velocity kick; a realistic distribution of velocities would not make a collisional cloud with such a prominent boundary.

Zoom In Zoom Out Reset image size

The change in the ratio of family members to background objects within some dynamical volume given by Δv_min ⩽ v_esc with a change in magnitude cutoff can be estimated given the size distributions of the family and the background. Given the ratio at some fixed magnitude m_v = m₁, the ratio at m₂ is

$$\begin{equation} \frac{N_{{\rm fam}}}{N_{{\rm bg}}} \big\vert _{m_{v}=m_{2}} = \frac{N_{{\rm fam}}}{N_{{\rm bg}}} \big\vert _{m_{v}=m_{1}} \times 10^{(\alpha _{{\rm fam}} - \alpha _{{\rm bg}})(m_{2}-m_{1})}, \end{equation} \tag{ 6 }$$

where α = (q − 1)/5. Thus, for a family with the same size distribution as the background, the ratio is independent of limiting magnitude. However, the ratio decreases by a factor of 100 with a change in limiting magnitude from 28 to 24.5 (the expected limiting magnitude of single exposures by LSST) if q_fam ∼ 4.5 and q_bg ∼ 2, as is expected below the break at ∼50 km in radius.

Figures 4 and 5 (panels 1 and 2) show histograms and cumulative number distributions versus log Δv_min for families with nearly identical progenitors to that of Figure 2 but located in different regions of the belt. In both Figures 4 (∼490 km radius progenitor, i ∼ 25) and 5 (∼500 km radius progenitor, i ∼ 15°), the family members are dominated in number by the background even at small Δv_min values even when no magnitude limit is included. A plot of the KBO number density including the family is shown for both Figures 4 and 5 in panels 3 and 4. The central region of the family in the cold classical belt does not stand out above the background, although some overdensity does stand out at semimajor axes interior to the cold classical region, particularly in the inclinations. This region of low inclination interior to the cold classical region, is, however, unstable. Note that, as discussed in Section 3.1, it is unlikely that a ∼490 km radius KBO would be strongly disrupted in the cold classical region anyway because of the low velocity dispersion (neglecting the possibility of a high-velocity collision with a scattered disk object). The effect of progenitor inclination on family identifiability will be discussed further in Section 5.7. In general, those searching for families in the Kuiper Belt should keep in mind that even relatively large clusterings could be the visible tip of a larger family. Note also how collisions can place relatively large numbers of objects on quite atypical orbits.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figures 6 and 7 show collisional families in the hot classical belt with progenitors of radius 250 km and 140 km, respectively. Although the dynamical volume Δv_min ⩽ v_esc is much smaller for these families, the small size of the fragments and the relatively small number of fragments make these families blend into the background population. With all else being equal, decreasing the size of the progenitor by a factor of two decreases the ratio of family members to background objects in the volume Δv_min ≲ v_esc by a factor of ∼2–3 (see Section 5.7). While these families will be difficult to identify using only dynamical clustering, they are by far the most likely to be present in the Kuiper Belt given the strong size dependence of the collision probability. As discussed in Section 3.1, 250 km is close to the maximum radius at which we would expect that there has most likely been at least one collision in the last several billion years given the current population densities. Note that the slight overdensities caused by the family are apparent to the naked eye in inclinations (panel 4) of both figures, though this is partly due to our choice of Δv = v_esc, with no spread in velocities. This shows that N_fam/N_bg ⩾ 1 is not a requirement for family identification. The effect of progenitor size on family identifiability will be discussed further in Section 5.7.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

When the collisional family members are more tightly clustered, with all members having Δv ⩽ 0.25v_esc, the situation improves greatly. Such a tightly clustered family—analogous to the Haumea collisional family in orbital distribution, but still with a size distribution consistent with a catastrophic disruption event—results in family member to background object number ratios greater than one for radii throughout the range 100–500 km. However, the inclinations at which this occurs are still ⩾10°. It is not clear how frequently a family would form with a considerable fraction of the mass within Δv ≲ 0.25v_esc, but the Haumea family has Δv ≲ 0.15v_esc, so such families are plausible. Note, also, that equipartition of momentum, though not necessarily an outcome of these collisions, would imply that the largest (and brightest) objects would be generally more tightly clustered.

Figure 8 (panels 1 and 2) shows a histogram and cumulative number distributions versus log Δv_min for a family originating from the same progenitor as that in Figure 6, but with a typical ejection velocity of only 0.25v_esc. The family members dominate in number over the background population much more so than when the relative velocities are ∼v_esc. Panels 3 and 4 of Figure 8 show the tight clustering in orbital elements of the family, which stands out easily above the background. In general, decreasing the typical ejection velocity from v_esc to 0.5v_esc increases the ratio N_fam/N_bg by a factor of ∼5. Further decreasing the typical ejection velocity to 0.25v_esc increases this ratio by another factor of ∼5, suggesting an enhancement in N_fam/N_bg of k^{−ln 5/ln 2} over the range measured.

Zoom In Zoom Out Reset image size

Thus far in this paper, we have been using the criterion that N_fam/N_bg ⩾ 1 is necessary for a family to be identifiable. However, this is not strictly true. Where the background population is well understood, a family can be identified even when this criterion is not met. Consider a smooth background that can be accurately modeled in a particular region. In this region, the background can be subtracted from the distribution of observed KBOs. In the absence of families, the minimum fluctuations in the remaining population should be due to Poisson noise and have magnitude ${\sim} \sqrt{N_{{\rm bg}}}$. It is now clear that families should be identifiable not only if N_fam ≳ N_bg, but also if $N_{{\rm fam}} \ge \sqrt{N_{{\rm bg}}}$, provided the background distribution can be well modeled and there are no "systematic" effects. In reality, there will be "systematic" effects such as clustering created by dynamical sculpting but unrelated to collisions, as in Neptune mean-motion resonances. The importance of these effects will depend greatly on the location in the belt and size of the family being considered. We consider this the best case to point out that it is extremely difficult or impossible to find a family where $N_{{\rm fam}} \lesssim \sqrt{N_{{\rm bg}}}$.

This additional constraint now leaves us with three regimes into which a family's detectability may fall: (1) for N_fam ≳ N_bg, the family can be identified and characterized—family members can be distinguished from interlopers with some confidence, (2) for $\sqrt{N_{{\rm bg}}} \le N_{{\rm fam}} < N_{\rm bg}$, the family may be identified in the form of overdensities above the expected noise level in the background population in the absence of confounding systematics, and (3) for $N_{{\rm fam}} < \sqrt{N_{{\rm bg}}}$, the family cannot be identified by dynamical clustering alone.

Figure 9 shows a histogram and cumulative number distribution for the "base case" collisional family of Section 5.1, but now with the noise level ($\sqrt{N_{{\rm bg}}}$) shown for the background population. It is clear that this family that had previously been deemed only marginally identifiable would stand out well above the background population, provided the background was well behaved.

Zoom In Zoom Out Reset image size

While the existence of such families can be proven by the statistically significant overdensity, unless the number of family members approaches the number of background objects, it is not possible to determine which objects in the overdensity belong to the family and which are interlopers without additional information. The larger the value of N_fam/N_bg, the more confidence can be placed in the identification of individual objects as members of the family. Simple identification of families is useful, since even the number of families can help constrain the collision history of the Kuiper Belt. However, insights into the properties of collisions, interiors, and surfaces require distinguishing family members from interlopers, so there is also a clear desire to characterize families, where possible.

The effects of size and location of the progenitor are shown again in Figure 10. The two panels show the ratio of family members to background objects, N_fam/N_bg, versus (1) size of the progenitor and (2) inclination of the progenitor, with a magnitude limit of m_v ⩽ 28. The ratio is strongly correlated with both size and inclination, with the family "enhancement" increasing with both size and inclination of the progenitor. Thus, the easiest families to identify would be those with large progenitors at high inclinations.

Zoom In Zoom Out Reset image size

The inclination dependence comes from the drop-off in background objects with increasing inclination. The size dependence comes from two factors, the number of family members and the number of background objects contained within the volume Δv_min ≲ v_esc. For $dN/ds \sim s^{-q_{{\rm fam}}}$, with q_fam > 4, the mass is concentrated at size s_min. With half the mass in the largest remnant of size R/2^1/3, the number of family members at cutoff size s_min scales with R as

$$\begin{equation} \frac{dN_{{\rm fam}}}{ds}s \big\vert _{s_{{\rm min}}} \sim \frac{\frac{1}{2}\frac{4}{3}\pi R^3 \rho }{\frac{4}{3}\pi s_{{\rm min}}^3} \sim \left(\frac{R}{s_{{\rm min}}}\right)^3. \end{equation} \tag{ 7 }$$

The number of background objects scales as

$$\begin{equation} N_{{\rm bg}} \sim \delta v^{2} \sim \sqrt{\frac{M}{R}}^{2} \sim R^{2}. \end{equation} \tag{ 8 }$$

Thus, the ratio N_fam/N_bg ∼ R (as in Figure 10). The full size dependence, including the normalization, for the cold classical belt objects in Figure 10 is given by N_fam/N_bg ∼ 4 × 10⁻⁵ (R/1 km). For hot classical belt objects, this dependence is N_fam/N_bg ∼ 2 × 10⁻⁴ (R/1 km). This difference in the normalization, a factor of ∼5, comes from the different number densities of the background population in the hot and cold classical belt regions. In Figure 10(b), the mean value of N_fam/N_bg is also a factor of ∼5 higher in the hot belt than the cold belt (at a given size) because of the lower background density. These ratios are for a limiting magnitude m_v = 28 and for a typical ejection velocity of v_esc, but can be scaled to any magnitude limit with Equation (6) and estimated for tighter clusterings using the results of Section 5.5.

If the background population can be well modeled, it may be possible to identify (but not characterize) families as statistical overdensities larger in size than the expected fluctuations in the background. Figure 11 shows the ratio of family members to the square root of the background number (the typical expected size of the fluctuations in the background), $N_{{\rm fam}}/\sqrt{N_{{\rm bg}}}$, versus (1) size of the progenitor and (2) inclination of the progenitor. The ratio $N_{{\rm fam}}/\sqrt{N_{{\rm bg}}} \sim R^{2}$, and again families stand out more at higher inclination due to the diminished background.

Zoom In Zoom Out Reset image size

Eventually, the search for families can be reduced to the following algorithm, which could in theory be applied to every KBO. Assume that this KBO is the center of a collisional family. Take the nearby objects and iteratively sort them into "possible-family" and "background" categories by using the Δv distribution, size distribution, colors, past orbital angles, and other properties. For example, you could reject objects that were larger than the central KBO or nearly as large but with unphysically large Δv values. The goal of the search would be to optimize (separately or in combination) various figures of merit that quantify the likelihood that this group is a family, such as difference between average color of family members and average color of background objects. Spatial point processes, a general statistical term for cluster algorithms, could also be effectively employed to determine figures of merit (e.g., Illian et al. 2008). For example, these could be used to identify regions of proper element space that contained significant overabundances compared to a model of the background. This would allow for statistical identification of families that cannot be detected independently. A specific definition of these merit criteria for family finding is beyond the scope of this paper. After repeating this for all KBOs, you could rank the results and then investigate the most promising cases. In order words, do a full investigation of family properties within a very large, but guided, search for the most plausible combinations of KBOs. Computational expediency may limit this technique, but most other methods are, in a sense, approximations to this most general technique.

A significant increase in detectability can come by using our understanding of the shapes of families in proper element space. All calculations of Δv_min presented here have been using the optimal orbital angles for each object individually as suggested by Ragozzine & Brown (2007). By fixing the orbital angles (ω and f; Ω does not affect family shape) to the angle of the largest remnant, the ratio N_fam/N_bg with Δv ⩽ v_esc can be increased; the number of background objects with small Δv at a specific set of orbital angles drops off rapidly.

In these simulations, we are using the unrealistic assumption that all family members are launched from the parent body with Δv = v_esc. In this case, the family lies along a two-dimensional (2D) manifold in a–e–i space that is approximately an ellipsoid in osculating elements (as in the figures of Brown et al. 2007; Ragozzine & Brown 2007, where this distribution is called the collisional "cloud"). If the shape of this ellipsoid were preserved in the transformation to proper elements, then using the optimal orbital angles as described above would recover nearly all of the family members in a single Δv bin. In families that cover a large range of semimajor axes, the change in secular frequencies as a function of a causes significant distortion of this ellipsoid, so that specifying the orbital angles only results in an improvement of N_fam/N_bg by an additional factor of ∼5. It is possible to imagine attempting a search for distorted ellipsoids by scanning over the plausible set of secular frequencies in the Kuiper Belt. This would effectively allow a family searching algorithm to zero in on the "arcs" visible in the distributions seen in the figures (which are the 2D projections of the ellipsoid surface), allowing for the identification and/or characterization of families even where our metric of N_fam/N_bg and $N_{{\rm fam}}/\sqrt{N_{{\rm bg}}}$ would suggest it is difficult to detect family. However, the improvement would be reduced in real families that have a relatively wide range of Δv values instead of the single value we have used here.

The Pan-STARRS and LSST surveys promise to provide uniformly measured colors for a large sample of KBOs. Identification of KBO families using purely dynamical means is attractive because the physical origin of KBO colors is currently unknown and dynamical techniques allow for unbiased searches for family members. Nevertheless, the addition of color information is likely to significantly enhance family identification in the Kuiper Belt. Spectral similarities were essential to the discovery of the Haumea collisional family (Brown et al. 2007). In the asteroid belt, families exhibit smaller spreads in colors than the spread in colors averaged over the entire belt (Ivezić et al. 2002; Parker et al. 2008). Identification techniques that include color information should therefore be developed.

The degree to which color information can enhance family identification depends on the mean color, μ_fam, and color dispersion, σ_fam, within a family and on the overall mean color, μ_bg, and color dispersion, σ_bg, in the family's region of the belt. Collisions may produce colors that are disjoint from the background color distribution, such that μ_fam ± σ_fam and μ_bg ± σ_bg do not overlap, allowing easy identification of family members using colors. We now estimate the extent to which colors enhance identification in the opposite extreme in which the two color distributions entirely overlap. We consider a family with N_fam members within an orbital element volume defined by Δv_min ⩽ v_esc containing N_bg background members, as above. Considering only this dynamically defined population, a family may be found and its members identified if N_fam ≳ fN_bg, where f ≡ σ_fam/σ_bg ⩽ 1. Assuming that the background color distribution is well characterized, the presence of a family may be determined if $fN_{{\rm bg}} \gtrsim N_{{\rm fam}} \gtrsim \sqrt{fN_{{\rm bg}}} + G(N_{{\rm bg}})$, though in this case individual family members will not be identifiable without additional information. The factor G(N_bg) quantifies both uncertainties in the background color distribution and intrinsic variation within that distribution, which is currently unmeasured. The factor f may be viewed as an enhancement factor for both family identification and characterization and, in general, is the fraction of background objects that cannot be distinguished from family members (e.g., by colors).

The value of f is not available for undetected families in the Kuiper Belt, but we can look to asteroid belt families and the Haumea family for guidance. Values of the spread in i − z and a* colors from Parker et al. (2008) suggest f = 0.1–0.5 for asteroid belt families, with i − z generating lower numbers than a*. The standard deviation in B−R measured for Haumea-family members compiled by Snodgrass et al. (2010) is ≈0.06 about a mean of ≈1.06. Peixinho et al. (2008) find that B−R colors in the Kuiper Belt may be fit with two components: 1.71 ± 0.11 for objects with inclination i ≲ 12° and 1.33 ± 0.2 for i ≳ 12°. If we ignore the offset in the mean, which significantly eased the identification of the Haumea family, and only consider the dispersion, we may estimate f ∼ 0.5 for the cold classical belt and f ∼ 0.25 for the hot population. Fortunately, family searches do not require prior knowledge of the value of f. Choosing a value of f = 0.25, we estimate that color information will likely reduce the number of family members required to find and characterize a family by a factor of four and reduce the number required to separate the presence of a family from the statistical noise by a factor of two. Lower values of f and the possibility that the mean color of a family may be offset from the background distribution make color measurements even more valuable. Pan-STARRS and LSST are expected to produce uniformly measured, 0.01–0.1 mag photometry for KBOs, precise enough to exploit color differences in family searches.

In the case where a smooth model background can be subtracted, the number of family members should be compared to the typical fluctuations in this background. Figure 11 shows the ratio $N_{\rm {fam}}/\sqrt{N_{\rm {bg}}}$ versus (1) size of the progenitor and (2) inclination of the progenitor. This figure shows that families could be identifiable (but not necessarily characterizable) down to progenitor radii of ∼100 km and that the family number increasingly dominates over Poisson noise with increasing inclination.

The method of family finding via backward integration has been not been used directly in the asteroid belt to our knowledge. Rather, very tight young asteroid families are identified and then back integrated (either with or without the Yarkovsky effect) to confirm that the objects were tightly clustered in their past and to obtain an age estimate (Nesvorný et al. 2002; Nesvorný & Vokrouhlický 2006). This technique works best when the objects are on orbits that are rather stable, e.g., Lyupanov timescales that are not much shorter than the duration of the integration (Nesvorný & Vokrouhlický 2006) and can give very accurate ages.² Backward integration could be used in the asteroid belt for finding families and could even potentially include the effect of Yarkovsky (e.g., following Nesvorný & Vokrouhlický 2006) with the main drawback being the computational limitation in integrating dozens of clones of the hundreds of thousands of known asteroids over potentially long times. This drawback has led to the more practical and presumably equally effective technique of searching for tight clusters in proper elements.

In the Kuiper Belt, however, finding collisional families via back integration has a number of advantages. The main advantage is that families are now given as clusters in six-dimensional space (a, e, i, ω, Ω, and time), and contamination with background objects is much reduced. Thus, many of the difficulties with finding families using proper elements alone in the current Kuiper Belt are avoided. The statistical strength of these clusters can be compared with random clusterings that occur during most of the history of the solar system, which should allow for rigorous identification of families as more than random clumpings, which are generally very rare even for small numbers of objects (Nesvorný & Vokrouhlický 2006). An additional advantage is gained by the much slower evolution of orbits in the Kuiper Belt as compared to the asteroid belt; scaling from known asteroid families, this suggests clusters older than ∼100 Myr could be found. Furthermore, the Yarkovsky effect, which plagues older and/or smaller families in the asteroid belt, is not an issue in the Kuiper Belt. An excellent by-product of backward integration is that it also directly determines the age of the collisional family, which significantly helps the process of using the family to place constraints on the formation and evolution of the Kuiper Belt.

Despite its potential advantages, there are several potential issues that may limit the applicability of back integration. Since this technique requires preserving the actual value of the secular angles into the past, the propagation of orbital errors from observational uncertainties could potentially be a serious problem. This problem is compounded by weak chaotic regions, especially for objects in or near weak mean-motion resonances with Neptune. A preliminary investigation has demonstrated that some KBOs have sufficiently well-determined orbits and reside in calm enough regions that the integration of multiple clones (accurately using the full covariance from observational errors) maintained differential apsidal and nodal angles with a standard deviation of ∼40° over the age of the solar system. Though larger than the dispersion used in asteroid families, this is small enough to robustly identify families if enough objects are used. With the development of large sky surveys, the improved accuracy of orbits as well as the large increase in the number of discovered KBOs will probably allow these problems to be overcome even for back integrations approaching billions of years.

Even if KBO orbits are well known and well behaved, this does not ensure that back integration will find families: to do this, the integrator needs to accurately reproduce the history of the actual solar system. Hence, a more serious drawback is global chaos, which ensures that insignificantly small errors in the back integration will grow exponentially (with some Lyapunov timescale) effectively disallowing any integration from accurately reproducing the solar system. While this certainly implies that the mean anomalies of ancient KBO families will never be reconstructable, more study is needed to determine the timescale of unavoidable chaotic divergence of differential apsidal and nodal angles in the Kuiper Belt. Our preliminary integrations did not consider small perturbations in the positions of the giant planets on the history of these angles. It is plausible that global chaos for these angles will either have a sufficiently long timescale or that the chaos will be "bounded" in a way that back integration will be effective. The main parameters that determine precession rates (masses, semimajor axes, eccentricities, and inclinations of the outer planets) are very stable (quasi-periodic) over the age of the solar system (Laskar 2008).

Finally, the integrator must take into account any effects that would cause the differential apsidal and nodal angles to vary from their true values in the actual solar system. This implies a search for all the relevant effects. Integrations with all eight planets and general relativity are presumably much more likely to succeed. It may be that gravitational interactions between family members or the additional weak precession caused by the (evolving) mass of the Kuiper Belt disk itself must be included.

The severity of these problems increases as a function of the age of the family and, though it seems likely that young families with ages less than perhaps 100 Myr could be identified in this manner, a more detailed investigation will be needed to show whether or not back integration over the age of the solar system is plausible for Kuiper Belt family identification. One excellent aspect of this problem, however, is that it is self-proving, i.e., if an integration finds a family that is statistically unlikely to occur randomly, then the above problems can be considered solved, especially if independently confirmed by families found in other ways.