ABSTRACT
The nonlinear stability of the triangular libration point, L4, when both of the primaries are oblate spheroids as well as sources of radiation has been studied. It is found that L4 is stable for all mass ratios in the range of linear stability except for three mass ratios depending upon oblateness coefficients and mass reduction factors.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The restricted three-body problem describes the motion of an infinitesimal mass moving under the gravitational effect of the two finite masses, called primaries, which move in circular orbits around their center of mass on account of their mutual attraction and the infinitesimal mass not influencing the motion of the primaries. It is originally formulated due to the approximately circular motion of the planets around the sun, and the small masses of the asteroids and the satellites of the planets compared to the planets' masses.
This classical restricted three-body problem is not valid when at least one of the interacting bodies is an intense emitter of radiation. In this connection, it is reasonable to modify the model by superposing a light repulsion field whose source coincides with the source of the gravitational field provided by the radiating body on the gravitational field of the main bodies. According to Radzievsky (1950, 1953), the problem in such a statement is called the photogravitational problem. He discussed it for three specific bodies: the sun, a planet, and a dust particle. It was found that an allowance for direct solar radiation pressure results in a change in the positions of the libration points.
In certain stellar dynamics problems it is altogether inadequate to consider solely the gravitational interaction force. For example, when a star acts upon a particle in a cloud of gas and dust, the dominant factor is by no means gravity, but the repulsive force of the radiation pressure. Since a large fraction of all stars belong to binary systems, the particle motion in the field of a double star offers special interest. Probably the simplest dynamical model of such a system is the restricted circular photogravitational three-body problem. Among the possible motions of a particle, the equilibrium states at the libration points in a reference frame sharing the orbital motion of the stars were studied by Schuerman (1980) and Kunitsyn & Tureshbaev (1985).
In stellar systems numerous examples are available where a body is moving under the gravitational field of two radiating bodies. Simmons et al. (1985) obtained a complete solution of the restricted three-body problem. They discussed the existence and linear stability of the equilibrium points for all values of radiation pressures of both luminous bodies and all values of mass ratios. The participating bodies in the classical restricted three-body problem are strictly spherical in shape, but in actual situations we find that several heavenly bodies, such as Saturn and Jupiter, are sufficiently oblate. The minor planets and meteoroids have irregular shapes. In these cases, on account of the small dimensions of the bodies in comparison with their distances from the primaries, they are considered to be point masses, but in many cases the dimensions of the bodies are larger than the distances from their respective primaries. Thus, the above assumption is not justified, and the results obtained are far from a realistic approach. The lack of sphericity, or the oblateness, of the planet causes large perturbations from a two-body orbit. The motions of artificial Earth satellites are examples of this. This enables many researchers to study the restricted problem by taking into account the shapes (oblateness) of the bodies (Subba Rao & Sharma, 1975; Bhatnagar & Chawla, 1979, Elipe & Ferrer, 1985; Elipe 1992; Markellos et al. 1996; Chandra & Kumar, 2004).
An investigation of the positions of libration points, when the more massive primary is a source of radiation and the smaller one is an oblate spheroid, was carried out by, e.g., Sharma (1987). He showed that the triangular points are linearly stable for the mass parameter 0 < μ < μcrit and the critical mass value μcrit decreases with the increase in oblateness and radiation force.
The effect of oblateness and radiation pressure forces of the primaries on the location and the linear stability of the triangular points in the restricted three-body problem was analyzed by Singh & Ishwar (1999). They considered both primaries as sources of radiation as well as oblate spheroids, and observed that these points are stable for 0 < μ < μco and unstable for μco < μ < 1/2, where μco is the critical value of the mass parameter and depends on the radiating and oblateness coefficients. The same problem under the influence of small perturbations in the Coriolis and the centrifugal forces was studied by AbdulRaheem & Singh (2006). Dealing with the overall effect they observed that the range of stability of triangular points decreases.
Many mathematicians and astronomers have been interested in the study of the stability of an equilibrium point for all time and all the orders of the terms in the expansion of the Hamiltonian. The nonlinear stability of the trianglar libration points in the classical restricted three-body problem was investigated by Deprit & Deprit-Bartholome (1967). Bhatnagar & Hallan (1983) discussed the effect of perturbations in the Coriolis and centrifugal forces on the nonlinear stability of equilibrium points. Later, analytical studies of the nonlinear stability of L4 under different aspects were also carried out by Niedzielska (1994), Subba Rao & Sharma (1997), Hallan et al. (2000), Gozdziewski (2003), and Chandra & Kumar (2004).
Our aim is to study the combined effects of oblateness and radiation of the primaries on the nonlinear stability of the libration point L4 as it has been found that they produce significant changes in the location and stability (Singh & Ishwar 1999) of the triangular points. We also know that the inclusion of the nonlinear terms sometimes changes the entire pattern of the stability and, hence, we intend to study the stability in the nonlinear sense as well. By applying Lyapunov's theorem (Lyapunov 1956) to the linear stability results in Singh & Ishwar (1999) mentioned earlier, we can state that L4 for μco < μ < 1/2 is unstable in the nonlinear sense also. So, we need to study the nonlinear stability of L4 for 0 < μ < μco. For this, we will apply Arnold's theorem (Arnold 1961) and follow the procedure adopted by Bhatnagar & Hallan (1983). Arnold (1961) proved that if
- 1.k1ω1 + k2ω2 ≠ 0 for all pairs (k1, k2) of rational integers where ω1, ω2 are the basic frequencies for the linear dynamical system and
- 2.The determinant D ≠ 0, where D = det(bij) (i, j = 1, 2, 3),
 ,
,  ,
,
b33 = 0 and  is the normalized Hamiltonian with I1, I2 as the action momenta coordinates, and A, B, C as second-order coefficients in the frequencies, then on each energy manifold H = h in the neighborhood of equilibrium, there exists invariant tori of quasi-periodic motions which divide the manifolds, and consequently, the equilibrium is stable. This is valid for a system with two degrees of freedom, which is the case under consideration. Moser (1962) showed that Arnold's theorem is true if the first condition of the theorem is replaced by k1ω1 + k2ω2 ≠ 0 for all pairs (k1, k2) of rational integers such that |k1| + |k2| ⩽ 4.
is the normalized Hamiltonian with I1, I2 as the action momenta coordinates, and A, B, C as second-order coefficients in the frequencies, then on each energy manifold H = h in the neighborhood of equilibrium, there exists invariant tori of quasi-periodic motions which divide the manifolds, and consequently, the equilibrium is stable. This is valid for a system with two degrees of freedom, which is the case under consideration. Moser (1962) showed that Arnold's theorem is true if the first condition of the theorem is replaced by k1ω1 + k2ω2 ≠ 0 for all pairs (k1, k2) of rational integers such that |k1| + |k2| ⩽ 4.
Markellos et al. (1996), Subba Rao & Sharma (1997), and Chandra & Kumar (2004) studied the nonlinear stability of L4 when the bigger primary is an oblate spheroid. We consider here the case where both primaries are oblate spheroids as well as sources of radiation. We use Ai(i = 1, 2) for the oblateness coefficients of the bigger and smaller primaries, respectively, such that 0 < Ai ≪ 1 (McCuskey 1963). We denote the radiation factors as qi(i = 1, 2) for the bigger and smaller primaries and these are given by Fp = Fg(1 − qi) such that 0 < 1 − qi ≪ 1 (Radzievsky 1950). For simplicity we further substitute q1 = 1 − ∈, q2 = 1 − ∈', | ∈ | ≪ 1, | ∈ '| ≪ 1 and restrict ourselves to linear terms in Ai, ∈, and ∈'. Then the coefficients of A1 throughout the paper are exactly the same as worked out in the paper of Markellos et al. (1996), Subba Rao & Sharma (1997), Chandra & Kumar (2004).
This paper should be read in conjunction with the papers by Bhatnagar & Hallan (1983) and Subba Rao & Sharma (1997) as, to save space, we are not mentioning the values of various variables given in those papers, although they are used in this paper.
2. EQUATIONS OF MOTION
Using dimensionless variables and a synodic coordinate system (x, y) as Szebehely (1967) and Singh & Ishwar (1999) did, the equations of motion of the infinitesimal mass can be written as
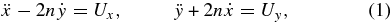
where
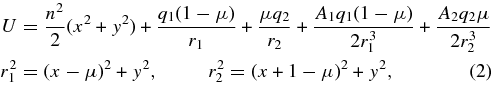
where r1 and r2 are the distances of the infinitesimal mass from the primaries and μ is the ratio of the mass of the smaller primary to the total mass of the primaries and 0 < μ ⩽ 1/2. The perturbed mean motion of the primaries, n, is given by
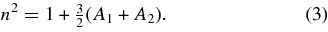
The coordinates of the triangular point L4, obtained by Singh & Ishwar (1999), are
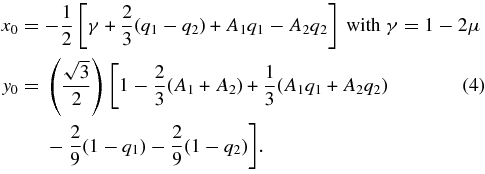
3. LINEAR STABILITY
The Lagrangian function of the problem can be written as
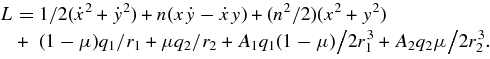
Shifting the origin to L4 and expanding in power series of x and y, we have

Consequently,

where

with considerations
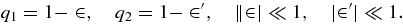
All these values are different from the classical case due to the radiation and oblateness of both primaries. When A2 = ∈ = ∈' = 0, these values agree with those found by Subba Rao & Sharma (1997).
The characteristic equation corresponding to Hamiltonian H2 is given by
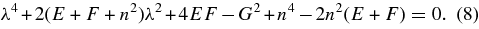
The roots of Equation (8) are purely imaginary if its discriminant Δ>0 and thus it is a necessary condition for the stability, in the linear sense, around the L4 point. The solution of the equation Δ = 0 for μ gives the critical mass value μco of the mass parameter.
This implies that (Singh & Ishwar 1999)
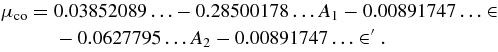
For A2 = ∈ = ∈' = 0 the value of μco agrees with that given by Subba Rao & Sharma (1975), Markellos et al. (1996), and Chandra & Kumar (2004). The range of stability, in the linear sense, can be written as 0 < μ < μco If Equation (8) has four imaginary roots, ±iωi, ± iω2 where ω1, ω2 are the basic frequencies, then we have
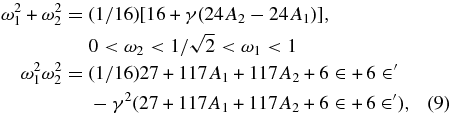
which give

The results given by Equations (9) and (10) in the case A2 = ∈ = ∈' = 0 agree with those found by Subba Rao & Sharma (1997).
4. FIRST-ORDER NORMALIZATION
Following the method given in Whittaker (1965), we use a canonical transformation from the phase space x, y, Px, Py into the phase space of the angles (ϕ1, ϕ2) and the actions (I1, I2) so that H2 be normalized:

where
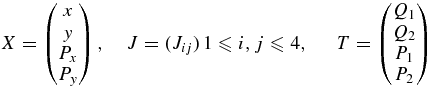
Qj = (2Ij/ωj)1/2sin ϕj Pj = (2Ij.ωj)1/2 cos ϕj(j = 1, 2), and the elements of the dyadic J can be obtained by adopting the method of Breakwell & Pringle (1966). Elements of J necessary for further analysis are given in Appendix A.
The transformation changes the second-order part of the Hamiltonian into the normal form H2 = ω1I1 − ω2I2.
5. SECOND-ORDER NORMALIZATION
For transforming the Hamiltonian H to the Birkhoff's normal forms, we have utilized Henrard's method (Deprit & Deprit-Bartholome 1967). We have expanded the coordinates (x, y) of the infinitesimal body in double d'Alembert series:
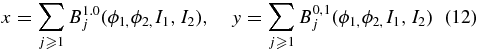
where the homogeneous components B1,0J and B0,1J are of degree j, I1 and I2 are to be taken as constants of integration, while ϕ1 and ϕ2 are to be determined as linear functions of time such that
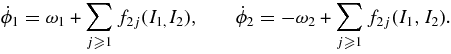
The first-order components B1,01 and B0,11 are the values of x and y obtained by Equation (11). Proceeding as in Deprit & Deprit-Bartholome (1967), we observe that the second-order components B1,02 and B0,12 are solutions of the partial differential equations
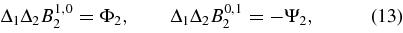
with
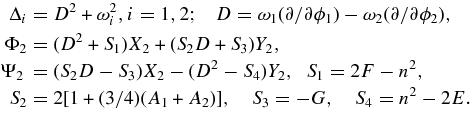
X2, Y2 are obtained by substituting respectively in ∂L3/∂x, ∂L3/∂y the first-order components for x and y.
Equation (13) can be solved for B1,02 and B0,12 by using the formula
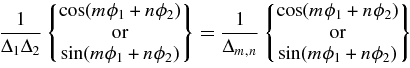
where
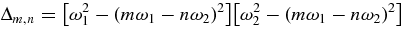
provided Δm,n ≠ 0.
Since Δ1,0 = Δ0,1 = 0, the terms cos ϕ1, sin ϕ1, cos ϕ2, and sin ϕ2 are the critical terms. Φ2 and Ψ2 are free from such terms. By condition (1) of Moser's theorem (Moser 1962), none of the divisors Δ2,0, Δ0,2, Δ1,1 Δ1,−1, is zero. The second-order components B1,02 and B0,12 are as follows:
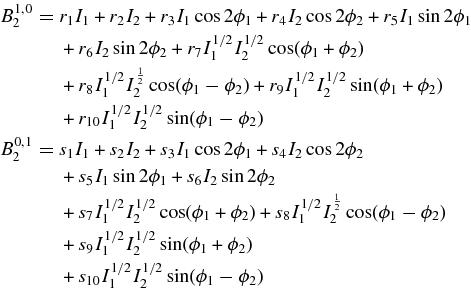
The coefficients rk and sk for k = 1, 2, ..., 10 are given in Appendix B.
6. SECOND-ORDER COEFFICIENTS IN THE FREQUENCIES
Following Henrard's method, we find that the third-order components B1,03 and B0,13 in the coordinates x, y and the second-order polynomials f2 and g2 in the frequencies  and
and  satisfy the partial differential equations:
satisfy the partial differential equations:
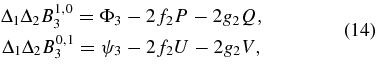
with
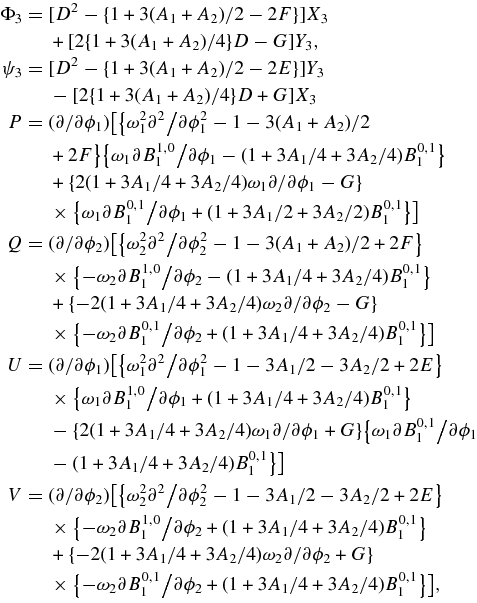
X3, Y3 are the homogeneous components of order 3 obtained by substituting, respectively,
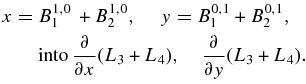
We do not require to find out the components B1,03 and B0,13. We find the coefficients of cos ϕ1 , sin ϕ1, cos ϕ2, and sin ϕ2 on the right-hand sides of Equation (14). They are the critical terms. We eliminate these terms by properly choosing the coefficients in the polynomials
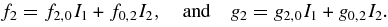
Further, we find that

with
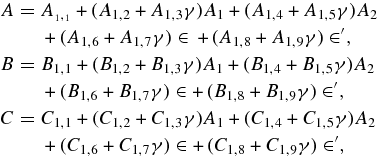
where the coefficients A, B, C are given in Appendix C.
7. STABILITY
Since condition (1) of Moser's theorem (Moser 1962) is applicable, Birkloff's normalization up to third order can be obtained. Condition (1) of Moser's theorem is satisfied in the interval 0 < μ < μco if the mass ratio does not take the critical values:

These results, in the case A2 = ∈ = ∈' = 0, agree with those found by Markellos et al. (1996), Subba Rao & Sharma (1997), and Chandra & Kumar (2004).
Normalized Hamiltonian up to fourth order is
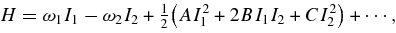
where the coefficients A, B, C are given in Appendix C.
Calculating the determinant D occurring in condition (2) of the Moser (1962) theorem, we have
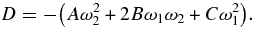
Putting the values of A, B, and C, we have
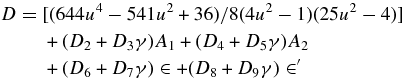
with

Moser's second condition is violated for the unperturbed problem, i.e., for A1 = A2 = ∈ = ∈' = 0 when μ0 = 0.0109136.... When A1, A2 ∈, ∈ ' ≠ 0, we take μ = μ0 + αA1 + α'A2 + α'' ∈ +α''' ∈ ' + such thatD = 0. It is seen that the second condition of Moser's theorem is satisfied, that is D ≠ 0 if in the interval 0 < μ < μco, the mass ratio does not take the value
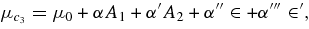
where
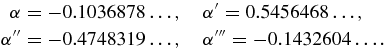
8. CONCLUSION
By taking both the primaries as oblate spheroids as well as sources of radiation, it has been seen that, in the nonlinear sense, the triangular point L4 is stable for all mass ratios in the range of linear stability except for three mass ratios,

at which the Moser (1962) theorem fails.
When A1A2 = ∈ = ∈' = 0, the values of μci(i = 1, 2, 3) agree with those found by Deprit & Deprit-Bartholome (1967).
When A2 = ∈ = ∈' = 0, the values of μci are the same as those found by Markellos et al. (1996), Subba Rao & Sharma (1997), and Chandra & Kumar (2004).
The author is extremely thankful to Professor B. Ishwar, Department of Mathematics, B. R. A. Bihar University, Muzaffarpur, India for his valuable suggestions.
APPENDIX A
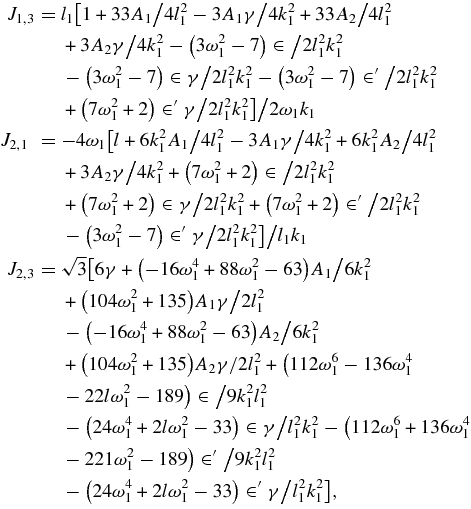
with
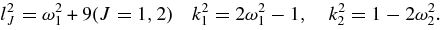
The values of J1,4J2,2J2,4 can be obtained respectively from J1,3, − J2,1, J2,3 by replacing ω1 by ω2, I1 by I2, k1 by k2, k21 by −k22 wherever they occur keeping A1, A2, ∈, ∈ ' unchanged.
APPENDIX B
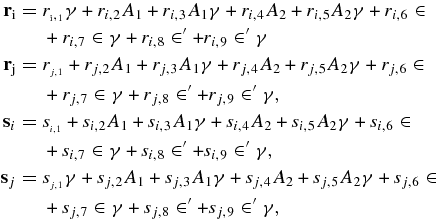
for i = 1, 2, 3, 4, 7, 8 and j = 5, 6, 9, 10.
The values of all ri,1, rj,1, ri,2, rj,2, ri,3, rj,3, si,1, sj,1, si,2, sj,2, si,3, sj,3 are the same as those in the paper by Subba Rao & Sharma (1997):

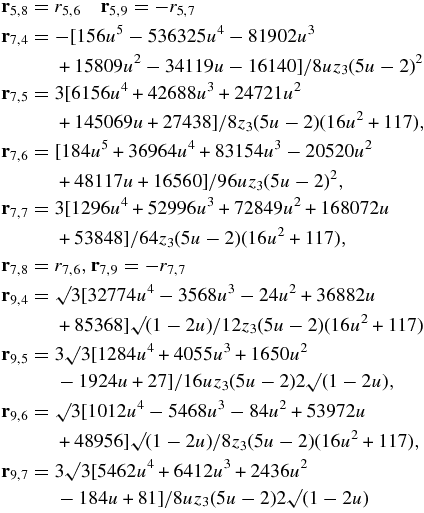


The values of rk, sk, for k = 2, 4, 6 can be obtained respectively from those for k = 1, 3, 5 by replacing ω1 by −ω2, l1 by l2k21 by −k22z1 by z2 wherever they occur and the values of rk, sk for k = 8, 10 can be obtained respectively from those for k = 7, 9 by replacing u by −u, keeping z3 unchanged, wherever they occur.
APPENDIX C
The values of all A1,1, A1,2, A1,3, B1,1, B1,2, B1,3, C1,1, C1,2, and C1,3 are the same as those in the paper by Subba Rao & Sharma (1997):
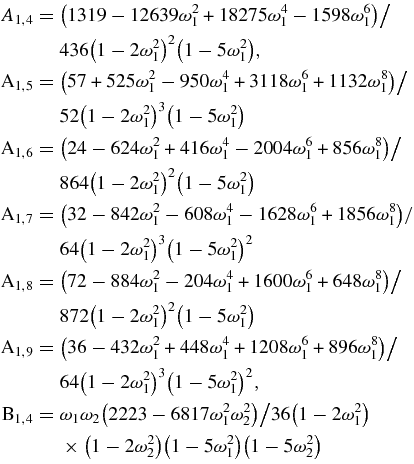
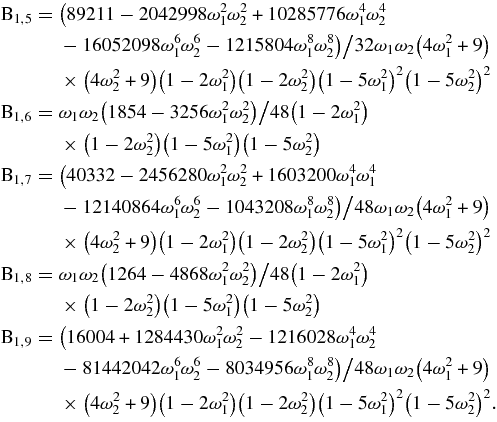
C1,i(i = 1, 2, 3, ..., 9) can be obtained respectively from A1i by replacing ω1 by ω2.




