THE ASTROPHYSICAL JOURNAL, 517:L31 L33, 1999 May 20
L33, 1999 May 20
© 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A.
Naval Undersea Warfare Center Division, 1176 Howell Street, Newport, RI 02841-1708
Received 1998 December 15; accepted 1999 March 16; published 1999 April 22
The concentrated mass at the Galactic center is considered as a gravitational lens that focuses gravitational-wave energy to the Earth. It is found that 60 Hz gravitational waves from a rotating neutron star outside our Galaxy are focused onto a region having an approximate radius of 1.1×10 m (assuming that the concentrated mass has the form of a supermassive black hole). The increase in intensity (which is proportional to the square of the increase in strain amplitude h) is by a factor of approximately 17,000. Sources within our Galaxy lead to increases in intensity by a factor that can exceed 4000.
m (assuming that the concentrated mass has the form of a supermassive black hole). The increase in intensity (which is proportional to the square of the increase in strain amplitude h) is by a factor of approximately 17,000. Sources within our Galaxy lead to increases in intensity by a factor that can exceed 4000.
Subject headings: Galaxy: center gravitation
gravitation gravitational lensing
gravitational lensing
Although the gravitational lensing of light is well known, the most promising focusing agents (i.e., the concentrated masses often located at the centers of galaxies) tend to block the focused light with clouds of dust and also tend to emit in-band "noise" that often dominates any desired focused signal. The focused "ring" of light rays can only be observed if its diameter is sufficiently large so as to avoid such dust and noise.
In principle, gravitational lensing of gravitational waves (GWs) should occur in the same way as it does for light (Thorne 1987). However, there are some key differences that can potentially favor the observation of such lensing over that of light. The most obvious difference is that dust clouds and noise are not a factor. Another difference is that the collinear requirement is less severe. Because gravitational waves are expected to occur at low frequencies, the resulting focused region will have a relatively large area because of diffraction. This leads to a relaxation of the collinear requirement, which increases the probability of observing such an event.
Assuming that the concentrated mass at the Galactic center (GC) is in the form of a supermassive black hole, it will focus GWs that pass through the Einstein radius RE to the Earth:

Here M is the mass of the supermassive black hole, estimated at 2.6×10 M
M (Genzel et al. 1997; Ghez et al. 1998); D is the distance to the GC, estimated at 8 kpc (Carney et al. 1995); d is the distance from the source to the GC; and G is the gravitational constant. The small gravitational deflection angle assumption leading to equation (1) is valid since the Einstein radius is much larger than the Schwarzschild radius of the supermassive black hole (Alexander & Sternberg 1999).
(Genzel et al. 1997; Ghez et al. 1998); D is the distance to the GC, estimated at 8 kpc (Carney et al. 1995); d is the distance from the source to the GC; and G is the gravitational constant. The small gravitational deflection angle assumption leading to equation (1) is valid since the Einstein radius is much larger than the Schwarzschild radius of the supermassive black hole (Alexander & Sternberg 1999).
The focused area is determined by D and the diffraction pattern for the circular annular region bounded by radii RE and R +
+ R
R (
( R
R
 R
R ), which can be shown to be
), which can be shown to be

The relative intensity is given by I=10

 , so the 3 dB points (the points of half-power) are located at kR
, so the 3 dB points (the points of half-power) are located at kR


 1.1, leading to sin
1.1, leading to sin 

 = ±1.1/kRE = ±0.175
= ±1.1/kRE = ±0.175 /RE, so that the approximate radius of the focused region (based on the half-power points) is
/RE, so that the approximate radius of the focused region (based on the half-power points) is 
 0.175
0.175 D/RE.
D/RE.
Assuming GWs emitted by a rotating neutron star (NS) or population of NSs in another galaxy, and neglecting D compared with d, the Einstein radius becomes

The radius  of the focused region at the Earth for 60 Hz GWs would be approximately 1.1×10
of the focused region at the Earth for 60 Hz GWs would be approximately 1.1×10 m. Taking into account that the Earth rotates about the GC approximately once every 200 million years, the time that such energy can be received (assuming detection only between the half-power points) would be approximately only 10.1 days. Assuming a sufficient signal-to-noise ratio, curve-fitting a number of such measurements to the expected diffraction pattern would lead to an accurate estimate of RE and hence to an accurate estimate of the magnitude of the concentrated mass at the GC.
m. Taking into account that the Earth rotates about the GC approximately once every 200 million years, the time that such energy can be received (assuming detection only between the half-power points) would be approximately only 10.1 days. Assuming a sufficient signal-to-noise ratio, curve-fitting a number of such measurements to the expected diffraction pattern would lead to an accurate estimate of RE and hence to an accurate estimate of the magnitude of the concentrated mass at the GC.
The increase in intensity depends on the ratio of the annular area bounded by radii RE and R +
+ R
R to that of the focused region. A larger radius R
to that of the focused region. A larger radius R +
+ R
R will focus GWs at a larger distance D+
will focus GWs at a larger distance D+ D. The annular area is determined by finding the radius R
D. The annular area is determined by finding the radius R +
+ R
R that will lead to GW rays that focus at distance D+
that will lead to GW rays that focus at distance D+ D and also intersect the diffraction lobe at distance D at the half-power points. This can be determined by the following equations:
D and also intersect the diffraction lobe at distance D at the half-power points. This can be determined by the following equations:


Solving for  D leads to
D leads to  RE
RE 
 /2 with an area or intensity ratio of approximately RE/
/2 with an area or intensity ratio of approximately RE/ . In this example, the intensity ratio is approximately 17,000. Since the strain amplitude h is proportional to the square root of the energy flux (Shapiro & Teukolsky 1983, p. 469), the increase in h is proportional to the square root of the area or intensity ratio.
. In this example, the intensity ratio is approximately 17,000. Since the strain amplitude h is proportional to the square root of the energy flux (Shapiro & Teukolsky 1983, p. 469), the increase in h is proportional to the square root of the area or intensity ratio.
The effective strength is (Flanagan 1999)

Assuming a rotational frequency of 30 Hz (producing 60 Hz waves), a observation time of 10.1 days, a distance D of 100 kpc, and an equatorial ellipticity 
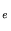 of 10
of 10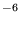 yields a value for heff of 1.4×10
yields a value for heff of 1.4×10 [which includes a factor of (17,000)1/2 due to lensing]. This is just at the expected noise floor of the advanced Laser Interferometric Gravitational-Wave Observatory (LIGO) at 60 Hz (Abramovici et al. 1992). If the rotational frequency is 500 Hz, the observation time reduces to approximately 14.5 hr, but the intensity ratio increases to approximately 293,000. The value for heff is then estimated at 1.5×10
[which includes a factor of (17,000)1/2 due to lensing]. This is just at the expected noise floor of the advanced Laser Interferometric Gravitational-Wave Observatory (LIGO) at 60 Hz (Abramovici et al. 1992). If the rotational frequency is 500 Hz, the observation time reduces to approximately 14.5 hr, but the intensity ratio increases to approximately 293,000. The value for heff is then estimated at 1.5×10 , compared with a noise floor of approximately 3×10
, compared with a noise floor of approximately 3×10 for LIGO at 1000 Hz (Abramovici et al. 1992).
for LIGO at 1000 Hz (Abramovici et al. 1992).
Determining the intensity ratio of waves emitted by NSs in our Galaxy requires the simultaneous solution of equation (4) and the following equation:

This leads to the following second-order equation in  D:
D:

Figure 1 shows the radius of the focused region as a function of d, while Figure 2 shows the area or intensity ratio as a function of d. The lensing process described here should have a significant impact on efforts to estimate the spatial distribution of the NS population by measuring the variance of the stochastic GW signal as a function of detector orientation (Giampieri 1999).
 Fig. 1
Fig. 1  Fig. 2
Fig. 2
- Abramovici, A., et al. 1992, Science, 256, 325 First citation in article | Crossref | ADS | PubMed
- Alexander, T., & Sternberg, A. 1999, ApJ, in press (astro-ph/9811038) First citation in article | ADS | Preprint
- Carney, B., Fulbright, J. P., Terndrup, D. M., Suntzeff, N., & Walker, A. 1995, AJ, 110, 1674 First citation in article | Crossref | ADS
- Flanagan, E. E. 1999, in Gravitation and Relativity: At the Turn of the Millennium, ed. N. Dadhich & J. Narlikar (Poona: Poona Univ. Press), in press (gr-qc/9804024) First citation in article | ADS | Preprint
- Genzel, R., Eckart, A., Ott, T., & Eisenhauer, F. 1997, MNRAS, 291, 219 First citation in article | Crossref | ADS
- Ghez, A. M., Klein, B. L., Morris, M., & Becklin, E. E. 1998, ApJ, 509, 678 First citation in article | IOPscience | ADS
- Giampieri, G. 1999, in Proc. Second Workshop on Gravitational-Wave Data Analysis, Orsay, France, 1997 November 13
 15, in press (astro-ph/9801019) First citation in article | Preprint
15, in press (astro-ph/9801019) First citation in article | Preprint
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects (New York: Wiley-Interscience) First citation in article | Crossref | ADS
- Thorne, K. S. 1987, in Three Hundred Years of Gravitation, ed. S. W. Hawking & W. Israel (Cambridge: Cambridge Univ. Press), 361 First citation in article
 Full image (20kb) | Discussion in text
Full image (20kb) | Discussion in text
FIG. 1. Radius of the focused region for NS sources in our Galaxy
Radius of the focused region for NS sources in our Galaxy
 Full image (20kb) | Discussion in text
Full image (20kb) | Discussion in text
FIG. 2. Intensity ratio for NS sources in our Galaxy
Intensity ratio for NS sources in our Galaxy
 m (assuming that the concentrated mass has the form of a supermassive black hole). The increase in intensity (which is proportional to the square of the increase in strain amplitude h) is by a factor of approximately 17,000. Sources within our Galaxy lead to increases in intensity by a factor that can exceed 4000.
m (assuming that the concentrated mass has the form of a supermassive black hole). The increase in intensity (which is proportional to the square of the increase in strain amplitude h) is by a factor of approximately 17,000. Sources within our Galaxy lead to increases in intensity by a factor that can exceed 4000.
 M
M +
+


 , so the 3 dB points (the points of half-power) are located at kR
, so the 3 dB points (the points of half-power) are located at kR




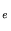 of 10
of 10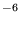 yields a value for heff of 1.4×10
yields a value for heff of 1.4×10 [which includes a factor of (17,000)1/2 due to lensing]. This is just at the expected noise floor of the advanced Laser Interferometric Gravitational-Wave Observatory (LIGO) at 60 Hz (
[which includes a factor of (17,000)1/2 due to lensing]. This is just at the expected noise floor of the advanced Laser Interferometric Gravitational-Wave Observatory (LIGO) at 60 Hz ( , compared with a noise floor of approximately 3×10
, compared with a noise floor of approximately 3×10 for LIGO at 1000 Hz (
for LIGO at 1000 Hz (

 Fig. 1
Fig. 1  Fig. 2
Fig. 2