Accretion flows onto compact astronomical sources are likely to be supersonic, and shock waves may therefore be common in such flows. Plasma passing through a shock front will be compressed and heated according to the jump conditions across the shock discontinuity. Shocks in accretion flows may therefore have important consequences for the flow structure and emission characteristics. The equations governing adiabatic (nonradiative) shocks in relativistic plasmas are presented. Relativistically correct equations of state are used that include the effects of radiation pressure and energy density, and pair equilibria are calculated for the postshock flow. Postshock states are determined for accretion flows with typical accretion-driven astronomical sources, and possible dynamics of the postshock flow are suggested. In particular, we find that cool, optically thick accretion flows undergoing shocks may become radiation or pair dominated and that the postshock plasma will likely become optically thin before returning to steady state conditions.
Subject headings: accretion, accretion disks![]() plasmas
plasmas![]() relativity
relativity![]() shock waves
shock waves
Matter in an accretion flow in the potential well of a compact object such as a black hole, neutron star, or white dwarf will likely form a quasi-spherical or disklike accretion structure in which angular momentum is transported outward, allowing accretion, and energy is lost from the system in the form of radiation and particle winds. For a wide range of accretion models discussed in the literature, supersonic accretion flows result within a sonic radius, rs, within which pressure forces become dynamically unimportant and the accreting plasma is essentially in free fall.
Steady state, spherical accretion models are constrained by the continuity equation in the radial direction, which within the sonic radius can be written as ![]() = const × v3, where
= const × v3, where ![]() is the plasma density and v is the free-fall velocity. The sound speed is easily found as cs = const × v(3/2)(
is the plasma density and v is the free-fall velocity. The sound speed is easily found as cs = const × v(3/2)(![]() -1), where
-1), where ![]() is the adiabatic index. Assuming a continuous flow of plasma with an adiabatic index of 5/3 or higher, we find that the sound speed is on the order of, or less than, the free-fall speed everywhere within rs.
is the adiabatic index. Assuming a continuous flow of plasma with an adiabatic index of 5/3 or higher, we find that the sound speed is on the order of, or less than, the free-fall speed everywhere within rs.
Keplerian thin disks are necessarily supersonic since the disk scale height, h, and hence the sound speed, cs, are determined by hydrostatic equilibrium in the axial direction, while the bulk flow Keplerian velocity, v![]() , is set by the full gravitational potential. The azimuthal Mach number can be written as M
, is set by the full gravitational potential. The azimuthal Mach number can be written as M![]() = v
= v![]() /cs
/cs ![]()
![]() -1(1 +
-1(1 + ![]() 2)3/4, where
2)3/4, where ![]() = h/r
= h/r ![]() 1 is the ratio of the disk scale height to radius (Frank, King, & Raine 1992). It is seen that supersonic flows are required for Keplerian thin disks.
1 is the ratio of the disk scale height to radius (Frank, King, & Raine 1992). It is seen that supersonic flows are required for Keplerian thin disks.
Accretion flows onto compact objects are therefore likely to be supersonic and, in the case of thin disks, highly supersonic. Shock waves are therefore possible and perhaps common in accretion flows, and, because shocks are efficient in heating the accreting plasma, they may play an important role in the dynamics and radiative processes within the accreting material. Solutions to the hydrodynamic equations for spherical and disklike accretion flows including shocks have been investigated (e.g., Babul, Ostriker, & Mészáros 1989; Park & Ostriker 1989; Chakrabarti 1989, 1990; Abramowicz & Chakrabarti 1990). Such solutions, when they exist, contain a "global" shock surface, which is an integral part of the disk structure, e.g., a radius r ![]() rs at which the flow undergoes a discontinuous change in its dynamic and thermodynamic properties. Several questions arise concerning the stability of such shocks. For example, how does the expected turbulent flow interact with a stationary shock front? Shocks within turbulent, high Reynolds number flows studied in the laboratory are characteristically unsteady and strongly distort the downstream flow characteristics (Smits 1992 and references therein). "Nonstructural" or "local" shocks may also form in supersonic accretion flows, which do not play a direct role in the global flow structure. Such shocks may result from many processes thought to be common in active galaxies, binary mass transfer systems, and other astronomical sources. For example, shocks may result from collisions between turbulent eddies, interaction of the accretion flow with the surface of the accreting object, interactions with Roche lobe overflow material, particle winds or jets, plasma accelerated by reconnecting magnetic field lines, unstable or nonlinear oscillatory modes, interaction with a star or other compact object on an orbit that intersects the disk (Sivron, Caditz, & Tsuruta 1996), etc. Shocks that are the result of local and transient disturbances in the flow may significantly alter the thermodynamic and radiative properties of the accreting plasma if they occur frequently. Infrequent shocks may be detectable as high-energy flares if they are sufficiently strong. Such local shock phenomena have previously been suggested for various classes of sources. Some recent contributions include extragalactic radio sources (Blackman 1996), gamma-ray sources (Bykov & Mészáros 1996), and protostellar disks (Neufeld & Hollenbach 1996).
rs at which the flow undergoes a discontinuous change in its dynamic and thermodynamic properties. Several questions arise concerning the stability of such shocks. For example, how does the expected turbulent flow interact with a stationary shock front? Shocks within turbulent, high Reynolds number flows studied in the laboratory are characteristically unsteady and strongly distort the downstream flow characteristics (Smits 1992 and references therein). "Nonstructural" or "local" shocks may also form in supersonic accretion flows, which do not play a direct role in the global flow structure. Such shocks may result from many processes thought to be common in active galaxies, binary mass transfer systems, and other astronomical sources. For example, shocks may result from collisions between turbulent eddies, interaction of the accretion flow with the surface of the accreting object, interactions with Roche lobe overflow material, particle winds or jets, plasma accelerated by reconnecting magnetic field lines, unstable or nonlinear oscillatory modes, interaction with a star or other compact object on an orbit that intersects the disk (Sivron, Caditz, & Tsuruta 1996), etc. Shocks that are the result of local and transient disturbances in the flow may significantly alter the thermodynamic and radiative properties of the accreting plasma if they occur frequently. Infrequent shocks may be detectable as high-energy flares if they are sufficiently strong. Such local shock phenomena have previously been suggested for various classes of sources. Some recent contributions include extragalactic radio sources (Blackman 1996), gamma-ray sources (Bykov & Mészáros 1996), and protostellar disks (Neufeld & Hollenbach 1996).
With the advent of X-ray observation, it has become clear that rapidly variable power-law X-ray spectra are a characteristic feature in compact accretion sources. Recent observations of Fe line features, hard X-ray bump, soft X-ray excess, and rapid variations of Fe line and X-ray continuum in some Seyfert nuclei (Matsuoka et al. 1990; Pounds et al. 1990; Nandra & Pounds 1994; Iwasawa et al. 1996; Yaqoob et al. 1996) suggest that there may be significant quantities of hot (T ![]() 109 K) and cool (T
109 K) and cool (T ![]() 106 K) material within or surrounding the central engines of many active galactic nuclei (AGNs) (Guilbert & Rees 1988; Lightman & White 1988). Such material has been suggested to be in the form of a "hybrid" hot and cold disk model (e.g., Wandel & Liang 1991; Tsuruta & Kellen 1995) in the form of clouds or filaments (e.g., Celotti, Fabian, & Rees 1992; Sivron & Tsuruta 1993; Kuncic, Blackman, & Rees 1996; Kuncic, Celotti, & Rees 1997) or within separate, localized regions (Poutanen et al. 1996).
106 K) material within or surrounding the central engines of many active galactic nuclei (AGNs) (Guilbert & Rees 1988; Lightman & White 1988). Such material has been suggested to be in the form of a "hybrid" hot and cold disk model (e.g., Wandel & Liang 1991; Tsuruta & Kellen 1995) in the form of clouds or filaments (e.g., Celotti, Fabian, & Rees 1992; Sivron & Tsuruta 1993; Kuncic, Blackman, & Rees 1996; Kuncic, Celotti, & Rees 1997) or within separate, localized regions (Poutanen et al. 1996).
While hot plasma is now commonly invoked to explain continuum spectra, the source of this material has rarely been discussed within the context of a self-consistent flow model. It is shown below that shocked material within a cool (T ![]() 105 K) optically thick accretion flow will, for a wide range of initial conditions and shock strengths, have characteristic temperatures T > 106 K and will thus contribute to X-ray emission (see § 5 for more details). This material may also become optically thin, and it may contribute to convective energy transport and advection of hot plasma to the disk surface. Bremsstrahlung emission from particles accelerated by first-order Fermi scattering in shocks may also produce X-ray emission in AGNs (Bregman & Boisseau 1989; Contini & Viegas-Aldrovandi 1990).
105 K) optically thick accretion flow will, for a wide range of initial conditions and shock strengths, have characteristic temperatures T > 106 K and will thus contribute to X-ray emission (see § 5 for more details). This material may also become optically thin, and it may contribute to convective energy transport and advection of hot plasma to the disk surface. Bremsstrahlung emission from particles accelerated by first-order Fermi scattering in shocks may also produce X-ray emission in AGNs (Bregman & Boisseau 1989; Contini & Viegas-Aldrovandi 1990).
In § 2 the equations governing the jump conditions across an adiabatic shock are presented. The thermodynamic properties of the pre- and postshock states, including gas and radiation energies and pressures are discussed in § 3. The form of these thermodynamic quantities is necessary to specify the jump condition. In § 4 we discuss possible dynamics of the postshock material within the accretion flow. A critical length scale is defined that differentiates those shocks that may participate in energy dissipation and those that may survive over dynamical timescales and contribute to the formation of a hot plasma component. Also, we give some example shock calculations for conditions expected in compact accretion flows, and we discuss possible consequences of "dissipative" and "dynamical" shocks for the flow structure and emission properties. A discussion of this work is presented in § 5. The Appendix presents characteristic timescales for the various competing microphysical processes.
General discussions of shocks are given by Landau & Lifshitz (1987) and Zeldovich & Raizer (1966). Astrophysical shocks have been investigated in many different contexts, including stellar processes, particle acceleration, jets, galaxy formation, supernova explosions, and cosmology. Shocks in AGNs have been discussed in the context of acceleration of particles and subsequent modification of the continuum and line spectra (Blondin & König 1987; Viegas-Aldrovandi & Contini 1989; Bregman & Boisseau 1989) and, as mentioned above, in the context of the global structure of accretion flows. Several authors have studied global standing shocks in spherical accretion flows (Park & Ostriker 1989; Babul et al. 1989) and in rotating flows (Chakrabarti 1989, 1990; Abramowicz & Chakrabarti 1990). Such shocks may occur when the infall or orbital speed exceeds the sound speed. Chakrabarti (1990) has studied spiral shocks in accretion disks and has found such shocks to transport angular momentum and thus to allow accretion even in the absence of viscous dissipative forces. Blondin & König (1987) have investigated the effects of copious pair production in standing shocks in sources with a high compactness parameter ![]() =
=![]()
 L/4
L/4![]() m
m c
c r>
r>![]() 1, where
1, where ![]() T is the Thomson cross section, me the electron mass, L the source luminosity, and R the source radius. We present here a careful study of the jump conditions for shocks as well as some possible scenarios for the postshock material.
T is the Thomson cross section, me the electron mass, L the source luminosity, and R the source radius. We present here a careful study of the jump conditions for shocks as well as some possible scenarios for the postshock material.
For simplicity, we assume a planar shock geometry, which is appropriate for regions not much larger than the shock source. To circumvent the need to specify boundary conditions at the surface of the accretion flow, we assume shock fronts not larger than the flow scale height. While magnetic fields are expected to be present in astronomical accretion flows (e.g., Balbus & Hawley 1991), we do not consider the effects of these fields on the shock solutions. Magnetic effects such as transverse and collisionless shocks will be considered elsewhere.
Propagation of the shock wave through the accretion flow is considered elsewhere (Sivron et al. 1996); however, we do discuss the possible behavior of the postshock material as it cools, expands, and/or diffuses into the surrounding medium. We assume that heat conduction and radiative losses within the shock discontinuity are negligible and therefore the shock is adiabatic. The conditions for adiabatic shocks are discussed in the Appendix.
The Taub adiabat relates pre- and postshock thermodynamic states for adiabatic shocks (Russo 1988; Iwamoto 1989):
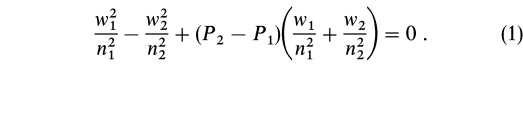
The nonrelativistic version of this equation is the well-known Rankine-Hugoniot equation for classical adiabatic shocks. The subscripts i = 1, 2 refer to the pre- and postshock quantities, respectively, and the enthalpy densities (wi) pressure (Pi) and the baryon number densities (ni) are to be expressed in the respective fluid element rest frames. Shock adiabats are obtained by inserting the appropriate functions wi(Pi, ni) into equation (1).
The speed of the shock front with respect to the preshock flow perpendicular to the shock front is (Iwamoto 1989)
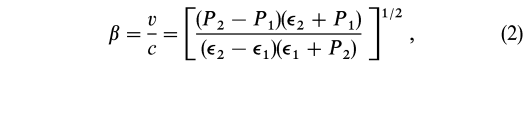
where ![]() i (=wi - Pi) is the energy density. The thermodynamic properties of the postshock material will be parameterized below in terms of this speed.
i (=wi - Pi) is the energy density. The thermodynamic properties of the postshock material will be parameterized below in terms of this speed.
The steady state, preshock accretion flow structure is determined by a simultaneous solution of the hydrodynamic and microphysical equations. Spherical accretion flows are discussed by, e.g., Frank et al. (1992). Cool, optically thick, geometrically thin disk solutions are given by, e.g., Shakura & Sunyaev (1973) and Novikov & Thorne (1973). Thick disks are discussed by e.g., Madau (1988) and Frank et al. (1992).
In this work we do not assume any particular accretion model. Rather, we are concerned with generic or typical preshock conditions for steady state accretion flows. Where appropriate, we give specific examples using physical conditions relevant to the models mentioned above.
Electron-electron, proton-proton, and electron-proton thermalization timescales, tee, tpp, and tep, are discussed in the Appendix. At sufficiently small accretion rates (or large radii), these timescales are smaller than the accretion timescale tr, and we expect a single-temperature accretion structure in thermal equilibrium (see Appendix § A1). The equilibrium temperature is found by equating the (local) gravitational heating rate to the (local) radiative cooling rate. Even assuming Eddington luminosity with all of the binding energy of the accreted material radiated at a few Schwarzschild radii, we find that ![]() = kbT/(mec2)
= kbT/(mec2) ![]() 1. Both protons and electrons are nonrelativistic, and the plasma is virtually pair free. In the case of a geometrically thin disk, this would be the cool, optically thick accretion disk model of, e.g., Shakura & Sunyaev (1973). In this temperature range, the preshock energy density is dominated by proton rest mass. The preshock material is therefore described by
1. Both protons and electrons are nonrelativistic, and the plasma is virtually pair free. In the case of a geometrically thin disk, this would be the cool, optically thick accretion disk model of, e.g., Shakura & Sunyaev (1973). In this temperature range, the preshock energy density is dominated by proton rest mass. The preshock material is therefore described by
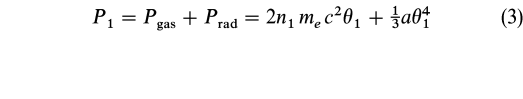
and

Here me and mp are the electron and proton masses, a = 4![]() /c(mec2/kb)4 = 9.42 × 1024 ergs cm-3,
/c(mec2/kb)4 = 9.42 × 1024 ergs cm-3, ![]() is the Stefan-Boltzmann constant, and kb is Boltzmann's constant. At higher accretion rates or smaller radii, the radial drift timescale may become as small as the thermalization timescales, and a two temperature plasma may result. This case will be considered elsewhere.
is the Stefan-Boltzmann constant, and kb is Boltzmann's constant. At higher accretion rates or smaller radii, the radial drift timescale may become as small as the thermalization timescales, and a two temperature plasma may result. This case will be considered elsewhere.
Since postshock temperatures may be much greater than the preshock temperature, we consider a general equation of state including radiation and pair effects.
We find

and
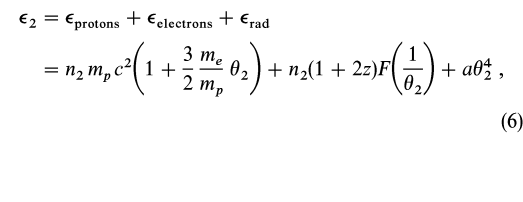
where z ![]() n+/np is the pair-to-proton ratio and the pair energy is included within the electron term. For electrons and positrons we have used a relativistic Maxwell-Boltzmann distribution:
n+/np is the pair-to-proton ratio and the pair energy is included within the electron term. For electrons and positrons we have used a relativistic Maxwell-Boltzmann distribution:

where K![]() is the modified Bessel function of the second kind of order
is the modified Bessel function of the second kind of order ![]() . The pair density ratio in thermal equilibrium is discussed by Wandel & Yahil (1979) and Svensson (1984). Following Svensson (1984), we find
. The pair density ratio in thermal equilibrium is discussed by Wandel & Yahil (1979) and Svensson (1984). Following Svensson (1984), we find
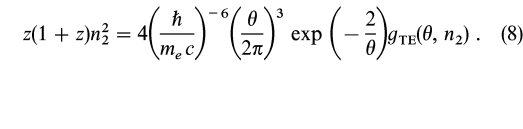
At densities of interest (n2 ![]() 1030 cm-3), pairs already dominate at subrelativistic temperatures, and we may approximate gTE as (Svensson 1984)
1030 cm-3), pairs already dominate at subrelativistic temperatures, and we may approximate gTE as (Svensson 1984)

Using equations (1) and (3)![]() (9), we may obtain the shock adiabats, P(1/n), for given initial conditions n1 and
(9), we may obtain the shock adiabats, P(1/n), for given initial conditions n1 and ![]() 1. The solid curve in Figure 1 shows the shock adiabat for gas-dominated initial conditions typical of standard accretion disk models describing the central engines of Seyfert nuclei (within a few tens of Schwarzschild radii) n1 = 1018 cm-3 and
1. The solid curve in Figure 1 shows the shock adiabat for gas-dominated initial conditions typical of standard accretion disk models describing the central engines of Seyfert nuclei (within a few tens of Schwarzschild radii) n1 = 1018 cm-3 and ![]() 1 = 1.7 × 10-5 (T1 = 105 K).
1 = 1.7 × 10-5 (T1 = 105 K).
 Fig. 1
Fig. 1
Every point on a shock adiabat represents a possible postshock state. The postshock state obtained by a given shock is determined by the Mach number or equivalently, by the shock front velocity ![]() . Mach numbers increase along the adiabat from right to left. Figure 1 is also divided into several regions determined by the dominant pressure and energy components. The lower solid line shows the transition from gas pressure dominance (below) to radiation pressure dominance (above), i.e., nmec2(2 + 2z)
. Mach numbers increase along the adiabat from right to left. Figure 1 is also divided into several regions determined by the dominant pressure and energy components. The lower solid line shows the transition from gas pressure dominance (below) to radiation pressure dominance (above), i.e., nmec2(2 + 2z)![]() = 1/3a
= 1/3a![]() 4. The upper solid line shows the transition from matter- to radiation-dominated energy density, i.e., nmpc2 = a
4. The upper solid line shows the transition from matter- to radiation-dominated energy density, i.e., nmpc2 = a![]() 4. For comparison, a shock adiabat is also given for the preshock conditions: (n1, T1) = (1020 cm-3, 104 K) (dashed curve), which may be appropriate at larger radii for higher mass and lower accretion rate sources. This adiabat remains gas dominated to high Mach numbers and approaches the asymptotic density ratio n2/n1
4. For comparison, a shock adiabat is also given for the preshock conditions: (n1, T1) = (1020 cm-3, 104 K) (dashed curve), which may be appropriate at larger radii for higher mass and lower accretion rate sources. This adiabat remains gas dominated to high Mach numbers and approaches the asymptotic density ratio n2/n1 ![]() 4 for an ideal monatomic gas, causing a sharp upturn of the adiabat. When radiation pressure becomes dominant, this ratio is increased to n2/n1
4 for an ideal monatomic gas, causing a sharp upturn of the adiabat. When radiation pressure becomes dominant, this ratio is increased to n2/n1 ![]() 7. The solid adiabat, representing shocks in a hotter, more diffuse plasma, becomes radiation pressure dominated at lower Mach numbers. The steeply increasing portion of the adiabats represents the transition from gas to radiation pressure dominance. At even higher Mach numbers, the shock becomes radiation energy dominated, and the postshock density will again increase. The radiation-dominated shock adiabat is given approximately by (Iwamoto 1989)
7. The solid adiabat, representing shocks in a hotter, more diffuse plasma, becomes radiation pressure dominated at lower Mach numbers. The steeply increasing portion of the adiabats represents the transition from gas to radiation pressure dominance. At even higher Mach numbers, the shock becomes radiation energy dominated, and the postshock density will again increase. The radiation-dominated shock adiabat is given approximately by (Iwamoto 1989)
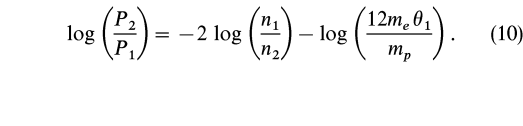
Using the maximum gas-dominated density limit of n2 ![]() 7n1 in equation (10), we find that the transition to radiation dominance occurs at approximately P2/P1
7n1 in equation (10), we find that the transition to radiation dominance occurs at approximately P2/P1 ![]() 4.1mp/(me
4.1mp/(me![]() 1).
1).
As expected, cooler plasmas become radiation dominated at greater pressures. Once radiation dominates the shock adiabat, the plasma density may increase with no bound. We see that relativistic effects allow for very large compressions across the shock front, far in excess of those allowed for purely gas-dominated shocks.
The characteristic size of a shocked region of plasma will depend on the size of the source or plasma perturbation causing the shock front as well as on the dynamics of the postshock material. The minimum size, ![]() min, is of order the particle deflection length, l, which is discussed in the Appendix § A2. Such small shocked regions will quickly thermalize into the surrounding plasma. Larger postshock regions will have longer thermal or viscous diffusion times (see Appendix § A3). The scale at which the diffusion time is of order the dynamical time indicates a shock size
min, is of order the particle deflection length, l, which is discussed in the Appendix § A2. Such small shocked regions will quickly thermalize into the surrounding plasma. Larger postshock regions will have longer thermal or viscous diffusion times (see Appendix § A3). The scale at which the diffusion time is of order the dynamical time indicates a shock size ![]() th, which is the largest capable of thermalization:
th, which is the largest capable of thermalization:

or
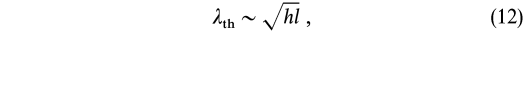
where h is the disk scale height. Shocks larger than ![]() th may maintain their identity over dynamical timescales and may therefore be seen as pockets of high-temperature plasma within the disk. Shocks of size
th may maintain their identity over dynamical timescales and may therefore be seen as pockets of high-temperature plasma within the disk. Shocks of size ![]() min <
min < ![]() <
< ![]() th may participate in energy dissipation within the disk. In the following sections, we discuss the possible behavior of "dynamic" [(hl)1/2 <
th may participate in energy dissipation within the disk. In the following sections, we discuss the possible behavior of "dynamic" [(hl)1/2 < ![]() < h] and "dissipative" [l <
< h] and "dissipative" [l < ![]() < (hl)1/2] shocks within accretion flows.
< (hl)1/2] shocks within accretion flows.
If the shock size is larger than ![]() th defined above, then the energy released within a shock cannot thermalize on dynamical timescales and is confined to an identifiable volume within the accretion flow. It is likely that such shocked regions will undergo adiabatic expansion until the plasma becomes optically thin. The shock energy will then be released in a burst of high-energy radiation on timescales determined ultimately by the distribution of shock length scales. High-energy variability is commonly observed in accretion-powered sources, and energy released from shocked plasma may, in some cases, be a plausible cause. In addition, at the high temperatures expected for the postshock plasma, pair processes may become important, altering the plasma composition.
th defined above, then the energy released within a shock cannot thermalize on dynamical timescales and is confined to an identifiable volume within the accretion flow. It is likely that such shocked regions will undergo adiabatic expansion until the plasma becomes optically thin. The shock energy will then be released in a burst of high-energy radiation on timescales determined ultimately by the distribution of shock length scales. High-energy variability is commonly observed in accretion-powered sources, and energy released from shocked plasma may, in some cases, be a plausible cause. In addition, at the high temperatures expected for the postshock plasma, pair processes may become important, altering the plasma composition.
The temperature for any point on the P-n plane is determined by the equation of state, equation (5). The preshock plasma is assumed to be within the optically thick region; however, at high enough temperatures, the postshock plasma may become effectively optically thin. The effective optical depth of a plasma of characteristic size ![]() is
is ![]() *
* ![]()
![]() mpn2[Kes(Kff + Kes)]1/2, where Kes = 0.4 cm-2g-1 is the electron scattering coefficient and K
mpn2[Kes(Kff + Kes)]1/2, where Kes = 0.4 cm-2g-1 is the electron scattering coefficient and K
![]() n
n (1+2z)T
(1+2z)T is the Rosseland mean free-free absorption coefficient for an electron (positron) density ne = n2(1 + 2z), with z determined from equation (8) above. Setting
is the Rosseland mean free-free absorption coefficient for an electron (positron) density ne = n2(1 + 2z), with z determined from equation (8) above. Setting ![]() * equal to 1 gives a critical length scale
* equal to 1 gives a critical length scale ![]() 1(P, n), below which (or equivalently, for a given
1(P, n), below which (or equivalently, for a given ![]() , a critical curve on the P-n plane above which) the postshock plasma becomes optically thin.
, a critical curve on the P-n plane above which) the postshock plasma becomes optically thin.
The shock adiabat, which assumes thermal equilibrium between gas and radiation field, is not self-consistent above the effectively thin transition curve for the relevant cloud size; shock adiabats appropriate to optically thin regions will be discussed in a future publication.
In addition, pair processes occurring in optically thin regions may significantly alter the accretion flow structure and emission properties (Blondin & König 1987; Park & Ostriker 1989; Tsuruta & Kellen 1995). The transition to pair-dominated optically thick plasma (i.e., z = 1 in eq. [8]) is shown by the short, dashed line marked "z > 1" in Figure 4. For typical thin disk (preshock) accretion disk densities, this region is obtained by relativistic shocks with ![]()
![]() 1. While such shocks may be infrequent, instabilities associated with copious pair production may have important consequences for spectral variability (Björnsson & Svensson 1992).
1. While such shocks may be infrequent, instabilities associated with copious pair production may have important consequences for spectral variability (Björnsson & Svensson 1992).
Figure 2 shows the postshock temperature and number density as a function of shock velocity for the same preshock parameters used for the solid adiabat in Figure 1.
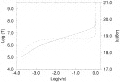 Fig. 2
Fig. 2
Inspection of these figures shows that even a moderate shock (![]()
![]() 10-2) may significantly increase the temperature (solid curve) and density (dashed curve) of the postshock material over their steady state equilibrium values. Because the density remains fairly constant in the gas energy regime, the pressure will increase with shock speed in proportion to the temperature increase. Pockets of hot, overdense, overpressure postshock plasma will therefore be embedded within the surrounding cool, preshock accretion flow. Since the thermalization time is long for the length scales considered here, these pockets of postshock plasma will experience dynamical effects. For example, overpressure regions will expand along a curve in the P-1/n plane to regain the ambient, preshock pressure.
10-2) may significantly increase the temperature (solid curve) and density (dashed curve) of the postshock material over their steady state equilibrium values. Because the density remains fairly constant in the gas energy regime, the pressure will increase with shock speed in proportion to the temperature increase. Pockets of hot, overdense, overpressure postshock plasma will therefore be embedded within the surrounding cool, preshock accretion flow. Since the thermalization time is long for the length scales considered here, these pockets of postshock plasma will experience dynamical effects. For example, overpressure regions will expand along a curve in the P-1/n plane to regain the ambient, preshock pressure.
Adiabatic expansion occurs with a characteristic timescale of
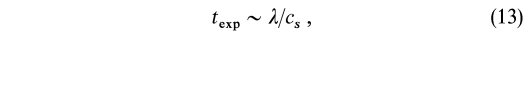
where ![]() is the postshock length scale and cs
is the postshock length scale and cs ![]() [P/(mpnp)]1/2 is the sound speed. The photon diffusion timescale is
[P/(mpnp)]1/2 is the sound speed. The photon diffusion timescale is
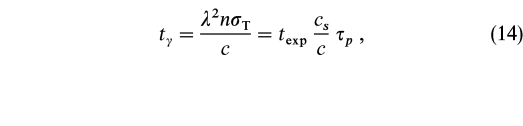
where ![]() p = n
p = n![]() T
T![]() is the proton optical depth. Adiabatic expansion will therefore dominate photon diffusion for length scales greater than
is the proton optical depth. Adiabatic expansion will therefore dominate photon diffusion for length scales greater than
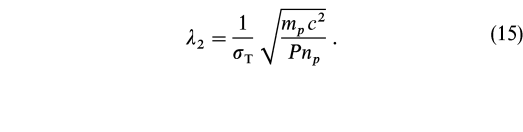
Radiation pressure![]() dominated postshock material with length scale
dominated postshock material with length scale ![]() >
> ![]() 2 will expand adiabatically and become effectively thin. For
2 will expand adiabatically and become effectively thin. For ![]() 1 <
1 < ![]() <
< ![]() 2, diffusion-driven cooling will dominate the return of the postshock material to steady state thermodynamic values, causing the expansion trajectory on the P-1/n plane to fall below the appropriate adiabatic expansion line.
2, diffusion-driven cooling will dominate the return of the postshock material to steady state thermodynamic values, causing the expansion trajectory on the P-1/n plane to fall below the appropriate adiabatic expansion line.
The two length scales ![]() 1 and
1 and ![]() 2 for our sample shock are plotted as a function of
2 for our sample shock are plotted as a function of ![]() in Figure 3. Notice that there is only a limited region of the parameter space that allows optically thick solutions. More importantly, for the preshock conditions considered, the postshock material must pass through an optically thin phase regardless of length scale for
in Figure 3. Notice that there is only a limited region of the parameter space that allows optically thick solutions. More importantly, for the preshock conditions considered, the postshock material must pass through an optically thin phase regardless of length scale for ![]() > 0.03. Once optically thin, the postshock plasma will quickly cool to the local equilibrium temperature, emitting the bulk of the shock energy in a burst of radiation of duration t
> 0.03. Once optically thin, the postshock plasma will quickly cool to the local equilibrium temperature, emitting the bulk of the shock energy in a burst of radiation of duration t ![]()
![]() /c and with characteristic temperature several orders of magnitude higher than the steady state disk temperature. At the temperatures and densities of interest, inverse Compton scattering of the emitted radiation will be important.
/c and with characteristic temperature several orders of magnitude higher than the steady state disk temperature. At the temperatures and densities of interest, inverse Compton scattering of the emitted radiation will be important.
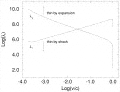 Fig. 3
Fig. 3
The effects described above are summarized in Figure 4. Figure 4 describes a possible trajectory taken by shocked plasma on the P-1/n plane. A short dashed line marked "z > 1" indicating the transition to high pair densities may be obtained for a very strong shock. The two dot-dashed lines indicate the transition to an optically thin plasma for postshock length scales ![]() = 107 cm and
= 107 cm and ![]() = 109 cm, which are appropriate for shocks of order the Keplerian disk scale height for Seyfert central engines.
= 109 cm, which are appropriate for shocks of order the Keplerian disk scale height for Seyfert central engines.
 Fig. 4
Fig. 4
The behavior of the postshock plasma is therefore determined by the shock strength and the characteristic length scale of the shocked region. For example, a shock of ![]()
![]() 0.1 will put the postshock plasma at the point marked "(n2, P2)" in Figure 4. If the shock size is
0.1 will put the postshock plasma at the point marked "(n2, P2)" in Figure 4. If the shock size is ![]()
![]() 107 cm, the shock front will be optically thin. If the shock size is
107 cm, the shock front will be optically thin. If the shock size is ![]()
![]() 108 cm, the postshock material will remain optically thick. However, the shocked plasma will expand freely along the adiabat marked "free expansion" and will cross into the optically thin region. The shock energy will then be lost in the form of radiation, and particle diffusion will return the plasma to the preshock conditions, (n1, P1).
108 cm, the postshock material will remain optically thick. However, the shocked plasma will expand freely along the adiabat marked "free expansion" and will cross into the optically thin region. The shock energy will then be lost in the form of radiation, and particle diffusion will return the plasma to the preshock conditions, (n1, P1).
In this section, we consider the possibility and ramifications of shocks that are produced internally by the accretion flow and, because of their small scale sizes, are dissipative in nature. If the accretion structure and energy conversion mechanisms are such that these shocks are frequent, they may play an important role in the conversion of gravitational energy into heat. Whether such shocks are sustainable in an accretion flow depends on the little-understood mechanism of turbulence production. If, for example, turbulence results from flow instabilities associated with a magnetic field (Balbus & Hawley 1991), then the Alfvén velocity may approach or exceed the sound speed and supersonic turbulence may persist in the flow. In addition, the largest turbulent cells in a thin accretion disk are expected to be of a scale size equal to the disk scale height, h. Such cells have a speed ![]() v
v ![]()
![]() v relative to the flow in a Keplerian disk a radial distance h away and are therefore nearly supersonic, with Mach numbers of order M
v relative to the flow in a Keplerian disk a radial distance h away and are therefore nearly supersonic, with Mach numbers of order M ![]() 1 relative to this flow. These simple arguments make it at least plausible that supersonic turbulent motion may be present within some accretion flows.
1 relative to this flow. These simple arguments make it at least plausible that supersonic turbulent motion may be present within some accretion flows.
It is likely that turbulent viscosity plays a role in angular momentum transport and energy dissipation within thin disks (Chakrabarti 1996 and references therein), and interactions between turbulent eddies may drive this dissipation (Balbus, Gammie, & Hawley 1994, hereafter BGH). Correlations between the fluctuating components of the gas and Alfvén velocities may be related to the "alpha" viscosity parameter via the fluctuation-dissipation theorem (see BGH for a more rigorous treatment):
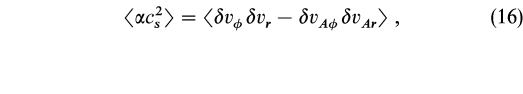
where ![]() vi and
vi and ![]() vAi represent the components of the fluctuating plasma and Alfvén velocities and the angle brackets signify a time average over several orbital periods and integration over disk height. On the other hand, as mentioned previously, it is possible that some fraction of the fluctuating velocities may become supersonic and collisions between supersonic turbulent eddies may result in shocks. Based on equation (16), we may expect that shocks play a role in field-free disks when the fluctuating velocities become supersonic or when
vAi represent the components of the fluctuating plasma and Alfvén velocities and the angle brackets signify a time average over several orbital periods and integration over disk height. On the other hand, as mentioned previously, it is possible that some fraction of the fluctuating velocities may become supersonic and collisions between supersonic turbulent eddies may result in shocks. Based on equation (16), we may expect that shocks play a role in field-free disks when the fluctuating velocities become supersonic or when ![]()
![]() 1. In the more likely case of equipartition magnetic fields,
1. In the more likely case of equipartition magnetic fields, ![]() need not be large to have supersonic turbulent velocities.
need not be large to have supersonic turbulent velocities.
Shocks due to supersonic turbulence are not likely to play a large role in viscous angular momentum transport, however, if they occur frequently, they may be important for energy dissipation and the radiative flux from the accretion flow. The adiabatic shocks considered here explicitly conserve energy; however, the postshock flow may possess significantly higher density, pressure, and internal energy, at the expense of turbulent kinetic energy. Fluctuations in these quantities may then be related to emissivity due to shocks. BGH neglected many such fluctuation terms in their analysis.
Following the procedure given by BGH, but including pressure and density fluctuation terms, we find that the vertically integrated radial energy flux is given by
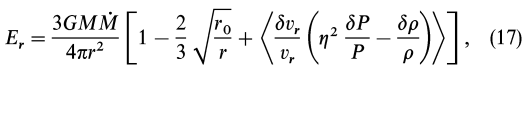
where we have assumed v![]()
![]() |
|![]()
 |
| ![]() vr; angular momentum flux is radial; viscosity vanishes at the inner disk boundary, r0; and magnetic effects at the shock front have been neglected. Setting (
vr; angular momentum flux is radial; viscosity vanishes at the inner disk boundary, r0; and magnetic effects at the shock front have been neglected. Setting (![]()
![]() ,
, ![]() P) equal to 0 reduces equation (17) to the standard Keplerian energy flux obtained for turbulent viscosity mechanisms (e.g., Shakura & Sunyaev 1973).
P) equal to 0 reduces equation (17) to the standard Keplerian energy flux obtained for turbulent viscosity mechanisms (e.g., Shakura & Sunyaev 1973).
The new terms, proportional to correlated velocity, pressure and density fluctuations may be associated with excess energy dissipation due to shocks.
The radiative flux density, Q=![]() h
h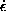 , through each disk face is obtained from the divergence of equation (17). The energy dissipation rate,
, through each disk face is obtained from the divergence of equation (17). The energy dissipation rate, ![]() s, associated with shocks is then:
s, associated with shocks is then:
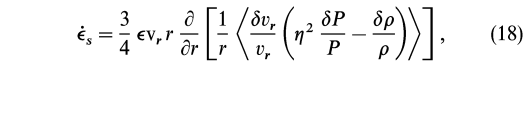
where ![]()
![]()
![]() v
v is the kinetic energy density. The opposing contributions of pressure and density fluctuations are due to the interaction of the density perturbations with the gravitational potential. We make the simplifying assumption that fluctuation magnitudes scale with their respective average values, independent of radius. This seems reasonable in the absence of a complete theory of turbulent processes in accretion disks. In addition, we assume that strong shocks are not common and therefore the pressure term may be neglected. In this case, we find
is the kinetic energy density. The opposing contributions of pressure and density fluctuations are due to the interaction of the density perturbations with the gravitational potential. We make the simplifying assumption that fluctuation magnitudes scale with their respective average values, independent of radius. This seems reasonable in the absence of a complete theory of turbulent processes in accretion disks. In addition, we assume that strong shocks are not common and therefore the pressure term may be neglected. In this case, we find
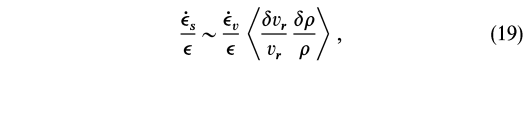
where 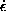
 /
/![]()
![]() v
v /r is the viscous energy dissipation rate. Since the relative magnitudes of the radial velocity and shock-induced density fluctuations may be large, we see that the energy dissipated within shocks may be significant. If shocks are frequent, then shock-induced energy dissipation may even dominate energy conversion within the disk, greatly enhancing disk luminosity.
/r is the viscous energy dissipation rate. Since the relative magnitudes of the radial velocity and shock-induced density fluctuations may be large, we see that the energy dissipated within shocks may be significant. If shocks are frequent, then shock-induced energy dissipation may even dominate energy conversion within the disk, greatly enhancing disk luminosity.
In this work, we have presented the adiabatic shock jump conditions appropriate to relativistic plasmas expected for shocked accretion flows onto compact objects. We have applied the resulting adiabatic equations to investigate shocks within cool, optically thick accretion flows. Such shocks may be the result of collisions between turbulent cells or other transient disturbances within the flow, or they may be structural in nature. For Keplerian disks with a viscosity parameter ![]()
![]() 1 or for disks with equipartition magnetic fields, we find that the heating produced within these shocks may be sufficient to account for a significant portion of the energy dissipation.
1 or for disks with equipartition magnetic fields, we find that the heating produced within these shocks may be sufficient to account for a significant portion of the energy dissipation.
Accretion flows onto compact objects are likely to be supersonic. Highly supersonic flows are expected in the case of the geometrically thin Keplerian accretion disks commonly discussed in the literature. Shocks that may be present in such flows result in highly efficient heating of the flow material. The observational evidence for radiation from accretion-powered AGNs points to the need for both cool and hot components. Shocks may therefore play an important role in the structure of an accretion flow by, e.g., naturally creating hot plasmas in a cold disk. It has been pointed out that observational evidence for some Galactic black hole candidates seems to argue against localized, disconnected regions of hot and cold emission (Vaughan & Nowak 1997). Also, it was noted that some characteristic features such as the Fe line and hard X-ray reflection humps observed in many Seyferts may support large distinct regions of the hot and cold matter, as in the case of, e.g., a promising AGN model involving a disk with a corona (e.g., Tsuruta & Kellen 1995; Haardt & Maraschi 1991) and another such model with clouds (e.g., Sivron & Tsuruta 1993; Nandra & George 1994). The latter requires optically thin, geometrically thick accretion flow, which is not considered in our current work. The former, however, has a direct connection to our current work on shocks in a cool, geometrically thin disk in the sense that our work can offer a natural origin for such a geometrical structure.
For instance, in a disk corona model, the cool component is in the form of a cool, thin disk while the hot component is envisioned as a corona above the disk. The hot component can be explained by both thermal and nonthermal plasmas (e.g., see Tsuruta & Kellen 1995).
In both types of models, however, the exact source of the hot radiation has been yet to be explained. The current paper is focused mainly on our studies of basic physics of shocks in the environment of a cold, thin accretion disk. However, it can offer a promising origin for the hot coronal radiation in the following way. The shock heating in a cold disk as discussed above is probably sufficient to generate hot material within the flow, which may be radiation and/or pair dominated. It is likely that they will pass through an optically thin phase before their return to equilibrium conditions. Although the detailed treatment of the dynamics of the postshock plasma will be postponed to our future work, we already note that as the larger postshock cells expand, they will become underdense and will be forced toward the disk surface. Shock-induced, buoyant cells within the cool disk most likely will appear as hot flares or outbursts above or on the surface of the cool disk, which will be responsible for the efficient acceleration of energetic particles responsible for high-energy radiation. The point is that the local hot regions produced in a disk need not stay there but will more likely move up to the disk surface. The surface of a thin accretion disk as a possible site of such particle acceleration was already pointed out by Galeev, Rosner, & Vaiana (1979).
Assuming such efficient acceleration near the surface, Tsuruta & Tritz (1992) and Tsuruta & Kellen (1995) constructed a successful disk corona model that is consistent with observed characteristics of Seyfert radiation. Our current shock studies show that the bulk of the shock energy can be released in a burst of high-energy radiation. The observed high-energy spectral fluctuations are then related to the distribution of length scales within the postshock plasma. In this way shocks will offer a plausible mechanism for the high-energy variability observed in these AGNs, and they may be responsible for supplying material and energy to a hot corona. The detailed presentation of the connection between our current basic work on shock physics and astrophysical application to the observed accretion-powered objects will be found in our Paper II (Tsuruta, Caditz, & Mola 1997).
We have considered only adiabatic shocks; we assume that energy is not lost from the shock front in the form of radiation or particle winds. This may be a good approximation for optically thick accretion flows, depending on the relevant microphysical timescales. Shocks in hot, optically thin flows may require a more careful treatment and will be discussed elsewhere. In addition, we have not considered the effects of magnetic fields on the shocks. Magnetic fields are expected to alter the various microphysical time and length scales and provide for additional shock solutions including new longitudinal and transverse magnetosonic shocks and collisionless shocks. Such shocks have been discussed generally by Sivron et al. (1996) and will be treated in more detail in a future work. The current work is presented as our first step toward more realistic models through a series of further improvements. Also, we emphasize that even when strong magnetic fields are present, the longitudinal, collision-dominated shocks discussed here remain valid shock solutions when the shock surface is perpendicular to the field lines. Since both the field and the supersonic flow are expected to be primarily azimuthal within the disk, field-free shock solutions are expected to be already very important for accretion flows with high angular momentum.
The authors would like to express gratitude Martin Rees for his useful comments and the anonymous referee for valuable guidance. This work is supported by NASA grant NAGW-2208
When a shock wave passes through a steady accretion flow, we expect the postshock material to be at least temporarily perturbed from its steady state accretion equilibrium. If runaway processes occur, then it is possible that the postshock material will undergo a catastrophic "change of state" before reaching a new equilibrium configuration. It is important, therefore, to compare the various timescales for approach to equilibrium of the macrophysical disk structure and the microphysical processes.
The orbital timescale is t![]() (r) = 1/
(r) = 1/![]() (r). Assuming Keplerian velocity (which is appropriate for a thin disk where radial pressure gradients are unimportant), we find
(r). Assuming Keplerian velocity (which is appropriate for a thin disk where radial pressure gradients are unimportant), we find
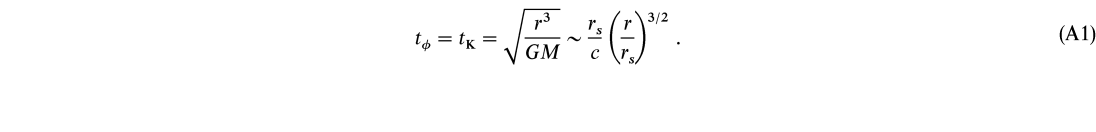
If particle and/or radiation pressure is significant, then we expect a deviation from Keplerian velocity and hence from Keplerian orbital timescales. For example, the orbital timescale for a vorticity-free torus (a thick disk in pure rotation with ![]()
![]() r-2) is
r-2) is
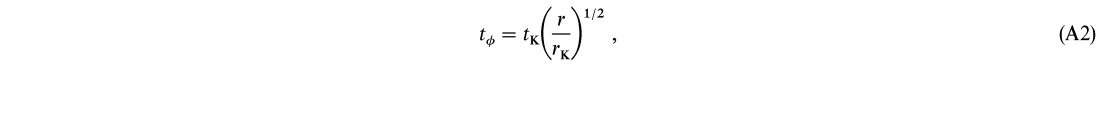
where rK(>rs) is the radius at which the velocity is Keplerian (e.g., Frank et al. 1992).
The hydrodynamic timescale is
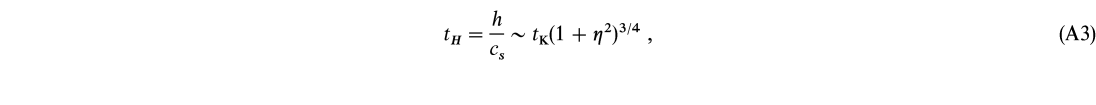
where cs ![]() (P/
(P/![]() )1/2 is the sound speed, h is the disk thickness,
)1/2 is the sound speed, h is the disk thickness, ![]()
![]() h/r, and we have used the z-component of the Euler equation with velocity terms neglected. For thin disks,
h/r, and we have used the z-component of the Euler equation with velocity terms neglected. For thin disks, ![]()
![]() 1, while for thick disks
1, while for thick disks ![]()
![]() 1.
1.
The viscous, radial drift, or proton heating timescale is
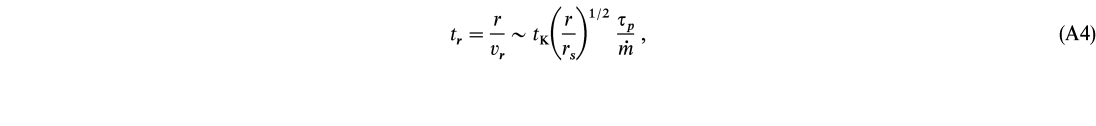
where we have used v
![]()
 /(
/(![]()
 rh) with
rh) with ![]() p as the proton density,
p as the proton density, 
![]()
 c
c /L
/L , and
, and ![]() p = np
p = np![]() Th as the proton optical depth. For typical disk accretion rates and proton optical depths (e.g., Björnsson & Svensson 1992) we find tr > tH
Th as the proton optical depth. For typical disk accretion rates and proton optical depths (e.g., Björnsson & Svensson 1992) we find tr > tH ![]() t
t![]() ; however, this need not be true in all cases.
; however, this need not be true in all cases.
The thickness ![]() of a strong shock is of order the mean free path or deflection length; i.e.,
of a strong shock is of order the mean free path or deflection length; i.e.,
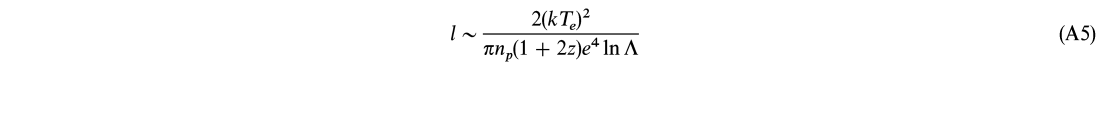
(Frank et al. 1992). The timescale for transition from preshock to postshock states is therefore
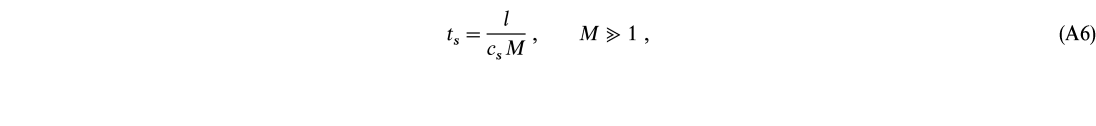
where M = vs/cs is the Mach number and vs and cs are the shock and sound speeds, respectively, in the preshock material. For weak shocks, where M ![]() 1, the thickness is increased by approximately 1.2/(M2 - 1) (Zeldovich & Raizer 1966), where we have assumed a monatomic gas adiabatic index
1, the thickness is increased by approximately 1.2/(M2 - 1) (Zeldovich & Raizer 1966), where we have assumed a monatomic gas adiabatic index ![]() = 5/3; therefore,
= 5/3; therefore,
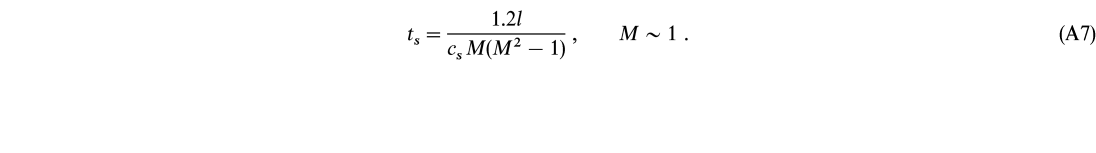
In the absence of a confinement mechanism, inhomogeneities of a size ![]() > l, where l is the particle mean free path, will dissipate by collisional diffusion. The diffusion timescale is (Reichl 1990)
> l, where l is the particle mean free path, will dissipate by collisional diffusion. The diffusion timescale is (Reichl 1990)
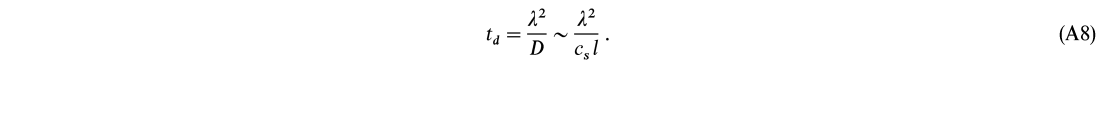
Here D ![]() cs l is the coefficient of self-diffusion. If a magnetic field exists, then the diffusion time perpendicular to the field lines is increased (Shkarofsky, Johnston, & Bachynski 1966):
cs l is the coefficient of self-diffusion. If a magnetic field exists, then the diffusion time perpendicular to the field lines is increased (Shkarofsky, Johnston, & Bachynski 1966):
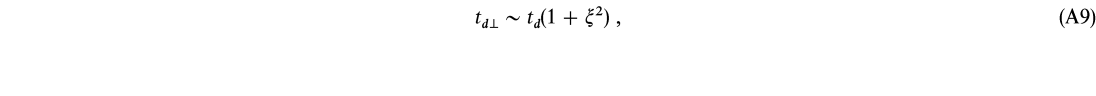
where ![]()
![]()
![]() b l/cs is the ratio of the cyclotron frequency
b l/cs is the ratio of the cyclotron frequency ![]() b = e|B|/mc to the collision frequency. Diffusion parallel to the field lines is unaffected. For an equipartition magnetic field, B
b = e|B|/mc to the collision frequency. Diffusion parallel to the field lines is unaffected. For an equipartition magnetic field, B /8
/8![]()
![]() 3nkT/2
3nkT/2![]() 3c
3c
![]() /2 and virial temperatures, kT/mc2
/2 and virial temperatures, kT/mc2 ![]() Rs/R, we find
Rs/R, we find

For typical accretion parameters, we expect significant confinement perpendicular to the field; however, for high enough pair densities such that ![]() < 1, magnetic confinement may be less important.
< 1, magnetic confinement may be less important.
Thermal relaxation timescales due to Coulomb interactions are discussed by Stepney (1983). Electron-electron, proton-proton, and electron-proton relaxation timescales are temperature dependent and are approximately in the ratio

for ![]()
![]() 1. For mildly relativistic electrons (
1. For mildly relativistic electrons (![]() e
e ![]() 1)
1)

where ln ![]() is the Coulomb logarithm, which we take to be 20. Comparing the thermal relaxation times with the diffusion timescale for shock-induced inhomogeneities of characteristic size
is the Coulomb logarithm, which we take to be 20. Comparing the thermal relaxation times with the diffusion timescale for shock-induced inhomogeneities of characteristic size ![]() , we find
, we find

where we have used equations (A5) and (A8), and the Thomson cross section ![]() T = 8
T = 8![]() /3(e2/mec2)2. The temperature dependence in this ratio comes mainly from the deflection length given in equation (A5). For
/3(e2/mec2)2. The temperature dependence in this ratio comes mainly from the deflection length given in equation (A5). For ![]() e >
e > ![]() (mp/me)1/2(l/
(mp/me)1/2(l/![]() ) we expect that Coulomb interactions will be sufficient to thermalize electrons (positrons) in the postshock material. The values of tpp/td and tep/td are larger by the ratios (1 + 2z)(mp/me)1/2 and (1 + 2z)(mp/me), respectively, and will therefore require larger postshock temperatures and/or sizes in order to obtain thermal equilibrium prior to diffusion. Plasma collective modes, however, may thermalize the plasma on timescales much shorter than the Coulomb thermalization times, and an equipartition magnetic field may confine the postshock inhomogeneity much longer than the diffusion time. Complete thermal equilibrium will therefore likely be obtained prior to dissipation of the postshock material.
) we expect that Coulomb interactions will be sufficient to thermalize electrons (positrons) in the postshock material. The values of tpp/td and tep/td are larger by the ratios (1 + 2z)(mp/me)1/2 and (1 + 2z)(mp/me), respectively, and will therefore require larger postshock temperatures and/or sizes in order to obtain thermal equilibrium prior to diffusion. Plasma collective modes, however, may thermalize the plasma on timescales much shorter than the Coulomb thermalization times, and an equipartition magnetic field may confine the postshock inhomogeneity much longer than the diffusion time. Complete thermal equilibrium will therefore likely be obtained prior to dissipation of the postshock material.
Photon-photon (![]()
![]() ), photon-particle (
), photon-particle (![]() e,
e, ![]() p, where e includes electrons and positrons), and particle-particle (ee, ep) pair production rates in hot plasma clouds are discussed by Svensson (1982, 1984). These quantities are functions of plasma temperature(s) and proton and pair densities. Low pair density (z
p, where e includes electrons and positrons), and particle-particle (ee, ep) pair production rates in hot plasma clouds are discussed by Svensson (1982, 1984). These quantities are functions of plasma temperature(s) and proton and pair densities. Low pair density (z ![]() 1) pair production is dominated by ee and ep interactions giving a pair production timescale
1) pair production is dominated by ee and ep interactions giving a pair production timescale
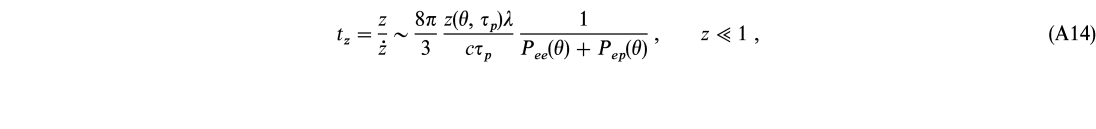
where ![]() is the size of the plasma cloud. The pair density, z, and the production rates, Pee and Pep, are highly temperature dependent.
is the size of the plasma cloud. The pair density, z, and the production rates, Pee and Pep, are highly temperature dependent.
For ![]()
![]() 25, the ratio is z/(Pee + Pep)
25, the ratio is z/(Pee + Pep) ![]() A(
A(![]() ), where A(
), where A(![]() ) is the dimensionless pair annihilation rate (Svensson 1982): A(
) is the dimensionless pair annihilation rate (Svensson 1982): A(![]() )
) ![]()
![]() /[1 + 2
/[1 + 2![]() 2/ln (1.12
2/ln (1.12![]() + 1.3)]. We therefore find
+ 1.3)]. We therefore find
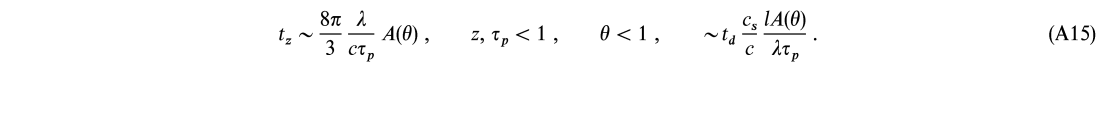
Low z plasma inhomogeneities of temperature ![]()
![]() 25 and of size
25 and of size ![]() >
> ![]() cr = [cslA/(cnp
cr = [cslA/(cnp![]() T)]1/2 will therefore reach pair equilibrium before diffusing into the surrounding medium. For
T)]1/2 will therefore reach pair equilibrium before diffusing into the surrounding medium. For ![]() > 25, pair annihilation cannot balance pair production, and no equilibrium exists.
> 25, pair annihilation cannot balance pair production, and no equilibrium exists.
For z ![]() 1 and
1 and ![]() < 10, photon-photon interactions dominate pair production. The pair production timescale is then
< 10, photon-photon interactions dominate pair production. The pair production timescale is then

For high z pair equilibria with ![]()
![]() 1, we find P
1, we find P![]()
![]() (1)
(1) ![]() 10 and z
10 and z ![]() 1/
1/![]() p (Svensson 1984) giving
p (Svensson 1984) giving
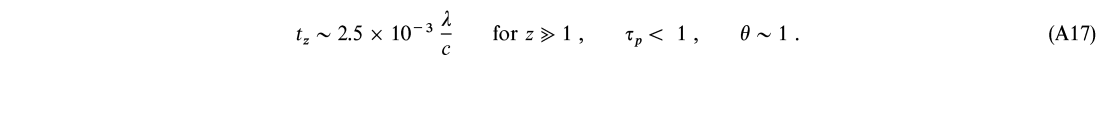
This expression is approximately correct for ![]()
![]() 10 and
10 and ![]() p < 0.1; however, for
p < 0.1; however, for ![]()
![]() 0.1, z
0.1, z ![]() 10/
10/![]() p and tz is 5 orders of magnitude shorter. Note that for shock-induced inhomogeneities {
p and tz is 5 orders of magnitude shorter. Note that for shock-induced inhomogeneities {![]()
![]() Max [l, 1.2l/(M2 - 1)]} the pair production timescale is always shorter than the diffusion timescale in high z pair equilibria, implying that new pair equilibria will be obtained prior to diffusion in shocked high z pair plasmas. If no pair equilibria exist for the postshock conditions, then pair runaway may result in rapid cooling and (local) collapse of the shocked region.
Max [l, 1.2l/(M2 - 1)]} the pair production timescale is always shorter than the diffusion timescale in high z pair equilibria, implying that new pair equilibria will be obtained prior to diffusion in shocked high z pair plasmas. If no pair equilibria exist for the postshock conditions, then pair runaway may result in rapid cooling and (local) collapse of the shocked region.
 Full image (34kb) | Discussion in text
Full image (34kb) | Discussion in text Full image (29kb) | Discussion in text
Full image (29kb) | Discussion in text Full image (31kb) | Discussion in text
Full image (31kb) | Discussion in text Full image (33kb) | Discussion in text
Full image (33kb) | Discussion in text