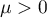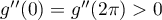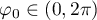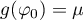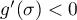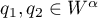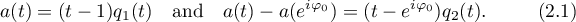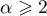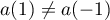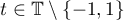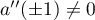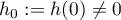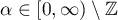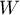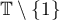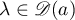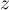Abstract
Analysis of the asymptotic behaviour of the spectral characteristics of Toeplitz matrices as the dimension of the matrix tends to infinity has a history of over 100 years. For instance, quite a number of versions of Szegő's theorem on the asymptotic behaviour of eigenvalues and of the so-called strong Szegő theorem on the asymptotic behaviour of the determinants of Toeplitz matrices are known. Starting in the 1950s, the asymptotics of the maximum and minimum eigenvalues were actively investigated. However, investigation of the individual asymptotics of all the eigenvalues and eigenvectors of Toeplitz matrices started only quite recently: the first papers on this subject were published in 2009–2010. A survey of this new field is presented here.
Bibliography: 55 titles.
Export citation and abstract BibTeX RIS
.
§ 1. Introduction
Let  be a Lebesgue integrable function on the unit circle
be a Lebesgue integrable function on the unit circle  and let
and let  denote the
denote the 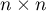 Toeplitz matrix formed by the Fourier coefficients of
Toeplitz matrix formed by the Fourier coefficients of  :
:
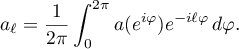
Then  is called the symbol of the sequence of matrices
is called the symbol of the sequence of matrices 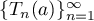 .
.
The behaviour of various spectral characteristics of Toeplitz matrices (eigenvalues and singular values, eigenvectors, determinants, condition numbers and so on) has been an object of active investigation for a century, starting with Szegő's paper [1] (see also the books [2]–[6] and the references there). First and foremost note the numerous versions of Szegő's theorem on the asymptotic distribution of the eigenvalues and the Avram-Parter-type theorems on the asymptotic behaviour of the singular values (see [7]–[12]). There is extensive literature on the asymptotic behaviour of the determinants of Toeplitz matrices (see the monographs [4]–[6] and the papers [13]–[19] and the references there). The asymptotics of the maximum and minimum eigenvalues has also been a focus of research (see [20]–[25]). The shape of the limit set of the eigenvalues and its stability have been investigated (see [26]–[28] and [15]). Note that the latter papers (by contrast with most of the papers cited before them) concern the more complicated case of essentially complex-valued symbols, which has not yet been analyzed in full generality.
This considerable interest in the asymptotic behaviour of the spectral characteristics of large Toeplitz matrices was motivated to a significant extent by many important applications: stochastic processes and time series analysis (see [2]); signal processing [29]; the numerical solution of differential and integral equations [30]; image processing [31]; quantum mechanics [32]. We point out the survey paper [19], which discusses the influence of the Ising model in statistical mechanics on the development of the asymptotic theory of the determinants of Toeplitz matrices.
Despite the considerable interest in this field that many authors have displayed, the individual asymptotic behaviour of all eigenvalues and eigenvectors was hardly investigated before 2008. In this connection we can only mention the well-known case of tridiagonal Toeplitz matrices (for instance, see [2] and [5]) and the case of linearly growing matrix elements considered recently in [33], where the eigenvalues and eigenvectors are calculated explicitly. On the other hand the importance of this problem is beyond doubt. For example, many papers are devoted to numerical methods for finding the spectrum of Toeplitz matrices of large size (see [34], [35] and the references there). For dimensions of order  –
–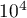 this problem can be solved effectively using modern hardware and the algorithms described in the above papers. However, in statistical physics and some other applied problems we encounter dimensions of order
this problem can be solved effectively using modern hardware and the algorithms described in the above papers. However, in statistical physics and some other applied problems we encounter dimensions of order  –
– , when no alternative to the asymptotic method exists. In addition, asymptotic formulae give more precise information on the local structure of the set of eigenvalues, the distances between them, accumulation points, their dependence on physical parameters and so on.
, when no alternative to the asymptotic method exists. In addition, asymptotic formulae give more precise information on the local structure of the set of eigenvalues, the distances between them, accumulation points, their dependence on physical parameters and so on.
In our opinion, the main difficulties arising in the implementation of the asymptotic method are as follows. First, the distances between successive eigenvalues are small (very small when we are in a neighbourhood of an accumulation point!) and our asymptotic formulae must be able to `separate' them. Furthermore, in addition to 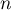 (the dimension of the matrix) being large, the problem involves another parameter, the index
(the dimension of the matrix) being large, the problem involves another parameter, the index  of the eigenvalue. So the asymptotic expansions with respect to
of the eigenvalue. So the asymptotic expansions with respect to 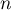 , as
, as 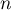 goes to infinity, which we construct must hold uniformly in
goes to infinity, which we construct must hold uniformly in  ,
,  . Finally, we stress that the determinants that appear in the eigenvalue problem in a natural way are related to one of the most complicated cases, when the symbol of the Toeplitz matrix has zeros on the unit circle.
. Finally, we stress that the determinants that appear in the eigenvalue problem in a natural way are related to one of the most complicated cases, when the symbol of the Toeplitz matrix has zeros on the unit circle.
In the papers [36]–[38], published in 2009–2010, asymptotic representations were constructed in the case of real-valued polynomial symbols (in other words, for Hermitian Toeplitz matrices with a finite number of nontrivial diagonals) that satisfy the so-called SL (simple loop) condition. This means that the real-valued symbol has precisely one minimum and one maximum on the unit circle (the precise definition is expressed by conditions (i) and (ii) in §2). The 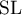 condition ensures a certain regularity in the arrangement of the eigenvalues; for instance, there are no multiple eigenvalues. In [36] and [37], based on Widom's well-known formula for the determinant of a Toeplitz matrix with polynomial symbol (see [21] and also [5], §2.4) we found an equation for the eigenvalues, with an exponentially small remainder term, and performed an asymptotic analysis of this equation. In [38] we also used explicit formulae from [39] to calculate eigenvectors of matrices with polynomial symbols, and on this basis we wrote down asymptotic formulae with a remainder term which is exponentially small in
condition ensures a certain regularity in the arrangement of the eigenvalues; for instance, there are no multiple eigenvalues. In [36] and [37], based on Widom's well-known formula for the determinant of a Toeplitz matrix with polynomial symbol (see [21] and also [5], §2.4) we found an equation for the eigenvalues, with an exponentially small remainder term, and performed an asymptotic analysis of this equation. In [38] we also used explicit formulae from [39] to calculate eigenvectors of matrices with polynomial symbols, and on this basis we wrote down asymptotic formulae with a remainder term which is exponentially small in 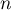 .
.
In the paper [40] published in 2012 the authors considered the case of infinitely smooth symbols also satisfying the SL condition. Using the asymptotic formula for determinants with Fisher-Hartwig singularities obtained in [18] the authors obtained the same nonlinear equation as in [36] and [37], but with remainder of the form 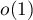 . Next they deduced two-sided estimates for the distance between arbitrary pairs of successive eigenvalues. Before the statement of this theorem the authors mentioned that the smoothness conditions imposed on the symbol can be relaxed.
. Next they deduced two-sided estimates for the distance between arbitrary pairs of successive eigenvalues. Before the statement of this theorem the authors mentioned that the smoothness conditions imposed on the symbol can be relaxed.
In [41] and [42] we considered an 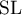 -symbol whose fourth derivative exists and has a certain regularity. We used a method distinct from [37] and [40]. It is based on a precise equation for the eigenvalues, which we derived, and on an asymptotic analysis of it. This equation is given in terms of the inverse matrix of a certain Toeplitz matrix of dimension
-symbol whose fourth derivative exists and has a certain regularity. We used a method distinct from [37] and [40]. It is based on a precise equation for the eigenvalues, which we derived, and on an asymptotic analysis of it. This equation is given in terms of the inverse matrix of a certain Toeplitz matrix of dimension  with positive symbol equal to the ratio of the difference
with positive symbol equal to the ratio of the difference 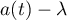 (where
(where 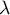 is the spectral parameter) and a second-order polynomial with the same zeros as this difference. We also point out [43], where the symbol is only assumed to have a first derivative and to satisfy certain additional conditions near the minimum and maximum points.
is the spectral parameter) and a second-order polynomial with the same zeros as this difference. We also point out [43], where the symbol is only assumed to have a first derivative and to satisfy certain additional conditions near the minimum and maximum points.
In [44] and [45] we abandoned the selfadjoint case and investigated Toeplitz matrices with complex-valued symbols. These symbols have a special feature: the corresponding function takes the unit circle to a curve without interior. In other words, the unit circle covers its image with multiplicity two by going in the `direct' and `reverse' direction along it. It is well known that then the limit set of the sequence of spectra coincides with this image curve, so for large 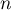 the eigenvalues lie close to this curve. Again, as in [36] and [37], in these papers we used known explicit formulae for determinants and inverse matrices because our symbols were polynomials. The resulting equation for the eigenvalues has the same structure as in the real-valued case; however, it must be considered in the complex domain, rather than on an interval of the real line, which brings in quite a number of significant technical difficulties.
the eigenvalues lie close to this curve. Again, as in [36] and [37], in these papers we used known explicit formulae for determinants and inverse matrices because our symbols were polynomials. The resulting equation for the eigenvalues has the same structure as in the real-valued case; however, it must be considered in the complex domain, rather than on an interval of the real line, which brings in quite a number of significant technical difficulties.
In 2009–2010 Kadanoff and his collaborators published the papers [46] and [47], where they considered a symbol, with power-like singularities, in the Fisher-Hartwig class. They presented formulae for the eigenvalues and eigenvectors. These formulae were deduced using heuristic arguments and justified by numerical experiment. In the same period of time, in 2008–2010 we considered a certain subclass of Fisher-Hartwig symbols. In this way, in [48]–[50] we refined and justified the formulae in [46] and [47] rigorously for symbols in the intersection of the classes under consideration.
We also point out the paper [51] close to this field. It looks at the asymptotic behaviour of the eigenvalues and eigenvectors of the Wiener-Hopf integral operator on a finite interval as the length of the interval tends to infinity, and it deals with the case of a symmetric rational (generally speaking, complex-valued) symbol. This problem is related to the same problem for Toeplitz matrices; however, its peculiarity consists in there being an infinite number of eigenvalues and eigenfunctions of the operator for an interval of any length.
Finally, we mention [52] and [53], where we go over from convergence in the sense of distributions (Szegő's theorem) to uniform convergence of the quantile function. For rather wide classes of symbols, approximation of eigenvalues can be expressed in terms of this function.
In §2 we state results for 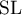 -symbols based on [43] and [42]. Toeplitz matrices with symmetric symbols are the subject of §3, where we present the main results of [44] and [45]. In §4 we look at Fisher-Hartwig symbols and discuss results from [48] and [50]. In §5 we investigate Wiener-Hopf operators on a finite interval (see [51]).
-symbols based on [43] and [42]. Toeplitz matrices with symmetric symbols are the subject of §3, where we present the main results of [44] and [45]. In §4 we look at Fisher-Hartwig symbols and discuss results from [48] and [50]. In §5 we investigate Wiener-Hopf operators on a finite interval (see [51]).
§ 2. SL-symbols
2.1. Eigenvalues
Assume that  and let
and let 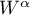 denote the weighted Wiener algebra of functions
denote the weighted Wiener algebra of functions  with representations
with representations
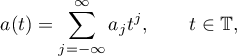
where the Fourier coefficients satisfy
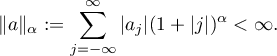
Along with  we look at the function
we look at the function ![$g\colon[0,2\pi]\to\mathbb R$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn22.gif) given by
given by  .
.
We define the class  as the set of symbols
as the set of symbols  in
in  such that
such that
- (i)
 is real-valued;
is real-valued; - (ii)the range of
 is an interval
is an interval ![$[0,\mu]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) where
where  ;
;  ,
,  , and there exists a point
, and there exists a point  such that
such that  ,
,  for
for  ,
,  for
for  and
and  .
.
Note that (i) is equivalent to all the matrices  ,
,  , being Hermitian (selfadjoint). If
, being Hermitian (selfadjoint). If  , then
, then ![$g\in C^{\lfloor\alpha\rfloor}[0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn40.gif) , where
, where  is the integer part of
is the integer part of  . Thus, if
. Thus, if  with
with 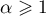 then, in particular,
then, in particular, 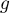 belongs to
belongs to ![$C^1[0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn45.gif) . Furthermore, in (ii) we assume that
. Furthermore, in (ii) we assume that 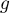 has second derivatives at the points
has second derivatives at the points  ,
,  and
and 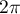 .
.
We will say that the symbol  belongs to the class
belongs to the class  with
with 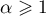 if
if  and the following additional condition is satisfied:
and the following additional condition is satisfied:
- (iii)there exist functions
 such that
such that 
By Lemma 3.1 in [41], if  , then the functions
, then the functions 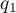 and
and  defined by (2.1) must belong to
defined by (2.1) must belong to 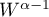 . In the definition of the class
. In the definition of the class  we impose the stronger condition (iii), that is, we assume that the symbol has additional smoothness at the points where it takes the minimum and maximum values. Using the same lemma we can show that each
we impose the stronger condition (iii), that is, we assume that the symbol has additional smoothness at the points where it takes the minimum and maximum values. Using the same lemma we can show that each 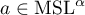 has the representations
has the representations
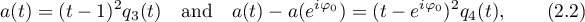
with 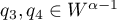 .
.
Let  ,
, 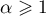 . For each
. For each ![$\lambda\in[0,\mu]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn57.gif) there exists precisely one point
there exists precisely one point  on the interval
on the interval ![$[0,\varphi_0]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn59.gif) such that
such that 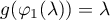 and precisely one point
and precisely one point ![$\varphi_2(\lambda)\in[\varphi_0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn61.gif) such that
such that  . In other words
. In other words  and
and 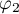 are the inverse functions of
are the inverse functions of 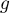 restricted to
restricted to ![$[0,\varphi_0]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn59.gif) and
and ![$[\varphi_0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn65.gif) , respectively. For each
, respectively. For each ![$\lambda\in[0,\mu]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn57.gif) ,
, 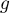 takes values not exceeding
takes values not exceeding 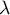 on the intervals
on the intervals ![$[0,\varphi_1(\lambda)]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn66.gif) and
and ![$[\varphi_2(\lambda),2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn67.gif) . Let
. Let 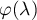 denote the arithmetic mean of the lengths of these two intervals:
denote the arithmetic mean of the lengths of these two intervals:
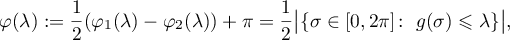
where  denotes Lebesgue measure on
denotes Lebesgue measure on ![$[0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn70.gif) . Note that
. Note that ![$\varphi\colon[0,\mu]\to[0,\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn71.gif) is continuous and bijective and let
is continuous and bijective and let ![$\psi\colon[0,\pi]\to[0,\mu]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn72.gif) denote its inverse function. Up to a linear change of the argument,
denote its inverse function. Up to a linear change of the argument,  and
and 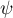 are the distribution function and the quantile function of the `random variable'
are the distribution function and the quantile function of the `random variable'  on the probability space
on the probability space ![$[0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn70.gif) with normalized Lebesgue measure. Set
with normalized Lebesgue measure. Set
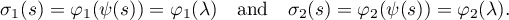
Note that the derivatives of  and
and 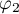 are unbounded in a neighbourhood of
are unbounded in a neighbourhood of  and
and 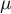 , whereas the functions
, whereas the functions  and
and  have continuous first derivatives on the whole of
have continuous first derivatives on the whole of ![$[0,\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn79.gif) . In addition, it is easy to see that
. In addition, it is easy to see that
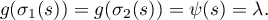
For each ![$s\in[0,\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn80.gif) the function
the function 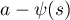 has two zeros,
has two zeros,  and
and 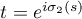 . We can define a positive function
. We can define a positive function  in terms of these:
in terms of these:
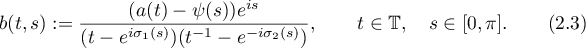
Let ![$\eta\colon[0,\pi]\to\mathbb R$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn85.gif) be defined by
be defined by
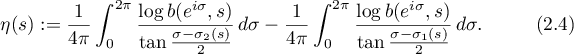
The singular integrals above are taken in the sense of the Cauchy principal value.
Let  denote the eigenvalues of the matrix
denote the eigenvalues of the matrix  . We can now state the main results in [43].
. We can now state the main results in [43].
Theorem 2.1. Let 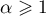 and
and 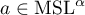 . Then for each
. Then for each 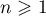 :
:
(i) all eigenvalues of  are distinct, so that
are distinct, so that 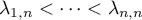 ;
;
(ii) the quantities  ,
, 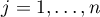 , satisfy the equations
, satisfy the equations
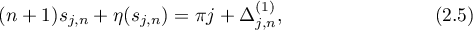
where  uniformly in
uniformly in  as
as  ;
;
(iii) for sufficiently large 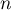 , equation (2.5) has a unique solution
, equation (2.5) has a unique solution ![$s_{j,n}\in[0,\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn93.gif) for each
for each 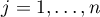 .
.
Set 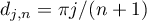 .
.
Theorem 2.2. If all the assumptions of Theorem 2.1 are fulfilled, then
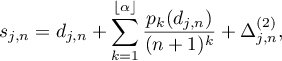
where 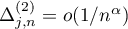 uniformly in
uniformly in  as
as  . The coefficients
. The coefficients  can be calculated explicitly; in particular,
can be calculated explicitly; in particular,
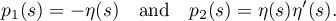
Theorem 2.3. If all the assumptions of Theorem 2.1 are fulfilled, then
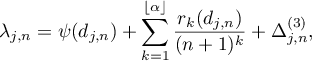
where 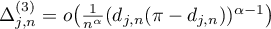 for
for 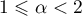 and
and  for
for 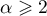 uniformly in
uniformly in  as
as  . The coefficients
. The coefficients 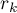 can be calculated explicitly; in particular,
can be calculated explicitly; in particular,
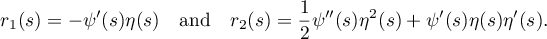
Remark 2.1. Let  and
and 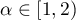 . Then the eigenvalues (for which
. Then the eigenvalues (for which 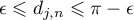 ) have the following asymptotics:
) have the following asymptotics:
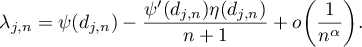
This means that the distance between two successive eigenvalues has the two-sided estimate
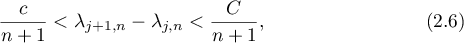
where the constants  and
and 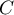 are independent of
are independent of  and
and 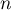 . On the other hand the difference
. On the other hand the difference  also has order
also has order  . In this connection an approximation
. In this connection an approximation

is often not sufficient for computations because the approximate formula (2.7) does not `separate' eigenvalues: a point 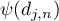 need not lie closest to the
need not lie closest to the  th eigenvalue, but perhaps to some other eigenvalue, for instance,
th eigenvalue, but perhaps to some other eigenvalue, for instance,  .
.
The assertion of Theorem 2.3 holds for all eigenvalues of 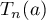 . However, bearing in mind the behaviour of
. However, bearing in mind the behaviour of  and
and 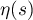 close to the endpoints of
close to the endpoints of ![$[0,\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn79.gif) (see Lemmas 4.2 and 4.6 in [43]) we can refine the asymptotic formulae for the extreme eigenvalues (cf. Corollary 2.5 in [41]).
(see Lemmas 4.2 and 4.6 in [43]) we can refine the asymptotic formulae for the extreme eigenvalues (cf. Corollary 2.5 in [41]).
(i) If 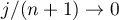 , then
, then
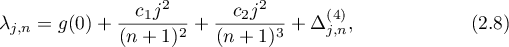
where  ,
,  and
and  as
as 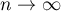 .
.
(ii) If 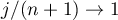 , then
, then
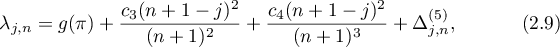
where 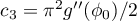 ,
,  and
and  as
as  .
.
Theorem 2.1 and, as a consequence, also Theorems 2.2 and 2.3 are based on the following result, which provides an exact equation for the eigenvalues. We introduce some further notation. As functions of the form (2.3) are positive, the operator  is invertible for each
is invertible for each 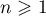 . Let
. Let ![$\Theta_k\colon\mathbb T\times[0,\pi]\to\mathbb C$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn125.gif) be defined by
be defined by
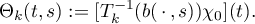
Here the Toeplitz matrix and the inverse matrix are realized as operators in the space
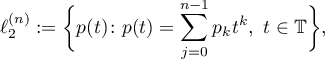
of polynomials of degree at most 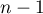 and the function
and the function 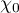 is identically equal to one:
is identically equal to one:  . In other words,
. In other words,  is a polynomial of degree at most
is a polynomial of degree at most 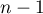 constructed from the entries in the zeroth column of
constructed from the entries in the zeroth column of 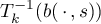 . For brevity we set
. For brevity we set  ,
, 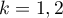 , so that we take
, so that we take  to be treated as
to be treated as 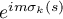 .
.
Theorem 2.5. Assume that 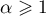 , and let
, and let 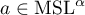 and
and 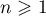 . Then
. Then  is an eigenvalue of the operator
is an eigenvalue of the operator  if and only if
if and only if
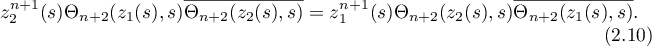
Note that (2.10) involves the action of the inverse operator  , so it is rather difficult to analyze directly. However, it can be analyzed asymptotically as
, so it is rather difficult to analyze directly. However, it can be analyzed asymptotically as  , when we replace
, when we replace  by the function
by the function }$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn137.gif) , where
, where  is the inverse of the (infinite) Toeplitz operator. As
is the inverse of the (infinite) Toeplitz operator. As 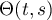 is easy to calculate in terms of the Wiener-Hopf factorization of
is easy to calculate in terms of the Wiener-Hopf factorization of  , we obtain equation (2.5) in this way.
, we obtain equation (2.5) in this way.
We conclude this subsection by observing that the formulae in Theorem 2.3 have proved to be numerically highly efficient and yield nice results for  (see [37], [41] and [43]).
(see [37], [41] and [43]).
2.2. Eigenvectors
The arguments resulting in the exact equation (2.10) enable us to deduce exact formulae for the components of the eigenvectors too. The results presented in this subsection were published in [42]. Keeping the notation used in §2.1, for brevity we write
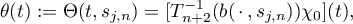
where we recall that 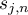 is related to the
is related to the  th eigenvalue of the matrix
th eigenvalue of the matrix  by
by 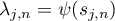 .
.
Theorem 2.6. Assume that 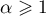 and let
and let 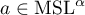 ,
,  and
and  . Then the vector
. Then the vector
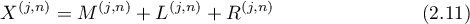
whose 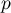 th component,
th component, 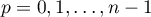 , is given by
, is given by
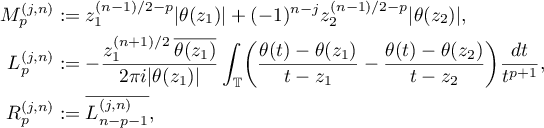
is an eigenvector corresponding to the eigenvalue 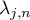 . In addition,
. In addition, 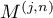 is conjugation symmetric:
is conjugation symmetric:  .
.
That is, the eigenvector 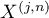 can be represented as a sum of three vectors: the leading term
can be represented as a sum of three vectors: the leading term 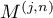 , the term
, the term  , concentrated in a neighbourhood of the left-hand endpoint (for small
, concentrated in a neighbourhood of the left-hand endpoint (for small 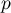 its components
its components  exceed significantly the other terms in absolute value) and the term
exceed significantly the other terms in absolute value) and the term  , concentrated in a neighbourhood of the right-hand endpoint. In other words,
, concentrated in a neighbourhood of the right-hand endpoint. In other words, 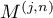 yields a rough approximation of the eigenvector, which is satisfactory for central components, while
yields a rough approximation of the eigenvector, which is satisfactory for central components, while  and
and  play the roles of left- and right-hand corrections, respectively.
play the roles of left- and right-hand corrections, respectively.
In the symmetric case, that is, when the symbol has the property  (which is equivalent to
(which is equivalent to  ), the statement of Theorem 2.6 can be simplified slightly.
), the statement of Theorem 2.6 can be simplified slightly.
Corollary 2.1. Assume that 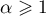 and let
and let 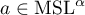 be a function with real Fourier coefficients (so that
be a function with real Fourier coefficients (so that  ). Then for each
). Then for each ![$s\in[0,2\pi]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn155.gif)
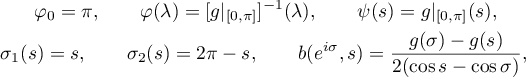
and the formulae in Theorem 2.6 can be written as follows:
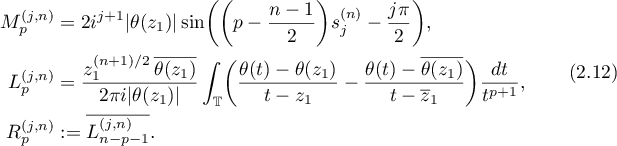
Theorem 2.6 reveals the structure of eigenvectors, but can only be implemented if we calculate the exact eigenvalues and can invert 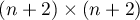 -matrices. To simplify the formulae in Theorem 2.6 we look at the `basic' approximation (see Theorem 2.1) of the equation for the eigenvalues,
-matrices. To simplify the formulae in Theorem 2.6 we look at the `basic' approximation (see Theorem 2.1) of the equation for the eigenvalues,

Note that if it has roots 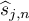 , then
, then
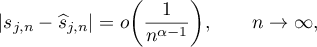
uniformly in  . Equation (2.13) is easy to solve numerically. In addition, asymptotic approximations to its solution are given by the formulae in Theorem 2.3. For
. Equation (2.13) is easy to solve numerically. In addition, asymptotic approximations to its solution are given by the formulae in Theorem 2.3. For ![${s\in[0,\pi]}$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn158.gif) we have the Wiener-Hopf factorization
we have the Wiener-Hopf factorization
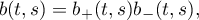
where
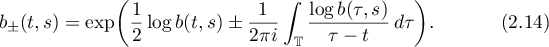
Theorem 2.7. Let 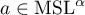 ,
, 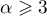 . Let
. Let 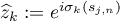 ,
, 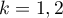 , and for
, and for 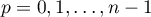 set
set
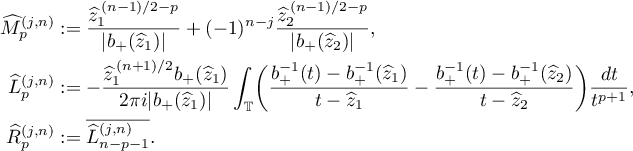
Let 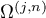 be the vector defined as the remainder term in the formula
be the vector defined as the remainder term in the formula
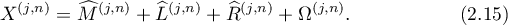
Then  as
as  and this relation holds uniformly in
and this relation holds uniformly in  and
and 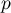 .
.
The integral involved in Theorem 2.7 can often be simplified. For example, if the symbol is rational, then the integral can be calculated using residue theory. In fact, in this case the function  given by (2.3) can be expressed by
given by (2.3) can be expressed by
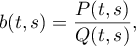
where  and
and 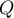 are polynomials in
are polynomials in 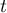 . It is easy to see that the symbol
. It is easy to see that the symbol  has a Wiener-Hopf factorization
has a Wiener-Hopf factorization  , where
, where
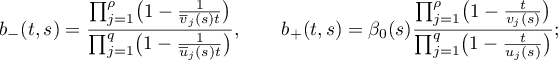
here 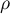 and
and 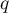 are positive integers,
are positive integers, 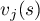 and
and 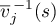 are formed from the
are formed from the 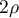 zeros of
zeros of 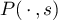 ,
,  and
and  are formed from the
are formed from the 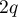 zeros of
zeros of 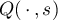 , and
, and  is a constant. Again, for brevity we write
is a constant. Again, for brevity we write  instead of
instead of  .
.
Theorem 2.8. Let  be a rational symbol in
be a rational symbol in  . Assume further that
. Assume further that  has only simple poles. Then an eigenvector can be expressed in the following form:
has only simple poles. Then an eigenvector can be expressed in the following form:
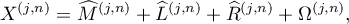
where, for 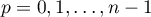 ,
,
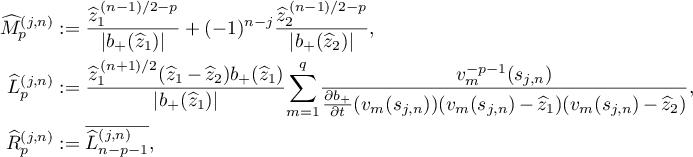
and for each 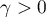 the limit relation
the limit relation  holds uniformly in
holds uniformly in  and
and 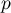 as
as  .
.
Note that if some of the poles of  are multiple, then we can also find an expression for
are multiple, then we can also find an expression for 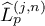 using residue theory.
using residue theory.
In [42] we presented numerical experiments validating the formulae in Theorems 2.7 and 2.8 and revealing the meaning of the different terms in these formulae.
§ 3. Symmetric symbols
In this section we consider complex-valued polynomial symbols of the form
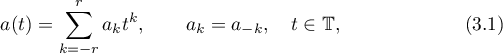
where 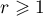 and
and  . Such a polynomial is an even function of the angle
. Such a polynomial is an even function of the angle  :
:
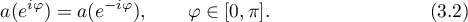
Let  denote the set of values of
denote the set of values of  , that is, the curve on the complex plane formed by the points
, that is, the curve on the complex plane formed by the points 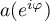 :
:
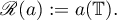
Then (for instance, see Theorems 5.28 and 5.32 in [3]) the limit as 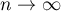 of the sequence of spectra of the
of the sequence of spectra of the  coincides with
coincides with  . Thus, for sufficiently large
. Thus, for sufficiently large 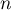 the eigenvalues of the matrix
the eigenvalues of the matrix  lie in a small neighbourhood of
lie in a small neighbourhood of  .
.
3.1. Eigenvalues of symmetric Toeplitz matrices
Consider a symbol of the form (3.1) and assume that
- (1)the curve
 does not intersect itself; in particular,
does not intersect itself; in particular,  ;
; - (2)
 for
for  ;
; - (3)
 .
.
As usual, set  . Then it follows from (3.2) that
. Then it follows from (3.2) that
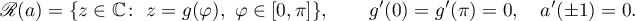
For sufficiently small  set
set  , where
, where
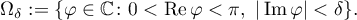
First we look at the equation 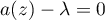 for
for 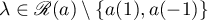 . It has
. It has  roots in the complex plane, which we arrange in the order of ascending absolute values. Taking the symmetry (3.2) into account we can represent this set of roots as follows:
roots in the complex plane, which we arrange in the order of ascending absolute values. Taking the symmetry (3.2) into account we can represent this set of roots as follows:
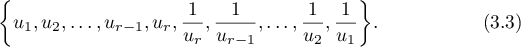
Thus, the root  ,
, 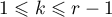 , which lies outside the unit circle
, which lies outside the unit circle  , corresponds to the root
, corresponds to the root 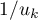 inside
inside  . By conditions 1 and 2 precisely two roots lie on
. By conditions 1 and 2 precisely two roots lie on  :
:
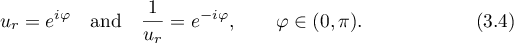
The other  roots are separated from
roots are separated from  uniformly in
uniformly in 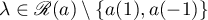 . Now let
. Now let  . It is easy to show that by 2 and 3, for sufficiently small
. It is easy to show that by 2 and 3, for sufficiently small 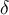 the equation
the equation 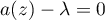 has a unique root in a neighbourhood of the upper half-circle, which has the form
has a unique root in a neighbourhood of the upper half-circle, which has the form  , where
, where  is an analytic function in
is an analytic function in 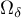 . In accordance with this definition
. In accordance with this definition  for
for  . We will regard the
. We will regard the 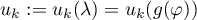 as functions of
as functions of  and denote them by
and denote them by  , where
, where  . Now there exists a positive
. Now there exists a positive  such that
such that
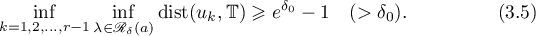
Consider the functions
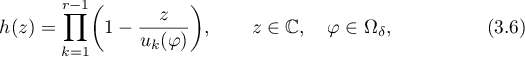
and

It follows from the definition (3.6) of 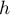 that
that  for
for  . Hence we can take a continuous branch of the function
. Hence we can take a continuous branch of the function 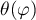 in the domain
in the domain 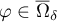 such that
such that  . We introduce the quantities
. We introduce the quantities
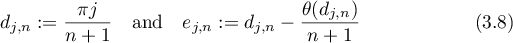
and the domains
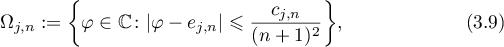
where  ,
, 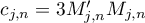 ,
,
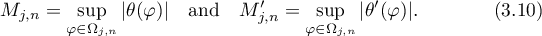
Note that 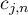 is bounded uniformly in
is bounded uniformly in  and
and 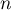 .
.
Now we state the main result of this subsection.
Theorem 3.1. Let  be a function of the form (3.1) such that conditions 1–3 are satisfied. Then the following results hold for sufficiently large
be a function of the form (3.1) such that conditions 1–3 are satisfied. Then the following results hold for sufficiently large 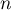 .
.
(i) All the eigenvalues of  are simple and
are simple and  for
for  .
.
(ii) The points  (
( ) such that
) such that 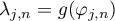 satisfy
satisfy
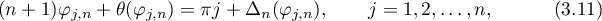
where  and
and 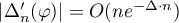 for some positive constant
for some positive constant 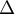 , uniformly in
, uniformly in 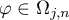 and
and  as
as 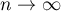 . Equation (3.11) has a unique solution in the domain
. Equation (3.11) has a unique solution in the domain  .
.
(iii) Each equation of the form

has a unique solution in  , and
, and  for some positive constant
for some positive constant 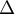 uniformly in
uniformly in  as
as 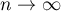 .
.
(iv) The function
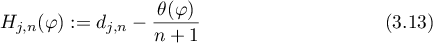
is a contraction mapping of  into itself; if
into itself; if
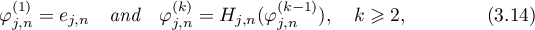
then
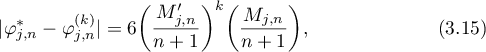
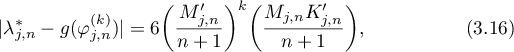
where 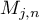 and
and 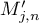 are defined by (3.10) and
are defined by (3.10) and 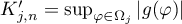 .
.
Setting  in (3.15) and (3.16) we obtain the following asymptotic expansions for
in (3.15) and (3.16) we obtain the following asymptotic expansions for  and
and 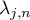 .
.
Theorem 3.2. Let 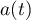 be a symbol of the form (3.1) such that conditions 1–3 are satisfied. Then
be a symbol of the form (3.1) such that conditions 1–3 are satisfied. Then
(i)

where  as
as 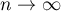 uniformly in
uniformly in  ;
;
(ii)
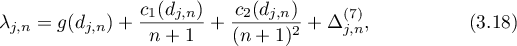
where  uniformly in
uniformly in  as
as 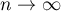 ,
,
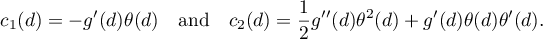
We have given the asymptotic formulae (3.17) and (3.18) as examples. Using estimates (3.15) and (3.16) for  we can find arbitrarily many terms of the expansions for
we can find arbitrarily many terms of the expansions for 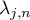 and
and  .
.
As a consequence of Theorem 3.2, we obtain a result on the extreme eigenvalues.
Theorem 3.3. Let  be a symbol of the form (3.1) and assume that conditions 1–3 are satisfied. Then the following results hold:
be a symbol of the form (3.1) and assume that conditions 1–3 are satisfied. Then the following results hold:
(i) if 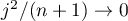 , then
, then
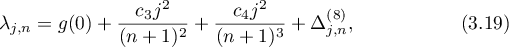
where 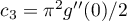 ,
,  and
and 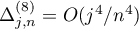 as
as 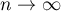 ;
;
(ii) if 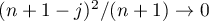 , then
, then
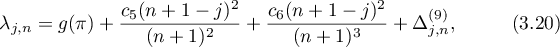
where 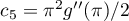 ,
,  and
and 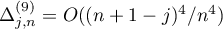 as
as 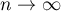 .
.
Remark 3.1. The leading term of the asymptotic expansion (3.18) corresponds to a point 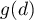 on the curve
on the curve  . This approximation to the eigenvalue
. This approximation to the eigenvalue  has accuracy
has accuracy  and cannot be considered satisfactory: the distance between successive eigenvalues also has order
and cannot be considered satisfactory: the distance between successive eigenvalues also has order  . Thus, this approximation `does not separate' eigenvalues (see Remark 2.1). On the other hand the approximation
. Thus, this approximation `does not separate' eigenvalues (see Remark 2.1). On the other hand the approximation  has accuracy
has accuracy  (see (3.16) for
(see (3.16) for  ) and can be treated as an individual approximation to the eigenvalue
) and can be treated as an individual approximation to the eigenvalue 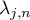 . In particular, the expression
. In particular, the expression 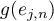 can be used to analyze the position of
can be used to analyze the position of 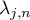 relative to the curve
relative to the curve  . In fact,
. In fact,
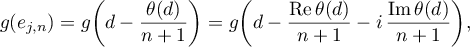
where
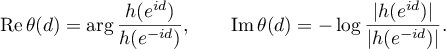
Setting
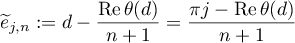
we obtain
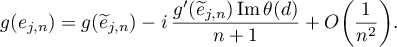
That is, to within  the eigenvalue
the eigenvalue 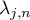 lies on the normal to
lies on the normal to  at the point
at the point  . The distance from
. The distance from 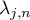 along the normal has order
along the normal has order  , provided that
, provided that 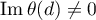 . Note that depending on the sign of
. Note that depending on the sign of  the point
the point 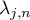 lies to the right or the left of
lies to the right or the left of  in the plane.
in the plane.
The numerical gain from the formulae in Theorems 3.1–3.3 was fairly comprehensively analyzed in [44].
3.2. Eigenvectors of symmetric Toeplitz matrices
Theorem 3.4. Let 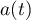 be a symbol of the form (3.1) and assume that conditions 1–3 are satisfied. Then eigenvectors
be a symbol of the form (3.1) and assume that conditions 1–3 are satisfied. Then eigenvectors  associated with the eigenvalues
associated with the eigenvalues 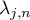 can be chosen so that the following asymptotic expressions (putting
can be chosen so that the following asymptotic expressions (putting  for brevity) hold:
for brevity) hold:
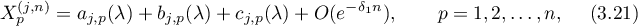
where the remainder estimate is uniform with respect to 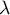 , and
, and 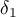 is independent of
is independent of 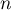 ,
,  and
and 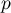 . Furthermore,
. Furthermore,
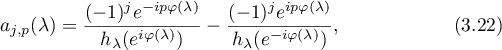

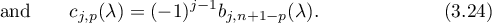
Remark 3.2. Theorem 3.4 was established as Theorem 2.3 in [45], albeit under the additional assumption that the function 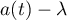 has only simple zeros for each
has only simple zeros for each  in
in  . Now, after [42], we can drop this technical condition.
. Now, after [42], we can drop this technical condition.
Remark 3.3. Let us analyze the formulae in Theorem 3.4. As the root 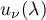 lies outside the unit circle, the term
lies outside the unit circle, the term 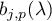 is small for components with large index
is small for components with large index 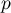 , and the term
, and the term  is small when
is small when  is large. In addition, it is easy to see that, as
is large. In addition, it is easy to see that, as 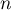 grows, the contribution of these terms can be significant for a few of the first and last components, respectively. Note however, that the number of these components does not depend significantly on
grows, the contribution of these terms can be significant for a few of the first and last components, respectively. Note however, that the number of these components does not depend significantly on 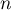 . Components in the middle part of the vector
. Components in the middle part of the vector 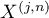 are mostly well approximated by
are mostly well approximated by 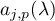 from (3.22). A numerical illustration of this observation can be found in [45].
from (3.22). A numerical illustration of this observation can be found in [45].
Remark 3.4. In (3.22)–(3.24) we can replace the exact eigenvalues by their approximations (asymptotic expressions), for instance, the ones given by (3.18).
Remark 3.5. Formulae (3.22)–(3.24) become much simpler for eigenvectors corresponding to the extreme eigenvalues (see Theorem 2.4 in [45]).
§ 4. Eigenvalues and eigenvectors of Hessenberg Toeplitz matrices and a problem of Dai, Geary and Kadanoff's
4.1. Eigenvalues
Dai, Geary and Kadanoff [46] and Kadanoff [47] considered symbols of the form
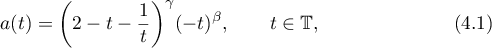
where  . They conjectured that for large
. They conjectured that for large 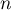 the corresponding eigenvalues
the corresponding eigenvalues  satisfy
satisfy
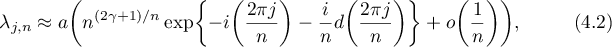
where  is some function (unknown to them). This conjecture was supported by numerical experiment and a certain heuristic argument.
is some function (unknown to them). This conjecture was supported by numerical experiment and a certain heuristic argument.
Now we state the main results of [48] and compare these with (4.2).
As usual, let  be the Hardy space of bounded analytic functions in the unit disc
be the Hardy space of bounded analytic functions in the unit disc  . For a fixed function
. For a fixed function 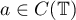 let
let 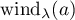 denote the number of windings of the image of
denote the number of windings of the image of  , that is, the curve
, that is, the curve  , about the point
, about the point 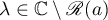 , and let
, and let  be the set of points
be the set of points 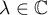 for which
for which  . In this subsection we treat matrices
. In this subsection we treat matrices  with symbols of the form
with symbols of the form 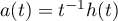 , where
, where
- (1.1)
 and
and  ;
; - (2.1)
 , where
, where  and
and  ;
; - (3.1)
 extends analytically to an open neighbourhood
extends analytically to an open neighbourhood  of the set
of the set  which does not contain
which does not contain  ;
; - (4.1)
 is a Jordan curve in
is a Jordan curve in  and
and  for each
for each  .
.
Note that if we set 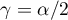 and
and 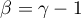 in (4.1), then the symbol satisfies conditions
in (4.1), then the symbol satisfies conditions  .
.
Let 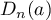 denote the determinant of
denote the determinant of  . Then the eigenvalues of the matrix
. Then the eigenvalues of the matrix  are the roots of the equation
are the roots of the equation  . By our assumptions
. By our assumptions  is a Hessenberg matrix, that is, it can be obtained from a lower triangular matrix by adding one nontrivial diagonal. In combination with the Baxter-Schmidt formula (see [5], §2.3, for instance) this enables us to represent
is a Hessenberg matrix, that is, it can be obtained from a lower triangular matrix by adding one nontrivial diagonal. In combination with the Baxter-Schmidt formula (see [5], §2.3, for instance) this enables us to represent  as a Fourier integral. Its value depends significantly on the pole at
as a Fourier integral. Its value depends significantly on the pole at 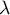 and the singularity of the term
and the singularity of the term 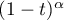 at
at  . Let
. Let  be a small neighbourhood of zero in
be a small neighbourhood of zero in 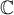 . We can show that for each
. We can show that for each  there exists a unique point
there exists a unique point  such that
such that  . An asymptotic analysis of the Fourier integral just mentioned yields an asymptotic representation for
. An asymptotic analysis of the Fourier integral just mentioned yields an asymptotic representation for  .
.
In all the statements in this subsection we take
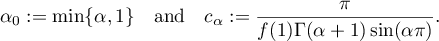
Theorem 4.1. Let 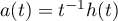 be a symbol satisfying conditions
be a symbol satisfying conditions  of zero in
of zero in 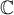 and points
and points 
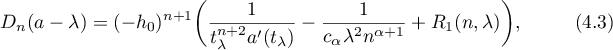
where 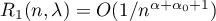 as
as  uniformly in
uniformly in  .
.
We now turn to the main results in this subsection. Set  . For the values of
. For the values of 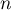 under consideration there exist positive integers
under consideration there exist positive integers  and
and  such that
such that  , but
, but  . Recall that
. Recall that  .
.
Theorem 4.2. Let 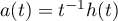 be a symbol with properties
be a symbol with properties  of zero and for each
of zero and for each  between
between  and
and  ,
,
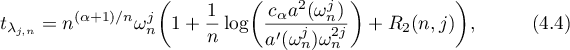
where 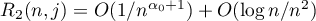 as
as  uniformly in
uniformly in  .
.
Thus formula (4.4) proves the conjecture (4.2) in the special case when 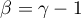 . In addition, we have found the function
. In addition, we have found the function

and have refined the order of the error term.
Taking the value of  at the point (4.4) we obtain the following asymptotic expression for
at the point (4.4) we obtain the following asymptotic expression for 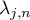 .
.
Theorem 4.3. Let 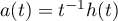 be a symbol with properties
be a symbol with properties  of zero in
of zero in 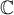 and
and  between
between  and
and  ,
,
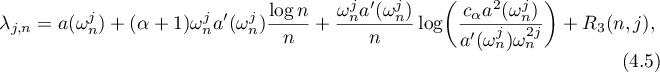
where  as
as  uniformly for
uniformly for  between
between  and
and  .
.
Remark 4.1. Here we have written out only a few of the first terms of the asymptotic expansion. Note however that using our method an arbitrary number of terms in this expansion can be obtained.
A numerical illustration of Theorem 4.3 can be found in [48].
4.2. Eigenvectors
To present the formulae for eigenvectors we define a function 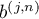 on
on  by
by
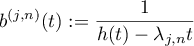
and let 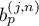 denote its
denote its 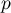 th Fourier coefficient.
th Fourier coefficient.

is an eigenvector of  corresponding to the eigenvalue
corresponding to the eigenvalue 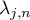 .
.
The next result describes the asymptotic behaviour of 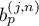 for large
for large 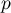 and
and 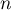 .
.
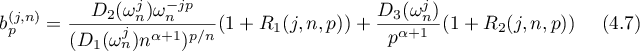
holds, where
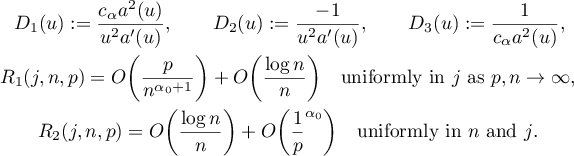
We stress that we only consider points 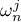 in
in 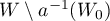 . In this domain the functions
. In this domain the functions  and
and  are bounded and separated away from zero. Hence the
are bounded and separated away from zero. Hence the  ,
, 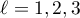 , are also bounded and separated away from zero there. Note also that since
, are also bounded and separated away from zero there. Note also that since 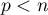 ,
,  tends to zero as
tends to zero as  .
.
Remark 4.2. We compare the above results on the asymptotics of eigenvectors and the results in [46] and [47] concerning symbols of the form (4.1).
We have already mentioned that for 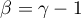 the function (4.1) becomes `our' symbol of the form
the function (4.1) becomes `our' symbol of the form 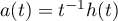 , with
, with 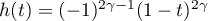 . In [46] the authors conjectured that an eigenvector has the form
. In [46] the authors conjectured that an eigenvector has the form

as  . Theorem 4.2 refines this conjecture and proves it while giving a rigorous estimate for the error term. Note that
. Theorem 4.2 refines this conjecture and proves it while giving a rigorous estimate for the error term. Note that

This shows that (4.8) corresponds to the first term on the right-hand side of (4.7) in the case when the ratio  is close to zero. Otherwise the representation (4.8) can give a large error: the corresponding numerical examples were presented in [50].
is close to zero. Otherwise the representation (4.8) can give a large error: the corresponding numerical examples were presented in [50].
Remark 4.3. Our asymptotic expansion (4.7) holds for 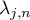 outside a small neighbourhood
outside a small neighbourhood  of zero and for large
of zero and for large 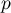 . For small
. For small 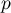 , for instance,
, for instance, 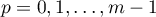 ,
, 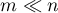 , the values of
, the values of  can be calculated using the relation between the Fourier coefficients of
can be calculated using the relation between the Fourier coefficients of  and
and 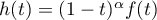 . Here we obtain a triangular system of equations, which can be solved by
. Here we obtain a triangular system of equations, which can be solved by 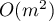 operations, and taking
operations, and taking ![$m=[\sqrt{n}\,]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn331.gif) we need
we need  operations. We can calculate the remaining components using asymptotic formulae (4.7), which also have order of complexity
operations. We can calculate the remaining components using asymptotic formulae (4.7), which also have order of complexity  from a numerical standpoint.
from a numerical standpoint.
§ 5. Spectral theory of Wiener-Hopf operators with symmetric complex kernels and rational symbols on a large interval
A truncated Wiener-Hopf operator has the form

We assume here that 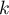 is a function in
is a function in 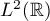 , so the integral operator in (5.1) is a compact Hilbert-Schmidt operator on
, so the integral operator in (5.1) is a compact Hilbert-Schmidt operator on  for every
for every  . Let
. Let  denote the spectrum of
denote the spectrum of 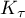 . As
. As 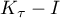 is compact, all points in
is compact, all points in  are eigenvalues.
are eigenvalues.
Here we make the two basic assumptions. First, 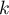 is a symmetric complex function, that is
is a symmetric complex function, that is  for
for  . Second,
. Second,
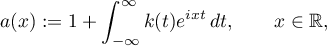
the so-called symbol of the operator, is rational. These two assumptions are equivalent to a representation of the form
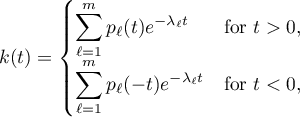
where the 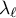 are complex numbers with
are complex numbers with 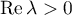 and the
and the  are polynomials with complex coefficients. Since
are polynomials with complex coefficients. Since  for all
for all  if and only if
if and only if 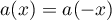 for all
for all 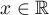 , the symbol is an even rational function, and we can write
, the symbol is an even rational function, and we can write
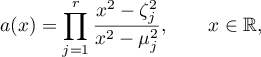
where 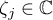 ,
,  ,
, 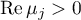 and
and  for all
for all  and
and 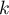 . To stress the dependence of
. To stress the dependence of 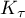 on the symbol
on the symbol  , following [54] we denote
, following [54] we denote 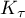 by
by 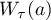 .
.
Putting 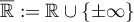 we extend the symbol by setting
we extend the symbol by setting 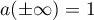 . As before, let
. As before, let 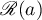 be the essential image of
be the essential image of  , that is,
, that is,  . By our assumptions
. By our assumptions 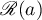 is an analytic curve in the plane such that as
is an analytic curve in the plane such that as 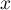 varies from
varies from 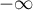 to
to  the value
the value 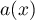 of the symbol ranges from
of the symbol ranges from  to
to  on this curve, and when
on this curve, and when 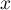 varies further from
varies further from  to
to 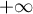 , the value of the symbol traverses
, the value of the symbol traverses 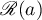 from
from  to
to  in the reverse direction.
in the reverse direction.
It was shown in [54] that in our case the limit of 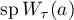 coincides with
coincides with 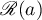 . So we will look for eigenvalues in a neighbourhood of
. So we will look for eigenvalues in a neighbourhood of 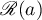 . We assume in addition that
. We assume in addition that 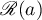 is a curve without self-intersections.
is a curve without self-intersections.
With each positive number 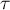 we associate the half-strip
we associate the half-strip
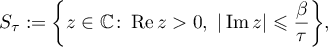
where 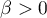 is fixed and sufficiently large. Consider a finite covering of the half axis by open intervals
is fixed and sufficiently large. Consider a finite covering of the half axis by open intervals  . For each interval
. For each interval  we consider either the closed subintervals of
we consider either the closed subintervals of  of the form
of the form

or the closed intervals of the form
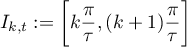
lying in  (depending on the position of
(depending on the position of 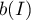 1 in
1 in 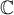 ); see (3.6) and (3.7) in [51]. In this way we obtain
); see (3.6) and (3.7) in [51]. In this way we obtain  families of rectangles
families of rectangles
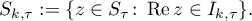
The proofs of the main results in this section are based on an explicit formula (see [55]) for the Fredholm determinants
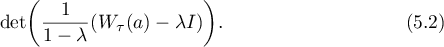
Note that for each  the equation
the equation  has precisely
has precisely  complex roots
complex roots
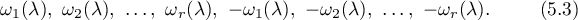
We can number them so that  and
and 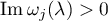 for
for  .
.
Fix an open neighbourhood 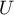 of
of 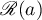 . Then
. Then  if
if 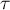 is sufficiently large. Set
is sufficiently large. Set 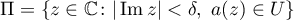 . For
. For  consider the two functions
consider the two functions
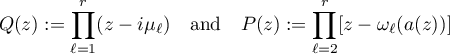
and set
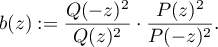
The main result of this section is the following.
Theorem 5.1. Let 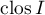 be the closure of
be the closure of  in
in ![$[0,\infty]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn380.gif) and assume that for
and assume that for 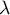 in
in  all the roots
all the roots 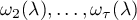 are distinct. Then there exists
are distinct. Then there exists  such that the following results hold for all
such that the following results hold for all  .
.
(i) If  is an eigenvalue of
is an eigenvalue of 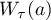 such that
such that  for some
for some 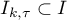 , then
, then  .
.
(ii) For each 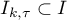 the set
the set  contains a unique eigenvalue
contains a unique eigenvalue  of
of 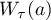 , which has algebraic multiplicity 1.
, which has algebraic multiplicity 1.
(iii) The function

is a contraction mapping of 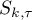 into itself; for
into itself; for
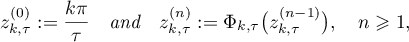
the relation
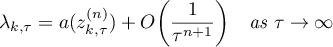
holds uniformly in 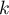 : there exist constants
: there exist constants  independent of
independent of 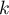 and
and 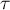 such that
such that
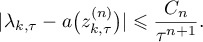
(iv) The following asymptotic expression holds for the points 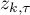 2:
2:
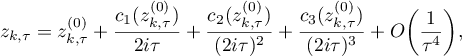
where
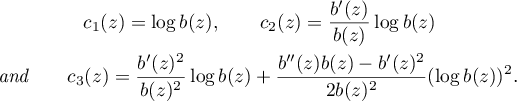
(v) The following asymptotic expression holds for  :
:
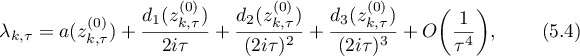
where
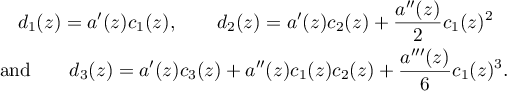
Remark 5.1. We have presented formula (5.4) as an example of an explicit calculation of a few of the first terms in the asymptotic expansion. Using our method we can find an arbitrary number of these terms.
In conclusion we present a result concerning eigenfunctions.
Theorem 5.2. Assume that all the numbers 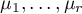 are distinct. Let
are distinct. Let 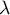 be an eigenvalue of the operator
be an eigenvalue of the operator 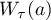 such that all the roots
such that all the roots 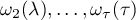 are distinct. Then each eigenfunction
are distinct. Then each eigenfunction  of
of 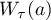 corresponding to
corresponding to 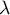 has the following form:
has the following form:
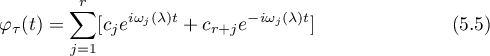
and satisfies the relation 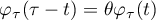 with
with 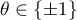 for all
for all 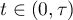 ; it can also be expressed by
; it can also be expressed by
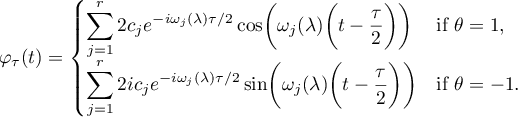
Note that the coefficients  in the last formulae can be calculated using a system of
in the last formulae can be calculated using a system of 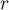 linear equations with known coefficients.
linear equations with known coefficients.
The numerical aspects of the above formulae have been discussed in [51].
Footnotes
- 1
See the definition of the function
 below.
below. - 2
This appears as
 in (i).
in (i).




![$[0,\mu]$](https://content.cld.iop.org/journals/1064-5616/208/11/1578/revision1/MSB_208_11_1578ieqn27.gif)