Abstract
A method for the representation of Delaunay's solutions and some other particular solutions to the problem of the motion of a heavy rigid body in the Kovalevskaya case in terms of the Weierstrass  - and
- and  -functions is put forward. The Hess case in the problem of the motion of a heavy rigid body is shown to be nonintegrable by quadratures.
-functions is put forward. The Hess case in the problem of the motion of a heavy rigid body is shown to be nonintegrable by quadratures.
Bibliography: 24 titles.
Export citation and abstract BibTeX RIS
§ 1. Introduction
The classical Kovalevskaya case of the problem of the motion of a heavy rigid body is one of those results blessed with good fortune. Kovalevskaya's paper [1] containing this result was awarded a prize by the French Academy. Kovalevskaya's prediction, to the effect that the functions integrating the problem would prove extremely useful in the future, came true (see [2]). The method used to search for exact solutions turned out to be quite effective in the study of Hamiltonian systems and, finally, very recently, a solution to a multivariate generalization of the Kovalevskaya case has been obtained within the framework of the L-A pair method with a spectral integration parameter of Hamiltonian systems (see [3]–[6]), which makes Kovalevskaya's remarkable result relevant even in the context of very advanced modern ideas.
The classical Kovalevskaya case is known to be integrable by quadratures, which is recognized as a yardstick for the complete integrability of the problem without reserve.
Nevertheless, we would like to return to just this classical problem. Indeed, though the calculations leading to the linearization of the Kovalevskaya problem on the Jacobian of the curve  of degree 5 are remarkable, the complicated dependence of the original coordinates on those obtained after all the changes, and even the final integrals, which define the solutions implicitly as a system of two equations with three unknowns (see [1])
of degree 5 are remarkable, the complicated dependence of the original coordinates on those obtained after all the changes, and even the final integrals, which define the solutions implicitly as a system of two equations with three unknowns (see [1])
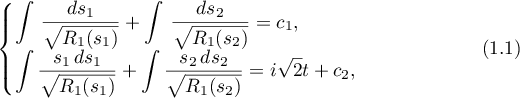
mean that we cannot use the exact solution thus obtained efficiently (see [2]).
This paper is concerned with some applications of the method for analysing Hamiltonian systems proposed in [7] and [8]. Namely, we write down some periodic solutions to the Kovalevskaya case explicitly (in the coordinates in which the problem was set), using the Weierstrass  - and
- and  -functions. Furthermore, we show that the Hess case cannot be integrated by quadratures (see [9]–[13]). In essence, our approach is a development of Kovalevskaya's idea of employing the analytic properties of the solutions of the differential equations under consideration. In finding her solution to the problem of the motion of a heavy rigid body, Kovalevskaya also obtained constraints on the parameters of the body such that, for any initial data, all solutions are single-valued (that is, they have the most simple form). It is worth noting that the same condition for solutions to be single valued holds in the Euler and Lagrange cases. These were obtained before Kovalevskaya's results, by simplifying the equations of the problem with appropriate parameters.
-functions. Furthermore, we show that the Hess case cannot be integrated by quadratures (see [9]–[13]). In essence, our approach is a development of Kovalevskaya's idea of employing the analytic properties of the solutions of the differential equations under consideration. In finding her solution to the problem of the motion of a heavy rigid body, Kovalevskaya also obtained constraints on the parameters of the body such that, for any initial data, all solutions are single-valued (that is, they have the most simple form). It is worth noting that the same condition for solutions to be single valued holds in the Euler and Lagrange cases. These were obtained before Kovalevskaya's results, by simplifying the equations of the problem with appropriate parameters.
It is natural to believe that in investigating nonlinear differential equations more general results can be obtained by looking at the whole of the asymptotic behaviour of solutions near singular points, rather than by just using the condition for solutions to be single valued. In this sense our paper continues the investigations in [7]–[9]. Note that we do not regard the method for finding exact solutions in this paper as independent of other methods of integration. On the contrary, the more information is available using other methods for analysing nonlinear differential equations (see [14]–[20]) the more easily we can construct exact solutions from a knowledge of their analytic properties.
This paper is written in a rather informal style. This is to show how, starting from asymptotic formulae and using natural, but not necessarily rigorously justified assumptions, one can obtain exact solutions of a prescribed form or prove that they do not exist. Of course, some calculation is unavoidable, and we present the intermediate results.
The author is grateful to A. V. Borisov and A. E. Mironov for helpful discussions.
§ 2. Statement of the main results
The classical problem of the motion of a heavy rigid body defined by the Euler- Poisson equations (see, for example, [21]) reads as follows:
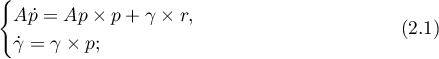
here  ,
,  ,
, 
 ,
,  .
.
System (2.1) has the first integrals of energy and angular momentum,  and
and  , and the trivial integral
, and the trivial integral  .
.
The Kovalevskaya case is defined by the following conditions imposed on the rigid body:
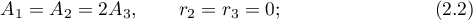
we also set  so that our equations are exactly the same as Kovalevskaya's.
so that our equations are exactly the same as Kovalevskaya's.
With these restrictions system (2.1) takes the form
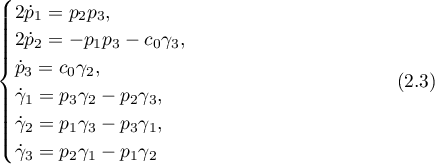
and admits the additional fourth integral
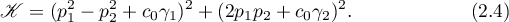
Owing to the presence of the fourth integral, the Kovalevskaya case is completely integrable, which means that the solution can be obtained by quadratures.
Among the solutions of system (1.1) is Delaunay's case (see [21]), which appears under the condition  . When we consider real solutions, this is equivalent to the two conditions
. When we consider real solutions, this is equivalent to the two conditions
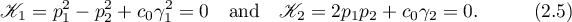
In this case, the solution can be expressed in terms of the variable  , for example:
, for example:
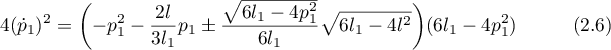
(see [21]).
Developing Kovalevskaya's approach based on the study of the analytic properties of solutions to Hamiltonian systems, this author found all possible asymptotic formulae for the solutions to the Kovalevskaya problem in neighbourhoods of singular points in [7] and [8]. The explicit form of these asymptotic formulae lets us put forward a representation of Delaunay's solution in terms of the Weierstrass  - and
- and  -functions.
-functions.
Theorem 1. Let  ,
,  be the Weierstrass functions and let
be the Weierstrass functions and let  .
.
Let  ,
,  ,
,  ,
,  denote the functions
denote the functions  ,
,  ,
,  and
and  , and let
, and let  ,
,  ,
,  ,
,  denote their derivatives taken with the opposite signs,
denote their derivatives taken with the opposite signs,  ,
,  ,
,  ,
,  .
.
Then any solution to the Delaunay case has the representation
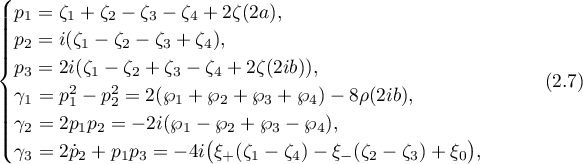
where
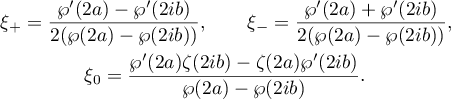
Representation (2.7) is real three-parameter: the free parameters are the sizes of the period-parallelogram of the functions  and
and  ; the real parameters
; the real parameters  ,
,  are connected via
are connected via  .
.
In addition to the above Delaunay case, [21] gives a solution to the Bobylev- Steklov case, whose conditions  and
and  are satisfied in the Kovalevskaya case, but in addition has the special initial conditions
are satisfied in the Kovalevskaya case, but in addition has the special initial conditions

The solution to this problem can be expressed, for example, in terms of the function  :
:
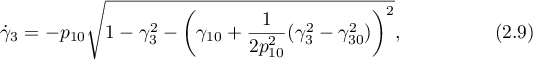
that is, it can be written down using the Jacobi elliptic functions (see [22]).
It turns out that in addition to the above particular periodic solutions, in the Kovalevskaya case there exist other particular periodic solutions, which cannot be picked up as obvious degenerations of the general solution. They become evident specifically through the analysis of the asymptotic behaviour of singular points of solutions. More precisely, there are asymptotic formulae for periodic solutions that are distinct from those for solutions in the above cases; however, this means that the solutions themselves must also exist.
Such solutions form a four-parameter family depending on the values of the first integrals: the energy and angular momentum integrals, the trivial integral, and the Kovalevskaya integral. In this paper, we present a two-parameter family of such solutions.
Theorem 2. Let  ,
,  be the Weierstrass functions, and let
be the Weierstrass functions, and let  .
.
Let  ,
,  ,
,  ,
,  denote the functions
denote the functions  ,
,  ,
,  and
and  and let
and let  ,
,  ,
,  ,
,  denote their derivatives taken with the opposite signs,
denote their derivatives taken with the opposite signs,  ,
,  ,
,  ,
,  .
.
Then there exists a periodic solution which is rationally expressible in terms of the Weierstrass  - and
- and  -functions:
-functions:
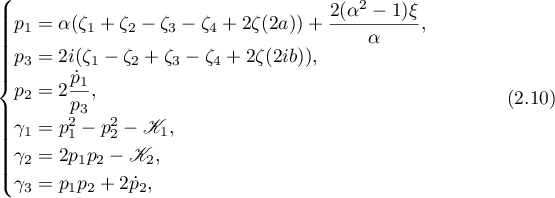
where
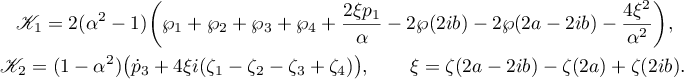
Representation (2.10) is real two-parameter: the free parameters are  and
and  , which define the
, which define the  -function by
-function by
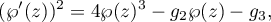
and define the period-parallelogram. The parameters  ,
,  and
and  are determined from the conditions
are determined from the conditions
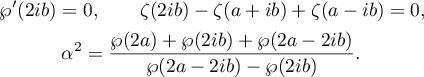
By investigating the analytic properties of the class of solutions to the problem of the motion of a heavy rigid body in the Hess case (see [9]) we can find out whether they can be represented by quadratures.
Theorem 3. The solution to the Euler-Poisson equations (2.1) in the Hess case cannot be expressed by quadratures.
Remark 1. The proof that the Hess problem is not integrable (see Theorem 12) makes essential use of the properties of the parametric Poincaré map (see Theorem 4).
Integrability in the sense of Theorem 4 becomes the basic tool for investigating the Hess problem in the absence of classical integrability.
§ 3. Preliminary results pertaining to the Kovalevskaya and Hess problems
We first give a brief description of Kovalevskaya's method of reducing equations (2.3) to the completely integrable system (1.1). Kovalevskaya set
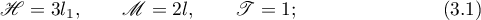
and the additional fourth integral was written as
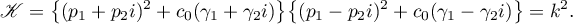
Kovalevskaya then introduced the notation
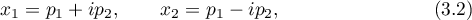
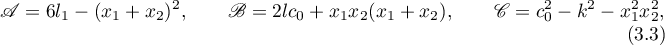

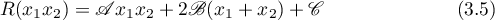
and considered the new variables

for which relations (1.1) hold and the fifth-degree polynomial reads as
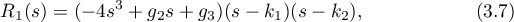
where
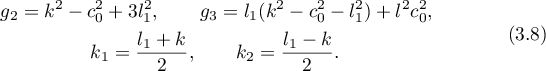
All the required intermediate steps were carried out by Kovalevskaya, but she never explained how she came up with these highly nontrivial integrating changes.
A modern view of the classical Kovalevskaya solution can be found in Perelomov [23].
In addition to Delaunay's case above, [21] gives a solution to the Bobylev-Steklov case, whose conditions  and
and  are satisfied in the Kovalevskaya case, but where there are special initial conditions
are satisfied in the Kovalevskaya case, but where there are special initial conditions

A solution to this problem is expressed, for example, in terms of the function  :
:
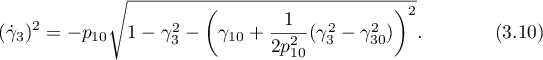
We also mention the case when only the condition  is imposed on the parameters, and the initial conditions are
is imposed on the parameters, and the initial conditions are

It has the solution
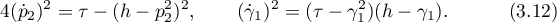
In the Kovalevskaya problem the condition  is satisfied, and so the above solution exists. Note that there is also a similar solution corresponding to the case
is satisfied, and so the above solution exists. Note that there is also a similar solution corresponding to the case  .
.
It is worth noting that all the aforementioned particular cases present periodic solutions.
The results we need for the Hess case will be formulated as the following four theorems.
Theorem 4. (see [9]) Any solution to the Euler-Poisson equations
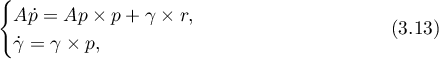
where  ,
,  ,
,  ,
,  ,
,  , in the Hess case specified by the conditions
, in the Hess case specified by the conditions
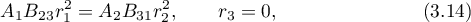

has the following representation expressing the variables  ,
,  ,
,  , in terms of the functions
, in terms of the functions  and
and  :
:
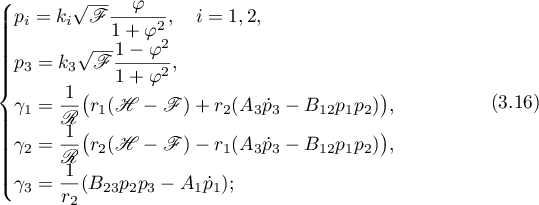
here
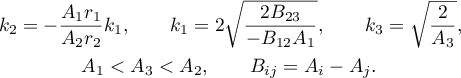
In the general case,  is the elliptic function defined by the differential equation
is the elliptic function defined by the differential equation
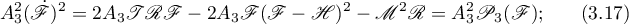
here  ,
,  and
and  are first integrals of the original Euler-Poisson system of equations,
are first integrals of the original Euler-Poisson system of equations,  , and
, and  is the
is the  -inner product in
-inner product in  .
.
If  are the roots of the polynomial
are the roots of the polynomial  , then
, then

where
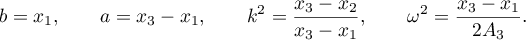
Moreover,

The function  is defined by Riccati's differential equation
is defined by Riccati's differential equation
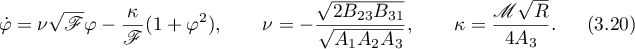
It will be shown later (see Theorem 3) that the solution to (3.20) cannot be expressed by quadratures, so we will represent this solution by describing its asymptotic behaviour at the singular points.
Theorem 5. (see [9]) The zeros and poles of the function  are singular points
are singular points  , and the asymptotic behaviour of
, and the asymptotic behaviour of  in neighbourhoods of these points has the following form:
in neighbourhoods of these points has the following form:
 in a neighbourhood of either of the conjugate points at which
in a neighbourhood of either of the conjugate points at which  ,
,  ,
,  , and either
, and either
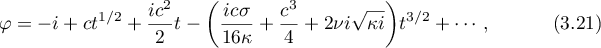
where  is a free parameter specifying a solution in the one-parameter family of solutions on the two-dimensional torus defined by the integrals
is a free parameter specifying a solution in the one-parameter family of solutions on the two-dimensional torus defined by the integrals  ,
,  ,
,  and
and  , or
, or
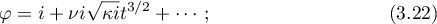
 in a neighbourhood of the point at which
in a neighbourhood of the point at which  ,
,  , where
, where  , and either
, and either
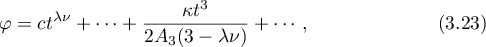
where  is a free parameter specifying a solution in the one-parameter family of solutions on the two-dimensional torus defined by the integrals
is a free parameter specifying a solution in the one-parameter family of solutions on the two-dimensional torus defined by the integrals  ,
,  ,
,  and
and  , or
, or

Since all the asymptotic formulae contain a free parameter, to describe a solution we must find the relation between the parameters in the asymptotic formulae which hold in neighbouring period-parallelograms of the function  . This relation is expressed by linear fractional transformations, which do not commute in general because solutions are not necessarily single-valued.
. This relation is expressed by linear fractional transformations, which do not commute in general because solutions are not necessarily single-valued.
Theorem 6. (see [9]) The linear-fractional transformations connecting the free parameters in the asymptotic formulae at two singular points with  are compositions of the following transformations:
are compositions of the following transformations:
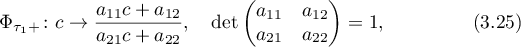
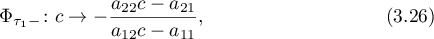
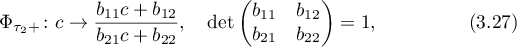
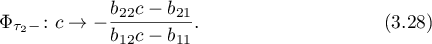
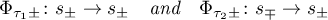
are the parametric Poincaré maps along the real and imaginary axes, respectively;  are singular points at which
are singular points at which  and the parameter in the expansion takes the values
and the parameter in the expansion takes the values  , and
, and
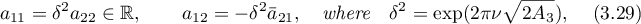
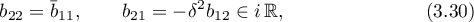

Taking the dependencies (3.25), (3.27), (3.29)–(3.31) into account, the quantities  and
and  can be regarded as free parameters defining the real three-parameter family of real invariant tori of the problem in the Hess case (as can the parameters
can be regarded as free parameters defining the real three-parameter family of real invariant tori of the problem in the Hess case (as can the parameters  ,
,  , or
, or  ,
,  and
and  for fixed parameters
for fixed parameters  and
and  ,
,  , of the rigid body).
, of the rigid body).
The solutions to the Hess problem are limit-periodic if  and quasi-periodic (see [24]) if
and quasi-periodic (see [24]) if  .
.
Theorem 7. The system of differential equations (3.13) in the Hess case (3.14) has two real periodic solutions, and the other solutions approach one of these two solutions asymptotically on the invariant tori on which, under the assumptions of Theorem 4,
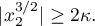
In this case, the periodic solutions  and
and  satisfy the estimates
satisfy the estimates
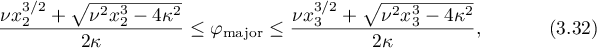

The solutions  and
and  are related by
are related by
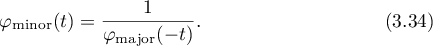
If the values of the integrals  and
and  are fixed and the value of
are fixed and the value of  (or, equivalently, the parameter
(or, equivalently, the parameter  ) is increasing, then the trajectories of the periodic solutions
) is increasing, then the trajectories of the periodic solutions  and
and  approach each other, and these solutions coincide for some
approach each other, and these solutions coincide for some  such that
such that

That is, for this value of  only one periodic solution exists on the invariant torus, and the other solutions approach this periodic solution asymptotically.
only one periodic solution exists on the invariant torus, and the other solutions approach this periodic solution asymptotically.
Increasing  further for fixed values of
further for fixed values of  and
and  results in quasi-periodic, and in particular, periodic solutions
results in quasi-periodic, and in particular, periodic solutions  .
.
The solutions to the system of differential equations (3.13), (3.14) are quasi- periodic for almost all  such that
such that
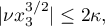
and the set of periodic solutions is a nullset.
§ 4. Classification of singular points of solutions and entire solutions to the classical problem of the motion of a heavy rigid body
In this section we briefly recall some facts in [7] (see also [8]) which we require for our discussion.
Making the change of variables  ,
,  in the Euler- Poisson equations (2.1) we obtain
in the Euler- Poisson equations (2.1) we obtain
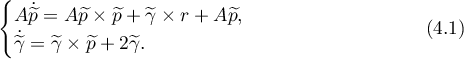
Solutions to (2.1) and (4.2) are related as follows:
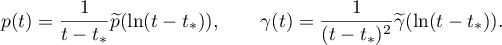
Now let  be a singular point of the system of differential equations (4.2). Then after the inverse change of variables the trajectory
be a singular point of the system of differential equations (4.2). Then after the inverse change of variables the trajectory  ,
,  going to
going to  is defined by a solution with singular point
is defined by a solution with singular point 
 :
:

Now in order to find the asymptotic behaviour of solutions to the original system (2.1) at singular points it suffices to ascertain the asymptotic behaviour of the solutions to (4.1) near singular points, which is a pretty standard task. To this end we first need to solve the linearized system near a singular point and then apply the Picard operator to the first approximation thus obtained.
Definition 1. The algebraic system

defining the singular points of (4.1) is called the characteristic system.
The characteristic system for the Euler-Poisson equations has two types of root,  and
and  ,
,  . These are the coefficients of the leading terms of the asymptotic formulae for two types of singular points of solutions to the Euler- Poisson equations; these will be called
. These are the coefficients of the leading terms of the asymptotic formulae for two types of singular points of solutions to the Euler- Poisson equations; these will be called  -singular and
-singular and  -singular points
-singular points
Remark 2. The characteristic system for the Euler-Poisson equations is completely solvable if the following degeneracy condition is satisfied: at least one of the coordinates  vanishes or some eigenvalues of the inertia operator
vanishes or some eigenvalues of the inertia operator  are equal.
are equal.
In the nondegenerate case we can solve the system once we know the zeros of a certain polynomial of degree 8 with coefficients depending on  and
and  .
.
In solving the characteristic system we shall ascertain the degeneracy cases corresponding to the well-known Euler, Lagrange, Kovalevskaya and Grioli integrable cases.
Finding the asymptotic behaviour of singular points of the Euler-Poisson equations by means of the method described above does not guarantee that we get the complete list of asymptotic formulae for all the singular points. To find all the singular points we consider the quotient of the flow on the phase space, when the phase space is transformed into a compact complex manifold with the structure of holomorphic foliation with singularities. An analysis of all the singular points of this foliation enables us to determine all the singular points of solutions to the Euler-Poisson equations.
Let  ,
,  be a solution to the Euler-Poisson equations; then
be a solution to the Euler-Poisson equations; then  ,
,  is too. This allows us to take a quotient of the set of trajectories of solutions to (2.1).
is too. This allows us to take a quotient of the set of trajectories of solutions to (2.1).
Theorem 8. Let  act on
act on  as follows:
as follows:
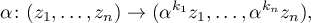
 . Then the quotient space
. Then the quotient space  by this action is a compact complex manifold.
by this action is a compact complex manifold.
Theorem 9. The canonical projection  ,
,  ,
,  , maps the foliation defined by the flow (2.1) to a holomorphic foliation
, maps the foliation defined by the flow (2.1) to a holomorphic foliation  of the compact complex manifold
of the compact complex manifold  .
.
All the singular points of the foliation  of
of  are the
are the  -projections of singular points of system (4.1) and the
-projections of singular points of system (4.1) and the  -projections of solutions to the characteristic system.
-projections of solutions to the characteristic system.
Remark 3. The foliation  is integrable because there exists a leafwise invariant map
is integrable because there exists a leafwise invariant map
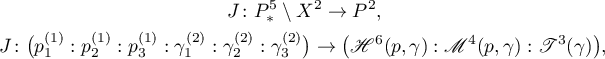
where  .
.
In addition, the surface  is invariant for
is invariant for  .
.
Theorem 10. All the singular points of solutions to the Euler-Poisson equations (2.1) are either  - or
- or  -singular points or limit singular points of
-singular points or limit singular points of  - or
- or  -singular points, or are approximated by the asymptotics of
-singular points, or are approximated by the asymptotics of  -singular points (which can only hold if the linear approximation in a neighbourhood of a
-singular points (which can only hold if the linear approximation in a neighbourhood of a  -singular point of system (4.1) has eigenvalue zero).
-singular point of system (4.1) has eigenvalue zero).
In the statement of Theorem 10 we do not mention singular points that are the projections of singular points of equations (2.1). This is because such points are responsible for the asymptotic behaviour as  , by contrast with
, by contrast with  - or
- or  -singular points, for which
-singular points, for which  . The proof of this theorem only depends substantially on the compactness of the manifold
. The proof of this theorem only depends substantially on the compactness of the manifold  .
.
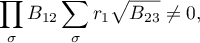
then all nonconstant solutions  to the Euler-Poisson equations have singular points
to the Euler-Poisson equations have singular points  .
.
The condition in Theorem 11 gives a condition which ensures the absence of singular points that are the  -projections of singularities of equations (4.1).
-projections of singularities of equations (4.1).
Theorem 12. The set of entire solutions to the Euler-Poisson equations (2.1) is exhausted by particular solutions to the Euler, Lagrange and Grioli cases.
§ 5. Asymptotic behaviour of singular points of solutions to the classical problem of the motion of a heavy rigid body in the Kovalevskaya case
Following the approach of §4, our next aim is to find the asymptotic behaviour of singular points for solutions to the Kovalevskaya problem. The characteristic system reads as
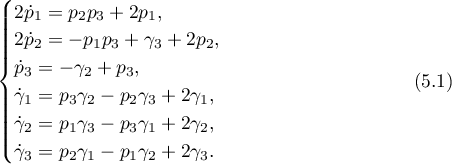
For simplicity and without loss of generality we assume here that  .
.
System (5.1) can easily be solved; its solution consists of the one-parameter family of points
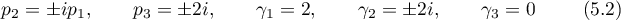
with free parameter  and the isolated solution
and the isolated solution
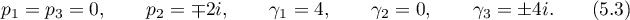
Theorem 13. All the singular points of the solutions to the problem of the motion of a heavy rigid body in the Kovalevskaya case are  -singular points (see Definition 1) and have the following asymptotic formulae
-singular points (see Definition 1) and have the following asymptotic formulae
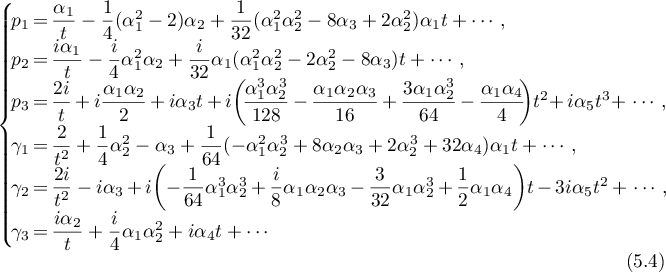
and
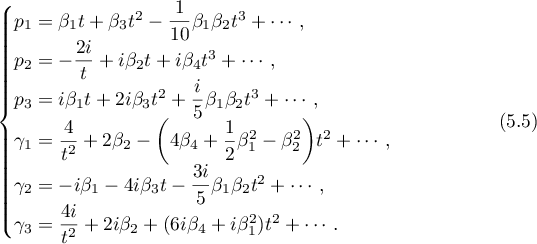
According to Theorem 13 the asymptotic formula (5.4) contains five free parameters, while (5.5) has only four. For the convenience of references to these formulae we need the following definition.
Definition 2. Singular points of solutions to the Euler-Poisson equations which have the asymptotic formula (5.4) or (5.5) will be called  - or
- or  -singular points, respectively.
-singular points, respectively.
Substituting the above asymptotic formulae into the first integrals and assuming that the values of these integrals are  ,
,  ,
,  and
and  we arrive at the following relations for the
we arrive at the following relations for the  -asymptotic formula:
-asymptotic formula:
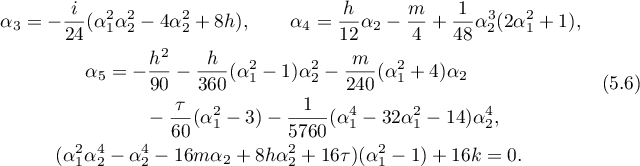
All the parameters in the  -asymptotic formula can be found from similar relations:
-asymptotic formula can be found from similar relations:
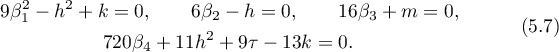
Thus we know the set of singular points of solutions to the Kovalevskaya problem in total. However, the asymptotic behaviour of the singular points of a particular solution is not at all obvious. We shall start to study this problem with the following simple particular cases.
§ 6. Solution to the Delaunay problem in terms of Weierstrass functions
Our first aim is to ascertain the nature of the asymptotic behaviour of singular points in the most simple cases.
For the solutions in case (3.11), (3.12) the answer is almost clear: a solution is expressible in terms of the Jacobi elliptic functions (see [22]), it has two free parameters, its singular points satisfy a  -asymptotic formula with constraints on the parameters,
-asymptotic formula with constraints on the parameters,
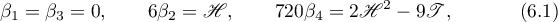
and moreover,  ,
,  ,
,
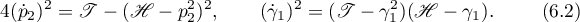
In the analogous case

when the solution has the form

the parameters of the  -asymptotic formula are as follows:
-asymptotic formula are as follows:
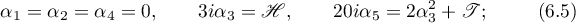
also,  and
and  .
.
We see that the cases (6.2) and (6.4), which are outwardly similar, differ quite substantially in the Kovalevskaya problem both in the type of asymptotic behaviour and in the relations between the values of the integrals for which these cases are realized.
In addition, the particular case (6.2) with  is found to be the Delaunay case, which cannot be said of (6.3). In turn, the case (6.3) for
is found to be the Delaunay case, which cannot be said of (6.3). In turn, the case (6.3) for  is the Bobylev-Steklov particular case (3.9), as distinct from (6.2). And even in the degenerate case
is the Bobylev-Steklov particular case (3.9), as distinct from (6.2). And even in the degenerate case  , in which both particular solutions are realized, they do not merge into a single solution. This again points up the importance of the difference in the asymptotic behaviour of the singular points of solutions.
, in which both particular solutions are realized, they do not merge into a single solution. This again points up the importance of the difference in the asymptotic behaviour of the singular points of solutions.
The Bobylev-Steklov case (3.9), as well as the cases treated above, has a solution in terms of Jacobi elliptic functions, which has  -singular points.
-singular points.
Furthermore, the solution in the Delaunay case has an integral representation as a hyperelliptic function (2.6), rather than as an elliptic function, and hence it can hardly be expressed in terms of Jacobi functions by simple formulae, even though such a representation is known to exist (see [22]).
However, although there exists a possibility that convenient formulae expressing the solution in the Delaunay case in terms of the Jacobi elliptic functions can be found, we believe in the potency of the approach which follows naturally from the analysis of the singular points of solutions in the original coordinates.
So, we now substitute the asymptotic formulae for singular points in the integrals  . in the Delaunay case. For the
. in the Delaunay case. For the  -asymptotic formulae, we have
-asymptotic formulae, we have
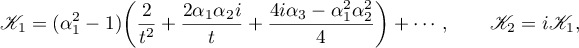
that is,  . Again putting this relation into
. Again putting this relation into  , we obtain a relation for
, we obtain a relation for  :
:
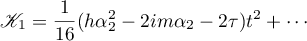
and further, using (5.6), determine the remaining  .
.
For the  -asymptotic formulae we have
-asymptotic formulae we have
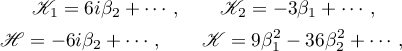
which readily implies that the generic Delaunay solutions (for example, the ones for which the energy integral has a nonzero value) do not have  -singular points. This establishes the following.
-singular points. This establishes the following.
Proposition 1. Each solution of the Delaunay case is defined by a periodic function which has a  -asymptotic formula at singular points with certain finite-valued parameters
-asymptotic formula at singular points with certain finite-valued parameters  ,
,  , depending on the initial values of the first integrals by virtue of the following relations:
, depending on the initial values of the first integrals by virtue of the following relations:
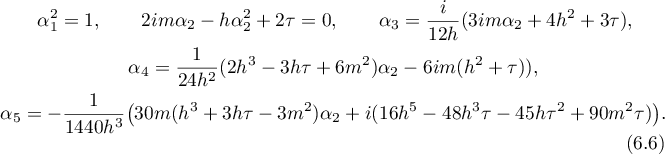
Thus, we see that the solution in the Delaunay case has the same leading terms in its asymptotic formula at the singular points as the functions  ,
,  and
and  ; in addition,
; in addition,  . However, in this case the parity properties do not hold for the functions
. However, in this case the parity properties do not hold for the functions  ,
,  , meaning that the coordinates of the singular points are shifted.
, meaning that the coordinates of the singular points are shifted.
Thus, for the doubly-periodic functions  ,
,  , the solutions can be expressed in terms of the Weierstrass
, the solutions can be expressed in terms of the Weierstrass  -function (see [11]) up to constants and permutations:
-function (see [11]) up to constants and permutations:
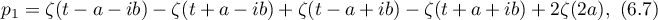
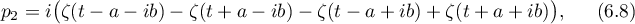

In (6.7)–(6.9) the coefficients are chosen with due regard to the  -asymptotic formula and the constants are taken so that the functions
-asymptotic formula and the constants are taken so that the functions  are doubly-periodic not only in the variable
are doubly-periodic not only in the variable  , but also in
, but also in  and
and  . This helps us to calculate products of these functions more easily, as both their products and their derivatives will be doubly-periodic in all these arguments.
. This helps us to calculate products of these functions more easily, as both their products and their derivatives will be doubly-periodic in all these arguments.
Definition 3. For brevity, the functions  ,
,  ,
,  and
and  will be denoted, respectively, by
will be denoted, respectively, by  ,
,  ,
,  and
and  . The derivatives of these functions taken with minus sign,
. The derivatives of these functions taken with minus sign,  ,
,  ,
,  and
and  , will be denoted by
, will be denoted by  ,
,  ,
,  and
and  , respectively.
, respectively.
We must verify that the representations (6.7)–(6.9) define a solution in the Delaunay case. To this aim we must also find expressions for the functions  ,
,  , and show that six independent relations connecting these variables hold. The required relations, some of which hold up to a constant, are
, and show that six independent relations connecting these variables hold. The required relations, some of which hold up to a constant, are
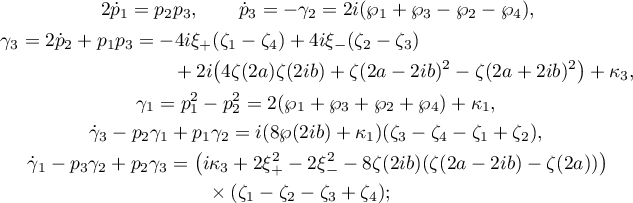
here  and
and  .
.
Among the above six relations, the first, second and fifth are exact. The additional exact relations are obtained by differentiating the relations that hold up to a constant. When they hold, these six exact relations impose a constraint on the parameters that were undefined ab initio. The result of some fairly cumbersome calculations, which we omit, is given in the statement of Theorem 1.
§ 7. Periodic  -solutions to the Kovalevskaya problem on generic level surfaces
-solutions to the Kovalevskaya problem on generic level surfaces
In this section we shall prove Theorem 2.
Looking at all the particular periodic cases in [21] and at their solutions in terms of the Jacobi and Weierstrass elliptic functions we see that these cases do not involve singular points with a general  -asymptotic formula.
-asymptotic formula.
As we have already pointed out, such an asymptotic formula contains only four free parameters, which implies that there should be a solution with a  -asymptotic formula on each surface level of the integrals
-asymptotic formula on each surface level of the integrals  ,
,  ,
,  and
and  and this solution must be periodic.
and this solution must be periodic.
Clearly, finding such an isolated periodic solution presents a challenge, because, as in the general Kovalevskaya case, it cannot be spotted in the original formulae of the problem. This solution could perhaps be detected using classical methods by a very careful investigation of all degenerate or limiting cases that appear after integrating the problem. However, to start investigating in this direction we need some motivation — and such motivation appears in the study of the asymptotic behaviour of singular points of the Kovalevskaya problem.
In order to produce the solution we seek we have to find the types of its singular points and their coordinates on the complex time-plane. This becomes easier the more necessary information we acquire before proceeding with the method of undetermined coefficients to represent the solution in terms of the Weierstrass functions.
Definition 4. Consider the problem of the motion of a heavy rigid body in the Kovalevskaya case. A particular periodic solution to this problem featuring  -singular points is called a
-singular points is called a  -solution. A quasi-periodic solution of general form to this problem featuring only
-solution. A quasi-periodic solution of general form to this problem featuring only  -singular points is called an
-singular points is called an  -solution.
-solution.
Remark 4. The parameters  ,
,  ,
,  of
of  -singular points can be determined uniquely from the values of the first integrals. The parameter
-singular points can be determined uniquely from the values of the first integrals. The parameter  obeys the equation
obeys the equation  (see (5.7)), and hence, on a level surface of the first integrals, either all
(see (5.7)), and hence, on a level surface of the first integrals, either all  -singular points belong to a single solution or there exist two
-singular points belong to a single solution or there exist two  -solutions.
-solutions.
It is not clear, without further analysis, whether the  -solutions are real-valued. But even if this is not the case, finding explicit formulae for such solutions is of great interest with regard to the structure of the solutions to the Kovalevskaya problem.
-solutions are real-valued. But even if this is not the case, finding explicit formulae for such solutions is of great interest with regard to the structure of the solutions to the Kovalevskaya problem.
We will derive an equation for the invariant surface in the Kovalevskaya problem. In view of (2.4), we can set
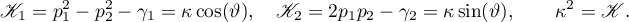
This enables us to derive one relation with three free parameters  ,
,  and
and  from the relations involving first integrals. This can be put into the form
from the relations involving first integrals. This can be put into the form
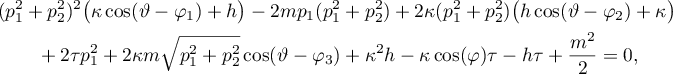
where
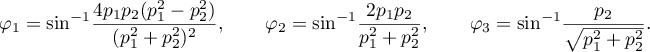
This implies that if, for example,  , then in order for this relation to hold in the general case it is necessary that
, then in order for this relation to hold in the general case it is necessary that  . This means that almost all solutions whose trajectories lie on the surface under consideration feature a
. This means that almost all solutions whose trajectories lie on the surface under consideration feature a  -asymptotic formula at a singular point corresponding to
-asymptotic formula at a singular point corresponding to  .
.
In order to find solutions with singular points that obey a  -asymptotic formula we expand the equation for the invariant surface in powers of
-asymptotic formula we expand the equation for the invariant surface in powers of  , starting from the highest power. As a result, we have
, starting from the highest power. As a result, we have
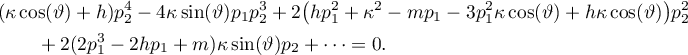
From this representation we find two more trajectories which go off to infinity along the invariant surface. Namely,
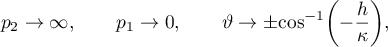
which corresponds to a  -asymptotic formula.
-asymptotic formula.
To find a representation for a  -solution, we shall employ, first, the fact that the functions
-solution, we shall employ, first, the fact that the functions  ,
,  ,
,  ,
,  are related by the simple formulae
are related by the simple formulae
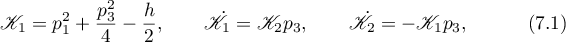
and second, the important observation that these functions have no singularities at a  -singular point.
-singular point.
In view of the asymptotic formula (5.4), since the sum of the residues is equal to zero, the periodic functions  and
and  can be put into the form
can be put into the form
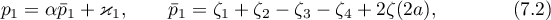
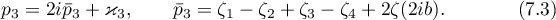
For convenience of notation, we also consider the functions
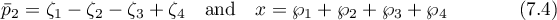
and define the constant
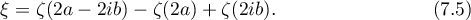
Using (7.1) we find the functions
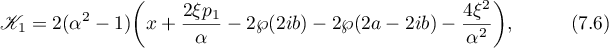
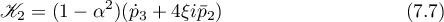
and the parameters
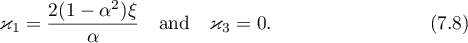
This also gives the following constraints on the chosen parameters:
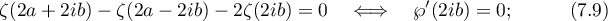
the last condition means that  is a half-period.
is a half-period.
Knowing the way  ,
,  ,
,  and
and  depend on time, one easily finds representations for the remaining variables:
depend on time, one easily finds representations for the remaining variables:
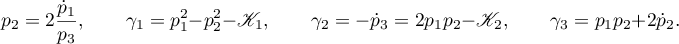
Remark 5. The representation  shows that in accordance with the asymptotic formula (5.5) the function
shows that in accordance with the asymptotic formula (5.5) the function  has a pole of first order at the zero of the function
has a pole of first order at the zero of the function  . The function
. The function  , being the derivative of the function
, being the derivative of the function  , does not have a singularity at the same point, while the function
, does not have a singularity at the same point, while the function  has a first-order zero. The function
has a first-order zero. The function  has a second-order zero also in accordance with (5.5).
has a second-order zero also in accordance with (5.5).
Substituting the solution thus obtained in the original system of differential equations (2.3) with  we see that the first five equations are satisfied automatically by the definition of
we see that the first five equations are satisfied automatically by the definition of  and
and  and the properties of
and the properties of  ,
,  ,
,  and
and  .
.
It is more convenient to verify the last (sixth) relation for the angular momentum
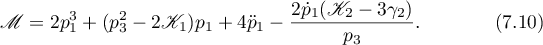
The value of the fraction in (7.10) can be found using the relation
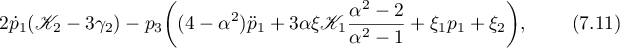
where
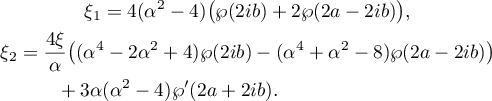
For the expression in (7.10) to be a constant, the parameters  ,
,  and
and  must satisfy the following relations in addition to (7.9):
must satisfy the following relations in addition to (7.9):
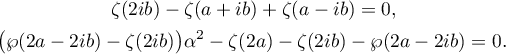
This proves Theorem 2.
Remark 6. From the four-parameter family of solutions we are looking for we have only found a two-parameter family. To add further free parameters, instead of four points on the period-parallelograms of the original functions  and
and  we can take eight singular points. This will result in more involved formulae, but the computational scheme will be the same.
we can take eight singular points. This will result in more involved formulae, but the computational scheme will be the same.
§ 8. Nonintegrability of the Hess problem by quadratures
The purpose of the present section is to prove that the Hess problem is not integrable by quadratures. However, a good deal of the proof will be devoted to an attempt to find a compact surface defining a singular periodic solution among the trajectories  .
.
We have to follow this approach in our analysis of the integrability of the Hess case because the proof of nonintegrability is based on properties of the parametric Poincaré map, and many remarkable facts supporting the existence of a singular solution with compact trajectory are thus left out of consideration. Of course, mathematical intuition is personal, but we believe that many experts interested in the Hess problem, including this author, would be eager to comprehend why no solution actually exists2, not just on the abstract level of the parametric Poincaré map, but also on the more concrete level of singular asymptotic formulae.
We first state Remarks 3, 4 and 13 from [9], but using the numbering of entities and formulae adopted in this paper.
Remark 7. When passing from the variable  (see (3.20)) to the original variables
(see (3.20)) to the original variables  ,
,  the solutions
the solutions
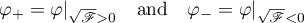
give the same solution.
Remark 8. Since the equations for  are linear, we can take the quotient of the corresponding flow by a homogeneous dilation, after which we obtain a holomorphic foliation with singularities on the compact complex manifold
are linear, we can take the quotient of the corresponding flow by a homogeneous dilation, after which we obtain a holomorphic foliation with singularities on the compact complex manifold  . There is an obvious correspondence between
. There is an obvious correspondence between  and
and  .
.
For real  we obtain two invariant tori, with
we obtain two invariant tori, with  and
and  .
.
Remark 9. The asymptotic formulae (3.23) and (3.24) with  are not asymptotic relations in general position, because only in these cases is the function
are not asymptotic relations in general position, because only in these cases is the function  locally single-valued in a neighbourhood of the singular point with
locally single-valued in a neighbourhood of the singular point with  ; otherwise it is infinite-valued.
; otherwise it is infinite-valued.
Here, if we consider the Hess problem not just with complex time but on the direct product  (see Remark 8), then a periodic solution will be single- valued on the real circle, while an aperiodic one will be infinite-valued.
(see Remark 8), then a periodic solution will be single- valued on the real circle, while an aperiodic one will be infinite-valued.
It would be natural to conjecture that the two single-valued solutions near the singular point with  are the two periodic solutions treated in Theorem 7.
are the two periodic solutions treated in Theorem 7.
However, if there does exist a link between the solutions mentioned above, it is likely to be highly nontrivial, because under appropriate assumptions, which we indicated in Theorem 7, all the real solutions can be quasi-periodic, meaning that there are no periodic solutions at all, but in any case solutions which are single-valued in a neighbourhood of the point  still exist.
still exist.
In addition to the above remarks we mention the following.
Remark 10. The asymptotic formula (3.23) involves a single-valued singular solution for  and a solution (3.24) for
and a solution (3.24) for  .
.
It would be wonderful if these singular asymptotic formulae described the same solution to the problem and this solution were periodic. In this case we would look for a solution whose behaviour at singular points agrees with the above single-valued asymptotic formulae. Undoubtedly, if such a solution does exist, then it is finite- valued, and its real part defines a periodic solution. Here we can assume that such a solution exists only for certain special values of the original parameters of the rigid body.
For equation (3.20), at a point with  we have four singular asymptotic formulae (3.23), (3.24), which we will put together into a single solution. For convenience, we set
we have four singular asymptotic formulae (3.23), (3.24), which we will put together into a single solution. For convenience, we set  .
.
Dividing the resulting equation by  we arrive at an expression depending on
we arrive at an expression depending on  :
:

here the  ,
,  , are polynomials of the
, are polynomials of the  th degree in
th degree in  .
.
Proceeding in a similar manner, for  we get
we get

The coefficients of the  ,
,  , in the polynomials in (8.1) and (8.2) are polynomial in
, in the polynomials in (8.1) and (8.2) are polynomial in  . But they are distinct, which shows that the coefficients multiplying
. But they are distinct, which shows that the coefficients multiplying  , which we require, must be rational; that is, we are looking for a solution in the form
, which we require, must be rational; that is, we are looking for a solution in the form
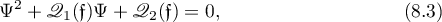
where the  ,
,  , are rational functions in
, are rational functions in  .
.
Solving (8.3) with respect to  we obtain
we obtain
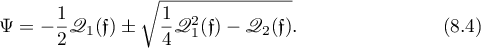
The discriminant, which depends on  and hence on
and hence on  , must be nonnegative for real
, must be nonnegative for real  exactly when the derivative
exactly when the derivative  is also real. Hence (8.4) can be refined as follows:
is also real. Hence (8.4) can be refined as follows:
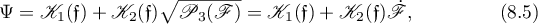
where the  ,
,  , are rational functions of
, are rational functions of  , for which we must write down differential equations.
, for which we must write down differential equations.
In view of (3.20) and setting  , we obtain
, we obtain
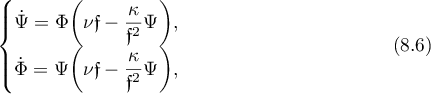
the first integral being

From (8.6) and (8.5) we have the representation
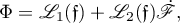
where the  are rational functions in
are rational functions in  .
.
Now we consider a very important particular case of the Hess problem — namely, the case when two periodic solutions on the torus merge. First, it is clear that if a pair of periodic solutions is defined by polynomial relations, then these merged solutions will also be defined by polynomial relations. Second, it is no less obvious that when a pair of periodic solutions coincides, this can be looked upon as a certain degeneration of the problem, and hence, a simplification.
Now, the two solutions (8.4) to equation (8.3) are the two periodic solutions. Hence, in order to get an equation for the merged solution we have to set  in (8.5), and hence, using (8.6),
in (8.5), and hence, using (8.6),
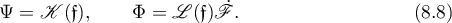
Substituting this into (8.6) yields:
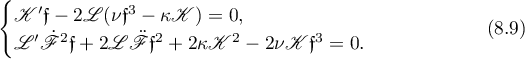
From these relations it follows that we can take the function  to be even, and the function
to be even, and the function  to be odd. We finally have the representation
to be odd. We finally have the representation
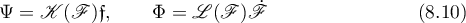
and for it we have the corresponding differential equations and the first integral,
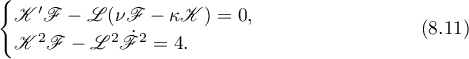
Thus it remains to find  from the first equation in (8.11) and to substitute it into the second.
from the first equation in (8.11) and to substitute it into the second.
From the asymptotic behaviour of the function  it follows that it has degree 3 at infinity and a zero of order 3 at the origin. Hence, by (8.10) the function
it follows that it has degree 3 at infinity and a zero of order 3 at the origin. Hence, by (8.10) the function  has degree 1 at infinity and a zero of the first order in
has degree 1 at infinity and a zero of the first order in  at the origin.
at the origin.
Starting with the minimum possible degree of the numerator and the denominator in  we write
we write
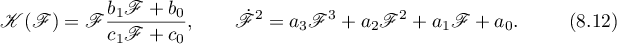
Substituting this into (8.11) we arrive at a polynomial system of eight equations with the eight unknowns  ,
,  and
and  , which has a solution in complex numbers. That the numbers
, which has a solution in complex numbers. That the numbers  ,
,  may be complex is irrelevant, since from a pair of complex conjugate solutions to the Riccati equations for the function
may be complex is irrelevant, since from a pair of complex conjugate solutions to the Riccati equations for the function  one may get a real solution, but the parameters
one may get a real solution, but the parameters  must be real, which is impossible in (8.10), because for the highest power in this representation the equation for the coefficients is
must be real, which is impossible in (8.10), because for the highest power in this representation the equation for the coefficients is  whereas
whereas  by the hypothesis of the problem.
by the hypothesis of the problem.
This cannot be circumvented by increasing the power of the rational function  . Hence, if we are still to find the solution in this way we need to change the form of the representation for the function
. Hence, if we are still to find the solution in this way we need to change the form of the representation for the function  with the aim of gaining a more precise matching between its true asymptotic formula and our representation. Clearly, the problem then becomes more involved, while on the other hand we do not know whether it is actually solvable. We turn to the properties of the parametric Poincaré map (Theorem 4).
with the aim of gaining a more precise matching between its true asymptotic formula and our representation. Clearly, the problem then becomes more involved, while on the other hand we do not know whether it is actually solvable. We turn to the properties of the parametric Poincaré map (Theorem 4).
We have seen that single-valued asymptotic formulae are characterized by the condition  on the free parameter at points with
on the free parameter at points with  . As a result, the matrices of the linear fractional transformation
. As a result, the matrices of the linear fractional transformation  and
and  must be diagonal.
must be diagonal.
Such matrices correspond to a singular solution since for a generic solution the parameter  in the asymptotic formula cannot have an infinite limit value. In addition, relation (3.31) degenerates on the singular solution.
in the asymptotic formula cannot have an infinite limit value. In addition, relation (3.31) degenerates on the singular solution.
Now compare the properties of the singular solution with a diagonal matrix of the parametric Poincaré map and those of the well-known integrable Hess solution with zero angular momentum.
In the notation of our paper, the Hess case with zero angular momentum has the form  , the function
, the function  being elliptic and given by differential equation (3.17).
being elliptic and given by differential equation (3.17).
In this case, the solution is
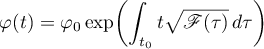
and so, after a time shift by period  of
of  the solution is multiplied by
the solution is multiplied by
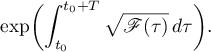
Near the singular point with  the asymptotic formula for the solution
the asymptotic formula for the solution  has the form (see (3.23))
has the form (see (3.23))
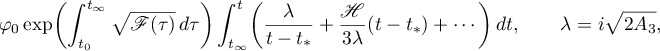
where  is the singular point and
is the singular point and  is a point near
is a point near  .
.
After a shift by  the asymptotic formula reads
the asymptotic formula reads
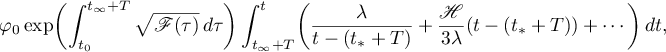
which supports the correspondence between the case of a diagonal matrix of the parametric Poincaré map and the integrable Hess case with zero angular momentum. There is no other possibility for a singular solution with single-valued asymptotic formulae at infinity for the function  .
.
Theorem 14. The trajectory of the solution  (see Remark 8),
(see Remark 8),  , to the Hess problem (see Theorem 4) can only be compact for
, to the Hess problem (see Theorem 4) can only be compact for  .
.
Proof of Theorem 3 Consider the question of the integrability of the Hess problem by quadratures. Integrability by quadratures (see, for example, (1.1)) usually means that by an appropriate change of variables  a system of differential equations
a system of differential equations  can be taken to a polynomial system
can be taken to a polynomial system
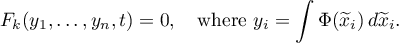
In the Hess problem, all the unknowns functions  and
and  ,
,  , can be expressed in terms of
, can be expressed in terms of  , which can be regarded as a function of
, which can be regarded as a function of  ,
,
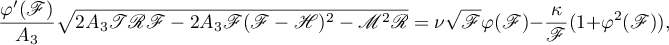
so we need to find a representation
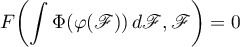
for this.
If  , then such a representation exists and takes the form
, then such a representation exists and takes the form
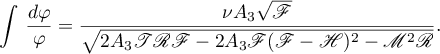
Otherwise, Theorem 12 shows that no such representation exists.
To be precise, for any analytic function  the function
the function  does exist. However, to speak about integrability we need
does exist. However, to speak about integrability we need  to be sufficiently nice (that is, it should lie in the class of commonly known functions, for example, finite-valued ones). The class of well-known infinitely-valued functions involves both the logarithm and the inverse trigonometric functions, but at the present time a function with singularities of the form
to be sufficiently nice (that is, it should lie in the class of commonly known functions, for example, finite-valued ones). The class of well-known infinitely-valued functions involves both the logarithm and the inverse trigonometric functions, but at the present time a function with singularities of the form  ,
,  , at the points in the integral lattice can by no means be considered convenient for describing the solution to the Hess problem.
, at the points in the integral lattice can by no means be considered convenient for describing the solution to the Hess problem.
This proves Theorem 3.
Footnotes
- 1
All the known particular solutions to the problem of the motion of a heavy rigid body include the case with these conditions, so that this case is included in all other particular cases. This makes it difficult to assign authorship.
- 2
The possible existence of a singular integrable solution to the Hess problem was pointed out to us by the referee of [9].



