Abstract
We have carried out numerical simulations of oblique incidence of a laser pulse with an intensity of 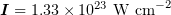 on a planar plasma layer and found the plasma density and the angle of incidence of p-polarised laser pulses that correspond to the highest gamma-ray generation efficiency and high gamma-ray directivity. The shape of the plasma surface has been determined by simulation and conditions have been considered that lead to an increase in generation efficiency.
on a planar plasma layer and found the plasma density and the angle of incidence of p-polarised laser pulses that correspond to the highest gamma-ray generation efficiency and high gamma-ray directivity. The shape of the plasma surface has been determined by simulation and conditions have been considered that lead to an increase in generation efficiency.
Export citation and abstract BibTeX RIS
1. Introduction
Since their discovery at the beginning of the 20th century, gamma rays have found application in many areas of science, technology and medicine. At present, the operating principle of most existing gamma-ray sources is based on radioactive decay, bremsstrahlung and inverse Compton scattering, requiring the presence of a radioactive material or the use of large electron accelerators.
A potential alternative approach to gamma-ray generation is to use ultrahigh power laser systems. State-of-the-art femtosecond lasers offer light intensities above 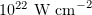 , and laser systems are being constructed [1] and designed [2] which are expected to allow even more impressive results to be achieved. One of the proposed ways of employing such laser systems is laser wakefield acceleration (LWFA) of electrons using a laser pulse propagating through a plasma and bremsstrahlung gamma-ray generation using the resulting high-energy electron beams [3]. It is worth noting that, at the intensities in question, the dimensionless laser pulse amplitude is
, and laser systems are being constructed [1] and designed [2] which are expected to allow even more impressive results to be achieved. One of the proposed ways of employing such laser systems is laser wakefield acceleration (LWFA) of electrons using a laser pulse propagating through a plasma and bremsstrahlung gamma-ray generation using the resulting high-energy electron beams [3]. It is worth noting that, at the intensities in question, the dimensionless laser pulse amplitude is 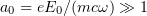 and, driven by the laser field, the electrons begin to efficiently emit photons due to Compton scattering. The photons have a synchrotron spectrum with a characteristic energy of the order of
and, driven by the laser field, the electrons begin to efficiently emit photons due to Compton scattering. The photons have a synchrotron spectrum with a characteristic energy of the order of  . Previous estimates suggest that, at a sufficiently high laser field intensity, a considerable part of the laser pulse energy can be converted into the energy of gamma-ray photons: several percent for
. Previous estimates suggest that, at a sufficiently high laser field intensity, a considerable part of the laser pulse energy can be converted into the energy of gamma-ray photons: several percent for 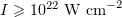 [4 – 6] and tens of percent for
[4 – 6] and tens of percent for 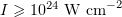 [7 – 9]. Because of this, such gamma-ray sources appear very attractive compared to conventional ones and even to LWFA-based sources.
[7 – 9]. Because of this, such gamma-ray sources appear very attractive compared to conventional ones and even to LWFA-based sources.
In this paper, we examine gamma-ray generation in the case of oblique incidence of laser pulses on flat targets. Since the ionisation time at the intensities in question is much shorter than the laser wave period, we can consider the interaction of laser pulses with a plasma layer. Section 2 describes the main phenomena that take place in the course of this interaction and lead to efficient gamma-ray generation. In addition, we perform semianalytical modelling of the shape of the plasma surface at oblique incidence of radiation. In Section 3, we present and analyse results of numerical simulation for wide ranges of plasma densities and angles of incidence of laser pulses. We optimise gamma-ray generation parameters and discuss physical effects that ensure the most efficient generation.
2. Interaction process.
We consider a p-polarised pulsed laser radiation incident at an angle 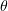 on a planar supercritical plasma layer. In this configuration, the electric field vector
on a planar supercritical plasma layer. In this configuration, the electric field vector 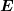 lies in the plane of incidence and, hence, there is an electric field component
lies in the plane of incidence and, hence, there is an electric field component 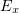 normal to the layer (Fig. 1).
normal to the layer (Fig. 1).
Figure 1. Configuration of the problem of a laser pulse incident at an angle 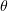 on a planar plasma layer.
on a planar plasma layer.
Download figure:
Standard imageAt a plasma density 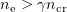 [where
[where 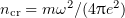 is the critical plasma density at the laser field frequency
is the critical plasma density at the laser field frequency 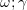 is the characteristic Lorentz factor of electrons interacting with the laser field; and
is the characteristic Lorentz factor of electrons interacting with the laser field; and  is the electron charge], the plasma is relativistically opaque to the laser pulse and the pulse penetration depth in the substance does not exceed the thickness of its skin layer. As a rule,
is the electron charge], the plasma is relativistically opaque to the laser pulse and the pulse penetration depth in the substance does not exceed the thickness of its skin layer. As a rule, 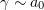 in such processes, so the opacity threshold can be estimated at
in such processes, so the opacity threshold can be estimated at  .
.
In the regime under consideration, the ponderomotive force of the laser field shifts electrons to the bulk of the plasma, and they form a thin (compared to the wavelength 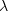 ) layer, which to a significant degree screens the external field in the bulk of the plasma (this is suggested by numerical simulation and, moreover, there are models based on this approach [6, 10 – 12]). Ions have a considerably larger mass, so their motion in the initial stage of interaction (the first few laser field periods) can be neglected. The result is a charge separation field, which can be evaluated to a first approximation using the formula for the field in a planar capacitor:
) layer, which to a significant degree screens the external field in the bulk of the plasma (this is suggested by numerical simulation and, moreover, there are models based on this approach [6, 10 – 12]). Ions have a considerably larger mass, so their motion in the initial stage of interaction (the first few laser field periods) can be neglected. The result is a charge separation field, which can be evaluated to a first approximation using the formula for the field in a planar capacitor: 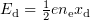 , where
, where 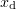 is the displacement of the electron layer relative to its unperturbed position. As the displacement increases, so does the restoring force, and at some instant in time the electron layer begins to move back. The result is an oscillatory process with a period equal to half the laser field period. Because of this, this laser – plasma interaction regime is also referred to as a 'relativistic electron spring' [11]. The above models analytically describe this oscillatory process. Gamma-ray photon emission by electrons in a layer was also modelled previously [12].
is the displacement of the electron layer relative to its unperturbed position. As the displacement increases, so does the restoring force, and at some instant in time the electron layer begins to move back. The result is an oscillatory process with a period equal to half the laser field period. Because of this, this laser – plasma interaction regime is also referred to as a 'relativistic electron spring' [11]. The above models analytically describe this oscillatory process. Gamma-ray photon emission by electrons in a layer was also modelled previously [12].
It is worth noting one important distinction between the behaviour of electrons at oblique incidence and that at normal incidence. At normal incidence, 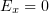 and the motion of electrons along the
and the motion of electrons along the  axis is only influenced by the magnetic component of the Lorentz force, which is proportional to
axis is only influenced by the magnetic component of the Lorentz force, which is proportional to 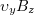 . At oblique incidence, since there is the component
. At oblique incidence, since there is the component 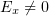 and
and 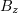 is the same as at normal incidence, the force exerted by the laser field on electrons moving along the
is the same as at normal incidence, the force exerted by the laser field on electrons moving along the  axis increases. This may lead to an increase in the amplitude of electron oscillations in this direction. Numerical simulation indicates that, even at angles of incidence from
axis increases. This may lead to an increase in the amplitude of electron oscillations in this direction. Numerical simulation indicates that, even at angles of incidence from 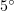 to
to 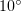 , some electrons are plucked out of the plasma (at least in part of their trajectory) and, as the angle of incidence and longitudinal field
, some electrons are plucked out of the plasma (at least in part of their trajectory) and, as the angle of incidence and longitudinal field 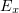 increase, so does the maximum distance of the electrons from the boundary. This process was analysed by Brunel [13] and Pan et al. [14].
increase, so does the maximum distance of the electrons from the boundary. This process was analysed by Brunel [13] and Pan et al. [14].
Since the transverse field component ( in the case of the polarisation under consideration) is large, as above, such electrons, being essentially in free space, are effectively accelerated by the field along the
in the case of the polarisation under consideration) is large, as above, such electrons, being essentially in free space, are effectively accelerated by the field along the 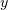 axis and acquire high values of the Lorentz factor
axis and acquire high values of the Lorentz factor 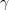 . At external field intensities
. At external field intensities 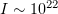 to
to 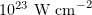 and higher, electrons are accelerated to a level
and higher, electrons are accelerated to a level 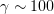 and above. The synchrotron emission mechanism then prevails and the emission spectrum lies in the gamma region. Of particular importance is that, according to theoretical calculations and numerical simulation, with increasing
and above. The synchrotron emission mechanism then prevails and the emission spectrum lies in the gamma region. Of particular importance is that, according to theoretical calculations and numerical simulation, with increasing 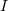 an ever larger part of the laser pulse energy converts to the energy of hard photons. In particular, Ji et al. [8] obtained
an ever larger part of the laser pulse energy converts to the energy of hard photons. In particular, Ji et al. [8] obtained  efficiency (for
efficiency (for  ) at normal incidence.
) at normal incidence.
It is therefore reasonable to expect that more effective electron acceleration at oblique incidence of laser pulses will lead to an increase in the energy-conversion efficiency from laser radiation to hard photons (relative to the case of normal incidence).
2.1. Modelling of the shape of the plasma surface
At oblique incidence, different points on the boundary plane of a plasma experience the action of the external field with different phases, so the oscillatory process converts into a wave travelling on the plasma surface with a velocity 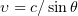 . Using equations of a previously reported model [12], we can determine the shape of the plasma surface. To this end, we transform to a frame of reference moving at a velocity
. Using equations of a previously reported model [12], we can determine the shape of the plasma surface. To this end, we transform to a frame of reference moving at a velocity 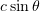 along the
along the 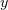 axis. It can be shown that, in this frame of reference, a laser pulse is incident on the plasma along the normal to its surface [15], but we will have to determine the amplitude and equation of the external field and the plasma density in the moving frame:
axis. It can be shown that, in this frame of reference, a laser pulse is incident on the plasma along the normal to its surface [15], but we will have to determine the amplitude and equation of the external field and the plasma density in the moving frame:
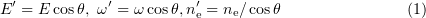
(where the primes refer to the moving frame). Moreover, the equations will include an additional term, describing the field of ions moving at a velocity 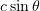 in the
in the 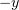 direction.
direction.
Modifying equations from Ref. [12] (with no allowance for the reaction force of the light, which has no significant effect on the shape of the plasma surface), we obtain the following system:

All the quantities in Eqns (2) are considered in the moving frame (the primes are omitted). Here 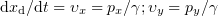 ; and
; and 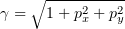 . In the normalisation used,
. In the normalisation used, 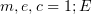 is normalised to
is normalised to 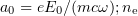 is normalised to
is normalised to 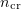 ; and
; and 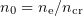 .
.
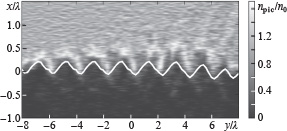
Integrating these equations, we can find 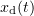 in the moving frame and then return to the laboratory frame. Figure 2 presents the spatial distribution of the electron concentration at a fixed instant of time and numerical simulation results. It is seen that the shape of the plasma surface is rather well described by Eqns (2). More details about the numerical simulation can be found in Section 3.
in the moving frame and then return to the laboratory frame. Figure 2 presents the spatial distribution of the electron concentration at a fixed instant of time and numerical simulation results. It is seen that the shape of the plasma surface is rather well described by Eqns (2). More details about the numerical simulation can be found in Section 3.
Figure 2. Shape of the plasma surface at 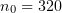 for a laser pulse with
for a laser pulse with 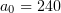 incident at
incident at 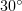 to the
to the  axis. The solid line represents theoretical predictions and the gray-scale pattern represents the electron concentration obtained by PIC simulation.
axis. The solid line represents theoretical predictions and the gray-scale pattern represents the electron concentration obtained by PIC simulation.
Download figure:
Standard image3. Numerical simulation
We performed several series of numerical simulations of gamma-ray generation as a result of interaction between obliquely incident laser pulses and a plasma. Three-dimensional simulation was carried out by the particle-in-cell (PIC) method, which has been shown to be effective in simulating laser – plasma interaction processes. The code used allows quantum electrodynamic effects to be taken into account. Emitted hard photons, whose wavelengths are considerably smaller than the mesh size, are modelled as quasiparticles. This is justified at sufficiently high laser field intensities, because a 'synchrotron peak' emerges in the electron emission spectrum at energies corresponding to the synchrotron radiation maximum: 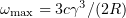 , where
, where 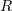 is the radius of curvature of the electron trajectory at a given point. At lower energies, the spectrum has a dip (down to laser harmonics), and waves with wavelengths of the order of the mesh size fall in this zone and are essentially not emitted by the electrons. The applicability of this approach was examined in greater detail by Gonoskov et al. [16]. Photon generation during electron motion along curved trajectories can be simulated by the Monte Carlo method (see the 'alternative' method in Elkina et al. [17]). This allows hard radiation in the region above hundreds of kiloelectron volts to be described with sufficient accuracy.
is the radius of curvature of the electron trajectory at a given point. At lower energies, the spectrum has a dip (down to laser harmonics), and waves with wavelengths of the order of the mesh size fall in this zone and are essentially not emitted by the electrons. The applicability of this approach was examined in greater detail by Gonoskov et al. [16]. Photon generation during electron motion along curved trajectories can be simulated by the Monte Carlo method (see the 'alternative' method in Elkina et al. [17]). This allows hard radiation in the region above hundreds of kiloelectron volts to be described with sufficient accuracy.
The longitudinal profile of an incident laser pulse had the form
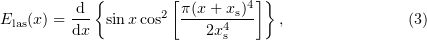
where the parameter  determines the pulse duration (in our simulations, it was taken to be
determines the pulse duration (in our simulations, it was taken to be  ). The transverse profile had a similar form. The profile has an essentially constant electromagnetic field amplitude in the central part of the pulse and falls off sharply distance
). The transverse profile had a similar form. The profile has an essentially constant electromagnetic field amplitude in the central part of the pulse and falls off sharply distance 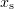 from the centre. Thus, the problem is brought nearer to an idealised case of incidence of a plane wave on a target and allows the effects resulting from the finite pulse size to be minimised.
from the centre. Thus, the problem is brought nearer to an idealised case of incidence of a plane wave on a target and allows the effects resulting from the finite pulse size to be minimised.
The target used was a 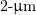 -thick plain film with an ion mass-to-charge ratio four times that of the proton. This roughly corresponds to a heavy element (e.g. Au) target with a degree of ionisation reaching 50 % to 70 % at the laser pulse intensity and duration under consideration. The laser wavelength was
-thick plain film with an ion mass-to-charge ratio four times that of the proton. This roughly corresponds to a heavy element (e.g. Au) target with a degree of ionisation reaching 50 % to 70 % at the laser pulse intensity and duration under consideration. The laser wavelength was 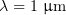 . The mesh size was
. The mesh size was 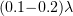 and the number of particles per cell was two (test simulations with eight particles per cell revealed no significant differences in results).
and the number of particles per cell was two (test simulations with eight particles per cell revealed no significant differences in results).
3.1. Influence of the angle of incidence and target density on gamma-ray generation efficiency
If the dimensionless laser field amplitude is 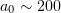 , the electron energy in the course of interaction may reach
, the electron energy in the course of interaction may reach 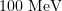 or more and, in the case of synchrotron emission, most of the energy is emitted in the gamma region. At such high intensities, gamma radiation takes away a considerable part of the incident laser pulse energy (up to tens of percent). Gamma-ray generation efficiency
or more and, in the case of synchrotron emission, most of the energy is emitted in the gamma region. At such high intensities, gamma radiation takes away a considerable part of the incident laser pulse energy (up to tens of percent). Gamma-ray generation efficiency 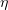 can be determined as the ratio of the energy of all emitted gamma-ray photons
can be determined as the ratio of the energy of all emitted gamma-ray photons 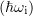 to the initial laser pulse energy
to the initial laser pulse energy  :
:

where  is the end point time of the simulation. Efficiency can be found by numerical calculations using (4) provided that the simulation time is sufficiently long and the size of the simulation region is sufficiently large (the laser pulse should completely interact with the target over time
is the end point time of the simulation. Efficiency can be found by numerical calculations using (4) provided that the simulation time is sufficiently long and the size of the simulation region is sufficiently large (the laser pulse should completely interact with the target over time 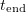 and the gamma-ray photons should not have time enough to leave the simulation region).
and the gamma-ray photons should not have time enough to leave the simulation region).
For a laser pulse with 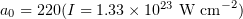 , we carried out a series of 78 numerical experiments with a variable angle of incidence on the film, 0 to
, we carried out a series of 78 numerical experiments with a variable angle of incidence on the film, 0 to 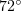 , and different electron concentrations,
, and different electron concentrations, 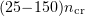 (
(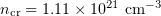 at the parameters used). The laser light intensity and the ranges of angles of incidence and electron concentrations correspond to realistic experimental conditions, where targets from various materials are bombarded in an existing laser system.
at the parameters used). The laser light intensity and the ranges of angles of incidence and electron concentrations correspond to realistic experimental conditions, where targets from various materials are bombarded in an existing laser system.
Figure 3 shows gamma-ray generation efficiency 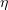 as a function of
as a function of 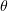 and
and 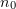 . The maximum value of
. The maximum value of 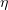 is 29 %, at
is 29 %, at 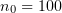 and
and 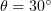 . The existence of an optimum is an important result, which can be used e.g. in experimental design. The presence of an optimal plasma density can be accounted for as follows: On the one hand, reducing the plasma density leads to a decrease in the number of electrons capable of interacting with the laser field and emitting photons. On the other, with increasing plasma density the penetration depth of laser pulses in the film decreases (at plasma densities above the relativistic self-induced transparency threshold [18], laser pulses are completely reflected from the plasma surface). We also observed a threshold in our numerical experiments. At normal incidence, the
. The existence of an optimum is an important result, which can be used e.g. in experimental design. The presence of an optimal plasma density can be accounted for as follows: On the one hand, reducing the plasma density leads to a decrease in the number of electrons capable of interacting with the laser field and emitting photons. On the other, with increasing plasma density the penetration depth of laser pulses in the film decreases (at plasma densities above the relativistic self-induced transparency threshold [18], laser pulses are completely reflected from the plasma surface). We also observed a threshold in our numerical experiments. At normal incidence, the 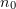 corresponding to the highest gamma-ray generation efficiency was approximately a factor of 2 – 3 lower than the threshold,
corresponding to the highest gamma-ray generation efficiency was approximately a factor of 2 – 3 lower than the threshold, 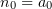 .
.
Figure 3. Gamma-ray generation efficiency as a function of plasma density 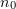 and angle of incidence
and angle of incidence 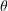 .
.
Download figure:
Standard imageIt should be noted that the relativistic self-induced transparency threshold depends on 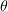 . When we transform to a frame of reference moving at a velocity
. When we transform to a frame of reference moving at a velocity 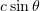 , the external field equation transforms according to (1), whereas the dimensionless amplitude
, the external field equation transforms according to (1), whereas the dimensionless amplitude 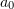 remains unchanged. The critical plasma density in the new frame has the form
remains unchanged. The critical plasma density in the new frame has the form

In laser – plasma interaction problems, a similarity law is typically valid [12, 19]: characteristics of interaction (dynamics of particles and radiation parameters) remain similar upon changes in  and
and 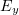 if the
if the  ratio remains unchanged. Also, a similarity parameter
ratio remains unchanged. Also, a similarity parameter 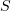 , which determines interaction conditions, can be introduced as the ratio of the dimensionless plasma density to the dimensionless laser field amplitude:
, which determines interaction conditions, can be introduced as the ratio of the dimensionless plasma density to the dimensionless laser field amplitude:

Substituting the transformations from (1), we find that, for 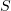 to remain constant, the dimensionless plasma density should vary as follows:
to remain constant, the dimensionless plasma density should vary as follows:

If the maximum gamma-ray generation efficiency corresponds to a certain value of the parameter 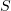 , the position of the maximum
, the position of the maximum 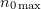 should also be described by (7). In the map presented in Fig. 3,
should also be described by (7). In the map presented in Fig. 3,  is seen to have a tendency to decrease roughly as
is seen to have a tendency to decrease roughly as 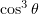 as the angle of incidence
as the angle of incidence 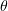 increases from
increases from  to
to 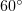 . At the same time, there is a region in the angular range
. At the same time, there is a region in the angular range  where
where  increases with increasing
increases with increasing 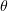 . It seems likely that the variation of the characteristics of interaction with
. It seems likely that the variation of the characteristics of interaction with  is inadequately described by the similarity law. This may be due to the presence of additional, angle-dependent terms in the equations [like in (2)].
is inadequately described by the similarity law. This may be due to the presence of additional, angle-dependent terms in the equations [like in (2)].
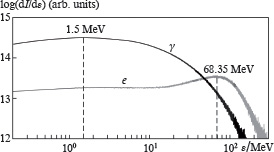
Figure 4 shows the gamma-ray and electron spectra of the target at the optimal parameters for effective generation 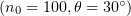 . The electron spectrum has a well-defined peak at about
. The electron spectrum has a well-defined peak at about 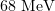 . Thus, the typical Lorentz factor (140) is of the same order as
. Thus, the typical Lorentz factor (140) is of the same order as 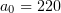 . The highest gamma-ray intensity is observed around
. The highest gamma-ray intensity is observed around  , but the intensity decreases rather slowly with frequency, so there is a considerable fraction of gamma-ray photons with energies of tens of megaelectron volts.
, but the intensity decreases rather slowly with frequency, so there is a considerable fraction of gamma-ray photons with energies of tens of megaelectron volts.
Figure 4. Gamma-ray and electron spectra of the target at 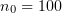 and
and 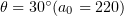 .
.
Download figure:
Standard image3.2. Radiation pattern of gamma-ray photons
In practical applications, not only high efficiency but also good directivity of gamma-ray generation are important. In contrast to the optical range, gamma rays cannot be focused, so directivity requirements are imposed on sources.
In the case of relativistic laser – plasma interaction, gamma-ray directivity is due to the dynamics of electrons, which emit by the synchrotron mechanism within a narrow cone of angle 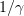 along their trajectory at each point. The power of the radiation is proportional to the fourth power of the Lorentz factor and the square of the trajectory curvature,
along their trajectory at each point. The power of the radiation is proportional to the fourth power of the Lorentz factor and the square of the trajectory curvature,

so necessary conditions for efficient and directional emission are that electrons have a large Lorentz factor over an extended part of their trajectory and that the direction of their velocity vector vary only slightly in this part (but the direction should still vary because the radius of curvature of the trajectory should remain not very large). In the case of oblique incidence, this may be facilitated by the fact that electrons enter the 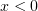 region and the longitudinal field component
region and the longitudinal field component 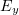 strongly accelerates them.
strongly accelerates them.
Three-dimensional simulation allows one to construct the radiation pattern of gamma rays because the velocity direction and the energy of each photon are known. By analogy with antenna theory, we introduce radiation directivity 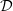 as the ratio of the maximum radiation intensity in the radiation pattern to the intensity averaged over all directions. Thus,
as the ratio of the maximum radiation intensity in the radiation pattern to the intensity averaged over all directions. Thus, 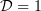 in the case of an isotropic radiation pattern and
in the case of an isotropic radiation pattern and 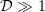 in a highly anisotropic system.
in a highly anisotropic system.
We can also introduce a gain 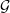 as the product of efficiency
as the product of efficiency 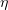 and directivity
and directivity 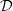 .
.  quantifies the ability of a source to emit intense directional radiation.
quantifies the ability of a source to emit intense directional radiation.
Figure 5 shows the  map for the same values of parameters as in Fig. 3. As above, the distribution has an optimum at an angle
map for the same values of parameters as in Fig. 3. As above, the distribution has an optimum at an angle 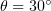 , but the corresponding plasma density is lower:
, but the corresponding plasma density is lower:  (against
(against  in Fig. 3). The most interesting result is the presence of another region with high
in Fig. 3). The most interesting result is the presence of another region with high 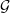 , at larger angles
, at larger angles 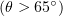 . In spite of the low efficiency, owing to the very high radiation directivity this region is favourable for the generation of relatively intense, directional radiation. Figure 6 illustrates the effect of the angle of incidence on the radiation pattern at
. In spite of the low efficiency, owing to the very high radiation directivity this region is favourable for the generation of relatively intense, directional radiation. Figure 6 illustrates the effect of the angle of incidence on the radiation pattern at 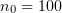 .
.
Figure 5. Gain 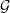 as a function of plasma density
as a function of plasma density 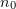 and angle of incidence
and angle of incidence 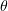 .
.
Download figure:
Standard imageFigure 6. Radiation patterns of gamma rays in the  plane at
plane at 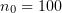 and different angles of incidence
and different angles of incidence 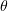 . The emission angle is measured counterclockwise from the
. The emission angle is measured counterclockwise from the  axis (see Fig. 1).
axis (see Fig. 1).
Download figure:
Standard imageOur numerical experiments did not cover the angular range 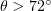 because simulation of a laser pulse incident at a grazing angle to the film requires a substantial increase in the size of the simulation region and computation time and complexity. Nevertheless, we obtained valuable simulation results that allow important effects at large angles of incidence to be highlighted.
because simulation of a laser pulse incident at a grazing angle to the film requires a substantial increase in the size of the simulation region and computation time and complexity. Nevertheless, we obtained valuable simulation results that allow important effects at large angles of incidence to be highlighted.
The radiation patterns in the 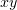 plane in Fig. 6 help to understand the origin of the second optimal region. There are three distinct types of radiation patterns: two symmetric lobes at
plane in Fig. 6 help to understand the origin of the second optimal region. There are three distinct types of radiation patterns: two symmetric lobes at  ; an asymmetric, but rather broad pattern at intermediate angles of incidence (approximately from
; an asymmetric, but rather broad pattern at intermediate angles of incidence (approximately from 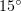 to
to  ); and a pattern strongly elongated along the
); and a pattern strongly elongated along the 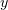 axis for
axis for 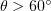 (in numerical simulations, it is observed at
(in numerical simulations, it is observed at 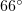 and
and 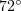 ). In the last case, the radiation is focused essentially in the propagation direction of the laser pulse.
). In the last case, the radiation is focused essentially in the propagation direction of the laser pulse.
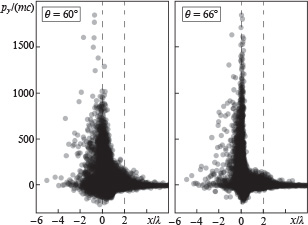
To understand the cause of the qualitative change in the shape of the radiation pattern for 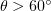 , the characteristics of plasma electrons should be analysed in greater detail using numerical simulation. Figure 7 shows the electron distributions obtained by numerical simulation in
, the characteristics of plasma electrons should be analysed in greater detail using numerical simulation. Figure 7 shows the electron distributions obtained by numerical simulation in 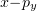 space at angles of incidence of
space at angles of incidence of 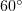 and
and 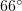 . These values of
. These values of  were chosen due to the qualitative change in the shape of the radiation pattern (see Fig. 6). Both distributions are obtained at the instants when the trailing edge of the laser pulse reaches the boundary of the plasma. It is seen that, in both cases, electrons with high longitudinal momenta are concentrated mainly near the left boundary of the plasma layer. Moreover, a considerable part of them are located outside the layer
were chosen due to the qualitative change in the shape of the radiation pattern (see Fig. 6). Both distributions are obtained at the instants when the trailing edge of the laser pulse reaches the boundary of the plasma. It is seen that, in both cases, electrons with high longitudinal momenta are concentrated mainly near the left boundary of the plasma layer. Moreover, a considerable part of them are located outside the layer 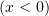 .
.
Figure 7. Distributions of the electron momentum component along the layer,  , obtained by numerical simulation at
, obtained by numerical simulation at 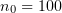 and
and 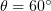 and
and  .
.
Download figure:
Standard imageAn essential distinction is that, at 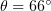 , the number of electrons with very high energies
, the number of electrons with very high energies ![$[p_{y}/(mc) > 1000]$](https://content.cld.iop.org/journals/1063-7818/46/4/299/revision1/qel_46_4_299ieqn152.gif) increases considerably. since the synchrotron radiation intensity is proportional to
increases considerably. since the synchrotron radiation intensity is proportional to 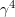 , an increase in longitudinal momentum has a very strong effect on the rise in gamma-ray generation efficiency along the
, an increase in longitudinal momentum has a very strong effect on the rise in gamma-ray generation efficiency along the 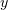 axis, as observed in our numerical experiments.
axis, as observed in our numerical experiments.
It is also worth noting that, at 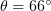 , electrons with high
, electrons with high 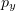 are present in the
are present in the 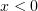 region somewhat more often than in the
region somewhat more often than in the 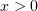 region. This seems to be due to the strong
region. This seems to be due to the strong 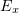 field at large angles of incidence. The increase in the number of electrons outside the plasma layer, in the region of the strong laser field, may be responsible for the increase in radiation intensity at large angles, but further work is needed to identify the exact physical mechanism of this process.
field at large angles of incidence. The increase in the number of electrons outside the plasma layer, in the region of the strong laser field, may be responsible for the increase in radiation intensity at large angles, but further work is needed to identify the exact physical mechanism of this process.
4. Conclusions
At oblique incidence on a flat target with a near-critical relativistic plasma density, relativistic laser pulses with an intensity from 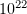 to
to 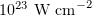 are reflected from the film surface, and electrons in the ionised substance are accelerated to relativistic velocities (with
are reflected from the film surface, and electrons in the ionised substance are accelerated to relativistic velocities (with 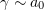 ). In this process, electrons effectively emit in the hard X-ray and gamma regions. We have carried out three-dimensional simulation of the interaction process and observed efficient conversion of the laser pulse energy to the gamma-ray photon energy with efficiencies up to tens of percent. Optimising the angle of incidence and plasma density, we were able to find efficient generation conditions, which correspond to an angle of
). In this process, electrons effectively emit in the hard X-ray and gamma regions. We have carried out three-dimensional simulation of the interaction process and observed efficient conversion of the laser pulse energy to the gamma-ray photon energy with efficiencies up to tens of percent. Optimising the angle of incidence and plasma density, we were able to find efficient generation conditions, which correspond to an angle of  . The highest efficiency obtained in numerical experiments at a dimensionless laser field amplitude
. The highest efficiency obtained in numerical experiments at a dimensionless laser field amplitude 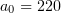 is 29 %.
is 29 %.
Analysis of gamma-ray directivity also demonstrates conditions, at large angles of incidence 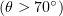 , under which radiation is well-focused along the
, under which radiation is well-focused along the 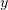 axis, but the gamma-ray generation efficiency is then not so high. If the purpose is to obtain both an intense and directional radiation source, an optimum is reached in both regimes at
axis, but the gamma-ray generation efficiency is then not so high. If the purpose is to obtain both an intense and directional radiation source, an optimum is reached in both regimes at 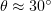 and
and 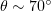 . We also have analysed the cause of the qualitative change in the shape of the radiation pattern (radiation localisation along the
. We also have analysed the cause of the qualitative change in the shape of the radiation pattern (radiation localisation along the 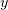 axis) at large angles. Numerical simulation indicates a substantial increase in the
axis) at large angles. Numerical simulation indicates a substantial increase in the 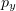 component of the electron momentum between the
component of the electron momentum between the 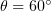 and
and  simulations and an increase in the number of electrons outside the plasma layer. It seems likely that, as a result of the increase in the
simulations and an increase in the number of electrons outside the plasma layer. It seems likely that, as a result of the increase in the 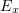 component of the electric field with increasing
component of the electric field with increasing  , electrons are more and more often removed from the plasma and begin to effectively interact with the
, electrons are more and more often removed from the plasma and begin to effectively interact with the  field. As a result,
field. As a result, 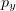 strongly increases and the emission along the
strongly increases and the emission along the 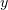 axis prevails.
axis prevails.
We also have carried out a semianalytical modelling of the shape of the plasma surface in the case of interaction with an obliquely incident laser pulse. To this end, we used a modified model for normal incidence [12]. The function thus obtained adequately describes the shape of the plasma surface, which has the form of a wavy structure.
Acknowledgements.
This work was supported by the RF Government (Grant No. 14.V25.31.0008) and the Russian Foundation for Basic Research (Grant No. 15-02-06079).