Abstract
There has been growing interest in investigating chiral phonons since they are theoretically found and experimentally verified recently. In a magnetic system with time inversion symmetry breaking, phonon can have nonzero angular momentum, which makes a correction to the gyromagnetic ratio measured in the Einstein–de Haas effect. Though total phonon angular momentum is zero in a nonmagnetic two-dimensional (2D) hexagonal system with space inversion symmetry breaking, phonons at high symmetry points of the Brillouin zone can have nonzero phonon angular momentum, which means they are chiral phonons. Chiral phonons decide selection rules in the electronic intervalley scattering, which has been experimentally verified in tungsten-diselenide monolayers very recently (Zhu et al 2018 Science 359 579). In this review, after a brief introduction of related background and some basic concepts, we mainly report recent progress of phonon angular momentum in magnetic systems and chiral phonon in nonmagnetic systems. We also review known experiments in verifications of the phonon chirality and finally conclude with an outlook of future developments.
Export citation and abstract BibTeX RIS
1. Introduction
Chirality, which is different from its mirror image, is a basic property of matter and denotes the asymmetric property of a system or an object. The chirality is an important quantum concept in modern physics for elementary and quasi-particles [1]. In graphene systems, the electronic chirality can distinguish the transport properties such as the Klein tunneling and the Landau quantization [2, 3]. On one hand, in the valley-electron interband scattering, the emergence of optical chirality leads to the valleytronics [4]. On the other hand, in the intervalley scattering of electrons, the valley phonons will be involved [5]. Thus a natural question is whether the phonons involved in the scattering process have chirality? Traditionally, people in both theories and experiments hold that phonon angular momentum is zero, i.e. phonon has no chirality.
However, it was reported that phonons in magnetic materials can be distorted by the spin–phonon interaction and thus led to the phonon Hall effect [6, 7]. Recent theoretical work [8] also found that phonon can have nonzero angular momentum in magnetic systems with time inversion symmetry breaking, which can correct the measurement of gyromagnetic ratio in the Einstein–de Haas effect [9]. Besides, in nonmagnetic two-dimensional (2D) hexagonal systems, where the space inversion symmetry is broken, valley phonons were found to have definite chiralities though the total phonon angular momentum is zero [10]. Very recently, the predicted circularly rotating chiral phonons were experimentally verified in monolayer WSe [11]. The finding of phonon chirality is a significant progress since it reveals that phonon, a kind of Bosonic collective excitation, can attain the chirality. Considering that we can vastly excite chiral phonons by a optical pump-probe technique [11], the manipulation of phonon chirality becomes possible, which is very important for the future applications. The chiral phonons are also important for the control of topological states [12], the electronic phase transition [13, 14], the intervalley scattering [4, 5, 15], as well as the solid state quantum information applications [16, 17]. The finding of chiral phonons also promotes the progress of other fields such as the valley transport of sonic crystals [15], the polarization in two-dimensional (2D) materials [18] and so on.
[11]. The finding of phonon chirality is a significant progress since it reveals that phonon, a kind of Bosonic collective excitation, can attain the chirality. Considering that we can vastly excite chiral phonons by a optical pump-probe technique [11], the manipulation of phonon chirality becomes possible, which is very important for the future applications. The chiral phonons are also important for the control of topological states [12], the electronic phase transition [13, 14], the intervalley scattering [4, 5, 15], as well as the solid state quantum information applications [16, 17]. The finding of chiral phonons also promotes the progress of other fields such as the valley transport of sonic crystals [15], the polarization in two-dimensional (2D) materials [18] and so on.
In this review, we first give a brief introduction of the related background and some basic concepts, including Einstein–de Haas effect, phonon Hall effect, phonon angular momentum, phonon chirality, phonon pseudo-angular momentum. Then, focusing on the 2D systems, the progress of chiral phonons and phonon-chirality induced new effects are specially reviewed. Finally, we summarize the known experiments verifications of the phonon chirality and conclude with an overview of future developments of chiral phonons.
1.1. Einstein–de Haas effect
The Einstein–de Haas effect [9, 19] is a phenomenon of mechanical rotation that is induced by the magnetization change. It is Einstein's only experiment during his life, which collaborated with de Haas. As shown in figure 1, the experiment was originally designed to prove the existence of Ampere's molecular currents. Einstein considered that the electron rotation around the nucleus and the electron spin formed the molecule electric current, which was the origin of the magnetism of matter. The ratio of atomic magnetic moment ( )
)
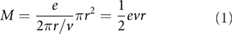
to the total 

denotes the gyromagnetic ratio

where  is the Lande factor. The published results of
is the Lande factor. The published results of  in the Einstein–de Haas experiment was 1.02, but later experiments showed that
in the Einstein–de Haas experiment was 1.02, but later experiments showed that  which indirectly confirmed the electron spin found in the Stern–Gerlach experiment. In the ferromagnet, the atomic magnetic moment mainly comes from the spin instead of the orbital moment. According to the relation of
which indirectly confirmed the electron spin found in the Stern–Gerlach experiment. In the ferromagnet, the atomic magnetic moment mainly comes from the spin instead of the orbital moment. According to the relation of  with respect to
with respect to  and the conservation of
and the conservation of  , we have
, we have


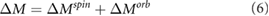
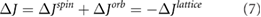

Figure 1. The mechanical rotation of a freely suspended body caused by the change of its magnetization.
Download figure:
Standard image High-resolution imageThe Einstein–de Haas effect provided an effective way to measure the  of different materials. The accuracy of
of different materials. The accuracy of  is key to determine the contribution of orbit and spin to the total
is key to determine the contribution of orbit and spin to the total  . The macroscopic visible mechanic rotation just reflects the motion of rigid body. The
. The macroscopic visible mechanic rotation just reflects the motion of rigid body. The  of phonon (
of phonon ( ), which is zero in the traditional sense, was not taken into account in the Einstein–de Haas effect. If phonon has nonzero
), which is zero in the traditional sense, was not taken into account in the Einstein–de Haas effect. If phonon has nonzero  , the total
, the total  should consider the contribution of phonon so that the
should consider the contribution of phonon so that the  need to be corrected.
need to be corrected.
1.2. Phonon Hall effect
Since the discovery of classic Hall effect of electrons, Leduc [20] proposed that the heat conductor of metal should have similar behavior. The transverse heat current arose once the temperature gradient was exerted, which was the thermal Hall effect or the Righi-Leduc effect. Different from the case of metal where the electron are main carriers, the phonons are the carrier of the heat current in the electric insulating crystal. The phonon Hall effect (PHE) was subsequently found by Strohm et al [6] and subsequently reproduced by Inyushkin and Taldenkov [22]. As shown in figure 2, when the magnetic field is exerted in the paramagnetic insulating thin film with longitudinal temperature gradient, we can observe the transverse temperature difference in the direction perpendicular to the longitudinal temperature gradient. The PHE is a exciting finding because phonon is a neutral pasi-particle which can not directly interacts with the magnetic field and thus suffers from the Lorentz force. This creative finding provides a new degree to manipulate the phonon by the magnetic field.
Figure 2. The phonon Hall effect: the direction of the heat flow is deflected by the magnetic field [21].
Download figure:
Standard image High-resolution imageSince the discover of PHE, some theories [23, 24] such as the spin–phonon interaction were proposed to understand the PHE. The magnetic field, which can not directly interacts with the phonon, only induces the polarization of the paramagnetic ion. The coupling between the paramagnetic ion and the phonon induces the PHE, which is also called the Raman spin–phonon interaction. For phonon Hall effect, the topological nature was investigated and topological phase transition was found [7], and a recent review on topological phonons is also reported [25]. The magnetic field exerts an effective force to distort the transport of phonon so that a transverse heat current emerges [26]. Thus, a natural question is whether the phonon current has nonzero angular momentum with some new macroscopic effects?
2. Basic concepts
2.1. Phonon angular momentum
The lattice angular momentum corresponding to the mechanical rotation of rigid-body motion of the sample is
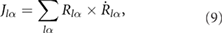
it only reflects the rigid-body motion. In a microscopic picture, similar to the lattice angular momentum (rigid-body part), the phonon angular momentum can be defined as [8]
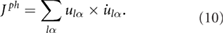
In the equation,  is a displacement vector which belong to the
is a displacement vector which belong to the  th atom in the
th atom in the  th unit cell, here we're going to do the mass normalization by multiplying the square root of the mass, and the purpose is to simplify the angular momentum. Along
th unit cell, here we're going to do the mass normalization by multiplying the square root of the mass, and the purpose is to simplify the angular momentum. Along  direction,
direction,  . In the second quantization form, the displacement can be given as
. In the second quantization form, the displacement can be given as

with  ,
,  and
and  are the wave vector and branch, respectively.
are the wave vector and branch, respectively.  is a displacement polarization vector. Then the total phonon angular momentum can be written as [8]
is a displacement polarization vector. Then the total phonon angular momentum can be written as [8]
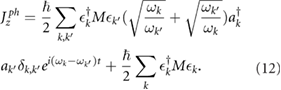
Here

 is the quantity of atoms in a unit cell. In equilibrium, the total phonon angular momentum changes into [8],
is the quantity of atoms in a unit cell. In equilibrium, the total phonon angular momentum changes into [8],
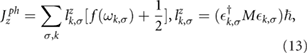
 is the Bose–Einstein distribution. In equation (13), all the wave vectors and all phonon branches are summed
is the Bose–Einstein distribution. In equation (13), all the wave vectors and all phonon branches are summed  . Here,
. Here,  is the phonon angular momentum with wave vector
is the phonon angular momentum with wave vector  and branch
and branch  , it is real and in proportion to
, it is real and in proportion to  . At zero temperature, the form of the total phonon angular momentum is
. At zero temperature, the form of the total phonon angular momentum is  , it means that every phonon mode
, it means that every phonon mode  has a zero-point energy of
has a zero-point energy of  and has a nonzero angular momentum(zero-point angular momentum)
and has a nonzero angular momentum(zero-point angular momentum)  .
.
2.2. Phonon chirality
Recently, the helicity-resolved Raman scattering has been experimentally observed in transition-metal dichalcogenide (TMD) atomic layers [27]. The authors found that the helicity of incident photons can be completely reversed by the Brillouin-zone-center  phonons. Such a finding implies that not only the valley phonons but also the
phonons. Such a finding implies that not only the valley phonons but also the  phonons which involved in the intravalley scattering of electrons can have chirality. Therefore, in the Brillouin zone high-symmetry points of the hexagonal lattices, investigating chirality of the phonons is highly desirable.
phonons which involved in the intravalley scattering of electrons can have chirality. Therefore, in the Brillouin zone high-symmetry points of the hexagonal lattices, investigating chirality of the phonons is highly desirable.
The two-dimensional honeycomb AB lattice, which has two sublattices (A and B) in each unit cell, can be used as a simplified model to demonstrate the general features of chiral phonons in monolayer materials, such as gapped graphene with isotopic doping [28] or staggered sublattice potential [29], hexagonal boron nitride [30]. By calculating the eigenvectors, the sublattice vibrations at valleys can be plotted, as shown in figure 3(a). We can see that the whole vibrations at the valleys are circularly polarized. The valley phonon modes from band 1 to band 4 are shown in the figure. Among it, two sublattices of band 1 and band 4 do circular motion in the opposite direction; two sublattices of band 2 and band 3 are different from the above, one is still, the other is a circular motion. The direction of the circular motion will be reversed from  to
to  .
.
Figure 3. Valley phonons of a honeycomb AB lattice. (a) Phonon dispersion relation and phonon vibrations for sublattices A and B in one unit cell of a honeycomb AB lattice. (b) Phase correlation of the phonon nonlocal part for sublattice A (upper two panels) and sublattice B (lower two panels) at  (left panels) and
(left panels) and  (right panels). (c) Phonon pseudoangular momentum for bands 1–4 at valleys
(right panels). (c) Phonon pseudoangular momentum for bands 1–4 at valleys  and
and  [10].
[10].
Download figure:
Standard image High-resolution imageThe phonon chirality can be characterized by the polarization of phonons along the  direction. The phonon eigenvectors can be written as [10]
direction. The phonon eigenvectors can be written as [10]  . A new basis of
. A new basis of  and
and  ) can be used to represent the right-handed circular polarization and left-handed circular polarization.
) can be used to represent the right-handed circular polarization and left-handed circular polarization.

Using above basis, the phonon eigenvector  can be represented as
can be represented as
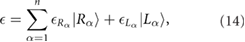
where  ,
, 
 . The phonon circular polarization operator along the
. The phonon circular polarization operator along the  direction is defined as
direction is defined as
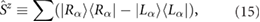
phonon circular polarization can be expressed as
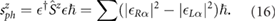
Here, the hexagonal lattices has two atoms in a unit cell, so the value of  is 2. Since
is 2. Since  , the value of the phonon circular polarization is between
, the value of the phonon circular polarization is between  . Along the
. Along the  direction, the
direction, the  has the same form with the phonon angular momentum
has the same form with the phonon angular momentum  [8]. We use
[8]. We use  to represent the contribution of each sublattice of the unit cell to the phonon circular polarization. As shown in figure 3(a), at valley
to represent the contribution of each sublattice of the unit cell to the phonon circular polarization. As shown in figure 3(a), at valley  , for band 2,
, for band 2,  ; for band 3,
; for band 3,  ; for band 1 and band 4, the magnitudes of sublattices A and B are different with opposite circular vibrations. Therefore,the circular polarization of phonon
; for band 1 and band 4, the magnitudes of sublattices A and B are different with opposite circular vibrations. Therefore,the circular polarization of phonon  which is at the valleys can be nonzero. As mentioned above, introducing a staggered sublattice on-site potential or isotope doping can lead to the similar chiral phonons at the valleys. At the Brillouin zone center
which is at the valleys can be nonzero. As mentioned above, introducing a staggered sublattice on-site potential or isotope doping can lead to the similar chiral phonons at the valleys. At the Brillouin zone center  , we can see doubly degenerate acoustic modes and optical modes, both of which are not circularly polarized. Through superposing the degenerated modes the circularly polarized phonon modes can always be obtained.
, we can see doubly degenerate acoustic modes and optical modes, both of which are not circularly polarized. Through superposing the degenerated modes the circularly polarized phonon modes can always be obtained.
2.3. Phonon pseudoangular momentum
At the high-symmetry points  in a honeycomb lattice,the phonons are invariant to the threefold discrete rotations in the direction perpendicular to the two-dimensional honeycomb lattice plane (figure 3(b)). The eigenvector has a phase change [10]
in a honeycomb lattice,the phonons are invariant to the threefold discrete rotations in the direction perpendicular to the two-dimensional honeycomb lattice plane (figure 3(b)). The eigenvector has a phase change [10]
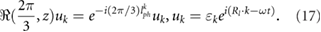
Here  is the rotation operator,
is the rotation operator,  in the equation is defined as the pseudoangular momentum (PAM) and has values of 1,
in the equation is defined as the pseudoangular momentum (PAM) and has values of 1,  , or 0,
, or 0,  is the phonon wave function. The phonon wave function is consisted of two parts, the local (intracell) part
is the phonon wave function. The phonon wave function is consisted of two parts, the local (intracell) part  and the nonlocal (intercell) part
and the nonlocal (intercell) part  . Thus, under the threefold rotation, we can get the spin phonon PAM (
. Thus, under the threefold rotation, we can get the spin phonon PAM ( ) for the intracell part and the orbital phonon PAM (
) for the intracell part and the orbital phonon PAM ( ) for the intercell part. The total phonon PAM
) for the intercell part. The total phonon PAM

For the left-handed or right-handed polarization of A and B atoms, it can be represented by the spin PAM  ,
,  .
.
The orbital PAM is obtained by the change of the phase  under the threefold rotation. As shown in figure 3(b), at the valley
under the threefold rotation. As shown in figure 3(b), at the valley  or
or  , the orbital PAM of the sublattices A and B is opposite and the value is 1 or
, the orbital PAM of the sublattices A and B is opposite and the value is 1 or  . At the
. At the  point, the sublattices A and B have no phase change, so the orbital PAM is zero. The spin PAM is obtained by the phase change of
point, the sublattices A and B have no phase change, so the orbital PAM is zero. The spin PAM is obtained by the phase change of  . At the valley
. At the valley  ,
,  for bands 1 and 4; For band 2,
for bands 1 and 4; For band 2,  = 0,
= 0,  ; for band 3,
; for band 3,  ,
,  . At the valley
. At the valley  , the value of spin PAM is opposite to the valley
, the value of spin PAM is opposite to the valley  .
.
As the phonon wave function  is the eigenstate of the rotation operator
is the eigenstate of the rotation operator  , if both sublattices are vibrating, the phonon PAM equals to
, if both sublattices are vibrating, the phonon PAM equals to
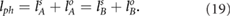
The values of phonon PAM are listed in figure 3(c). We can see that the orbital PAM and spin PAM of A and B can verify above equation. If one of the sublattices does not vibrate, the phonon PAM is determined by the other vibrational sublattice. At the  point, the orbital PAM is zero, so the above equation changes into
point, the orbital PAM is zero, so the above equation changes into

As mentioned in the end of above section, the sublattices can do circular vibration by superposing the doubly degenerate modes. Therefore, the value of the  is 1 or
is 1 or  .
.
In the unit cell, each sublattice can be selected as the center of the threefold rotation with a zero orbital phonon PAM. Thus, the spin PAM is equal to the phonon PAM according to equation (20). That is to say the value of spin PAM is  or 0. Therefore, all the phonon modes at valleys (figure 3(a)) do circular motion, otherwise the phonon modes are still.
or 0. Therefore, all the phonon modes at valleys (figure 3(a)) do circular motion, otherwise the phonon modes are still.
3. Phonon angular momentum in magnetic systems
3.1. The Hamiltonian
In a uniform external magnetic field, the Hamiltonian for ionic crystals is written as [23, 24]
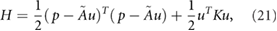
 is a column vector which from lattice equilibrium positions of displacements, the quality normalization has been completed by multiplying square root of mass,
is a column vector which from lattice equilibrium positions of displacements, the quality normalization has been completed by multiplying square root of mass,  is a force constant matrix,
is a force constant matrix,  is a conjugate momentum vector, the
is a conjugate momentum vector, the  term reflects the Raman spin–phonon interaction [31, 32],
term reflects the Raman spin–phonon interaction [31, 32],  is an antisymmetric real matrix [33], the dimension of the matrix is
is an antisymmetric real matrix [33], the dimension of the matrix is  ,
,  is the dimension of the lattice vibrations and
is the dimension of the lattice vibrations and  is the number of total sizes.
is the number of total sizes.  can be block diagonal, and the element is
can be block diagonal, and the element is
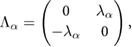
where we only consider two-dimensional motion in the honeycomb lattice, so  (
( and
and  directions).
directions).  has the dimension of frequency, and it is proportional to the magnetization and the spin–phonon interaction.
has the dimension of frequency, and it is proportional to the magnetization and the spin–phonon interaction.
When there is no spin–phonon interaction on the system, the Hamiltonian is reduced to
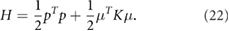
Use  to solve the eigenvalue equation
to solve the eigenvalue equation  , we can get
, we can get  ,
,  and
and  . The total phonon angular momentum
. The total phonon angular momentum  1 if we sum over all phonon modes. However, when the system has a spin–phonon interaction,
1 if we sum over all phonon modes. However, when the system has a spin–phonon interaction,  , the total phonon angular momentum
, the total phonon angular momentum  , which is shown in figure 4.
, which is shown in figure 4.
Figure 4. (a) The phonon angular  as a function of
as a function of  . (b) The contour plot of the phonon angular momentum a function of
. (b) The contour plot of the phonon angular momentum a function of  and
and  . (c)The phonon angular momentum from different phonon bands as a function of temperature
. (c)The phonon angular momentum from different phonon bands as a function of temperature  at
at  THz, where the arrow denotes the Debye temperature of the model (
THz, where the arrow denotes the Debye temperature of the model ( K). (d) The phonon angular momentum from different phonon bands as a function of
K). (d) The phonon angular momentum from different phonon bands as a function of  at
at  K [8].
K [8].
Download figure:
Standard image High-resolution image3.2. Phonon angular momentum of a two-dimensional lattice
With spin–phonon interaction, the phonon angular momenta at zero temperature for different lattices are shown in figure 4(a). The phonon angular momenta of honeycomb and kagome lattices are larger than the triangle and square lattices. The honeycomb and kagome lattices have more sites in one unit cell than the triangle and square lattices, which means the more sites of lattices, the more phonon angular momentum they have. This trend can be understood from the fact that the contribution of optical bands to phonon angular momentum is greater than that of acoustic bands. As shown in figures 4(c) and (d), if the value of  is small,the phonon angular momentum of the acoustic bands almost vanishes at low temperature, so the optical bands do the main contribution to the total phonon angular momentum. Therefore, the more sites of per unit cell, the more optical bands it has, thus the phonon angular momentum will be bigger. As shown in figure 4(a), the total angular momentum
is small,the phonon angular momentum of the acoustic bands almost vanishes at low temperature, so the optical bands do the main contribution to the total phonon angular momentum. Therefore, the more sites of per unit cell, the more optical bands it has, thus the phonon angular momentum will be bigger. As shown in figure 4(a), the total angular momentum  increased with the increase of
increased with the increase of  . As shown in figure 4(b), since
. As shown in figure 4(b), since  is proportional to the magnetization, the sign of phonon angular momentum also changes when the sign of magnetization changes
is proportional to the magnetization, the sign of phonon angular momentum also changes when the sign of magnetization changes  . This can explain the phenomenon that the transverse temperature difference reverses when the magnetic field is reversed in the phonon hall effect.
. This can explain the phenomenon that the transverse temperature difference reverses when the magnetic field is reversed in the phonon hall effect.
3.3. Phonon angular momentum in the classical limit
At the high temperature limit, because of
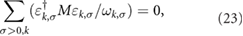
the phonon angular momentum goes to zero. Whether or not the magnetic field is applied, the phonon angular momentum of each unit cell decreases with the increase of temperature and goes to zero at the high temperature limit (the temperature is far greater than the Debye temperature). As the temperature increases, more phonon modes are stimulated. The angular momentums of these modes have opposite direction to the zero-point angular momentum. In the high temperature limit, all stimulated modes are offset by zero-point angular momentum. The vanish of phonon angular momentum can be understood as follows: at high temperature, the classical statistical mechanics is applied to the calculation of phonon angular momentum. A phase-space integral with respect to  and
and  can be obtained by the summation over quantum states, it can change to a pure harmonic system by variable substitution. As discussed earlier, the phonon angular momentum is zero. Furthermore, the Bohr-van Leeuwen theorem illuminates that the average magnetization in the classical mechanics is always zero [34], which makes the phonon angular momentum vanish in the classical limit. Therefore, only in the low-temperature quantum systems that the phonon angular momentum is meaningful.
can be obtained by the summation over quantum states, it can change to a pure harmonic system by variable substitution. As discussed earlier, the phonon angular momentum is zero. Furthermore, the Bohr-van Leeuwen theorem illuminates that the average magnetization in the classical mechanics is always zero [34], which makes the phonon angular momentum vanish in the classical limit. Therefore, only in the low-temperature quantum systems that the phonon angular momentum is meaningful.
3.4. Correction of gyromagnetic ratio
The Einstein–de Haas effect shows that a freely suspended body has mechanical rotation due to its change of magnetization. Einstein and De Haas adopted the resonance method in the experiment. The periodic magnetic field is tuned to be the intrinsic frequency of the suspended objects. Their experiment provide a way to measure the ratio between the change of magnetization and the change of total angular momentum. It is traditionally believed that the total angular momentum of the system is equal to the sum of the lattice angular momentum, spin angular momentum and orbital angular momentum

Due to the conservation of angular momentum, we known that the change of the lattice angular momentum is equal to the sum of the change of the spin angular momentum and the orbital angular momentum
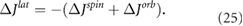
The change of the lattice angular momentum is determined by the mechanical rotation of the sample [35]. But from the microscopic point of view, the angular momentums of all atoms in the sample are equal to the sum of the lattice angular momentum and the phonon angular momentum in equilibrium. So the total angular momentum will have one more phonon angular momentum [8].
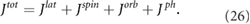
As discussed in the previous section, when there is a spin–phonon interaction, the total phonon angular momentum is not zero. According to the conservation of total angular momentum
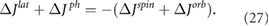
On the other hand, the total magnetization change can be measured using
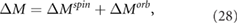
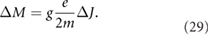
Obviously the  now needs to be corrected. Since the spin–phonon interaction is ubiquitous in the magnetic lattices, the phonon angular momentum is very important.
now needs to be corrected. Since the spin–phonon interaction is ubiquitous in the magnetic lattices, the phonon angular momentum is very important.
3.5. Experimental proposals to measure phonon angular momentum
Phonons have important contribution to total angular momentum, and the magnitude of phonon angular momentum depends on the value of  . The calculation shows that in the presence of spin–phonon interaction, the degenerate phonon modes split at
. The calculation shows that in the presence of spin–phonon interaction, the degenerate phonon modes split at  point and the gap is 2
point and the gap is 2 , so the parameter
, so the parameter  can be obtained from the phonon dispersion relation. This kind of split of the degenerate acoustic modes can be measured by the inelastic neutron scattering or Raman scattering. Because the phonon angular momentum proportional to the magnetization, larger phonon angular momentum can be observed when magnetization in paramagnetic materials is saturated. In the phonon hall effect experiment, the paramagnetic insulator is used to highlight the contribution of phonons in the thermal transport, while the contribution of the electrons and the magnons can be ignored. However, spin–phonon interaction extensively exist in various magnetic materials [36]. A very large magnetization do Ferromagnetic materials have, so we can observe the obvious phonon angular momentum if the spin–phonon interaction is strong.
can be obtained from the phonon dispersion relation. This kind of split of the degenerate acoustic modes can be measured by the inelastic neutron scattering or Raman scattering. Because the phonon angular momentum proportional to the magnetization, larger phonon angular momentum can be observed when magnetization in paramagnetic materials is saturated. In the phonon hall effect experiment, the paramagnetic insulator is used to highlight the contribution of phonons in the thermal transport, while the contribution of the electrons and the magnons can be ignored. However, spin–phonon interaction extensively exist in various magnetic materials [36]. A very large magnetization do Ferromagnetic materials have, so we can observe the obvious phonon angular momentum if the spin–phonon interaction is strong.
For the materials with large magnetization and strong spin–phonon interaction, the zero-point phonon angular momentum is important. According to previous studies, the orbital magnetic moment calculated in some ferromagnetic materials are only a small part of the total magnetic moment, which means that the orbital angular momentum is approximately  times a small value [37]. The phonon angular momentum is comparable to the size of the electron orbital angular momentum, so the phonon angular momentum cannot be ignored.
times a small value [37]. The phonon angular momentum is comparable to the size of the electron orbital angular momentum, so the phonon angular momentum cannot be ignored.
In ferromagnetic insulators, the transport of electrons are negligible. Because the phonon angular momentum decreases with the rising temperature and it tends to zero under the condition of the classical limit, the change of lattice angular momentum can be measured under the low temperature ( ) and the high temperature (
) and the high temperature ( ), so that the the phonon angular momentum can be separated. Here, the dividing line between the low temperature and the high temperature should be the Debye temperature (
), so that the the phonon angular momentum can be separated. Here, the dividing line between the low temperature and the high temperature should be the Debye temperature ( ), which is the critical temperature divides the quantum and classical regions. On the other hand, in order to avoid the participation of the magnon, the high temperature needs to be lower than the Curie temperature, which makes the Curie temperature to be much higher than Debye temperature. So the angular momentum of magnon is almost constant, but the phonon angular momentum changes significantly with the temperature. Fortunately, many ferromagnetic materials can satisfy
), which is the critical temperature divides the quantum and classical regions. On the other hand, in order to avoid the participation of the magnon, the high temperature needs to be lower than the Curie temperature, which makes the Curie temperature to be much higher than Debye temperature. So the angular momentum of magnon is almost constant, but the phonon angular momentum changes significantly with the temperature. Fortunately, many ferromagnetic materials can satisfy  ,
,  , their Curie temperature is about 1000 K, and their Debye temperature is lower than 500 K [38].
, their Curie temperature is about 1000 K, and their Debye temperature is lower than 500 K [38].
Except for the application in measuring the gyromagnetic ratio, the nonzero phonon angular momentum also provides an effective method to study the spin–phonon interaction of magnetic materials. In ferromagnetic materials, there is an open question to separate the contributions to the thermal hall effect from phonons and magnons, a method to obtain the phonon contribution is gived by the phonon angular momentum.
4. Chiral phonons in nonmagnetic systems
4.1. Brief introduction of valleytronics
Due to the breaking of spatial inversion symmetry, the separated valleys  and
and  in momentum space are no longer equivalent, this kind of nonequivalence property can be described by the Berry curvature or orbital magnetic moment. The two valleys constitute another degree of freedom for the electrons besides charge and spin. Therefore, the construction of the valley degree of freedom depends on the spatial inversion symmetry breaking of the material systems. The emergence of valley degree of freedom leads to the the valleytronics.
in momentum space are no longer equivalent, this kind of nonequivalence property can be described by the Berry curvature or orbital magnetic moment. The two valleys constitute another degree of freedom for the electrons besides charge and spin. Therefore, the construction of the valley degree of freedom depends on the spatial inversion symmetry breaking of the material systems. The emergence of valley degree of freedom leads to the the valleytronics.
There are many graphene-like hexagonal lattice materials, such as boron nitride, TMD, gallium selenide, etc. Unlike graphene, the A and B sublattice structures in these materials are composed of different atoms, which destroys the spatial inversion symmetry. The existence of valley degree of freedom in these materials create conditions for the study of valleytronics.
On the  double-layer graphene materials, we can apply a electric field perpendicular to the two-dimensional plane to break the spatial inversion symmetry of graphene, which make the Berry curvature and the orbital magnetic moment of
double-layer graphene materials, we can apply a electric field perpendicular to the two-dimensional plane to break the spatial inversion symmetry of graphene, which make the Berry curvature and the orbital magnetic moment of  and
and  have opposite direction with the same magnitude [39]. The Berry curvature and orbital magnetic moment which are associated with the valleys lead some novel effects carried such as the valley hall effect and the optical transition selection rules [39]. As shown in figure 5, because of the inverse Berry curvature, the electrons in
have opposite direction with the same magnitude [39]. The Berry curvature and orbital magnetic moment which are associated with the valleys lead some novel effects carried such as the valley hall effect and the optical transition selection rules [39]. As shown in figure 5, because of the inverse Berry curvature, the electrons in  and
and  valleys move in the direction perpendicular to the applied electric field, and they deflect transversely with opposite direction, which is called the valley Hall effect. As shown in figure 6, only the left-handed(right-handed) circularly polarized photos are involved in the interband transition of
valleys move in the direction perpendicular to the applied electric field, and they deflect transversely with opposite direction, which is called the valley Hall effect. As shown in figure 6, only the left-handed(right-handed) circularly polarized photos are involved in the interband transition of  valley electrons. This is just the optical transition selection rules which are relevant to valleys, i.e. the circular polarization dichroism of valleys. All of these provide possible physical methods to regulate a particular valley state.
valley electrons. This is just the optical transition selection rules which are relevant to valleys, i.e. the circular polarization dichroism of valleys. All of these provide possible physical methods to regulate a particular valley state.
Figure 5. Valley electronic Hall effect diagram [40].
Download figure:
Standard image High-resolution imageFigure 6. Valley optical selection rules:  circularly polarized light couples only to bandedge transitions in valley
circularly polarized light couples only to bandedge transitions in valley  [40].
[40].
Download figure:
Standard image High-resolution imageThe scattering of the electrons in the intravalley involves a polarized photoexcitation and photoluminescence, and the phonons of the brillouin-zone-corner(valley) are also involved in intervalley electron scattering [5]. In view of the deterministic chirality of valley electrons, it is natural to ask two questions: do the valley phonons have definite chirality? what role do the chiral phonons play in the intervalley scattering of electrons? It was later observed in the TMDs that the phonons of the Brillouin-zone-center could completely reverse the polarization of the incident photons, i.e. the optical polarity inversion phenomena. This finding imply that, except for the phonons in the valleys, the
could completely reverse the polarization of the incident photons, i.e. the optical polarity inversion phenomena. This finding imply that, except for the phonons in the valleys, the  phonons which involved in the intralley scattering of electrons also have the chirality [27]. Therefore, it is necessary to study the chiral phonons at the high-symmetry points of the brillouin zone.
phonons which involved in the intralley scattering of electrons also have the chirality [27]. Therefore, it is necessary to study the chiral phonons at the high-symmetry points of the brillouin zone.
4.2. Selection rules of inter/intra-valley scattering
4.2.1. The helicity-resolved Raman scattering in TMD
The moment of the electrons along the direction  is 0, the state will not change under the threefold rotation, the orbits of the sublattices A and B determine the PAM. If we assume that the orbit of sublattice A corresponds to the valence band and the orbit of sublattice B corresponds to the conduction band, the pseudoangular momentum
is 0, the state will not change under the threefold rotation, the orbits of the sublattices A and B determine the PAM. If we assume that the orbit of sublattice A corresponds to the valence band and the orbit of sublattice B corresponds to the conduction band, the pseudoangular momentum  . Therefore, in the gapped graphene, electrons absorb the right-handed or left-handed circularly polarizated photons to have interband transition. Because of the conservation of the PAM, the selection rule can be obtained
. Therefore, in the gapped graphene, electrons absorb the right-handed or left-handed circularly polarizated photons to have interband transition. Because of the conservation of the PAM, the selection rule can be obtained
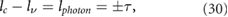
the difference between the conduction bands angular momentum and the valence bands angular momentum is equal to the photon angular momentum, as is shown in figure 7.
Figure 7. Selection rules in electronic intervalley scattering [41].
Download figure:
Standard image High-resolution imageThe electron in the conduction band is scattered in the intravalley by a phonon at  , then through emitting a photon it can combine with a hole in the valence band. First order Raman scattering is named for this process. Because the PAM is conserved in this process, the selection rule is
, then through emitting a photon it can combine with a hole in the valence band. First order Raman scattering is named for this process. Because the PAM is conserved in this process, the selection rule is

At  point, doubly degenerate optical modes are Raman active, has PAM of 1,
point, doubly degenerate optical modes are Raman active, has PAM of 1,  , so it is expected to have a helicity-resolved Raman
, so it is expected to have a helicity-resolved Raman  peak in the honeycomb lattice (gapped graphene or a boron nitride monolayer). In the whole process, the incident right-handed (left-handed) photon emits a left-handed (right-handed) phonon or absorbs a right-handed (left-handed) phonon, then turns to the left-handed (right-handed) photon. As shown in figure 8 [10], the helicity-resolved Raman scattering in layered TMD is explained by this selection rule.
peak in the honeycomb lattice (gapped graphene or a boron nitride monolayer). In the whole process, the incident right-handed (left-handed) photon emits a left-handed (right-handed) phonon or absorbs a right-handed (left-handed) phonon, then turns to the left-handed (right-handed) photon. As shown in figure 8 [10], the helicity-resolved Raman scattering in layered TMD is explained by this selection rule.
Figure 8. Photon helicity changed by phonons at  (a) left-handed photon changes its helicity at
(a) left-handed photon changes its helicity at  valley; (b) right-handed photon changes its helicity at
valley; (b) right-handed photon changes its helicity at  valley [41].
valley [41].
Download figure:
Standard image High-resolution image4.2.2. Intervalley scattering of electrons
The intervalley scattering of electrons can be achieved by emitting a circularly polarized valley phonon  . Because phonons have PAM under a threefold rotational symmetry, under the condition that both momentum and energy are conserved, the selection rule
. Because phonons have PAM under a threefold rotational symmetry, under the condition that both momentum and energy are conserved, the selection rule

can be obtained. The difference between the conduction band (valence band) angular momentum at  and
and  point is equal to the PAM of the valley phonon. It is well known that the doubly resonance peak
point is equal to the PAM of the valley phonon. It is well known that the doubly resonance peak  in the graphene Raman spectrum reflects the intervalley scattering of phonons which adjacent to the
in the graphene Raman spectrum reflects the intervalley scattering of phonons which adjacent to the  point [42, 43]. Therefore, according to the Raman spectrum, a valley phonon with definite PAM and frequency can be observed [10].
point [42, 43]. Therefore, according to the Raman spectrum, a valley phonon with definite PAM and frequency can be observed [10].
4.2.3. Chiral phonons in monolayer 
There is a band-gap  eV in the spin–orbit coupling MoS
eV in the spin–orbit coupling MoS (the single layer is converted into a direct band-gap) and a spin splitting
(the single layer is converted into a direct band-gap) and a spin splitting  meV for the highest valence band at
meV for the highest valence band at  valley. For the lowest conductance band, there is a
valley. For the lowest conductance band, there is a  meV splitting, which can be neglected [44]. By absorbing or transmitting a photon, a valley center phonon is involved in the intervalley electron scattering at valley centers, and the selection rules and energy conservation are
meV splitting, which can be neglected [44]. By absorbing or transmitting a photon, a valley center phonon is involved in the intervalley electron scattering at valley centers, and the selection rules and energy conservation are
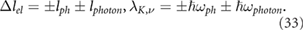
The change of electron angular momentum is equal to the algebraic sum of the phonon angular momentum and photon angular momentum, and the spin splitting of the valence band is equal to the algebraic sum of the phonon energy and photon energy, where  means emission and − means absorbtion.
means emission and − means absorbtion.
For monolayer MoS , at valleys, the PAM of the conduction bands are
, at valleys, the PAM of the conduction bands are  , and the PAM of the valence band is
, and the PAM of the valence band is  [45]. The right-handed polarized photon excites a pair of excitons (conduction electron and valence band hole) at valley
[45]. The right-handed polarized photon excites a pair of excitons (conduction electron and valence band hole) at valley  , the right-handed photon has a band-gap energy. Because the stimulated electrons are in the center of the valleys, and the phonons have energy, so by emitting a phonon, they cannot be scattered to another valley center. However, since the valence band has a large spin splitting, through absorbing a stimulated circular polarized photon the hole can be scattered to another valley, and a chiral valley phonon can be emitted, the spin of electron is fixed here.
, the right-handed photon has a band-gap energy. Because the stimulated electrons are in the center of the valleys, and the phonons have energy, so by emitting a phonon, they cannot be scattered to another valley center. However, since the valence band has a large spin splitting, through absorbing a stimulated circular polarized photon the hole can be scattered to another valley, and a chiral valley phonon can be emitted, the spin of electron is fixed here.
As shown in figure 9(a), there is a resonance peak with energy  can be observed by the stimulated right-handed light which scanning on the sample. According to the selection rule, the chiral phonon emitted at
can be observed by the stimulated right-handed light which scanning on the sample. According to the selection rule, the chiral phonon emitted at  point has the PAM of
point has the PAM of  . The resonance peak is in
. The resonance peak is in  meV (due to the small phonon polarization of 48.0 meV, the peak of 98.0 meV is not evident). For stimulated left-handed photons, only a peak of
meV (due to the small phonon polarization of 48.0 meV, the peak of 98.0 meV is not evident). For stimulated left-handed photons, only a peak of  meV is observed, which is corresponding to the phonon mode of
meV is observed, which is corresponding to the phonon mode of  meV. The other two modes do not participate because they are odd under the mirror operation since in the scattering process the whole system keeps even under a mirror operation relative to the
meV. The other two modes do not participate because they are odd under the mirror operation since in the scattering process the whole system keeps even under a mirror operation relative to the  -
- plane. Different valleys are electrons and holes located in, which after being scattered by phonons and photons, respectly. This is consistent with the recent discovery that the low energy excitons have large momentum [46]. Similarly, a left-handed photon with 1.65 eV excits a hole of
plane. Different valleys are electrons and holes located in, which after being scattered by phonons and photons, respectly. This is consistent with the recent discovery that the low energy excitons have large momentum [46]. Similarly, a left-handed photon with 1.65 eV excits a hole of  and emits a chiral phonon of
and emits a chiral phonon of  . So by a stimulated photon, we can obtain a chiral phonon at a definite valley. By irradiating samples using the two-step polarized light, there created a large quantity of valley phonons which has definite frequencies [10].
. So by a stimulated photon, we can obtain a chiral phonon at a definite valley. By irradiating samples using the two-step polarized light, there created a large quantity of valley phonons which has definite frequencies [10].
Figure 9.  -valley phonon emitted in hole scattering of MoS
-valley phonon emitted in hole scattering of MoS (a) A stimulated right-handed photon is absorbed and a phonon with
(a) A stimulated right-handed photon is absorbed and a phonon with  is emitted; (b) A stimulated left-handed photon is absorbed and a phonon with
is emitted; (b) A stimulated left-handed photon is absorbed and a phonon with  is emitted [10].
is emitted [10].
Download figure:
Standard image High-resolution image4.2.4. Chiral phonons in other 2D systems
Chiral phonons not only exit in monolayer MoS , but also exist in many other 2D systems. In graphene/hexagonal boron nitride (G/h-BN) heterostructure, the broken inversion symmetry and the interlayer interaction of G/h-BN open the band gap of ZO1(K) and ZO3(K), LO1(K) and LO3(K), shown in figures 10(a)–(c). The nonzero phonon polarization at the first-Brillouinzone corners (valleys) is shown in figure 10(d). The phonon chirality can be characterized by the polarization of phonons [10], which means the chiral phonons occur at valleys. Furthermore, the vertical stress is effective to adjust the band gap while holding the phonon chirality of G/h-BN heterostructure, which is favorable for the ultrafast infrared spectroscopy or Raman measurement [47]. In addition, chiral phonons also be found in center-stacked bilayer triangle lattices [48]. In this model, there are two atoms in one unit cell and considers three dimensional motion—six phonon bands can be obtained. Because the two sublattices have different masses, the spatial inversion symmetry is broken. The band gap is opened with nonzero phonon polarization, which is shown in figure 11. In bilayer lattice structure, the interaction between layers (interlayer coupling) can not be ignored and the mass of sublattice in different layers must be considered, too. By adjusting these parameters, they find that the phonon chirality remain robust with changing interlayer coupling and mass ratio of sublattices [48].
, but also exist in many other 2D systems. In graphene/hexagonal boron nitride (G/h-BN) heterostructure, the broken inversion symmetry and the interlayer interaction of G/h-BN open the band gap of ZO1(K) and ZO3(K), LO1(K) and LO3(K), shown in figures 10(a)–(c). The nonzero phonon polarization at the first-Brillouinzone corners (valleys) is shown in figure 10(d). The phonon chirality can be characterized by the polarization of phonons [10], which means the chiral phonons occur at valleys. Furthermore, the vertical stress is effective to adjust the band gap while holding the phonon chirality of G/h-BN heterostructure, which is favorable for the ultrafast infrared spectroscopy or Raman measurement [47]. In addition, chiral phonons also be found in center-stacked bilayer triangle lattices [48]. In this model, there are two atoms in one unit cell and considers three dimensional motion—six phonon bands can be obtained. Because the two sublattices have different masses, the spatial inversion symmetry is broken. The band gap is opened with nonzero phonon polarization, which is shown in figure 11. In bilayer lattice structure, the interaction between layers (interlayer coupling) can not be ignored and the mass of sublattice in different layers must be considered, too. By adjusting these parameters, they find that the phonon chirality remain robust with changing interlayer coupling and mass ratio of sublattices [48].
Figure 10. (a) Phonon dispersion of G/h-BN heterostructure along the  –K direction. ((b) and (c)) Magnified dispersion diagrams for ZO1(K), ZO3(K), and LO1(K), LO3(K). (d) Phonon polarization of G/h-BN along the
–K direction. ((b) and (c)) Magnified dispersion diagrams for ZO1(K), ZO3(K), and LO1(K), LO3(K). (d) Phonon polarization of G/h-BN along the  –K direction [47].
–K direction [47].
Download figure:
Standard image High-resolution imageFigure 11. (a) Phonon polarization for all bands along the  -directions. ((b) and (c)) Contour plots of the phonon polarization for band 3 and band 4. Here,
-directions. ((b) and (c)) Contour plots of the phonon polarization for band 3 and band 4. Here,  = 1 and
= 1 and  ; the spring constants are
; the spring constants are  ,
,  , and
, and  [48].
[48].
Download figure:
Standard image High-resolution imageIn all above 2D systems, chiral phonons exist at Brillouin-zone corners (valleys). But the nondegenerate chiral phonons also can be observed near to  point [49]. As shown in figure 12(a), through the periodic atomic mass doping of sublattice
point [49]. As shown in figure 12(a), through the periodic atomic mass doping of sublattice  , the
, the  superlattices are tailored on a honeycomb AB lattice. Considering two dimensional motion and the model has six atoms in one unit cell, there are twelve phonon branches, shown in figure 12(b). Moreover, the nondegenerate chiral phonons of two valleys are folded to
superlattices are tailored on a honeycomb AB lattice. Considering two dimensional motion and the model has six atoms in one unit cell, there are twelve phonon branches, shown in figure 12(b). Moreover, the nondegenerate chiral phonons of two valleys are folded to  point, thus we can obtain nonzero phonon polarization at Brillouin-zone center, see figures 12(c) and (d). Since the nonzero phonon polarization occur at
point, thus we can obtain nonzero phonon polarization at Brillouin-zone center, see figures 12(c) and (d). Since the nonzero phonon polarization occur at  point where the LO/TO splitting can not be ignored, the relation between LO/TO splitting and phonon polarization has also been discussed in this article [49].
point where the LO/TO splitting can not be ignored, the relation between LO/TO splitting and phonon polarization has also been discussed in this article [49].
Figure 12. (a) Schematic representation of the  honeycomb superlattices. The blue balls represent sublattices 1, 3 and 5 with
honeycomb superlattices. The blue balls represent sublattices 1, 3 and 5 with  , the red balls represent sublattices 2 and 6 with
, the red balls represent sublattices 2 and 6 with  , the cyan balls represent sublattice 4 with
, the cyan balls represent sublattice 4 with  . The lattice primitive cells basic vectors
. The lattice primitive cells basic vectors  and
and  are represented by the magenta lines. (b) and (c) Phonon dispersion and phonon polarization along the
are represented by the magenta lines. (b) and (c) Phonon dispersion and phonon polarization along the  -directions. The red solid, blue dash, olive dash dot and orange short dash lines, correspond to branches 5, 6, 7 and 8, respectively. (d) Contour plot denotes value of phonon polarization from
-directions. The red solid, blue dash, olive dash dot and orange short dash lines, correspond to branches 5, 6, 7 and 8, respectively. (d) Contour plot denotes value of phonon polarization from  to
to  for branch 7. Here,
for branch 7. Here,  ,
,  and
and  ; the spring constants are
; the spring constants are  and
and  [49].
[49].
Download figure:
Standard image High-resolution image4.3. Possible effects of chiral valley phonons
4.3.1. Circularly polarized infrared absorption or emission
Because the phonons of different bands at valleys have different PAM, we can observe the circular polarization infrared spectra in the intervalley scattering of the valley phonons (phonon bands).The nonzero ionic magnetic moment is caused by the circular polarization vibrations of the sublattices at the valleys, and it can couple to photons directly. So through polarized infrared absorption or emission, the valley phonons can be observed. As discussed earlier, the valley phonons can be excited during the electron or hole intervalley scattering process. As shown in figure 13, assuming the electrons can excite the phonons of band  at the valley
at the valley  massively, through a photon with energy
massively, through a photon with energy  stimulation which is left-circularly-polarized infrared or a photon with energy
stimulation which is left-circularly-polarized infrared or a photon with energy  simulation which is right-handed infrared, the corresponding left-handed or right-handed photoluminescence can be observed.
simulation which is right-handed infrared, the corresponding left-handed or right-handed photoluminescence can be observed.
Figure 13. Polarized infrared absorption or emission by valley phonons [10].
Download figure:
Standard image High-resolution imageIf a lot of valley phonons at band  are created, through the infrared stimulation, we can observe the left-handed photoluminescence with energy
are created, through the infrared stimulation, we can observe the left-handed photoluminescence with energy  (
( ), or the right-handed photoluminescence with energy
), or the right-handed photoluminescence with energy  . Therefore, the resonance peak of infrared spectrum can distinguish the valley phonons. Figure 13 shows the bands and corresponding PAM of phonons at valley
. Therefore, the resonance peak of infrared spectrum can distinguish the valley phonons. Figure 13 shows the bands and corresponding PAM of phonons at valley  , the blue ellipses mark the valley phonons which are excited during the intervalley electron scattering, the green lines reflect all possible absorption or emission of polarized infrared lights [10].
, the blue ellipses mark the valley phonons which are excited during the intervalley electron scattering, the green lines reflect all possible absorption or emission of polarized infrared lights [10].
4.3.2. Valley phonon hall effect
Because of the opposite Berry curvature, electrons in different valleys flow to opposite transverse edges under an in-plane electric field, which is called the electronic valley hall effect [39, 50]. Recently, in monolayer MoS transistors [51] and in graphene superlattices [52] the valley hall effect of electrons has been observed experimentally. As discussed above, phonons with definite frequencies at the valleys can be produced massively. So, analogy to the electronic valley hall effect, if the Berry curvature of valley phonons is nonzero, the valley phonon hall effect can be observed when there is an in-plane gradient strain field, this provides another method to observe valley phonons.
transistors [51] and in graphene superlattices [52] the valley hall effect of electrons has been observed experimentally. As discussed above, phonons with definite frequencies at the valleys can be produced massively. So, analogy to the electronic valley hall effect, if the Berry curvature of valley phonons is nonzero, the valley phonon hall effect can be observed when there is an in-plane gradient strain field, this provides another method to observe valley phonons.
Due to breaking of the spatial inversion symmetry, the nonzero phonon Berry curvature is observed in the valley, as shown in figure 14(a). At the valleys, band 2 and band 3 have large Berry curvature, while band 1 and band 4 has small Berry curvature. Because of the nonzero Berry curvature, when applying a strain gradient  along the
along the  direction, the phonons excited at different valleys will move along different transverse direction since
direction, the phonons excited at different valleys will move along different transverse direction since
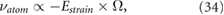
which is analogous to the electrons. As shown in figure 14(b), if the polarization of the photon is reversed, the direction of the transverse phonon current is also reversed. Because the phonons accumulated on one edge, we can observe the transverse temperature difference. If the circular polarization of the stimulated photon is reversed, the temperature difference changes sign. The phenomenon of phonon hall effect can be obtained in the paramagnetic insulator, and the transport of phonons can be distorted by the magnetic field so that the transverse temperature difference can be observed, which has led to many researches in this field [23]. At nonmagnetic system with broken inversion symmetry, the transverse valley phonon hall effect induced by Berry curvature will bring new applications.
Figure 14. Phonon Berry curvature and valley phonon Hall effect in a honeycomb lattice. (a) Berry curvature of band 1 (bottom contour plot) and band 2 (top 3D plot). (b) and (c) Schematic of the valley phonon Hall effect under a strain gradient (the orange arrows) [10].
Download figure:
Standard image High-resolution image5. Experiments verifications of chiral phonons
The phonon chirality at the Brillouin-zone-center is first verified by the experiment of 2D semiconducting TMDCs (MX , M = Mo/W, X = S/Se) [27]. The authors performed helicity-resolved Raman scattering of the TMDC atomic layers. As shown in figure 15, it is found the in-plane relative motion of transition metal and chalcogen atoms, i.e. the IMC phonon mode can always switch the incident photon helicity. In the process of first order Raman scattering, due to the conservation of the PAM, we have
, M = Mo/W, X = S/Se) [27]. The authors performed helicity-resolved Raman scattering of the TMDC atomic layers. As shown in figure 15, it is found the in-plane relative motion of transition metal and chalcogen atoms, i.e. the IMC phonon mode can always switch the incident photon helicity. In the process of first order Raman scattering, due to the conservation of the PAM, we have  . The doubly degenerate optical modes at
. The doubly degenerate optical modes at  can have a pseudoangular momenta of
can have a pseudoangular momenta of  by superposition. Therefore the chiral phonons can completely reverse the helicity of incident photons. At
by superposition. Therefore the chiral phonons can completely reverse the helicity of incident photons. At  point, the orbital part of PAM is always zero, the total PAM is equal to the spin PAM and layer thickness will not affect spin PAM, i.e. layer thickness has no effect on pseudo-angular momentum of Brillouin zone center doubly degenerate chiral phonons. But for nondegenerate chiral phonons of Brillouin zone corners (valleys), the stacking types of two layers affect the sublattices' relative position and thus affects the orbital PAM of it. Because of
point, the orbital part of PAM is always zero, the total PAM is equal to the spin PAM and layer thickness will not affect spin PAM, i.e. layer thickness has no effect on pseudo-angular momentum of Brillouin zone center doubly degenerate chiral phonons. But for nondegenerate chiral phonons of Brillouin zone corners (valleys), the stacking types of two layers affect the sublattices' relative position and thus affects the orbital PAM of it. Because of  [10], the spin PAM and total PAM change as orbital PAM changes, which has been researched in a theoretical work [47].
[10], the spin PAM and total PAM change as orbital PAM changes, which has been researched in a theoretical work [47].
Figure 15. The helicity-resolved Raman spectra of monolayer (1 L) and two-layers (2 L) MoS . The excitation wavelength is 488 nm with
. The excitation wavelength is 488 nm with  polarization [27].
polarization [27].
Download figure:
Standard image High-resolution imageVery recently, at the corner of the Brillouin-zone of the monolayer tungsten diselenide, the chiral phonons are directly observed by the group of Zhang [11]. As shown in figure 16, the authors first inject the holes at the  valley using a left circularly polarized (LCP) optical pump pulse. The hole at the
valley using a left circularly polarized (LCP) optical pump pulse. The hole at the  valley relaxes to the valence band edge with a initial linear momentum
valley relaxes to the valence band edge with a initial linear momentum  . The hole can transit to the
. The hole can transit to the  valley with a final momentum
valley with a final momentum  . During this process, a
. During this process, a  phonon is emitted because
phonon is emitted because  . However, due to the spin–orbit interactions, the energy of the spin-conserving state is much higher, thus the intermediate state is virtual [11]. Then they send an infrared pulse to satisfy the energy conservation, and the hole is placed in the spin-split band at the
. However, due to the spin–orbit interactions, the energy of the spin-conserving state is much higher, thus the intermediate state is virtual [11]. Then they send an infrared pulse to satisfy the energy conservation, and the hole is placed in the spin-split band at the  valley. Note that the hole here has zero PAM, thus the phonon PAM must equal to the IR photon spin angular momentum. Therefore, only the creation of LO(K) phonons are controled by the LCP pulse. The final spin-split state in the opposite valley can be recognized by the energy and the right circular polarization (RCP) of its radiative decay, which is signaled by the RCP luminescence.
valley. Note that the hole here has zero PAM, thus the phonon PAM must equal to the IR photon spin angular momentum. Therefore, only the creation of LO(K) phonons are controled by the LCP pulse. The final spin-split state in the opposite valley can be recognized by the energy and the right circular polarization (RCP) of its radiative decay, which is signaled by the RCP luminescence.
Figure 16. Nondegenerate chiral phonons in monolayer WSe [11].
[11].
Download figure:
Standard image High-resolution imageThe valley phonon PAM is determined from the polarization selection of the absorbed IR photon. Different IR absorptions can be observed when the probe has the same/opposite ( ) polarization as the pump light. Due to the different electron–phonon coupling strength, the IR circular dichroism (CD), which is calculated by CD
) polarization as the pump light. Due to the different electron–phonon coupling strength, the IR circular dichroism (CD), which is calculated by CD  , demonstrates that scattering cross sections of the two processes are not equal. We can see from figure 17 that the CD of the valley-polarized holes is always positive at 82 K. The initial intravalley intervalence band transition (IVBT) has positive CD, which is because the electronic spin at the valence band edge of
, demonstrates that scattering cross sections of the two processes are not equal. We can see from figure 17 that the CD of the valley-polarized holes is always positive at 82 K. The initial intravalley intervalence band transition (IVBT) has positive CD, which is because the electronic spin at the valence band edge of  valley flips from
valley flips from  to
to  1/2. But this contribution decays fast with the delay of IR. When
1/2. But this contribution decays fast with the delay of IR. When  ps, the intervalley phonon-creating transition becomes the dominant source of the positive CD, which means the indirect IR absorption is mostly contributed by the LO branch now.
ps, the intervalley phonon-creating transition becomes the dominant source of the positive CD, which means the indirect IR absorption is mostly contributed by the LO branch now.
Figure 17. Chirality of phonons measured by transient IR circular dichroism [11].
Download figure:
Standard image High-resolution image6. Summary and outlook
In this review, the phonon angular momentum in magnetic system is introduced firstly. Raman spin–phonon interaction is the reason of creating nonzero phonon angular momentum, and the phonon angular momentum is an odd function of the magnetization, which can explain the phenomena in the phonon hall effect that the reverse of transvrse thermal current when the magnetic field reversed. Except for the zero-point energy, phonons at zero temperature also have nonzero angular momentum. Under the classical limit condition, the total phonon angular momentum vanishes, which is because the angular momentum of the thermal stimulated phonon modes are offset by the zero-point angular momentum. The contribution of phonon angular momentum in total angular momentum cannot be neglected in magnetic materials with large magnetization and strong spin–phonon interaction. Revisit the Einstein–de Haas effect, the phonon angular momentum is deducted from the angular momentum of electrons, and the spin angular momentum and the orbital angular momentum can be accurately confirmed by modification.
In addition to the existence of phonon angular momentum found in the magnetic system, chiral phonons are found at the high-symmetry points of brillouin zone in the nonmagnetic hexagonal lattices system. At these high-symmetry points, there is a threefold rotational symmetry, which endow the phonon modes quantized PAM. The breaking of spatial inversion symmetry of two-dimensional lattice plane and the time reversal symmetry breaking at  and
and  are the fundamental reasons for the non-degeneracy valley phonon modes and the determined PAM. There is a time reversal symmetry at point
are the fundamental reasons for the non-degeneracy valley phonon modes and the determined PAM. There is a time reversal symmetry at point  , and the phonon modes with opposite PAM are degenerate. The chiral phonons at these high-symmetry points not only determine the selection rules of intervalley and intravalley electron scattering, and endow the other potential effects of phononics, such as valley phonon Berry curvature and valley phonon hall effect. The dispersion of phonons in the adjacent zone of these high-symmetry points has extremes, so it has a large density of states. Therefore, chiral phonons play an important role in valleytronics, especially in the intervalley or the intravalley scattering of electrons or holes.
, and the phonon modes with opposite PAM are degenerate. The chiral phonons at these high-symmetry points not only determine the selection rules of intervalley and intravalley electron scattering, and endow the other potential effects of phononics, such as valley phonon Berry curvature and valley phonon hall effect. The dispersion of phonons in the adjacent zone of these high-symmetry points has extremes, so it has a large density of states. Therefore, chiral phonons play an important role in valleytronics, especially in the intervalley or the intravalley scattering of electrons or holes.
According to the above discussions, nondegenerate chiral phonons exist in the system where time reversal symmetry or spatial inversion symmetry is broken. In the magnetic system with time reversal symmetry broken, phonons carry nonzero angular momentum, which has an important influence on the correction of the gyromagnetic ratio. In the nonmagnetic system where the spatial inversion symmetry is broken, chiral phonons are found at high-symmetry points at the brillouin zone, it has quantized PAM, which provides another way to study valleytronics.
Phonon angular momentum can be used to accurately measure the gyromagnetic ratio, study the spin–phonon coupling and the thermal hall effect, etc. In the study of the resonance quantum magnon-electron coupling effect using the multiferroic metal organics, the Beijing national key magnetism laboratory research team point out that the spin–phonon interaction can cause the change of the dielectric permittivity, the change of phonon angular momentum of the system well explain the magnetization of the tunneling effect [53]. Chiral phonons play an important role in the selection rules in the intervalley or intravalley scattering of electrons and in the valley phonon hall effect, which establish the basis for the applications of valley-based electronics and phononics. The research team from the university of Massachusetts connect the electron-photon coupling and the interactions of chiral phonons with the electrons or circular polarization photons in TMDCs materials, and study the coupling between electrons and phonons, photons and phonons in two-dimensional materials, which is very important for understanding the basic properties of condensed matter systems [54]. The research team from Wuhan university consider the concept of valley in phonon crystals, obtain its important vortex properties and establish the excitation selection rule [55].
Researches about phonon angular momentum and chiral phonons have just begun, relevant theories and applications deserve further investigating, such as the connection between spin–phonon interaction and phonon angular momentum, the intrinsic relationship between lattice symmetry and chiral phonons, the effect of chiral phonons in the electron–phonon interaction, the transport property of chiral phonon, the manipulation of chiral phonon transport, the measurement and applications for phonon angular momentum and chiral phonons, etc. Due to the phonons widely exist in condensed matter physics, such as superconductivity, electron–phonon interaction, brillouin zone and Raman scattering, thermoelectric effect, thermal effect, chiral phonons in these areas will be inevitable and will play an important role. The study of phonon angular momentum and chiral phonons will lead to the exploration and new development of phonons in condensed matter physics.
Acknowledgments
We acknowledge support from NSFC (Nos. 11574154, 11704189). WZ is sponsored by the Jiangsu Postdoctoral Research Funding Program (1701118C).
Footnotes
- 1
See supplemental material at http://link.aps.org/supplemental/10.1103/PhysRevLett.112.085503 for detailed derivations.



















