Abstract
Gapless bilayer graphene is susceptible to a variety of spontaneously gapped states. As predicted by theory and observed by experiment, the ground state is, however, topologically trivial, because a valley-independent gap is energetically favorable. Here, we show that under the application of interlayer electric field and circularly polarized light, one valley can be selected to exhibit the original interaction instability while the other is frozen out. Tuning this Floquet system stabilizes multiple competing topologically ordered states, distinguishable by edge transport and circular dichroism. Notably, quantized charge, spin, and valley Hall conductivities coexist in one stabilized state.
Export citation and abstract BibTeX RIS
1. Introduction
Chirally stacked few-layer graphene, ranging from the Bernal bilayer to its thicker cousins with Rhombohedral stacking, has become a paradigmatic platform for studying fascinating two-dimensional electron physics [1–4]. Unlike the linear Dirac bands in monolayer graphene, the bands in an N-layer system exhibit flatter dispersions ∼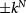 . Notably, the Fermi surface only consists of band touching points at two inequivalent hexagonal Brillouin zone corners, known as K and
. Notably, the Fermi surface only consists of band touching points at two inequivalent hexagonal Brillouin zone corners, known as K and 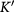 valleys. Intriguingly, the Fermi points are protected by the quantized Berry phases
valleys. Intriguingly, the Fermi points are protected by the quantized Berry phases 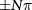 in the presence of a chiral symmetry between the two sublattices located at the top and bottom layers. This unique feature leads to band gap opening when an interlayer electric field breaks the chiral symmetry [5–10]. More remarkably, due to the large density-of-states near the Fermi points, the
in the presence of a chiral symmetry between the two sublattices located at the top and bottom layers. This unique feature leads to band gap opening when an interlayer electric field breaks the chiral symmetry [5–10]. More remarkably, due to the large density-of-states near the Fermi points, the 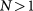 systems are susceptible to a variety of broken chiral symmetry states [11], in which each spin-valley flavor spontaneously transfers charge between layers to yield opening of quasiparticle energy gaps [12–15] and spreading of momentum-space Berry curvature [3].
systems are susceptible to a variety of broken chiral symmetry states [11], in which each spin-valley flavor spontaneously transfers charge between layers to yield opening of quasiparticle energy gaps [12–15] and spreading of momentum-space Berry curvature [3].
The order competing is enriched by the 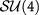 spin-valley symmetry [11–44]. The nearly-degenerate ground states can be topologically classified based on the signs of spontaneous gaps at each spin-valley [3, 18], analogous to those single-particle states in Haldane and Kane-Mele models [45, 46]. The intervalley exchange interactions, although extremely weak and often negligible, energetically favor those candidates with valley degeneracy [19], i.e. the same layer polarization at the two valleys. In order to minimize the electrostatic energy, hence the two spin flavors must polarize toward opposite layers. These two facts yield a topologically trivial layer-antiferromagnetic (LAF) ground state [3, 19, 20, 29], as recently confirmed by experiment [37–41].
spin-valley symmetry [11–44]. The nearly-degenerate ground states can be topologically classified based on the signs of spontaneous gaps at each spin-valley [3, 18], analogous to those single-particle states in Haldane and Kane-Mele models [45, 46]. The intervalley exchange interactions, although extremely weak and often negligible, energetically favor those candidates with valley degeneracy [19], i.e. the same layer polarization at the two valleys. In order to minimize the electrostatic energy, hence the two spin flavors must polarize toward opposite layers. These two facts yield a topologically trivial layer-antiferromagnetic (LAF) ground state [3, 19, 20, 29], as recently confirmed by experiment [37–41].
One may naturally wonder whether and how the more exotic topologically ordered states [3, 18] can be stabilized. The key is to relax the aforementioned valley degeneracy; a possible route is to explicitly break both time reversal (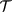 ) and spatial inversion (
) and spatial inversion (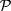 ) symmetries that dictate the valley degeneracy. We find that under the application of interlayer electric field and circularly polarized light in bilayer graphene, one valley can be selected to exhibit the original
) symmetries that dictate the valley degeneracy. We find that under the application of interlayer electric field and circularly polarized light in bilayer graphene, one valley can be selected to exhibit the original 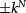 -band touching [3] and weak interaction instability [12–15], whereas the other valley is frozen out due to a large field-induced gap, as illustrated in figure 1. When the interaction-driven gap at the selected valley is opposite to the field-induced gap at the frozen valley, the ground state is a quantum anomalous Hall (QAH) state.
-band touching [3] and weak interaction instability [12–15], whereas the other valley is frozen out due to a large field-induced gap, as illustrated in figure 1. When the interaction-driven gap at the selected valley is opposite to the field-induced gap at the frozen valley, the ground state is a quantum anomalous Hall (QAH) state.
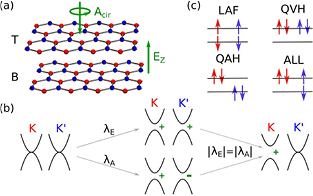
Figure 1. (a) Sketch of bilayer graphene under the application of an interlayer electric field and a circularly polarized light. (b) The electric (light) field opens an energy gap with the same (opposite) sign(s) at the two valleys. If both fields generate equal gap magnitudes, the energy gap of a selected valley vanishes. (c) Illustration of the layer polarizations in the four competing ordered states. The up/down arrows denote the two spins; the red/blue colors denote the two valleys.
Download figure:
Standard image High-resolution imageRemarkably, when the selected-valley gaps become opposite between the two spin flavors, quantized charge, spin, and valley Hall conductivities coexist. As we will examine, such an exotic ordered state dubbed 'ALL' hereafter, elusive in the absence of the delicately applied fields or the electron-electron interactions, can be stabilized by tuning the interacting Floquet system, and different ordered states can be distinguished by edge transport and circular dichroism. We note that a light-irradiated Floquet state has been observed on a topological insulator (TI) surface [47, 48], and our predicted ordered Floquet states may be similarly studied in chiral graphene experiments [33–44].
2. Floquet theory
We first establish our notation by discussing the effective Hamiltonian [3] that can coherently describe graphene (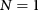 ), its Bernal bilayer (
), its Bernal bilayer (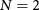 ), and its Rhombohedral few-layers (
), and its Rhombohedral few-layers (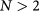 ), to which our main results derived for the bilayer system can be generalized. Such a model reads
), to which our main results derived for the bilayer system can be generalized. Such a model reads
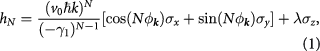
where v0 is the Fermi velocity of graphene, 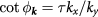 , and
, and  label the K and
label the K and 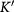 valleys.
valleys. 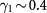 eV is the interlayer nearest-neighbor hopping energy, which sets the largest energy scale of the model. The Pauli matrices
eV is the interlayer nearest-neighbor hopping energy, which sets the largest energy scale of the model. The Pauli matrices 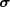 act on the layer-pseudospin space spanned by the two sublattices relevant at low energy, i.e. the top A and bottom B without interlayer nearest neighbors. For
act on the layer-pseudospin space spanned by the two sublattices relevant at low energy, i.e. the top A and bottom B without interlayer nearest neighbors. For 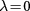 , the gapless spectrum of
, the gapless spectrum of  has two band touch points at K and
has two band touch points at K and 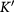 , protected by the chiral (
, protected by the chiral (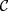 ) symmetry between the two sublattices.
) symmetry between the two sublattices.
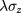 is a mass term that characterizes
is a mass term that characterizes 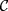 symmetry breaking and hence opens an energy gap whenever
symmetry breaking and hence opens an energy gap whenever 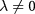 . It turns out that the mass term can be explicitly induced by an interlayer electric field or a circularly polarized light, or spontaneously generated by electron-electron interactions. In the first scenario, as demonstrated by the experiments in
. It turns out that the mass term can be explicitly induced by an interlayer electric field or a circularly polarized light, or spontaneously generated by electron-electron interactions. In the first scenario, as demonstrated by the experiments in 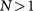 systems [5–10], the interlayer electric field Ez breaks
systems [5–10], the interlayer electric field Ez breaks  and
and  symmetries by producing
symmetries by producing
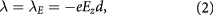
where d is the layer separation. 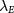 is spin-valley independent, as required by
is spin-valley independent, as required by 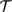 and spin
and spin 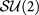 symmetries.
symmetries.
To demonstrate the second scenario, consider a circularly polarized light shining on a few-layer. This amounts to applying a time-dependent electromagnetic gauge potential 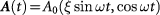 to the system, where
to the system, where 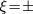 denote the light helicities. In Floquet theory, such a periodically driven system can effectively be described by a static Hamiltonian [49, 50]
denote the light helicities. In Floquet theory, such a periodically driven system can effectively be described by a static Hamiltonian [49, 50]
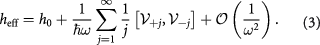
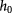 is the time-independent Hamiltonian without the periodic drive;
is the time-independent Hamiltonian without the periodic drive; 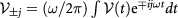 are the Fourier components of the time-dependent periodic potential
are the Fourier components of the time-dependent periodic potential 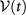 . Similarly to how equation (2) was derived [51], we apply
. Similarly to how equation (2) was derived [51], we apply 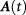 to the original full-band model of N-layer graphene, followed by a projection to the two-band model at low energy. In the high-frequency limit, to the leading order the circularly polarized light yields
to the original full-band model of N-layer graphene, followed by a projection to the two-band model at low energy. In the high-frequency limit, to the leading order the circularly polarized light yields
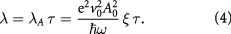
The radiation field can yield a mass term 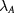 as its definite helicity breaks
as its definite helicity breaks 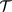 and
and 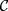 symmetries. The intact spin
symmetries. The intact spin 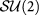 and
and 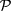 symmetries dictate
symmetries dictate 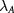 to be spin independent but opposite at the two valleys.
to be spin independent but opposite at the two valleys. 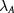 was originally derived in the seminal work on radiated monolayer graphene [52–55], and a similar gap has been experimentally observed on the TI surface [47, 48]. Here we generalize the idea to graphene few-layers and demonstrate the general validity of equation (4).
was originally derived in the seminal work on radiated monolayer graphene [52–55], and a similar gap has been experimentally observed on the TI surface [47, 48]. Here we generalize the idea to graphene few-layers and demonstrate the general validity of equation (4).
In a many-body scenario, Coulomb interactions can generate masses in the quasiparticle spectra of 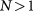 systems [3]. While a microscopic theory will be given later, the ground state turns out to be LAF [38–43], breaking all the symmetries. The two spin flavors are polarized to opposite layers spontaneously as if they are subjected to opposite
systems [3]. While a microscopic theory will be given later, the ground state turns out to be LAF [38–43], breaking all the symmetries. The two spin flavors are polarized to opposite layers spontaneously as if they are subjected to opposite 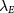 mean-fields, i.e.
mean-fields, i.e. 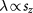 in equation (1).
in equation (1).
In each scenario, the mass generation in equation (1) spreads the Berry curvature, which is integrated to 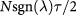 for each spin-valley [3]. Hence,
for each spin-valley [3]. Hence, 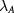 induces a QAH state with Chern number 2N, which is reminiscent of the Haldane model [45];
induces a QAH state with Chern number 2N, which is reminiscent of the Haldane model [45]; 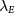 produces a quantum valley Hall (QVH) state since the valley Chern numbers are opposite for different valleys [3, 56–61], analogous to the quantum spin Hall state [46]. Metallic in-gap states have indeed been experimentally observed [62–65] along a QVH domain wall in bilayer graphene where the edge conductance appears to approach
produces a quantum valley Hall (QVH) state since the valley Chern numbers are opposite for different valleys [3, 56–61], analogous to the quantum spin Hall state [46]. Metallic in-gap states have indeed been experimentally observed [62–65] along a QVH domain wall in bilayer graphene where the edge conductance appears to approach 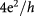 . By contrast, the LAF state is topologically trivial since it can be viewed as two opposite copies of QVH states. As motivated in Introduction and illustrated in figure 1(b), when
. By contrast, the LAF state is topologically trivial since it can be viewed as two opposite copies of QVH states. As motivated in Introduction and illustrated in figure 1(b), when 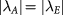 , one valley can be selected to exhibit the original
, one valley can be selected to exhibit the original 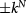 -band touching, whereas the other valley is almost frozen out due to a large field-induced gap. The interactions generate masses at the selected valley, whose signs determine three competing ordered states: QAH, QVH, and the emergent ALL states. With masses opposite (the same) in sign for the two spins at the selected (frozen) valley, the ALL state can be viewed as a QVH state for one spin but QAH for the other. Remarkably, such a state breaks all the symmetries and exhibits charge, spin, and valley Chern numbers of N. More remarkably, the ALL state is a synergistic consequence of intrinsic interactions and external fields, instead of due to any magnetic moment or spin-orbit coupling.
-band touching, whereas the other valley is almost frozen out due to a large field-induced gap. The interactions generate masses at the selected valley, whose signs determine three competing ordered states: QAH, QVH, and the emergent ALL states. With masses opposite (the same) in sign for the two spins at the selected (frozen) valley, the ALL state can be viewed as a QVH state for one spin but QAH for the other. Remarkably, such a state breaks all the symmetries and exhibits charge, spin, and valley Chern numbers of N. More remarkably, the ALL state is a synergistic consequence of intrinsic interactions and external fields, instead of due to any magnetic moment or spin-orbit coupling.
3. Hartree–Fock theory and phase diagram
We now study the phase diagram enrichment in terms of the following ordered state quasiparticle Hamiltonian [3, 38, 39]:
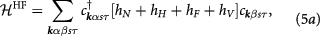
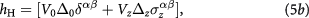
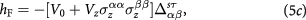
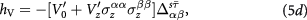
which has well reproduced the experimentally observed gap size and Tc in bilayer graphene. In equation (5), Greek letters label layer, s labels spin, and τ labels valley. 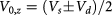 denotes the average (difference) of intralayer and interlayer interactions at the same valley, and likewise
denotes the average (difference) of intralayer and interlayer interactions at the same valley, and likewise 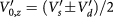 for valley-exchange interactions [19]. The density matrix
for valley-exchange interactions [19]. The density matrix 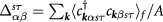 must be determined self-consistently. We introduce
must be determined self-consistently. We introduce 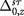 as the density sum (difference) of the top and bottom layers for one spin-valley flavor and
as the density sum (difference) of the top and bottom layers for one spin-valley flavor and 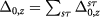 as the total density sum (difference). The mean-field interaction vertices must be diagonal in layer due to in-plane rotational symmetry; neither spin nor valley coherence can be established spontaneously since the long-range Coulomb interactions
as the total density sum (difference). The mean-field interaction vertices must be diagonal in layer due to in-plane rotational symmetry; neither spin nor valley coherence can be established spontaneously since the long-range Coulomb interactions 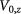 dominate. Therefore, in equation (1) λ reads
dominate. Therefore, in equation (1) λ reads
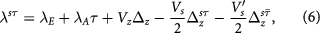
where 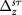 minimize the energy density functional
minimize the energy density functional
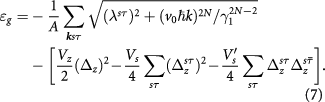
Given that the subtracted in the second line of equation (7) is exactly half of the mean-field interactions that are implicit in the first line, the three interaction parameters (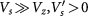 ) play different roles in order competing. The intralayer exchange Vs causes spontaneous layer polarization in each spin-valley, whereas the Hartree energy determined by Vz prevents any total layer polarization. Although rather weak, the valley-exchange interaction
) play different roles in order competing. The intralayer exchange Vs causes spontaneous layer polarization in each spin-valley, whereas the Hartree energy determined by Vz prevents any total layer polarization. Although rather weak, the valley-exchange interaction 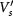 favors a ground state in which different valleys have the same layer polarization. Therefore, for
favors a ground state in which different valleys have the same layer polarization. Therefore, for 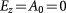 , the ground state must be the LAF state in which different spin (valley) flavors are layer polarized in the opposite (same) sense, as observed in experiment [38–43].
, the ground state must be the LAF state in which different spin (valley) flavors are layer polarized in the opposite (same) sense, as observed in experiment [38–43].
We now examine how the circularly polarized radiation enriches the order competing and stabilizes the ordered QAH and ALL states. We focus on the 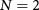 case to facilitate our numerics; the qualitative results should apply to
case to facilitate our numerics; the qualitative results should apply to 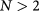 cases. Figure 2(a) shows the phase diagram, which exhibits four competing orders and mirror symmetries with respect to
cases. Figure 2(a) shows the phase diagram, which exhibits four competing orders and mirror symmetries with respect to 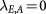 lines. The LAF state exists in the limit of vanishing external fields. A sufficiently large
lines. The LAF state exists in the limit of vanishing external fields. A sufficiently large 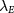 (
(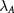 ) favors the QVH (QAH) state. Near the
) favors the QVH (QAH) state. Near the 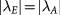 line, there emerges the ALL state.
line, there emerges the ALL state.
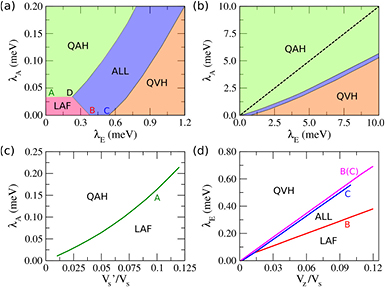
Figure 2. ((a) and (b)) Phase diagram of bilayer graphene at small and large fields, respectively. The Hartree interaction 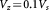 ; the valley-exchange interaction
; the valley-exchange interaction  . ((c)–(d)) The dependences of the critical points A–C in (a) on
. ((c)–(d)) The dependences of the critical points A–C in (a) on 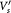 and on Vz, respectively. The red and blue lines are for
and on Vz, respectively. The red and blue lines are for 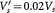 , and the purple line is for
, and the purple line is for 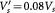 .
.
Download figure:
Standard image High-resolution imageIn the phase diagram figure 2(a), the positions of the critical points A–D are determined by the strengths of three interaction parameters. This has also been discussed in the above analysis of equations (6) and (7). (i) The experimental LAF gap is about 2 meV at zero fields [38, 39]; it follows from equations (6) and (7) that the dominating intralayer exchange 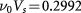 , where
, where 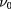 is the density of states per flavor. (ii) Although both QAH and LAF states are ordered without total layer polarization, it is the weak valley-exchange interaction
is the density of states per flavor. (ii) Although both QAH and LAF states are ordered without total layer polarization, it is the weak valley-exchange interaction 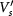 that favors the LAF state [19], in which different valleys have the same layer polarization. Consequently, the A point shifts toward a larger
that favors the LAF state [19], in which different valleys have the same layer polarization. Consequently, the A point shifts toward a larger 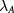 if
if 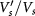 is stronger, as shown in figure 2(c). (iii) The weak Hartree interaction Vz prevents any total layer polarization induced by finite
is stronger, as shown in figure 2(c). (iii) The weak Hartree interaction Vz prevents any total layer polarization induced by finite 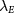 . Thus, both B and C shift toward larger
. Thus, both B and C shift toward larger 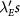 if
if 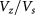 is stronger, as shown in figure 2(d). (iv) Interactions favor the QAH state over the QVH state and produces the novel ALL state near their transition. The ALL-state phase boundaries in figure 2(b) are shifted away from the
is stronger, as shown in figure 2(d). (iv) Interactions favor the QAH state over the QVH state and produces the novel ALL state near their transition. The ALL-state phase boundaries in figure 2(b) are shifted away from the 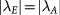 line, which separates the QAH and QVH states in the absence of interactions. Such a shift arises from the compensation of the Hartree energy by the
line, which separates the QAH and QVH states in the absence of interactions. Such a shift arises from the compensation of the Hartree energy by the 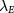 mass in the frozen valley τ, and it is given by
mass in the frozen valley τ, and it is given by 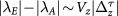 . The width of the ALL-state regime is similarly determined, but by the selected valley
. The width of the ALL-state regime is similarly determined, but by the selected valley  , and it is given by
, and it is given by 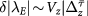 . Note that since B is sensitive to the change of
. Note that since B is sensitive to the change of 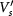 whereas C is not, the ALL state may disappear at
whereas C is not, the ALL state may disappear at 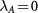 if
if 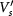 exceeds a critical value, as exemplified by the magenta line in figure 2(d). (Here we predict that a circularly polarized light can stabilize and control the ALL state without Landau levels. Its quantum Hall ferromagnetic variant has been experimentally observed at
exceeds a critical value, as exemplified by the magenta line in figure 2(d). (Here we predict that a circularly polarized light can stabilize and control the ALL state without Landau levels. Its quantum Hall ferromagnetic variant has been experimentally observed at 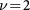 [42].)
[42].)
The parameters for the emergence of the intriguing ALL state in the phase diagram figure 2(b) can be fitted to 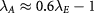 meV at relatively large fields. To observe the ALL state, e.g. one can scan the parameter region around
meV at relatively large fields. To observe the ALL state, e.g. one can scan the parameter region around 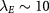 meV and
meV and 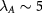 meV. Given equation (2), the electric field strength is
meV. Given equation (2), the electric field strength is 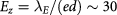 mV
mV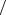 nm where
nm where 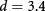 Å is the interlayer separation. The laser frequency, which should be much larger than the interaction-driven or field-induced energy gap ∼
Å is the interlayer separation. The laser frequency, which should be much larger than the interaction-driven or field-induced energy gap ∼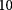 meV but much smaller than
meV but much smaller than 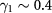 eV, can be chosen as
eV, can be chosen as 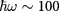 meV. This corresponds to a light frequency ∼
meV. This corresponds to a light frequency ∼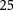 THz or a light wavelength ∼
THz or a light wavelength ∼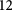 μm. Given equation (4), we can obtain the energy flux of the light is
μm. Given equation (4), we can obtain the energy flux of the light is 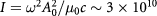 W
W 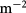 .
.
4. Circular dichroism
In addition to the number of valley-projected chiral edge states (figures 3(d) and (e)) dictated by the aforementioned Chern numbers, different topologically ordered states may also be characterized by optical means. Here we consider terahertz absorbance [66, 67] and its dichroism [68–71] using a second, circularly polarized, normally incident light. Consider a weak probe beam 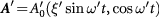 , and to the first order the induced perturbation reads
, and to the first order the induced perturbation reads
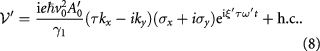
Figure 3. ((a) and (b)) Ordered state masses 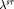 and (c) circular dichroism
and (c) circular dichroism 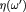 of bilayer graphene, as functions of
of bilayer graphene, as functions of 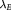 . The square and circle denote different spins,
. The square and circle denote different spins, 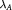 is fixed at 10 meV, and other parameter values are the same as in figure 2(b). ((d)–(f)) Protected zigzag edge states for the three phases. The red and green states, spin degenerate in (d) and (f) but non degenerate in (e), localize at opposite edges. Note that a zigzag edge is the best to observe the charateristic edge states but not required. The edge states are robust as long as the two valleys are well separated in the edge Brillouin zone and the boundary (or domain wall) is smooth in a scale much larger than the inverse of the separation.
is fixed at 10 meV, and other parameter values are the same as in figure 2(b). ((d)–(f)) Protected zigzag edge states for the three phases. The red and green states, spin degenerate in (d) and (f) but non degenerate in (e), localize at opposite edges. Note that a zigzag edge is the best to observe the charateristic edge states but not required. The edge states are robust as long as the two valleys are well separated in the edge Brillouin zone and the boundary (or domain wall) is smooth in a scale much larger than the inverse of the separation.
Download figure:
Standard image High-resolution imageUsing Fermi's golden rule, we obtain the interband transition probability, followed by the flavor absorbance
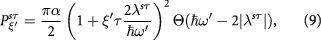
where α is the fine structure constant. We further define the total absorbance and the circular dichroism as
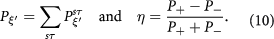
In the limit of 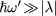 or
or 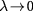 , the total absorbance recovers the universal result
, the total absorbance recovers the universal result 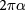 , independent of the light helicity or polarization. This results in
, independent of the light helicity or polarization. This results in 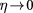 . Close to the thresholds,
. Close to the thresholds, 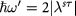 , a circularly polarized light is either destructively blocked or constructively absorbed, depending on the light helicity, the valley index, and the mass sign. This leads to sharp peaks in η.
, a circularly polarized light is either destructively blocked or constructively absorbed, depending on the light helicity, the valley index, and the mass sign. This leads to sharp peaks in η.
Figure 3 plots 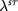 and
and 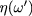 as functions of
as functions of 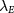 for the case of
for the case of 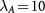 meV. As the electric field increases, the ground state undergoes QAH-ALL-QVH transitions. At the frozen valley the masses are large and of uniform sign for the two spins, whereas at the selected valley the masses are small and relatively inverted for zero, one, and two spin flavors, respectively, in QVH, ALL, and QAH states. Universally, η shows a marked jump when the selected valley starts to be probed and gradually falls upon increasing
meV. As the electric field increases, the ground state undergoes QAH-ALL-QVH transitions. At the frozen valley the masses are large and of uniform sign for the two spins, whereas at the selected valley the masses are small and relatively inverted for zero, one, and two spin flavors, respectively, in QVH, ALL, and QAH states. Universally, η shows a marked jump when the selected valley starts to be probed and gradually falls upon increasing 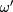 , except that η switches sign for the ALL state due to the different magnitudes of
, except that η switches sign for the ALL state due to the different magnitudes of 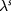 . Distinctively, when the frozen valley starts to be probed, η exhibits a tiny jump for the QAH and ALL states but switches sign for the QVH state and progressively vanishes with further advancing
. Distinctively, when the frozen valley starts to be probed, η exhibits a tiny jump for the QAH and ALL states but switches sign for the QVH state and progressively vanishes with further advancing  . By contrast, the LAF state exhibits little circular dichroism, because the two spin flavors have opposite masses
. By contrast, the LAF state exhibits little circular dichroism, because the two spin flavors have opposite masses 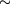
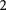 meV.
meV.
5. Discussion
The absorption spectroscopy (or optical conductivity) and circular dichroism provides efficient means not only to measure the flavor dependent mass 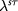 but also to distinguish the competing ordered states. It follows that the photoluminescence can also be circularly and valley polarized, controllable by the external fields. Similarly, opto-valley, -spin, and -charge Hall effects may be feasible upon the pumping of these fields, given the nontrivial conduction-band Berry curvature [3].
but also to distinguish the competing ordered states. It follows that the photoluminescence can also be circularly and valley polarized, controllable by the external fields. Similarly, opto-valley, -spin, and -charge Hall effects may be feasible upon the pumping of these fields, given the nontrivial conduction-band Berry curvature [3].
Three comments are in order. (i) Graphene does not reflect a significant amount of light as opposed to TI's, and the interaction effects are more pronounced in suspended samples. Transmission spectroscopy is thus suggested to study the predicted effects. (ii) In non-equilibrium periodically driven systems, interactions and band populations are important and delicate issues for Floquet states [50, 72, 73]. In our case, additional terms beyond equation (4) produced by interactions can be safely ignored, as we focus on the weak interaction instability implied by peculiar band structures. Given the fact that absorbance per graphene layer is only  [66, 67], presumably the band population is almost intact in the presence of the high-frequency light. (iii) Our Hartree–Fock theory only captures the most essential physics of Floquet bilayer graphene. The weak yet important interaction parameters Vz and
[66, 67], presumably the band population is almost intact in the presence of the high-frequency light. (iii) Our Hartree–Fock theory only captures the most essential physics of Floquet bilayer graphene. The weak yet important interaction parameters Vz and 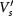 may vary from case to case and should be determined by future experiments. The phase boundaries in figure 2 are likely to be quantitatively modified by the thermal proliferation of domain walls separating different ordered states [31].
may vary from case to case and should be determined by future experiments. The phase boundaries in figure 2 are likely to be quantitatively modified by the thermal proliferation of domain walls separating different ordered states [31].
At single-particle level, the Floquet idea [52–55] was theoretically applied to TI's [74] and semimetals [75–77], and experimentally realized in photonic crystals [78], TI surfaces [47, 48], and ultracold atoms [79]. Our proposal paves the way for generalizing the idea to a paradigmatic many-body system (i.e. chiral few-layer graphene), and revealed the significant roles played by interactions in stabilizing topologically ordered states (e.g. the ALL state) hardly accessible at single-particle level.
Acknowledgments
This work is supported by NSF (PHY-1505496), ARO (W911NF-17-1-0128), AFOSR (FA9550-16-1-0387), and UTD Research Enhancement Funds.