Abstract
The present work is an attempt to formulate the quantum theory of plasmons in metallic structures starting from basic laws of electrodynamics and quantum theory as first principles. In particular, the dynamical integral equation of plasmon in any metallic structure was established. As a test, this general dynamical equation was used to determine the dispersion of plasmon in bulk metal and the obtained result completely agreed with the formula derived in conventional theories. Then the general method for determining the energy spectrum of plasmons in any metallic nanostructure was presented.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
On the basis of the achievements of the fundamental research of physical phenomena related to the interaction of the light with the collective excitations in the electron gas called plasmons, the resonances in the fluctuations of the electron density in metallic structures, including metallic nanostructures, a newly emerging and very promising area of quantum physics called plasmonics has been created and was rapidly developing [1–8]. However, due to the complicated quantum structure of the devices and systems exhibiting the plasmonic effect, formulating and solving theoretical problems related to the wide variety of plasmonic phenomena and processes is very difficult work. Therefore, although there has been significant attention towards the theoretical interpretation or explanation of the experimental data [9–29], there still exists a visible gap between the contents of the theoretical works [30–47] and the subjects of the experimental investigations [48–63]. Moreover, the theoretical works are either based on simplified models of electron gas or on the phenomenological interaction Hamiltonians. Therefore, it is very desirable to find a theory capable of application to the study of the same subjects as those of the experimental works, starting from the basic laws of electrodynamics and quantum theory as the first principles. The present work is an attempt to realize this intention.
In order to overcome the difficulties related to the complicated geometrical forms of the plasmonic structures, it was proposed to apply the functional integral technique using the integration and the integral equations instead of the differentiation and the differential equations in traditional quantum mechanics [64]. The formulation of the physical problems mainly in terms of the integration and the integral equations facilitates the elaboration of computational methods.
The present work is the first attempt to demonstrate the application of the general principles and formulae of the functional integral technique in many-body problems [65, 66] to the study of plasmonic processes and phenomena, starting from the study of the dispersion of plasmon in bulk metal and the energy spectra of plasmons in metallic nanostructures.
The general theory of scalar field of collective excitations in electron gas is presented in section 2. The application of the general theory to the electron gas in bulk metal, as the simplest example, is realized in section 3. Section 4 is devoted to the study of the plasmon spectrum in electron gas of any metallic nanostructure; section 5 contains the conclusion and the discussions.
2. Scalar field of collective excitations in electron gas
Consider the electron gas consisting of itinerant electrons moving in a domain Ω of some metal and denote U(r) the potential energy of electron in the electrostatic field of positive ions in the crystalline lattice of the metal. The single-electron Hamiltonian has the form
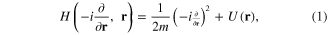
where m is the effective mass of the electron (we use the unit system with 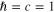 ). This Hamiltonian has eigenstates with wave functions
). This Hamiltonian has eigenstates with wave functions 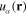 and eigenvalues
and eigenvalues 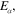
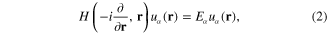
the symbol α labeling the eigenstates and eigenvalues is a group of indices to be identified in each concrete case.
When the mutual electron–electron Coulomb interaction in the electron gas is neglected, it is called the free electron gas. The Green function 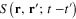 of the electron in the free electron gas is the solution of the inhomogeneous differential equation
of the electron in the free electron gas is the solution of the inhomogeneous differential equation

with the condition

where
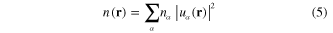
is the electron density in the electron gas, 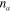 being the occupation number of the quantum state with the wave function
being the occupation number of the quantum state with the wave function 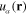 . It has the following explicit expression
. It has the following explicit expression
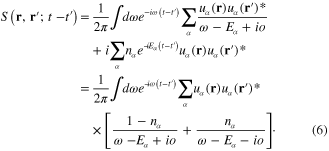
Denote 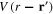 the electrostatic potential energy of the Coulomb interaction between two electrons with the coordinates r1 and r2
the electrostatic potential energy of the Coulomb interaction between two electrons with the coordinates r1 and r2
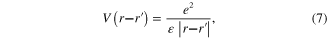
where ε is the background dielectric constant of the metal and e is the absolute value of the electron charge. In the previous work [64] it was shown that the collective excitations in the electron gas can be described by a scalar field 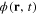 with the effective action being a functional A[φ] of this scalar field. In the harmonic approximation, the second-order approximation with respect to the scalar field
with the effective action being a functional A[φ] of this scalar field. In the harmonic approximation, the second-order approximation with respect to the scalar field  , the effective action functional of this field has following expression
, the effective action functional of this field has following expression
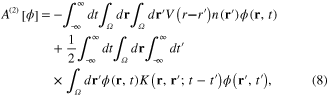
where the kernel 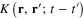 has the form
has the form

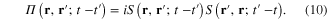
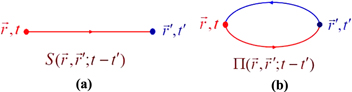
In the diagrammatic representation the function 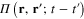 , which is similar to the self-energy part in quantum field theory, and the Green function
, which is similar to the self-energy part in quantum field theory, and the Green function  can be represented as in figure 1.
can be represented as in figure 1.
Figure 1. Diagrammatic representation of (a) 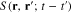 and (b)
and (b) 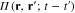 .
.
Download figure:
Standard image High-resolution imageFrom th extreme action
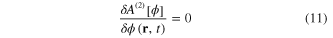
we derive the following integral equation determining the scalar field 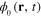 corresponding to the extreme action
corresponding to the extreme action

The solution of the integral equation (12) is a time independent (static) field 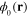 describing the ground state of the electron gas.
describing the ground state of the electron gas.
The fluctuations of the scalar field  around the extreme static field
around the extreme static field 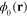 corresponding to the ground state of the electron gas are described by the difference
corresponding to the ground state of the electron gas are described by the difference
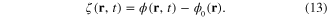
In terms of this new field, the difference
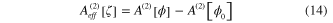
has the quadratic form

It can be interpreted as the effective action of the scalar field 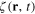 describing the fluctuations of the electron gas around its static ground state in the harmonic approximation. From the expression (15) of the effective action
describing the fluctuations of the electron gas around its static ground state in the harmonic approximation. From the expression (15) of the effective action ![$A_{eff}^{(2)}[\zeta ]$](https://content.cld.iop.org/journals/2043-6262/5/3/035004/revision1/ansn497431ieqn20.gif) of the scalar field
of the scalar field  it follows that this field must satisfy the following integral equation
it follows that this field must satisfy the following integral equation
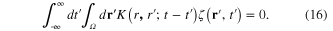
The quanta of the quantized scalar field 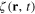 are called the plasmons, and integral equation (16) can be interpreted as the dynamical equation for free plasmon.
are called the plasmons, and integral equation (16) can be interpreted as the dynamical equation for free plasmon.
The kernel 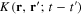 of integral equation (16) is expressed in terms of the function
of integral equation (16) is expressed in terms of the function  defined by formula (10). The explicit expression of this function depends on the form of the metallic structure and the physical parameters of its electron gas. Using the expression (6) of the electron Green function (6), we obtain following general formula
defined by formula (10). The explicit expression of this function depends on the form of the metallic structure and the physical parameters of its electron gas. Using the expression (6) of the electron Green function (6), we obtain following general formula
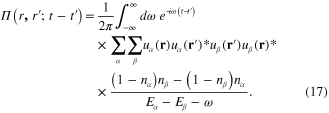
On the basis of this formula for  it is straightforward to establish the expressions of the kernel
it is straightforward to establish the expressions of the kernel 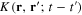 of the dynamical equation (16) of plasmons in the metallic structures and derive their dispersion equations or energy spectra.
of the dynamical equation (16) of plasmons in the metallic structures and derive their dispersion equations or energy spectra.
3. Plasmons in bulk metal
As the first simple example we start from considering the homogeneous and isotropic electron gas in the three-dimensional space. In this case the integration domain Ω is the whole three-dimensional space, the potential energy U(r) in the single electron Hamiltonian (1) can be set to be zero U(r) = 0 and the wave function 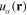 ,
, 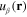 in formulae (6) and (17) are the normalized plane waves
in formulae (6) and (17) are the normalized plane waves
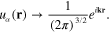
Due to the translational invariance, the free electron Green function  as well as the functions
as well as the functions  and
and 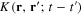 depend only on the difference
depend only on the difference 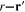 of two coordinates. The electron Green function has the following explicit expression
of two coordinates. The electron Green function has the following explicit expression
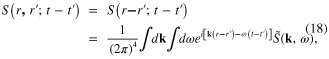
where all integrations are performed from −∞ to +∞ and
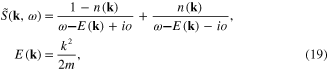
n(k) being the electron distribution function 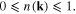
Denote 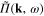 ,
,  and
and  the Fourier transforms of
the Fourier transforms of 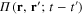 ,
, 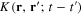 and of the Coulomb interaction potential between two electrons:
and of the Coulomb interaction potential between two electrons:
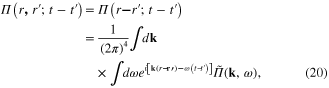
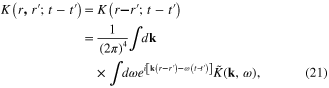
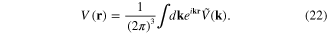
Using formula (9) for the function  we can express its Fourier transform in terms of the Fourier transform
we can express its Fourier transform in terms of the Fourier transform 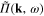 and
and 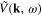 as follows:
as follows:
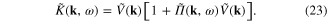
In order to find the expression of 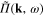 we start from formula (17) and substitute
we start from formula (17) and substitute
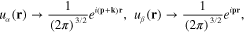
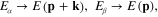
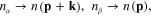
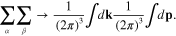
We obtain
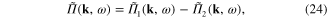
where

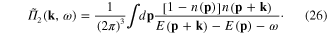
By means of the substitution  we rewrite formula (25) in the form
we rewrite formula (25) in the form
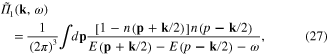
By changing the integration variable 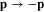 we rewrite expression (26) as follows
we rewrite expression (26) as follows
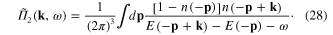
Because both 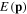 and
and  are the functions of p2, we have
are the functions of p2, we have
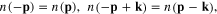
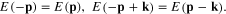
Therefore,
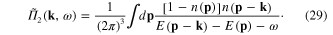
By means of the substitution  , we obtain
, we obtain
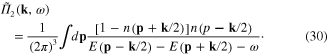
Combining (27) and (30), finally we derive following expression of 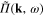 :
:
Consider the case of the electron gas at vanishing absolute temperature T = 0 and denote pF the magnitude of the momentum of electrons at the Fermi surface. Because n(p) is equal to unity inside and on the Fermi surface, i.e. at  , and vanish outside this surface, i.e. at p > pF, the domain of integration in the rhs of formula (31) must be the common volume of the region inside the spherical surface
, and vanish outside this surface, i.e. at p > pF, the domain of integration in the rhs of formula (31) must be the common volume of the region inside the spherical surface 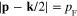 and the region outside the spherical surface
and the region outside the spherical surface 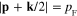 . At small values of k (k/2 < pF) two spheres
. At small values of k (k/2 < pF) two spheres 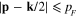 and
and 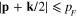 are overlapping (figure 2) and the domain of integration is the region bounded by two above-mentioned spherical surfaces. Let us choose the direction of vector k to be that of the vertical axis Oz in the rectangular coordinate system. Then for small values of k the domain of integration is the region bounded from above by the spherical surface
are overlapping (figure 2) and the domain of integration is the region bounded by two above-mentioned spherical surfaces. Let us choose the direction of vector k to be that of the vertical axis Oz in the rectangular coordinate system. Then for small values of k the domain of integration is the region bounded from above by the spherical surface  and bounded from below by the spherical surface
and bounded from below by the spherical surface  (figure 2). In this case formula (31) becomes
(figure 2). In this case formula (31) becomes
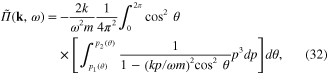
where
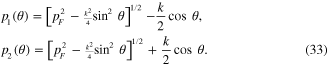
Figure 2. The integration domain Ω is confined inside the region with the yellow colour. 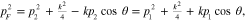

Download figure:
Standard image High-resolution imageExpanding the rhs of formula (32) into the power series of the small variable k2 and limiting at the second-order approximation, we obtain [31, 67]
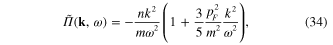
where
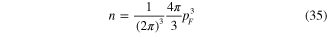
is the electron density in the metal. Substituting expression (34) into the rhs of formula (23), using expression

and setting
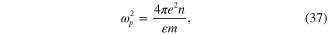
we obtain
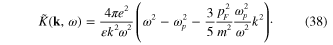
Finally consider the dynamical equation (16) for the free plasmons in the metal. In this case the kernel 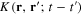 has the form (21) with the Fourier transform
has the form (21) with the Fourier transform 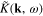 of the form (38). Introduce the Fourier transformation of the scalar field
of the form (38). Introduce the Fourier transformation of the scalar field 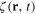 :
:
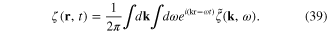
From the dynamical equation (16) it follows that
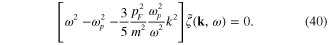
Therefore, the energy ω and the momentum k of free plasmons must satisfy following dispersion equation
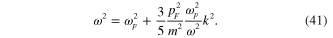
In the first order with respect to the small ratio 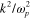 this dispersion equation can also be written as follows
this dispersion equation can also be written as follows
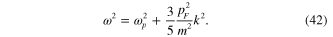
Previously, formula (42) was derived in the framework of the conventional theory of plasma oscillations in metal [68, 69].
We have established formula (41) by using the expression (32) of  , expanding the integral over momentum p into a power series of k2 and limiting at the approximation of the second order. In principle we can derive the approximate expression of ω in the form of a polynome of any order of the variable k2, starting from the expression (32) of
, expanding the integral over momentum p into a power series of k2 and limiting at the approximation of the second order. In principle we can derive the approximate expression of ω in the form of a polynome of any order of the variable k2, starting from the expression (32) of  and cutting each power series of the small variable k2 at the appropriate order. Moreover, expression (32) and other complicated analytical formulae can be effectively used for the numerical calculation of the k2-dependence of ω by means of the simulation technique.
and cutting each power series of the small variable k2 at the appropriate order. Moreover, expression (32) and other complicated analytical formulae can be effectively used for the numerical calculation of the k2-dependence of ω by means of the simulation technique.
4. Plasmons in metallic nanostructures
For the application in subsequent works to study plasmons in various plasmonic devices, now we consider the electron gas in some metallic nanostructure occupying a domain Ω of the three- dimensional space. In this case, instead of the expressions (20) and (21), we must use following formulae of the Fourier transformation of functions  and
and 
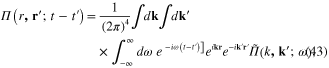

where all integrations over the momenta k and k' are performed over the whole three-dimensional momentum space, and
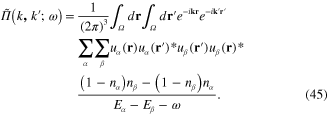
In term of the Fourier transforms  ,
, 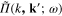 and
and  , formula (9) becomes
, formula (9) becomes
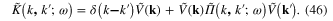
Substituting the Fourier transformation formulae (39) for the wave function 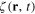 and (44) for the kernel
and (44) for the kernel  into the lhs of the relation (16), we derive following integral equation
into the lhs of the relation (16), we derive following integral equation
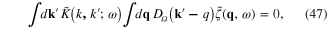
where
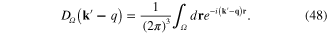
When the domain Ω is the whole three-dimensional space,  becomes the function
becomes the function  . Using expression (46) of
. Using expression (46) of  and setting
and setting

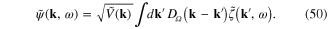
Finally, we obtain the dynamical integral equation of plasmon in the following form
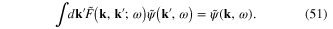
The plasmon energy (frequency) spectrum consists of the values of the parameter ω satisfying the requirement of the existence of the solution of the integral equation (51).
5. Conclusion and discussion
In our previous work [64] we have elaborated the functional integral technique for the theoretical study of the elementary collective excitations of the electron gas. It was shown that the fluctuations of the electron density in the electron gas can be described by a scalar field whose quanta are the elementary collective excitations called plasmons—the plasmon field. The present work is the continuation of the previous one [64]. In the harmonic approximation we have established the dynamical integral equation of the plasmon field in the most general form capable of application to any electron gas. In the case of the isotropic homogeneous electron gas in the bulk metal, from the established dynamical integral equation of the plasmon field it follows the well-known plasmon dispersion formula. This agreement would be a good test of the validity of the established plasmon dynamical integral equation.
The above-mentioned dynamical integral equation of the plasmon field can be used in order to find the plasmon energy spectrum of the electron gas in a metallic nanostructure by means of corresponding approximate computational methods. For this purpose we have performed Fourier transformation of all functions of the coordinates and derived the dynamical integral equation (51) containing a real parameter ω. The plasmon energy (frequency) spectrum consists of the values of this parameter satisfying the requirement of the existence of the solution of the newly established dynamical integral equation. For the study of the plasmon energy (frequency) spectrum it is necessary to establish the explicit form of the last integral equation, elaborate the appropriate simulation method for solving this dynamical equation and find the values of the parameter ω such that at these values the solution of equation (51) does exist.
Acknowledgment
The authors would like to express their gratitude to Vietnam Academy of Science and Technology for the support.