Isotropic negative refractive index at near infrared

In the last decade great efforts have been made to develop negative-index metamaterials (NIMs). The first NIMs consisted of thin metal wires and split-ring resonators (SRRs). These constitutive elements, when combined, provided both negative electric and magnetic responses within the same frequency range, therefore demonstrating negative beam deflection in a prism [1]. Various modifications of this microwave design were proposed for the far and mid infrared frequency regions (see [2, 3]). However, further increase in the operating frequency encountered fundamental limitations on the magnitude of the magnetic resonance of SRRs related with to kinetic inductance [4]. This problem has been eliminated by the invention of multi-split SRRs [5]. However, the implementation of wire-SRR metamaterials in the near IR and visible ranges has encountered technological problems [6].

Other works utilized various approaches to achieve negative refraction at optical frequencies. The strong development of wired structures resulted in the well-known fishnet metamaterial (see e.g. [7–9]), i.e. a set of parallel plasmonic meshes. In fishnet metamaterials the resonant magnetic response results from the non-equidistant arrangement of resonant meshes. The fishnet geometry effectively shares out pairs of meshes, which at certain frequencies operate as effective magnetic layers. The resonance of the magnetic mode can overlap over the frequency range of the electric mode. This overlapping results in a negative refractive index (see [7–9]). The negative refractive index has been experimentally retrieved from the plane-wave reflection and transmission coefficients of a fishnet layer [7–10]. However, as was shown in [11], this negative index refers only to incidence angles which are close to zero. One can conclude that fishnet structures are very anisotropic and reveal their unusual properties only for a narrow angular spectrum. The same observation refers to such optical metamaterials as cut-wire pairs [12], cut-patch pairs [13], and other design solutions based on the planar technology (e.g. [14, 15]).

In this work we are looking at a feasible design solution for isotropic NIMs for the visible or at least near-infrared range. The simplest particle geometry that has an isotropic response is spherical. Spherically symmetric inclusions for isotropic negative effective material parameters were suggested in several works. In [16] the idea of effective nanorings of plasmonic spheres allowed the authors to predict a negative refractive index in the visible range for a metamaterial which would comprise a mixture of these nanorings with different orientations. In [17] this idea was developed, and negative permeability was predicted for a cubic lattice of raspberry-like nanoclusters with a central dielectric core covered by silver nanospheres. These silver particles were assumed to be rather substantial (20–30 nm) and covered by organic molecules (e.g. proteins) so as to avoid electrical contact. If the solid dielectric core of such a nanocluster was replaced by a core–shell particle with a golden core, the approximate analytical theory predicted a negative refractive index for such lattices (though in the background of high optical losses). However, in [17] the simplified Drude model was adopted for the dielectric constant of silver. This model did not take into account the peculiarities of the permittivity at the optical transitions which occur in the operational frequency range of the suggested metamaterial. As shown in [18], experimental data for the dissipative losses in silver substituted instead of the Drude fitting model ruined the effects claimed in [17]. More complicated silver particles replacing the simple nanospheres in the raspberry nanocluster allowed us to simulate the negative effective permeability of the lattice in [19]. However, beyond the Drude model for silver negative refraction has not been revealed for any of the composites of raspberry nanoclusters we have extensively studied. Therefore we have started to try other geometries.

In [20] a photonic crystal of metal spheres operating in the visible range performed as a NIM. This NIM resulted from spatial dispersion effects related to the rather large optical size of constituents at the operating frequency. Therefore, the optical properties of such lattices are very anisotropic: at the operating frequency the isofrequency surface of the lattice is far from a spherical shape.

At microwave frequencies one often tries to design NIMs using the idea of combined electric and magnetic Mie resonances in dimers of rather distant spheres. Then the lattice contains two identical sublattices of two different spheres. One sphere (the smallest one) experiences the magnetic Mie resonance at the same frequency while another (the larger one) experiences the electric Mie resonance (see [21]). After [21] a number of theoretical and experimental papers appeared developing this idea. However, the spatial dispersion which is also inherent to such lattices resulted in strong optical anisotropy, as shown in [22]. To avoid the strong spatial dispersion in the lattice exploiting the Mie resonance one has to miniaturize the unit cell. The obvious way is to replace the dimer of two different spheres by a single core–shell particle. The optical properties of such particles were previously studied in the literature (see [23, 24]). Since in a transparent particle the electric and magnetic Mie resonances can hardly occur at the same frequency, the electric Mie resonance can be replaced (in the optical range) by the plasmon resonance.

This approach to the design solution for isotropic NIMs at optical frequencies was first claimed in [25]. The metamaterial under study was formed by LiTaO₃ spheres covered with metallic shells. LiTaO₃ in the far IR range is a so-called polaritonic material with high permittivity and rather small optical losses. Nanospheres experienced a magnetic Mie resonance at frequencies where their diameter was much smaller than the wavelength. This optical smallness allowed the absence of strong spatial dispersion in the metamaterial which was isotropic in the simulations of [25]. Metallic nanoshells of constitutive particles provided negative permittivity of the lattice due to their plasmon resonance, whereas the polaritonic cores provided negative permeability. By tailoring all sizes these resonances were obtained in the same frequency region.

However, the design solution with the dielectric core and metal shell results in a NIM only for the far-infrared range and, perhaps, also for the mid IR. In the visible and near IR ranges only very lossy materials demonstrate such a high permittivity as polaritonic materials show in the far and mid infrared. Probably, crystalline silicon is the material which is the closest analog of polaritonic materials for the visible range. The real part of the complex permittivity equals 13–25 at frequencies of 300–800 THz (at higher frequencies silicon becomes very lossy). These values are not high enough to obtain the magnetic Mie resonance in a very small particle. A nanosphere of c-Si demonstrates the magnetic Mie resonance at a wavelength λ where its diameter is only three to five times smaller than λ. These spheres, though optically substantial, are small enough to avoid the strong spatial dispersion of a densely packed cubic lattice. However, we have found that such spheres when covered with metal nanoshells do not allow isotropy to be reached. If the lattice is not very dense and its unit cell is significantly larger than the particle size, the strong spatial dispersion cannot be avoided due to the Bragg phenomenon. The dense package of the lattice means small distances between adjacent metal shells and consequently their high capacitive coupling. The strong coupling of adjacent metal shells dramatically changes the operation of the lattice unit cell compared to an individual core–shell particle. All attempts to deduce collective properties from those of an individual particle are useless.

In our present paper we develop the approach suggested in [25], so that the plasmon resonance is now due to the metal core and the magnetic Mie resonance holds for the spherical shell. We saw that this (at first glance slight) modification of the known design leads to a qualitatively new result: the optical isotropy of a NIM is now achievable with optically rather substantial particles. Our NIM operates in the inter-band region (700–900 nm). In our case the core is made of silver and the shell is made of silicon (crystal or amorphous), as shown in figure 1. Below we analytically calculate the electric and magnetic response of the single core–shell particle, then compare it with the results of the retrieval. Individual polarizabilities are retrieved from the scattering matrix of a monolayer grid which is obtained by full-wave simulations. The retrieval is done in accordance with the model of a resonant monolayer grid of magnetic and electric dipoles, suggested in [26] (we call such grids metafilms). We discuss the isotropy of the lattice and finally we numerically demonstrate negative refraction in a metamaterial prism.

Zoom In Zoom Out Reset image size

Let us consider a particle consisting of a central core with radius r₁ and a shell (outer radius r₂), shown in figure 1. The electromagnetic response of spherical particles can be analytically estimated using the Mie theory generalized for core–shell particles in [27, 28]. Being excited by a plane wave, such a particle produces a scattered field, which can be decomposed into multipole terms. The proportionality constant of the 2^m-pole term for the electric field is given by the following expression:

$$\begin{eqnarray} &&\fl {a}_{m}=({\psi }_{m}(y)[{\psi }_{m}^{\prime}({n}_{2}y)-{A}_{m}{\chi }_{m}^{\prime}({n}_{2}y)]-{n}_{2}{\psi }_{m}^{\prime}(y)[{\psi }_{m}({n}_{2}y)\nonumber\\ &&-~{A}_{m}{\chi }_{m}({n}_{2}y)])({\xi }_{m}(y)[{\psi }_{m}^{\prime}({n}_{2}y)-{A}_{m}{\chi }_{m}^{\prime}({n}_{2}y)]\nonumber\\ &&-~{n}_{2}{\xi }_{m}^{\prime}(y)[{\psi }_{m}({n}_{2}y)-{A}_{m}{\chi }_{m}({n}_{2}y)])^{-1}, \end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray} &&\fl {A}_{m}=\frac{{n}_{2}{\psi }_{m}({n}_{2}x){\psi }_{m}^{\prime}({n}_{1}x)-{n}_{1}{\psi }_{m}^{\prime}({n}_{2}x){\psi }_{m}({n}_{1}x)}{{n}_{2}{\chi }_{m}({n}_{2}x){\psi }_{m}^{\prime}({n}_{1}x)-{n}_{1}{\chi }_{m}^{\prime}({n}_{2}x){\psi }_{m}({n}_{1}x)} \end{eqnarray} \tag{ 2 }$$

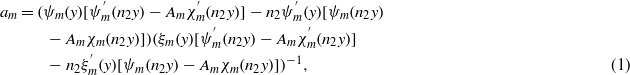
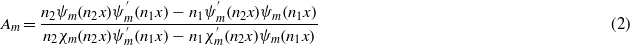
and for the magnetic field:

$$\begin{eqnarray} &&\fl {b}_{m}=({n}_{2}{\psi }_{m}(y)[{\psi }_{m}^{\prime}({n}_{2}y)-{B}_{m}{\chi }_{m}^{\prime}({n}_{2}y)]-{\psi }_{m}^{\prime}(y)[{\psi }_{m}({n}_{2}y)\nonumber\\ &&-~{B}_{m}{\chi }_{m}({n}_{2}y)])({n}_{2}{\xi }_{m}(y)\left [{\psi }_{m}^{\prime}({n}_{2}y)-{B}_{m}{\chi }_{m}^{\prime}({n}_{2}y)\right ]\nonumber\\ &&-~{\xi }_{m}^{\prime}(y)[{\psi }_{m}({n}_{2}y)-{B}_{m}{\chi }_{m}({n}_{2}y)])^{-1}, \end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray} &&\fl {B}_{m}=\frac{{n}_{2}{\psi }_{m}({n}_{1}x){\psi }_{m}^{\prime}({n}_{2}x)-{n}_{1}{\psi }_{m}^{\prime}({n}_{1}x){\psi }_{m}({n}_{2}x)}{{n}_{2}{\chi }_{m}^{\prime}({n}_{2}x){\psi }_{m}({n}_{1}x)-{n}_{1}{\chi }_{m}({n}_{2}x){\psi }_{m}^{\prime}({n}_{1}x)}, \end{eqnarray} \tag{ 4 }$$

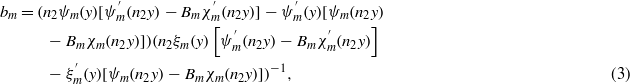
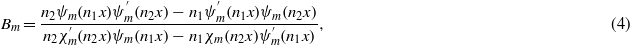
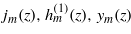where n₁ and n₂ are complex refractive indices of the core and shell, respectively, $x={k}_{0}{r}_{1},y={k}_{0}{r}_{2},{\psi }_{m}(z)=z{j}_{m}(z),{\xi }_{m}(z)=z{h}_{m}^{(1)}(z),{\chi }_{m}(z)=-z{y}_{m}(z)$ and ${j}_{m}(z),{h}_{m}^{(1)}(z), {y}_{m}(z)$ are spherical Bessel functions.

For electrically small particles we may take into account only electric and magnetic dipole terms in the scattered field, neglecting high-order terms. Then, as shown in [29], the expressions for the electric and magnetic polarizabilities for the particle are as follows:

$$\begin{eqnarray} &&{\alpha }_{\mathrm{ee}}=\frac{6 \pi \mathrm{i}{a}_{1}}{{k}_{0}^{3}}, \end{eqnarray} \tag{ 5 }$$

$$\begin{eqnarray} &&{\alpha }_{\mathrm{mm}}=\frac{6 \pi \mathrm{i}{b}_{1}}{{k}_{0}^{3}}. \end{eqnarray} \tag{ 6 }$$

In order to obtain negative refraction in the composite one needs to have both strong electric and magnetic responses of the individual particles in the same frequency range. In our design the core of the particle is made of silver. A strong electric response is provided by the plasmonic resonance of the core, due to the negative permittivity of silver in the optical region (the data for the permittivity of silver was taken from [30]). The resonant magnetic response is offered by the silicon shell. We studied both crystalline and amorphous Si shells (the data for complex permittivity were taken from [32, 31]). Analytical expressions of the Mie theory (1)–(4) allowed us to quickly optimize the dimensions of the core particle in order to obtain both resonances in the same frequency range.

These analytical calculations gave us the following geometric parameters of the particle with overlapping electric and magnetic resonances of large magnitudes (amorphous silicon shell): r₁ = 30 nm and r₂ = 130 nm. The particle size is close to λ/4 at the resonant frequency.

In order to verify this approximate analytical model we have utilized an independent method to calculate the individual electric and magnetic polarizabilities. This method was first suggested by the groups of C Holloway and E Kuester in [26] and later successfully used in our works [33, 19]. The procedure for the retrieval of individual polarizabilities of particles is as follows. First, one should obtain amplitudes and phases of both reflection and transmission coefficients of a metafilm (a planar grid of such particles) for the normal incidence. Second, the collective electric and magnetic polarizabilities of the metafilm (called in [26] surface susceptibilities) are calculated using the expressions:

$$\begin{eqnarray} &&{\chi }_{\mathrm{ES}}=-\frac{2\mathrm{i}}{{k}_{0}}\frac{R+T-1}{R+T+1} \end{eqnarray} \tag{ 7 }$$

$$\begin{eqnarray} &&{\chi }_{\mathrm{MS}}=-\frac{2\mathrm{i}}{{k}_{0}}\frac{R-T+1}{R-T-1}. \end{eqnarray} \tag{ 8 }$$

Finally, one retrieves individual electric and magnetic polarizabilities of particles through the surface susceptibilities using the formulae

$$\begin{eqnarray} &&{\alpha }_{\mathrm{ee}}=\frac{1}{\frac{1}{{a}^{2}{\chi }_{\mathrm{ES}}}+\frac{{k}_{0}{C}_{0}}{4{a}^{2}}-\frac{\mathrm{i}{k}^{3}}{6 \pi }}, \end{eqnarray} \tag{ 9 }$$

$$\begin{eqnarray} &&{\alpha }_{\mathrm{mm}}=\frac{1}{\frac{1}{{a}^{2}{\chi }_{\mathrm{MS}}}+\frac{{k}_{0}{C}_{0}}{4{a}^{2}}-\frac{\mathrm{i}{k}^{3}}{6 \pi }}. \end{eqnarray} \tag{ 10 }$$

Here C₀ = cos(k₀as)/(k₀as) − sin(k₀as),s = 0.6956 is a quasi-static interaction constant of a planar dipole grid and a is the grid period. In [26] the authors assumed 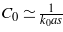${C}_{0}\simeq \frac{1}{{k}_{0}a s}$, which corresponds to the limiting case k₀a ≪ 1. The term −ik³/6π for time dependence exp(−iωt) corresponds to the compensation of individual radiation losses of electric and magnetic dipoles in their regular infinite arrays (see e.g. [36]).

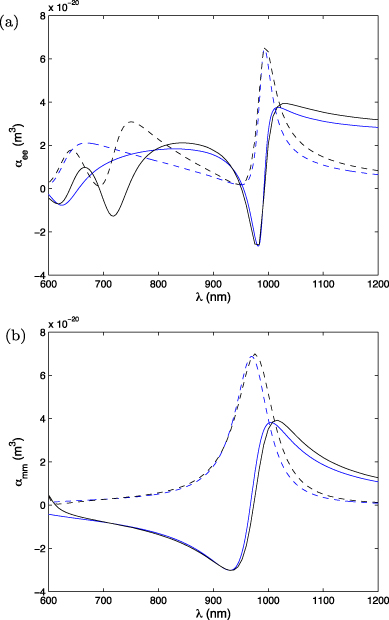
The reflection and transmission coefficients R and T for the planar array of coated spheres with r₁ = 30 nm,r₂ = 130 nm and a = 270 nm were obtained using Ansoft HFSS. Figure 2 shows the comparison between polarizabilities calculated in accordance with the Mie theory and those extracted from numerical simulations. It is clearly seen that up to wavelengths lower than 830–850 nm the two methods give very similar results. This means that for a planar array the quasi-static model is adequate until the frequency at which the grid period is equal to one-third of the operational wavelength. Such a high frequency bound for validity of the quasi-static model gives hope that the spatial dispersion effects will be avoided also for a bulk lattice.

Zoom In Zoom Out Reset image size

Notice, that the frequency shape of the electric individual polarizability does not correspond to the Lorentz resonance. This is typical for a Fano resonance. Such a result for a dipole electric polarizability of a rather small particle seems to be strange, but it is not new. Fano resonances require an observable that is sensitive to interference. When referred to individual responses of the particles this interference can be provided by the overlapping of two resonances (the dipole plasmonic one and the magnetic Mie one). The possibility of this situation for scatterers whose size is smaller than λ/2 has been already pointed out in [37].

Using the well-known Maxwell Garnett model (modified in [16] so that to take into account the compensation of dipole radiation damping) we calculated the effective permittivity and permeability for a simple cubic lattice. These effective material parameters are expressed through individual polarizabilities of core–shell particles as follows:

$$\begin{eqnarray} &&{\epsilon }_{\mathrm{eff}}=1+\frac{1}{{N}_{\mathrm{d}}^{-1}[{\alpha }_{e}^{-1}+\mathrm{i}({k}_{0}^{3}/6 \pi )]-1/3}, \end{eqnarray} \tag{ 11 }$$

$$\begin{eqnarray} &&{\mu }_{\mathrm{eff}}=1+\frac{1}{{N}_{\mathrm{d}}^{-1}[{\alpha }_{m}^{-1}+\mathrm{i}({k}_{0}^{3}/6 \pi )]-1/3}, \end{eqnarray} \tag{ 12 }$$

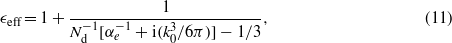
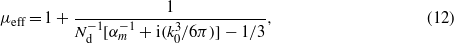
where N_d is the particle concentration. The term −ik³/6π corresponds to the compensation of radiation losses of an individual particle in an infinite array (see [34, 35] for details). Notice that for finite regular arrays radiation losses are not fully compensated. This term should be multiplied by a certain weight factor W which is evidently between 0 and 1 (see [36]). The same refers to non-regular infinite arrays. If the distribution of the particle concentration is fully random then W = 0 and the term −ik³/6π is absent.

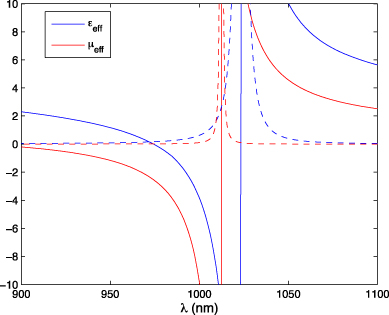
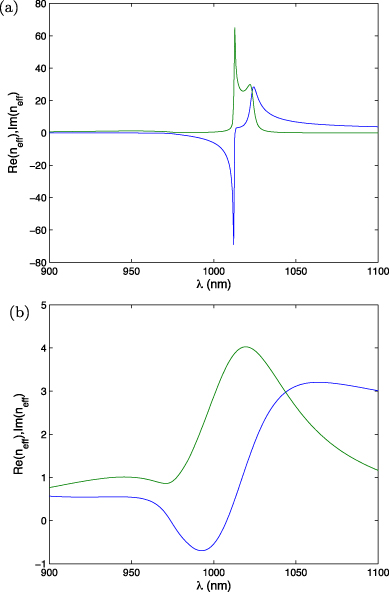
The unit cell size in the analytically optimized simple cubic lattice is 270 nm, which at the combined electric and magnetic resonance is four times smaller than the wavelength. Figure 3 shows the effective material parameters of the lattice. One can clearly see the frequency region where both permittivity and permeability are negative. Figure 4 gives the effective negative refractive index of the composite for two cases: (1) a periodic arrangement of the particles in a cubic lattice (a simple cubic lattice with period 270 nm, body-centered cubic (bcc) or face-centered cubic (fcc) lattice with the same concentration of particles), (2) a fully random arrangement of particles with the same averaged concentration. In the second case the term −ik³/6π is absent in both (11) and (12). We see from this comparison that the effective parameters are extremely sensitive to the presence or absence of radiation losses.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

It is worth mentioning that the quasi-static interaction model for a bulk lattice becomes inadequate at lower frequencies than for a planar array. For the period λ/4 the Maxwell Garnett theory is inaccurate and the design parameters (dimensions) analytically optimized using this theory can be considered only as preliminary estimations of the required sizes. To find parameters which reliably implement the NIM we performed numerous simulations in the vicinity of the values predicted by this analytical model. We simulated the dispersion in a simple and bcc lattice using HFSS software and have not seen features of the strong spatial dispersion up to frequencies lying in the 3d pass band at which the period approaches λ/2. At the operating frequencies there is no optical anisotropy, and the propagation along the crystal axes and the oblique propagation hold with nearly the same refractive index.

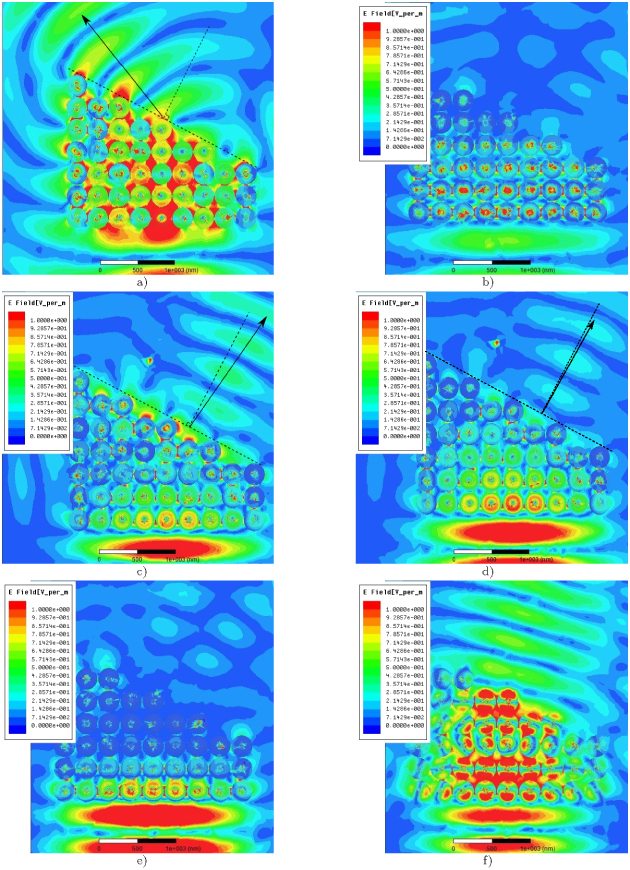
In order to demonstrate the negative refractive index we simulated the incidence of a Gaussian beam on the metamaterial prism of finite size shaped as a wedge (see figure 5). The design parameters were optimized for the negative refractive (the optimization implied the refractive index to be as close as possible to (−1) at a certain wavelength) and are as follows: r₁ = 30 nm, r₂ = 140 nm, amorphous silicon, simple cubic lattice. The reason for the 10 nm increase in the outer radius is discussed below.

Zoom In Zoom Out Reset image size

The field distributions are shown in descending order starting from the largest wavelengths. At lower frequencies corresponding to the simulation depicted in figure 5(a) the prism in our model possesses a positive refractive index. The model prediction at this wavelength fits the simulated refraction. Then the resonant stop-band follows for which the quasi-static model predicts huge optical losses and the simulation figure 5(b) confirms it. However, it occurs at a higher frequency than the quasi-static model predicts (the difference is nearly 15%). Its width is about 100 nm in terms of λ. This value is close to that predicted by the homogenization model with non-compensated radiation losses and disagrees with the predictions for an infinite periodic array figure 4(a). This difference can be explained by the presence of radiation losses in the finite array despite its internal periodicity. The extreme sensitivity of the structure under study to this factor has been discussed above. The prism is optically not very large (for larger prisms we could not achieve a reliable convergence of simulations), and its size is not sufficient for total compensation of individual radiative losses of particles. Moreover, spheres located at the edges of the prism scatter strongly since the output side of the prism is not very large compared to the width of the Gaussian beam.

First we performed the simulations with r₁ = 30 nm and r₂ = 130 nm, but found no negative refraction. The reason for this failure turned out to be the additional shift of the magnetic resonance in the three-dimensional composite. The magnetic response is due to the excitation of the Si shells. These shells are very close to one another, unlike the cores which are sufficiently distanced. The dynamic interaction between adjacent Si shells resulted in a resonance frequency shift. As a result, the magnetic and electric resonances, which overlap over frequency within the MG model, are not overlapping any more. We needed to perform further numerical optimization to find the true geometrical parameters for the negative refraction: r₂ = 140 nm is very close to the initial estimations by the quasi-static model, but not exactly the same. The negative refraction illustrated by figure 5(c) also occurs at the frequency blue-shifted by 15% with respect to the analytical prediction. The effective refractive index of the prism retrieved from the beam deviation angle has an absolute value whose maximum nearly equals 0.5 and it better fits the model predictions for the random array figure 4(b) than those for the infinite periodic array figure 4(a). Looking at the attenuation of the refracted beam one can estimate the imaginary part of the refractive index, which approximately equals 0.12 and gives FOM ≈ 4. The range of the NIM operation is centered at 877 nm with width about 10 nm. The incident beam in this range feels the presence of the edges, and this results in a distortion of the phase fronts in the negatively refracted beam in the vicinity of the prism, where the phase fronts are not exactly orthogonal to the averaged Poynting vector of the beam. In the NIM range the effective impedances of the metamaterial and free space are mismatched, which leads to the strong reflection. We need to note that the far-field spectra calculated in HFSS show no refraction at all, which is surprising and contradicts the theoretical predictions. We can explain this by the following. The HFSS code calculates the far-field pattern on the basis of the field distribution in the array spatial domain. The wedge array simulations are very resource intensive and require large meshing. Inaccuracies in the near-field distribution are inevitable in this case. Small errors in the near fields for such a large bulk array, especially in the phase distribution, perhaps are not visible in our color map, but may lead to the large errors in the far-field spectra. In our opinion the calculation of the far-field pattern of such large bulk arrays of resonant scatterers is unreliable in HFSS. This explains why the field distribution inside the array spatial domain and around it is in good agreement with theoretical model, but the calculation of the far-field pattern fails.

Figure 5(d) shows the almost zero refraction near the bound of the second stop-band. This stop-band corresponds to figure 5(e) and also fits the analytical model for the random array. It refers to the case when the resonant permeability is still negative, but the resonant permittivity passes its second zero and becomes positive. In this range the complex refractive index has a small real part whereas its imaginary part is close to unity (see figure 4(b)). As a result, in this range the reflectance is almost total. After the second stop-band the region with small positive refraction follows. Here the resonant permeability also passes its second zero and becomes positive. We can see the simulation for this region in figure 5(f). At wavelengths of less than 700 nm the homogenization model becomes inadequate and the simulations have shown that in this range the prism scatters the incident beam.

Analogous results have also been obtained for the case when shells of nanoparticles are made of crystal silicon. Since the optical constants of the crystal and amorphous silicon in the inter-band frequency range are close to one another, the changes in the optimal design parameters and frequencies of the NIM operation are negligible. Concerning the possible ways of creating of such a metamaterial, using current fabrication methods one may already obtain uniform silver nanospheres [38], hollow silicon nanospheres [39] and even core–shell structures with a silver core and silica shell [40]. It seems very likely that development of these methods will allow us to build silver–silicon core–shell particles with controlled thickness in the near future.

We suggested and studied a design for a metamaterial based on spherical nanoparticles with a silver core and a silicon shell. The electromagnetic responses of individual particles were studied using the Mie theory and successfully validated by the theory of surface susceptibilities of a metafilm. In this validation the scattering matrix of the metafilm was obtained from full-wave numerical simulations. In this way it was shown that up to frequencies where the particle size is equal to λ/3 the analytical model of the single particle is rather accurate. Then we performed the analytical optimization of the particle dimensions to combine electric and magnetic resonances with resonance magnitudes sufficient for obtaining a negative refractive index for a composite medium. Using the modified Maxwell Garnett model we calculated the effective material parameters and revealed the possibility of an isotropic negative refractive index in the near-infrared frequency range. It was shown that material parameters are strongly dependent on the level of compensation of radiative losses of a single particle. This compensation is absent for a random array and is complete for a periodic array. We simulated the dispersion in an infinite lattice and found no features of spatial dispersion and anisotropy at the operating frequencies. Finally, our predictions were validated by the numerical simulation of the refraction of a Gaussian beam by a metamaterial prism. We obtained a negative deviation angle which is the most convincing numerical demonstration of a negative refractive index. Extended simulations are in agreement with the analytical model. The main difference is the frequency blue shift, equal to nearly 15%.

To our knowledge, our work is the first study describing an optically isotropic NIM operating at frequencies as high as those of the inter-band range (700–900 nm).

The research leading to these results has received funding from the European Community's Seventh Framework Programme (FP7/2007–13) under grant agreement no 228762 and was carried out in the frame of the METACHEM project (2009–13).