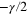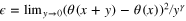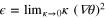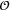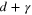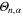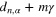Abstract
We discuss general features of the operator product expansion and use it to infer multi-point manifestations of the energy cascade in turbulence. We calculate explicitly the possible form of the three-point velocity correlation function when one distance is smaller than two others. We elucidate manifestation of direct and inverse energy cascades in the three-point velocity correlation function.
Export citation and abstract BibTeX RIS
1. Introduction
Operator product expansion (OPE), also known as the 'fusion of correlations', is a powerful general tool for analyzing multi-point correlations of random fields. It claims, essentially, that for local quantities, whose correlations decay with distances, the correlations between values of the fields taken at a set of close points can be separated from their correlations with the values of the fields at distant points. That makes it possible to replace a product of closely located fields by a sum of composite local quantities (see e.g. [1]).
Originally, OPE was introduced in quantum field theory (QFT) [2, 3] and in (mathematically equivalent) equilibrium statistical mechanics of classical fields [4, 5]. In these contexts, OPE have proven to be a remarkably useful analytic tool, especially in conformal field theories, where it can even be promoted into the basic dynamical principle [5, 6]. In any case, OPE provides a natural way to separate local properties of the field statistics from global aspects such as the geometry of the space and the boundary conditions.
It is natural to ask if and to which degree OPE can be extended to more general cases of fluctuating fields, away from thermal equilibrium, such as the velocity field of developed turbulence. We are not aware of any first-principle derivation of the (equal-time) OPE in turbulence: while standard justifications of the equilibrium OPE are based on the Renormalization group analysis, no appropriate RG scheme in fluid turbulence is yet developed. The question of validity of OPE is important in particular in view of recent discovery of the traces of conformal invariance in the statistics of isolines in 2d inverse turbulent cascades in the whole family of fluid-mechanical models [7–9], including Euler hydrodynamics. In fact, conformal invariance of the statistics of fields in 2d turbulence was conjectured by Polyakov over 20 years ago [10]. We note that, regardless of the validity of this conjecture, even its general formulation requires the notion of OPE. More generally, in turbulence different symmetries (Galilean and scale invariance, time reversibility) are broken spontaneously i.e. at the level of correlation functions, see e.g. [11]. Those symmetries, however, may be present on a deeper level of OPE. For these reasons, we believe that establishing (or disproving) the validity of OPE in non-equilibrium statistics, in particular in turbulence, would be an important step in understanding its structure and symmetries [11–15].
There are several models of non-equilibrium field statistics for which OPE is known to hold. Most important is the Kraichnan model of passive scalar turbulence, which admits closed description in terms of equal-time correlation functions and analytic solution. The latter is fully consistent with OPE (see [12, 13, 16–18] and appendix). Another class of models is provided by many cases of weak wave turbulence. Here stationary distribution is essentially gaussian, and the associated correlation functions obey OPE trivially [19]. OPE for the velocity field exists in Burgers turbulence (see appendix). Yet another case amenable to straightforward perturbative and RG treatment is quasi-linear dynamics dominated at all scales by an external force with power-law spectrum [16, 20], where OPE can be derived as well.
In this situation, our strategy will be to assume validity of OPE for the velocity field and try to extract testable predictions. We believe that the natural setting to test this strategy is the stationary energy cascade in incompressible fluid in two or three spatial dimensions.
2. Generalities of OPE
Mathematically, OPE may be formulated as follows. One assumes existence of a 'complete' set of local fluctuating fields  , such that any product expands as
, such that any product expands as

Here 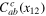 are c-number (non-fluctuating) coefficients which depend on the spatial separation
are c-number (non-fluctuating) coefficients which depend on the spatial separation 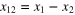 . Irrespective of the number of independent local degrees of freedom, the set
. Irrespective of the number of independent local degrees of freedom, the set  is always infinite—at the very least, it includes any field together with all its coordinate derivatives. It can be regarded as the extension of the notion of Taylor expansions to fields with fractal properties. Generally, the expansions (1) are understood as the relations between the correlation functions
is always infinite—at the very least, it includes any field together with all its coordinate derivatives. It can be regarded as the extension of the notion of Taylor expansions to fields with fractal properties. Generally, the expansions (1) are understood as the relations between the correlation functions
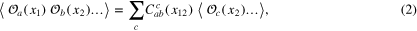
where ⋯ stands for any product of local fields 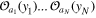 . The sum (2) is assumed convergent, or at least asymptotic, to the correlation function in the lhs as long as the separation
. The sum (2) is assumed convergent, or at least asymptotic, to the correlation function in the lhs as long as the separation 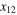 is sufficiently small.
is sufficiently small.
Formally (i.e. ignoring the issues of the convergence and analyticity), successive applications of (1) allows one to reduce generic N-point correlation functions to one-point expectation values

This relation clearly separates the 'local dynamics' of the theory, which is encoded in the coefficient functions, from global properties of the state, incorporated in the one-point expectation values.
Intuitively, OPE may be explained on the basis of some sort of RG procedure. Averaging over small-scale fluctuations with the wave numbers larger then  , with subsequent re-scaling
, with subsequent re-scaling 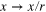 , leads to r-dependent 'renormalization' of interactions between the remaining long-range degrees of freedom, while transforming original operators
, leads to r-dependent 'renormalization' of interactions between the remaining long-range degrees of freedom, while transforming original operators 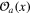 to certain linear combinations
to certain linear combinations 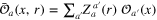 , with c-number factors
, with c-number factors 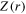 [37]. This allows one to relate correlations at different scales. Consider the lhs of (2), and apply the RG transformation with
[37]. This allows one to relate correlations at different scales. Consider the lhs of (2), and apply the RG transformation with  , where
, where  is the microscopic scale. This relates it to the correlation function with 'microscopic' separation between the points 1 and 2, which obviously obeys OPE. Comparing with the RG transformed right-hand side (rhs) of (2), and assuming that the matrices
is the microscopic scale. This relates it to the correlation function with 'microscopic' separation between the points 1 and 2, which obviously obeys OPE. Comparing with the RG transformed right-hand side (rhs) of (2), and assuming that the matrices  are invertible, one concludes that (2) should hold at all scales, as long as
are invertible, one concludes that (2) should hold at all scales, as long as  is much smaller then all other separations
is much smaller then all other separations  . While this argument (borrowed from similar consideration in equilibrium statistics, see e.g. [4, 21, 37], and used in [15]) does not constitute a proof of OPE in turbulence, it makes it tempting to assume OPE for the velocity field and other fluctuating fields in turbulent flows in 3d and 2d, and explore its possible form and consequences. This is the subject of the present note.
. While this argument (borrowed from similar consideration in equilibrium statistics, see e.g. [4, 21, 37], and used in [15]) does not constitute a proof of OPE in turbulence, it makes it tempting to assume OPE for the velocity field and other fluctuating fields in turbulent flows in 3d and 2d, and explore its possible form and consequences. This is the subject of the present note.
3. OPE and scaling
In this discussion we always have in mind stochastic fields in stationary, homogeneous, and isotropic regime. Thus, in the case of fluid turbulence that means pumped turbulence in the inertial interval. Spatial homogeneity was already taken into account in (1) when we claimed that the functions 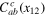 depend on the separations
depend on the separations 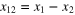 only. Also, in the isotropic case the fields
only. Also, in the isotropic case the fields  can be classified according to representations of
can be classified according to representations of  , the group of rotations of the d-dimensional space. Thus, the fields
, the group of rotations of the d-dimensional space. Thus, the fields 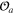 may be scalars, vectors, or irreducible tensors of the higher ranks. In the cases of the vectors and tensors the coefficient functions
may be scalars, vectors, or irreducible tensors of the higher ranks. In the cases of the vectors and tensors the coefficient functions 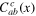 will have tensor structures such that the whole OPE (1) is rotationally invariant.
will have tensor structures such that the whole OPE (1) is rotationally invariant.
In many physical situations (and those include fluid turbulence) the statistics of the random fields exhibits certain scaling properties. Assumption of the OPE allows one to incorporate those in a simple and unified way. We say that the OPE (1) is scale invariant if the fields 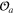 can be assigned scale dimensions da (which determine how the correlation functions depend on the large scale L), so that the OPE does not change under the space dilations accompanied by suitable rescalings of the fields,
can be assigned scale dimensions da (which determine how the correlation functions depend on the large scale L), so that the OPE does not change under the space dilations accompanied by suitable rescalings of the fields, 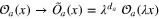 . It follows that the coefficient functions
. It follows that the coefficient functions 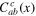 are homogeneous functions of the separation x,
are homogeneous functions of the separation x,

Thus, if the three fields 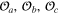 are all scalars, then
are all scalars, then 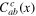 is fixed up to a single overall constant,
is fixed up to a single overall constant,  , but when vectors and tensors are involved one may have several tensor structures. In all cases the scale invariance fixes
, but when vectors and tensors are involved one may have several tensor structures. In all cases the scale invariance fixes  up to a few numbers.
up to a few numbers.
Physically, the scale invariant regime is limited to certain interval of scales,

In equilibrium statistics, the 'UV' scale  is usually the microscopic scale, such as the lattice size or interatomic distance, while the 'IR' scale is either the correlation length Rc, or the size of the system. In the case of turbulence, the origin of both UV and IR scales can be quite different. In the regime of the direct cascade (for instance, in incompressible 3d turbulence), the energy is injected by a large scale stirring and L is the pumping scale. The injected energy then 'propagates' through the inertial interval (5), to be dissipated at the viscous UV scale
is usually the microscopic scale, such as the lattice size or interatomic distance, while the 'IR' scale is either the correlation length Rc, or the size of the system. In the case of turbulence, the origin of both UV and IR scales can be quite different. In the regime of the direct cascade (for instance, in incompressible 3d turbulence), the energy is injected by a large scale stirring and L is the pumping scale. The injected energy then 'propagates' through the inertial interval (5), to be dissipated at the viscous UV scale  . In 2d, the energy cascade is inverse:
. In 2d, the energy cascade is inverse:  is the force scale, while L is either the box size or the scale where the energy is dissipated (say, by uniform friction). It is important to note that one cannot treat
is the force scale, while L is either the box size or the scale where the energy is dissipated (say, by uniform friction). It is important to note that one cannot treat 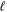 as the smallest scale even considering an inverse cascade, the viscous dissipative scale must be assumed the smallest scale; if one subject fluid to thermal driving (short-correlated random force and viscous friction related by the fluctuation–dissipation theorem), the resulting state is equilibrium rather than inverse turbulent cascade.
as the smallest scale even considering an inverse cascade, the viscous dissipative scale must be assumed the smallest scale; if one subject fluid to thermal driving (short-correlated random force and viscous friction related by the fluctuation–dissipation theorem), the resulting state is equilibrium rather than inverse turbulent cascade.
In scale-invariant theories the coefficients  can be made independent on both the scales
can be made independent on both the scales 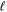 and L. Generally, the structure of the OPE (1) is thought to be determined by local properties of fluctuations, so L-independence is expected. In equilibrium statistical mechanics at criticality all properties of the scale invariant theory are determined by the associated fixed point of the RG flow [37], while all dependence of the correlation functions on the UV scale
and L. Generally, the structure of the OPE (1) is thought to be determined by local properties of fluctuations, so L-independence is expected. In equilibrium statistical mechanics at criticality all properties of the scale invariant theory are determined by the associated fixed point of the RG flow [37], while all dependence of the correlation functions on the UV scale 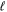 can be eliminated by (generally
can be eliminated by (generally 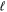 -dependent) renormalization of the fields
-dependent) renormalization of the fields 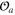 . We assume that these properties extend to the OPE in turbulence.
. We assume that these properties extend to the OPE in turbulence.
However, even if the OPE exhibit scale invariance according to (4), the correlation functions may not be scale invariant. This happens, for instance, if 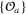 includes scalar fields S of negative dimensions
includes scalar fields S of negative dimensions 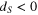 , having non-zero expectation values
, having non-zero expectation values

where the constant BS depends not only on the field S but also on the details of the IR cutoff, that is on the form and the boundary conditions of the box containing the system, or, as is the case in the direct cascade, on the detailed statistics of the pumping force. In such cases the correlation functions are dominated by the negative dimension terms in (3), which diverge with the IR scale L. Formally, the situation is analogous to spontaneous symmetry breaking in field theory, and here we refer to this possibility as 'broken scale symmetry'. In all known cases of turbulence (energy cascades, vorticity cascade, turbulent convection etc), the velocity field itself has a negative dimension between 0 and −1, so that its derivatives, like vorticity, have positive dimensions. While velocity statistics necessarily depends on L, whether the correlation functions of the velocity derivatives are L-independent seems to be determined by the direction of the cascade: self-similarity is broken and the moments contain extra factors 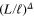 with the whole spectrum of anomalous dimensions Δs in all direct cascades [12]. Particularly, the local energy flux
with the whole spectrum of anomalous dimensions Δs in all direct cascades [12]. Particularly, the local energy flux ![$\epsilon (x)={{{\rm lim} }_{y\to 0,\ell \to 0}}{{\{[v(x+y)-v(x)]\cdot y\}}^{3}}/{{y}^{4}}$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn42.gif) is strongly fluctuating in 3d energy cascade and its pair correlation function decays as a power law in the inertial interval:
is strongly fluctuating in 3d energy cascade and its pair correlation function decays as a power law in the inertial interval: 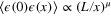 with
with 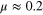 . On the contrary, there are claims that velocity derivatives and differences in the inverse cascade have self-similar probability distribution [11, 22], but the subject deserves more careful study.
. On the contrary, there are claims that velocity derivatives and differences in the inverse cascade have self-similar probability distribution [11, 22], but the subject deserves more careful study.
Note that for a direct turbulent cascade of the passive scalar the OPE is scale-invariant and the correlation functions are not, while for an inverse cascade, the correlation functions are scale invariant, see [12, 13, 16–18].
4. OPE and correlation functions of the velocity field
In fluid turbulence, the main object of interest is the statistics of the velocity field 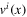 , i.e. the collection of the correlation functions
, i.e. the collection of the correlation functions

In this discussion we always have in mind incompressible flow, so that 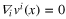 .
.
We are interested in the behavior of the correlation functions in the inertial interval (5), that is the domain where 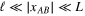 for all the separations
for all the separations 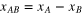 in (7). Known data (experimental and numerical) suggest that the velocity field in the inertial interval has the following properties:
in (7). Known data (experimental and numerical) suggest that the velocity field in the inertial interval has the following properties:
(a) The correlation functions (7) with xAB fixed admit finite limit 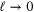 . Assuming this property, in what follows we discuss the correlation functions with the limit
. Assuming this property, in what follows we discuss the correlation functions with the limit 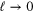 taken.
taken.
(b) The velocity field remains continuous in this limit, i.e. even after  is sent to zero, the correlation functions (7) approach finite limits when two or more of the points xA are brought together,
is sent to zero, the correlation functions (7) approach finite limits when two or more of the points xA are brought together, 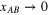 . Note that this property implies existence of the composite field
. Note that this property implies existence of the composite field  , whose dimension is twice the dimension dv of the velocity field. Similarly, multiple powers of v can be defined, and their dimensions are multiples of dv.
, whose dimension is twice the dimension dv of the velocity field. Similarly, multiple powers of v can be defined, and their dimensions are multiples of dv.
As is well known, the fluid dynamics is invariant with respect to Galilean transformations. In the stationary regime of forced turbulence the external forcing fixes a preferable frame, characterized by the condition

The OPE is determined by the intrinsic dynamics of the turbulent flow, and therefore must be invariant with respect to the Galilean transformations. On the other hand, the correlation functions (7) can not be Galilean invariant, even in the inertial interval, where the forcing and dissipation manifest themselves only via the cascade. The symmetry is broken at the level of correlation functions, due to the non-invariance of the one-point expectation values in (3). The situation is formally similar to the spontaneous breaking of symmetry in phase transitions in statistical mechanics and in QFT. Possibility of breaking of scale symmetry in a similar manner was pointed out in the previous section.
The two-point correlation function has the following well known form
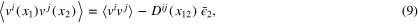
where the first term involves the expectation value of the field 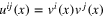 , which is independent of
, which is independent of  but depends on the IR scale L. From now on, we consider energy cascades determined by the mean energy dissipation rate per unit mass
but depends on the IR scale L. From now on, we consider energy cascades determined by the mean energy dissipation rate per unit mass  . In this case it follows from isotropy and dimensional reasoning that
. In this case it follows from isotropy and dimensional reasoning that

i.e. the dimension dv of the velocity field is exactly 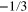 . The second term in (9) is as follows:
. The second term in (9) is as follows:

The factor  in the second term in (9) generally is L-dependent,
in the second term in (9) generally is L-dependent, 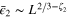 , and in our treatment will be interpreted as the expectation value of a certain local field
, and in our treatment will be interpreted as the expectation value of a certain local field 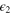 , the exponent
, the exponent 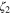 being related to its dimension,
being related to its dimension,  . Kolmogorov and Obukhov assumed that
. Kolmogorov and Obukhov assumed that  . Observed values are different in different d and in different regimes, but in all known cases
. Observed values are different in different d and in different regimes, but in all known cases  turns out to be close to this value. It can be related to the law of de-correlation of the velocities of two fluid particles or the scaling of the respective statistical Lagrangian integral of motion [12, 23].
turns out to be close to this value. It can be related to the law of de-correlation of the velocities of two fluid particles or the scaling of the respective statistical Lagrangian integral of motion [12, 23].
The correlation function (9) is the special case n = 2 of the n momenta of the velocity difference

Here in general 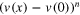 stands for the tensor product of the velocity difference vectors, so that the rhs is a symmetric n-tensor built from the components of xi. The exponents
stands for the tensor product of the velocity difference vectors, so that the rhs is a symmetric n-tensor built from the components of xi. The exponents 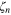 may depend on d, and also may be different in the direct and inverse cascades in 2d, but
may depend on d, and also may be different in the direct and inverse cascades in 2d, but 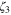 always equals 1, as follows from the flux constancy. With the tensor structure restored, this linear scaling of the third moment gives the exact correlation function
always equals 1, as follows from the flux constancy. With the tensor structure restored, this linear scaling of the third moment gives the exact correlation function
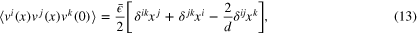
where 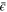 is a dimensional constant identified with the energy dissipation rate. In particular,
is a dimensional constant identified with the energy dissipation rate. In particular,
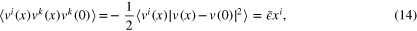
since  . The (non-trivial) generalization of the flux relation for a curved space can be found in [24].
. The (non-trivial) generalization of the flux relation for a curved space can be found in [24].
The form (14) is regarded as a manifestation of the energy cascade for two points: when the squared velocity difference between two points is larger than average, then the velocity difference is directed inwards for 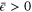 (the direct cascade) and outwards for
(the direct cascade) and outwards for  (the inverse cascade). Further manifestations of the cascade behavior must exist at the level of multi-point correlation functions. In particular, one may ask how correlations of the velocities in three different points distinguish between direct and inverse cascade? Very little is known about the three point function from the first principles. Here we attempt to address this question by assuming the validity of OPE for the velocity field, and exploring its consequences.
(the inverse cascade). Further manifestations of the cascade behavior must exist at the level of multi-point correlation functions. In particular, one may ask how correlations of the velocities in three different points distinguish between direct and inverse cascade? Very little is known about the three point function from the first principles. Here we attempt to address this question by assuming the validity of OPE for the velocity field, and exploring its consequences.
Let us assume that the velocity field  , its derivatives and infinitely many other fields, constitutes the set
, its derivatives and infinitely many other fields, constitutes the set 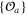 closed with respect to the OPE (1). Consider the product
closed with respect to the OPE (1). Consider the product 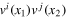 ; by the assumption it admits the expansion
; by the assumption it admits the expansion

As was explained above, the fields 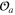 may have tensor indices; here we incorporate those into the index a. The coefficient functions
may have tensor indices; here we incorporate those into the index a. The coefficient functions 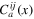 must satisfy a number of conditions, some of them general properties of OPE, and some specific for the velocity field in turbulence. The most important, but also the most difficult, of the general conditions is the associativity of the algebra of OPE. With the exception of CFT, no efficient way of analysis of this condition is known, and we will not address this question here, limiting our attention to elementary properties.
must satisfy a number of conditions, some of them general properties of OPE, and some specific for the velocity field in turbulence. The most important, but also the most difficult, of the general conditions is the associativity of the algebra of OPE. With the exception of CFT, no efficient way of analysis of this condition is known, and we will not address this question here, limiting our attention to elementary properties.
Those include the symmetry with respect to the interchange  , which the lhs of (15) obviously enjoys. In the rhs one can replace
, which the lhs of (15) obviously enjoys. In the rhs one can replace 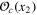 by
by  at the price of adding terms with the derivatives of
at the price of adding terms with the derivatives of 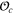 , according to the Taylor expansion, with the result consistent with the symmetry of the lhs. When
, according to the Taylor expansion, with the result consistent with the symmetry of the lhs. When  is an independent field (i.e. is not a derivative of another local field), this simple condition demands
is an independent field (i.e. is not a derivative of another local field), this simple condition demands
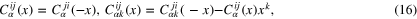
where 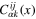 is the coefficient at
is the coefficient at 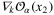 in (15).
in (15).
There are several conditions specific for velocity:
(i) Incompressibility, which demands

Note that the divergence 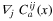 does not necessarily vanish for every field
does not necessarily vanish for every field 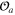 ; however, it vanishes for independent (non-derivative) operators
; however, it vanishes for independent (non-derivative) operators  .
.
(ii) Continuity of the velocity field. This condition demands that, when the limit 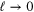 is already taken, the limit
is already taken, the limit 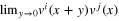 still exists, and defines the product field
still exists, and defines the product field  , which necessary has the dimension
, which necessary has the dimension  . The field
. The field 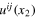 enters the OPE (15) as the dominating term, with the coefficient 1.
enters the OPE (15) as the dominating term, with the coefficient 1.
(iii) Galilean invariance: under the fixed-time Galilean transformation 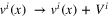 the lhs of (15) changes as
the lhs of (15) changes as

where we assumed Vi to be infinitesimal. The invariance demands that the Galilean transformation of the rhs must generate the same terms. Similar but not identical terms are generated by the leading term 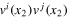 in the rhs of (15). The mismatch
in the rhs of (15). The mismatch ![${{V}^{j}}[{{v}^{i}}({{x}_{1}})-{{v}^{i}}({{x}_{2}})]$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn94.gif) can be written as the Taylor series in
can be written as the Taylor series in  , where the coefficients are the derivatives of
, where the coefficients are the derivatives of 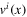 evaluated at the point x2. Therefore the sum in (15) must include additional non-invariant fields which generate linear in V terms needed to fix the mismatch. Since the mismatch is a power series (PS below) in
evaluated at the point x2. Therefore the sum in (15) must include additional non-invariant fields which generate linear in V terms needed to fix the mismatch. Since the mismatch is a power series (PS below) in 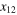 , the non-invariant fields must come with the coefficients involving only integer powers of
, the non-invariant fields must come with the coefficients involving only integer powers of 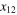 . Emergence of such terms is not unexpected. Indeed, the OPE (15) must include, along with the leading term
. Emergence of such terms is not unexpected. Indeed, the OPE (15) must include, along with the leading term 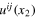 , all the spatial derivatives of this field. However, the above mismatch can not always be closed with the help of these derivatives alone; in general one needs to introduce an additional non-derivative tensor field of the dimension
, all the spatial derivatives of this field. However, the above mismatch can not always be closed with the help of these derivatives alone; in general one needs to introduce an additional non-derivative tensor field of the dimension 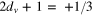 (see below).
(see below).
With these properties taken into account, the OPE (15) should have the following structure

where PS and GIT stand for 'power series' (in 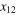 ) and 'Galilean Invariant Terms', analyzed separately below.
) and 'Galilean Invariant Terms', analyzed separately below.
Let us analyze power series part first. Its leading terms look as follows:

The first term in the bracket involves the derivative of the product field 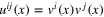 , and is symmetric in the indices
, and is symmetric in the indices 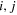 . The new field
. The new field  in the second term is antisymmetric in
in the second term is antisymmetric in 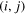 and transforms as
and transforms as

under the Galilean transformation. The equation (17) demands that

This new field can be understood as follows. As the velocity field is not smooth (not continuously differentiable), generally the limit 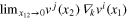 does not exist. That is clear, in particular, from the fact that the correlation function
does not exist. That is clear, in particular, from the fact that the correlation function 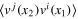 contains terms with
contains terms with 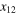 in the power less than 1. It is possible, however, that a non-zero limit
in the power less than 1. It is possible, however, that a non-zero limit 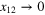 exists in the antisymmetric combination
exists in the antisymmetric combination

Our arguments here suggest that consistency of OPE with the Galilean invariance demands this to be the case, and the limit  of (22) then defines the field
of (22) then defines the field  in (19). By the transformation property (20) this field is identical to the microscopic field
in (19). By the transformation property (20) this field is identical to the microscopic field 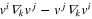 . Generally, it is possible to show that the full Galilean invariance of the OPE (18) can be satisfied by the contributions from the fields
. Generally, it is possible to show that the full Galilean invariance of the OPE (18) can be satisfied by the contributions from the fields 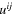 ,
,  , and their derivatives. Moreover, it is not difficult to collect all these contributions explicitly; we do not present the full expression here as it is not used below.
, and their derivatives. Moreover, it is not difficult to collect all these contributions explicitly; we do not present the full expression here as it is not used below.
The cases d = 1 and d = 2 are special. In d = 1 (Burgers equation) the field  vanishes identically, and the terms with the derivatives of
vanishes identically, and the terms with the derivatives of  are sufficient to satisfy the Galilean invariance. This case is briefly described in the appendix. In d = 2 the filed
are sufficient to satisfy the Galilean invariance. This case is briefly described in the appendix. In d = 2 the filed  is not zero, but its components can be reduced to derivatives of
is not zero, but its components can be reduced to derivatives of 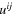 using the identity
using the identity

verified component-wise.
Let us note that the separation between PS and GIT in (18) is ambiguous. Thus, the fields  and
and 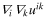 which may appear in the PS term (18) at the order
which may appear in the PS term (18) at the order 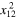 are Galilean invariant, and their contributions can well be attributed to the GIT part. The coefficients in front of these and similar higher order regular terms are not fixed by Galilean symmetry.
are Galilean invariant, and their contributions can well be attributed to the GIT part. The coefficients in front of these and similar higher order regular terms are not fixed by Galilean symmetry.
The GIT generally involve fractional powers of  . The associated Galilean invariant fields may carry any representations of
. The associated Galilean invariant fields may carry any representations of 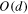 , but it is natural to expect that the leading contributions come from low spins. Including only scalar, vector and second-rank tensor fields, the OPE would look like this
, but it is natural to expect that the leading contributions come from low spins. Including only scalar, vector and second-rank tensor fields, the OPE would look like this
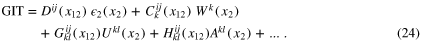
Here 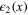 denotes the scalar field of the lowest dimension
denotes the scalar field of the lowest dimension 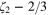 , whose expectation value
, whose expectation value 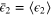 generates the second term in the correlation function (9). Note that
generates the second term in the correlation function (9). Note that 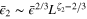 . Other terms explicitly written in (24) exemplify a priory admissible contributions of a vector field
. Other terms explicitly written in (24) exemplify a priory admissible contributions of a vector field 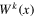 , and antisymmetric and irreducible symmetric tensors,
, and antisymmetric and irreducible symmetric tensors, 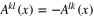 and
and 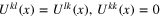 , respectively. Further terms may involve additional scalars, vectors and tensors, as well as independent fields with higher spins. Note that in homogeneous isotropic flow all derivatives and all fields with non-zero spin have zero expectation values, hence bring no contribution to the two-point function (9) (the situation changes when the isotropy is broken, as we discuss below). Contributions from additional scalar fields S of higher dimensions are possible, but assuming their dimensions dS are positive, their expectation values (6) bring negligible contribution in the inertial interval
, respectively. Further terms may involve additional scalars, vectors and tensors, as well as independent fields with higher spins. Note that in homogeneous isotropic flow all derivatives and all fields with non-zero spin have zero expectation values, hence bring no contribution to the two-point function (9) (the situation changes when the isotropy is broken, as we discuss below). Contributions from additional scalar fields S of higher dimensions are possible, but assuming their dimensions dS are positive, their expectation values (6) bring negligible contribution in the inertial interval 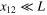 .
.
The coefficient functions  ,
,  ,
, 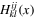 are severely restricted by the conditions (16) and (17). Let us first show that the non-vanishing contributions from Wk and
are severely restricted by the conditions (16) and (17). Let us first show that the non-vanishing contributions from Wk and 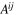 are inconsistent with these conditions. Indeed, by isotropy and (16) the coefficient
are inconsistent with these conditions. Indeed, by isotropy and (16) the coefficient 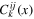 must have the form
must have the form ![$\left[ {{\delta }^{ik}}{{x}^{j}}-{{\delta }^{jk}}{{x}^{i}} \right]\;C({{x}^{2}})$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn137.gif) with scalar
with scalar  , and then the incompressibility condition (17) leads to
, and then the incompressibility condition (17) leads to  . Next, for the coefficient
. Next, for the coefficient  the antisymmetry in
the antisymmetry in 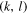 and the condition
and the condition 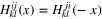 , which follows from (16), allow for only one structure
, which follows from (16), allow for only one structure ![$H_{kl}^{ij}(x)\sim \left[ {{\delta }^{ik}}{{x}^{j}}{{x}^{l}}+{{\delta }^{jk}}{{x}^{i}}{{x}^{l}}-(k\leftrightarrow l) \right]\;{{({{x}^{2}})}^{b}}$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn143.gif) , and then (17) fixes b to be
, and then (17) fixes b to be  , which is not acceptable because of singularity at coinciding points. We conclude that in the OPE (24) contributions from vector and antisymmetric tensor fields, which are not derivatives of other local fields, are forbidden. Note that the derivatives like
, which is not acceptable because of singularity at coinciding points. We conclude that in the OPE (24) contributions from vector and antisymmetric tensor fields, which are not derivatives of other local fields, are forbidden. Note that the derivatives like  may well be present. Similar analysis of the term with the symmetric tensor
may well be present. Similar analysis of the term with the symmetric tensor 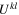 allows one to fix the coefficient function
allows one to fix the coefficient function 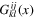 up to two constants,
up to two constants,

where a relates to the dimension of the field U, 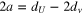 , and the numerical factor depends on the normalization of the field
, and the numerical factor depends on the normalization of the field 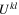 .
.
The presence and nature of one such tensor field can be inferred from what is known about anisotropic turbulence. Indeed, the term with a symmetric tensor should describe, in particular, the response of the pair correlation function to the strain of a mean flow. It is reasonable to assume and is known empirically that the correction to the spectrum is proportional to the gradient of the mean-flow velocity, which suggests that the OPE (18) must involve terms with the first derivatives of the velocity field, and allows to identify

Then  must scale as a typical turn-over time at the scale x, that is in Kolmogorov phenomenology
must scale as a typical turn-over time at the scale x, that is in Kolmogorov phenomenology 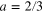 , consistent with
, consistent with 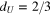 . That scaling was suggested for the anisotropic part of the spectrum, which carries the momentum flux
. That scaling was suggested for the anisotropic part of the spectrum, which carries the momentum flux 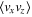 in [25–27] through a dimensional argument. Experimental evidence for it was found in [28] and [29], among others. Similar identification for the case of power-law force was made in [20]. With this in mind, here we assume that the tensor field of the lowest dimension contributing to (24) is the strain field (26). It is worth stressing, that the Kolmogorov scaling for anisotropic correction to the second moment within OPE follows from the assumption that it is linearly proportional to the external gradient i.e. from the identification (26), and it is independent of the scaling exponent
in [25–27] through a dimensional argument. Experimental evidence for it was found in [28] and [29], among others. Similar identification for the case of power-law force was made in [20]. With this in mind, here we assume that the tensor field of the lowest dimension contributing to (24) is the strain field (26). It is worth stressing, that the Kolmogorov scaling for anisotropic correction to the second moment within OPE follows from the assumption that it is linearly proportional to the external gradient i.e. from the identification (26), and it is independent of the scaling exponent 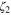 (whether Kolmogorov or not) of the isotropic part of the second moment. To avoid misunderstanding, note that all our results are valid for isotropic homogeneous turbulence only; we briefly invoked the data on turbulence anisotropy only to justify (26).
(whether Kolmogorov or not) of the isotropic part of the second moment. To avoid misunderstanding, note that all our results are valid for isotropic homogeneous turbulence only; we briefly invoked the data on turbulence anisotropy only to justify (26).
The overall factor B in (25) depends on 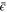 . The character of this dependence can be inferred from the fact that the single-point value of the cross-correlation function
. The character of this dependence can be inferred from the fact that the single-point value of the cross-correlation function 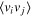 can be related to the gradient of the mean flow
can be related to the gradient of the mean flow 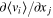 and the energy flux
and the energy flux 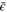 . Indeed, the energy exchange rate between turbulence and the mean flow is
. Indeed, the energy exchange rate between turbulence and the mean flow is 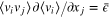 , which is positive in 3d [30] and negative in 2d [31]. If we now assume that the different-point correlation function
, which is positive in 3d [30] and negative in 2d [31]. If we now assume that the different-point correlation function  decreases with the distance x, we must require B and
decreases with the distance x, we must require B and 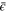 to be of the same sign, i.e. up to a positive order-unity factor
to be of the same sign, i.e. up to a positive order-unity factor  .
.
With all the non-vanishing contributions found above, the OPE (15) has the form

where all fields v and 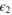 in the rhs are taken at the point x2, and we omitted terms which involve
in the rhs are taken at the point x2, and we omitted terms which involve 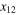 in powers higher then 4/3. According to (11) and (25), the coefficients
in powers higher then 4/3. According to (11) and (25), the coefficients  and
and  involve fractional powers of
involve fractional powers of  . One can say that while the first and the third terms in the rhs represent smooth component of the field
. One can say that while the first and the third terms in the rhs represent smooth component of the field 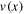 , the second and the fourth terms there should be regarded as the manifestation of its fractal nature.
, the second and the fourth terms there should be regarded as the manifestation of its fractal nature.
5. Three-point function
The OPE (27) suggests certain behavior of the correlation functions (7) in the situation when the separation between two points, say x1 and x2, is much smaller then all other separations. Here we limit attention to the three point function

At zero separation 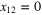 we have the exact form (13). Conventional derivation of this form implies that the limit
we have the exact form (13). Conventional derivation of this form implies that the limit 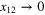 in (28) is taken before the limit
in (28) is taken before the limit 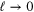 . However, the OPE (15) suggests that this form is retained if the limits are taken in the opposite order, i.e.
. However, the OPE (15) suggests that this form is retained if the limits are taken in the opposite order, i.e. 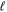 is sent to zero first, while all separations in (28) are kept within the inertial interval, see also [32]. The form (13) represents the contribution of the leading term
is sent to zero first, while all separations in (28) are kept within the inertial interval, see also [32]. The form (13) represents the contribution of the leading term 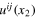 in (27), which is the only survivor in the limit
in (27), which is the only survivor in the limit  . The behavior of (28) at
. The behavior of (28) at  finite but small as compared to
finite but small as compared to  is determined by further terms in (27). There is no contribution from the term with the scalar field
is determined by further terms in (27). There is no contribution from the term with the scalar field 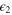 because the two-point function
because the two-point function 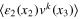 vanishes. Indeed, by isotropy and incompressibility (17) the two-point function must have the form Const
vanishes. Indeed, by isotropy and incompressibility (17) the two-point function must have the form Const  at all scales, including the domain
at all scales, including the domain  . Then absence of singularity at x = 0 demands Const = 0. Therefore the leading corrections are determined by the term
. Then absence of singularity at x = 0 demands Const = 0. Therefore the leading corrections are determined by the term  and the contribution of the symmetric tensor
and the contribution of the symmetric tensor 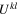 in (27). To find these contributions we need the two-point correlations of the corresponding composite operators at x2 with
in (27). To find these contributions we need the two-point correlations of the corresponding composite operators at x2 with 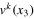 . From the flux law (13) we have
. From the flux law (13) we have

The correlation function 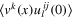 is also dimensionless, and the conditions (17) and (21) fix its form up to single constant A,
is also dimensionless, and the conditions (17) and (21) fix its form up to single constant A,
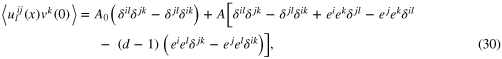
where  , and
, and  is the unit vector in the direction of xi.
is the unit vector in the direction of xi.
Remarkably, in 2d the square brackets in (30) vanishes identically and this correlation function is fixed completely. This relates to the identity (23), but can be verified directly: note that at d = 2 the form is antisymmetric in both ij and kl, thus it has only one independent component. Taking, say 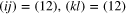 one finds that the three terms in (30) combine to zero.
one finds that the three terms in (30) combine to zero.
Finally, with the identification (26), the correlation function 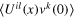 is equal to
is equal to

Here 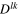 is given by (11). To write the leading terms of the expansion of (28) at
is given by (11). To write the leading terms of the expansion of (28) at 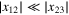 in a compact form, it is useful to split it into parts symmetric and antisymmetric in
in a compact form, it is useful to split it into parts symmetric and antisymmetric in  . The contribution of
. The contribution of  is symmetric in
is symmetric in  , and thus drops out from the antisymmetric part. As a result, we have
, and thus drops out from the antisymmetric part. As a result, we have
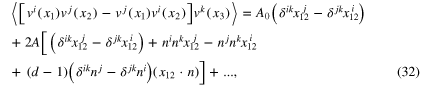
where  , and dots are
, and dots are 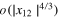 . It is tempting to assume that
. It is tempting to assume that 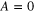 at all d, but it needs to be checked in numerical simulations.
at all d, but it needs to be checked in numerical simulations.
To treat the symmetric part, consider the velocity difference 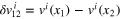 and note that the product
and note that the product  , being evidently Galilean invariant, receives contributions from (24) only. The leading contribution comes from the term with
, being evidently Galilean invariant, receives contributions from (24) only. The leading contribution comes from the term with 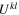 ,
,

where 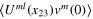 is given by (31), and the dots represent further terms which involve powers of
is given by (31), and the dots represent further terms which involve powers of 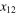 higher then
higher then 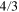 . In particular
. In particular
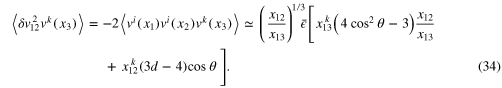
Here θ is the angle between the vectors  and
and 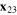 . Note that the terms (25) did not contribute. It is interesting that if we take the longitudinal velocity difference
. Note that the terms (25) did not contribute. It is interesting that if we take the longitudinal velocity difference  then the moment has an opposite sign in 2d:
then the moment has an opposite sign in 2d:
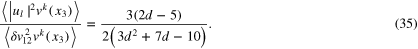
Analytical closures predict that fusing points 1 and 2 inside the triple velocity moment gives the second moment times interaction time i.e.  [27, 33, 34], which is supported by the numerical data [35, 36] and agrees with the leading term of (34).
[27, 33, 34], which is supported by the numerical data [35, 36] and agrees with the leading term of (34).
Two-point manifestation of the energy cascade,  , has
, has  positive/negative for direct/inverse cascade. The physical meaning is quite simple: ul is negative for larger
positive/negative for direct/inverse cascade. The physical meaning is quite simple: ul is negative for larger  in 3d, i.e. when there is more energy at a given scale the points tend to approach so that the energy goes to shorter distance. It is opposite in 2d: two fluid particles having large velocity difference tend to separate. Three-point correlation function (34) tells us more intimate information about the energy cascade. The sign of the correlation function (34) depends not only on the sign of the energy flux but on the geometry as well. Consider first the simplest situation when all three points are on a line (i.e.
in 3d, i.e. when there is more energy at a given scale the points tend to approach so that the energy goes to shorter distance. It is opposite in 2d: two fluid particles having large velocity difference tend to separate. Three-point correlation function (34) tells us more intimate information about the energy cascade. The sign of the correlation function (34) depends not only on the sign of the energy flux but on the geometry as well. Consider first the simplest situation when all three points are on a line (i.e. 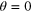 ). Apparently, the velocity at the distant point is more correlated with the velocity at the point which is closer. That means that the velocity at a distant point has the same sign as ul. When there is a strong vortex in some region (large
). Apparently, the velocity at the distant point is more correlated with the velocity at the point which is closer. That means that the velocity at a distant point has the same sign as ul. When there is a strong vortex in some region (large 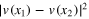 ), the velocity far away is predominantly directed towards it in the direct cascade and away from it in the inverse cascade. For arbitrary angle, the projection of this correlation function on the long direction is proportional to
), the velocity far away is predominantly directed towards it in the direct cascade and away from it in the inverse cascade. For arbitrary angle, the projection of this correlation function on the long direction is proportional to 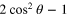 in 2d, i.e. changes sign at
in 2d, i.e. changes sign at 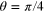 and has zero average over the angle due to incompressibility (generally
and has zero average over the angle due to incompressibility (generally  ). In other words, when
). In other words, when 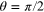 the velocity is opposite to that at
the velocity is opposite to that at  . The projection on the short direction is proportional to
. The projection on the short direction is proportional to 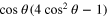 and turns into zero for
and turns into zero for 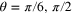 (generally
(generally 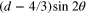 ).
).
6. Discussion
The general expansion equation (27) determines behavior of any correlation function (7) when two points are brought close together, much closer then the distances to all remaining points. This behavior was derived on the basis of two assumptions: the general assumption of the validity of equal-time OPE in fluid turbulence, and the identification of the leading tensor contribution with the strain (26). We believe that elucidating validity of these assumptions, especially the first one, would be an important step in understanding statistics of velocity field in turbulence. The expansion leads to the asymptotic forms (32)–(34) of the three-point correlation function, providing testable predictions of the above assumptions.
Acknowledgments
The work of GF was supported by the grants of the BSF, ISF and Minerva foundations and by the RScF grant 14-22-00259 (analytic theory). GF acknowledges kind hospitality of the Rutgers University and AZ acknowledges kind hospitality of the Weizmann Institute of Science, where most of this work was done. Research of AZ was supported in part by DOE grant DE-FG02-96ER40959, and by the BSF grant.
Appendix
A.1. OPE in Burgers turbulence
For one-dimensional Burgers model in the limit of large Reynolds numbers, it is known that the statistics of velocity differences and derivatives is largely determined by dilute shocks. In particular, one can write the Burgers OPE for  regarding
regarding  as smooth field distorted by shocks. Contributions non-analytic in the inviscid limit are determined by a single shock
as smooth field distorted by shocks. Contributions non-analytic in the inviscid limit are determined by a single shock 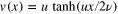 in the main order in x. Typical size of the shock
in the main order in x. Typical size of the shock 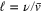 (which is determined by viscosity ν and the mean velocity
(which is determined by viscosity ν and the mean velocity 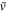 ) plays the role of the UV scale in (5). In the inertial interval
) plays the role of the UV scale in (5). In the inertial interval  we have
we have

where  is related to 'shock operator' [38, 39], namely
is related to 'shock operator' [38, 39], namely  returns the squared velocity of the shock (
returns the squared velocity of the shock ( where
where  are the velocity immediately to the right and to the left of the shock) if a shock is present in the interval
are the velocity immediately to the right and to the left of the shock) if a shock is present in the interval 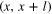 , and zero otherwise. Its expectation value is
, and zero otherwise. Its expectation value is 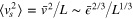 , where L is the mean distance between the shocks, which plays the role of the upper bound for the inertial interval (5).
, where L is the mean distance between the shocks, which plays the role of the upper bound for the inertial interval (5).
One can develop further terms in the above OPE. In the order x2 we have the terms ![${{x}^{2}}[v(x){{v}_{xx}}(x)/2+({{v}_{x}})_{s}^{2}(x)]$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn231.gif) , where the operator
, where the operator  measures the square of the velocity gradient immediately outside the shock if the shock is present in
measures the square of the velocity gradient immediately outside the shock if the shock is present in 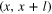 .
.
One can write OPE of another type, considering  . Namely, we can expect relation like
. Namely, we can expect relation like 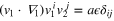 + time derivative + space derivative and the coefficient a can be determined exactly. There are infinity of such relations [40, 41].
+ time derivative + space derivative and the coefficient a can be determined exactly. There are infinity of such relations [40, 41].
A.2. Passive scalar model.
The scalar field 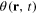 satisfies the equation
satisfies the equation

Here the random force is assumed to be Gaussian with the variance 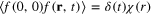 where
where  decays on the scale L. In the Kraichnan model, we also consider the velocity field incompressible white Gaussian with
decays on the scale L. In the Kraichnan model, we also consider the velocity field incompressible white Gaussian with ![$\langle {{v}_{i}}(0,0){{v}_{j}}({\bf r},t)\rangle =\delta (t)[{{v}^{2}}{{\delta }_{ij}}-{{K}_{ij}}(r)]$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn239.gif) , where
, where ![${{K}_{ij}}(r)={{r}^{2-\gamma }}[(d+1-\gamma ){{\delta }_{ij}}-(2-\gamma ){{r}_{i}}{{r}_{j}}{{r}^{-2}}]$](https://content.cld.iop.org/journals/1751-8121/48/18/18FT02/revision1/jpa512350ieqn240.gif) . Here γ is the degree of non-smoothness, Kolmogorov cascade would correspond to
. Here γ is the degree of non-smoothness, Kolmogorov cascade would correspond to 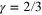 .
.
In the model, the passive scalar correlation functions  satisfy the equation
satisfy the equation

where 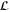 is the n-point differential operator [12]
is the n-point differential operator [12]

Building OPE is straightforward in this case, see also [12, 13, 18, 42]. The OPE must be invariant with respect to the following two symmetries: (a) shift 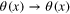 + constant, and (b) renormalization symmetry
+ constant, and (b) renormalization symmetry 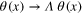 . By the last symmetry, generic operator is characterized by its 'degree' n related to the transformation property
. By the last symmetry, generic operator is characterized by its 'degree' n related to the transformation property 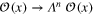 , and the degrees of the operators in the rhs of the (1) must agree with the degree of the lhs. The OPE also have the scale symmetry (4).
, and the degrees of the operators in the rhs of the (1) must agree with the degree of the lhs. The OPE also have the scale symmetry (4).
Operators can be described explicitly in the case 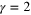 . In this case we just have all polynomials of θ and derivatives. The dimensions are
. In this case we just have all polynomials of θ and derivatives. The dimensions are 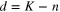 , where n is the degree and K is the total number of derivatives. Thus, in this case the spectrum of dimensions is highly degenerate. At
, where n is the degree and K is the total number of derivatives. Thus, in this case the spectrum of dimensions is highly degenerate. At 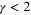 the space of operators does not change, but the degeneracy of dimensions is lifted. The spectrum of the dimensions changes continuously with γ, therefore it is natural to assume that for fixed n the spectrum of dimensions remains bounded from below, at least in some range of γ. From the differential equations (37) certain general properties can be deduced [12]:
the space of operators does not change, but the degeneracy of dimensions is lifted. The spectrum of the dimensions changes continuously with γ, therefore it is natural to assume that for fixed n the spectrum of dimensions remains bounded from below, at least in some range of γ. From the differential equations (37) certain general properties can be deduced [12]:
- (1)The dimension of θ is exactly
 .
. - (2)The zero-dimension operator can be defined as the flux
 , where it is assumed that the limit
, where it is assumed that the limit  is taken first, so that y is always kept within the inertial interval
is taken first, so that y is always kept within the inertial interval  . Alternatively, starting with finite κ one can define the flux operator as suitably renormalized square of the gradient of θ, i.e.
. Alternatively, starting with finite κ one can define the flux operator as suitably renormalized square of the gradient of θ, i.e.  .
. - (3)For any operator
 of degree n and dimension d there is at least one operator of the same degree and spin, and dimension
of degree n and dimension d there is at least one operator of the same degree and spin, and dimension  . We call such operators 'descendants'. Thus, for each degree n there are 'primary' operators (denoted below as
. We call such operators 'descendants'. Thus, for each degree n there are 'primary' operators (denoted below as  , where α distinguishes between different primaries of the same degree), each accompanied by a string of its descendants, with the dimensions
, where α distinguishes between different primaries of the same degree), each accompanied by a string of its descendants, with the dimensions  . For instance,
. For instance,  is the first descendant of
is the first descendant of  .
.
There is the correspondence between the primary operators of degree n and zero modes  of the operator
of the operator  . The zero modes are homogeneous functions with the degree of homogeneity
. The zero modes are homogeneous functions with the degree of homogeneity 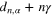 . The n-fold product of θ's can be written as
. The n-fold product of θ's can be written as

where dots stand for contribution of the descendants of 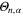 and their derivatives.
and their derivatives.
For n = 2 there is only one scalar primary field 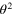 of the dimension
of the dimension  , and all other scalar operators are its descendants. The mth descendant can be understood as the regularized composite fields
, and all other scalar operators are its descendants. The mth descendant can be understood as the regularized composite fields 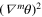 (it reduces to this product at
(it reduces to this product at 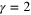 ). In addition, there are primary fields of any spin
). In addition, there are primary fields of any spin
For n = 4 we have infinitely many scalar primaries (and of course primaries with any spin), but only three have negative dimensions: the operator 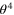 has the dimension
has the dimension  , while the dimensions of the other two—the regularized products
, while the dimensions of the other two—the regularized products 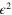 and
and  —are related to the exponents
—are related to the exponents  and
and  of [12, 18]. For general n, the operator with the lowest negative dimension
of [12, 18]. For general n, the operator with the lowest negative dimension 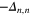 is shift invariant, and can be understood as the regularized
is shift invariant, and can be understood as the regularized  . It corresponds to the dominant zero mode of the n-point operator
. It corresponds to the dominant zero mode of the n-point operator  [12].
[12].
Computation of the two-point OPE can be done, for instance, by using the decomposition of the operator (38) from [18],  , where
, where
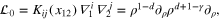
and R is the short-hand for  . Assume that
. Assume that 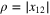 is much smaller then all other separations in the correlation function Fn. Then equation (37), written as
is much smaller then all other separations in the correlation function Fn. Then equation (37), written as 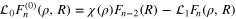 , can be solved iteratively, starting with the zeroth-order approximation
, can be solved iteratively, starting with the zeroth-order approximation  . The iterations generate series which is interpreted in terms of the OPE. To put it simply, for passive scalar in the Kraichnan model, the OPE follows from the two facts: (i) the main ρ-dependent part of the operator
. The iterations generate series which is interpreted in terms of the OPE. To put it simply, for passive scalar in the Kraichnan model, the OPE follows from the two facts: (i) the main ρ-dependent part of the operator 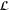 separates and (ii) the rhs of (37) is a sum of reducible contributions.
separates and (ii) the rhs of (37) is a sum of reducible contributions.
Realization of that scheme requires specifying whether distances between points are larger or smaller than the correlation radius L of the pumping correlation function χ. For an incompressible velocity, which we consider here, the cascade of the scalar is direct i.e. takes place at 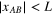 . For such non-equilibrium (flux) state, we have
. For such non-equilibrium (flux) state, we have
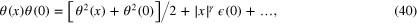
where further terms involve the descendants of  as well as operators of higher spin. Non-zero-dimensions and non-zero expectation values of the powers of
as well as operators of higher spin. Non-zero-dimensions and non-zero expectation values of the powers of  mean that the scale invariance is spontaneously broken at the level of correlation functions.
mean that the scale invariance is spontaneously broken at the level of correlation functions.
One can also build an OPE for the fluxless state at  (it tends to equilibrium as
(it tends to equilibrium as  ). This OPE is simpler. The main contributions into correlation functions have normal scaling. There are anomalous dimensions in subleading terms. The leading part
). This OPE is simpler. The main contributions into correlation functions have normal scaling. There are anomalous dimensions in subleading terms. The leading part  gives the leading contribution due to the identity operator I, normalized by
gives the leading contribution due to the identity operator I, normalized by 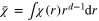 ; the next iteration yields
; the next iteration yields  , which gives the first subleading contribution:
, which gives the first subleading contribution: 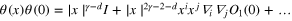 , where
, where 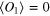 and
and 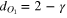 , see [43] for the details.
, see [43] for the details.