Abstract
This work investigates the possible integration of an energy harvester in a bioinspired fish-like aquatic unmanned vehicle. The defined fish-like system utilizes a reduced complexity prescribed motion as the representation for energy harvester to be subjected to. Nonlinear electromechanical modeling is performed by considering the geometric and piezoelectric nonlinearities. A convergence analysis is carried out in order to determine the required modes in the Galerkin discretization due to the presence of nonlinear interactions between the prescribed and relative motions. The utilization of higher-order modeling for the strain and material leads to the identification of impactful prescribed motions terms that can activate the nonlinearities in the system, results in more harmonics to consider, and leads to the presence parametric excitation terms. Considering a reduced-complex model by decreasing the value of the quadratic constraint envelope that the fish-like system would be forced with, the soft-robotic system behaves more with a base excitation characteristic. Small damping would allow this prescribed motion with reduced quadratic envelope forcing still induces a hardening behavior, but the other harmonics and parametric resonance seen are greatly reduced. Considering this reduced complexity system, the interaction between the prescribed and base excitations is also investigated to demonstrate that when the two excitations are of similar nature constructive and destructive build of the response waveform can occur when looking at near the first natural resonance. It is shown that the quenching phenomenon can take place which may result in a destructive response of the piezoelectric energy harvester. The results show that the robustness of the fish-like robot is directly dependent on the design parameters including the damping of the structure, importance of the undulatory motion, and activation of the resonances.
Export citation and abstract BibTeX RIS
1. Introduction
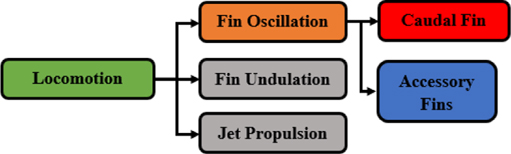
The development of soft robotic actuators exploited in aquatic unmanned vehicles (AUVs) designs allows for a more biomimetic motion to boost performance, replicate biological locomotion, and replace the usage of disruptive propellers [1, 2]. Figure 1 gives a simplified representation of the different categories of locomotion that these systems inspire from. Soft robotic actuators attempt to improvise cutting edge mechanical design to produce an undulating–oscillatory body motion in fish-like caudal fin swimming AUVs [2, 3]. These bioinspired AUVs are attempting to blend more naturally into their environment which would expand their mission capabilities as they are less disruptive and stealthier [4, 5]. The advancement of sensory networks is beginning to push these systems toward autonomy and make them capable to move in more complex 3D environments [2, 6, 7]. By creating a more capable swimming fishlike system that is able to sense its environment would provide a platform to be exploited for conservation, research, and espionage missions.
Figure 1. Locomotion categorization with emphasis on caudal fin categorization.
Download figure:
Standard image High-resolution imageThe development of bioinspired AUVs utilizing the caudal fin locomotion has led to designs being constructed to perform a defined prescribed motion. Depending on the species, this motion varies in undulatory and oscillatory characteristics depending on the body composition and nature of their lifestyle. Therefore, depending on the species selected, this sinusoidal waveform can be represented as a spatio-temporal cosine function that has a polynomial envelope constraint for the amplitude of the spinal column motion, as shown in table 1. This spatio-temporal function is the inspiration for the locomotion of these caudal fin bioinspired AUVs and is considered as the prescribed motion vp(x, t). The polynomial constraint envelope for the amplitude of the spinal column can have constants a0, a1, and a2 and are defined as 0.02, −0.0825, and 0.1625 for a Carangiform motion [8]. The undulatory term, K, defines the periodic nature of the spinal column. Length, L, scales this prescribed motion for the respective spinal column structure. Frequency is defined by ωp for the prescribed motion in rad s−1, and fp in Hz. The prescribed motion is found to be of great importance. Table 1 outlines the two cases to be discussed in this study. Case A is the biomimetic defined case that includes the undulatory term K. Case B is a bioinspired considers K = 0 to remove complications that stem from this term. Figure 2 demonstrates the case B motion when the periodic undulation term is removed.
Table 1. Classifications of vp cases.
| Case | Equation | Description |
|---|---|---|
| A |
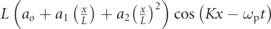
| • Undulating–oscillatory motion with |
| original backbone polynomial | ||
| B |
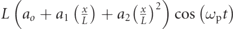
| • Oscillatory motion with original |
| backbone polynomial |
Figure 2. Example of case B motion where the undulatory term K = 0.
Download figure:
Standard image High-resolution imageThe endurance challenge for these soft robotic AUVs has led to the investigations of an energy harvester patch integrated into the architecture of these systems. Piezoelectric energy harvester patches are becoming more commercially available products. One of the most commonly utilized materials in these patches is a lead zirconium-titanate (PZT) as its atomic structure can be formulated into the highly performative perovskite crystal structure [9]. Depending on the fabrication recipe used by a vendor, the piezoelectric transduction material may have doping agents added to control the properties of the final developed patch [10–12]. Typical commercial energy harvester patches organized transduction material into thin-films or macro-fiber composite (MFC) configurations which offer distinct capabilities for various applications [13–19]. The MFC patch architecture is more applicable for large deformation architectures as the composite nature of the patch allows for more flexibility. The flexibility introduced by the soft material actuators to produce a prescribed motion for propulsion in bioinspired AUVs offers a platform to scavenge energy using one of these MFC patches. Works by Cha et al [20] and Salazar et al [21, 22] attempted to investigate this complex problem using a piezoelectric material. These works did not account for the prescribed motion for a biomimetic AUV interacting with the structure of these energy harvester systems.
The adaptation of soft materials actuated through a variety of means like hydraulic, pneumatic, and smart material actuators require investigations to understand how these structures vibrationally behave. As these actuators' types advance the ability to excite a structure over the span can be more easily accomplished. The design of a structure that has a natural frequency within the operating conditions is possible. Therefore, in this work, the development of an electromechanical piezoelectric energy harvester integrated into a representative AUV model is conceived to investigate these undulatory prescribed motion capable soft robot AUV. This will help to identify the complexities and potential robustness issues that these systems can suffer from.
The rest of this work is organized as follows. Section 2 describes the identification of the motion to be used for actuating the AUV system. Section 3 details the methodology for the derived nonlinear electromechanical energy harvester. Section 4 breaks apart the reduced-order model to discern the impact of the various components of the model to enlighten how a prescribed motion could be impactful and how the defined prescribed motion, structural damping, electrical load resistance, and external influence are important. Section 5 offers insight into how the influence of external excitation interacting with the structures prescribed motion could be damaging and affect the robustness of the system. Section 6 offers conclusions of work and recommendations for future researchers.
2. Piezoelectric AUV energy harvester nonlinear modeling
The undulatory nature of such a soft robotic biomimetic AUV with integrated energy harvester constructed that can perform the defined motion is shown in figure 3. The construction of this body caudal fin energy harvester (BCFEH) is considered as a thin beam that undergoes the case B bioinspired prescribed motion. The defined BCFEH has a tail tip patch configuration as it was found to be the best performing configuration under this motion [21, 22]. In addition, the other possible vibratory sources of excitations are assumed in the form of a harmonic base excitation with acceleration (ab) and base excitation frequency (ωb). The dimensions and material properties of this bioinspired AUV are detailed in table 2. The intention of this work is to enlighten how the prescribed and base motions can heavily influence these soft robotic systems near resonance and cause damage for the system.
Figure 3. Diagram of a Carangifrom bioinspired AUV with a beam substrate backbone with a potential energy harvester patch attached on the tail section (a) side view and (b) top down view showing the prescribed motion bending over the length and base excitation at the base.
Download figure:
Standard image High-resolution imageTable 2. Fixed characteristics of the BCFEH [13].
| Symbol | Parameter | Value |
|---|---|---|
| bp | Width of piezoelectric layer (mm) | 7 |
| bs | Width of substrate layer (mm) | 7 |
| hp | Thickness of piezoelectric layer (mm) | 0.2 |
| hs | Thickness of aluminum substrate (mm) | 0.6 |
| Ep | Piezoelectric material Young's modulus (GN m−2) | 30.336 |
| Es | Aluminum Young's modulus (GN m−2) | 69.5 |
| ρs | Density of aluminum substrate (kg cm−3) | 2700 |
| ρp | Density of piezoelectric patch (kg cm−3) | 5440 |
| m1 | Mass per unit length (0 ⩽ x ⩽ L1) | ρs bs hs |
| m2 | Mass per unit length (L1 < x ⩽ L2) | ρs bs hs + ρp bp hp |
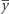
| Position to the neutral axis |
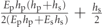
|
| y1 | Position of aluminum relative to the neutral axis |
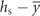
|
| y2 | Position of piezoelectric layer relative to the neutral axis |

|
| y0 | Start of aluminum layer relative to neutral axis |
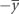
|
| EI1 | Stiffness constant of beam for (0 ⩽ x ⩽ L1) |
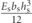
|
| EI2 | Stiffness constant of beam for (L1 < x ⩽ L1) |
![$\left(\frac{1}{3}\right)\left[{E}_{\mathrm{s}}{b}_{\mathrm{s}}\left({y}_{1}^{3}-{y}_{0}^{3}\right)+{E}_{\mathrm{p}}{b}_{\mathrm{p}}\left({y}_{2}^{3}-{y}_{1}^{3}\right)\right]$](https://content.cld.iop.org/journals/1748-3190/16/4/046001/revision3/bbabe54cieqn9.gif)
|
| e31 | Piezoelectric stress constant (C m−2) | −5.16 |
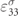
| Permittivity constant (nF m−1) | 12.563 |
| α | Nonlinear elastic constant (GPa) | −33.76 |
| γ | Nonlinear piezoelectric constant (C m−2) | −28 × 10−3 |
It is desired that the BCFEH operates near the first primary resonance, thus the length of 0.5 m is defined for the robotic system under consideration. The piezoelectric patch length is defined to be 0.3L and to be attached at L1 = 0.35 m and L = 0.5 m so it is at the tail tip. A system of equations constructed from an eigenvalue problem analysis using the boundary and continuity conditions of the representative backbone beam with partial patch coverage is used to solve for the natural frequencies and mode shapes of the BCFEH [13]. The first three natural frequencies are determined and shown in table 3.
Table 3. First three natural frequencies (Hz) of the BCFEH under investigation.
| L = 0.5 m and L1 = 0.35 m | |
|---|---|
| First natural frequency (f1) | 1.6640 |
| Second natural frequency (f2) | 12.1528 |
| Third natural frequency (f3) | 35.0773 |
To accurately account for the multiple excitations and response of the structure, an energy model formulation is adopted [14, 22, 23]. In [22], the nonlinear electrostrictive and nonlinear permittivity material terms were found to not be essential so are neglected in this work. The kinetic energy (T), shown in equation (1), of the BCFEH is dependent on 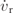 ,
, 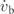 , and
, and 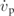 which are the velocity of the relative, base, and prescribed motion, respectively. Equation (2) is the potential energy (Π) of the BCFEH as it undergoes motion
which are the velocity of the relative, base, and prescribed motion, respectively. Equation (2) is the potential energy (Π) of the BCFEH as it undergoes motion
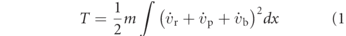
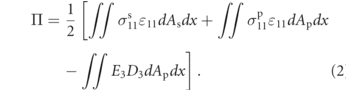
The main focus in this study will be near the primary resonance. The presence of large deformation in these kinds of undulatory systems needs to be estimated more accurately to predict resonance. The large deformation additionally could activate the nonlinear response of the material. To this end, both geometric nonlinearity for the strain and piezoelectric nonlinearities are considered. Nonlinear effects of the strain are added through a geometric nonlinearity [16]. The large deformation nature of this prescribed motion requires higher order modeling to approximate the influence of this motion on the fish-like energy harvester. It was demonstrated in [22] that the inclusion of geometric and material nonlinearities has a dramatic effect. In this current work, the case B motion is utilized as it keeps some of the complexity of the prescribed motion to show how it can be very impactful for a nonlinear coupled energy harvester when the system is operating near the first primary resonance. Forcing the prescribed fish-like motion onto the structure and incorporating the structural response, vr, into the nonlinear strain, equation (3) is determined as:
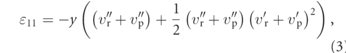
where y is the relationship of the beam thickness and is dependent on the location along the beam.
The response of the piezoelectric materials undergoing stress has commonly been accounted for in the Gibb's free energy (G) by Amin et al [24], Sherrit and Mukherjee [25], and Wang et al [26]. This formulation can be expanded to higher-order piezoelectric, permittivity, and electrostrictive terms as by Guyomar et al [27, 28] and Joshi [29] to be:
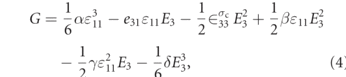
where G depends on the piezoelectric strain constant (e31), strain the material is subjected to (ɛ11), electric field (E3), permittivity under constant stress (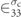 ), nonlinear elastic constant (α), nonlinear electrostriction constant (β), nonlinear piezoelectricity constant (γ), and nonlinear permittivity constant (δ).
), nonlinear elastic constant (α), nonlinear electrostriction constant (β), nonlinear piezoelectricity constant (γ), and nonlinear permittivity constant (δ).
The electric displacement (D3) is found by deriving equation (4) function with respect to the electric displacement [29] which yields the nonlinear electric displacement [30] as follows:
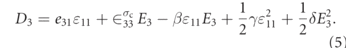
The stress of the piezoelectric is determined by deriving equation (4) with respect to the strain. The traditional Hooke's law relationship is also accounted for. Thus, the piezoelectric materials nonlinear stress response can be expressed as [31]:
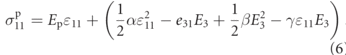
The mass, m, is dependent on the location along the length, where m = m1 for the first section of the backbone without the piezoelectric patch and m = m2 for the tail section covered by the piezoelectric patch. The stress of the structure (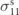 ) is related through Hooke's law.
) is related through Hooke's law.
The electric field is related to the voltage generation through the piezoelectric patch thickness by:
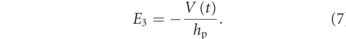
The relative displacement from the response of the structure is accounted for in a Galerkin discretization as:
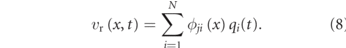
The displacement is dependent on the mode shape (ϕji (x)), where subscripts are dependent on both the section of the beam and mode of vibration. j = 1 or 2 corresponds to the first or second section of beam's length, respectively, and i denotes the vibration mode number. The number of modes used is determined by N. Modal coordinates are denoted as qi (t).
Equations (1) and (2) are combined with equa-tions (3), (5), and (6) while considering equations (7) and (8). The electromechanical equations of motion are found using the Euler–Lagrange principle as:
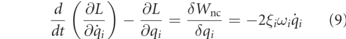
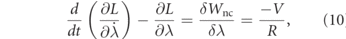
where (L = T − Π) and 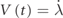 . The damping ratio (ξ) is defined for the structure and R denotes the electrical load resistance of the circuit that harvests the energy.
. The damping ratio (ξ) is defined for the structure and R denotes the electrical load resistance of the circuit that harvests the energy.
Using the Euler–Lagrange equations, the following nonlinear reduced-order model is obtained:
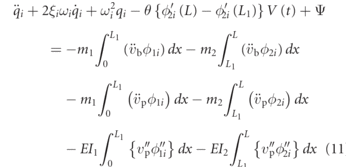

where the nonlinear terms are grouped and defined by:

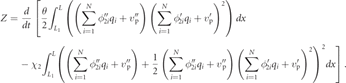
The piezoelectric coupling term and capacitance of the piezoelectric patch and nonlinear elastic and nonlinear piezoelectric term are defined as:
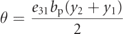
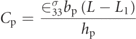
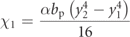
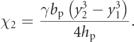
It should be noted that equation (12) is dependent on the mode shape and natural frequency number, as such, a system of (N + 1) coupled equations is constructed. This system of equations is different to typical vibrational energy harvesters noted before as it has additional terms that come from the prescribed motion. As this term has a polynomial envelope of quadratic order due to the term a2, shear terms begin to appear that influence the robotic system dramatically. If the prescribed motion is considered to have K ≠ 0, these terms were found to influence this system of equations and cause so much complication, thus case B is considered to remove much of these complications. By removing the undulation term, the mechanical and electrical equations are more affected by the envelope contribution of the system. Indeed, how this envelope impacts the system is next investigated, but the additional terms brought about by the geometric nonlinearities and material nonlinearities also must be investigated.
3. Importance of model formulation and convergence analysis: impacts of nonlinear strain, nonlinear material, prescribed motion envelope, and structural damping
The investigation of the nonlinear response of BCFEH when its architecture and operating conditions could induce the first primary resonance to be activated is carried out. Two nonlinear reduced-order models are defined considering a robotic system with and without parametric excitation terms created by the coupling between the prescribed motion and the geometric and piezoelectric nonlinearities to distinguish their importance. The amplitude envelopes influence by creating additional forcing terms on the convergence of the system is studied. The nonlinear interaction between prescribed motion and external excitation is also investigated and discussed. The presence of these excitations and how they could activate the nonlinear effects of the energy harvester depending on the structural damping are also examined in this study.
3.1. Importance of nonlinear strain and nonlinear piezoelectric terms
The geometric nonlinearity and nonlinear piezoelectric components of Ψ and Z are defined for the two models, as shown in table 4. Due to the complexity of the expansion due to the geometric nonlinearity, only N = 1 is considered in order to study the effects of the parametric excitation terms and the piezoelectric nonlinearities. For the full model case, the modal coordinate terms are considered up to third-order. Parametric excitation-resulted terms of the prescribed motion combined with modal coordinate are kept in this case and are again considered for terms up until the third order. The modal coordinate and voltage combinations are considered to not exceed the third order. The prescribed motion terms combined with voltage term are removed in the full case as well. In the reduced-complex model case, all parametric excitations terms are removed. All the other considerations in the full model case with orders of q and combinations of q and V are considered for the reduced-complex model case.
Table 4. Model case assumptions' considerations.
| Model case | Component considerations |
|---|---|
| Full model | • Orders of modal coordinate q are considered to result in terms of |
| no more than cubic-order for q after Euler–Lagrange equations | |
| • No combinations of vp and V(t) after Euler–Lagrange equations | |
| • Considers combinations of parametric excitation terms | |
| • Examples of parametric excitation terms pre-Euler–Lagrange equations: | |
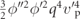 , , 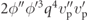 , , 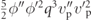 , , 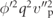
| |
| Reduced-complex model | • No combinations of vp(x, t) to q(t) and V(t) after Euler–Lagrange equations |
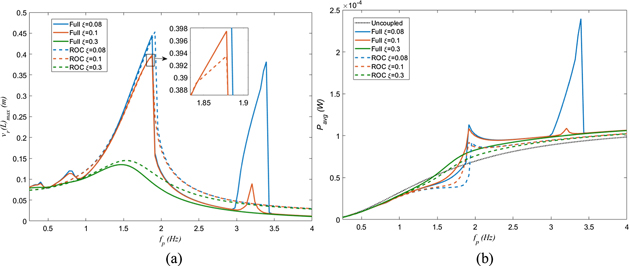
The comparison between the full and reduced-complex system is important as the complexity of the full system with the increasing number of N will make the numerical modeling difficult and time consuming. The presence of quadratic and cubic nonlinearities due to the geometric and piezoelectric nonlinearities may activate sub- or super-harmonic resonances. As for the parametric excitation terms in the full system, they can result in the appearance of parametric excitation resonances where the excitation frequency is almost twice one of the natural frequencies of the system under investigation. It should be noted that this is not a converged result, but those parametric excitation term impacts are still very likely for larger number of modes. Additionally, as the main focus is placed on the first primary resonance, the range of interest to this region may be unaffected, and thus, a reduced-complex case may be applicable. Figure 4 shows a comparison between the frequency-response curves of the full and reduced-complex models when considering one mode in the Galerkin discretization. It should be mentioned that the nonlinear elastic (α) and nonlinear piezoelectric (γ) terms are also present in this analysis. The load resistance is considered as R = 1/(Cp ω1) and multiple damping ratio values are considered in order to study their impact on the system's response and presence of super- and sub-harmonic resonances and parametric resonance.
Figure 4. Comparison of N = 1 full model with parametric terms to model with terms removed with α = −33.76 GPa and γ = −28 × 10−3 C m−2, investigating the impact of structural damping on (a) relative displacement and (b) average harvested power.
Download figure:
Standard image High-resolution imageA comparative uncoupled model is adopted which was used in [21, 22]. In these works, a biomimetic system was defined to have very high damping so there is no structural influence in the electrical Gauss law system. This would be the case when equation (12) no longer has any relationship with the mechanical equation (11). Thus, the system would be uncoupled and the electrical equation would only be dependent on the prescribed motion.
The plotted curves in figure 4 demonstrate that the full nonlinear model exhibits a clear superharmonic resonance of order 2 and 3 (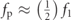 and
and 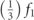 ) due to the presence of the quadratic and cubic nonlinearities in the system [32]. It is also clear that the full model detects the parametric resonance corresponding to fp ≈ 2f1 which is dependent on the damping ratio. The parametric resonance and super-harmonic resonances of order 2 and 3 are more easily recognizable in the relative displacement at the tail tip, as depicted in figure 4(a). The effects of damping are also much clearer in the relative displacement. It is also clear, at the first primary resonance when fp ≈ f1, a hardening behavior occurs for both the full and reduced-complex case when structural damping is decreased, and these nonlinear effects become more influential.
) due to the presence of the quadratic and cubic nonlinearities in the system [32]. It is also clear that the full model detects the parametric resonance corresponding to fp ≈ 2f1 which is dependent on the damping ratio. The parametric resonance and super-harmonic resonances of order 2 and 3 are more easily recognizable in the relative displacement at the tail tip, as depicted in figure 4(a). The effects of damping are also much clearer in the relative displacement. It is also clear, at the first primary resonance when fp ≈ f1, a hardening behavior occurs for both the full and reduced-complex case when structural damping is decreased, and these nonlinear effects become more influential.
The full model case exhibits a reduction of the maximum relative displacement for the first primary resonance compared to the reduced-complex case. It should be mentioned that the superharmonic resonances of order 2 and 3 and parametric resonance are not observed when the parametric excitation terms are neglected. Moreover, it follows from the plotted curves in figure 4(b) that the harvested power is influence significantly in the parametric resonance region when considering the full model. Additionally, the uncoupled model is in good agreement for various prescribed frequencies in the off-resonance regions.
It is known that the harvested power is a combination of the prescribed motion and the structural input in the Gauss law equation. The superharmonic resonance does not come through in the average power as this has large impact on the displacement, as shown in figure 4(b). The harvested power at the first primary resonance is impacted by the combination of the resonance response from the displacement and the prescribed motion. The maximum power for the different cases of damping show how this combination is influenced by the phase response of the system with this change of ξ. The decrease of structural damping does not correspond to an increase in the harvested power as the structure can move more freely. There is a complex interaction between the structural motion phase and the prescribed motion.
To further explore the various resonances in figure 4, the time histories and fast Fourier transform (FFT) are presented for selected frequencies of interest from the full model and are shown in figure 5. The super-harmonic corresponding to 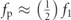 , is shown when fp = 0.818 Hz. Primary resonance is taken at the hardened peak. The parametric resonance frequency is taken at the peak of the resonance as well. Figure 5(a) demonstrates that the superharmonic is moving with two frequencies [32, 33]. The parametric resonance time history shows that the response is of similar frequency as the primary resonance, shown in figure 5(b). The FFT shows the working frequencies in each case of these specified time histories. Indeed, the superharmonic is working with the two frequencies of
, is shown when fp = 0.818 Hz. Primary resonance is taken at the hardened peak. The parametric resonance frequency is taken at the peak of the resonance as well. Figure 5(a) demonstrates that the superharmonic is moving with two frequencies [32, 33]. The parametric resonance time history shows that the response is of similar frequency as the primary resonance, shown in figure 5(b). The FFT shows the working frequencies in each case of these specified time histories. Indeed, the superharmonic is working with the two frequencies of 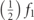 and f1. The primary resonance is working solely at the point. The parametric resonance case operates with f1 and further demonstrates that this is a typical parametric excitation resonance [17].
and f1. The primary resonance is working solely at the point. The parametric resonance case operates with f1 and further demonstrates that this is a typical parametric excitation resonance [17].
Figure 5. Relative displacement time histories and FFT of N = 1 full model with parametric terms and α = −33.76 GPa, γ = −28 × 10−3 C m−2, and ξ = 0.08 for multiple prescribed frequency conditions.
Download figure:
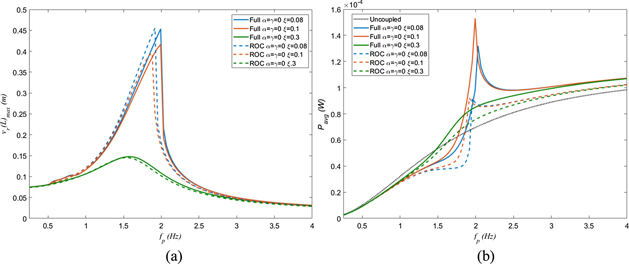
Standard image High-resolution imageTo this point, the nonlinear elastic and nonlinear piezoelectric terms are included in the full and reduced-complex models. By equating these two terms to zero, the impacts of the geometric nonlinearity in the linear elastic and linear piezoelectric term can be distinguished. The plotted curves in figure 5 show the frequency-response curves of the maximum relative displacement and average harvested power. The same load resistance and multiple structural damping for both models are used. It is easily evident in figure 6 that this soft robotic system is affected much differently compared to the one shown in figure 4 when considering the nonlinear piezoelectric material terms. It follows from the maximum relative displacement frequency curves shown in figure 6(a) that there are no clearly defined super-harmonic resonances of order 2 and 3 influences like the superharmonic resonances seen in figure 4(a). A superharmonic resonance region can be seen in the full model results for the smaller damping, but again, are not clearly defined. The system also exhibits a slight shift in characteristic for the hardening behavior of the full and reduced-complex models. The difference between the two models near the first primary resonance is clearer when there are no piezoelectric nonlinearities. Indeed, when considering the reduced-complex model, the strength of the nonlinear hardening effect is lowered, and smaller amplitudes are obtained. It should be noted that the parametric resonance is disappeared when the nonlinear piezoelectric terms are neglected from the full model.
Figure 6. Comparison of N = 1 full model with parametric excitation terms to model with terms removed with α = γ = 0, investigating the impact of structural damping on (a) relative displacement and (b) average harvested power.
Download figure:
Standard image High-resolution imageThe average harvested power is dramatically more affected by the first primary resonance when the nonlinear piezoelectric terms are considered zero. Additionally, as there are no parametric excitation terms activated in this case, the harvested power is solely impacted near the primary resonance. The damping also has interesting induced results in the harvested power. The damping does not directly correspond to a predictable power output as an increase in the damping causes an increase in power as seen before, but much more dramatic in the full model. The reduced-complex model is less affected by the constructive build due to the phase as in the full model. This demonstrates that these terms affect the phase interaction of the structure and the prescribed motion.
After performing this investigation on the nonlinear piezoelectric terms and how they result in the activation of the superharmonic resonances and parametric resonance, it can be concluded that these kinds of fish-like energy harvesting systems are complex due to the interaction between the prescribed motion and relative response of the system. Using one mode in the Galerkin approach, it is shown that the primary resonance is not much affected by the absence of the nonlinear piezoelectric terms which may be less influential depending on the type of the piezoelectric material and its nonlinear characteristics. To this end, for the remaining of this study, only the linear piezoelectric constitutive relations are considered in order to minimize the possible nonlinear interactions which are outside the scope of this study.
3.2. Impact of higher number of modes and envelope term on the system's response
After distinguishing the impactful nonlinear piezoelectric terms and removal of the parametric excitation terms, an investigation on the effects of considering more number of modes in the Galerkin discretization is examined. The reduced-complex model with α = γ = 0 is used to investigate the effects of the geometric nonlinearity and prescribed motion (without the existence of the parametric excitation terms) on the convergence of the Galerkin discretization. It should be noted that the envelope term a2 of the prescribed motion directly causes the presence of additional terms in the mechanical and electrical equations.
The plotted curves in figure 7 depict the results of the convergence for N = 1, 2, 3 when considering different damping ratios. Again, the electrical load resistance is defined to be R ≈ 1/(Cp
ω1). The convergence analysis is evidently impacted with every increase in the number of modes in the Galerkin discretization. Figure 7(a) shows that the hardening of the relative displacement frequency-response curves is affected when N = 3. When N = 1, the maximum relative displacement is higher for the smaller structural damping. Then, as N = 2, the relative displacement decreases compared to N = 1. However, when N = 3, the relative displacement increases in amplitude. This variability can be explained by the impact of the forcing term stemming from the prescribed motion. As N increases, the new forcing term, ϕ''i
v''p, increases as the shear increases at the tail tip with each additional mode shape, as shown in table 5. This is especially true when the original envelope term  is considered.
is considered.
Figure 7. Convergence of reduced-complex model with α = γ = 0, investigating the impact of structural damping on (a) relative displacement and (b) average harvested power for N = 1, 2, 3.
Download figure:
Standard image High-resolution imageTable 5. Table of values for additional forcing term considering different a2.
![$\left[{\int }_{0}^{{L}_{1}}{\phi }_{1i}^{{\prime\prime}}{v}_{\mathrm{p}}^{{\prime\prime}}dx+{\int }_{{L}_{1}}^{L}{\phi }_{2i}^{{\prime\prime}}{v}_{\mathrm{p}}^{{\prime\prime}}dx\right]=\frac{2}{L}\left[{\int }_{0}^{{L}_{1}}{\phi }_{1i}^{{\prime\prime}}{a}_{2}dx+{\int }_{{L}_{1}}^{L}{\phi }_{2i}^{{\prime\prime}}{a}_{2}dx\right]\mathrm{cos}\left({\omega }_{\mathrm{p}}t\right)$](https://content.cld.iop.org/journals/1748-3190/16/4/046001/revision3/bbabe54cieqn26.gif)
| |||
|---|---|---|---|
![${{\Gamma}}_{i}=\frac{2}{L}\left[{\int }_{0}^{{L}_{1}}{\phi }_{1i}^{{\prime\prime}}{a}_{2}dx+{\int }_{{L}_{1}}^{L}{\phi }_{2i}^{{\prime\prime}}{a}_{2}dx\right]$](https://content.cld.iop.org/journals/1748-3190/16/4/046001/revision3/bbabe54cieqn27.gif)
| |||
| Value of Γi | |||
| Mode shape number | i = 1 | i = 2 | i = 3 |
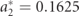
| 0.3428 | −1.4061 | 2.9148 |
Figure 7(b) demonstrates that the combining of the structural response terms and the prescribed motion term in the Gauss law equation causes a wide variety of impact on the system. The structural component is not a constant input into this equation because of the variation of the mechanical response impacted by Γ in table 5. The interesting influence of the damping ratio on the power combined with the number of modes can be seen for these different cases of mode number and when ξ = 0.08 and 0.1. Depending on the combination of the mode number and damping, the average harvested power at resonance is influenced by the phase combination of the structural response and prescribed motion. Thus, the harvested power at resonance can be larger for the different cases of these small ξ values. Additionally, the increase in the number of modes in the Galerkin discretization increases the overall impact of the structural response in the electrical equation and decreases the overall power and, thus, does not reach convergence due to the high forcing resulted by the prescribed motion when the number of modes is increased, as shown in table 5.
The obtained results in figure 7 and table 5 lead to the necessary investigation of reducing the influence of the impactful forcing term due to the envelope. Indeed, by considering a smaller envelope term to the original 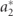 , the BCFEH behaves more like a typical base-excited system once the influence of this term is overcome. Therefore, a range of a2 are considered as
, the BCFEH behaves more like a typical base-excited system once the influence of this term is overcome. Therefore, a range of a2 are considered as 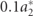 ,
, 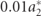 , and
, and  which are investigated for their relationship to convergence, as depicted in figure 7. By considering the increasingly smaller envelope term, the value of Γ is analogous to the multiple of
which are investigated for their relationship to convergence, as depicted in figure 7. By considering the increasingly smaller envelope term, the value of Γ is analogous to the multiple of 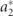 . The case where a2 = 0 is used to compare the other cases of envelope to that which is of time dependent nature. The same load resistance and ξ = 0.08 are considered as the convergence investigation with
. The case where a2 = 0 is used to compare the other cases of envelope to that which is of time dependent nature. The same load resistance and ξ = 0.08 are considered as the convergence investigation with 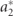 .
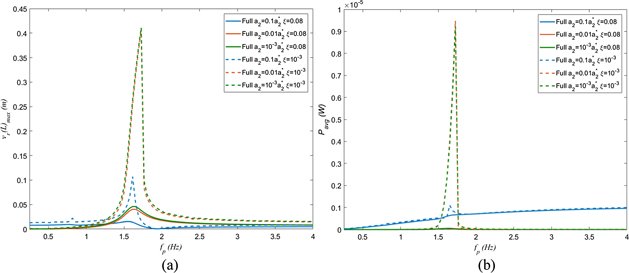
.
The plotted curves in figure 8 show that when  , the relative displacement of the system is still influenced by the increase in the number of modes. As for the average power, there is a significant effect with respect to the number of modes when
, the relative displacement of the system is still influenced by the increase in the number of modes. As for the average power, there is a significant effect with respect to the number of modes when 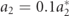 . As
. As 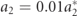 , the effects of the forcing term due to the prescribed motion and stiffness of the system are dramatically decreased. The relative displacement and harvested power dramatically shift to a response more similar to the synonymous base excitation case (a2 = 0), but of decreased value. Clearly, as the value decreases for a2 beyond this point, the effects in the Γ are so little that the system just converges to the a2 = 0 case. The more mode numbers considered also reach convergence much more quickly within N = 3, when
, the effects of the forcing term due to the prescribed motion and stiffness of the system are dramatically decreased. The relative displacement and harvested power dramatically shift to a response more similar to the synonymous base excitation case (a2 = 0), but of decreased value. Clearly, as the value decreases for a2 beyond this point, the effects in the Γ are so little that the system just converges to the a2 = 0 case. The more mode numbers considered also reach convergence much more quickly within N = 3, when 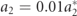 or smaller. This is especially evident in the harvested power, as there is less impact from the interaction between the structure and the prescribed motion term in the Gauss law equation. The uncoupled modeling displays how the prescribed term becomes less influential when a2 is decreased, as shown in figure 8(b).
or smaller. This is especially evident in the harvested power, as there is less impact from the interaction between the structure and the prescribed motion term in the Gauss law equation. The uncoupled modeling displays how the prescribed term becomes less influential when a2 is decreased, as shown in figure 8(b).
Figure 8. Convergence of system with impactful motion envelope term a2 is reduced, with α = γ = 0, investigating the impact of structural damping on (a) relative displacement and (b) average harvested power for N = 1, 2, 3.
Download figure:
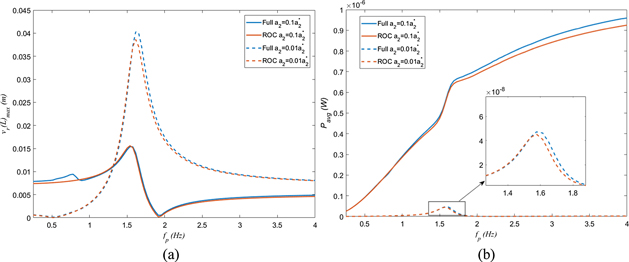
Standard image High-resolution imageIt should be noted that the results shown in figure 8 demonstrate that as the forcing term coming from the prescribed motion for sure impact the activation of the nonlinearity which depends on the structural damping. As smaller values of Γ are considered, the damping needs to be also decreased for the nonlinear phenomenon to be activated. To determine if the full model would be impacted by the change in envelope term, the full model with N = 1 is reconsidered using the same load resistance and two different ξ, as shown in figure 9. It follows from the plotted curves in figure 8 that the impact of a2 on the full model results in a similarity to the reduced-complex model results and hence the disappearance of the parametric resonance and superharmonic resonances as the prescribed motion coupling terms become less influential. As seen before, the hardening phenomenon of the first natural resonance is not apparent for the different a2 when ξ = 0.08. However, when a much smaller value of damping is considered, this hardening behavior begin to appear as seen in figure 9 when ξ = 10−3.
Figure 9. Full model, N = 1, with impactful motion envelope term a2 is reduced, investigating the impact of structural damping on (a) relative displacement and (b) average power.
Download figure:
Standard image High-resolution imageThe identification that the envelope term is highly impactful on the system leads to the reinvestigation of the full and reduced-order complex models. The presence of undulatory terms which give rise to the additional derived forcing terms, defined in table 5, cause challenges for the justification of using the reduced-order complex model. However, when smaller a2 are used, these terms become less impactful and the reduced-order complex model can be justified, which is shown in figure 10. Additionally, when a2 is reduced, the full model with material nonlinearities has reduced superharmonic resonance and parametric resonance activated.
Figure 10. Comparison full and reduce-order complex models with impactful motion envelope term a2 reduced and its impact on (a) relative displacement and (b) average harvested power when ξ = 0.08, α = −33.76 GPa, and γ = −28 × 10−3 C m−2.
Download figure:
Standard image High-resolution image3.3. Investigation on the external effect due to base excitation
During the implementation of the BCFEH in a natural environment, external impulse on this robotic system could induce a structural resonance which could cause damage. To gain grasp of a possible scenario of external excitation, the kinetic energy of the system accounts for the possibility of an excitation that impulses the system at the head which would be synonymous with a base excitation case. As such, the prescribed motion is defined to equal zero. The other assumptions in this case are R = 1/(Cp ω1) and ab = 1 m s−2 while a variety of structural damping are considered, as shown in figure 11. It is clear that a base excitation with acceleration of 1 m s−2 can still activate the nonlinear hardening at the first primary resonance when structural damping is small enough. When ξ = 0.08, the appearance of this behavior is not clear. However, the convergence of this system happens quickly for all cases of ξ and three modes in the Galerkin discretization is enough. This supports the observations seen in the smaller a2 cases to reach convergence with three modes. Now that it is established how the base excitation affects the system's response, the interaction between the base excitation and prescribed motion excitation are investigated in the next sections.
Figure 11. Convergence of base excitation for reduced-complex model with α = γ = 0, investigating the impact of structural damping on (a) relative displacement and (b) average power.
Download figure:
Standard image High-resolution image4. Impacts of prescribed and base excitations on the system's behavior and robustness
As stated earlier, a functioning bioinspired body caudal fin AUV would be subjected to not only the prescribed motion but additional excitation from the surrounding environment. The challenge comes when the waveforms of these excitations are of some nature that the phase interaction results in constructive/destructive build or are in some similar regime that the beating phenomenon occurs for the response waveform [34–37].
Considering the reduced-complex model, the prescribed motion case is considered to have 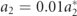 so converged responses for both the relative motion and harvested power are reached when considering three modes in the Galerkin discretization. Figure 11 has distinguished that the base excitation will have a much larger influence on the system with ab = 1 m s−2. As such, a range of values of ab = 0.01, 0.1, 0.5, and 1 m s−2 are considered to determine the influence of the base acceleration for this defined prescribed motion case, as shown in figure 12. Multiple base excitation frequencies are considered close to the first natural frequency of the system. The structural damping is considered to be equal to 0.08 as this would reduce the nonlinear hardening in the system for these conditions of prescribed envelope and base acceleration. The load resistance is considered as R = 1/(Cp
ω1).
so converged responses for both the relative motion and harvested power are reached when considering three modes in the Galerkin discretization. Figure 11 has distinguished that the base excitation will have a much larger influence on the system with ab = 1 m s−2. As such, a range of values of ab = 0.01, 0.1, 0.5, and 1 m s−2 are considered to determine the influence of the base acceleration for this defined prescribed motion case, as shown in figure 12. Multiple base excitation frequencies are considered close to the first natural frequency of the system. The structural damping is considered to be equal to 0.08 as this would reduce the nonlinear hardening in the system for these conditions of prescribed envelope and base acceleration. The load resistance is considered as R = 1/(Cp
ω1).
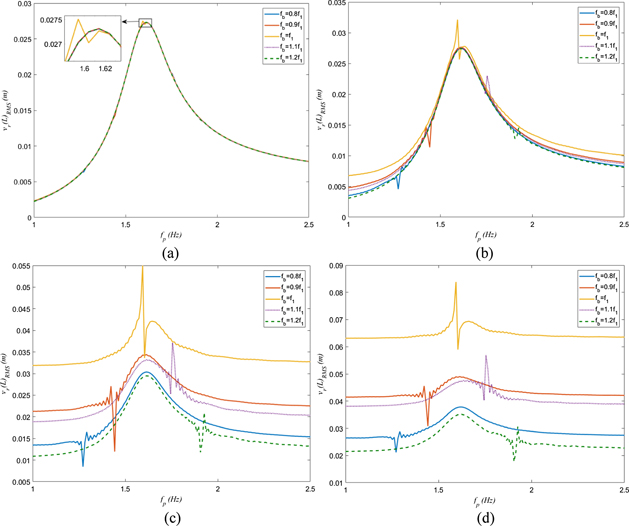
Figure 12. Impact of base acceleration considering multiple fb, ξ = 0.08, and R = 1/(Cp ω1). RMS relative displacement when (a) ab = 0.01 m s−2, (b) ab = 0.1 m s−2, (c) ab = 0.5 m s−2, and (d) ab = 1 m s−2.
Download figure:
Standard image High-resolution imageThe interaction of the prescribed motion and base excitation is displayed for the root mean square (RMS) relative motion of the BCFEH at the tail tip. This allows for the identification of regions where the interaction between the two excitations causes variation of the response. It is clear in figure 12(a) that the prescribed motion is dominant when ab is small. The variation of results when fb = f1 is due to the slight off phase interaction caused by the load resistance. This suggests that the BCFEH could be largely unaffected except when fb is at resonance for small amplitudes of acceleration. However, when the acceleration increases, all the base excitation frequencies near the resonance experience some phase interaction. Obviously, since the structural damping and load resistance are kept constant, the prescribed frequencies that have this induced interaction of phase all occur at the same value independent of the base acceleration. Indeed, however, the amplitude of the base acceleration causes these regions to become more pronounced, as depicted in figure 12(c). As the base acceleration increases beyond 0.5 m s−2, the base excitation becomes more dominant and increases the RMS relative displacement to higher values. Considering figure 12(c), the phase interaction region for the different base excitation frequencies correspond to the related prescribed motion near that same value. It should be noted that these regions when the excitation frequencies coincide can cause constructive and destructive build of the response waveform which could to the BCFEH being damaged or inoperable. It should be mentioned that the quenching phenomenon takes place when the prescribed frequency of excitation and the base excitation frequency are close to each other. This is particularly clear when fb = 0.8f1 and fb = 1.2f1, as shown in figures 12(b)–(d).
To investigate how these waveforms are interacting in these regions, time histories are plotted for some selected cases, as shown in figure 13. Time histories are necessary to distinguish if the RMS of the response waveform is over enough time to give an appropriate timeframe and to describe how there is a wide variability of response for the various frequencies defined. Additionally, when these two excitation frequencies are interacting, the aforementioned beating phenomena can occur. This phenomenon occurs when the two excitations are close to each other and when the excitations become more different the response is pulled-out to whichever excitation which is more dominant. These responses are all periodic in nature but are dependent on this combination of the two excitations [34–37]. The variability of the synchronization and pull-out conditions are shown in figure 13. In figure 13(a), the selected fp is closer to the synchronization region when the beating phenomenon occurs. Figures 13(c) and (d) show that when fp is further away from the synchronization region the system works with one frequency.
Figure 13. Relative displacement at the tail tip time histories of select frequency points when ab = 0.5 m s−2, ξ = 0.08, and 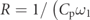 ).
).
Download figure:
Standard image High-resolution imageAfter studying the impacts of the base excitation and relationship between the prescribed frequency and base frequency of excitations, the effects of the electrical load resistance is investigated, as presented in figure 14. The harvested power frequency-response curves corresponding to figure 12 is of similar nature when the load resistance is fixed. However, when the load resistance is varied for a fixed base acceleration, the harvested power response is greatly varied while the impact of the relative motion is minimal. Therefore, the average power is considered to demonstrate the effects of load resistance on the system's performance, as shown in figure 14. The variation of the load resistance in figure 14 has a clear impact on the electrical response of the system. It should be noted that R = 106 Ω is the closest case to R = 1/(Cp ω1) = 1.4398 × 106 that was considered for previous investigations. This demonstrates that this considered load resistance for the previous investigations is very close to the optimal performing load resistance and as such this assumptive load resistance is in good agreement with the approximate optimal load resistance for optimal electrical performance. As the load resistance allows for the optimal performance for the electrical response of the harvester, the effects seen in the relative motion become more pronounced and defined. As the load resistance begins to decrease to short circuit-configuration or increase to closed-circuit configuration, the effects of the combination of the prescribed and base excitation diminish in response of the fish-like energy harvester.
Figure 14. Variation of Pavg frequency response for different load resistance considering (a) fb = 0.8f1, (b) fb = 0.9f1, (c) fb = f1, and (d) fb = 1.2f1, where ξ = 0.08 and ab = 0.5 m s−2.
Download figure:
Standard image High-resolution imageThe damping is purposely chosen to be in a region where the two excitations are not suppressed but also not free to activate nonlinearities in the system. By selecting ξ = 0.08 and focusing on the primary resonance region, the superharmonic resonances and parametric resonance are not activated or of focus. For sure, the smaller value damping you have the more complex the interaction, and the larger the damping the more suppressed the whole response is.
5. Discussion of robustness of soft robotic system and integration of energy harvesting
It is evident that the application of an energy harvester in a system that is defined with undulatory motion comes with many challenges. The undulatory nature of the prescribed motion can lead to the activation of parametric resonance and superharmonic resonances of the structure which are challenging to model and fully grasp. This is due to the possible presence of the piezoelectric nonlinearities and their interactions with the undulatory prescribed motion. It should be mentioned that the analysis performed in this study assumed that the prescribed motion defined does not contain the term including the undulatory motion as the fish that it is inspired from. If the term captured in the cosine that defines the periodic nature of the spinal column was included in the model, many challenges and issues would arise from the additional forcing terms in the coupled system of equations. By simplifying the system to neglect these highly undulatory terms, it was still shown that controlling the envelope of oscillation to bend with a quadratic nature leads to challenges from these terms as well. It was required to assume and minimize the impact of these terms as much as possible to even achieve a response of the system that behaves with conventional thought.
The additional terms that are brought about due to the quadratic nature of the oscillation envelope can greatly impact the robotic system. The new forcing terms can activate the nonlinear response the system when the appropriate representation of the strain is used. However, the structural component of the strain was represented in a Galerkin discretization and with each additional mode number considered, the shear of the mode shape combining with the prescribed motion component grows in value and does not converge. This leads to the system varying greatly with higher modes. These kinds of responses hugely affect the robustness of the system and hence unpredictable responses may take place and results in damaging the robot. The mechanical coupling in the electrical equation means there is also impact with each additional mode as well as the phase interaction of this response and the additional prescribed motion term in the electrical equation.
In order to be able to control the soft robotic system to produce results without the impacts of these terms, there are two methods. One being, that the undulation of the system is removed as much as possible. This was demonstrated in this study by decreasing the quadratic envelope term till its effects become negligible and the system behaves more like that with a base excitation as the prescribed motion. This gives rise to the issues of (1) biomimicry and desire to create a structure that moves as the biological with large undulation with a prescribed motion and (2) the endurance of the system due to low thrust produced. It should be cautioned that the induction of a motion that forces a structure with such undulation could lead to these many issues. This leads to point two, create a damping mechanism that effectively silences the mechanical response of the structure, if the designer is able to achieve an undulatory prescribed motion with some developed actuator. This a monumental challenge as there would be a constant question of efficiency which is the ultimate desire when even considering the application of an energy harvester. The prescribed motion would still have to be fully functional regardless of this high damping for a functioning system, but if done, the system could operate without activating some resonances in the system which could be beneficial for operation. Additionally, if one is able to create such a system, the uncoupled electrical equation described could be an appropriate approximative model for the harvested power.
6. Conclusions
The development of a nonlinear fish-like robotic energy harvester model has led to the identification of the complexities that extend from the undulatory motion that is conceived for bioinspiration. Additional terms related to the prescribed motion of the structure are highly influential in the response of the system. The additional prescribed terms may activate the nonlinearities in the system and can cause parametric and superharmonic resonances for a system that considers terms to a certain order. Due to the complexity of the system, a step-by-step reduction in the complexity was performed to demonstrate how even in a reduced-complex system there are still many challenges and possible issues. The reduction of the quadratic envelope influence was shown to result in more of a base excitation response. By considering another external stimulus in the system as a base excitation, it was demonstrated that the interaction between these excitations can cause quenching of the motion in destructive build of the two waveforms when they are similar to each other. Additionally, the variation of the load resistance has a large impact on the harvested power harvested. At a value closest to the optimal configuration of the circuit for the system, the interaction regions between the two excitation waveforms was most pronounced. This study has reduced the complexity to gain understanding, but the full nonlinear model with impactful terms still considered requires more in-depth studies to grasp.
Acknowledgments
The authors would like to thank Brian Saunders of New Mexico State University for help in numerical simulations in this work.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.