ABSTRACT
Using local N-body simulation, we examine viscosity in self-gravitating planetary rings. We investigate the dependence of viscosity on various parameters in detail, including the effects of particle surface friction. In the case of self-gravitating rings with low optical depth, viscosity is determined by particle random velocity. Inclusion of surface friction slightly reduces both random velocity and viscosity when particle random velocity is determined by inelastic collisions, while surface friction slightly increases viscosity when gravitational encounters play a major role in particle velocity evolution, so that viscous heating balances with increased energy dissipation at collisions due to surface friction. We find that including surface friction changes viscosity in dilute rings up to a factor of about two. In the case of self-gravitating dense rings, viscosity is significantly increased due to the effects of gravitational wakes, and we find that varying restitution coefficients also change viscosity in such dense rings by a factor of about two. We confirm that our numerical results for viscosity in dense rings with gravitational wakes can be well approximated by a semianalytic expression that is consistent with a previously obtained formula. However, we find that this formula seems to overestimate viscosity in dense rings far from the central planet, where temporary gravitational aggregates form. We derive semianalytic expressions that reproduce our numerical results well for the entire range of examined parameters.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Angular momentum transport is a key process that drives the large-scale structures of planetary rings. It determines the timescale of radial spreading, the behavior of wave structures, and the condition of gap formation in rings in the vicinity of embedded moonlets, and it is also related to the stability of dense rings (see, e.g., Goldreich & Tremaine 1978; Stewart et al. 1984; Schmidt et al. 2009). Furthermore, recent studies show that Saturn's small moons orbiting just outside the main rings likely formed by an accretion of radially spreading particles from the outer edge of the rings (Charnoz et al. 2010; Canup 2010); thus, the spreading rate of the ring is also related to the formation of these moons.
In planetary rings, angular momentum transport is caused by collisions and gravitational interactions between particles and satellites, and the rate of the transport is expressed in terms of viscosity. In most previous works on the viscosity of planetary rings, effects of the self-gravity of the rings were either neglected or only taken into account in an approximate manner (e.g., Goldreich & Tremaine 1978; Borderies et al. 1985; Araki & Tremaine 1986). Wisdom & Tremaine (1988) performed local simulation of planetary rings with nongravitating particles and studied their equilibrium properties, including viscosity. In addition to the local component of angular momentum transport due to particle radial random motion examined by Goldreich & Tremaine (1978), Wisdom & Tremaine (1988) also evaluated the nonlocal component due to collision. They found that the nonlocal component dominates the viscosity in dense rings, and they confirmed that the values of the viscosity agree well with the result of Araki & Tremaine (1986). They also examined effects of self-gravity in an approximate manner by enhancing the vertical frequency of particle orbital motion, and they found that the viscosity is enhanced by a factor of five. Richardson (1994) calculated ring viscosity using N-body simulation of self-gravitating rings, but did not examine the angular momentum transport due to gravitational interactions between particles.
On the other hand, Daisaka et al. (2001) studied viscosity in self-gravitating rings using local N-body simulation. In addition to the local and nonlocal components studied by Wisdom & Tremaine (1988), Daisaka et al. (2001) calculated the gravitational component of viscosity based on the formulation of Takeda & Ida (2001), who studied angular momentum transport in proto-lunar disks. Takeda & Ida (2001) and Daisaka et al. (2001) found that the viscosity is strongly enhanced when particle disks become gravitationally unstable and gravitational wakes are formed. From their numerical results, Daisaka et al. (2001) derived a formula of the viscosity in self-gravitating dense rings given by ν ∼ CG2Σ2/Ω3, where G is the gravitational constant, Σ and Ω are the surface density and angular velocity of the ring, respectively, and C is a correction factor that depends on the ratio of the Hill radius of the particles to their physical size (see Section 5). However, the range of parameters studied by Daisaka et al. (2001) was somewhat limited; for example, they did not examine viscosities in dense rings far from the planet, where temporary gravitational aggregates can form. Also, they assumed that particles are smooth spheres and did not examine the effects of surface friction of particles on the viscosity.
Spins of ring particles arise as a natural outcome of oblique impacts between particles with surface friction. Spin rate of ring particles is an important parameter in modeling thermal emission from Saturn's rings, and it has been studied in detail, using analytic calculation, three-body orbital integration, and N-body simulation (Salo 1987; Richardson 1994; Ohtsuki 2005, 2006a, 2006b; Ohtsuki & Toyama 2005; Morishima & Salo 2006). These studies show that the spin period of the particles is on the order of their orbital period in rings of equal-sized particles, while small particles spin faster than larger ones when size distribution is included. Considering energy balance between viscous gain and dissipation due to an inelastic collision with surface friction, Morishima & Salo (2006) examined the effects of particle surface friction on viscosity in rings consisting of nongravitating particles, but such effects on the viscosity in self-gravitating rings were not studied.
On the other hand, Tanaka et al. (2003) derived a new formulation for the calculation of the total viscosity (i.e., the sum of the local, nonlocal, and gravitational components) in particle disks. Under Hill's approximations in the three-body problem, they derived an expression of angular momentum flux in terms of the changes of orbital elements of constituent particles due to mutual collisions and gravitational interactions. In the case of planetary rings with low optical depth, they showed that viscosity can be evaluated by three-body orbital integration. They also derived a formula to calculate viscosity in dense rings using N-body simulation. In this case, viscosity in rings in a quasisteady state can be obtained from energy dissipation at inelastic collisions between particles (see Section 2). In the case of rings with the effect of vertical overall self-gravity, Salo et al. (2001) also found agreement between viscous heating and energy dissipation due to inelastic collision using N-body simulation. Tanaka et al. (2003) confirmed that viscosities in planetary rings calculated using their new formula agree with those obtained by the method used by Daisaka et al. (2001). This new method of viscosity calculation can also be used in the case of particles with surface friction, and the method is convenient when investigating detailed parameter dependence of the total viscosity of the rings.
In this work, we examine the viscosity of planetary rings consisting of spinning, self-gravitating particles. Using an N-body simulation code similar to the one developed by and used in Daisaka & Ida (1999) and Daisaka et al. (2001) and on the basis of the above viscosity calculation formula derived by Tanaka et al. (2003), we calculate ring viscosity for a wide range of parameters, including cases of particles with surface friction. We also examine viscosities in dense rings far from the central planet, where temporary gravitational aggregates can form. In Section 2, we describe our numerical methods. Numerical results of our N-body simulation are presented in Sections 3 and 4. First, in Section 3, we describe the effects of surface friction on viscosity in rings with low optical depth. Then, we show results for dense rings of spinning self-gravitating particles in Section 4. In Section 5, we derive semianalytic expressions of ring viscosity based on our numerical results. Our conclusions are summarized in Section 6.
2. NUMERICAL METHOD
We adopt the method of local N-body simulation (e.g., Wisdom & Tremaine 1988; Richardson 1994; Salo 1995; Daisaka & Ida 1999; Ohtsuki & Emori 2000; Daisaka et al. 2001) and use a code based on Daisaka & Ida (1999) and Daisaka et al. (2001). We erect a rotating Cartesian coordinate system with the origin at the center of the square simulation cell that moves on a circular orbit with a semimajor axis a0 at the Keplerian angular velocity Ω = (GMc/a30)1/2 (Mc is the mass of the central planet). The x-axis points radially outward, the y-axis points in the direction of the orbital motion, and the z-axis is normal to the equatorial plane. In this case, the equations of motion of particle i are written as
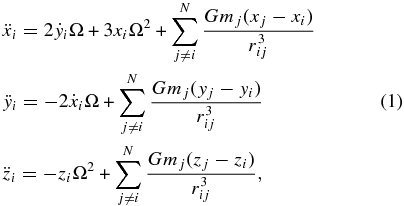
where rij = [(xi − xj)2 + (yi − yj)2 + (zi − zj)2]1/2, N is the particle number, mj is the mass of particle j, and the last terms on the right-hand side of Equation (1) denote gravitational forces between particles. We directly calculate the gravitational forces between particles using GRAPE-7, which is a special-purpose hardware for calculating gravitational forces, and orbits of particles are integrated with the second-order leap-frog method. In this work, we assume that all particles have identical sizes of 1 m radius.
When collisions between particles are detected, velocity changes are calculated based on the hard-sphere model, including surface friction (e.g., Salo 1987; Richardson 1994; Ohtsuki & Toyama 2005). Velocity changes are described in terms of the normal and tangential restitution coefficients, εn and εt, where 0 ⩽ εn ⩽ 1 and −1 ⩽ εt ⩽ 1. (Perfectly smooth spheres have εt = 1.) Let the normal and the tangential components of the relative velocity (v) of colliding particles to the tangent plane be vn and vt, respectively, and the normal and the tangential components of the relative velocity of the two contacting points at the time of impact be un and ut, respectively. Then, the normal and the tangential components of the relative velocity of the two contacting points after impact are given as

Using these relations, we calculate changes in velocities and rotation rates of the colliding particles (Appendix A). In this study, we assume that εt is constant and examine the dependence of viscosity on εt. As for the normal restitution coefficient, in addition to cases with constant εn's, we also examine cases with the velocity-dependent coefficient based on laboratory impact experiments (Bridges et al. 1984), which is given as

where vc = 1 cm s−1.
We calculate ring viscosities based on the formulation derived by Tanaka et al. (2003). Deriving an expression for angular momentum flux in terms of changes in particle orbital elements and assuming a quasisteady state in a local ring region, Tanaka et al. (2003) showed that the averaged viscosity in the ring region can be obtained by calculating energy dissipation due to inelastic collisions using N-body simulation. In the case of N-body simulation using a square simulation cell of width L, the viscosity averaged over the cell and a time interval T is written as (Tanaka et al. 2003)
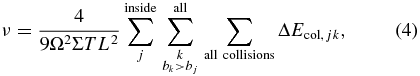
where Σ is the averaged surface density and ΔEcol, jk(> 0) is an amount of energy dissipated at a collision between particle j and particle k. ΔEcol, jk can be calculated, for example, from the change of the orbital elements for the relative motion of particles due to a collision (Appendix B). The first summation is taken over particle j whose guiding center is inside the simulation cell, while the second summation is over particle k, which have a semimajor axis of the guiding center (b) larger than that of particle j. The above expression can also be obtained by assuming a balance between energy loss due to inelastic collisions and the viscous gain due to the shear motion (Tanaka et al. 2003; see also Salo et al. 2001).
In the case of nongravitating rings or self-gravitating rings with low optical depth, N ∼ 103 or an even smaller number of particles is sufficient to examine such equilibrium properties, e.g., velocity dispersion. However, in the case of self-gravitating dense rings, a sufficiently large simulation cell (thus, a sufficiently large number of particles) should be used to accurately obtain various dynamical quantities (Salo 1995). Following Salo (1995), we set the size of the simulation cell so that L ⩾ 4λcr, where λcr = 4π2GΣ/Ω2 is the critical wavelength for axisymmetric gravitational instability. We performed simulations for sufficiently long time periods to achieve a quasisteady state; these were typically at least 20–50TK (TK is the Keplerian orbital period) for dense rings (10TK for τ = 1 and rh = 1, where rh is defined by Equation (5)), and still longer periods in the case of dilute rings. The time average for calculating viscosities from Equation (4) is carried out after a quasisteady state is achieved.
3. EFFECTS OF SURFACE FRICTION ON VISCOSITY IN OPTICALLY THIN RINGS
In this section, we first show results for nongravitating rings. Then we describe, in detail, results for self-gravitating rings with a low optical depth. Numerical results for self-gravitating dense rings will be presented in Section 4.
Figure 1 shows numerical results for the viscosity in the case of nongravitating rings as a function of optical depth. First, to confirm the validity of our code for N-body simulation and viscosity calculation, we compare our results with Wisdom & Tremaine (1988) by performing simulations for the same parameters, i.e., smooth particles (εt = 1) with εn = 0.5. In Figure 1(a), the crosses represent results from Wisdom & Tremaine (1988), and the line shows our results. We find excellent agreement between the two results. Figure 1(b) shows our numerical results for the velocity-dependent normal restitution coefficient given by Equation (3) with εt = 1, 0.5, and 0. We find that the dependence of viscosity on the value of εt is different between the low and high optical depth cases, and this difference is related to the behavior of particle random velocity. In the case of low optical depth, random velocity is somewhat reduced with the increasing strength of surface friction (Salo 1987; Ohtsuki & Toyama 2005), and the reduced radial excursion of particles lowers the rate of angular momentum transport and viscosity (Goldreich & Tremaine 1978). On the other hand, in the case of high optical depth, the dependence of random velocity on τ or εt becomes rather weak (Wisdom & Tremaine 1988). In this case, viscosity becomes larger with decreasing εt, because viscous heating increases to balance the additional energy dissipation due to surface friction.
Figure 1. Viscosity in the case of nongravitating rings as a function of optical depth. (a) Solid line shows our numerical results with εn = 0.5 and εt = 1, and the crosses are those obtained by Wisdom & Tremaine (1988) for the same parameters. (b) Our numerical results with the velocity-dependent normal restitution coefficient εn(v) given by Equation (3), with εt = 1 (circles), 0.5 (triangles), and 0 (squares).
Download figure:
Standard image High-resolution imageNext, we examine the case of self-gravitating rings with a low optical depth. The relative importance of self-gravity to mutual collision between particles depends on the relative size of the Hill radius of the particles to their physical size (Ohtsuki 1993, 1999; Salo 1995; Daisaka et al. 2001). In the case of rings of equal-sized particles (mass m, radius R, internal density ρ) at a distance a0 from the planet, the ratio of the mutual Hill radius RH(= a0(2m/3Mc)1/3) of colliding particles to the sum of their radii is written as (Daisaka et al. 2001)
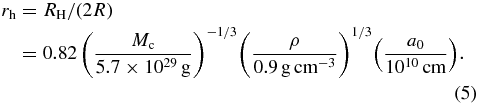
Figure 2 shows the plots of rh as a function of the distance from Saturn for several values of ρ. When ρ = 0.9 g cm−3, rh = 0.5, 0.71, and 1 (see, e.g., Figure 3) correspond to a/1010 cm = 0.61, 0.87, and 1.22, respectively. However, if ρ = 0.5 g cm−3, the above three values of rh correspond to a/1010 cm = 0.74, 1.05, and 1.48, respectively. Although the actual physical properties of ring particles are poorly known, comparisons between the observations and dynamical studies suggest that it is likely they are underdense (e.g., Schmidt et al. 2009).
Figure 2. Dependence of rh on the distance from Saturn for the case of equal-sized particles and several values of particle internal density. Cases for ρ = 0.3–0.9 g cm−3 are shown with an interval of 0.1 g cm−3.
Download figure:
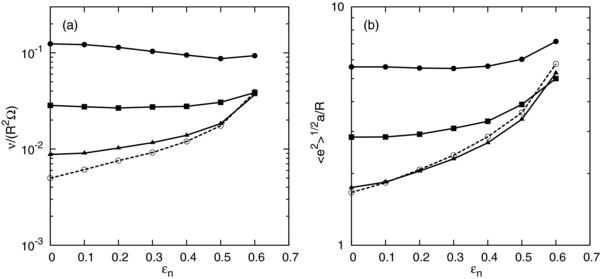
Standard image High-resolution imageFigure 3. (a) Dependence of viscosity on εn for rh = 0 (dashed line with open circles), 0.5 (triangles), 0.71 (squares), and 1 (solid circles) (τ = 0.01, εt = 1, N = 103). (b) Same as (a), but for random velocity.
Download figure:
Standard image High-resolution imageFigure 3 shows the dependence of viscosity and random velocity on εn for low optical depth rings (τ = 0.01) with four different values of rh, including the nongravitating case (rh = 0). Figure 3(b) confirms the dependence of random velocity on εn and rh (or the distance from the planet for a given density) obtained by previous studies (e.g., Salo 1995; Ohtsuki 1999). In the case of no or weak gravity, random velocity is determined by a mutual collision and the equilibrium random velocity increases with increasing εn, while the εn-dependence becomes weak in the case of larger rh, where gravitational encounters between particles become important. More importantly, the random velocity significantly increases with increasing rh, i.e., the increasing effect of gravitational encounters. The εn-dependence of viscosity shown in Figure 3(a) is similar to, but somewhat weaker than, that of random velocity. However, we find that the rh-dependence of the viscosity is similar to that of random velocity, indicating that viscosity in self-gravitating rings with low optical depth can be roughly expressed in terms of random velocity, as in the case of the dilute nongravitating rings discussed above.
Figure 4 shows the dependence of viscosity and random velocity on εt in self-gravitating rings with low optical depth. We also show the results for the nongravitating case (rh = 0) for comparison. The curves for the random velocity in the case of weak gravity (rh = 0.5) are very close to those for the nongravitating case. In these cases, energy dissipation due to surface friction is most effective at εt = 0; thus, the random velocity becomes the smallest at εt ≃ 0 (Morishima & Salo 2006). Then, the reduced radial excursion of particles results in the reduction of viscosity (Figure 4(a)), as mentioned above. The behavior in the case of rh = 0.71 is similar, although the εt-dependence of the viscosity seems rather weak. In the case of rh = 1, on the other hand, gravitational encounters between particles play a major role in determining random velocity. As a result, the random velocity becomes almost independent of εt. In this case, impact velocity also becomes nearly independent of εt, and energy dissipation at the collision is the largest when surface friction is the strongest, i.e., at εt ≃ 0. Therefore, the viscosity in the case of rh = 1 becomes larger when εt ≃ 0 by a factor of about two compared with the case of smooth particles (εt = 1). Here, we emphasize that both viscosity and random velocity increase with increasing rh and, if we neglect the above rather weak εt-dependence, viscosity in self-gravitating rings with low optical depth seems to be expressed in terms of random velocity (Section 5).
Figure 4. Scaled viscosity and random velocity as a function of εt obtained from N-body simulation (N = 103). Symbols represent the results for different values of rh; rh = 0 (open circles), 0.5 (triangles), 0.71 (squares), and 1 (solid circles), respectively. Each line type represents a corresponding combination of τ and εn used in the simulation; solid lines, dashed lines, and dot-dashed lines represent τ = 0.01 with εn = εn(v), τ = 0.01 with εn = 0.5, and τ = 0.05 with εn = 0.5, respectively.
Download figure:
Standard image High-resolution image4. VISCOSITY IN DENSE RINGS
Next, we examine the case of dense, self-gravitating rings. First, we show results for smooth particles to compare with cases with surface friction shown later. The solid line with marks in Figure 5(a) shows the plots of the viscosity obtained by our N-body simulation as a function of optical depth (rh = 0.82, εn = 0.5, εt = 1). In the case of low optical depth, viscosity is proportional to the optical depth, because angular momentum is transferred via successive binary collisions and gravitational encounters between particles, and the frequency of interactions is proportional to the particle surface number density. The coefficient of proportionality in the case of self-gravitating rings with low optical depth can be obtained from results of three-body orbital integration (Tanaka et al. 2003). In this case, equilibrium random velocity for given parameters (i.e., rh, εn, and εt) is first calculated by solving the velocity evolution equation with the velocity stirring rates obtained from the three-body orbital integration (Ohtsuki 1999). Then, we evaluate the coefficient for the viscosity for this equilibrium velocity by also using the results of the three-body orbital integration, and the result is shown in Figure 5(a) with the dotted line. We find that the results obtained by the two different methods perfectly agree with each other in the case of low optical depth. On the other hand, the results of N-body simulation deviate from the three-body results for τ ≳ 0.2. This is because the viscosity is dominated by the angular momentum transfer related to the gravitational torques exerted by the wake structures formed in such dense, self-gravitating rings (Figure 6; Daisaka et al. 2001).
Figure 5. (a) Scaled viscosity as a function of optical depth. Solid line represents results of N-body simulation, while the dotted line was drawn using a coefficient evaluated by the three-body orbital integration (i.e., ν/(R2Ω) = 4.44τ). In both cases, rh = 0.82 (corresponding to a = 1010 cm in Saturn's rings if ρ = 0.9 g cm−3), εn = 0.5, and εt = 1 are used. In the N-body simulations, N = 5000 for τ ⩽ 0.5, while N = 36, 000 is used for τ = 1 so that L/λcr ≃ 4. (b) Same as (a), but results of N-body simulation for four different combinations of εn and εt are shown. εn = 0.5 and εt = 1 (dashed line with circles); εn = 0.5 and εt = 0.5 (dot-dashed line); εn = 0.5 and εt = 0 (dotted line); and εn = εn(v) and εt = 0.5 (solid line). (c) Same as (b), but the viscosity values are scaled by those for the case of εn = 0.5 and εt = 1.
Download figure:
Standard image High-resolution imageFigure 6. Snapshots of the spatial distribution of particles for simulations with four different values of τ (rh = 0.82, εn = 0.5, εt = 1). Particle radius is 1 m, and the size of the simulation cell for the cases shown here is about 340 m. Note that, in our simulations, the size of the simulation cell is varied depending on τ and rh. Here (and in Figure 8) we show snapshots with a common size of the simulation cell to facilitate comparison between the panels.
Download figure:
Standard image High-resolution imageIn addition to the smooth particles case, we show the results of our N-body simulation for self-gravitating rings of particles with surface friction in Figure 5(b). We find that the overall behavior in the case with surface friction is similar to the case with smooth particles. Figure 5(b) shows the numerical results for four combinations of εn (0.5 or εn(v) given by Equation (3)) and εt(1, 0.5, or 0). Figure 5(c) is the same as Figure 5(b), but the viscosity values are scaled by those in the case of εn = 0.5 and εt = 1, to facilitate a comparison among the four cases. We note that the viscosity values change systematically when the restitution coefficients are varied. In dense rings where gravitational wakes are formed, the balance between gravitational heating by wakes and inelastic dissipation leads to a quasisteady state with Q ≃ 1–2, where Q is the Toomre parameter, and the dependence of the particle random velocity (thus their impact velocity) on elastic properties is rather weak (Salo 1995). In this case, the average energy dissipation rate is larger when the effect of the surface friction is stronger, resulting in somewhat larger viscosity values (Figures 5(b) and (c)). We also note that the slope of the curve for the case with εn(v) in Figure 5(b) becomes somewhat steeper at τ ≳ 0.2. This is because the increased impact velocities at a larger optical depth results in the increase in energy dissipation and viscosity in the case with the velocity-dependent restitution coefficient. Figure 5(c) shows that varying restitution coefficients can change the viscosity in dense self-gravitating rings by a factor of about two.
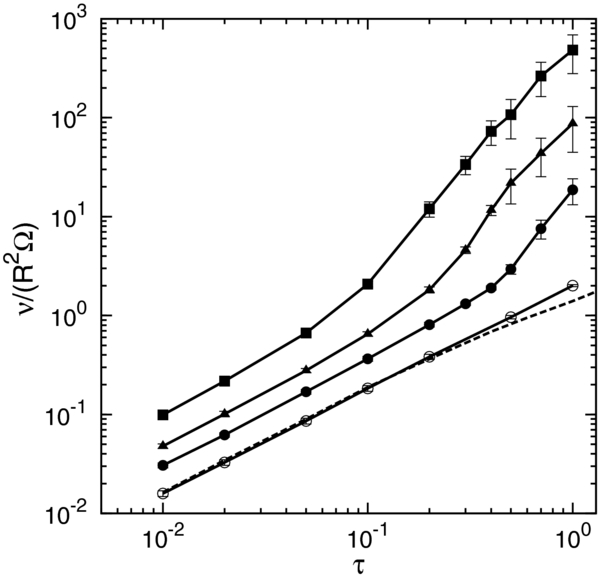
Figure 7 shows the τ-dependence of viscosity for various values of rh, including the nongravitating case (rh = 0; dashed line), with surface friction and the velocity-dependent εn. As in the case shown in Figure 5, viscosity in dilute rings is proportional to the optical depth, while it significantly increases at large τ in the case with self-gravity. We confirmed that Q takes on values smaller than 2–3 when viscosities begin to deviate from the linear τ-dependence. The deviation begins at τ ∼ 0.1 in the case of strong gravity (rh = 1). On the other hand, in the case of weak gravity (rh = 0.5), the deviation is very small and the viscosity values are close to those for the nongravitating case, even at τ ≃ 1. In this case of weak self-gravity, the tendency of wake formation is not strong, even at τ ≃ 1 (Figure 8). The wake structures for τ = 1 become notable with increasing rh; even temporary aggregates can form in the case of rh = 1.
Figure 7. Dependence of viscosity on τ for five values of rh (εn = εn(v), εt = 0.5). Solid lines with marks represent results of N-body simulation for rh = 0.5 (open circles), 0.71 (solid circles), 0.82 (triangles), and 1 (squares). Dashed line represents the nongravitating case (rh = 0). In these simulations, N = 5000 for cases of low optical depth, weak gravity (small rh), or both. The particle number is increased in the cases of dense rings with self-gravity, so that L/λcr ⩾ 4 is satisfied. For example, in the case of τ = 1, particle numbers are N = 5000, 15,000, 36,000, 115,800 for rh = 0.5, 0.71, 0.82, 1, respectively.
Download figure:
Standard image High-resolution imageFigure 8. Snapshots of the spatial distribution of particles in simulations for four different values of rh in the case of τ = 1 (εn = εn(v), εt = 0.5). Particle radius is 1 m, and the size of each panel shown here is about 450 m.
Download figure:
Standard image High-resolution imageThe τ-dependence of viscosity, often expressed in terms of β ≡ dln ν/dln τ, is related to the condition for the onset of viscous overstability in dense rings; Salo et al. (2001) found that β > βcr ∼ 1 as a rough condition for the onset of overstability. In the high-τ regime where viscosity is enhanced by the effect of self-gravity, the slope of the curves shown in Figure 7 seems to change with increasing optical depth. For example, in the case of rh = 0.82, viscosity increases more rapidly than the ν∝τ2 dependence (i.e., β > 2) when the effect of gravitational wakes becomes important at τ ≃ 0.2–0.3, then β ≃ 2 at τ ≃ 0.5–1. Similar behavior can be seen in the cases of rh = 0.71 and 1. Figure 14.8 (upper right panel) of Schmidt et al. (2009), drawn by Heikki Salo, shows the change of β in the case of rh = 0.82 in more detail, where β increases from 1 to about 3 as τ increases from 0.1 to 0.5, then decreases to about 2 as τ further increases to ∼1. In the range of parameters shown here and studied in other works (e.g., Daisaka et al. 2001; Schmidt et al. 2009), we find that 1 ≲ β ≲ 3 in self-gravitating dense rings, satisfying the condition for the onset of overstability. Simulations of dense rings for much longer periods with a larger simulation cell are necessary for a more detailed study of viscous overstability (Daisaka et al. 2001; Salo et al. 2001).
5. SEMIANALYTIC EXPRESSION
On the basis of our numerical results presented above, here we derive a semianalytic expression for viscosity in rings of equal-sized particles. As we discussed above, ring viscosity depends on various parameters. We have shown that varying restitution coefficients can change ring viscosity for a given τ and rh by a factor of about two. On the other hand, ring viscosity changes by orders of magnitude when τ, rh, or both are varied. In the following, we will use our numerical results in the case of εn = εn(v) and εt = 0.5 and derive semianalytic expressions that approximately reproduce the dependence of these results on τ and rh.
First, in the case of low optical depth, viscosity is determined by particle velocity dispersion c, as shown by Goldreich & Tremaine (1978) for nongravitating rings. We also discussed this in Section 3 for the case of self-gravitating rings. Viscosity in this case can be written as

where α is a constant. In optically thin rings, the velocity dispersion c can be written as (e.g., Salo 1995; Ohtsuki 1999)

depending on either inelastic collisions or gravitational encounters dominate particle velocity evolution. Substituting Equation (7) into Equation (6), viscosity in low optical depth rings can be expressed in terms of optical depth, distance from the planet, and particle internal density, as
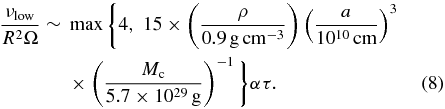
We find that α ∼ 0.35 from the comparison with our numerical results, which is roughly consistent with the nongravitating case (Goldreich & Tremaine 1978).
Next, we examine the case of high optical depth. From a dimensional analysis (see also Lynden-Bell & Kalnajs 1972; Ward & Cameron 1978), Daisaka et al. (2001) argued that the viscosity in dense rings is expected to be proportional to that of a self-gravitating disk,

with a correction factor C(rh), which depends on the relative importance of inelastic collisions to the self-gravity of a ring. In terms of τ and rh, Equation (9) can be rewritten as (Daisaka et al. 2001)

Daisaka et al. (2001) found C(rh) = 26r5h from a comparison with their numerical results.
Although our results of N-body simulations show that the dependence of the viscosity on optical depth is somewhat stronger than that given by Equation (9) (i.e., dln ν/dln τ > 2) when viscosity begins to deviate from the ν∝τ relation with increasing τ (Section 4), the τ-dependence of our numerical results for the high-τ cases is roughly consistent with Equation (9). Therefore, following Daisaka et al. (2001), we evaluate the correction factor  using our numerical results (Figure 9(a)). We find that a correction factor given by
using our numerical results (Figure 9(a)). We find that a correction factor given by

seems to well reproduce our numerical results for dense rings with gravitational wakes (i.e., rh ∼ 0.7–0.8 and τ ≳ 0.5). The fifth-power dependence of the correction factor on rh is consistent with Daisaka et al. (2001), but the numerical coefficient is a factor of about two larger than Daisaka et al. (2001). This is due to the difference in restitution coefficients adopted in these simulations. We used our numerical results for the case with εn = εn(v) and εt = 0.5, while Daisaka et al. (2001) derived their correction factor from their simulations with smooth particles with normal restitution coefficients independent of impact velocity. In fact, we confirmed that our numerical results as well as those obtained by Schmidt et al. (2009) for εn = 0.5 and εt = 1 are consistent with Daisaka et al. (2001; Figure 9(b)). As we discussed in Section 4, including surface friction as well as using the velocity-dependent normal restitution coefficient somewhat increases the viscosity values, which explains the above difference in the correction factor. Thus, it should be noted that our semianalytic expressions shown below include uncertainty of a factor of 2–3 due to uncertainty in elastic properties of ring particles.
Figure 9. Correction factor C ≡ ν/(G2Σ2/Ω3) as a function of rh. (a) Solid lines with symbols represent the results obtained from our N-body simulations (εn = εn(v), εt = 0.5) with τ =0.2 (crosses), 0.5 (triangles), 0.7 (circles), and 1 (squares). Dashed line represents the relation  , which agrees well with our numerical results for the case of the dense rings with gravitational wakes. Note that the tendency to form gravitational wakes is rather weak in the case of τ = 0.2; thus, the values of the correction factor in this case deviate from the line for the semianalytic expression even at rh = 0.8–1. (b) Comparison of our numerical result (circle) with the results obtained by Daisaka et al. (2001) (triangles) and Schmidt et al. (2009) (squares) for εn = 0.5 and εt = 1 with τ = 0.5. Dashed line is the same as the one shown in (a). Dot-dashed line represents the relation C = 26r5h obtained by Daisaka et al. (2001).
, which agrees well with our numerical results for the case of the dense rings with gravitational wakes. Note that the tendency to form gravitational wakes is rather weak in the case of τ = 0.2; thus, the values of the correction factor in this case deviate from the line for the semianalytic expression even at rh = 0.8–1. (b) Comparison of our numerical result (circle) with the results obtained by Daisaka et al. (2001) (triangles) and Schmidt et al. (2009) (squares) for εn = 0.5 and εt = 1 with τ = 0.5. Dashed line is the same as the one shown in (a). Dot-dashed line represents the relation C = 26r5h obtained by Daisaka et al. (2001).
Download figure:
Standard image High-resolution imageDaisaka et al. (2001) argued that the rh-dependence of the correction factor is related to "compressibility" of particle disks due to self-gravity. When rh is significantly smaller than unity (e.g., rh ∼ 0.5), collisions suppress the tendency of formation of gravitational wakes; thus, the enhancement of viscosity due to self-gravity is insignificant. This compressibility discussed in Daisaka et al. (2001) can be quantitatively demonstrated by calculating the physical optical depth τphys using a spatial distribution of particles obtained by N-body simulation; here, τphys is defined so that exp (− τphys) is the average fraction of skewers that penetrate the ring without piercing any particles (Figure 10; Wisdom & Tremaine 1988; Robbins et al. 2010). In the case of large τ and rh, we confirm significant reduction in τphys compared with the dynamical optical depth τ(= NπR2/L2); thus, there is a stronger tendency of particle clumping and wake formation, which results in a significant increase in viscosity.
Figure 10. Physical optical depth τphys as a function of dynamical optical depth τ(= NπR2/L2). τphys is calculated from snapshots of the spatial distribution of particles obtained by our N-body simulation (εn = εn(v), εt = 0.5). Results for various values of rh are shown; rh = 0.5 (open circles), 0.71 (solid circles), 0.82 (triangles), and 1 (squares), respectively. Nongravitating case (rh = 0) is also shown by the dashed line.
Download figure:
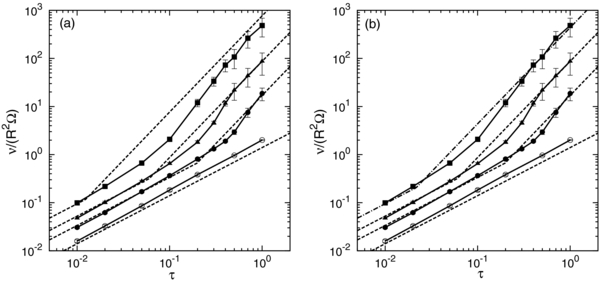
Standard image High-resolution imageFigure 11(a) shows the plots of our analytic results obtained by  (
(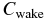 is given by Equation (11)) together with numerical results of our N-body simulation. We confirm excellent agreement in both low and high optical depth regimes for rh = 0.5–0.82, as expected. On the other hand, the above analytic expression significantly overestimates the numerical results for rh = 1, as can be predicted from the plots of the correction factor in Figure 9(a). In the cases of rh ≃ 1, the relatively large size of the Hill sphere compared with the particle physical size allows the formation of temporary aggregates rather than gravitational wakes (Salo 1995), as we mentioned above (Figure 8). Therefore, the above disagreement between the analytic result for the viscosity that is valid in the case of wake formation and the numerical results for rh ≃ 1 is not surprising; viscosity in rings with temporary aggregate formation, which likely corresponds to the outer A ring of Saturn, should be treated separately from the case of rings with gravitational wakes. Our numerical results show that the τ2-dependence suggested by Equation (9) also seems to be approximately valid in the case of rh = 1 and τ ≃ 1, but the correction factor should be separately determined. Since our numerical results for rh ≃ 1 suggest that the dependence of the correction factor on τ is rather weak (Figure 9(a)), here we adopt
is given by Equation (11)) together with numerical results of our N-body simulation. We confirm excellent agreement in both low and high optical depth regimes for rh = 0.5–0.82, as expected. On the other hand, the above analytic expression significantly overestimates the numerical results for rh = 1, as can be predicted from the plots of the correction factor in Figure 9(a). In the cases of rh ≃ 1, the relatively large size of the Hill sphere compared with the particle physical size allows the formation of temporary aggregates rather than gravitational wakes (Salo 1995), as we mentioned above (Figure 8). Therefore, the above disagreement between the analytic result for the viscosity that is valid in the case of wake formation and the numerical results for rh ≃ 1 is not surprising; viscosity in rings with temporary aggregate formation, which likely corresponds to the outer A ring of Saturn, should be treated separately from the case of rings with gravitational wakes. Our numerical results show that the τ2-dependence suggested by Equation (9) also seems to be approximately valid in the case of rh = 1 and τ ≃ 1, but the correction factor should be separately determined. Since our numerical results for rh ≃ 1 suggest that the dependence of the correction factor on τ is rather weak (Figure 9(a)), here we adopt

as a simple remedy for the correction factor in the case of temporary aggregate formation. Figure 11(b) shows a comparison between the results obtained from the revised semianalytic expression with our results of N-body simulation, where we find excellent agreement for the entire parameter regime examined here.
Figure 11. (a) Comparison of results obtained by our semianalytic expression (dashed lines) with the numerical results of our N-body simulation (solid lines) for εn = εn(v) and εt = 0.5. The four lines correspond to the cases with rh =0.5, 0.71, 0.82, and 1, as in Figure 7. For the semianalytic results shown here, we used 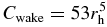 given by Equation (11) for all the values of rh. (b) Same as (a), but
given by Equation (11) for all the values of rh. (b) Same as (a), but 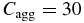 is used instead of
is used instead of 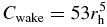 to obtain the semianalytic results for the case with rh = 1 (dot-dashed line).
to obtain the semianalytic results for the case with rh = 1 (dot-dashed line).
Download figure:
Standard image High-resolution imageIn summary, our numerical results can be well approximated by the following expression:

where νlow and 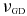 are given by Equations (8) and (9), respectively, and the correction factor is C = min {Cwake(rh), Cagg}, where Cwake(rh) and Cagg are given by Equations (11) and (12), respectively. Again, it should be noted that viscosity values obtained by the above expression include an uncertainty factor of about 2–3 due to uncertainty in the elastic properties of particles.
are given by Equations (8) and (9), respectively, and the correction factor is C = min {Cwake(rh), Cagg}, where Cwake(rh) and Cagg are given by Equations (11) and (12), respectively. Again, it should be noted that viscosity values obtained by the above expression include an uncertainty factor of about 2–3 due to uncertainty in the elastic properties of particles.
6. CONCLUSIONS AND DISCUSSION
In this work, using local N-body simulation, we examined viscosity in self-gravitating rings for a wide range of parameters. We calculated ring viscosity based on the formulation developed by Tanaka et al. (2003), in which viscosity is evaluated by calculating the average energy dissipation rate due to inelastic collisions in N-body simulation. We investigated the dependence of viscosity on various parameters in detail, including the effects of particle surface friction.
In the case of self-gravitating rings with low optical depth, we found that viscosity is determined by particle random velocity, as in the case of nongravitating rings with low optical depth. The effects of surface friction on viscosity were found to depend on the importance of the mutual gravity of the particles relative to collisions, which can be expressed in terms of the ratio of the mutual Hill radius of colliding particles to their physical size (rh). When the effects of gravitational encounters are unimportant (rh ∼ 0.5) and particle random velocity is determined by inelastic collisions, the inclusion of surface friction slightly reduces both random velocity and viscosity. On the other hand, when rh ∼ 1 and gravitational encounters do play a major role in particle velocity evolution, the inclusion of surface friction results in the increase of viscosity, since the viscous heating increases to balance the increased energy dissipation at collisions due to surface friction. We found that varying restitution coefficients can change the viscosity in dilute rings by a factor of about two.
On the other hand, viscosity is significantly enhanced in dense self-gravitating rings where gravitational wakes are formed (Daisaka et al. 2001). We found that viscosity in dense rings with a given τ and rh is larger when collisions are more dissipative, for example, by the inclusion of surface friction, and the enhancement of viscosity due to this effect can be a factor of about two. Following Daisaka et al. (2001), we assumed that the dependence of viscosity on the optical depth can be approximated by that for a self-gravitating disk (Equation (9)), so we evaluated a correction factor using our numerical results of N-body simulation. We found that the expression for the correction factor of the dense rings with gravitational wakes is similar to the one obtained by Daisaka et al. (2001); the difference of a factor two in the numerical coefficient can be explained by the difference in restitution coefficients that were adopted. On the other hand, in the case of the outer rings where temporary aggregates form due to self-gravity, the above expression overestimates the viscosity values; thus, we derived a revised expression for such a case. We confirmed that the semianalytic expressions we obtained reproduce our numerical results well for the entire range of parameters examined here.
The expression we obtained for the viscosity in the case with low optical depth is consistent with previous theoretical works for nongravitating rings (e.g., Goldreich & Tremaine 1978). However, the expressions for the viscosity (or the expression for the correction factor) for dense rings were empirically obtained by comparing numerical results. Although the strong rh-dependence of the viscosity in the case of the rings with gravitational wakes has been explained by ring compressibility (i.e., the degree of density contrast created as a result of the formation of gravitational wakes), more detailed theoretical modeling of viscosity in self-gravitating collisional disks would be useful for a better understanding of the dynamics in dense planetary rings.
This work was supported by the Japanese Society for Promotion of Science and NASA's Outer Planets Research Program and Planetary Geology and Geophysics Program. We thank Ryuji Morishima, Heikki Salo, Jürgen Schmidt, and Hidekazu Tanaka for their discussion and useful comments. A portion of the numerical simulations was performed using the GRAPE-7 system at the Center for Computational Astrophysics of the National Astronomical Observatory of Japan.
APPENDIX A: CHANGES IN PARTICLE VELOCITY AND ROTATION RATE DUE TO COLLISION
When two particles, i and j, collide with each other, the changes of their velocities and rotation rates are calculated as follows. We assume that ring particles are spheres, and we let the mass, radius, and spin angular velocity vector of particle j be given by mj, Rj, and ωj, respectively. Suppose that two particles, i and j, collide with each other with relative velocity of the centers of the two bodies in the rotating coordinate system, v, and that their relative position at impact is given by r. Let vn and vt denote the normal and the tangential component of v to the tangent plane, respectively. In this case, the normal and the tangential components of the relative velocity of the two contacting points at the time of impact can be written as (e.g., Araki & Tremaine 1986; Richardson 1994; Ohtsuki 2006a, 2006b)

where λ ≡ r/|r| is the unit vector pointing from the center of particle i to that of particle j, and Ω ≡ (0, 0, Ω) is the Keplerian angular velocity vector of the coordinate system. In the above equation, we used the relation r = (Ri + Rj)λ at impact. In terms of the normal and the tangential restitution coefficients, εn and εt, the normal and the tangential components of the relative velocity of the two contacting points after impact are given by Equation (2). From Equation (2) and the conservation of linear and angular momenta, the change of the normal and the tangential components of the relative velocity of the centers of the two spheres are given as
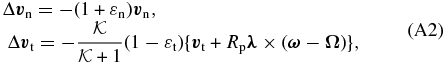
where Rp ≡ Ri + Rj, and

In the above, 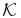 is the coefficient of the moment of inertia, e.g.,
is the coefficient of the moment of inertia, e.g.,  . In the present work, we set
. In the present work, we set  , assuming a homogeneous sphere. The change of spin angular velocity of particle j due to the collision is written as
, assuming a homogeneous sphere. The change of spin angular velocity of particle j due to the collision is written as

where μ is the reduced mass.
APPENDIX B: ENERGY DISSIPATION DUE TO AN INELASTIC COLLISION BETWEEN PARTICLES
When a local ring region is in a quasisteady state, its average viscosity can be calculated by summing up the amount of energy dissipated at collisions that occur in the region during a certain time interval (Equation (4)). Following Tanaka et al. (2003, their Equation (43)), we calculate the amount of energy dissipated at a collision between particles j and k as

In the above, μ = (1/mj + 1/mk)−1 (mj is the mass of particle j, and mj = m in the equal-sized case studied in the present work); h = (2m/3Mc)1/3; and  ,
, 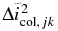 and
and 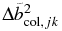 are the changes in the square of the scaled relative orbital elements
are the changes in the square of the scaled relative orbital elements 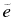 ,
, 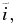 and
and 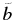 due to the collision, where
due to the collision, where 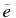 and
and  are the eccentricity and the inclination of the relative motion scaled by h (see Ohtsuki 1999), and
are the eccentricity and the inclination of the relative motion scaled by h (see Ohtsuki 1999), and  is the difference in the semimajor axes of the two particles scaled by ha0. Note that the effects of time variation of the total self-gravitational energy, random kinetic energy, or rotational energy of particles do not appear in Equation (B1) because we assume the region is in a quasisteady state.
is the difference in the semimajor axes of the two particles scaled by ha0. Note that the effects of time variation of the total self-gravitational energy, random kinetic energy, or rotational energy of particles do not appear in Equation (B1) because we assume the region is in a quasisteady state.