Abstract
The low-lying rotational bands of triaxially deformed nuclei 137Pr, 137Pm and 139Eu are studied with a modified particle-rotor model following the nonadiabatic quasiparticle approach. The matrix elements of the odd-A nucleus are obtained in terms of a coupling matrix and the rotational energies of the even–even core. The spectra of the cores 136Ce, 136Nd and 138Sm indicate a strong influence of triaxial deformation and vibrational degrees of freedom. These properties are appropriately carried forward to the calculations for the odd-A nucleus. We demonstrate that the ground and side bands of the odd-A nucleus and its core can be explained with the same set of deformation parameters (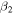 , γ). We argue that this method could be useful in studying the low-lying states in exotic nuclei also.
, γ). We argue that this method could be useful in studying the low-lying states in exotic nuclei also.
Export citation and abstract BibTeX RIS
1. Introduction
Nuclei in the mass region A = 136 and just below the shell closure N = 82 show several interesting phenomena related to their structure. The role of triaxial deformation is predicted to be strong in these nuclei through the calculation of potential energy surfaces with respect to the shape asymmetry parameter (γ) [1–3]. Their shape changes with increasing angular momentum through rotation alignment of high-j quasiparticle pairs [4]. Study of triaxial nuclei reveals unexpected characteristics in nuclei like chiral doublet [5], wobbling motion [6], signature inversion [7], exotic rotations involving sudden changes of the rotation axis [8, 9] etc. Microscopic models like the 3D relativistic Hartree–Bogoliubov model have predicted strong triaxiality in the ground states of even-A Pt isotopes and γ-softness in Sm nuclei [10]. In the present work, we analyze a few chosen nuclei (137Pr, 137Pm and 139Eu) with 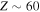 , which correspond to the transitional region [11]. In these nuclei, generally the valence protons occupy the lower half of the
, which correspond to the transitional region [11]. In these nuclei, generally the valence protons occupy the lower half of the 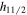 orbital (lean to collective prolate shape) and the valence neutrons occupy the upper half of the
orbital (lean to collective prolate shape) and the valence neutrons occupy the upper half of the  orbital (lean to collective oblate shape) [12, 13]. Such configurations drive these nuclei to be triaxial in shape or γ-soft. The macroscopic–microscopic calculations [14, 15] predict these nuclei to be moderately deformed. For such moderate deformations the
orbital (lean to collective oblate shape) [12, 13]. Such configurations drive these nuclei to be triaxial in shape or γ-soft. The macroscopic–microscopic calculations [14, 15] predict these nuclei to be moderately deformed. For such moderate deformations the 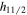 orbital is decoupled from the neighboring orbitals and hence leads to the formation of decoupled bands [16, 17] with
orbital is decoupled from the neighboring orbitals and hence leads to the formation of decoupled bands [16, 17] with  . Recently [18], we have formulated a modified particle-rotor model (MPRM) to study the ground and side bands of the triaxial odd-A nuclei. This model incorporates the measured energies of the rotor which are coupled to the particle states in a microscopic manner. This coupling requires eigen vectors of the triaxial rotor, which are calculated with a variable moment of inertia (VMI) approach including the vibrational degrees of freedom in a simple way. The following sections of this article comprise the outline of our formalism and highlights of our results obtained for 137Pr, 137Pm and 139Eu, followed by a succinct conclusion.
. Recently [18], we have formulated a modified particle-rotor model (MPRM) to study the ground and side bands of the triaxial odd-A nuclei. This model incorporates the measured energies of the rotor which are coupled to the particle states in a microscopic manner. This coupling requires eigen vectors of the triaxial rotor, which are calculated with a variable moment of inertia (VMI) approach including the vibrational degrees of freedom in a simple way. The following sections of this article comprise the outline of our formalism and highlights of our results obtained for 137Pr, 137Pm and 139Eu, followed by a succinct conclusion.
2. Formalism
The total Hamiltonian for an odd-A system is given by 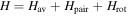 , where
, where 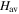 represents the mean field of the single-particles,
represents the mean field of the single-particles,  is the pairing interaction and
is the pairing interaction and 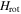 corresponds to the rotor (core). The total wave function can be written as
corresponds to the rotor (core). The total wave function can be written as
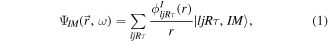
where 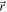 is the position of the valence particle with respect to the core and ω is the orientation of the core.
is the position of the valence particle with respect to the core and ω is the orientation of the core. 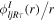 and
and 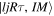 are the radial and angular parts of the wave function, respectively. The particle quantum numbers are given by usual notations l and j. The total angular momentum of the odd-A system is given by I with M and K being its projections on the z-axis (laboratory frame) and the third axis (body fixed frame), respectively. Similarly, we have the quantum numbers of the rotor as R, τ and KR, respectively.
are the radial and angular parts of the wave function, respectively. The particle quantum numbers are given by usual notations l and j. The total angular momentum of the odd-A system is given by I with M and K being its projections on the z-axis (laboratory frame) and the third axis (body fixed frame), respectively. Similarly, we have the quantum numbers of the rotor as R, τ and KR, respectively.
In terms of the rotor energies ETRi and eigen vectors 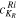 , the matrix elements of Hrot in the K representation can be written as [18, 19]
, the matrix elements of Hrot in the K representation can be written as [18, 19]
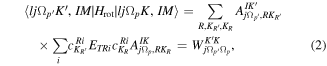
where the transformation amplitude
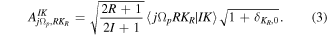
 is the projection of j on the third axis.
is the projection of j on the third axis. 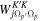 represents the coupling matrix, with the help of which, the matrix elements of the particle-plus-rotor system can be written in the K representation as
represents the coupling matrix, with the help of which, the matrix elements of the particle-plus-rotor system can be written in the K representation as
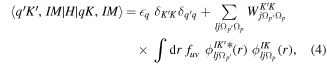
where q defines the single-particle state. 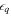 is the quasiparticle energy, which is calculated from the single-particle energy (eq) through the relation
is the quasiparticle energy, which is calculated from the single-particle energy (eq) through the relation 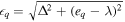 . As
. As 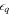 is with reference to the chemical potential, the yrast states naturally come out as lowest in energy [20]. We consider the pairing interaction through the BCS approach with a frozen gap
is with reference to the chemical potential, the yrast states naturally come out as lowest in energy [20]. We consider the pairing interaction through the BCS approach with a frozen gap 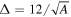 MeV. The chemical potential λ is calculated by imposing the particle number conservation. In the BCS approach, the occupation (Vq) and un-occupation (Uq) probabilities are given by
MeV. The chemical potential λ is calculated by imposing the particle number conservation. In the BCS approach, the occupation (Vq) and un-occupation (Uq) probabilities are given by ![${V}_{q}^{2}=\tfrac{1}{2}[1-({e}_{q}-\lambda )/{\epsilon }_{q}]$](https://content.cld.iop.org/journals/1402-4896/92/9/094002/revision1/psaa81ecieqn21.gif) and
and  . The matrix elements between the particle states to the quasiparticle states are transformed through the factor
. The matrix elements between the particle states to the quasiparticle states are transformed through the factor  . The single-particle wave function in the intrinsic frame is given by
. The single-particle wave function in the intrinsic frame is given by 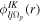 . The single-particle energies and wave functions are calculated by diagonalizing Hav, which consists of the Woods–Saxon potential along with the Coulomb and the spin–orbit potential for triaxial nucleus. We utilize the universal set of parameters [21] for the mean field potential.
. The single-particle energies and wave functions are calculated by diagonalizing Hav, which consists of the Woods–Saxon potential along with the Coulomb and the spin–orbit potential for triaxial nucleus. We utilize the universal set of parameters [21] for the mean field potential.
The rotor energies ETRi correspond to the measured energies. For missing data and eigen vectors 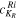 , we employ a VMI approach defined by the Hamiltonian [22, 23]
, we employ a VMI approach defined by the Hamiltonian [22, 23]
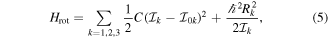
where C is the restoring force constant related to the vibrational degrees of freedom. The vibrations are with respect to the quadrupole and triaxial shape degrees of freedom which are represented by the parameters  and γ, respectively.
and γ, respectively. 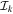 and Rk are the moments of inertia and total angular momenta of the rotor in three directions, respectively.
and Rk are the moments of inertia and total angular momenta of the rotor in three directions, respectively. 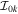 are the ground state moments of inertia and related to the deformation parameter γ through the relation
are the ground state moments of inertia and related to the deformation parameter γ through the relation
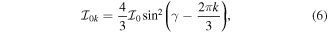
where 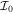 is the VMI parameter. Here the total energy of the rotor ETRi is calculated using method 2 for triaxial rotor, as in [18], by diagonalizing the Hamiltonian Hrot (5),
is the VMI parameter. Here the total energy of the rotor ETRi is calculated using method 2 for triaxial rotor, as in [18], by diagonalizing the Hamiltonian Hrot (5),
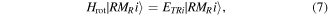
with the wave function
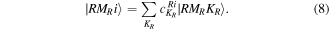
The different eigenstates for a given value of R are labeled by i with coefficient 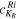 specifying the contribution of each KR. Here the two VMI parameters C and
specifying the contribution of each KR. Here the two VMI parameters C and 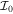 can be calculated by fitting the rotor energies ETRi with the experimental energies [18, 19].
can be calculated by fitting the rotor energies ETRi with the experimental energies [18, 19].
The rotational spectra of even–even nuclei can be understood in a microscopic way also, e.g. through the algebraic collective model [24]. A direct comparison between microscopic models and our collective model is not attempted here. In the present work, we focus on the collective model (to explain even–even nuclei) which is reliable to work in the framework of rotation-particle coupling for the odd-A nuclei.
3. Results and discussions
In this work, we analyze the rotational spectra of the nuclei 137Pr, 137Pm and 139Eu which are predicted as triaxial according to macroscopic–microscopic calculations [15] with 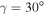 ,
, 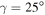 and
and 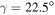 , respectively. The corresponding cores 136Ce, 136Nd and 138Sm [10], are also predicted as triaxially deformed [15] with
, respectively. The corresponding cores 136Ce, 136Nd and 138Sm [10], are also predicted as triaxially deformed [15] with 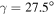 ,
,  and
and 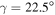 , respectively. These nuclei are near the β-stability region, and hence we have enough experimental data to compare with our calculated results. In our calculations, we vary the deformation parameters
, respectively. These nuclei are near the β-stability region, and hence we have enough experimental data to compare with our calculated results. In our calculations, we vary the deformation parameters 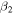 and γ such that best fit is achieved for both the odd-A nucleus and its core. In figure 1, the ground and γ bands are shown for the cores. We can identify that for all these nuclei the ground band is decoupled with
and γ such that best fit is achieved for both the odd-A nucleus and its core. In figure 1, the ground and γ bands are shown for the cores. We can identify that for all these nuclei the ground band is decoupled with  . In our calculations for the core, the quadrupole deformation parameter
. In our calculations for the core, the quadrupole deformation parameter 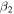 does not appear explicitly as the information is contained in the spectrum. In the axially symmetric case, one can obtain a relation between
does not appear explicitly as the information is contained in the spectrum. In the axially symmetric case, one can obtain a relation between  and the energy of
and the energy of  state through the Grodzins formula [33]. The γ band is very sensitive to γ deformation [23], which enables us to unambiguously fix γ by considering it as a parameter in the fit along with the VMI parameters C and
state through the Grodzins formula [33]. The γ band is very sensitive to γ deformation [23], which enables us to unambiguously fix γ by considering it as a parameter in the fit along with the VMI parameters C and 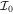 . Only a small variation of γ near this fitted value is required to have a better fit for the spectrum of the corresponding odd-A nucleus. As evident from figure 1, the calculated spectra for the ground band agrees well with the data and the γ band is reasonably reproduced. The placement of the γ band with respect to the ground band, i.e. energy difference between
. Only a small variation of γ near this fitted value is required to have a better fit for the spectrum of the corresponding odd-A nucleus. As evident from figure 1, the calculated spectra for the ground band agrees well with the data and the γ band is reasonably reproduced. The placement of the γ band with respect to the ground band, i.e. energy difference between 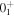 and
and 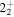 , is well reproduced in our calculations. A common feature of the γ band is that
, is well reproduced in our calculations. A common feature of the γ band is that 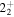 and
and 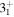 lie closer and similarly the levels
lie closer and similarly the levels 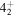 and
and  lie closer contrary to the experimental feature where
lie closer contrary to the experimental feature where 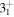 and
and 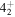 lie closer. This feature is inherent to the rigid triaxial rotor which is not affected by incorporating VMI. The discrepancy with data in this regard could be attributed to several effects like the mixing of γ band with the two quasiparticle states or other higher vibrational bands, which are neglected in this work. The softness with regard to vibration of the nucleus is proportional to
lie closer. This feature is inherent to the rigid triaxial rotor which is not affected by incorporating VMI. The discrepancy with data in this regard could be attributed to several effects like the mixing of γ band with the two quasiparticle states or other higher vibrational bands, which are neglected in this work. The softness with regard to vibration of the nucleus is proportional to 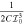 [22, 23]. The resulted values of C and
[22, 23]. The resulted values of C and 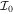 indicate that these nuclei are soft and hence the spectra are quite influenced by the vibration also, as they show a large deviation from the rigid rotor spectrum.
indicate that these nuclei are soft and hence the spectra are quite influenced by the vibration also, as they show a large deviation from the rigid rotor spectrum.
Figure 1. Rotational spectra of rotors 136Ce, 136Nd and 138Sm for the ground (g) and γ bands. The g band contains only positive parity even angular momentum states, while the γ band contains both even and odd angular momentum states with positive parity. Gray lines correspond to the experimental spectra [25–28] which are used in the fit. The solid black lines represent our calculations with best fitting values of γ and VMI parameters C and 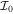 .
.
Download figure:
Standard image High-resolution imageIn figure 2, we present the spectra of 137Pr, 137Pm and 139Eu. These calculations involve the single-particle energies and wavefunctions which are calculated in a triaxially deformed mean field and hence require the explicit values of the deformation parameters 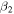 and γ. The γ values are constrained by the γ band in the rotor and for the nuclei 137Pr, 137Pm and 139Eu, the deformation parameters (
and γ. The γ values are constrained by the γ band in the rotor and for the nuclei 137Pr, 137Pm and 139Eu, the deformation parameters (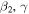 ) turn out to be (0.12, 24°), (0.23, 25°) and (0.19, 25°), respectively. These values are compatible with the macroscopic–microscopic calculations which yield (0.12, 30°), (0.19, 25°) and (0.21,
) turn out to be (0.12, 24°), (0.23, 25°) and (0.19, 25°), respectively. These values are compatible with the macroscopic–microscopic calculations which yield (0.12, 30°), (0.19, 25°) and (0.21,  ), respectively. We have considered the hexadecapole deformations (
), respectively. We have considered the hexadecapole deformations ( ) also, with a constraint between
) also, with a constraint between 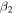 and
and 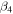 satisfying the values given in [14]. The positive and negative parity bands, for 137Pr are shown in figure 2(a) with the band built on the
satisfying the values given in [14]. The positive and negative parity bands, for 137Pr are shown in figure 2(a) with the band built on the 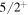 state being the ground band. From the analysis of the corresponding wave functions we find that these bands have the configurations
state being the ground band. From the analysis of the corresponding wave functions we find that these bands have the configurations 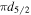 and
and  , respectively [29]. In case of the negative parity it is well known that all the quasiparticle states originating from
, respectively [29]. In case of the negative parity it is well known that all the quasiparticle states originating from  orbital will mix strongly through Coriolis interaction [16]. Similarly, we see a strong Coriolis mixing of quasiparticle states in the positive parity also. Hence it is difficult to point out a particular quasiparticle (Nilsson) state on which the band is built on. These bands having different configurations (and opposite in parity) ensure that we cannot obtain the energy difference between these two band-heads. These bands are presented in figure 2(a) with reference to their individual band-heads. In case of 137Pm (figure 2(b)), both the ground and side bands have the same configuration
orbital will mix strongly through Coriolis interaction [16]. Similarly, we see a strong Coriolis mixing of quasiparticle states in the positive parity also. Hence it is difficult to point out a particular quasiparticle (Nilsson) state on which the band is built on. These bands having different configurations (and opposite in parity) ensure that we cannot obtain the energy difference between these two band-heads. These bands are presented in figure 2(a) with reference to their individual band-heads. In case of 137Pm (figure 2(b)), both the ground and side bands have the same configuration 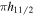 and hence we get the correct relative placement of these bands. We have presented the energies of ground band of 137Pm up to the angular momentum
and hence we get the correct relative placement of these bands. We have presented the energies of ground band of 137Pm up to the angular momentum 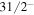 , whereafter the configuration changes to that of three quasiparticles [30] which is beyond the scope of the present work. This is a decoupled band and hence its energies are not sensitive to the
, whereafter the configuration changes to that of three quasiparticles [30] which is beyond the scope of the present work. This is a decoupled band and hence its energies are not sensitive to the 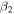 deformation. However, the side band is sensitive to
deformation. However, the side band is sensitive to 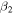 , and hence enables us to have an unambiguous fit. The spectra of ground and side bands for 139Eu are shown in figure 2(c). In this case also, both the bands have the same configuration
, and hence enables us to have an unambiguous fit. The spectra of ground and side bands for 139Eu are shown in figure 2(c). In this case also, both the bands have the same configuration 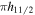 and hence we get the right placement of the side band.
and hence we get the right placement of the side band.
Figure 2. Rotational spectra of 137Pr, 137Pm and 139Eu for the ground (g) and side bands. Gray lines correspond to the experimental spectra [29–32]. The solid black lines represent results of our calculations.
Download figure:
Standard image High-resolution image4. Conclusion
We present MPRM with nonadiabatic quasiparticle approach for triaxially deformed nuclei. The rotation-particle coupling is carried out by expressing the matrix elements of the odd-A nucleus in terms of the measured energies of the rotor. We consider that the odd-A system and its core have the same deformation. We could successfully explain the ground and side bands in the nuclei 137Pr, 137Pm and 139Eu and their corresponding cores 136Ce, 136Nd and 138Sm. In the cases of 137Pm and 139Eu, we obtain the relative energy difference between two bands arising from the same configuration. This aspect could be very useful in studying low-lying states in exotic nuclei where the data is scarce. It will be interesting to utilize the wave functions resulting from this approach to calculate the decay widths of particle emission from the low-lying states of triaxial nuclei [34, 35].
Acknowledgments
This work is supported by the Council of Scientific and Industrial Research, Government of India, via project no. 03(1338)/15/EMR-II.




