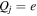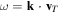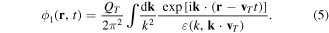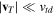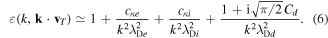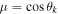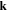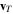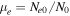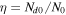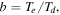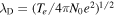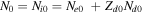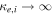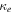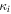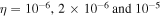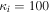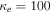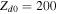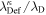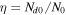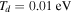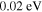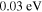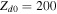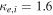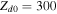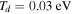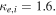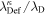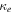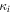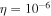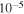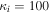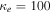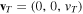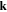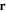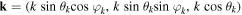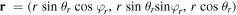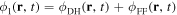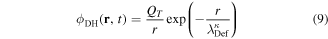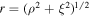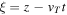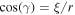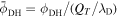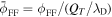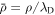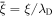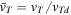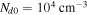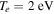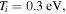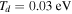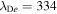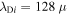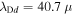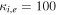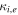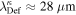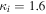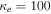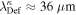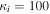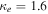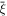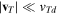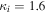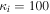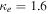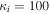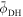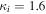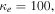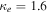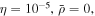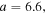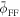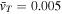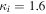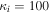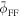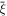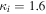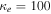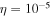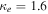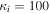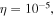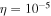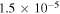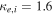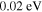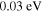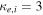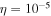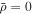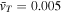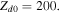Abstract
The electrostatic potential around a slowly moving test charge is studied in a dusty plasma where the ions and electrons follow a powerlaw Kappa distribution in velocity space. A test charge moving with a speed much smaller than the dust thermal speed gives rise to a short-scale Debye–Hückel potential as well as a long-range far-field potential decreasing as inverse cube of the distance to the test charge along the propagation direction. The potentials are significantly modified in the presence of high-energy tails, modeled by lower spectral indices in the ion and electron Kappa distribution functions. Plasma parameters relevant to laboratory dusty plasmas are discussed.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Fluid and kinetic models are two common approaches to study waves and instabilities in plasma [1, 2]. Test charge techniques [3–6] are often utilized for studying shielding phenomena such as electrostatic potential and energy loss caused by a moving test charge in plasma. In this technique, a test charge with a given charge and velocity is externally inserted into the plasma and its charge is coupled with the plasma charge density through the space charge effects, leading to the shielding of the charge by a cloud of opposite charges in the plasma. Problems involving shielded electrostatic potentials around charged particles and energy loss of particles moving in plasma occur in many different areas of physics, such as particle acceleration [7, 8], the formation of new materials in low-temperature dusty plasma [9–11], heating and ignition in inertial confinement fusion [12–16], heavy ion energy deposition in dense plasma [17], and the interaction of ion clusters with condensed matter [18–21].
Taking into account moving and stationary test charges, a far-field (FF) potential distribution depending as the inverse third power of the distance to the test charge was found around a test charge in a Maxwellian plasma of dynamical electrons with static ions [4]. Later, the effects of ionic motions [22, 23], collisions [24–26] and turbulence [27, 28] were taken into account. A kinetic description was used to study the electrostatic potential around a test charge with low and high velocities [29, 30], revealing the excitation of long-range wakefields in a Maxwellian plasma. The effects of magnetic field, collisions and plasma density gradients have also been studied for slowly and rapidly moving test charges [31–33]. The Debye shielding has been studied in a dusty plasma with Boltzmann distributed electrons and ions in the presence of static negatively charged dust grains [34], taking into account both small and finite amplitude potential distributions. Collisions, Landau damping, and dust-charge perturbation effects on the dipole-like FF potential have been taken into account for a slow test charge in a Maxwellian dusty plasma [35, 36]. Oscillatory wake-field, Debye–Hückel (DH) and FF potentials caused by a test charge in a colloidal Maxwellian plasma in the presence of streaming ions and dust grains have also been studied theoretically [37] and numerically [38]. Recently, the shielding of two slow co-moving teset charges in collisional plasma has also been studied theoretically [39].
There is a growing interest in studying non-Maxwellian power-law distributions involving superthermal particles, accelerated by wave-particle interactions and turbulence. It has opened up new research avenues for researchers to model plasma collective interactions and instabilities in astrophysical environments [40]. Suprathermal electrons often occur in plasmas where modulational instabilities and Langmuir turbulence take place [41], such as beam-plasma interactions [42], in the solar wind where type III solar radio emissions occurs [43], intense microwave-plasma interactions [44] and ionospheric heating experiments [45, 46]. Superthermal energetic tails in the velocity distribution function of particle species s (s = e for electrons and i for ions) can be modeled by a three-dimensional Kappa distribution function [47] with normalization constant . Here Ns0 and is the equilibrium density and effective thermal speed, respectively. The Kappa distribution is valid for . The temperature is denoted by Ts and the mass by ms. The Kappa distribution function tends to a Maxwellian distribution function, in the limit . Vasyliunas [47] first pointed out the relevance of the Kappa distribution function by fitting empirical data from the solar wind to show its importance for low spectral index κ ∼ 2–4. After that, the investigation of several dispersive modes and instabilities have been carried out for power-law Kappa-distributed plasmas [48–51]. Recently, the potential around a slowly moving test charge in a Kappa-distributed plasma was studied [52] using a Vlasov model, containing supra-thermal hot and cold electrons with immobile ions. It was shown that the short-range DH potential decreases as an exponential decay of the distance and long-range FF potential as the inverse cube of the distance from the test charge.
In this paper, we present a theory for the potential distributions around a slowly moving test charge in an unmagnetized dusty plasma having supra-thermal electrons and ions, as well as negatively charged dynamical dust grains.
2. Vlasov–Poisson model
The electrostatic potential due to a moving test charge in a collisionless dusty plasma is in the small-amplitude limit governed by the linearized Vlasov–Poisson system
where QT is the charge of the test particle and δ is Dirac's delta function representing the test charge located at . We have used the equilibrium charge-neutrality condition , where Nj0 is the particle number density of the jth species (j = e for electrons, i for positive ions, and d for the negatively charged dust grains), and Zd0 is the equilibrium dust charge state. We assume that all dust grains are spherical in shape with radius r d and mass m d. The linearized electron and ion density fluctuations and are, respectively, obtained in the limits and for Kappa-distributed inertialess electrons and ions with temperatures Te and Ti. Furthermore, the perturbation of the dust distribution function is assumed to be much smaller compared to the equilibrium Maxwellian distribution, , where is the dust thermal speed and T d the dust temperature. Note that the effects of suprathermal tails are accounted for through the parameters , where in the Maxwellian limits . The shielded test charge QT gives rise to the screened potential , which depends on its speed in comparison with the thermal speeds.
3. Dielectric response to a test charge
Applying the space-time Fourier transform to equations (1) and (2), we obtain
Here ω and are the angular frequency and wave vector, is the Fourier transformed potential,
is the plasma dielectric constant, the plasma dispersion function [53], and . Here stands for the Debye length of jth species, where the charge for the electrons, for the ions, and for the dust grains. Setting describes the dispersion relation of plane dust acoustic waves.
Taking the inverse Fourier transform of equation (3) gives , and the potential is obtained as [2, 54]
The dielectric constant can in the limit be simplified as
In equation (6), we have made an expansion of function in the limit , with , to account for a slowly moving test charge, ignoring the higher order terms. Note that the plasma response function, and in turn the test charge distribution, are modified by the dust Landau damping term [4] proportional to C d in right-hand side of equation (6). For , the dust Landau damping vanishes, and the shielded test charge gives rise to the standard DH potential [52, 55–57].
Taking the inverse of equation (6) in the limit we obtain
with the angle between the vectors and . The effective Debye length, modified by the superthermal electrons and ions, is given by
where and are the normalized electron and dust concentrations, respectively. The temperature ratios are denoted by and while we denoted and . In the Maxwellian limit , equation (8) exactly coincides with previous results [34] in the limit of static dust grains. Figure 1 displays the impact of the dust temperature and charge state on the normalized effective Debye length given by equation (8). Since all plasma species participate in the shielding process when the test charge is moving slowly, the effective shielding length is also influenced by the dust temperature and charge state. We note that the effective shielding length is reduced in a dusty plasma compared to an electron–ion plasma due to the cold dust population shielding the test charge. Figure 2 exhibits how the normalized effective Debye length varies as function of the electron and ion spectral indices and for different values of dust concentration , in figures 2(a)–(c) having and in figures 2(d)–(f) with . Other parameters are taken as a = 6.6, b = 66.6 and . Consistent with previous results [60], the effective Debye length is smaller for smaller values of the spectral indices.
Figure 1. The normalized effective Debye length () given by equation (8) against the dust concentration for (a) the dust temperatures (black dotted curve), (blue dashed curve) and (red solid curve), with fixed values of and , (b) the dust charge states (black dotted curve), 600 (blue dashed curve) and 1000 (red solid curve), with and
Download figure:
Standard image High-resolution imageFigure 2. The normalized effective Debye length as a function of the electron and ion spectral indices and for the normalized dust concentrations , 2 × 10−6, and , respectively, in panels (a)–(c) with and panels (d)–(f) with . Other parameters are fixed as b = 66.6 and .
Download figure:
Standard image High-resolution image4. Profiles of the DH and FF potentials
Choosing a coordinate system in which the test charge is moving in the z-direction, , the vectors and can be expressed into the spherical polar coordinates as and , allowing us to write the total electrostatic potential (5) as the sum of DH and FF potentials as with
and
Equation (9) describes the short-range DH potential, accounting for small distances between the test charge and the observer, and equation (10) the long-range FF potential derived in the limit , which to leading order decays as the inverse cube of the distance to the test charge. Here is the distance from a test charge to observer with radial position ρ and axial position . When the spectral indices the superthermailty parameters approach unity, and the modified effective shielding length tends to the effective shielding length for a Maxwellian plasma, . Consequently, equations (8) and (9) are consistent with the results of [35, 36] (with ), who also considered the effects of collisions and dust charge fluctuations on the FF potential.
As a numerical illustration, we have normalized equations (8)–(10) using , , , with and chosen typical values from laboratory [58, 59], as , , , , and . This gives the electron Debye length μm, the ion Debye length m, and the dust Debye length m. Consequently, the effective Debye length for . Significant effects due to superthermal tails in the electron and ion distribution functions appear only at low values of , leading to a reduction of the effective Debye length for and , and for and . In figure 3, the profiles of the short-range DH potential due to a slowly moving test charge QT are shown as a function of the axial distance . Since the test charge moves with a very slow speed , it is shielded by all the plasma species, contributing to an effective shielding length In figure 3(a), small ion spectral indices, and 2, lead to a visible reduction of the DH potentials in comparison to the Maxwellian case . On the other hand, the electron spectral index , 2, and 100 with a fixed give a relatively small impact on the DH potentials (see figure 3(b)). This is expected, since the shielding is primarily due to the colder species (ions and dust), while the hot electrons do not significantly participate in the DH shielding.
Figure 3. The normalized DH potential as a function of normalized axial distance for changing (a) the ion spectral index, (black dotted curve), 2 (blue dashed curve), and 100 (red solid curve) with (b) the electron spectral index (black dotted curve), 2 (blue dashed curve), and 100 (red solid curve) with Other parameters are fixed as b = 66.6 and .
Download figure:
Standard image High-resolution imageFigure 4 exhibits how supra-thermal tails of the ions and electrons, as well as the dust concentration and temperature, affect the FF potential for a test charge speed . The shielding FF potential is more localized for smaller ion spectral indices and 2 compared to the near-Maxwellian case (see figure 4(a)), and the shielding is also more efficient for lower values of the dust temperatures (figure 4(d)). The values of the electron spectral index and the dust concentration have only minor effects on the FF shielding potential in figures 4(b) and (c).
Figure 4. The normalized FF potential against the normalized axial distance for different values of (a) (black dotted curve), 2 (blue dashed curve), and 100 (red solid curve) with and , (b) (black dotted curve), 2 (blue dashed curve), and 100 (red solid curve) at and (c) dust concentration (black dotted curve), (blue dashed curve), and 2 × 10−5 (red solid curve), for , and (d) dust temperature (black dotted curve), (blue dashed curve), and (red solid curve), for and . Other fixed parameters are , a = 6.6, b = 66.6, , and
Download figure:
Standard image High-resolution image5. Summary
To summarize, we have presented slow response of a moving test charge in a non-Maxwellian dusty plasma, whose constituents are supra-thermal and inertialess electrons and ions in the presence of Maxwell-distributed inertial dust grains. For this purpose, linearized Vlasov equation for the dust, coupled with the electron and ion density responses and Poisson's equation for the potential are solved with a Fourier transform technique to obtain the modified electrostatic potential modified by the supra-thermal tails of the ions and electrons. When the test charge moves with a constant speed, slowly in comparison with the dust thermal speed, it gives rise to a shielded potential that can be decomposed into a short-range DH and long-range FF potential. The variation of FF potential is to leading order proportional to the inverse cube of the distance to the test charge. Both the DH and FF shielding potentials are more localized (i.e. more efficient shielding) for smaller spectral indices. For large spectral indices, the DH and FF potentials approach the Maxwellian case.
Acknowledgments
It is our pleasure to dedicate this article to Professor Hans L Pécseli on the occasion of his 70th birthday. S Ali acknowledges the support from the Abdus Salam International Centre for Theoretical Physics (AS-ICTP) for his visit under the Regular Associateship Scheme. BE acknowledges the support from the EPSRC (UK), grant no. EP/M009386/1.



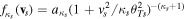
![${a}_{{\kappa }_{s}}={N}_{s0}{\pi }^{-3/2}{\rm{\Gamma }}({\kappa }_{s}+1)/[\sqrt{{\kappa }_{s}}{\theta }_{{Ts}}^{3}{\rm{\Gamma }}({\kappa }_{s}-1/2)]$](https://content.cld.iop.org/journals/1402-4896/92/8/084003/revision1/psaa7c09ieqn2.gif)
![${\theta }_{{Ts}}={[2{T}_{s}({\kappa }_{s}-3/2)/({\kappa }_{s}{m}_{s})]}^{1/2}$](https://content.cld.iop.org/journals/1402-4896/92/8/084003/revision1/psaa7c09ieqn3.gif)
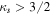
![${f}_{{\kappa }_{s}}({{\bf{v}}}_{s})\to {f}_{{M}_{s}}({{\bf{v}}}_{s})={[{m}_{s}/(2\pi {T}_{s})]}^{3/2}\exp [-{m}_{s}{v}_{s}^{2}/(2{T}_{s})]$](https://content.cld.iop.org/journals/1402-4896/92/8/084003/revision1/psaa7c09ieqn5.gif)
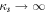
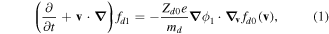

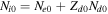
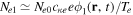

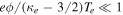


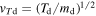
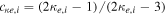
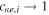
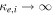
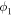
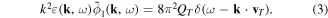
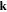
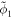
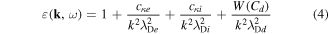
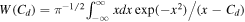

![${\lambda }_{{\rm{D}}{j}}={[{T}_{j}/(4\pi {N}_{j0}{Q}_{j}^{2})]}^{1/2}$](https://content.cld.iop.org/journals/1402-4896/92/8/084003/revision1/psaa7c09ieqn23.gif)