Abstract
We suggest and demonstrate a new protocol based on correlated beams of light: the 'optical illusionist game'. An 'illusionist' at first shows that if two uncorrelated light beams excited in the same Gaussian state are mixed in a beam splitter, then no correlations arise between them, as it was not present. On the other hand, when correlations with an ancillary state are exploited, the presence of the beam splitter can be unveiled.
Export citation and abstract BibTeX RIS
1. Introduction
Gaussian states, i.e. states with Gaussian Wigner functions (e.g. coherent, thermal and squeezed states), play a crucial role in developing quantum technologies [1–21] and in quantum optics.
They possess the interesting property of being generated through linear and bilinear interactions feasible in quantum optics laboratories and, remarkably, led to the realization of the first quantum protocols, such as continuous variable quantum teleportation [22]. Furthermore, in order to optimize the generation of entanglement and to preserve it during propagation through realistic channels, very recently interest has emerged in analyzing the effects of linear optical elements on the correlations of Gaussian states [22–29].
In this paper, we address the general question of the invariance of two uncorrelated Gaussian states, irrespective of whether classical (e.g. thermal) or quantum (e.g. squeezed vacuum), mixed at a beam splitter (BS); in particular, we demonstrate that, even when they are left unchanged, as when the BS is not present, one can distinguish between the two situations when a third ancillary state is included. In the following, we present this physical phenomenon as a fancy game.
2. The illusionist game: theory
An illusionist displays on the stage an amazing game involving two light beams, a beam splitter (BSI) and two photodetectors able to measure the correlations between the beams. He specifies that he will use only Gaussian states of light with zero first moments. The illusionist starts his performance by crossing two uncorrelated beams of light excited in the same Gaussian state and showing, as one may expect, that no correlations arise between them (figure 1(a)). Then, he inserts BSI and shows that the counters continue to reveal zero correlations (figure 1(b)). This effect is a consequence of the linear interaction of modes performed by the BSI and the Gaussian nature of the states [18, 19]. In fact, the most general single-mode Gaussian state can be written as ϱ = D(α)S(ξ)νth(N)S†(ξ)D†(α), where  is a thermal equilibrium state with N average number of quanta,
is a thermal equilibrium state with N average number of quanta, ![$S(r) = \exp \{\frac 12 [\xi (\skew3\hat {a}^{\dagger })^2-\xi ^* \skew3\hat {a}^2]\}$](https://content.cld.iop.org/journals/1402-4896/2013/T153/014006/revision1/pscr454554ieqn2.gif) and
and ![$D(\alpha ) = \exp [ \alpha \skew3\hat {a}^{\dagger } - \alpha ^*\skew3\hat {a}]$](https://content.cld.iop.org/journals/1402-4896/2013/T153/014006/revision1/pscr454554ieqn3.gif) are the squeezing and the displacement operators, respectively, a being the annihilation operator. The state ϱ is fully characterized by its 2 × 2 covariance matrix (CM)
are the squeezing and the displacement operators, respectively, a being the annihilation operator. The state ϱ is fully characterized by its 2 × 2 covariance matrix (CM)  ,
, ![$[\boldsymbol {\sigma }]_{hk}=\frac 12\langle R_hR_k + R_kR_h \rangle - \langle R_h\rangle \langle R_k \rangle $](https://content.cld.iop.org/journals/1402-4896/2013/T153/014006/revision1/pscr454554ieqn5.gif) , k = 1,2, and first moment vector
, k = 1,2, and first moment vector ![$\overline {\boldsymbol {X}}^{\mathrm {T}} = \langle \boldsymbol {R}^{\mathrm {T}} \rangle = \sqrt {2}(\Re {\mathrm { e}}[\alpha ],\Im {\rm m}[\alpha ])$](https://content.cld.iop.org/journals/1402-4896/2013/T153/014006/revision1/pscr454554ieqn6.gif) , with 〈A〉 = Tr[A ϱ], where
, with 〈A〉 = Tr[A ϱ], where  and
and  and
and  are the position- and momentum-like operators. In the following, according to the requirements of the performer, we set α = 0, i.e.
are the position- and momentum-like operators. In the following, according to the requirements of the performer, we set α = 0, i.e.  . Now, when two uncorrelated, single-mode Gaussian states ϱk with CMs
. Now, when two uncorrelated, single-mode Gaussian states ϱk with CMs  , k = 1,2, interact through a BSI with transmissivity τ, the initial 4 × 4 CM
, k = 1,2, interact through a BSI with transmissivity τ, the initial 4 × 4 CM  of the two-mode state ϱ1⊗ϱ2 transforms as [30–33]
of the two-mode state ϱ1⊗ϱ2 transforms as [30–33]

where

and
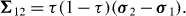
Note that  denotes the presence of correlation between the outgoing modes. It is now clear that if the input states are in the same initial state, namely
denotes the presence of correlation between the outgoing modes. It is now clear that if the input states are in the same initial state, namely  and
and  , then the output beams are left uncorrelated (
, then the output beams are left uncorrelated ( ).
).
Figure 1. The illusionist game. (a) Two uncorrelated light beams excited in the same Gaussian state are crossed: no correlations arise. (b) A beam splitter (BSI) lets the two beams interfere: still no correlations are detected. (c) The illusionist can always say whether the BSI is hidden under the hat or not: the trick is behind the curtain (where the illusionist has access to a further beam). Dk, k = 1,2,3, are detectors to measure the correlations.
Download figure:
Standard imageIn the second part of the game, the public is now asked to insert at will the BSI hiding it under a hat (figure 1(c)). The illusionist argues that he is able to say whether it is present or not and he succeeds, despite the fact that the interaction through the BSI does not seems to affect the output states.
Now we explain how the use of a third ancillary mode correlated with one of the two input modes allows us to discriminate between the two cases. Although the public sees only modes 1 and 2 on the stage excited in the state ϱ1 = ϱ2 = ϱ, however, mode 2 is actually correlated with mode 3 (kept by the illusionist behind the curtain, figure 1(c)), i.e. ϱ2 = Tr[ϱ23] with ϱ23 ≠ ϱ2⊗ϱ3. On the one hand, modes 1 and 2 are left unchanged and uncorrelated after the interference; because of the interaction, part of the correlations shared between modes 2 and 3 are now shared between modes 1 and 3. This can be seen by looking at the evolved CM of the whole state of the three modes in the presence of the BSI. The 6 × 6 CM of the initial state ϱ123 = ϱ1⊗ϱ23 reads

where  is the 2 × 2 single-mode CM of mode k = 1,2,3,
is the 2 × 2 single-mode CM of mode k = 1,2,3,  and the matrix
and the matrix  contains the correlations between modes 2 and 3. Since the BSI acts only on modes 1 and 2, we have
contains the correlations between modes 2 and 3. Since the BSI acts only on modes 1 and 2, we have
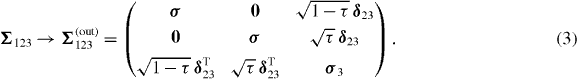
The comparison between equations (2) and (3) shows that while the states of modes 1 and 2 are (locally) left unchanged and, in turn, uncorrelated, both modes 1 and 2 are now correlated with mode 3 (again, the presence of non-zero off-diagonal blocks denotes the presence of correlations between the corresponding modes). Furthermore, the degree of correlations between modes 2 and 3 is decreased ( ) for the benefit of the birth of correlations between the previously uncorrelated modes 1 and 3 (
) for the benefit of the birth of correlations between the previously uncorrelated modes 1 and 3 ( ). We conclude that BSI is present, since mode 1 becomes correlated with mode 3 at the expense of the initial correlations between modes 1 and 2. Nevertheless, this happens in such a way that no overall correlations arise between the interacting modes. The illusionist, who has access also to the third mode can discover the presence of the BSI by exploiting the 'hidden correlations'. Remarkably, the correlations are not hidden 'behind the curtain': in fact, the two beams are actually mixed (part of the photons from each beam are reflected and transmitted according to the interference rules of quantum physics) and, shot by shot, correlation may arise due to the quantized nature of the light, but, overall, this effect is 'washed out' by the very statistical nature of the Gaussian states and the linear interaction itself. Thus, the use of the ancillary mode allows us to retrieve this particular information.
). We conclude that BSI is present, since mode 1 becomes correlated with mode 3 at the expense of the initial correlations between modes 1 and 2. Nevertheless, this happens in such a way that no overall correlations arise between the interacting modes. The illusionist, who has access also to the third mode can discover the presence of the BSI by exploiting the 'hidden correlations'. Remarkably, the correlations are not hidden 'behind the curtain': in fact, the two beams are actually mixed (part of the photons from each beam are reflected and transmitted according to the interference rules of quantum physics) and, shot by shot, correlation may arise due to the quantized nature of the light, but, overall, this effect is 'washed out' by the very statistical nature of the Gaussian states and the linear interaction itself. Thus, the use of the ancillary mode allows us to retrieve this particular information.
For the sake of clarity, we described the illusionist game addressing only single-mode beams; however, the same results hold also in the presence of multimode Gaussian beams, provided that each mode interferes with the corresponding one. This is essentially due to the tensor product nature of the multimode state and the pairwise interaction.
3. The illusionist game: experiment
We have experimentally realized the protocol by addressing the most simple Gaussian states, i.e. thermal beams (figure 2). Two speckled, i.e. spatial multimode and single temporal mode (pseudo)-thermal beams, a and b, were generated by scattering two 1 ns laser pulses (λ = 532 nm and 12.4 Hz repetition rate) on two independent rotating ground glasses (R1 and R2) [34]. While beam b is directly sent to BSI as beam 1 (figure 2(a)), beam a is divided into the two correlated beams 2 and 3, needed for the trick, by means of the balanced beam splitter BS23. A system of half waveplates (λ/2) and polarizers (P) compensated unbalancing in intensity of the modes and selected only modes with the same polarization, in order to realize the theoretical condition ϱ1 = ϱ2. The lens LI (focal length 20 cm) imaged the beams on an electron multiplying charge coupled device (EMCCD) array (Andor Luca, sensitive area 658 × 498 pixels, squared pixel dimension 10 μm) with 0.16 magnification of the beams. Each mode of the beams corresponded to a point on the EMCCD array. For each beam k = 1,2,3 we selected an area Ak with 40 × 40 pixels collecting M ≈ 41 modes. Each mode collected in the area Ak interferes with its correlated one in the corresponding other areas. Optimal selection of the correlated areas Ak is performed maximizing the (pixel-by-pixel) spatial correlation [35].
Figure 2. Sketch of the experimental setup. Implementation of the illusionist game with the BSI (a) and without it (b). In the right panels of figures (a) and (b) the thermal beams detection area Ak are reported. The numbers of photoelectrons I(j)k per frame j collected in the area Ak are used to evaluate the correlation coefficients c1,2, c1,3 and c2,3 according to equation (4).
Download figure:
Standard imageThe pseudo-thermal beams show the typical speckle structure, and we put the BSI in their far field zone in order to associate each mode of the multimode thermal beam with a point on the BSI, i.e. on the detection plane. In this way, our setup allows us to identify properly each pair of single modes and make them interacting at the BSI.
To evaluate the intensity correlations between the modes, which are due to the presence of non-zero off-diagonal blocks of the CM, each beam k = 1,2,3 was registered by an area Ak of an EMCCD array (right panel of figure 2), corresponding to the detector Dk of figure 1. We actually measure the number of photoelectrons I(j)k corresponding to the light intensity impinging on the whole area Ak. By averaging I(j)k over the number of frames, due to the presence of many spatial modes per area, one has a reasonable estimate of the operator  , where η is the quantum efficiency of the EMCCD and
, where η is the quantum efficiency of the EMCCD and  is the field operator of the mth mode impinging on Ak and M is the total number of collected modes. The correlation between the beams h and k (h,k = 1,2,3) is estimated by using the second-order correlation coefficient ch,k, namely
is the field operator of the mth mode impinging on Ak and M is the total number of collected modes. The correlation between the beams h and k (h,k = 1,2,3) is estimated by using the second-order correlation coefficient ch,k, namely

where  is the average over Nframe frames and Δfr(Ik)2 = 〈I2k〉fr − 〈Ik〉fr2. If ch,k = 1, one has maximum correlation; if ch,k = 0, the beams are uncorrelated. It is remarkable to note that if all the spatial modes belonging to a beam have the same intensity, the correlation coefficient ch,k is independent of the number of modes M, i.e. ch,k is equal to the one calculated for the single mode.
is the average over Nframe frames and Δfr(Ik)2 = 〈I2k〉fr − 〈Ik〉fr2. If ch,k = 1, one has maximum correlation; if ch,k = 0, the beams are uncorrelated. It is remarkable to note that if all the spatial modes belonging to a beam have the same intensity, the correlation coefficient ch,k is independent of the number of modes M, i.e. ch,k is equal to the one calculated for the single mode.
To ensure proper mode matching at BSI and perfect superposition of the correlated areas A1 and A2, we alternatively stopped beams a or b and measured and maximized the correlation c(a)1,2 and c(b)1,2, respectively, between beams 1 and 2 outgoing the BSI. We then investigated the two configurations proposed by the illusionist: with the BSI and without it. Our results fully demonstrate the theoretical protocol. Figure 3 shows the correlation coefficient c1,2 for different configurations and as a function of the number of frames. With the BSI inserted, the correlation falls from almost 1 in the presence of only one of the two beams a and b (c(a)1,2 and c(b)1,2), to almost zero when both beams are present, thus efficiently hiding the correlation (c(BS)1,2). A very small residual correlation persists due to experimental imperfections, such as the non-perfect superpositions of the optical modes and the unbalancing of the BSI. The question that naturally arises is whether this residual correlation is enough to discriminate the presence from the absence of the BSI. The answer is 'no' where a relatively small number of frames is used to estimate c1,2. As shown in the insets of figure 3, the large overlap between the probability density functions (pdf) [36] of c(BS)1,2 and of c(no)1,2 (obtained for Nframe = 10,30,50) does not allow us to discriminate between the two cases with sufficiently small error probability and the 'hidden correlations' are needed.
Figure 3. Plot of the correlation c1,2 for different experimental configurations (dots), together with the confidence intervals at 99% (shaded regions), as a function of the number of frames used to evaluate it. c(a)1,2 (black) and c(b)1,2 (orange) correspond to the correlation of beams 1 and 2 outgoing BSI when only mode a or b, respectively, is switched on. c(BS)1,2 (blue) and c(no)1,2 (red) refer to the correlation of modes 1 and 2 with and without the BSI, respectively, when both a and b are switched on. As expected, the width of the confidence intervals decreases as Nframes increases. The insets of the figure show the probability density function of the correlation coefficients for Nframe = 10,30 and 50.
Download figure:
Standard imageIn figure 4(a) we report c1,3 with and without BSI: the correlation between beams 1 and 3, which are initially uncorrelated, is evident in the presence of BSI. In the absence of BSI, beams 1 and 3 are uncorrelated, hence c(no)1,3 ≈ 0; inserting BSI, correlations appear and c(BS)1,3 ≈ 0.5. Similar results concern c2,3 (figure 4(b)): one has c(no)2,3 ≈ 1 without BSI and c(BS)2,3 ≈ 0.5 with BSI. However, to perform the trick, the illusionist should be able to discriminate between the two cases with low error probability and, thus, he should choose a suitable Nframe. In figure 4(c) we plotted the probability of error P(1,2)err as expected by the public, i.e. addressing c1,2, and that of the illusionist, P(1,3)err or P(2,3)err, i.e. addressing c1,3 or c2,3, respectively. Also in the presence of experimental imperfections, for Nframe ≈ 50, he is indeed able to discriminate between the two configurations, since P(1,3)err ≈ 1% (P(2,3)err ≈ 1%) and P(1,2)err ≈ 35%: we conclude that the illusionist succeeded in his game!
Figure 4. (a) Plot of c1,3 (dots), together with their confidence intervals at 99% (dashed lines and shaded regions), as functions of Nframe. c(BS)1,3 (blue) and c(no)1,3 (red) refer to correlations between beams 1 and 3 with and without BSI, respectively. (b) Plot of c(BS)2,3 (blue) and c(no)2,3 (red), referred to correlations between beams 2 and 3 with and without BSI, respectively. (c) Log-linear plot of the error probability P(h,k)err of the discrimination presence/absence of BSI as a function of Nframe obtained from ch,k.
Download figure:
Standard image4. Conclusions
In summary, we have suggested and demonstrated a novel scheme to illustrate and exploit the correlations of quantized light. In our illusionist game, two identical Gaussian beams of light are addressed to the BSI and do not acquire any correlation revealing the action of the BS itself. On the other hand, the presence of the BS can be identified by using the pre-existing correlations of one of the beams with a third one. Our protocol represents a paradigmatic example of hidden correlations of quantized optical beams, and paves the way for future applications, e.g. innovative interferometric schemes and generation scheme for highly excited photon number entangled states [37].
Acknowledgments
This work was supported by MIUR (progetto Premiale 'Oltre i limiti classici di misura'; FIRB 'LiCHIS'—RBFR10YQ3H) and by Compagnia di San Paolo. SO acknowledges financial support from the University of Trieste (FRA 2009).





