Long-lived double periodic patterns in dipolar cigar-shaped Bose–Einstein condensates in an optical lattice

The properties of dipolar Bose–Einstein condensates (BEC) in an optical lattice have been in the focus of research during the last few years [1–7]. Here we study dipolar BEC in a one-dimensional (1D) very deep optical lattice (1D OL), modeling the system by the discrete nonlinear Schrödinger equation (DNLSE) with a dipole–dipole (DD) interaction term. We demonstrate the existence of stationary states with periods equal to twice that of the optical lattice. Their occurrence nearly coincides with the onset of dynamical instability of states of the usual Bloch form with lattice periodicity [8] by applying a small perturbation with the doubled lattice periodicity.

Two branches of double periodic patterns (DPPs) have been found analytically and numerically. To generate a spatial doubled periodic pattern in the condensate, the presence of nonlinear interaction is necessary. We show that the DPP are formed not only in the presence of local (contact) interaction as discussed in previous works [8], but also in the presence of only nonlocal, nonlinear DD interaction and in the combination of local and nonlocal interactions. The DPP occurs in the form of an unstaggered (US) or staggered (ST) periodic pattern. Close to the anticontinuum limit, DPPs are long-lived, while the instability grows with an increase of the inter-site coupling. This is a known property of the DNLSE with contact nonlinearity [9]. Moreover, in a repulsive condensate with a certain strength of repulsion between the constituents' dipolar moments, stable DPP branches may be created via the supercritical pitchfork bifurcation from the CW background in an OL with finite depth.

The trapped quasi-1D condensate is modelled by the scaled DNLSE with cubic local and nonlocal DD terms [6]:

$$\begin{eqnarray} \mathrm{i}\frac{\mathrm{d}f_{n}}{\mathrm{d}t}&=&-C(f_{n+1}+f_{n-1}-2f_{n})+\sigma \left\vert f_{n}\right\vert ^{2}f_{n}\nonumber\\ &&-\Gamma \sum_{m\neq n}\frac{\left\vert f_{m}\right\vert ^{2}}{|m-n|^{3}}f_{n}, \end{eqnarray} \tag{ 1 }$$

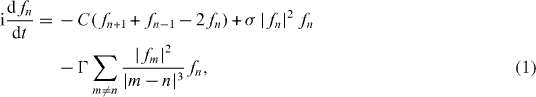
where parameter σ ≡ γ/|γ| = −1 and +1 corresponds to attractive or repulsive contact interaction with γ being the nonlinearity parameter which is proportional to the s-wave scattering length [6]. The parameter C > 0 (scaled with respect to |γ|) is the inter-site coupling constant that accounts for the tunnelling of atoms between adjacent sites of the lattice, and Γ is the relative strength of the DD interaction, in comparison to the local nonlinearity. Γ > 0 and Γ < 0 correspond to the long-range attraction and repulsion, respectively. Time is in units of ω⁻¹_⊥, where ω_⊥ is the radial frequency which defines the transversal radius of the condensate trap 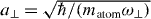$a_{\bot }=\sqrt {\hbar /(m_{\mathrm {atom}} \omega _{\bot })}$.

Stationary solutions to equation (1) with chemical potential μ are sought in the form, 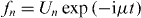$f_{n}=U_{n}\exp {(-\mathrm {i}\mu t)}$. The corresponding stationary equation for the discrete wave function U_n is

$$\begin{eqnarray} \mu U_{n}&=&-C(U_{n+1}+U_{n-1}-2U_{n})+\sigma \left\vert U_{n}\right\vert ^{2}U_{n}\nonumber\\ &&-\Gamma \sum_{m\neq n}\frac{\left\vert U_{m} \right\vert^{2}}{|m-n|^{3}}U_{n}. \end{eqnarray}\noindent \tag{ 2 }$$

It supports solutions with lattice periodicity which are actually the uniform chains of BEC droplets trapped in the OL. They are discrete equivalents of the continuous waves (CWs) [10]. A straightforward analysis of the modulation instability [9] of the CW (U_n ≡ U) was performed in [6] by linearizing equation (1) for small perturbations. It is shown that the CW is stable in a relatively narrow parameter region [6] (see figure 1(a)).

Zoom In Zoom Out Reset image size

The stationary equation (2) allows the existence of multi-periodic patterns with respect to lattice periodicity. Here we are interested in the DPP, U_2n−1 = ϕ₁, U_2n = ϕ₂, n = 1,2,...,[N/2], where N is the total number of lattice sites. We showed that the DPP can be formed in the presence of any type of nonlinear interaction, local and long-ranged ones (figure 2). A new finding is the creation of the DPP in a condensate with only nonlinear, nonlocal DD interaction, either repulsive or attractive as illustrated in figure 2(a).

Zoom In Zoom Out Reset image size

The amplitudes ϕ₁ ≠ ϕ₂ satisfy the following relations which were exactly analytically derived from equation (2):

$$\begin{equation} \phi _{1}^2+\phi _{2}^2=4\frac{\mu -2C}{4\sigma -\Gamma \zeta(3)},\quad \phi _{1}\phi _{2}= \frac{-4C}{2\sigma +3\Gamma\zeta(3)}, \end{equation} \tag{ 3 }$$

where ζ is Riemann's zeta function. Two classes of DPPs have been identified as in [8]. One class is characterized by |ϕ₁|² ≠ |ϕ₂|² and the phase difference is equal to 0 (US pattern) or π (ST pattern). Another class of solutions is that with arbitrary phase difference and |ϕ₁| = |ϕ₂|. In figure 2, US and ST DPPs are illustrated for different types of inter-atomic interaction.

The formation of DPPs is a consequence of the modulation (dynamical) instability of the CW states to added small perturbation with doubled lattice periodicity as confirmed by numerical dynamical simulation (figures 3(a) and (b)).

Zoom In Zoom Out Reset image size

3.1. Stability properties of DPPs

In 1D optical lattices with weak linear coupling, long-lived DPPs can be observed in dipolar BEC. They can be created in the presence of any type of nonlinear interaction between the condensate atoms (contact and or/ DD interaction). A significant finding here is the possibility to generate stable DPP only in the presence of DD interaction of both kinds, attractive and repulsive ones.

It is shown analytically and numerically that the DPP originates from the unstable CW solution modulated by a small perturbation with doubled lattice periodicity. The long-lived DPPs are found in the anti-continuum limit. Moreover, in the repulsive condensate in the presence of repulsive DD interaction, a stable DPP can be created in the OL via the supercritical pitchfork bifurcation.

The DPP as well as the multi-periodic patterns, which are allowed in the present system, may be understood in terms of trains of solitons [8]. The role of the DD interaction in this framework is under investigation. Moreover, the transition from CW to long-lived DPP can be phenomenologically related to the Peierls instability which occurs in spatially periodic electron systems in condensate matter physics [11] and leads to the transition from the conduction to the isolator phase.

We acknowledge support from the Ministry of Education and Science, Serbia (project no. III45010).