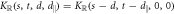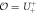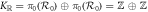Abstract
Chiral and helical Majorana fermions are two archetypal edge excitations in two-dimensional topological superconductors. They emerge from systems of different Altland–Zirnbauer symmetries and characterized by 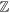 and
and 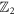 topological invariants respectively. It seems improbable to tune a pair of co-propagating chiral edge modes to counter-propagate in a single system without symmetry breaking. Here, we explore the peculiar behaviors of Majorana edge modes in topological superconductors with an additional 'mirror' symmetry which changes the bulk topological invariant to
topological invariants respectively. It seems improbable to tune a pair of co-propagating chiral edge modes to counter-propagate in a single system without symmetry breaking. Here, we explore the peculiar behaviors of Majorana edge modes in topological superconductors with an additional 'mirror' symmetry which changes the bulk topological invariant to  type. A theoretical toy model describing the proximity structure of a Chern insulator and a px-wave superconductor is proposed and solved analytically to illustrate a direct transition between two topologically nontrivial phases. The weak pairing phase has two chiral Majorana edge modes, while the strong pairing phase is characterized by mirror-graded Chern number and hosts a pair of counter-propagating Majorana fermions protected by the mirror symmetry. The edge theory is worked out in detail, and implications to braiding of Majorana fermions are discussed.
type. A theoretical toy model describing the proximity structure of a Chern insulator and a px-wave superconductor is proposed and solved analytically to illustrate a direct transition between two topologically nontrivial phases. The weak pairing phase has two chiral Majorana edge modes, while the strong pairing phase is characterized by mirror-graded Chern number and hosts a pair of counter-propagating Majorana fermions protected by the mirror symmetry. The edge theory is worked out in detail, and implications to braiding of Majorana fermions are discussed.
Export citation and abstract BibTeX RIS
1. Introduction
A defining feature of topological quantum matter [1, 2] is the existence of protected boundary/edge modes due to the nontrivial topology of the bulk material. Gapped bulk Hamiltonians can be classified into different Altland–Zirnbauer (AZ) classes based on their symmetries [3–6]. Each symmetry class has its own manifestation of the bulk-boundary correspondence. A well-known example is the two-dimensional (2D) quantum Hall insulator in class A, which is characterized by an integer Chern number and has gapless chiral edge modes. Another example is the quantum spin Hall insulator [7–9] in class AII with counter-propagating edge modes protected by time-reversal symmetry, and characterized by a 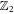 invariant. Analogously, in 2D topological superconductors, chiral Majorana edge modes appear in class-D superconductors such as
invariant. Analogously, in 2D topological superconductors, chiral Majorana edge modes appear in class-D superconductors such as 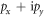 [10], while helical Majorana modes emerge in class-DIII superconductors with time-reversal symmetry [11–18] (the term 'helical' here refers to a pair of counter-propagating modes with pseudospin-momentum locking). These edge modes, commonly referred to as Majorana fermions, are dispersive and differ from Majorana zero modes which obey anyonic statistics. Recently, however, it is shown that the propagation of chiral Majorana fermions can lead to the same unitary transformation as the braiding of Majorana zero modes [19]. This opens up a new route for topological quantum computing [20–26] based on electrical manipulation of chiral Majorana fermions on the mesoscopic scale. Experimentally, chiral Majorana fermions have been observed in a proximity structure of quantum anomalous Hall insulator (QAHI) and an s-wave superconductor, which behaves effectively as a
[10], while helical Majorana modes emerge in class-DIII superconductors with time-reversal symmetry [11–18] (the term 'helical' here refers to a pair of counter-propagating modes with pseudospin-momentum locking). These edge modes, commonly referred to as Majorana fermions, are dispersive and differ from Majorana zero modes which obey anyonic statistics. Recently, however, it is shown that the propagation of chiral Majorana fermions can lead to the same unitary transformation as the braiding of Majorana zero modes [19]. This opens up a new route for topological quantum computing [20–26] based on electrical manipulation of chiral Majorana fermions on the mesoscopic scale. Experimentally, chiral Majorana fermions have been observed in a proximity structure of quantum anomalous Hall insulator (QAHI) and an s-wave superconductor, which behaves effectively as a 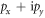 superconductor [27], and superconducting ferromagnetic hybrid system Pb/Co/Si(111) [28]. They are also expected to emerge in the ν = 5/2 fractional quantum Hall state [10, 29, 30–32], which was recently confirmed from the quantized thermal Hall conductance [33].
superconductor [27], and superconducting ferromagnetic hybrid system Pb/Co/Si(111) [28]. They are also expected to emerge in the ν = 5/2 fractional quantum Hall state [10, 29, 30–32], which was recently confirmed from the quantized thermal Hall conductance [33].
In this paper, we investigate whether braiding can also be achieved by using other (non-chiral) kinds of Majorana fermions protected by certain symmetries. We introduce a toy model of a 2D p-wave superconductor and analyze its quantum phases and topological invariants. We show that it changes from the host of a pair of chiral Majorana modes to the host of a pair of counter-propagating Majorana modes, schematically shown in figures 1(a) and (b), as the magnitude of the superconducting pairing is increased. At first sight, such a direct transition seems impossible without any symmetry breaking because these two types of edge modes require distinct symmetries of the bulk Hamiltonian according to the standard AZ classification [3–6]. However, as we show explicitly below, the presence of additional symmetry (besides time reversal, particle-hole and chiral symmetry) gives rise to richer physics beyond the AZ classes, and it is indeed possible to realize both types of edge modes within the same material. This implies that the direction of the Majorana fermions can be controlled to yield new quantum gates. Furthermore, we show that these counter-propagating Majorana fermions, in addition to their chiral cousins, can also be used to achieve braiding-like operations. This broadens the choice of topological superconductors for topological quantum computation.
Figure 1. Schematic of (a) chiral and (b) counter-propagating Majorana edge modes in the weak and strong pairing phase of model (2). The red/green line depicts edge modes in different subspaces of mirror symmetry, with the arrow indicating the propagating direction. Panels (c)–(f) show the quasiparticle spectra of model (2) in a half-infinite geometry with open boundary along a 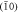 or
or 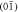 edge. Left column, (c) and (d): Δ = 0.5t0, the bulk is in the weak pairing phase. Right column, (e) and (f): Δ = 2t0, the strong pairing phase. M = 0.5t0. The red/green lines label edge modes in different mirror-subspace. In (c), the chiral edge modes are doubly degenerate.
edge. Left column, (c) and (d): Δ = 0.5t0, the bulk is in the weak pairing phase. Right column, (e) and (f): Δ = 2t0, the strong pairing phase. M = 0.5t0. The red/green lines label edge modes in different mirror-subspace. In (c), the chiral edge modes are doubly degenerate.
Download figure:
Standard image High-resolution imageCentral to our proposal and analysis is a 'mirror' symmetry. Within the pair of edge modes, indicated by the red and green arrows in figures 1(a) and (b), each belongs to a specific sub-eigenspace of the symmetry operator and one of them changes its chirality across the topological phase transition. In the weak pairing (WP) phase, the two Majorana modes belonging to different subspace propagate unidirectionally. In contrast, in the strong pairing (SP) phase with large pairing amplitude, the two Majorana modes move in opposite directions. We construct a new bulk topological invariant to characterize both the WP and SP phases and demonstrate the bulk-edge correspondence by working out the effective edge theory for both phases. The edge modes are shown to be stable against any perturbations that preserve the mirror symmetry.
The remainder of this paper is organized as follows. In section 2, we introduce the p-wave superconductor model with the required symmetry and discuss its band structures. In section 3, we construct the bulk topological invariant based on the mirror symmetry, which dictates the appearance of different types of Majorana edge modes. Further, we present the edge theory and solve the Majorana edge modes directly from the Dirac-like low-energy Hamiltonian in section 4. The edge theory yields predictions that coincide with the bulk analysis. Finally in section 5, we show the tunability of the propagation of Majorana edge modes and its possible applications in topological quantum computation. We draw conclusions and discuss potential experimental realizations in section 6. Note that our primary goal here is to show a theoretical scenario, a possibility, using a toy model rather than a proposal that can be realized immediately in experiments.
2. Model and two phases
Our starting point is a minimal model of Chern insulator with two orbitals, referred to as pseudospin  and
and  , per site on a square lattice described by Hamiltonian
, per site on a square lattice described by Hamiltonian

Here t0 = 1 is the intra-orbital hopping amplitude and sets the energy unit, αx/y is the inter-orbital hopping (analogous to spin–orbit coupling) along the x/y direction, M denotes an effective Zeeman field, and the Pauli matrices σi are defined in orbital (pseudospin) space. This model is introduced in [34, 35] and recently realized using cold atoms in optical lattices [36, 37]. The topological properties of 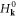 is well known and characterized by Chern number
is well known and characterized by Chern number  . For
. For 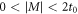 ,
, 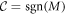 is simply given by the sign of M; while in other parameter regions,
is simply given by the sign of M; while in other parameter regions,  and the system is a trivial band insulator.
and the system is a trivial band insulator.
Now let us introduce on top of 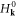 an effective px-wave pairing term similar to the one in the Kitaev chain [38]. Fermions of the same pseudospin at neighboring sites along the x direction form Cooper pairs with amplitude Δ5
. The Bogoliubov de Gennes Hamiltonian
an effective px-wave pairing term similar to the one in the Kitaev chain [38]. Fermions of the same pseudospin at neighboring sites along the x direction form Cooper pairs with amplitude Δ5
. The Bogoliubov de Gennes Hamiltonian 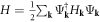 in Nambu basis
in Nambu basis 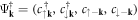 reads
reads

where the Pauli matrices τi operate in the particle-hole space. We have assumed that the chemical potentials for each spin, 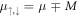 , satisfy
, satisfy 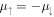 , i.e. the average chemical potential μ is at the band crossing points, which we set as energy zero, μ = 0. Hk belongs to class D in the AZ classification table, with particle-hole symmetry
, i.e. the average chemical potential μ is at the band crossing points, which we set as energy zero, μ = 0. Hk belongs to class D in the AZ classification table, with particle-hole symmetry  , where
, where 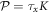 and K is the complex conjugate [3–6]. In addition, there exists another important symmetry
and K is the complex conjugate [3–6]. In addition, there exists another important symmetry 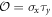 , which satisfies
, which satisfies
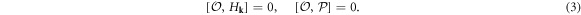
We emphasize that 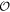 flips the pseudospin and converts a particle into a hole. It is helpful to visualize the system as a bilayer, with each orbital confined to one of the two layers slightly shifted away from each other. Then
flips the pseudospin and converts a particle into a hole. It is helpful to visualize the system as a bilayer, with each orbital confined to one of the two layers slightly shifted away from each other. Then 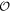 exchanges the two layers and generalizes the 2D mirror reflection [39]. For this reason, we shall refer to it as a mirror symmetry. It plays a crucial role in our analysis. Of course, in general μ can be tuned away from zero, then pairing would occur at two mismatched Fermi surfaces for
exchanges the two layers and generalizes the 2D mirror reflection [39]. For this reason, we shall refer to it as a mirror symmetry. It plays a crucial role in our analysis. Of course, in general μ can be tuned away from zero, then pairing would occur at two mismatched Fermi surfaces for 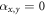 , and involve parity mixing for finite spin–orbit coupling αx,y. Under these circumstances, the
, and involve parity mixing for finite spin–orbit coupling αx,y. Under these circumstances, the 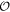 -symmetry will be broken, but we will not consider such cases where our model loses its simple appeal. The quasiparticle energy spectrum of
-symmetry will be broken, but we will not consider such cases where our model loses its simple appeal. The quasiparticle energy spectrum of 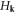 is given by
is given by
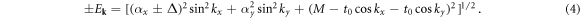
We will focus on the parameter region 0 < M < 2t0 to ensure the base insulator is topologically nontrivial. From (4), one observes with increasing Δ, the gap closes when Δ = αx for a fixed M. The gap closing occurs at two Dirac points 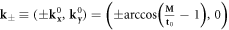 . We will refer to the gapped superconducting phase at Δ < αx as the WP phase; and the phase at Δ > αx as the SP phase.
. We will refer to the gapped superconducting phase at Δ < αx as the WP phase; and the phase at Δ > αx as the SP phase.
Both phases turn out to be topologically nontrivial and give rise to Majorana edge states. Figure 1 illustrates the quasiparticle spectra of Hk in a half-infinite geometry with 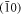 edge (along y-direction), or
edge (along y-direction), or 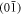 edge (along x-direction). For the WP phase (figures 1(c), (d), left column), a pair of chiral Majorana modes propagate in the same direction on each edge. In particular, for the
edge (along x-direction). For the WP phase (figures 1(c), (d), left column), a pair of chiral Majorana modes propagate in the same direction on each edge. In particular, for the 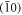 edge, the two modes are completely degenerate and they cross zero energy exactly at kx = 0. At the phase transition point Δ = αx, the bulk bands touch at the two Dirac points, triggering a dramatic change in the edge spectrum. Within the SP phase (figures 1(e), (f), right column), a pair of Majorana modes still cross zero energy at k = 0, but they have opposite group velocity and propagate in opposite directions along each edge.
edge, the two modes are completely degenerate and they cross zero energy exactly at kx = 0. At the phase transition point Δ = αx, the bulk bands touch at the two Dirac points, triggering a dramatic change in the edge spectrum. Within the SP phase (figures 1(e), (f), right column), a pair of Majorana modes still cross zero energy at k = 0, but they have opposite group velocity and propagate in opposite directions along each edge.
3. Topological invariant
According to the bulk-boundary correspondence, the emergence of edge states is governed by a nontrivial topological invariant in the bulk. For 2D class-D superconductors, the topological invariant is the Chern number defined as

where 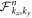 is the Berry curvature [40, 41] for the nth band, and the sum is over all the occupied bands (with negative quasienergy). Note that for our model, the two lower bands overlap,
is the Berry curvature [40, 41] for the nth band, and the sum is over all the occupied bands (with negative quasienergy). Note that for our model, the two lower bands overlap,  has to be calculated with care [42, 43]. We find for the WP phase,
has to be calculated with care [42, 43]. We find for the WP phase,  , in agreement with the number of chiral Majorana edge modes. This phase is adiabatically connected to a Chern insulator at Δ = 0, which hosts chiral, complex fermion as edge state. Such a chiral fermion can be decomposed into two chiral Majorana fermions. Accordingly, one observes two gapless chiral modes on each edge in the WP phase. For the SP phase, the Chern number vanishes,
, in agreement with the number of chiral Majorana edge modes. This phase is adiabatically connected to a Chern insulator at Δ = 0, which hosts chiral, complex fermion as edge state. Such a chiral fermion can be decomposed into two chiral Majorana fermions. Accordingly, one observes two gapless chiral modes on each edge in the WP phase. For the SP phase, the Chern number vanishes,  . The change in
. The change in  at the topological phase transition can be understood by expanding Hk around the two Dirac points. This leads to the following two-band Dirac Hamiltonian describing the gap closing:
at the topological phase transition can be understood by expanding Hk around the two Dirac points. This leads to the following two-band Dirac Hamiltonian describing the gap closing:
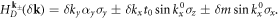
Here δm = αx − Δ plays the role of Dirac mass. As the gap closes and reopens, δm changes sign, accompanied by the change of Chern number ![${\rm{\Delta }}{{ \mathcal C }}_{{{\bf{k}}}_{\pm }}=\tfrac{1}{2}[\mathrm{sgn}(\delta m\lt 0)-\mathrm{sgn}(\delta m\gt 0)]=-1$](https://content.cld.iop.org/journals/1367-2630/21/12/123014/revision2/njpab5cadieqn39.gif) through each Dirac point. Hence
through each Dirac point. Hence  changes by −2, yielding
changes by −2, yielding  for the SP phase, consistent with a pair of counter-propagating Majorana modes with no net chirality. Obviously
for the SP phase, consistent with a pair of counter-propagating Majorana modes with no net chirality. Obviously 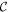 by itself cannot characterize the topology of the SP phase, or predict the number of Majorana edge modes in each direction.
by itself cannot characterize the topology of the SP phase, or predict the number of Majorana edge modes in each direction.
We need to construct a new topological invariant. This can be accomplished by taking into account the symmetry  and following the general procedure of K-theory [44]. In the presence of
and following the general procedure of K-theory [44]. In the presence of 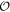 , the topological invariant takes the form of
, the topological invariant takes the form of 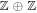 , i.e. a pair of integers6
. More physically, as
, i.e. a pair of integers6
. More physically, as ![$[{ \mathcal O },{H}_{{\bf{k}}}]=0$](https://content.cld.iop.org/journals/1367-2630/21/12/123014/revision2/njpab5cadieqn50.gif) , we can decompose Hk into two sectors. Each sector belongs to a specific sub-eigenspace of
, we can decompose Hk into two sectors. Each sector belongs to a specific sub-eigenspace of 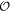 , labeled by ±1, the eigenvalues of
, labeled by ±1, the eigenvalues of 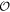 . For example, the transformation
. For example, the transformation 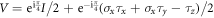 , which diagonalizes
, which diagonalizes  via
via 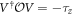 , will take H(k) to
, will take H(k) to 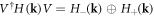 , with
, with
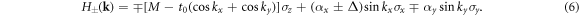
As ![$[{ \mathcal O },{ \mathcal P }]=0$](https://content.cld.iop.org/journals/1367-2630/21/12/123014/revision2/njpab5cadieqn57.gif) ,
,  each belongs to class D. Therefore, we can define the corresponding Chern number
each belongs to class D. Therefore, we can define the corresponding Chern number  in each
in each  -subspace. The total Chern number discussed above is simply
-subspace. The total Chern number discussed above is simply 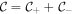 , while the
, while the 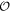 -graded Chern number is defined as
-graded Chern number is defined as
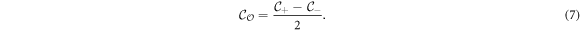
This new invariant 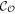 counts how many pairs of counter-propagating Majorana edge modes exist along each edge. For the WP phase,
counts how many pairs of counter-propagating Majorana edge modes exist along each edge. For the WP phase, 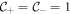 ,
,  and
and 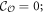 while for the SP phase,
while for the SP phase, 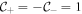 , yielding
, yielding  and
and 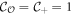 . The topological invariants and bulk-edge correspondence are summarized in table 1.
. The topological invariants and bulk-edge correspondence are summarized in table 1.
Table 1. Bulk-edge correspondence for the WP and SP topological superconductors described by model (2).
| Condition |

|
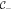
|
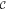
|
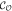
|
Edge modes |
|---|---|---|---|---|---|
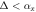 (WP) (WP) |
1 | 1 | 2 | 0 | Co-propagating |
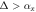 (SP) (SP) |
1 | −1 | 0 | 1 | Counter-propagating |
It is clear from these discussions that each Majorana edge mode belongs to a specific 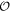 -subspace. They are protected by
-subspace. They are protected by 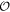 in both phases. As long as this symmetry is preserved, the hybridization between them is forbidden. In comparison, for the time-reversal symmetry protected topological superconductors discussed in [11], the helical edge modes form a Kramers pair, and they will switch partners under the time-reversal symmetry (time-reversal symmetry is absent in our model). Recent work on the ν = 5/2 fractional quantum Hall state also showed a WP phase with Chern number 2 and a trivial SP phase with Chern number 0 [45]7
. Another recent work observed a transition from helical to chiral phase driven by Zeeman field in a 2D superconducting domain consisting of a Pb monolayer covering magnetic Co–Si islands grown on Si(111). There, the Chern numbers of the chiral and helical phase are
in both phases. As long as this symmetry is preserved, the hybridization between them is forbidden. In comparison, for the time-reversal symmetry protected topological superconductors discussed in [11], the helical edge modes form a Kramers pair, and they will switch partners under the time-reversal symmetry (time-reversal symmetry is absent in our model). Recent work on the ν = 5/2 fractional quantum Hall state also showed a WP phase with Chern number 2 and a trivial SP phase with Chern number 0 [45]7
. Another recent work observed a transition from helical to chiral phase driven by Zeeman field in a 2D superconducting domain consisting of a Pb monolayer covering magnetic Co–Si islands grown on Si(111). There, the Chern numbers of the chiral and helical phase are  and
and  , respectively. Furthermore, their model does not possess any mirror symmetry, and the superconducting order parameter contains both singlet and triplet pairing [28].
, respectively. Furthermore, their model does not possess any mirror symmetry, and the superconducting order parameter contains both singlet and triplet pairing [28].
4. Edge theory
The essential features of the Majorana edge modes, and their symmetry properties, can be described by their low-energy theory. Quite generally, an edge mode crossing zero energy can be regarded as bound state formed at a domain wall of the Dirac mass. The BdG Hamiltonian near k = (0, 0) can be expanded to the second order in k. It consists of three terms

Here 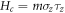 with m = M − 2t0 being the effective Dirac mass,
with m = M − 2t0 being the effective Dirac mass, 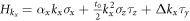 , and
, and 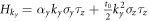 . To simplify the algebra, we take
. To simplify the algebra, we take 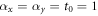 as example and assume Δ > 0 below.
as example and assume Δ > 0 below.
Let us first consider the  edge. The domain wall is located at x = 0 and is described by a spatially varying m(x) which changes sign at x = 0, i.e. m(x > 0) < 0 is the topological superconductor while m(x < 0) > 0 is the vacuum. We can replace kx with −i∂x and treat
edge. The domain wall is located at x = 0 and is described by a spatially varying m(x) which changes sign at x = 0, i.e. m(x > 0) < 0 is the topological superconductor while m(x < 0) > 0 is the vacuum. We can replace kx with −i∂x and treat 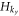 as a perturbation in (8). A trial wave function for the zero-energy bound state at the domain wall is given by
as a perturbation in (8). A trial wave function for the zero-energy bound state at the domain wall is given by 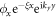 , where ϕx is a four-component spinor and the real number ξ > 0 is the inverse localization length. The eigenvalue problem reduces to
, where ϕx is a four-component spinor and the real number ξ > 0 is the inverse localization length. The eigenvalue problem reduces to ![$\det [{H}_{{k}_{x}}+{H}_{c}]=0$](https://content.cld.iop.org/journals/1367-2630/21/12/123014/revision2/njpab5cadieqn87.gif) , which gives an equation for ξ,
, which gives an equation for ξ, 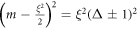 . It has different solutions for the two phases.
. It has different solutions for the two phases.
For the WP phase with Δ < 1, ξ has four solutions
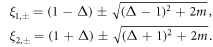
And the corresponding spinors are 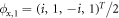 and
and 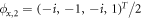 , which transform as
, which transform as 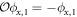 ,
, 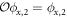 . The superposition of these independent solutions have to satisfy the boundary condition
. The superposition of these independent solutions have to satisfy the boundary condition 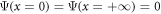 . This leads to the wavefunctions of the zero-energy bound states:
. This leads to the wavefunctions of the zero-energy bound states:
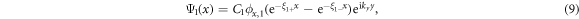
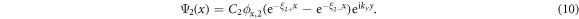
Here C1 and C2 are the normalization factors. The perturbation 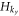 within the Hilbert space spanned by Ψ1(x) and Ψ2(x) is proportional to the identity matrix,
within the Hilbert space spanned by Ψ1(x) and Ψ2(x) is proportional to the identity matrix, 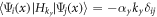 . Thus there are two degenerate chiral Majorana modes along the
. Thus there are two degenerate chiral Majorana modes along the 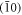 edge with group velocity vF = −αy, in agreement with
edge with group velocity vF = −αy, in agreement with  .
.
For the SP phase with Δ > 1, ξ again has four solutions 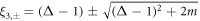 , and
, and  , with spinor
, with spinor 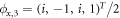 and
and 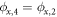 , respectively. And we observe that
, respectively. And we observe that 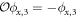 . The wavefunctions of the bound states are
. The wavefunctions of the bound states are
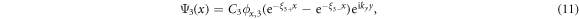
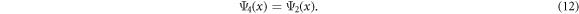
The perturbation 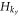 in the Hilbert space spanned by Ψ3(x) and Ψ4(x) is found to be
in the Hilbert space spanned by Ψ3(x) and Ψ4(x) is found to be 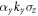 . Therefore, there exist a pair of counter-propagating edge modes with group velocity
. Therefore, there exist a pair of counter-propagating edge modes with group velocity  , in accordance with
, in accordance with  and
and 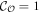 . Note that the resulting edge theory is analogous to that of the quantum spin Hall system [46]. Moreover, one of the edge modes, described by Ψ2(x) and Ψ4(x), smoothly evolves across the topological phase transition, while the other mode reverses the direction of travel.
. Note that the resulting edge theory is analogous to that of the quantum spin Hall system [46]. Moreover, one of the edge modes, described by Ψ2(x) and Ψ4(x), smoothly evolves across the topological phase transition, while the other mode reverses the direction of travel.
Similar analysis can be performed for the 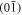 edge by treating
edge by treating 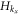 as perturbation. With a trial wave function
as perturbation. With a trial wave function  , the existence of zero-energy bound states requires
, the existence of zero-energy bound states requires 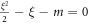 , yielding two solutions
, yielding two solutions  and corresponding spinor
and corresponding spinor 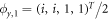 ,
, 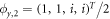 obeying
obeying 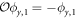 ,
,  . The perturbation
. The perturbation 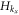 in the reduced Hilbert space is then
in the reduced Hilbert space is then 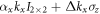 . For Δ < 1 in the WP phase, the second term lifts the degeneracy of the two edge modes while preserves the chirality; for Δ > 1 in the SP phase, the second term dominates, driving the reversal of group velocity for one of the edge modes. Taking together, the edge theory corroborates the Majorana edge modes depicted in figure 1.
. For Δ < 1 in the WP phase, the second term lifts the degeneracy of the two edge modes while preserves the chirality; for Δ > 1 in the SP phase, the second term dominates, driving the reversal of group velocity for one of the edge modes. Taking together, the edge theory corroborates the Majorana edge modes depicted in figure 1.
Based on the edge state wavefunctions Ψj, we can construct the effective edge Hamiltonian in second quantization form. For example, 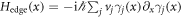 , where x is the coordinate along the edge and γj is the field operator of Majorana fermions corresponding to Ψj. The edge theory forms the basis to understand the low-energy quantum transport of Majorana fermions in the next section.
, where x is the coordinate along the edge and γj is the field operator of Majorana fermions corresponding to Ψj. The edge theory forms the basis to understand the low-energy quantum transport of Majorana fermions in the next section.
5. Braiding
The propagation of Majorana edge modes in heterostructures can mimic the braiding operation to implement topologically protected quantum bits and gates. Previously, [19] demonstrated braiding-like unitary transformation using QAHI and 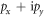 chiral topological superconductor, which can be realized for example using a QAHI in proximity with an s-wave superconductor [27]. Here, we show that the WP and SP superconductors above can form a junction to carry out similar braiding transformations of Majorana fermions, shown schematically in figure 2. The junction consists of a SP phase in the middle region with large Δ sandwiched between two WP regions with smaller Δ. In proximity-induced superconductors, the spatially dependent pairing can be realized by controlling the proximity coupling strength.
chiral topological superconductor, which can be realized for example using a QAHI in proximity with an s-wave superconductor [27]. Here, we show that the WP and SP superconductors above can form a junction to carry out similar braiding transformations of Majorana fermions, shown schematically in figure 2. The junction consists of a SP phase in the middle region with large Δ sandwiched between two WP regions with smaller Δ. In proximity-induced superconductors, the spatially dependent pairing can be realized by controlling the proximity coupling strength.
Figure 2. The WP–SP–WP topological superconductor junction. For the WP superconductor (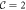 ) on the two sides, two co-propagating Majorana fermions flow on the edge. For the SP superconductor in the middle,
) on the two sides, two co-propagating Majorana fermions flow on the edge. For the SP superconductor in the middle, 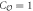 , a pair of Majorana fermions are counter-propagating. A potential barrier (shaded region) is located at the interface. The incoming electrons from leads A and B propagating along the edge are detected in leads C and D. Here
, a pair of Majorana fermions are counter-propagating. A potential barrier (shaded region) is located at the interface. The incoming electrons from leads A and B propagating along the edge are detected in leads C and D. Here 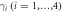 and
and 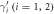 label the corresponding Majorana edge modes.
label the corresponding Majorana edge modes.
Download figure:
Standard image High-resolution imageAccording to the above edge theory, each edge hosts two Majorana modes, e.g. γ1 and γ2 in the WP region and γ3 and γ4 in the SP region (see figure 2). Note that at the interfaces between WP and SP phases, a pair of modes γ1 (or  ) and γ3 co-propagate, in contrast to the proposal in [19]. However, their spinor wavefunctions are orthogonal to each other, and their spatial overlap is exponentially suppressed by introducing a potential barrier controlled by a gate. Hence their couplings can be neglected. Consider four external leads, A to D, attached to the junction. A complex fermion (say an electron) φA injected from lead A becomes fractionalized into two Majorana fermions,
) and γ3 co-propagate, in contrast to the proposal in [19]. However, their spinor wavefunctions are orthogonal to each other, and their spatial overlap is exponentially suppressed by introducing a potential barrier controlled by a gate. Hence their couplings can be neglected. Consider four external leads, A to D, attached to the junction. A complex fermion (say an electron) φA injected from lead A becomes fractionalized into two Majorana fermions, 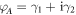 . γ1 and γ2 follow different propagation paths, e.g. γ2 will reach lead D while γ1 cannot. Similarly, electron from lead B gives rise to
. γ1 and γ2 follow different propagation paths, e.g. γ2 will reach lead D while γ1 cannot. Similarly, electron from lead B gives rise to 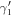 and
and 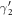 . The outgoing electron states in leads C and D, which are spatially separated, then become entangled. As the wave packet of the injected electron evolves, γ2 will ditch its original partner γ1 and merge with
. The outgoing electron states in leads C and D, which are spatially separated, then become entangled. As the wave packet of the injected electron evolves, γ2 will ditch its original partner γ1 and merge with 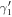 to form an outgoing electron in lead D.
to form an outgoing electron in lead D.
Compared to the braiding of Majorana zero modes in the vortex core, braiding of Majorana edge modes is due to the effective exchange of these edge channels during the propagation through the junction. Physically, in the low-current limit, as shown in [19], using the occupation number 0 and 1 as the qubit states for the leads (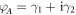 ,
, 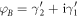 ,
, 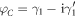 ,
, 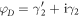 ), the unitary evolution of switching Majorana partners is identical mathematically to braiding of these qubits and the unitary transformation between the four leads can be shown to be
), the unitary evolution of switching Majorana partners is identical mathematically to braiding of these qubits and the unitary transformation between the four leads can be shown to be
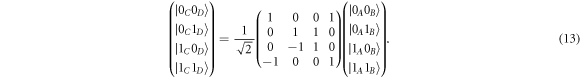
Further, if we constrain to the odd-parity or even-parity subspace, the above unitary transformation is exactly a topologically protected Hadamard gate H followed by a Pauli-Z gate. Key to this process is the non-local nature of Majorana fermions.
6. Discussions
We have demonstrated a scenario of topological transitions in a p-wave superconductor model, in which the Majorana edge modes change from co-propagating to counter-propagating. The bulk topological invariant and edge theory are worked out in detail and the implications of these results to topological quantum computing are discussed. While the proposal of [19] requires all edge states to be chiral, here we show that pairs of counter-propagating Majorana edge modes protected by symmetry can also be used to braid Majorana fermions for topological quantum computing.
Besides superconducting proximity structures, our model (2) can also be potentially realized in quantum gas experiments. The base Chern insulator 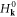 has been realized in 2D retro-reflected optical Raman lattice [36, 37] with highly controllable synthetic spin–orbit coupling [47] and a long lifetime. One way to induce the desired px-wave pairing is to couple the fermionic atoms with a Bose gas [48, 49] or the p-orbital degrees of freedom [50, 51]. Another approach is based on degenerate dipolar Fermi gases [52, 53] where px-wave pairing is natural by tilting the dipole towards the x-axis. The challenge then is to create spin–orbit coupling, as achieved recently for dysprosium [54], and integrate it with optical lattice. While experimental realization of our model seems demanding at current stage, our main goal here is to theoretically explore the role of symmetries on the tunability of Majorana edge modes. The mechanism of inducing topological phase transition in each symmetry subspace is general and can be extended to other symmetry classes and models.
has been realized in 2D retro-reflected optical Raman lattice [36, 37] with highly controllable synthetic spin–orbit coupling [47] and a long lifetime. One way to induce the desired px-wave pairing is to couple the fermionic atoms with a Bose gas [48, 49] or the p-orbital degrees of freedom [50, 51]. Another approach is based on degenerate dipolar Fermi gases [52, 53] where px-wave pairing is natural by tilting the dipole towards the x-axis. The challenge then is to create spin–orbit coupling, as achieved recently for dysprosium [54], and integrate it with optical lattice. While experimental realization of our model seems demanding at current stage, our main goal here is to theoretically explore the role of symmetries on the tunability of Majorana edge modes. The mechanism of inducing topological phase transition in each symmetry subspace is general and can be extended to other symmetry classes and models.
Acknowledgments
This research is supported by NSF PHYS-1707484 and AFOSR Grant No. FA9550-16-1-0006.