Abstract
There is increasing experimental interest in mechanotransduction in multi-cellular tissues as opposed to single cells. This is driven by a growing awareness of the importance of physiologically relevant three-dimensional culture and of cell–cell and cell–gel interactions in directing growth and development. The paradigm biophysical technique for investigating tissue level mechanobiology in this context is to grow model tissues in artificial gels with well-defined mechanical properties. These studies often indicate that the stiffness of the encapsulating gel can significantly alter cellular behaviours. We demonstrate here potential mechanisms linking tissue growth with stiffness-mediated mechanotransduction. We show how tissue growth in gel systems generates points at which there is a significant qualitative change in the cellular stress and strain experienced. We show analytically how these potential switching points depend on the mechanical properties of the constraining gel and predict when they will occur. Significantly, we identify distinct mechanisms that act separately in each of the stress and strain fields at different times. These observations suggest growth as a potential physical mechanism coupling gel stiffness with cellular mechanotransduction in three-dimensional tissues. We additionally show that non-proliferating areas, in the case that the constraining gel is soft compared with the tissue, will expand and contract passively as a result of growth. Central compartment size is thus seen to not be a reliable indicator on its own for growth initiation or active behaviour.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Mechanical interactions are now known to play a role in tissue growth and development [1, 2]. This awareness has driven a rapid expansion in the development of advanced biophysical techniques that probe the responses of cells to physical cues and to measure cell derived forces, including e.g. traction force microscopy, optical tweezers, molecular force sensors and atomic force microscopy-based approaches [3–7]. In parallel there has been much success in developing engineered tissue scaffolds that can be used in conjunction with cell experiments to control the physical properties of the cellular microenvironment, including substrate stiffness [8, 9], topology [9, 10] and ligand density and patterning [6, 11]. These advances together have demonstrated that a plethora of individual cellular behaviours respond to physical cues [12–14], with gel stiffness identified as a key control parameter. Indeed, it has even been demonstrated that cells can actively adapt gel stiffness to this end [15].
A potential explanation for the role of gel stiffness in controlling cellular behaviour is that stiffer gels alter the stress, and significantly the stretch, experienced by contractile cells. This hypothesis has been tested across cell types using stretch-based assays [16]. For example, [17] clearly demonstrates that stretch activates and promotes cell division. Other instances in the literature include tissues under stretch or compression affecting cytoskeletal fluidisation [18] or cell alignment and reorientation [19]. A range of potential molecular pathways have also been identified for cellular force transduction with focal adhesions (FAs) identified as a key structural component [20–22]. Despite this focus on FAs, there is an emerging realisation of the role of stretch activation across the whole cell including in chromatin [23] and at the nuclear envelope [24].
What has become evident as a result of these studies is that cells behave very differently in multi-cellular structures where cell–cell communication and coordination generates additional complexities, as compared with their behaviours in isolation. A key feature of this is that multi-cellular structures change how force can be generated and transmitted as opposed to studies involving single cells. For example, Sunyer et al [25] have demonstrated that cellular communities will exhibit durotaxis even where single cells cannot, while Trepat et al [26] showed that the force distributions within such migrating colonies are significantly altered by the cell–cell attachments. This effect is only further enhanced in three-dimensions where the geometry also alters the stress and strain distribution, with clear changes in tissue development in three-dimensional over two-dimensional environments [27–29]. Experimentally, biophysical investigations in three-dimensions tend to focus on in vitro tissue culture using carefully engineered gels to change the mechanical properties of the tissue environment. There are many paradigm tissues that can be investigated in this way with some of the most popular including avascular tumour spheroids [16, 30–32] and epithelial cyst cultures [33–35] across a range of cell types. Another similar tissue also investigated using in vitro culture is the ovarian follicle [36]. In each of the three paradigm systems, there is significant evidence that the material properties of the gels used for tissue culture affect cell behaviours within the tissue. Avascular tumours are arguably the most studied from this perspective, with many results showing that the stiffness of the gel alters tumour development [16, 30, 32, 37]. Similar studies, however, have also shown that, for example, gel stiffness can affect cyst growth and lumen formation [33, 38] and oocyte development [36].
We focus here on how tissue growth changes the stress and strain distribution in three-dimensional culture. We focus on the period following growth initiation as a results of e.g. biochemical signalling [39], stress relaxation in gel matrices [30, 40], or capillary growth [41]. We thus assume that the deformations are small enough following growth that we can use linear elasticity. To model growth, many different approaches have been developed, see for example the excellent review articles [42, 43]. We adopt a method based on decomposing the deformation tensor, introducing an interim 'target' stress-free configuration for the growing tissue, from which the grown tissue is elastically deformed, see figure 1. The decomposition method is usually combined with a nonlinear elastic constitutive relationship to account for long time growth [44–46], but the use of linear elasticity additionally enables us to obtain analytical expressions for potential mechanotransductive switching points. Linear elasticity-based models have frequently been used to model avascular tumour growth over longer time periods than those discussed here, although not in combination with decomposition, see e.g. [47–49]. We highlight, however, the linear elasticity based model described in [50] for a non-structured solid tumour, which can be shown to be formally equivalent to adopting a decomposition approach.
Figure 1. (a) In vitro tissue culture of multicellular tissues in an encapsulating gel. Γc, Γt and Γg represent the central region (green), proliferating tissue (blue) and the outer gel region (white), respectively. (b) Schematic representation of the decomposition approach to modelling growth, with tissue again assumed to be growing in an encapsulating gel. The growing shell is initially in configuration S0 with inner and outer radii r0 and r1, respectively, and after growth and deformation adopts the configuration Sd. The interim configuration Sg represents the configuration the proliferating shell would adopt if entirely released from stress, i.e. an idealised target configuration.
Download figure:
Standard image High-resolution imageWe identify separate mechanisms in each of the strain and stress fields where growth generates significant moments of qualitative change. In the first stress-based mechanism, we show that, where the effective stiffness of the gel is softer than that of the tissue, the inner compartment initially experiences a tensile radial pull before switching to compression at a time when the tissue expansion matches the ratio of effective stiffnesses. In contrast, where the gel is stiffer than the tissue, the entire tissue (including inner compartment) experiences compression throughout. In the radial strain field, we show that the tissue stretch can remain positive even when the radial stress is compressive but as the tissue grows this strain will also change sign, changing from stretch to compression. This strain-based switching point in the growing tissue will in general be at a different point to the stress-based mechanism, due to that fact that the stress depends on both the radial and azimuthal strains. We suggest that these points of qualitative change could represent robust switching points in the system. That the switching points each depend on the encapsulating gel stiffness has the potential to explain experimental observations of stiffness mediated tissue growth. We finally consider, in section 3.3, the central region and show that where the central region is deformable or empty, and the constraining gel is soft, this region will expand passively without internal growth or active processes. This highlights that tissue size is not a reliable indicator of growth with the need rather for additional biomarkers to confirm proliferative activity.
2. Elasticity model for encapsulated growing tissues
We consider a spherical system consisting of a tissue with a central compartment, a proliferating shell and an encapsulating gel (as depicted in figure 1(a)). This models experimental systems such as epithelial cysts, tumour spheroids or ovarian follicles in in vitro tissue culture. Specifically, epithelial acini (cysts) typically form a hollow shell with a fluid or gas filled central lumen, a structure observed in multiple tissue types including kidneys, lungs and mammary glands [29, 35]. Tumour spheroids begin as a proliferating ball of cells, however, as the tissue size increases the nutrients begin to be depleted nearer the centre so that eventually these tissues have a core of non-proliferating and necrotic cells [51]. Ovarian follicles are again spherically symmetric with an outer proliferating shell which now surrounds a single central oocyte, where we note that the oocyte is stiff compared with the tissue [52]. We look for points where the growth generates a qualitative change in either the stress or the strain. For example, where a cell under compression switches to being under tension. These are considered as potential robust switching points since a qualitative change in sign enables distinct molecular mechanisms to be employed. To do this we adopt a continuum linear elasticity approach solving for the displacements in both the gel and tissue and thus determining the strain and stress fields. The assumption of isotropic linear elasticity is of course a simplifying assumption when considering the constitutive response of the complex fibrous and viscoelastic nature of ECM [3]. Indeed the nonlinearity of biopolymer gels has been shown to have important implications for cell biomechanics, for example, it can increase the long-range interactions between embedded cells [53, 54]. However, the linear assumption is common in biophysics, in particular in combination with experimental assays where the data rarely justify the use of more complicated models.
Note that as the radial stress and strain are not simply proportional to each other, the system can have distinct critical points in each of stress and strain and these are considered separately in the discussion below. To see this, consider a force in the radial direction compressing a sphere; this force will generate strains in both the radial direction and also circumferentially around the sphere to accommodate the compression. The relationship between the radial stress σrr and radial strain  rr and circumferential strain
rr and circumferential strain  is described by the constitutive relation
is described by the constitutive relation
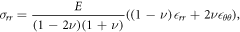
where E is the Young's modulus with units of kPa, and ν is the Poisson's ratio [55]. We can see that at the point where  rr = 0, we will, in general, not have σrr = 0.
rr = 0, we will, in general, not have σrr = 0.
2.1. Tissue growth
The shape changes that are observed as a tissue grows are in fact a combination of two physical processes, an increase in tissue volume and the consequent deformations due to mechanical interactions. To account for this within the framework of continuum elasticity theory we adopt the method of decomposition [42, 43, 45, 46]. This widely adopted approach explicitly separates the two physical processes into a growth phase and an elastic deformation, exploiting the separation of timescales between growth and elastic response. Specifically, we introduce an interim configuration Sg which is the configuration the tissue would adopt due to volume increase alone if all stresses were relaxed from every material element, see figure 1(b). The stresses are then calculated by considering how far from this target stress-free configuration Sg the tissue is currently observed to be (in configuration Sd). Throughout we assume volumetric isotropic growth so that there is no preferred direction of growth for the tissue.
Before considering complex structured tissues, we first consider as an instructional example a solid spherical tissue of unit radius that grows by 10%; in this case, if the growth is unconstrained, for example in a fluid medium, the tissue radius r1 would consequently increase to r1  1.03. However, if we now consider the growth within a constraining gel we can expect that the observed radius would be
1.03. However, if we now consider the growth within a constraining gel we can expect that the observed radius would be  due to compression from the outside gel. Indeed in the limit of an infinitely stiff gel culture we see that r1 = 1, where the unit radius now corresponds to a significant compression as compared with the target volume increase of 10%. Using the decomposition approach, the stress experienced within the tissue is calculated based on this difference from the target expanded state.
due to compression from the outside gel. Indeed in the limit of an infinitely stiff gel culture we see that r1 = 1, where the unit radius now corresponds to a significant compression as compared with the target volume increase of 10%. Using the decomposition approach, the stress experienced within the tissue is calculated based on this difference from the target expanded state.
In this paper, we consider structured tissues such as epithelial acini, tumour spheroids or follicles, which share a common morphology of a central non-growing core region surrounded by an outer layer of proliferating cells. In each of these cases the proliferating tissue forms a growing spherical shell (so that by spherical symmetry we can see that all deformations must be a function of radial direction only). Consider volumetric growth, where the material expands uniformly and isotropically so that every microscopic element making up the material expands its linear dimensions by a factor λ. Thus λ = 1 corresponds to no growth and e.g. when λ = 21/3 ≈ 1.3 each tissue element has doubled in volume. Now it follows in spherical coordinates that the original configuration [r, θ, ϕ] maps to the intermediate configuration [λr, θ, ϕ], figure 1(b) (see e.g. [46, 56]). It is worth reiterating that this swollen configuration is not observed in reality but is only the target configuration for the tissue. Note that as the factor λ models growth, λ is assumed to be varying (indeed monotonically increasing) with time as the tissue grows. Importantly, however, λ is slowly varying with respect to the elastic response (the essential assumption of decomposition theory) so that we need only solve for the static mechanical equilibrium.
For an alternative visualisation of how volume increase drives a radial expansion in this interim configuration, consider a spherical shell of material at radial position rA. As each volume element swells isotropically due to growth, the extra material must still, by symmetry, be accommodated into a spherical shell. Since the material cannot be compressed as this would violate the zero stress condition of the interim configuration, the spherical shell must increase in size, i.e. the radius must increase, and in fact scales with λ. This holds at all values of rA, hence a consequence of isotropic swelling is that the central hole naturally increases in size (in the interim configuration) as the inner radius scales with λ. This enlargement under expansion is analogous to the well-known fact that a metal pipe increases its diameter under thermal expansion (something that must be taken into account when joining pipes with different coefficients of thermal expansion). Within tissues, the idea that swelling and growth of a tube can increase the target radius (i.e. reduce curvature) was demonstrated experimentally by Fung (see [57]) in his seminal tissue cutting experiments on e.g. arteries and hearts, where he observed that a stress-free configuration necessitates a larger target radius with reduced tissue curvature.
2.2. Model for elastic deformations
Assuming linear elasticity, the stress tensor σij and strain tensor  ij satisfy the force balance equation
ij satisfy the force balance equation
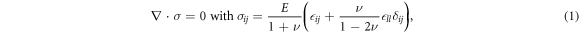
where the summation convention applies for repeated indices. Spherical symmetry implies that all displacements are in the radial direction so that  and that
and that ![$[r,\theta ,\phi ]\to [r+u(r),\theta ,\phi ]$](https://content.cld.iop.org/journals/1367-2630/20/4/043041/revision1/njpaab7e6ieqn5.gif) . The only non-zero strains are thus the radial component
. The only non-zero strains are thus the radial component  rr = du/dr and circumferential components
rr = du/dr and circumferential components  , which when substituted into (1) and integrated gives
, which when substituted into (1) and integrated gives  , where A, B are constants.
, where A, B are constants.
In the encapsulating gel (r > r1) we denote the displacement by ug(r), and find on applying the boundary condition  that
that
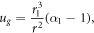
where  is the current observed position of the interface between outer gel and growing tissue.
is the current observed position of the interface between outer gel and growing tissue.
In the central compartment r < r0, in the case where this is deformable, the deformation is denoted by uc(r) and found (on applying the boundary condition uc(0) = 0) to be
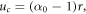
where  is the current observed radius of the inner compartment. Note that where the centre can be assumed to be infinitely stiff, as for example, would be the case for the ovarian follicle, uc(r) = 0 and α0 = 1, and it is shown in appendix B that this is the limiting solution of the full problem as the Young's modulus of the centre
is the current observed radius of the inner compartment. Note that where the centre can be assumed to be infinitely stiff, as for example, would be the case for the ovarian follicle, uc(r) = 0 and α0 = 1, and it is shown in appendix B that this is the limiting solution of the full problem as the Young's modulus of the centre  .
.
The only non-zero components of the stress tensor in the outside encapsulating gel are
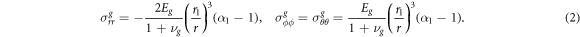
In the centre we have the constant solution
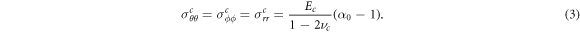
The unknown constants α0 and α1 are to be determined by continuity of stress with the growing shell.
2.3. Elastic deformations in the growing phase
Here we shall introduce the subscript t to denote the solution in the growing tissue region. The radial displacement that determines the elastic response is in this case the displacement from the interim grown configuration ![$r\in [\lambda {r}_{0},\lambda {r}_{1}]$](https://content.cld.iop.org/journals/1367-2630/20/4/043041/revision1/njpaab7e6ieqn12.gif) , due to the decomposition, and this displacement is denoted ut(r). ut(r) can be found similarly to section 2.2 as
, due to the decomposition, and this displacement is denoted ut(r). ut(r) can be found similarly to section 2.2 as
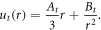
The radial component of the stress in this case in the interim configuration is
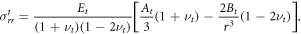
To determine the unknown constants At, Bt, along with α0, α1, we apply continuity conditions at the inner and outer boundaries as detailed in appendix A for an undeformable central compartment and in appendix B for a deformable central compartment. Note that as the deformations in the growing phase are considered relative to the interim configuration, the assumption of small strain can hold at relatively large values of λ depending on the deformations induced by the constraining gel.
3. Results and discussions
3.1. Stress-based mechanotransduction in the central compartment
Focusing first on the mechanical stress that the growing tissue and central compartment experience as growth progresses, we introduce the parameter
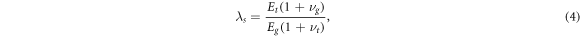
which, given that the Poisson's ratio of cells and matrix are in most circumstances likely to be very similar (typically in the range ν = 0.45 to ν = 0.49 [58]), quantifies the relative stiffnesses of the constraining gel and growing tissue. λs < 1 thus in practice translates to the circumstance of the outside constraining gel being stiffer than the growing tissue, while λs > 1 implies that the growing tissue is stiffer than the outside gel. We will consider these two cases separately as we will show that the stress experienced within the tissue differs markedly in each of these two regimes.
Consider first the case where the tissue is softer than the gel ( ) and in which the centre is rigid. We plot in figures 2(a), (b) typical profiles for the stresses σrr and
) and in which the centre is rigid. We plot in figures 2(a), (b) typical profiles for the stresses σrr and  , parameter values given in the figure caption (Young's modulus measured in
, parameter values given in the figure caption (Young's modulus measured in  ). We see in this case that the radial stress is uniformly compressive and at a maximum at the outer radius of the tissue, and the circumferential stresses are also compressive but with a maximum at the inner radius. The stress increases in magnitude as tissue grows, i.e. as λ increases. In particular, on the growth initiation of the surrounding tissue, the inner compartment, which may be considered to be e.g. the central oocyte of an ovarian follicle, experiences an immediate compressive radial stress, which increases over time as the tissue grows.
). We see in this case that the radial stress is uniformly compressive and at a maximum at the outer radius of the tissue, and the circumferential stresses are also compressive but with a maximum at the inner radius. The stress increases in magnitude as tissue grows, i.e. as λ increases. In particular, on the growth initiation of the surrounding tissue, the inner compartment, which may be considered to be e.g. the central oocyte of an ovarian follicle, experiences an immediate compressive radial stress, which increases over time as the tissue grows.
Figure 2. Spatial variation of the radial and circumferential stresses for an undeformable centre. Each line represents a different value for the growth factor λ, with λ = 1.05, 1.15, 1.25, 1.35 plotted in blue, green, red and light blue, respectively. For λs < 1 in (a), (b) the radial component of the stress is uniformly compressive, while for λs > 1 in (c), (d) the inner compartment initially experiences tension for a period of growth. Parameter values are in (a), (b) λs = 0.59 (Eg = 5 and Et = 3) and in (c), (d) λs = 1.96 (Eg = 5 and Et = 10). Note stresses are only considered in the region r ≥ r0, with  and
and  corresponding to the growing tissue and the constraining gel, respectively, and
corresponding to the growing tissue and the constraining gel, respectively, and  , νt = 0.46.
, νt = 0.46.
Download figure:
Standard image High-resolution imageIn stark contrast, if the tissue is stiffer than the surrounding gel (λs > 1), then initially at the inner surface there is a positive radial stress, indicating that the central compartment initially experiences a pulling force, while the circumferential stresses remain compressive, see figures 2(c), (d). At the outer surface r = r1, it can be seen from figure 2(c) that the radial stress is compressive, and that within the growing region there is a radius at which the stress is zero. As the tissue continues to grow, i.e. as λ increases, it can be seen that the compressive stress at the outer surface increases, and the radius at which σrr = 0 decreases.
We plot in figure 3 the radial and circumferential stresses at the inner radius in the regime λs > 1. Significantly the radial stress at this inner boundary is initially positive, so that the inner compartment is initially pulled outwards. This pulling force increases with growth until a maximum is reached, after this the radial stress decreases to zero before becoming negative so that the inner compartment now experiences a compressive force towards its centre.
Figure 3. Growth dependent evolution of the (a) radial stress σrr and (b) circumferential stress σθ θθ at the inner boundary with λs > 1. The radial stress switches sign when λ = λs changing from tension to compression (tensile region represented by the dotted line). Parameter values νg = 0.45, νt = 0.46, Eg = 5 and Et = 10 (corresponding to λs = 1.96) and with an undeformable centre. λ = 1 is the initial configuration.
Download figure:
Standard image High-resolution imageTo find the critical value of growth at which such a qualitative switch could occur, we set  in the solution from appendix A to obtain the following quadratic equation for the critical values of λ
in the solution from appendix A to obtain the following quadratic equation for the critical values of λ
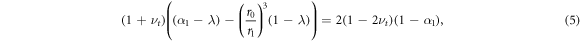
with α1(λ) given by (A.1). This has roots λ = 1, corresponding to the initial conditions of no growth and zero stress, and λ = λs. Thus we see that the point at which the radial stress at the inner surface switches from a tensile to a compressive force is λ = λs, thus giving an a posteriori justification for the significance of the parameter λs. This then can be termed a switching point of the system.
For a structured tissue with a deformable central compartment, corresponding to the solution presented in appendix B, similar dynamics are observed, see ESI figures S1, S2 available online at stacks.iop.org/NJP/20/043041/mmedia. Significantly, the parameter λs plays the same role as before. For λs < 1 the inner compartment experiences uniform compression, if λs > 1 then the inner compartment initially experiences tension before switching to compression once the growth parameter passes a critical threshold. To show this, we set  using the solution from appendix B to obtain a cubic equation corresponding to (5) for the critical values of λ
using the solution from appendix B to obtain a cubic equation corresponding to (5) for the critical values of λ
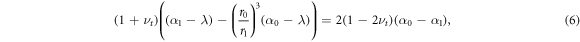
with α0 and α1 given now by (B.1) and (B.2). The solutions of (6) are λ = λs, λ = 1 (i.e. the initial conditions of zero stress, no growth) and λ = 0, which is unphysical. That λs plays the same role as before is initially surprising, however, it is clear that the switching condition for which the radial stress at the inner surface changes sign must be the same, for at this point the inner surface is transmitting zero stress and so the properties of the central region can have no influence on the mechanical equilibrium achieved.
We thus see, in both cases considered, that when the material surrounding the growing structured tissue is softer than the growing tissue, a new and interesting mechanism for growth induced mechanotransduction is introduced. In this case, the central compartment will initially experience tension as the tissue grows, before switching to compression when the growth is such that  . A switching mechanism based on such significant qualitative change has the potential to be particularly robust. Biological tissues vary greatly in their measured Young's modulus (ranging anything from kPa to MPa) for different tissues [44, 59–61], so the Young's modulus is relatively unconstrained, however note that it is only the relative stiffness of gel and tissue that determines the switching point. Equally, λs is independent of the shell thickness. The shell thickness and the respective Young's moduli and Possion's ratios, however, do determine the magnitude of the stress in each case. Experimentally changing the material properties of the external constraining gel would change λs and could potentially take this parameter through the critical threshold of λs = 1 generating significant change in the system.
. A switching mechanism based on such significant qualitative change has the potential to be particularly robust. Biological tissues vary greatly in their measured Young's modulus (ranging anything from kPa to MPa) for different tissues [44, 59–61], so the Young's modulus is relatively unconstrained, however note that it is only the relative stiffness of gel and tissue that determines the switching point. Equally, λs is independent of the shell thickness. The shell thickness and the respective Young's moduli and Possion's ratios, however, do determine the magnitude of the stress in each case. Experimentally changing the material properties of the external constraining gel would change λs and could potentially take this parameter through the critical threshold of λs = 1 generating significant change in the system.
3.2. Strain-based mechanotransduction mechanism in the growing compartment
Considering now how growth could generate qualitative changes in cellular strain, we see that the circumferential strains  within the growing tissues are always negative as a constraining gel will always induce negative displacements relative to the grown configuration. Considering the radial component of strain (in the case of a rigid central compartment) we find that
within the growing tissues are always negative as a constraining gel will always induce negative displacements relative to the grown configuration. Considering the radial component of strain (in the case of a rigid central compartment) we find that
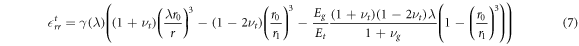
within the growing region ![$r\in [\lambda {r}_{0},\lambda {r}_{1}]$](https://content.cld.iop.org/journals/1367-2630/20/4/043041/revision1/njpaab7e6ieqn23.gif) , where
, where
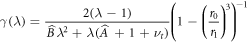
and we note that γ(λ) > 0 everywhere. Plots of this radial strain are shown in figure 4(a).
Figure 4. (a) The radial strain in the growing region with  . Lines represent different values of growth parameter λ = 1.05, 1.15, 1.25, 1.35 plotted in dark blue, green, red, light blue, respectively (Et = 10). (b) Radial strain at the inner boundary of the growing outer shell. Here each line is a different value of Et, with Et = 0.1, 0.4, 2, 10 plotted in dark blue, green, red, light blue, respectively. Note that the radial strain can switch from positive to negative as growth progesses. Other parameter values are νg = 0.45, νt = 0.46, Eg = 5, in both (a), (b).
. Lines represent different values of growth parameter λ = 1.05, 1.15, 1.25, 1.35 plotted in dark blue, green, red, light blue, respectively (Et = 10). (b) Radial strain at the inner boundary of the growing outer shell. Here each line is a different value of Et, with Et = 0.1, 0.4, 2, 10 plotted in dark blue, green, red, light blue, respectively. Note that the radial strain can switch from positive to negative as growth progesses. Other parameter values are νg = 0.45, νt = 0.46, Eg = 5, in both (a), (b).
Download figure:
Standard image High-resolution imageIn contrast to the circumferential strains, this radial strain can be positive and this can occur even when the radial component of stress is negative. To see this, consider first the case of a thin shell where r1 = r0 + δ, δ ≪ 1, which gives  for all values of the material properties. This counter-intuitive result can be understood in the context of the compressive circumferential strains. Given that the material is not infinitely compressible, these necessitate an expansion (or 'squeezing out' of the material) in the radial direction for these thin shells, even in the presence of compressive radial forces.
for all values of the material properties. This counter-intuitive result can be understood in the context of the compressive circumferential strains. Given that the material is not infinitely compressible, these necessitate an expansion (or 'squeezing out' of the material) in the radial direction for these thin shells, even in the presence of compressive radial forces.
As for stress, there is the possibility for strain to also exhibit sign switching under the action of growth, introducing an additional potential mechanotransductive mechanism linked to tissue growth in these structured tissues. To see this, consider again  as given by (7); this is a decreasing monotonic function of r (within the growing region
as given by (7); this is a decreasing monotonic function of r (within the growing region ![$r\in [\lambda {r}_{0},\lambda {r}_{1}]$](https://content.cld.iop.org/journals/1367-2630/20/4/043041/revision1/njpaab7e6ieqn27.gif) ) with a zero at
) with a zero at  where
where

For  the radial strain will be positive (indicating stretch) and for
the radial strain will be positive (indicating stretch) and for  the radial strain will be negative. The condition that positive radial strains exist within the growing region is thus that
the radial strain will be negative. The condition that positive radial strains exist within the growing region is thus that  , i.e. that the radius at which zero strain is felt lies in r > λ r0. However, as η(λ) is an increasing function, we see that eventually, at some value for the growth λ, these positive strains will be lost and that there will be a qualitative switch from positive to negative strains as the encapsulating gel begins to dominate. We note that this switching mechanism is controlled not just by the relative stiffnesses of the tissue and gel, but also by the thickness (r0/r1) of the proliferating shell.
, i.e. that the radius at which zero strain is felt lies in r > λ r0. However, as η(λ) is an increasing function, we see that eventually, at some value for the growth λ, these positive strains will be lost and that there will be a qualitative switch from positive to negative strains as the encapsulating gel begins to dominate. We note that this switching mechanism is controlled not just by the relative stiffnesses of the tissue and gel, but also by the thickness (r0/r1) of the proliferating shell.
Any such change in strain can underpin a stretch-activated mechanism of switching as it will induce molecular conformation changes at this point, see figure 4(b). Interestingly, in contrast to the stress-based mechanism this qualitative strain switching can occur even if the tissue is softer than the constraining gel, see figure 4(b). This behaviour may thus be more likely in vivo as the surrounding stiffness of tissues is typically softer than that of in vitro gels [59].
3.3. Central region growth or shrinkage driven by outer shell growth
When the outer gel is softer than the growing tissue (λs > 1), an additional consequence of the positive stress on the inner boundary is that the inner compartment can increase in size. This occurs even in the absence of material growth in this region, at least in the case that Ec is finite. To see this, we plot in figure 5(a) α0 as a function of the growth parameter λ. Where α0 > 1, this corresponds to an expansion of the inner compartment due to the shell expansion pulling it outwards. In this case, it might appear that there has been growth initiation in this central compartment, but in fact the inner region has expanded merely as a result of the stretch exerted by the outside tissue. This has particular significance in considerations of growth initiation, for example, in ovarian follicles, where an increase in oocyte size cannot alone be taken as a marker of growth initiation. This highlights the need for a full consideration of mechanics in interpreting the experimental data and the need for additional biologic readouts in interpreting growth data.
Figure 5. Expansion of the inner core as a function of the growth factor λ. α0 < 1 corresponds to the core shrinking and α0 > 1 corresponds to expansion. (a) For an inner deformable elastic core (Ec = 6), note that for a sufficiently stiff tissue there is a significant period of core growth before the external gel overcomes the tissue expansion. (b) Expansion factor for an interior void (epithelial cyst) again demonstrating significant lumen expansion due to the expansion of the proliferating rim in stiff tissues. In (a), (b) Et = 1,4,10,20 plotted in dark blue, green, red, light blue, respectively. (Other parameter values are νg = 0.45, νt = 0.46, νc = 0.45, Eg = 5, and in (a)  and in (b)
and in (b)  .)
.)
Download figure:
Standard image High-resolution imageIt is interesting to also compare this with the case where the central region is empty (so that we apply a zero stress boundary condition at the inner boundary), as is the case for an epithelial cyst. We plot this expansion factor α0 in figure 5(b) for different values of tissue stiffness Et with  . For all values of λs the model predicts that even without additional mechanical forces the central lumen will close (α0 → 0) when
. For all values of λs the model predicts that even without additional mechanical forces the central lumen will close (α0 → 0) when

although this may in practice be a point beyond the validity of the linear model, see figure 5(b). Variations in shell thickness have a weak influence on the expansion factor α0 as compared with variations in the constraining gel stiffness in this initial phase of growth. For example, for a growth factor of λ = 1.2, unless the outer gel is relatively soft, once  changes in shell thickness do not have a discernable affect on α0 for both the hollow centre and deformable centre cases, see ESI figures S3(a), (b).
changes in shell thickness do not have a discernable affect on α0 for both the hollow centre and deformable centre cases, see ESI figures S3(a), (b).
4. Conclusions
We have considered here biophysical studies of tissue growth in three-dimensions, which involve tissue culture within encapsulating gel matrices. We have specifically considered three paradigm tissue types that are commonly studied: avascular tumours, epithelial cysts and ovarian follicles. By developing a continuum elasticity model incorporating growth, we have demonstrated two new mechanisms by which initiation of growth in the outer shell could provide mechanical feedback throughout the growing tissue.
In the first case we considered the distribution of radial stresses in the tissue. We showed that where the constraining gel is softer than the tissue, there will be a stress experienced at the inner compartment that switches from tension to compression as the tissue grows. We identified that this will occur when the tissue has grown by a factor λs, where λs quantifies the relative stiffnesses of the gel and tissue.
The second mechanism is a strain-based mechanism situated within the growing compartment. Potentially counterintuitively, we show how even when the radial stress is compressive, the radial strains can be positive, indicating a stretch in this direction. This is driven by the relatively large circumferential compressive strain dominating the deformation and squeezing out tissue radially. However, as the expansion of the shell due to growth continues, we show that this positive radial strain will reduce, eventually becoming negative as the encapsulating gel begins to dominate. This suggests a second switching mechanism based on stretch-activation at the inner interface, with a stretch-activated channel being turned off as the tissue grows and the stretch is released. Significantly, this mechanism is controlled not just by the elastic properties of the tissue and gel but also depends on the shell thickness.
Both mechanisms have switching points dependent on the Young's modulus and Poisson's ratio of the tissue and gel. Thus, when the stiffness of the gel changes, the switching point will be moved to a higher or lower value, changing the observed dynamics, or alternatively taking the switching point outside of the achievable parameter space, so that the switch is removed entirely. This would, for example, be the case in the stress-based switch when a stiff gel was used such that the tissue stiffness was less than the constraining gel. We note that the strain-based switch and the stress-based switch do not, in general, occur at the same point, opening up the possibility for multiple mechanisms to act in parallel.
The model also emphasises the need for additional markers of tissue growth and retardation, apart from simple measurements of tissue size. We have shown how the expansion of the growing outer tissue shell can pull the inner compartment outwards, even when the central compartment is not growing. Thus, for example, an observation of oocyte expansion in follicles cannot be taken as a sufficient indication of growth initiation in the follicle, with growth needing to be additionally verified by suitable biomarkers. Equally, for epithelial cysts, lumen expansion or early closure can be seen to be a potentially passive response governed by the dynamics of the expanding shell at these early stages of growth. Studies such as [33] showing e.g. delay in lumen growth in response to stiffer gels, thus do not necessarily imply the need for active mechanical feedback. This emphasises the need to incorporate careful theoretical considerations of the mechanics of tissue growth into experimental studies on multicellular growth and mechanotransduction.
Although the results presented here are theoretical, they suggest experimental investigations which could, in principle, be used to verify the results. To compare the predicted stress and strain distributions to in vitro culture models is challenging as despite the plethora of techniques available for measuring forces in two-dimensions, most are not directly applicable in three-dimensions. There are, however, methods newly developed which can successfully measure forces in three-dimensions, for example the oil droplet method of Campàs et al [62] or fluorescence-resonance energy transfer based force sensors in 3D, see for example Grashoff et al [63], see also Roca-Cusachs et al [7]. Equally, we see that even without validation of the force distribution, the identification of e.g.  as a key switching point of the system can be tested by altering the relative gel stiffnesses of the experimental system and looking for the predicted correlation between tissue size and behavioural change. Note that as experimental techniques improve so it could be that nonlinear elastic effects are observed, which could be incorporated within this framework.
as a key switching point of the system can be tested by altering the relative gel stiffnesses of the experimental system and looking for the predicted correlation between tissue size and behavioural change. Note that as experimental techniques improve so it could be that nonlinear elastic effects are observed, which could be incorporated within this framework.
Acknowledgments
EL acknowledges PhD funding from the UK Engineering and Physical Sciences Research Council, institutional Doctoral Training Partnership grant (EP/M508160/1). CMD also acknowledges financial support from the UK EPSRC (grant EP/M012964/1). Data Availability: the authors confirm that all data underlying the findings are fully available without restriction. The data is held at the University of Surrey and requests for access can be sent to researchdata@surrey.ac.uk.
Appendix A.: Spheroidal tissues with rigid centres
To determine the constants At, Bt, α1 we impose continuity of radial stress at the outer boundary. This requires that the stress experienced by the growing tissue in being deformed from its interim grown configuration to the final configuration equals that imposed from the outside gel, i.e. we set  , as is consistent with decomposition theory. This, in conjunction with the knowledge that for a rigid centre
, as is consistent with decomposition theory. This, in conjunction with the knowledge that for a rigid centre  and
and  (α0 = 1), gives
(α0 = 1), gives
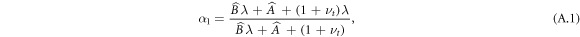
where
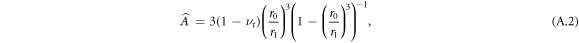
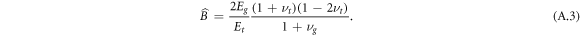
The constants At, Bt are
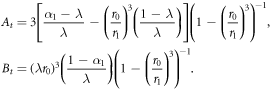
Appendix B.: Spheroidal tissues with deformable centres
For systems where the central region is deformable, we must additionally determine α0 from the continuity conditions. In this case, we set  as in appendix A and additionally take the corresponding condition at the inner boundary
as in appendix A and additionally take the corresponding condition at the inner boundary  . We also have that
. We also have that  and
and  . We thus obtain
. We thus obtain
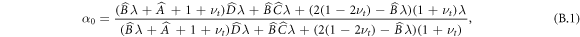

where  and
and  are given as before by (A.2), (A.3) and
are given as before by (A.2), (A.3) and
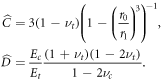
The constants At, Bt are
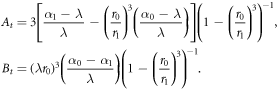
We note that as  , i.e. the limit of an infinitely stiff centre, α0 → 1 as expected, and we recover the rigid centre case from above.
, i.e. the limit of an infinitely stiff centre, α0 → 1 as expected, and we recover the rigid centre case from above.








