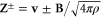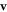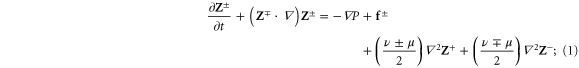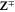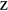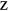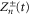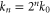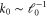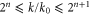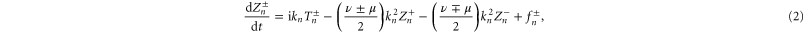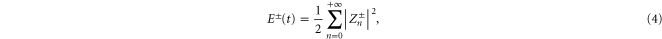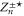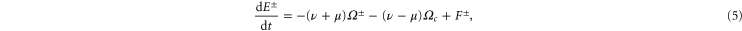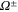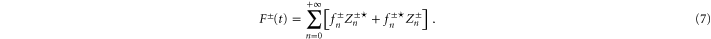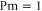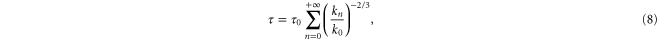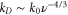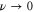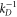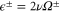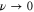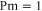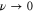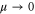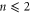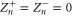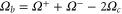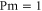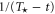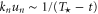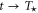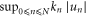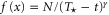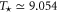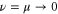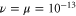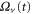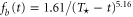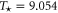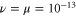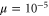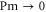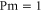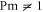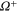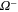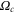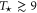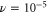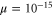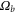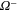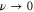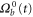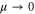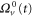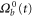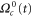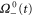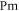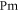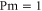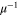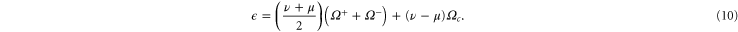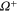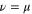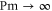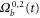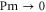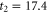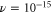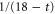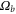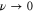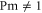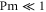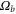Finite-time singularities and flow regularization in a hydromagnetic shell model at extreme magnetic Prandtl numbers

Turbulence is a complex and ubiquitous phenomenon, observed both in ordinary and electrically conducting fluids [1, 2]. Its complexity is due to the nonlinear cascade mechanism, the basic process of which involves a transfer of energy from the large injection scale ℓ₀ to smaller scales down to dissipative scales, exhibiting nontrivial scaling behavior [3]. Experiments suggest that the energy transfer is not steady but intermittent, hence fluctuations are amplified when the energy reaches smaller scales [4, 5]. This has been interpreted as a consequence of the spontaneous generation of isolated bursts of fluctuations at all scales [6–9] due to phase-synchronization [10]. Also it has been conjectured that bursts of activity in fluids seem to be related to development of singularities in a finite time, even for smooth forcing or smooth initial conditions [6, 7]. The hypothetical existence of singularities is the signature of a transfer of energy towards infinitesimal length scales in the limit of zero-viscosity in a finite time [1, 6, 7, 11]. The existence of these singularities is the subject of considerable debate; at present no definitive answer is available for ether ordinary or magnetohydrodynamic (MHD) flows. The lack of a conclusive answer, in part, is because the numerical experiments cannot reach high enough resolution to confirm or rule out their existence. In particular, while a two-dimentional (2D) non-magnetic incompressible ideal flow, with sufficiently regular initial data, stays regular for all times [12, 13], in the corresponding three-dimentional (3D) case it is not known [14, 15]. It has been conjectured that what may prevent, or at least slow down, a singularity is the depletion of nonlinearities: the phenomenon by which inviscid incompressible flows tend to organize themselves into structures having greatly reduced nonlinearities [16]. The tendency in MHD to form 2D structures, through current sheet formation, can be seen as a possible way to produce depletion of nonlinearities [17–19]. However the depletion may not be enough to prevent a blowup: in fact it depends on how strong this depletion is and also on how persistent it is. It is worth noting that most of the depletion mechanisms described in the literature are geometrical in origin [20].

Here we address the issue of the existence of finite time singularities from the purely dynamical point of view, i.e. not directly due to geometrical features. Accordingly, we adopt a simplified description of the dynamics that neglects spatial information but that can, on the other hand, reach an asymptotic regimes where the dissipation is vanishingly small. A suitable tool could be afforded by shell models [21], which provide a simplified description of the MHD turbulent cascade [22–30] while keeping the main dynamical properties even for extremely small or extremely large magnetic Prandtl numbers. Our strategy is to investigate if shell models, despite their simplified description, are able to capture the fundamental dynamic elements taking place in a turbulent cascade, which may lead to the formation of the avoidance of singularities. If a shell model is able to discriminate between singular and not-singular behavior, one possibility is that the mechanism controlling the formation of singularities is captured by the basic principles assumed in the derivation of shell models.

In MHD two different dissipation mechanisms are operative, the usual viscosity ν and the magnetic diffusivity μ. Their role can be made apparent by writing the MHD equations in terms of Elsässer variables ${{\bf{Z}}}^{\pm }={\bf{v}}\pm {\bf{B}}/\sqrt{4\pi \rho }$, where ρ is the constant mass density, ${\bf{v}}$ and ${\bf{B}}$ are the velocity and magnetic intensity, respectively,

$$\begin{eqnarray}\displaystyle \frac{\partial {{\bf{Z}}}^{\pm }}{\partial t}+({{\bf{Z}}}^{\mp }\cdot \nabla ){{\bf{Z}}}^{\pm }=-\nabla P & + & {{\bf{f}}}^{\pm }\\ & + & (\displaystyle \frac{\nu \pm \mu }{2}){\nabla }^{2}{{\bf{Z}}}^{+}+(\displaystyle \frac{\nu \mp \mu }{2}){\nabla }^{2}{{\bf{Z}}}^{-};\end{eqnarray} \tag{ 1 }$$

here P is the pressure and ${{\bf{f}}}^{\pm }$ are the forcing terms and ${{\bf{Z}}}^{\mp }$ describe the Alfvénic fluctuations propagating in opposite directions with respect to the large-scale magnetic field [31]. It is evident that for magnetic Prandtl numbers $\mathrm{Pm}\equiv \nu /\mu \neq 1$, a nonlinear coupling is at work between ${\bf{Z}}$⁺ and ${\bf{Z}}$⁻ in the dissipative range. In numerical work, to avoid complications, it is often chosen $\mathrm{Pm}=1$. However in most cases Pm is either extremely large, as in the dilute plasma forming the interstellar and intracluster medium, or extremely small, as in the dense plasma forming stellar interiors and in liquid metals [32]; this should have a deep influence on the energy cascade. While the extreme values of $\mathrm{Pm}$ prevalent in nature are still beyond the power of today's supercomputers for direct numerical simulations (DNS), shell models are able to describe the main dynamical features of MHD turbulence even in those cases. In fact shell models maintain one of the fundamental properties of the nonlinearities, i.e. the conservation of quadratic invariants. Shell models have already been used to study the occurrence of singularities in non-conducting fluids [33–36] and the development of time intermittency [8, 37, 38].

An MHD shell model consists of a set of coupled ordinary differential equations for the dimensionless dynamical variables ${Z}_{n}^{\pm }(t)$ describing the time evolution of discrete Fourier modes of equation (1) with wave-vectors ${k}_{n}={2}^{n}{k}_{0}$ ($n=0,1,2,...,N-1$ and ${k}_{0}\sim {{\ell }}_{0}^{-1}$), within a certain shell of wave-vectors ${2}^{n}\leqslant k/{k}_{0}\leqslant {2}^{n+1}$ [23, 24]. Here we use a modified version of the 3D MHD shell model, introduced for hydrodynamic flows by L'vov et al [39]. It is given by the dimensionless equations

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}{Z}_{n}^{\pm }}{{\rm{d}}t}={\rm{i}}{k}_{n}{T}_{n}^{\pm }-(\displaystyle \frac{\nu \pm \mu }{2}){k}_{n}^{2}{Z}_{n}^{+}-(\displaystyle \frac{\nu \mp \mu }{2}){k}_{n}^{2}{Z}_{n}^{-}+{f}_{n}^{\pm },\end{eqnarray} \tag{ 2 }$$

where the nonlinear terms are

$$\begin{eqnarray}{T}_{n}^{\pm } & = & \displaystyle \frac{5}{12}{Z}_{n+1}^{\pm \star }{Z}_{n+2}^{\mp }+\displaystyle \frac{7}{12}{Z}_{n+2}^{\pm }{Z}_{n+1}^{\mp \star }-\displaystyle \frac{1}{24}{Z}_{n+1}^{\pm }{Z}_{n-1}^{\mp \star }\\ & & -\displaystyle \frac{5}{24}{Z}_{n-1}^{\pm \star }{Z}_{n+1}^{\mp }+\displaystyle \frac{1}{48}{Z}_{n-1}^{\pm }{Z}_{n-2}^{\mp }-\displaystyle \frac{7}{48}{Z}_{n-2}^{\pm }{Z}_{n-1}^{\mp },\end{eqnarray} \tag{ 3 }$$

and ⋆ denotes complex conjugation. The pseudo-energies related to Elsässer fields, which in the shell model are defined by

$$\begin{eqnarray}&&{E}^{\pm }(t)=\displaystyle \frac{1}{2}\underset{n=0}{\overset{+\infty }{\displaystyle \sum }}{| {Z}_{n}^{\pm }| }^{2},\end{eqnarray} \tag{ 4 }$$

are ideal invariants (2), i.e. both are subject to a simultaneous cascade [31]. From equation (2), by multiplying by ${{Z}_{n}^{\pm }}^{\star }$ and summing over all shells, one can immediately obtain an equations describing the time evolution of ${E}^{\pm }(t)$, namely

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}{E}^{\pm }}{{\rm{d}}t}=-(\nu +\mu ){\Omega }^{\pm }-(\nu -\mu ){\Omega }_{c}+{F}^{\pm },\end{eqnarray} \tag{ 5 }$$

which involves the enstrophies ${\Omega }^{\pm }$ (in the following pseudo-enstrophies) related to the pseudo-energies, and the enstrophy ${\Omega }_{c}$ (hereafter cross-enstrophy) related to the cross-helicity

$$\begin{eqnarray}{\Omega }^{\pm }(t) & = & \displaystyle \frac{1}{2}\underset{n=0}{\overset{+\infty }{\displaystyle \sum }}{k}_{n}^{2}{| {Z}_{n}^{\pm }| }^{2}\ ,\\ {\Omega }_{c}(t) & = & \displaystyle \frac{1}{4}\underset{n=0}{\overset{+\infty }{\displaystyle \sum }}{k}_{n}^{2}[{Z}_{n}^{-}{Z}_{n}^{+\star }+{Z}_{n}^{-\star }{Z}_{n}^{+}],\end{eqnarray} \tag{ 6 }$$

as well as the externally injected total powers

$$\begin{eqnarray}&&{F}^{\pm }(t)=\underset{n=0}{\overset{+\infty }{\displaystyle \sum }}[{f}_{n}^{\pm }{Z}_{n}^{\pm \star }+{f}_{n}^{\pm \star }{Z}_{n}^{\pm }]\ .\end{eqnarray} \tag{ 7 }$$

In non-conducting fluids equation (5) simplifies to an equation for the kinetic energy, which involves a balance between the injected energy and a dissipative term proportional to the kinetic enstrophy (i.e. the mean square vorticity). In MHD when $\mathrm{Pm}=1$ the situation is similar to non-conducting fluids, even if in MHD two pseudo-energies and two estrophies are involved. In these cases, the cascade is realized in a time τ which is the sum of the eddy turnover times associated with all the intermediate scales of the cascade

$$\begin{eqnarray}&&\tau ={\tau }_{0}\underset{n=0}{\overset{+\infty }{\displaystyle \sum }}{(\displaystyle \frac{{k}_{n}}{{k}_{0}})}^{-2/3},\end{eqnarray} \tag{ 8 }$$

which is a convergent geometric series, while the dissipative wavevector scales as ${k}_{D}\sim {k}_{0}{\nu }^{-4/3}$. In the limit $\nu \to 0$ the energy should reach infinitesimal scales ${k}_{D}^{-1}$ in a finite time [11] in order to generate a full turbulent spectrum. Since in a stationary situation the injection energy rates must be equal to the dissipated energy rates ${\epsilon }^{\pm }=2\nu {\Omega }^{\pm }$, according to our description the pseudo-enstrophies should diverge as $\nu \to 0$ to ensure finite non-vanishing energy dissipation rates [1].

When only one of the dissipations goes to zero or one of the dissipations goes to zero faster than the other one, so that $\mathrm{Pm}\to 0$ or $\mathrm{Pm}\;\to \;\infty$, the development of a singularity is not guaranteed. In these cases the cross-enstrophy ${\Omega }_{c}$ is now involved in the dynamics ($\nu \neq\mu$), together with the pseudo-enstrophies, and this could lead to differences compared with the case $\mathrm{Pm}=1$. It is worth noting that the cross-enstrophy in equation (5) can play both the role of dissipation or injection rate for the pseudo-energies depending on the sign of the term ($\nu -\mu$). Therefore the turbulent cascade may have a different kind of behavior in the limit $\nu \to 0$ as opposed to $\mu \to 0$.

The shell model (2) has been numerically integrated with a fourth-order Runge–Kutta scheme with a time-step of 10⁻⁵, using N = 33 shells for different values of ν and μ. The forcing terms are set to ${f}_{n}^{+}={f}_{n}^{-}=(1+i)\times {10}^{-2}$ (for $n\leqslant 2$), and initial conditions are given by ${Z}_{n}^{+}={Z}_{n}^{-}=0$ for $n\gt 2$ and small values otherwise. This corresponds to an injection of kinetic energy, while the increase of magnetic energy results from a dynamo effect [26–29]. Together with the enstrophies in equation (6), we consider also the kinetic enstrophy ${\Omega }_{v}={\Omega }^{+}+{\Omega }^{-}+2{\Omega }_{c}$, which represents the mean square vorticity, and the magnetic enstrophy ${\Omega }_{b}={\Omega }^{+}+{\Omega }^{-}-2{\Omega }_{c}$, which is strictly related to the mean square current density.

First, as reference, we investigate the case $\mathrm{Pm}=1$. The zero-dissipation limit is achieved by a set of simulations with decreasing values of $\nu =\mu$ down to 10⁻¹⁵. When the energy is injected at large scales, a cascade towards small scales is observed, whereby the energy fills larger and larger shells, up to ${k}_{n}\sim {k}_{D}$ where it is strongly dissipated. As the dissipation decreases, the energy has to reach larger k_D in a finite time in order to guarantee not vanishing constant dissipation. During the dissipation decrease, ${\Omega }^{+}$ shows a divergent behavior as the time is approaching to a given instant ${T}_{\star }=9.054$ in the dimensionless unit (figure 1). The other enstrophies show a similar divergent behavior. A well-known criterion to establish whether a singularity might develop in a finite-time ${T}_{\star }$ is given by the BKM theorem [40] which for an MHD fluid requires that the magnitude of the vorticity and of the current density become infinite at least as fast as $1/({T}_{\star }-t)$. A corresponding criterion for the loss of regularity in a hydrodynamic (HD) shell model is derived in [41], which implies that the maximum shell vorticity must grow at least as ${k}_{n}{u}_{n}\sim 1/({T}_{\star }-t)$ as $t\to {T}_{\star }$ [45]. Therefore in order to establish the existence of singularities in shell models it is important to check the behavior of:

$$\begin{eqnarray}&&\underset{t\to {T}_{\star }}{\mathrm{lim}}\ \underset{0\leqslant n\leqslant N}{\mathrm{sup}}{k}_{n}| {u}_{n}| \ \ \ \ \ \ \mathrm{and}\ \ \ \ \ \ \underset{t\to {T}_{\star }}{\mathrm{lim}}\ \underset{0\leqslant n\leqslant N}{\mathrm{sup}}{k}_{n}| {b}_{n}| .\end{eqnarray} \tag{ 9 }$$

The time behavior of ${\mathrm{sup}}_{0\leqslant n\leqslant N}{k}_{n}| {u}_{n}|$ fulfills the shell model criterion for singularities as derived in [41] (see figure 2); ${\mathrm{sup}}_{0\leqslant n\leqslant N}{k}_{n}| {b}_{n}|$ has exactly the same time behavior of ${\mathrm{sup}}_{0\leqslant n\leqslant N}{k}_{n}| {u}_{n}|$. It is evident the strong exponential increase of the shell vorticity becomes more severe for increasing shell number n. Argument in favor of development of singularities is the shape of the fitting functions for the enstrophies, which turn out to be $f(x)=N/{({T}_{\star }-t)}^{\gamma }$ with ${T}_{\star }\simeq 9.054$ and $\gamma \gt 1$ (see figure 3). This can be taken as evidence of finite-time singularities in the MHD shell models when $\mathrm{Pm}=1$. It is worth noting that the same kind of behavior is observed for vanishing ν and μ but with a ratio such that Pm = 10 or Pm=100 (not shown).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Since we can easily reach very small values of ν and μ, we can investigate the existence of singularities when Pm vanishes or diverges. Keeping μ constant, e.g. we choose $\mu ={10}^{-5}$, and decreasing the viscosity ($\mathrm{Pm}\to 0$) we find the same kind of behavior as observed for the case $\mathrm{Pm}=1$ (shown in figure 1), except that the magnetic enstrophy ${\Omega }_{b}$ reaches a finite limit. This is due to the fact that, when $\mathrm{Pm}\;\neq\;1$, the cross-enstrophy enters into play, so that even though ${\Omega }^{+}$, ${\Omega }^{-}$ and ${\Omega }_{c}$ have a blowup their difference remains finite, thus representing a kind of self-renormalization process. The energy cascade in this case proceeds through the kinetic energy channel and the magnetic variable acts like a passive field.

In the zero-diffusivity limit ($\mathrm{Pm}\to \infty$ keeping constant the viscosity, e.g. $\nu ={10}^{-5}$) we find a completely different situation, namely a regularization of the system is observed. In fact, singularities disappear for every enstrophy and only a run-up of enstrophies is found up to a finite value at around the same time ${T}_{\star }\gtrsim 9$ (figure 4). The asymptotic behaviors for the different enstrophies are summarized in table 1.

Zoom In Zoom Out Reset image size

Table 1.  Enstrophy behavior for the zero-viscosity limit ($\nu \to 0$ keeping finite μ) and zero-diffusivity limit ($\mu \to 0$ keeping finite ν).

limit	${\Omega }_{v}$	${\Omega }_{b}$	${\Omega }_{c}$	${\Omega }^{+}\ \$	${\Omega }^{-}$
$\nu \to 0$	$+\infty$	${\Omega }_{b}^{0}(t)$	$+\infty$	$+\infty$	$+\infty$
$\mu \to 0$	${\Omega }_{v}^{0}(t)\ \$	${\Omega }_{b}^{0}(t)\ \$	${\Omega }_{c}^{0}(t)\ \$	${\Omega }_{+}^{0}(t)\ \$	${\Omega }_{-}^{0}(t)$

It is worth noting that our shell model considers local interactions between shells, namely, each shell interacts only with the first two neighbor shells on each side. At large $\mathrm{Pm}$ it is known that non-local interactions give an important contribution in the magnetic energy spectrum at small-scales [42–44]. This contribution, due to non-local interactions, was estimated by Plunian and Stepanov using a non-local shell model [43]. At large $\mathrm{Pm}$ they found that the non-local interactions play an important role in the transfer of energy from the kinetic scales with largest shear (near the viscosity range) to smaller sub-viscosity magnetic scales. In the same time this energy, or at least some part of it, is transferred back locally to kinetic scales belonging to the kinetic viscous range. This energy is then lost by viscous dissipation [43]. Therefore, considering the non-local interactions, the magnetic spectrum extending to scales smaller than the Kolmogorov scale will be different than what we obtain here, where only the local interactions have been considered. The importance of the contribution due to the non-local interactions on the development of a singularity in the magnetic energy channel depends on how fast the magnetic energy reaches the diffusivity scale and how much magnetic energy can reach this diffusivity scale (which is in sub-viscosity range) in a finite time. We think that it could be very interesting to investigate the existence of finite-time singularities by using a non-local shell model.

One of the basic consequences of the possible presence of the singularities in fluids is the non-vanishing energy dissipation rate for vanishing dissipation. This is still under debate in ordinary fluids [1], and some contradictory evidence is reported for MHD flows in DNS at $\mathrm{Pm}=1$ [17, 46]. The energy dissipation rate can be written as function of the hydrodynamic Reynolds number ${\nu }^{-1}$ and the magnetic Reynolds number ${\mu }^{-1}$ as follows:

$$\begin{eqnarray}&&\epsilon =(\displaystyle \frac{\nu +\mu }{2})({\Omega }^{+}+{\Omega }^{-})+(\nu -\mu ){\Omega }_{c}.\end{eqnarray} \tag{ 10 }$$

The energy dissipation rate approaches a finite limit as the Reynolds numbers diverge for all those values of Pm investigated, both in the the zero-viscosity limit, i.e. huge hydrodynamic Reynolds number, and in the zero-diffusivity limit, i.e. huge magnetic Reynolds number (see figure 5).

Zoom In Zoom Out Reset image size

An other set of simulations for the 2D MHD case turns out to be worthwhile in order to compare the 2D case with the 3D case. From this comparison, we can deduce useful information and gain some insight for the existence of singularities in hydromagnetic fluids. Therefore we integrate the equations of the 2D MHD shell model. This 2D model differs from the 3D version only by one of the conserved quadratic quantities, namely the square of the vector potential in the 2D MHD case as opposed to the magnetic helicity in the 3D case. This difference results in the same functional shape as in equation (3) with different numerical coefficients [21, 25–29]. Solutions of the 2D model reveal a tamer behavior, in which a finite-time blowup is completely absent. This result remains the same for every values of the magnetic Prandtl number we considered (see figures 6 and 7). Since in the shell model description the only difference between the 2D case and the 3D case is in the conservation of different ideal invariants, the comparison between the two aforementioned cases can suggest that the occurrence of singularities might depend on the above-given difference in the ideal invariants conservation. This statement does not mean that the phenomenon of depletion of nonlinearity due to the formation of 2D structures has nothing to do with preventing or slowing down the blowup. Probably the tendency to develop small-scale structures of the flow, which arrange themselves in such a way that locally the solution has an almost vanishing nonlinearity, may be a consequence of ideal invariants conservation. Hence in a 3D MHD fluid, the tendency to generate 2D current sheets may be a consequence of the magnetic helicity conservation. Therefore there may be a deep linkage between the conservation of some ideal invariants, instead of other invariants, and the depletion of nonlinearity due to the generations of 2D structures. This linkage could be a subject of further investigations. In addition to the theoretical importance of this linkage, it has useful implications for the existence of singularities. Indeed reaching a definitive answer to the existence of singularities through only searching for spatial features at small scales currently requires a computational effort too high for modern supercomputers.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The appearance of singularities in an MHD shell model is investigated in the present paper. Finite-time singularities exist when $\mathrm{Pm}=1$ in a 3D MHD shell model. Due to the flexibility of the shell model, we investigated the occurrence of singularities in the case of asymptotic value of the magnetic Prandtl number; this being a situation closer to what is expected in naturally occurring turbulent plasmas. In the 3D case, both the zero-viscosity limit and the zero-diffusivity limit are considered, showing an asymmetrical behavior with respect to the appear of singularities for the two different limits. One of the most important implications of this asymmetrical behavior is related to an intrinsically different nature within the turbulent cascade for kinetic and magnetic energy channels. In fact, this is a clear indication of different mechanisms that can be used to generate small scales in the two energy channels, showing how, under certain conditions, the magnetic field fluctuations cascade towards smaller scales as a passive field. This is what is suggested by the lack of singularities in ${\Omega }_{b}$ while the other pseudo-enstrophies blow up when $\nu \to 0$ and $\mathrm{Pm}\lt 1$. In this case the magnetic field fluctuations do not make a cascade by themselves but they reach the smaller scales because they are dragged there by the velocity field fluctuations. As a consequence, different modes of dissipation for the velocity and the magnetic field fluctuations can generally be at work in the turbulent cascade.

We demonstrated the absence of singularities only in the magnetic enstrophy at small Pm and the absence of singularities for all enstrophies at large Pm. This may be due to the fact that while at small Pm the kinetic energy still maintains a Komogorov-like cascade at small (subresistive) scales, at large Pm the magnetic spectrum is suppressed at small (subviscous) scales. The last point seems to suggest that the full MHD turbulent cascade up to the smaller scales, when $\mathrm{Pm}\ne 1$, is more efficient for small viscosity and finite magnetic diffusivity than the opposite case, namely small magnetic diffusivity and finite viscosity. This consideration can allow us to think that in the dissipation mechanism for an MHD system, the viscosity has a more important role than the magnetic diffusivity. Even if different cascades for kinetic and magnetic energies [47] seem to be present, at least at small scales, in MHD turbulence, we cannot rule out that in the shell model the difference may be due to a lack of spatial structures such as current sheets. These can eventually dissipate magnetic energy and produce accelerations in the development of small scales [15].

Finally, considering also the comparison between the 3D case and the 2D case for an MHD shell model, we can suggest that the different way of transferring ideal invariants throughout the turbulent range of scales is critical in the development of singularities. In other words, the tendency to conserve some quadratic invariants instead of other invariants can make a difference in the existence of singularities. For instance, in the 3D case when $\mathrm{Pm}\ll 1$ the system has the tendency to conserve the hydrodynamic invariants because of maintaining a Komogorov-like cascade at small (subresistive) scales and singularities are found for every pseudo-enstrophies except for ${\Omega }_{b}$. Moreover we think there is a linkage between the purely dynamical properties of an MHD system, such as the conservation of the ideal invariants, and the depletion mechanisms as due to the formation of 2D structures. These results and conclusions need more in-depth work and validations possibly even through direct numerical simulations. This paper provides an innovative way to look at this issue by using a simplified model.

The authors acknowledge the Marie Curie Project FP7 PIRSES-2010-269297. G Nigro thanks Prof Robert Rosner and Prof Fausto Cattaneo for useful comments.