Abstract
The order parameter of a quantum-coherent many-body system can include a phase degree of freedom, which, in the presence of an electromagnetic field, depends on the choice of gauge. Because of the relationship between the phase gradient and the velocity, time-of-flight measurements reveal this gradient. Here, we describe such measurements of initially trapped Bose–Einstein condensates (BECs) subject to an artificial magnetic field. Vortices nucleated in the BEC for artificial field strengths above a critical value, which represented a structural phase transition. By comparing to superfluid-hydrodynamic and Gross–Pitaevskii calculations, we confirmed that the transition from the vortex-free state gives rise to a shear in the released BEC's spatial distribution, representing a macroscopic method to measure this transition, distinct from direct imaging of vortex entry. Shear is also affected by an artificial electric field accompanying the artificial magnetic field turn-off, which depends on the details of the physical mechanism creating the artificial fields, and implies a most natural choice of gauge. Measurements of this kind offer opportunities for studying phase in less-well-understood quantum gas systems.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
While gauge invariance is central to our description of nature, specific physical situations lend themselves to a 'natural' choice of gauge, without violating gauge freedom. A Bose–Einstein condensate's (BEC's) order parameter includes a gauge-dependent phase. When a BEC is subjected to sufficiently rapid rotation (or a sufficiently strong artificial magnetic field6
,  ), the BEC exhibits vortices: points at which the density vanishes and the phase is singular. For a finite system, the structural phase transition from a state in which the phase varies smoothly to one with a single phase singularity occurs at a critical magnetic field
), the BEC exhibits vortices: points at which the density vanishes and the phase is singular. For a finite system, the structural phase transition from a state in which the phase varies smoothly to one with a single phase singularity occurs at a critical magnetic field  , dependent on both particle–particle interactions and geometry [1]. In quantum gas experiments, images of time-of-flight (TOF) expanded clouds can reveal the vortex-nucleation transition [1–5] via the appearance of local minima in the imaged atomic density, each associated with a vortex core. Here, we detected this structural phase transition via an abrupt shape-change in TOF-expanded BECs accompanying the appearance of vortices. As we see below, this change depends upon the our experiment's geometry, which in turn implies a most natural gauge choice.
, dependent on both particle–particle interactions and geometry [1]. In quantum gas experiments, images of time-of-flight (TOF) expanded clouds can reveal the vortex-nucleation transition [1–5] via the appearance of local minima in the imaged atomic density, each associated with a vortex core. Here, we detected this structural phase transition via an abrupt shape-change in TOF-expanded BECs accompanying the appearance of vortices. As we see below, this change depends upon the our experiment's geometry, which in turn implies a most natural gauge choice.
In the description of many-body systems subject to a (real or synthetic) uniform magnetic field, the vector potential is generally written in the gauge most convenient for the problem at hand. Although the symmetric and Landau gauges are common choices, there is no a priori 'natural' gauge. However, looking beyond the simple specification that the magnetic field is uniform, the physical mechanism that creates the magnetic field often suggests a specific gauge choice, for example: any magnetic field created by a single electric current has a natural gauge determined by the geometry in which the vector potential is proportional to the electrical current. In this sense, the symmetric gauge is a natural gauge for an infinite cylindrical solenoid (figure 1(a)), and the Landau gauge is a natural choice for two parallel counterflowing sheets of current (figure 1(b)). Analogous to an infinite solenoid, the synthetic magnetic field for rotating systems is most naturally expressed in the symmetric gauge  because changes to the rotation rate lead to changes of
because changes to the rotation rate lead to changes of  having the form of the symmetric gauge. As in the case for two sheet currents, our experiment's [5] synthetic magnetic field
having the form of the symmetric gauge. As in the case for two sheet currents, our experiment's [5] synthetic magnetic field  is derived from an engineered vector potential [6] that is most naturally expressed by the Landau form
is derived from an engineered vector potential [6] that is most naturally expressed by the Landau form  , because the coupling between laser fields along
, because the coupling between laser fields along  only affects the component of
only affects the component of  along
along  (figure 1(c)). The gauge freedom present in the initial formulation of the problem is inherited by the effective Hamiltonian describing laser dressed atoms. Two experiments starting with the same
(figure 1(c)). The gauge freedom present in the initial formulation of the problem is inherited by the effective Hamiltonian describing laser dressed atoms. Two experiments starting with the same  and ending with zero magnetic field can manifest different physical outcomes without violating gauge invariance, since the electric field
and ending with zero magnetic field can manifest different physical outcomes without violating gauge invariance, since the electric field  associated with the change [7] is determined by the physical mechanism that creates
associated with the change [7] is determined by the physical mechanism that creates  . The natural gauge is the gauge for which the vector potential is zero when any created fields are 'off'. Any changes in the vector potential (which are the measureable quantities) are then directly proportional to the vector potential in our choice of gauge. We emphasize that any gauge will do, but in the sense described above, one can be most natural in many physical situations.
. The natural gauge is the gauge for which the vector potential is zero when any created fields are 'off'. Any changes in the vector potential (which are the measureable quantities) are then directly proportional to the vector potential in our choice of gauge. We emphasize that any gauge will do, but in the sense described above, one can be most natural in many physical situations.
Figure 1. (a) Solenoid and (b) counterflowing current-sheet geometries, shown with electrical current flow (red), vector potential  (blue), and magnetic field
(blue), and magnetic field  (green). For each case, the natural gauge is illustrated: symmetric (suitable for rotating systems)
(green). For each case, the natural gauge is illustrated: symmetric (suitable for rotating systems)  in (a) and Landau (suitable for our Raman system)
in (a) and Landau (suitable for our Raman system)  in (b). (c) Experimental geometry. The elongated 87Rb BEC (black) experienced an artificial field
in (b). (c) Experimental geometry. The elongated 87Rb BEC (black) experienced an artificial field  created using counterpropagating Raman lasers (red and blue arrows). (d) Level diagram of the f = 1 ground state and excited
created using counterpropagating Raman lasers (red and blue arrows). (d) Level diagram of the f = 1 ground state and excited  states, showing two-photon Raman transitions.
states, showing two-photon Raman transitions.
Download figure:
Standard image High-resolution imageIn this work, we studied 87Rb BECs subject to uniform laser-induced synthetic magnetic fields. The constituent bosons experienced a Lorentz force, just as would charged particles in a magnetic field. This synthetic magnetic field was continuously tunable from 0 to above  . BECs are characterized by the complex-valued order parameter
. BECs are characterized by the complex-valued order parameter ![$\psi ({\bf r})=\sqrt{{\rho }_{c}({\bf r})}\mathrm{exp}[{\rm i}\phi ({\bf r})]$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn22.gif) with condensate density
with condensate density  and phase
and phase  . The Gross–Pitaevskii equation (GPE) gives the time dependence of
. The Gross–Pitaevskii equation (GPE) gives the time dependence of  . The single-valuedness of the phase lends the superfluid system one of its defining properties: irrotationality. The current density
. The single-valuedness of the phase lends the superfluid system one of its defining properties: irrotationality. The current density ![${\bf J}({\bf r})=\mathbb{R}{\rm e}[{\psi }^{*}({\bf r})\hat{{\bf v}}\psi ({\bf r})]$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn26.gif) ,where
,where ![$\hat{{\bf v}}=[-{\rm i}{\hslash }\boldsymbol{\nabla }-\boldsymbol{\mathcal{A}}({\bf r})]/m$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn27.gif) , describes the flow of particles and links the local velocity to its phase
, describes the flow of particles and links the local velocity to its phase  via
via ![${\bf v}({\bf r})=[{\hslash }\boldsymbol{\nabla }\phi ({\bf r})-\boldsymbol{\mathcal{A}}({\bf r})]/m$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn29.gif) for particles of mass m. Notice that irrotationality applies to the local per-particle canonical momentum
for particles of mass m. Notice that irrotationality applies to the local per-particle canonical momentum  , i.e.,
, i.e.,  , but neither to velocity nor mechanical momentum
, but neither to velocity nor mechanical momentum  .
.
We prepared trapped, equilibrated7
BECs in one of three configurations: (i)  , a reference case described by standard superfluid hydrodynamics (figures 2(a), (d)); (ii)
, a reference case described by standard superfluid hydrodynamics (figures 2(a), (d)); (ii)  , described by modified superfluid hydrodynamics (figures 2(b), (e)); and (iii)
, described by modified superfluid hydrodynamics (figures 2(b), (e)); and (iii)  , with vortices (figures 2(c), (f)). For all cases, we initiated TOF by abruptly removing the confining potential
, with vortices (figures 2(c), (f)). For all cases, we initiated TOF by abruptly removing the confining potential  and rapidly making the vector potential
and rapidly making the vector potential  . Effectively8
, this rapid turn-off left
. Effectively8
, this rapid turn-off left  unaltered and mapped the gauge-dependent canonical momentum
unaltered and mapped the gauge-dependent canonical momentum  just before TOF (at
just before TOF (at  ) onto the gauge-independent mechanical momentum just after TOF began (at
) onto the gauge-independent mechanical momentum just after TOF began (at  ):
):  . Measuring the shearing motion in TOF, which has contributions from the initial velocity field
. Measuring the shearing motion in TOF, which has contributions from the initial velocity field  and the position-dependent electric force, allows us to distinguish between cases (i), (ii), and (iii).
and the position-dependent electric force, allows us to distinguish between cases (i), (ii), and (iii).
Figure 2. GPE calculations of (a)–(f) in situ and (g)–(i) time-of-flight distributions. (a)–(c) Landau-gauge-in-situ phase, (d)–(f) in situ density, and (g)–(i) TOF density profiles in the  –
– plane for
plane for  (left, centre) and
(left, centre) and  (right). The dashed grey ellipse in (a) indicates the Thomas–Fermi edge of the cloud; the phase is everywhere zero. (j)–(l) Experimental TOF images for systems subject to magnetic fields with cyclotron frequencies,
(right). The dashed grey ellipse in (a) indicates the Thomas–Fermi edge of the cloud; the phase is everywhere zero. (j)–(l) Experimental TOF images for systems subject to magnetic fields with cyclotron frequencies,  . A small degree of shear is evident in (k), but the largest shear is found in (l), where the cloud is also spatially irregular, due to the vortices' phase singularities. The dashed red lines in the lower images indicate the primary axis, to emphasize the small shear in (h) and (k).
. A small degree of shear is evident in (k), but the largest shear is found in (l), where the cloud is also spatially irregular, due to the vortices' phase singularities. The dashed red lines in the lower images indicate the primary axis, to emphasize the small shear in (h) and (k).
Download figure:
Standard image High-resolution imageCase (i): the  expansion of a repulsively interacting BEC released from a harmonic trap is well-studied: zero-point energy is typically negligible and interactions between the atoms dominate. In the ground state, the constant (in situ) phase gives
expansion of a repulsively interacting BEC released from a harmonic trap is well-studied: zero-point energy is typically negligible and interactions between the atoms dominate. In the ground state, the constant (in situ) phase gives  . The familiar inverted-parabola Thomas–Fermi profile of harmonically trapped BECs [8] is preserved by the interaction-driven expansion during TOF [9].
. The familiar inverted-parabola Thomas–Fermi profile of harmonically trapped BECs [8] is preserved by the interaction-driven expansion during TOF [9].
Case (ii): modest magnetic fields ( ) alter the interaction-dominated TOF expansion, as was demonstrated in vortex-free rotating BEC systems [10]. The in situ phase
) alter the interaction-dominated TOF expansion, as was demonstrated in vortex-free rotating BEC systems [10]. The in situ phase  is everywhere well-defined and the canonical momentum
is everywhere well-defined and the canonical momentum  differs from the mechanical momentum
differs from the mechanical momentum  due to the presence of the vector potential that gives
due to the presence of the vector potential that gives  . The
. The  canonical momentum in the Landau gauge
canonical momentum in the Landau gauge
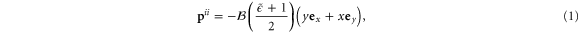
where  , also defines
, also defines  , where
, where  is a trap- and cyclotron-frequency-dependent anisotropy parameter (see equation (5) and [11]). Here the anisotropy is large, so that
is a trap- and cyclotron-frequency-dependent anisotropy parameter (see equation (5) and [11]). Here the anisotropy is large, so that  is nearly −1; compared to previous measurements [6] in a cylindrically symmeteric trap (
is nearly −1; compared to previous measurements [6] in a cylindrically symmeteric trap ( ), the canonical momentum components are small. (In the corresponding symmetric gauge expression
), the canonical momentum components are small. (In the corresponding symmetric gauge expression  is replaced by
is replaced by  .)
.)
Case (iii): vortices significantly affect the TOF expansion. At the location of each vortex, the phase is singular (figure 2(c)), with a  -winding around it. As an example, a vortex centered at the origin of a cylindrically symmetric system contributes a phase
-winding around it. As an example, a vortex centered at the origin of a cylindrically symmetric system contributes a phase  , and the
, and the  canonical momentum in the Landau gauge is approximately
canonical momentum in the Landau gauge is approximately

As before, this in-trap canonical momentum becomes the mechanical momentum  as TOF begins.
as TOF begins.
We estimate the relative shear of these configurations from their momenta at  . Case (i) is shear free. For case (ii), the momentum along
. Case (i) is shear free. For case (ii), the momentum along  has typical scale
has typical scale  . In the presence of many vortices (case (iii), in the diffused vorticity limit [12]) this increases by
. In the presence of many vortices (case (iii), in the diffused vorticity limit [12]) this increases by  , where R is the characteristic system size and
, where R is the characteristic system size and  is the total number of vortices. The difference is proportional to
is the total number of vortices. The difference is proportional to  , where
, where  is the areal vortex density, leading to an abrupt increase in the shearing momentum when vortices enter (figures 2(g)–(i)). Microscopically, this increased velocity originates from the spatial variations in phase associated with the vortices (figure 2(c)).
is the areal vortex density, leading to an abrupt increase in the shearing momentum when vortices enter (figures 2(g)–(i)). Microscopically, this increased velocity originates from the spatial variations in phase associated with the vortices (figure 2(c)).
The transition between configurations (ii) and (iii) at  occurs when the system can lower its energy by admitting a vortex; this critical field depends on the system's trap and interaction parameters [1]. The critical cyclotron frequency
occurs when the system can lower its energy by admitting a vortex; this critical field depends on the system's trap and interaction parameters [1]. The critical cyclotron frequency  , above which vortices are energetically stable [1, 13, 14] may be estimated as
, above which vortices are energetically stable [1, 13, 14] may be estimated as  (note that in rotating system experiments, the cyclotron frequency
(note that in rotating system experiments, the cyclotron frequency  differs by a factor of two from the rotation frequency, commonly referred to as Ω.)
differs by a factor of two from the rotation frequency, commonly referred to as Ω.) ![${R}_{\perp }={\left[4\mu /m({\omega }_{x}^{2}+{\omega }_{y}^{2})\right]}^{1/2}$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn79.gif) is the mean transverse Thomas–Fermi radius in a harmonic potential with frequencies
is the mean transverse Thomas–Fermi radius in a harmonic potential with frequencies  . The healing length
. The healing length  sets the characteristic vortex core size, where
sets the characteristic vortex core size, where  is the central mean-field energy,
is the central mean-field energy,  is the s-wave scattering length [15], and n0 is the central density. For the parameters in this experiment,
is the s-wave scattering length [15], and n0 is the central density. For the parameters in this experiment,  Hz.
Hz.
We prepared BECs with  in the f = 1 ground state hyperfine manifold at the intersection of two
in the f = 1 ground state hyperfine manifold at the intersection of two  laser beams (figure 1(c)). The resulting potential was approximately harmonic and had measured frequencies
laser beams (figure 1(c)). The resulting potential was approximately harmonic and had measured frequencies  (see supplementary data). We implemented an artificial magnetic field [5, 16] using the combination of two counterpropagating
(see supplementary data). We implemented an artificial magnetic field [5, 16] using the combination of two counterpropagating  nm Raman lasers (figure 1(d)) traveling along
nm Raman lasers (figure 1(d)) traveling along  in conjunction with a (real) magnetic field
in conjunction with a (real) magnetic field  , giving a gradient in detuning from Raman resonance
, giving a gradient in detuning from Raman resonance  along
along  ranging from 0 to
ranging from 0 to  . This gave effective cyclotron frequencies ranging from
. This gave effective cyclotron frequencies ranging from  to 20 Hz.
to 20 Hz.
To study the evolution of the density distribution after mean-field-driven expansion, we released the atoms from the trap, and adiabatically transformed the Raman-dressed superposition into a single Zeeman level for imaging [17] in the first 2 ms of TOF (see supplementary data). The cloud expanded for a total of 36.2 ms TOF before being imaged along  (figures 1(j)–(l)).
(figures 1(j)–(l)).
Figures 2(a)–(f) shows computed in situ phase and density distributions for a range of cyclotron frequencies. Vortices nucleate only above  , here only in panels (c) and (f). For this geometry, the system's ground state consists of a linear chain of vortices; larger cyclotron frequencies or less anisotropy would result in a regular vortex lattice. (In the experiment, the vortices have not equilibrated to their ground state configuration.) Figures 2(g)–(l) depicts calculated and measured TOF densities; the cloud's shear increases monotonically with increasing cyclotron frequency
, here only in panels (c) and (f). For this geometry, the system's ground state consists of a linear chain of vortices; larger cyclotron frequencies or less anisotropy would result in a regular vortex lattice. (In the experiment, the vortices have not equilibrated to their ground state configuration.) Figures 2(g)–(l) depicts calculated and measured TOF densities; the cloud's shear increases monotonically with increasing cyclotron frequency  (e.g., there is a small shear in figures 2(h), (k) and a large shear for figures 2(i), (l)). For strong artificial fields the observed density distributions were irregularly fragmented (figure 2(l)), while the computed clouds were ordered. These observations are both consistent with the presence of vortices — disordered in the case of experiment — whose characteristic phase gradients cause density modulations after TOF. The generic
(e.g., there is a small shear in figures 2(h), (k) and a large shear for figures 2(i), (l)). For strong artificial fields the observed density distributions were irregularly fragmented (figure 2(l)), while the computed clouds were ordered. These observations are both consistent with the presence of vortices — disordered in the case of experiment — whose characteristic phase gradients cause density modulations after TOF. The generic  -aligned stripes present in TOF (figures 2(i), (l)) result from the predominantly
-aligned stripes present in TOF (figures 2(i), (l)) result from the predominantly  -expansion from the anisotropic trap.
-expansion from the anisotropic trap.
We obtained TOF images at various artificial field strengths, and fit the resulting 2D column densities to a sheared Thomas–Fermi profile

where  is the central density;
is the central density;  are Thomas–Fermi radii; and axy is a dimensionless shear parameter. We obtain a measure of the spatial irregularity from the fit residuals
are Thomas–Fermi radii; and axy is a dimensionless shear parameter. We obtain a measure of the spatial irregularity from the fit residuals ![$\mathcal{F}={{\displaystyle \sum }}_{x,y}{[{n}_{2{\rm D}}^{\mathrm{meas}}(x,y)-{n}_{2{\rm D}}^{\mathrm{fit}}(x,y)]}^{2}$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn102.gif) . Figure 3(a) shows that
. Figure 3(a) shows that  sharply increases (see supplementary data) around
sharply increases (see supplementary data) around  Hz, an indication of the transition to the BEC's vortex phase.
Hz, an indication of the transition to the BEC's vortex phase.
Figure 3. Signatures of vortex formation. (a) Fit residuals,  , indicating spatial irregularity due to vortices. As more vortices enter the system, the TOF density variations increase in their spatial frequency, and due to the limited resolution of our imaging, this measure of irregularity decreases for higher spatial frequencies. (b) Shear parameter
, indicating spatial irregularity due to vortices. As more vortices enter the system, the TOF density variations increase in their spatial frequency, and due to the limited resolution of our imaging, this measure of irregularity decreases for higher spatial frequencies. (b) Shear parameter  . The experimental data points (grey circles) each reflect an average over tens of measurements, and the uncertainty bars denote the standard deviation of the mean. Pink marks the region, including uncertainty, where the vortex nucleation transition is expected:
. The experimental data points (grey circles) each reflect an average over tens of measurements, and the uncertainty bars denote the standard deviation of the mean. Pink marks the region, including uncertainty, where the vortex nucleation transition is expected:  Hz. The shear parameter calculated for irrotational BECs is denoted by the red dashed curve and the results of the Raman GPE calculations (diamonds) connected by lines; neither has any free parameters. All uncertainties are statistical.
Hz. The shear parameter calculated for irrotational BECs is denoted by the red dashed curve and the results of the Raman GPE calculations (diamonds) connected by lines; neither has any free parameters. All uncertainties are statistical.
Download figure:
Standard image High-resolution imageAdditional evidence for the entrance of vortices into this anisotropically trapped BEC is the behavior of the shear parameter axy: figure 3(b) shows axy sharply increasing above  Hz, in reasonable agreement with the predicted critical cyclotron frequency
Hz, in reasonable agreement with the predicted critical cyclotron frequency  . We compare this result to two calculations.
. We compare this result to two calculations.
The first calculation, the usual hydrodynamic description [11, 12], valid only in the absence of vortices, is modified to include the artificial magnetic field from a Landau-gauge vector potential [16], predicting the in situ density
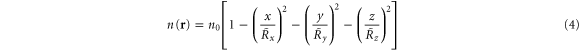
and the canonical momentum  (equation (1)). Here,
(equation (1)). Here, ![${\tilde{R}}_{i}={[2\mu /m{\tilde{\omega }}_{i}^{2}]}^{1/2}$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn111.gif) are modified Thomas–Fermi radii with effective trapping frequencies
are modified Thomas–Fermi radii with effective trapping frequencies  , where
, where ![${\tilde{\omega }}_{x}^{2}={\omega }_{x}^{2}+{\Omega }_{{\rm C}}^{2}{[(1+\tilde{\epsilon })/2]}^{2}$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn113.gif) ,
, ![${\tilde{\omega }}_{y}^{2}={\omega }_{y}^{2}+{\Omega }_{{\rm C}}^{2}{[(1-\tilde{\epsilon })/2]}^{2}$](https://content.cld.iop.org/journals/1367-2630/17/6/065016/revision1/njp514789ieqn114.gif) , and
, and  . The anisotropy parameter
. The anisotropy parameter
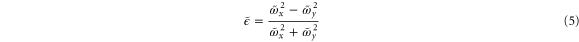
can be obtained self-consistently from these equations [12, 16]. These distributions are propagated in TOF using the hydrodynamic equations for comparison to the measured distributions. From these calculated TOF distributions, we extracted the shear parameter and compared it with the measurement, as shown in figure 3(b).
The second calculation uses the GPE, which is valid for all our cases. We numerically found the GPE ground state at each  and then used the time-dependent GPE to calculate TOF evolution (see supplementary data available at stacks.iop.org/njp/17/065016/mmedia). We find excellent agreement both with the amount of shear in the cloud for all configurations and in the location of the critical artificial field strength for vortex nucleation.
and then used the time-dependent GPE to calculate TOF evolution (see supplementary data available at stacks.iop.org/njp/17/065016/mmedia). We find excellent agreement both with the amount of shear in the cloud for all configurations and in the location of the critical artificial field strength for vortex nucleation.
To understand the impact of the experimentally dictated natural gauge, we investigated the effects of different gauge choices. We performed GPE calculations as described above to obtain axy for two alternate gauge choices with the same  : the symmetric and Landau gauges. We compared these to the Raman system described above (which does not have a simple analytical form, but is well-approximated for small deviations in momentum and position by a Landau gauge; figure 4(a) shows the Raman gauge deviates only slightly from the ideal Landau gauge choice). Though the Landau and symmetric gauge atomic systems are identical before release, their TOF responses differ because of their different electric field impulses at turn-off, which reflect each system's natural gauge (figure 4(b)). For
: the symmetric and Landau gauges. We compared these to the Raman system described above (which does not have a simple analytical form, but is well-approximated for small deviations in momentum and position by a Landau gauge; figure 4(a) shows the Raman gauge deviates only slightly from the ideal Landau gauge choice). Though the Landau and symmetric gauge atomic systems are identical before release, their TOF responses differ because of their different electric field impulses at turn-off, which reflect each system's natural gauge (figure 4(b)). For  , this electric field impulse produces a significantly larger shearing when the symmetric gauge is natural. This behavior reflects the fact that the gauge-dependent in situ canonical momentum, which becomes
, this electric field impulse produces a significantly larger shearing when the symmetric gauge is natural. This behavior reflects the fact that the gauge-dependent in situ canonical momentum, which becomes  , is different in the two cases. Each system reacted to the entrance of vortices with a marked change in axy, here positive, as set by the vortices' direction of circulation, but with a significantly different character.
, is different in the two cases. Each system reacted to the entrance of vortices with a marked change in axy, here positive, as set by the vortices' direction of circulation, but with a significantly different character.
Figure 4. (a) Vector potentials used to calculate TOF response for cyclotron frequency  Hz: the upper panel shows the vector potential corresponding to the exact-Raman dispersion relationship (black) and the central-region fit to the Landau gauge (dashed blue)
Hz: the upper panel shows the vector potential corresponding to the exact-Raman dispersion relationship (black) and the central-region fit to the Landau gauge (dashed blue)  (
( in both cases), while the lower panel shows the symmetric gauge components
in both cases), while the lower panel shows the symmetric gauge components  (blue dashed) and
(blue dashed) and  (red dashed). (b) Shear parameter axy computed via GPE for equivalent-field systems after TOF and
(red dashed). (b) Shear parameter axy computed via GPE for equivalent-field systems after TOF and  -turn-off for fields created by three physical mechanisms: Raman (blue); Landau gauge (red); and symmetric gauge (green).
-turn-off for fields created by three physical mechanisms: Raman (blue); Landau gauge (red); and symmetric gauge (green).
Download figure:
Standard image High-resolution imageIn conclusion, we showed that the shape of the cloud observed after TOF is strongly affected by the presence of vortices and signals the vortex nucleation transition. By exploiting the connection between phase and velocity, we were able to extract topological features of our system's order parameter from the TOF density distribution. Our experiment's anisotropic geometry and Landau-like natural gauge led to a signal that made this transition particularly clear. By comparing to what would have happened in the symmetric gauge, we showed that the gauge choice can make a significant difference in the experimental outcome. In the future, techniques that match a system's geometry to the artificial field's natural gauge might be used to selectively excite edge modes in cold-atom quantum-Hall-like systems [18–20].
Acknowledgments
We thank J V Porto for useful conversations; S Eckel, and D G Norris each for meticulously reading the manuscript; and J H Thywissen for the base code on which the GPE calculations were built. This work was partially supported by the ONR; by the ARO with funds both from the DARPA-OLE program and the Atomtronics MURI; and by the NSF through the Physics Frontier Center at JQI. L J L acknowledges the NSERC of Canada, K J-G acknowledges CONACYT, and M C B acknowledges NIST-ARRA. This research was undertaken, in part, thanks to funding from the Canada Research Chairs program.
Footnotes
- 6
Since there is no real electric charge in this system, we work in terms of charge-free quantities, e.g., for the magnetic field
 and vector potential
and vector potential  . Unless otherwise stated, the phrase 'magnetic field' refers to a synthetic magnetic field.
. Unless otherwise stated, the phrase 'magnetic field' refers to a synthetic magnetic field. - 7
As in previous work [5], the equilibration time for the BEC in the artificial field was sufficient to reach equilibrium vortex density, but too small for the formation of an Abrikosov lattice of the vortex cores.
- 8
In practice, the final vector potential is spatially uniform but non-zero; as explained in the supplemental data, this does not affect the shape of the TOF-expanded BEC.









