Abstract
We show how to create quantum gates of arbitrary speed between trapped ions using a laser walking wave, with complete insensitivity to the drift of the optical phase, and requiring cooling only to the Lamb–Dicke regime. We present pulse sequences that satisfy the requirements and are easy to produce in the laboratory.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
A variety of proposals exist for quantum logic gates between ions trapped in high vacuum [1–14], several of which have been experimentally implemented [15–26]. For quantum computing, the primary goal is fast, precise quantum logic. Methods are sought that are insensitive to those experimental parameters 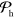 which are, in practice, harder to control [27–31]. Such methods still require accurate parameter settings, but only for
which are, in practice, harder to control [27–31]. Such methods still require accurate parameter settings, but only for  parameters whose precise control is available in the laboratory. Examples of
parameters whose precise control is available in the laboratory. Examples of  are ion temperature T and optical phases
are ion temperature T and optical phases 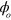 ; examples of
; examples of  are rf frequencies and phases. An optical phase is the phase of a travelling- or standing-wave of light which is sensitive to nm-scale changes in optical path lengths. Single-qubit gate methods, such as stimulated Raman transitions, can use co-propagating laser beams to avoid sensitivity to the slow drift of
are rf frequencies and phases. An optical phase is the phase of a travelling- or standing-wave of light which is sensitive to nm-scale changes in optical path lengths. Single-qubit gate methods, such as stimulated Raman transitions, can use co-propagating laser beams to avoid sensitivity to the slow drift of 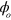 , and this is extremely important for the realization of the high degree of precision which is needed for quantum computing. Similar insensitivity is available in some two-qubit gate methods, but at a cost in speed. We show how to construct simple laser pulse sequences which allow arbitrarily fast gates robust against T and having complete insensitivity to the value of the optical phase
, and this is extremely important for the realization of the high degree of precision which is needed for quantum computing. Similar insensitivity is available in some two-qubit gate methods, but at a cost in speed. We show how to construct simple laser pulse sequences which allow arbitrarily fast gates robust against T and having complete insensitivity to the value of the optical phase  when the gate is applied.
when the gate is applied.
The issues of gate speed and sensitivity to 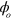 have been addressed separately in recent work. Methods broadly similar to those presented here have been used to perform gates on ions in linear chains where the objective is spatial selection of a subset of the ions rather than gate speed [32, 33]. Using the general concept of forced displacements in phase space [4, 5, 17], García-Ripoll et al [6, 7] showed how to find the time-dependence f(t) of a spin-dependent force which would allow a two-qubit gate of any speed in a given trap. The issue of optical phases arises when the force is produced by a laser standing wave: if
have been addressed separately in recent work. Methods broadly similar to those presented here have been used to perform gates on ions in linear chains where the objective is spatial selection of a subset of the ions rather than gate speed [32, 33]. Using the general concept of forced displacements in phase space [4, 5, 17], García-Ripoll et al [6, 7] showed how to find the time-dependence f(t) of a spin-dependent force which would allow a two-qubit gate of any speed in a given trap. The issue of optical phases arises when the force is produced by a laser standing wave: if  were not controlled then the ions would experience the wrong f(t) and the gate would not work in general. For 'slow' gates, on the other hand, i.e. with
were not controlled then the ions would experience the wrong f(t) and the gate would not work in general. For 'slow' gates, on the other hand, i.e. with 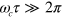 , where
, where 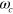 is the centre of mass (COM) mode frequency, and τ the gate time, one may use the simple laser pulse described in [17] and below, resulting in an entangling gate insensitive to
is the centre of mass (COM) mode frequency, and τ the gate time, one may use the simple laser pulse described in [17] and below, resulting in an entangling gate insensitive to 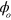 . The method of Mølmer and Sørensen involving spin flips [3, 4], as originally discovered, was sensitive to
. The method of Mølmer and Sørensen involving spin flips [3, 4], as originally discovered, was sensitive to 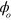 even in the slow regime, and this was an important limitation on its practical realizability. However, it was shown how to choose laser beam propagation directions so that insensitivity to
even in the slow regime, and this was an important limitation on its practical realizability. However, it was shown how to choose laser beam propagation directions so that insensitivity to 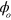 is possible for a slow implementation of the gate on a pair of ions [27]; see also [25]. Here we achieve both high speed and insensitivity to
is possible for a slow implementation of the gate on a pair of ions [27]; see also [25]. Here we achieve both high speed and insensitivity to 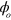 .
.
The gate methods mentioned above work by driving the system around a closed loop in phase space, using an oscillating force whose magnitude or direction depends on the qubit state. The closure and the loop area can depend on the initial phase of the force because for fast gates with 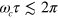 , the rotating wave approximation is not valid. A given oscillation
, the rotating wave approximation is not valid. A given oscillation 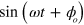 appears as an oscillation at two frequencies
appears as an oscillation at two frequencies  in an interaction picture. The phase
in an interaction picture. The phase 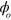 is half the phase difference between these two oscillations at t = 0, and it has significant physical consequences. Similar considerations arise in fast manipulation of spins by Rabi flopping.
is half the phase difference between these two oscillations at t = 0, and it has significant physical consequences. Similar considerations arise in fast manipulation of spins by Rabi flopping.
A summary of our analysis is as follows. We consider a pair of ions subject to a laser walking wave, of phase 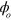 at some arbitrary position and time, which produces a spin-dependent oscillating force through the ac Stark shift. We extract the dependence of the dynamics on
at some arbitrary position and time, which produces a spin-dependent oscillating force through the ac Stark shift. We extract the dependence of the dynamics on  , and obtain four complex number conditions which suffice to ensure that all loops in the motional phase space are closed for any value of
, and obtain four complex number conditions which suffice to ensure that all loops in the motional phase space are closed for any value of 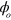 . We then extract a further two complex number conditions which ensure that loop areas are independent of
. We then extract a further two complex number conditions which ensure that loop areas are independent of 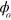 , and another condition which ensures that single-qubit rotations due to ac Stark shifts also vanish for all
, and another condition which ensures that single-qubit rotations due to ac Stark shifts also vanish for all  . Next, we search for pulse sequences that satisfy all the conditions. We show that some remarkably simple pulse sequences can succeed at fast speeds
. Next, we search for pulse sequences that satisfy all the conditions. We show that some remarkably simple pulse sequences can succeed at fast speeds  : for example, a symmetric five-pulse sequence of fixed frequency and phase origin (as could be produced by a single oscillator gated between zero and three output levels). Such a high speed requires high laser intensity, however, and this may be impractical. We also present a very simple symmetric four-pulse sequence, with all pulses at the same amplitude, which produces infidelity below
: for example, a symmetric five-pulse sequence of fixed frequency and phase origin (as could be produced by a single oscillator gated between zero and three output levels). Such a high speed requires high laser intensity, however, and this may be impractical. We also present a very simple symmetric four-pulse sequence, with all pulses at the same amplitude, which produces infidelity below 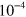 (averaged over a uniform distribution of
(averaged over a uniform distribution of  ) at gate speed
) at gate speed 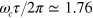 .
.
Consider a walking wave of light interacting with two ions in the same trap. The light field is produced by two laser beams of difference wavevector 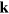 directed along x, difference frequency and phase
directed along x, difference frequency and phase 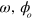 . The internal qubit states of the ions will be labelled
. The internal qubit states of the ions will be labelled 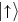 and
and 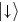 and referred to as 'spin states'; in practice they are usually a pair of levels in the ground state hyperfine structure. We assume the light polarization is adjusted so that the ac Stark shift from either laser beam acting alone is the same for
and referred to as 'spin states'; in practice they are usually a pair of levels in the ground state hyperfine structure. We assume the light polarization is adjusted so that the ac Stark shift from either laser beam acting alone is the same for  . This is usually the case in experiments and serves to eliminate an error source (random qubit rotations from laser intensity noise). The laser–ion interaction Hamiltonian is then
. This is usually the case in experiments and serves to eliminate an error source (random qubit rotations from laser intensity noise). The laser–ion interaction Hamiltonian is then

where  is shorthand for
is shorthand for  ,
, 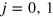 counts the ions,
counts the ions, 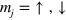 indicates the internal state, the C coefficients account for different coupling to different spin states,
indicates the internal state, the C coefficients account for different coupling to different spin states,  (real and positive) is proportional to the product of the two laser beam electric field amplitudes at ion j at time t, and
(real and positive) is proportional to the product of the two laser beam electric field amplitudes at ion j at time t, and  depend on the light polarization.
depend on the light polarization.
In general, for each two-ion spin state, both the COM and stretch modes of motion of the ions are excited, by differing amounts. After making the Lamb–Dicke approximation 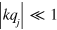 , where
, where 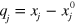 are the excursions from equilibrium, we have
are the excursions from equilibrium, we have
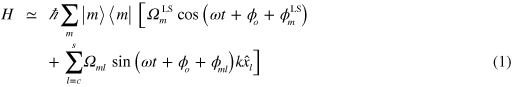
where  gives the amplitudes and phases of the various contributions, and
gives the amplitudes and phases of the various contributions, and  ,
, 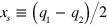 are the COM and stretch coordinates. The equations relating
are the COM and stretch coordinates. The equations relating 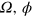 to
to 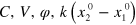 are easily derived but lengthy to write down.
are easily derived but lengthy to write down.
The first term in (1) is a time-dependent light shift (LS) (ac Stark shift) causing spin precession about z. Although for slow gates it can be negligible, it will be important here. The second term is a sum of time-dependent forces acting on the normal modes. It is well known that the effect of such a uniform force on quantum simple harmonic motion is simply to displace the motional state in its x–p phase space [34, 35]. Let  be a Fock state displaced by α, then the total evolution has the form
be a Fock state displaced by α, then the total evolution has the form
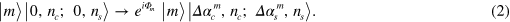
The phases 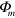 have a contribution from the LS term, and a contribution proportional to the sum of the (signed) areas enclosed by the phase space orbits
have a contribution from the LS term, and a contribution proportional to the sum of the (signed) areas enclosed by the phase space orbits 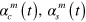 . The desired two-qubit phase gate is obtained when
. The desired two-qubit phase gate is obtained when  .
. 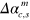 are the net displacements at the end of the gate operation. In an ideal case these would be zero so that the spin and motion are disentangled. We calculate the infidelity
are the net displacements at the end of the gate operation. In an ideal case these would be zero so that the spin and motion are disentangled. We calculate the infidelity 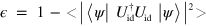 where
where 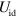 is an ideal operation and the outer brackets represent averaging over an initial thermal state, and over spin states
3
. For small errors we obtain
is an ideal operation and the outer brackets represent averaging over an initial thermal state, and over spin states
3
. For small errors we obtain

where 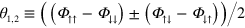 are the single-qubit rotation angles, and
are the single-qubit rotation angles, and 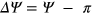 ,
, 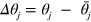 .
.
For an oscillator with mass M and natural frequency 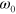 , the coherent state parameter in the laboratory frame is defined as
, the coherent state parameter in the laboratory frame is defined as  , where
, where  . The Argand diagram for α corresponds to an x–p phase space in which the motion can be conveniently described. For a uniform driving force f(t), the evolution is given by [34, 35]
. The Argand diagram for α corresponds to an x–p phase space in which the motion can be conveniently described. For a uniform driving force f(t), the evolution is given by [34, 35]
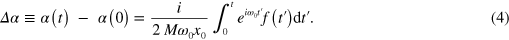
Consider the force owing to any one of the terms in (1):

where  ,
, 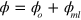 , with the Lamb–Dicke parameter
, with the Lamb–Dicke parameter 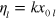 . One finds
. One finds

where 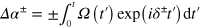 with
with 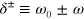 . Therefore
. Therefore  describes an ellipse in the Argand diagram as
describes an ellipse in the Argand diagram as 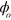 is varied. In order to guarantee that
is varied. In order to guarantee that 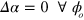 , it is sufficient and necessary that
, it is sufficient and necessary that  . If
. If 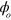 is uniformly distributed between 0 and
is uniformly distributed between 0 and 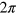 then the mean value of
then the mean value of  is
is 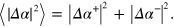
When  the orbit is closed, and the phase
the orbit is closed, and the phase 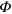 acquired by the quantum state is twice the enclosed area,
acquired by the quantum state is twice the enclosed area, ![$\Phi ={\rm{Im}}\left[ I \right]$](https://content.cld.iop.org/journals/1367-2630/16/5/053049/revision1/njp493744ieqn77.gif) where
where

with
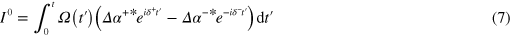

In order that  is independent of
is independent of 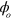 it is sufficient and necessary that
it is sufficient and necessary that 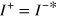 . When
. When 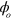 is uniformly distributed between 0 and
is uniformly distributed between 0 and 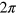 , the variance of
, the variance of 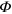 is
is 
Now consider the  term in (1). The contribution to
term in (1). The contribution to  is
is  where
where 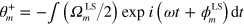 . This does not contribute to
. This does not contribute to  but produces single-qubit rotations. When
but produces single-qubit rotations. When  is uniformly distributed,
is uniformly distributed,  has mean zero and variance
has mean zero and variance 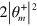 .
.
Now consider a sequence of laser pulses, where in general the amplitude, frequency and relative phases of the pulses may differ, although later we will restrict to all 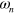 and
and 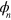 the same. The force on a given mode for a given spin state has the form
the same. The force on a given mode for a given spin state has the form
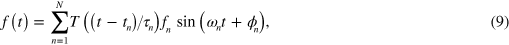
where the 'top hat' function T(x) is 1 for 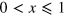 and zero otherwise. Thus the nth pulse begins at
and zero otherwise. Thus the nth pulse begins at  and has duration
and has duration  . Then during any given pulse the change in α is given by
. Then during any given pulse the change in α is given by 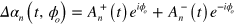 where
where
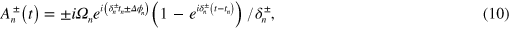
and  .
.  describes a cycloid.
describes a cycloid.
Let 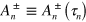 . The orbit area calculation (6) gives
. The orbit area calculation (6) gives


where

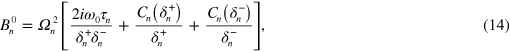
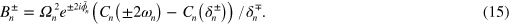
For brevity we introduced the circle function 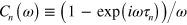 , and phase
, and phase 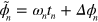 . The LS term gives
. The LS term gives

We are interested in the case where 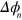 are well-defined but
are well-defined but  is not. Our problem is to find a sequence of pulses such that
is not. Our problem is to find a sequence of pulses such that 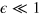 when
when  is uncontrolled, with the total time
is uncontrolled, with the total time 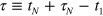 small. Smaller pulse magnitudes and areas are preferred, to minimize the laser intensity and decoherence from photon scattering. Also the number of parameters describing the sequence should be small, to reduce the control problem.
small. Smaller pulse magnitudes and areas are preferred, to minimize the laser intensity and decoherence from photon scattering. Also the number of parameters describing the sequence should be small, to reduce the control problem.
To solve for general values of the coupling coefficients, it is sufficient to find a sequence producing



for non-zero  , because orbits of different spin states only differ by an amplitude factor and phase origin. Therefore there are seven complex numbers that must be zero. By contrast, if we only needed a solution at one value of
, because orbits of different spin states only differ by an amplitude factor and phase origin. Therefore there are seven complex numbers that must be zero. By contrast, if we only needed a solution at one value of 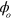 , there would be only two complex number conditions:
, there would be only two complex number conditions: 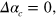
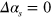 . One can drop the condition on the LS term
. One can drop the condition on the LS term 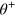 while doubling the total gate time by applying a given pulse sequence twice, with a spin-flip in between (spin-echo sequence). However
while doubling the total gate time by applying a given pulse sequence twice, with a spin-flip in between (spin-echo sequence). However 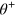 must not be ignored altogether because for fast gates the LS phases are greater than the orbit area phases by approximately
must not be ignored altogether because for fast gates the LS phases are greater than the orbit area phases by approximately 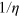 .
.
For each pulse, a change in 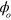 rotates and displaces the orbit along itself:
rotates and displaces the orbit along itself: 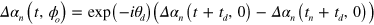 where
where 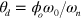 ,
, 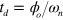 . Therefore if it were possible to close both orbits
. Therefore if it were possible to close both orbits  with a single pulse, then the closure would be guaranteed for all
with a single pulse, then the closure would be guaranteed for all  , and also the areas would be independent of
, and also the areas would be independent of 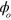 . However, because
. However, because  is irrational, this is not possible
4
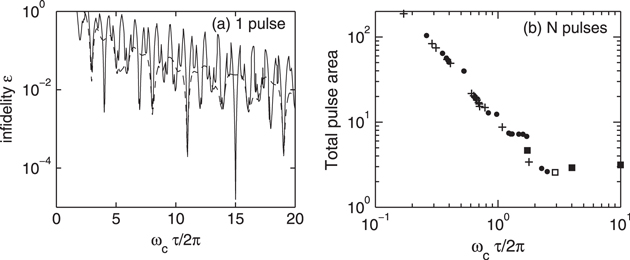
. We show in figure 1(a) the best that can be done with a single pulse. There are two free parameters, ω, τ. The minimum infidelity
is irrational, this is not possible
4
. We show in figure 1(a) the best that can be done with a single pulse. There are two free parameters, ω, τ. The minimum infidelity 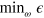 was calculated for durations in the range
was calculated for durations in the range  , at
, at 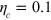 ,
, 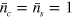 . It is seen that high fidelity can be obtained when
. It is seen that high fidelity can be obtained when  is near to the denominator of a rational approximation to
is near to the denominator of a rational approximation to 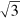 (i.e. the values 4,11,15), but
(i.e. the values 4,11,15), but 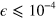 is not available for
is not available for  .
.
Figure 1. (a) Infidelity versus  for a gate using a single laser pulse. The case
for a gate using a single laser pulse. The case 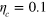 ,
, 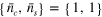 is shown, for
is shown, for 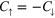 ,
,  ,
,  (equal and opposite light shifts, balanced intensities, ion separation an integer number p of standing wave periods). At each τ, ω is optimized. Full curve: single pulse, dashed curve: spin-echo sequence, with two pulses of duration
(equal and opposite light shifts, balanced intensities, ion separation an integer number p of standing wave periods). At each τ, ω is optimized. Full curve: single pulse, dashed curve: spin-echo sequence, with two pulses of duration 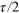 and
and 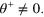 (b) Near-exact solutions: total pulse area versus total gate time, for example pulse sequences. The examples shown are time-symmetric with fixed
(b) Near-exact solutions: total pulse area versus total gate time, for example pulse sequences. The examples shown are time-symmetric with fixed  ,
,  .
.  :
: 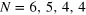 pulses;
pulses;  has all pulses of the same amplitude.
has all pulses of the same amplitude.
Download figure:
Standard image High-resolution imageWe performed a numerical search for fast pulse sequences that solve the problem. A sequence was deemed a 'solution'
5
if  at
at  ,
,  , or if
, or if 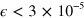 in the case of a pulse sequence with fewer than seven parameters. A sequence of N pulses has
in the case of a pulse sequence with fewer than seven parameters. A sequence of N pulses has  parameters, since the start time and phase origin are arbitrary, and the absolute amplitude is fixed by the requirement
parameters, since the start time and phase origin are arbitrary, and the absolute amplitude is fixed by the requirement 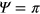 . This suggests that solutions might be possible with few pulses. However to simplify the experimental requirements we assumed fixed
. This suggests that solutions might be possible with few pulses. However to simplify the experimental requirements we assumed fixed 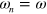 and restricted the values of
and restricted the values of 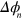 . For example, useful solutions were found with
. For example, useful solutions were found with 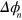 restricted to multiples of
restricted to multiples of 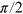 , and also with
, and also with  . For
. For  and fixed
and fixed  the number of parameters is
the number of parameters is 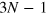 . We found that by further restricting to time-symmetric sequences
. We found that by further restricting to time-symmetric sequences  , the rapidity with which solutions were found increased. This is because the parameter space is smaller, but it shows that the symmetric space contains a good density of solutions. Another possibility is to remove the gaps between the pulses, so that the sequence describes a single shaped pulse, with
, the rapidity with which solutions were found increased. This is because the parameter space is smaller, but it shows that the symmetric space contains a good density of solutions. Another possibility is to remove the gaps between the pulses, so that the sequence describes a single shaped pulse, with  parameters if all sections of the pulse have the same frequency and phase origin. We find there are solutions at
parameters if all sections of the pulse have the same frequency and phase origin. We find there are solutions at 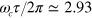 for a shaped pulse with three sections, and symmetric shaped pulses with five sections can give faster solutions (see for example figure 3).
for a shaped pulse with three sections, and symmetric shaped pulses with five sections can give faster solutions (see for example figure 3).
More generally, one may parametrize essentially any functional form (e.g. Gaussian, Blackman, etc) in terms of some modest numbers of parameters, and then seek solutions in the parameter space. In order to compute the effect of some such more general pulse shape, one may treat it for example by Fourier analysis, or simply model it numerically as a continuous sequence of a large number of short pulses, and then the equations of this paper apply.
Here we report examples using small numbers of square pulses. To find a solution, we searched among values of 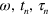 from a random starting point, for each case solving a set of linear equations for the
from a random starting point, for each case solving a set of linear equations for the 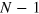 amplitudes
amplitudes 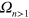 , and using the Nelder–Mead simplex method and simulated annealing to find a minimum of
, and using the Nelder–Mead simplex method and simulated annealing to find a minimum of  . The linear equations were a subset of (18), (17). We found that
. The linear equations were a subset of (18), (17). We found that 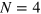 can give some quite fast pulse sequences (
can give some quite fast pulse sequences (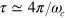 ) at
) at  , see figure 2, and N = 5 was sufficient and necessary to get fast solutions (
, see figure 2, and N = 5 was sufficient and necessary to get fast solutions (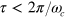 ,
, 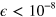 ). In figure 1(b) we show the total pulse area
). In figure 1(b) we show the total pulse area 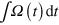 versus length of the pulse sequence, for sequences of minimal area at given τ. The area is important because the unwanted photon scattering is proportional to it. With a single (slow) pulse the area is approximately π. For
versus length of the pulse sequence, for sequences of minimal area at given τ. The area is important because the unwanted photon scattering is proportional to it. With a single (slow) pulse the area is approximately π. For 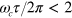 we find the same
we find the same 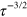 scaling law as was described in [7].
scaling law as was described in [7].
Figure 2. Behaviour of two example symmetric pulse sequences: (a) moderately fast and simple, (b) very fast. The orbit α is shown for COM (top) and stretch (bottom) modes, for two values of  (left) and
(left) and 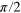 (right), with pulse amplitude versus t at the bottom, in units of the COM period,
(right), with pulse amplitude versus t at the bottom, in units of the COM period, 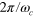 . Case (a) has
. Case (a) has 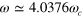 , pulse durations and gaps
, pulse durations and gaps 
 . Case (b) has
. Case (b) has 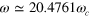 , τ1, t2 − τ1, τ2, ...,
, τ1, t2 − τ1, τ2, ..., 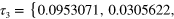
 relative pulse amplitudes
relative pulse amplitudes 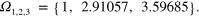
Download figure:
Standard image High-resolution imageWe studied the effect of experimental imprecision by evaluating  as a function of all the parameter values, for small departures from the optimum, for each of several interesting pulse sequences. The terms in (16) contribute single-qubit phases that are each of order
as a function of all the parameter values, for small departures from the optimum, for each of several interesting pulse sequences. The terms in (16) contribute single-qubit phases that are each of order  . They cancel when the frequency and timing are accurate, but in the presence of timing errors these are the main source of infidelity. However their influence can be reduced by employing a spin-echo, and as long as any timing error is constant, the value of
. They cancel when the frequency and timing are accurate, but in the presence of timing errors these are the main source of infidelity. However their influence can be reduced by employing a spin-echo, and as long as any timing error is constant, the value of 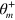 can be adjusted to high accuracy in practice by tweaking the pulse frequency ω. Once this is done, we found that the dependence of infidelity
can be adjusted to high accuracy in practice by tweaking the pulse frequency ω. Once this is done, we found that the dependence of infidelity  on the fractional inaccuracy
on the fractional inaccuracy  of other parameters p (such as pulse duration or height) is of order
of other parameters p (such as pulse duration or height) is of order 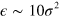 . For example, to achieve
. For example, to achieve 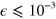 would typically require pulse areas accurate to one percent. The method does not require that the pulses be square; in practice one would seek solutions for whatever shape is conveniently produced in the laboratory; the examples given in this paper can serve as starting points of such a search.
would typically require pulse areas accurate to one percent. The method does not require that the pulses be square; in practice one would seek solutions for whatever shape is conveniently produced in the laboratory; the examples given in this paper can serve as starting points of such a search.
For a fast gate the orbits have to be large to enable the required phase difference to be acquired rapidly (cf figure 2(b)). Eventually the motion goes outside the Lamb–Dicke regime and then equations (1)–(10) must be replaced by a more general analysis or numerical integration.
A fast gate with low photon scattering leads to high laser power requirements, and this may in practice limit what speed one would aim to achieve. As an example case, consider the pulse sequence in figure 3(b), applied to a pair of calcium ions in a trap with COM frequency 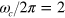 MHz, giving a COM Lamb–Dicke parameter
MHz, giving a COM Lamb–Dicke parameter  for the Raman transition at 397 nm laser wavelength. With 350 mW power in a beam waist of
for the Raman transition at 397 nm laser wavelength. With 350 mW power in a beam waist of 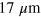 , the Rabi frequency on the
, the Rabi frequency on the 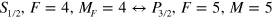 transition is 20 GHz. At a detuning of 3 THz the effective Rabi frequency for the 'stretched state' Raman transition (
transition is 20 GHz. At a detuning of 3 THz the effective Rabi frequency for the 'stretched state' Raman transition (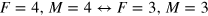 in
in 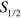 ) is 15 MHz on the carrier, and therefore 1.8 MHz on the first sideband. The gate time is 1.33 oscillation periods in the trap, which is
) is 15 MHz on the carrier, and therefore 1.8 MHz on the first sideband. The gate time is 1.33 oscillation periods in the trap, which is 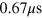 . The total Raman scattering rate from both ions during the gate is
. The total Raman scattering rate from both ions during the gate is 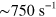 , so the number of scattered photons is
, so the number of scattered photons is  . The infidelity including the effect of Rayleigh scattering is approximately twice this. The sequence shown in figure 3(a) has a total pulse area smaller by a factor of two and hence requires approximately four times less laser power, at the same scattering error, to obtain a gate time of
. The infidelity including the effect of Rayleigh scattering is approximately twice this. The sequence shown in figure 3(a) has a total pulse area smaller by a factor of two and hence requires approximately four times less laser power, at the same scattering error, to obtain a gate time of  in the same trap. Overall, we have achieved a simple, practical solution which offers to increase gate speed by an order of magnitude, while maintaining insensitivity to optical phase drift, with the cost in photon scattering as expected for this general type of gate.
in the same trap. Overall, we have achieved a simple, practical solution which offers to increase gate speed by an order of magnitude, while maintaining insensitivity to optical phase drift, with the cost in photon scattering as expected for this general type of gate.
Figure 3. Behaviour of two further examples, both moderately fast and simple. (a) Has a small total pulse area, (b) illustrates a single shaped pulse. Case (a) has 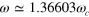 , pulse durations and gaps
, pulse durations and gaps 
![$1.10990,\;1.7475]/{{\omega }_{c}}$](https://content.cld.iop.org/journals/1367-2630/16/5/053049/revision1/njp493744ieqn202.gif) ; pulse amplitudes
; pulse amplitudes  . Case (b) has
. Case (b) has 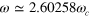 , segment durations
, segment durations 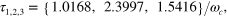 amplitudes
amplitudes 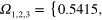
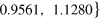 .
.
Download figure:
Standard image High-resolution imageThe gate method we have analyzed has the disadvantage that the qubits must be stored, for the duration of the gate, in levels whose energy difference has a first-order Zeeman effect. Supposing the qubits are ordinarily in 'clock' states, this can easily be achieved by fast microwave pulses before and after the gate, but it is natural to enquire whether this aspect can be avoided altogether, for example by exploiting the Mølmer–Sørensen gate [3, 4]. The latter does not require a first-order Zeeman effect. However, for running-wave-driven Mølmer–Sørensen gates, carrier transitions are only detuned on the order of the motional frequencies and cannot be neglected for the timescales anticipated in our method. The carrier terms do not commute with the sideband terms under the Mølmer–Sørensen interaction, therefore it is not straightforward to integrate the equations of motion [4]. The situation is different for Mølmer–Sørensen gates induced by standing waves or microwave near-fields where the fields can be designed so that the carrier term, which is proportional to the field strength, vanishes to first order and also commutes with the sideband terms [13, 23, 36]. Still, to produce standing wave fields with precise indexing to the position of single ions and high enough microwave gradients to drive sidebands with Rabi-frequencies sufficient for our method is very challenging with existing technology. It would be interesting to discover whether the simpler strategy of allowing a Zeeman effect during the gate would in fact be acceptable in the lab, because the gate is fast enough to make the accumulated phase owing to a magnetic field fluctuation sufficiently small.
Acknowledgments
We thank D M Lucas, D J Szwer and C Ballance for helpful discussions. This work was supported by the National Security Agency (NSA) and Disruptive Technology Office (DTO) (W911NF-05-1-0297), EPSRC (QIP IRC) and the Royal Society.
Footnotes
- 3
We average over product spin states where each spin is uniformly distributed over the Bloch sphere. The numerical factors in front of the terms in (3) depend on the averaging and on correlations amongst
 . However, for solutions
. However, for solutions  the values of these factors are irrelevant.
the values of these factors are irrelevant. - 4
One can have
 rational in an anharmonic trap, or in a trap with a potential 'sculpted' on the length scale of the inter-ion separation (e.g. into a double well). In the former case the mode frequencies and the ion separation become sensitive to stray dc electric fields.
rational in an anharmonic trap, or in a trap with a potential 'sculpted' on the length scale of the inter-ion separation (e.g. into a double well). In the former case the mode frequencies and the ion separation become sensitive to stray dc electric fields. - 5
When
 in (3), the fidelity will be limited in practice by other considerations, such as breakdown of the Lamb–Dicke approximation or laser intensity noise.
in (3), the fidelity will be limited in practice by other considerations, such as breakdown of the Lamb–Dicke approximation or laser intensity noise.