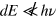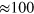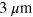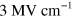Focus on nonlinear terahertz studies

A nonlinear response to the electromagnetic field requires high intensity. At first glance, it may seem improbable to achieve sufficiently large intensities (or electric field amplitudes) in the THz frequency range. Since intensity is pulse energy divided by pulse length and illuminated area, in the THz range all three factors reduce the reachable intensity: the pulse energy is much smaller than at higher optical frequencies, the pulses are longer (the minimum pulse length can be taken roughly as the inverse of the frequency), and the illuminated area is at least on the order of the wavelength squared. As the papers in this 'focus on' collection show, despite the lower intensities in the THz range, it is possible to observe THz nonlinearities. What are the reasons for this fact? For an answer to this question one first has to consider when nonlinearities occur. One possibility also present in other spectral ranges is a transition driven resonantly with high field amplitude. Here a nonlinearity occurs if the population transfer from the ground to the excited state is appreciable. With the transition dipole moment d and the electric field E this is equivalent to $dE/\;h\nu$, i.e. if the Rabi frequency reaches the order of magnitude of the transition frequency. Here it helps that in the THz range the transition dipole moments are typically larger than for higher frequencies. This can be seen simply from the uncertainty relation: increasing the size of a system reduces the momentum uncertainty and thus the energy, resulting eventually in THz-frequency transitions. At the same time, transition dipole moments scale with the system dimensions. Another possibility unique to the THz range that can lead to nonlinearities is the acceleration of charged carriers in the THz field. Here nonlinearities occur if the kinetic energy gained from the accelerating field becomes comparable to energies in the system, e.g. to the band gap in a semiconductor. Since the kinetic energy gained is proportional to the time the field acts in one direction, THz pulses have the advantage of comparatively long acceleration times. Therefore, in the THz range, much lower intensities are required to observe nonlinearities than for higher frequencies. Even these intensities only became available in the last decade or so, rendering the study of THz nonlinearities a relatively new field.

The generation of high THz intensities is still a topic of research. In this collection, several papers consider THz generation in a laser-generated plasma [1–3]. These sources can achieve very broad spectra, extending up to a frequency of $\approx 100$ THz (corresponding to a wavelength of $3\;\mu \text{m}$) if very short pump pulses are used. For many applications, they have the disadvantage that the spatial profile of their emission is quite complex. Three further papers consider other methods for THz generation, one by intracavity mixing [4] and two with quantum cascade lasers [5, 6].

Apart from generation, detection is also an important topic. In [7], the authors present a scheme to allow for the determination of the square of the electric field as a function of time over a broad frequency range by four-wave mixing in gases.

The remaining papers consider the action of high-intensity THz pulses on solids, among them antiferromagnets, superconductors, graphene and semiconductors.

The paper on antiferromagnets [8] is unique in this collection of articles in that the relevant interaction is with the THz magnetic field, while in all other papers it is only with the THz electric field. In this respect, one should note that an electromagnetic wave with an electric field amplitude of $3\;\text{MV}\;\text{c}{{\text{m}}^{-1}}$ is accompanied by a magnetic field with an amplitude of 1 T.

A natural object of THz studies is superconductors, since in conventional superconductors the superconducting gap is in the THz range. In this collection, there are three papers on superconductors, two on conventional [9, 10] and one on high-temperature [11] superconductors.

In graphene, which can be considered a two-dimensional semiconductor with a zero band gap, the THz range is particularly interesting, since here THz pulses can induce both resonant transitions between the valence and conduction band (one can find points in the k space where the energy difference is equal to the THz frequency), and lead to electrical transport by moving the charge carriers in real and reciprocal space. This interplay between inter- and intraband transitions is calculated in [12]. The predicted [12, 13] generation of THz higher harmonics was not observed in [14], but in [15]. In [16] surface plasmons in graphene are considered.

The majority of papers in this collection are concerned with the study of semiconductors [8, 17–23]. While their band gaps are typically much larger than THz photon energies (an exception to this is the narrow-gap semiconductor InSb [8]), one can still have resonant transitions in the THz range, either between discrete levels of impurities [17] or between discrete states caused by spatial confinement, e.g. in quantum wells [18–20]. As mentioned in the introduction, a second way for nonlinearities to occur is via transport over a large part of the Brillouin zone [21, 22].

This 'focus on' collection shows that it is possible to perform nonlinear THz studies for a wide range of materials. In many cases, such studies lead to new results not available with other techniques. Further advances in the generation and detection of THz pulses and in understanding their interaction with matter will certainly lead to a continued series of exciting results in the future.