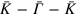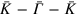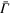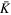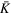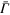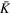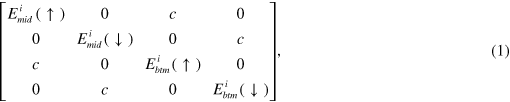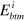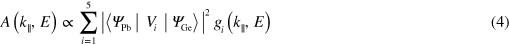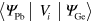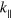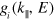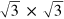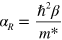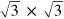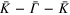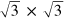Rashba effect within the space–charge layer of a semiconductor

The photoemission measurements were performed with photons of energy 21.2 eV from a He lamp and synchrotron radiation from beamline 21B1-U9 at the National Synchrotron Radiation Research Center in Taiwan. A highly doped n-type Ge(111) wafer, 10¹⁷ – 10¹⁸ cm⁻³, was used. The cleaning procedure for a Ge(111)-c(2 × 8) surface is described elsewhere [18]. To form the Pb/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° structure, we deposited ∼3 ML of the Pb film; the substrate was subsequently annealed from RT to 400 °C. The Pb/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° structure thus obtained is the β phase [19]. An overlayer uniform Pb film was formed on depositing Pb onto the Pb/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° structure kept at −150 °C. The film thickness was determined from a discrete evolution of the quantum-well states [20].

Our first–principles calculations are based on the generalized gradient approximation [21], using the full-potential projected augmented-wave method [22] as implemented in the VASP package [23]. The lattice structure of bulk Ge was optimized with a 13 × 13 × 7 Monkhorst–Pack k-point mesh over the Brillouin zone with cutoff energy of 500 eV. The Ge(111)-1 × 1 unreconstructed surface was simulated by a 18-layer Ge slab terminated by a hydrogen layer on the backside. The vacuum thickness was larger than 15 Å, satisfactorily separating the slabs. The self–consistent calculations were performed on 13 × 13 × 1 k-point mesh over the 2D irreducible Brillouin zone. The spin–orbital coupling was included in the band-structure calculations.

Figures 1(a) and (b) show the gray scale of 2D photoemission spectra of the energy-band dispersions for Pb/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° surface and a 2 ML Pb film on Ge(111), respectively, in the symmetry direction $\bar{K}-\bar{\Gamma }-\bar{K}$ in terms of a Ge(111) surface Brillioun zone. Three bands resembling heavy-hole(HH), light-hole(LH) and split-off(SO) band edges of Ge are observed in both spectra. On inspecting those bands and comparing them with the calculated bulk Ge band edges (yellow dashed curves in figures 1(c), (d)) in the symmetry direction K−Γ−K (parallel to $\bar{K}-\bar{\Gamma }-\bar{K}$), one finds significant differences. First, there exists an extra non-split-off(NSO) band (blue dotted curve), coinciding with the top of the HH and LH at the zone center and crossing the SOI gap between them. Second, the bands resembling the SO and LH band edges appear broader. Those bands must be resonances localized within the Ge SCL [18] so that they become observable from both a Pb/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° surface and a 2 ML Pb film on Ge(111), which have disparate lattice structures [18, 20]. According to preceding work [18], the HH-, LH-, and SO-like resonance bands are caused by the coupling between surface states (quantum-well states) and Ge band edges within the SCL, and the NSO-like band is a surface resonance within the Ge gap induced by SOI, but its origin was not addressed. Figure 2 shows the dependence of those band-edge-like resonance bands on photon energies at 21.2, 25, and 30 eV, respectively. As seen, those four bands don't shift or deform except the change in the intensities. Therefore, their 2D nature was further confirmed.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

To unravel the nature of these resonance bands, one must trace back to the original band edges of a bulk semiconductor. Figure 3(a) shows the prototype model for the formation of three main band edges, HH, LH and SO. The mechanism includes SOI, mostly an atomic effect, and band–band anticrossing interaction (BAI), which is mostly a solid-state effect [24, 25]. Without SOI, all three band edges are nested at the zone center and are approximately parabolic, but with different curvatures. Due to SOI, the middle band shifts downward by an energy Δ. The shifted middle band then interacts with the bottom band (indicated by the arrows), resulting in an anticrossing gap and consequently the so-called LH and SO band edges. However the formation of HH, which has distinct shape form the top band, is not account for in this crude model. In addition the repulsive anticrossing interaction could make the energy difference between LH and SO band edges at the zone center further larger than Δ. Figure 3(b) displays the subbands pertaining to HH (green), LH (blue) and SO (red) on the left-hand side and their corresponding precursors without interactions on the right hand side, superimposed onto the 2D photoemission data of 2 ML Pb on Ge(111). The yellow dashed curves denote the band edges, the same as those in figures 1 and 2, derived from the bulk band dispersions K−Γ−K. As seen, part of HH subbands aggregate densely onto the band edge of LH, causing the delusion of broadening of LH band edge (pink dashed-dot curve). This possibly explains the deviation between LH–like resonance band and LH band edge observed in figures 1 and 2. Such effect is also observed from the band edges without interaction (the right-hand side of figure 3(b)) however with less relevance. The first-principles calculated orbital symmetry of HH, LH and SO as well as their counterparts without interactions are exhibited in figure 3(c). The electron states of HH, LH and SO are mainly p_z , p_y and p_x type, manifesting themselves for the atomic spin–orbital splitting. However, one can see the orbital symmetry of SO band edge turns more s-like when being away from the zone center. In addition, HH, LH and SO band edges have slight mixture with p_y , p_x , and s-type symmetry, respectively, near the zone center, which are not observed for their counterparts without interaction. Hence, this confirms the band–band interactions among them for the formation of Ge band edges.

Zoom In Zoom Out Reset image size

Up to here, the deviation on the LH band edge between the calculation and data is likely resolved in the context of Ge bulk. Yet the existence of extra NSO band and the broadening of SO-like resonance band should be further investigated in light of SCL, within which electronic bands are inherently 2D. Due to the extra potential induced by charge accumulation on the semiconductor surfaces, the energy position of the bulk band edges in SCL shifts upward or downward as a function of the position in the direction normal to the surface––so-called band bending. Moreover, the confinement effect of the SCL, which is more evident in the highly doped condition, yields discrete or quantized subbands of band edges [24]. A further effect within the SCL, which might have been overlooked, is the Rashba effect. Figure 4(a) shows the precursors of three band edges, top, middle and bottom, of the Ge SCL without SOI; their tops coincide at the zone center, which is arbitrarily set at the Fermi level. Subsequently, as shown in figure 4(b), the middle band shifts down by Δ from the top band because of SOI. At this point, if the Rashba effect enters, those band edges would spin-split in the ±k_∥ direction following time-reversal symmetry. In turn, this condition produces a great change in the consequence of the following anticrossing interaction between the middle and bottom band edges because of the spin-selection rule for the interaction [26]. The spin splitting of the bottom band edge is considered to be negligible as it has quite large s-type symmetry with increasing k_∥ (figure 3(c)), resulting in a zero value of the matrix element for SOI. As shown in figure 4(c), the resulting HH, LH and SO bands are spin-polarized (red for spin up and blue for spin down); the inner parts of the spin-polarized LH bands constitute what appears to be the NSO band observed within the SCL of Ge. This is understandable since the spin–selection rule allows one of the degenerate bottom bands, equivalent to NSO band, to pass the anticrossing gap. The spin splitting of SO bands then leads to the observed broadening. Through the repulsive BAI, the top of the LH would slightly overshoot that of the precursor of the HH band, causing its deformation after the interaction.

Zoom In Zoom Out Reset image size

To make a full simulation, all subbands on behalf of the band edges ⁴ , middle and bottom, must be taken into account to undergo these three effects, namely SOI, BAI and the Rashba effect, which are summarized in terms of the Hamiltonian matrix as

$$\begin{eqnarray}\left[ \begin{matrix} E_{mid}^{i}\left( \uparrow \right) & 0 & c & 0 \\ 0 & E_{mid}^{i}(\downarrow ) & 0 & c \\ c & 0 & E_{btm}^{i}(\uparrow ) & 0 \\ 0 & c & 0 & E_{btm}^{i}(\downarrow ) \\ &&\end{matrix} \right],\end{eqnarray} \tag{ 1 }$$

Here c represents the matrix element for the BAI potential, which is assumed to be an overall constant, and arrows denote the spin polarization perpendicular to the momentum direction. The energy eigenvalues of subband i for the middle and bottom band edges before the BAI have forms

$$\begin{eqnarray}&&E_{mid}^{i}\left( \uparrow \downarrow \right)=E_{mid}^{i}\left( {{k}_{\|}}\pm \beta \right)-\Delta \end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&E_{btm}^{i}\left( \uparrow \downarrow \right)=E_{btm}^{i}\left( {{k}_{\|}} \right)\end{eqnarray} \tag{ 3 }$$

in which β and Δ represent respectively the momentum offset by Rashba splitting and the energy shift by atomic SOI. These two quantities are assumed to be constant over all subbands. With the calculated bulk Ge subbands (without SOI considered) for $E_{mid}^{i}$ and $E_{btm}^{i}$ and with c and β as fitting parameters, the 2D photoemission spectra of LH-, SO- and NSO-like bands in figure 5(a) from 2 ML Pb film on Ge(111) were then fitted by the spectra function [20, 25]

$$\begin{eqnarray}&&A\left( {{k}_{\shortparallel }},E \right)\propto \underset{i=1}{\overset{5}{\mathop \sum }}\,{{\left| \left \langle {{\Psi }_{\text{Pb}}} \right|{{V}_{i}}\left| {{\Psi }_{\text{Ge}}} \right \rangle \right|}^{2}}{{g}_{i}}\left( {{k}_{\shortparallel }},E \right)\end{eqnarray} \tag{ 4 }$$

Zoom In Zoom Out Reset image size

with the addition of a smooth background function and lifetime and instrumental broadening, where the hybridization matrix element $\left \langle {{\Psi }_{\text{Pb}}} \right|{{V}_{i}}\left| {{\Psi }_{\text{Ge}}} \right \rangle$, with i = 1–5 for the Ge valence bands, is each taken to be a constant in the thin film limit, ${{k}_{\shortparallel }}$ is the in-plane wave vector, and ${{g}_{i}}({{k}_{\shortparallel }},E)$ is the density of states of Ge in 1D form, adopted from the HH band edge and spin-polarized band edges of LH, SO and NSO derived through relations (1), (2) and (3). We sampled 50 k-points distributed uniformly between the bulk Ge symmetry points Γ and L for the onsets of all subbands. The resulting band edges are formed by the summations of a partial contribution from each subband. Nevertheless, a definite fitting result could still not be achieved due to the facts previously revealed through examining the band edges of a bulk Ge; first, the possible larger gap size between the tops of LH and SO bands than the actual spin–orbital splitting value Δ and second, the unreal broadening of the LH band edge due to the partial aggregation of HH subbands. Thus, we carry out the fitting on four different conditions. Figure 5(b) shows the fitting results with Δ value relaxed. Figures 5(c), (d) show the results with Δ value fixed to be 0.26 and 0.29 eV. The fitting goodness in figure 5(b) is the best with the resulting Δ = 0.24 eV, c = 0.1 eV and β = 0.06 Å⁻¹. The fitting goodness in figure 5(d) is apparently worse with much larger gap size ∼0.38 eV than Δ (0.29 eV). This enlargement of the gap size is, as mentioned before, due to the effect from the repulsive anticrossing interaction. Such result infers that the spin–orbital splitting value Δ within the SCL is substantially smaller than the commonly known value ∼0.29 eV for a bulk Ge [17]. On the other hand, the adsorbate (Pb atoms) on Ge(111) could also possibly decrease the spin–orbital splitting value of Ge, which was found to be 0.28 eV for Bi/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° [15]. In spite of that, the NSO band as well as the broadening of SO-like band is well reproduced in all fitting conditions, confirming the Rashba effects within Ge SCL. The Rashba splitting constants α_R extracted from the figures 5(b)–(d) via the relation ${{\alpha }_{R}}=\frac{{{\hbar }^{2}}\beta }{m*}$ (with the effective mass, 0.279 m_e, extrapolated from the calculated middle band edge before BAI) are 1.35, 1.44, and 1.52 eV Å, respectively. Figure 5(e) shows the fitting result with both Δ fixed at 0.29 eV and spin–polarized LH band edge fixed as that of bulk Ge depicted by the yellow dashed curve in figure 1. The corresponding Rashba splitting constant then reduces to 0.83 eV Å simply because the Rashba spin splitting is proportional to the k_∥ range the spin–polarized LH band edges span, as illustrated in figures 4(b), (c). As for the HH band edge, the Rashba splitting within the SCL is expected to be much smaller, and thus not resolved with the limited resolution of our measuring system. The Rahsba α_R values of HH (mainly p_z type) and other band edges (mainly p_x or p_y type) can differ largely because of the orbital-symmetry dependence of Rashba splitting [27].

Following from our model, the observed LH-, SO- and NSO-like bands must be spin-polarized. In order for further confirmation, we therefore performed first-principles calculation for a Ge slab composed of 18 layers with one surface terminated by hydrogen atoms. Figure 6(a) shows the calculated band dispersions in the symmetry direction $\bar{K}-\bar{\Gamma }-\bar{K}$, where the dashed and the solid curves represent the surface states and the resonance states. Certainly, our focus is on the latter. The spin polarizations of the electronic states of each subband were denoted by circles with the magnitudes proportional to their sizes and colors indicating the directions; red and blue colors denote the opposite in–plane directions. As seen, the spin polarizations of the subbands follow the time–reversal symmetry with respect to the surface zone center, the essential property of Rashba effects. Moreover, we pick up the calculated subbands most resembling the LH, NSO and SO band edges and superimposed them onto figure 6(b) with the adjustment of energy offset; one can see the resemblance of the spin-direction assignments for NSO and SO bands between figure 4(c) and figure 6(b). The spin textures of the constant energy contours of the calculated subbands resembling the LH, and NSO band edges are further examined at energy position −0.23 eV, indicated by the white dash-dotted line; they exhibit two hexagonal contours with major spin polarizations perpendicular to the momentum direction in k_x k_y plane rotating about the surface zone center in the similar manner to those formed by a typical Rashba splitting. The spin polarizations of the outer (LH) and inner (NSO) contours have opposite directions with their maximums as 50% and 30% of full polarization, respectively. The hexagonal warping shape is due to the fact that the electronic states at −0.3 eV are substantially subjected to the Ge crystal potential. It is very interesting to note that the hexagonal contours corresponding to LH and NSO band edges are 30° rotated to each other. Such behavior was also observed from the spin-splitting constant energy contours derived from the conduction band minimum of the giant bulk Rashba semiconductor BiTeI [28], which possesses trigonal layered structures. We further extrapolate the Rashba splitting value from the calculated spin-polarized subbands matching SO band edge shown in figure 6(b), and the resulting value α_R, 0.81 eV Å (Δk_∥ = 0.02 Å⁻¹, m* = 0.192 m_e), is very close to the value obtained from the fitting in figure 5(e). Due to the fact that actual LH band edge spans narrower than that observed in the data, the actual Rashba constant α_R is more likely within the range 0.8–1.5. Nevertheless, this range of values is larger than values α_R = 0.2 and 0.4 eV Å previously obtained for systems Bi/Ge(111)-R30°$\sqrt{3}\times \sqrt{3}$ [15] and 1 ML Br on Ge(111) [16], respectively, in which the observed spin splitting was also contributed mainly by Ge. The Rashba splitting in the latter cases were, however, focused on the energy range between −0.2 eV and E_F, in which the splitting derived from our model is also small, as is obvious in figure 4(c). It is worth noting that two surface resonances bands, S and S', in Bi/Ge(111)-$\sqrt{3}\times \sqrt{3}$ R30° (figure 3(a) of [15]) have opposite spin polarizations as those of LH and NSO bands in our model (figure 4(c)). The larger values that we obtained should thus stand scrutiny.

Zoom In Zoom Out Reset image size