Topological origin of quasi-flat edge band in phosphorene

The unit cell of phosphorene contains four phosphorus atoms, where two phosphorus atoms exist in the upper layer and the other two phosphorus atoms exist in the lower layer. In the momentum representation we obtain the four-band Hamiltonian ${{H}_{4}}={{\sum }_{{\boldsymbol{k}} }}{{c}^{\dagger }}({\boldsymbol{k}} ){{\hat{H}}_{4}}({\boldsymbol{k}} )c({\boldsymbol{k}} )$ with

$$\begin{eqnarray}{{\hat{H}}_{4}}=\left( \begin{array}{ccccccccccccccc} 0 & {{f}_{1}}+{{f}_{3}} & {{f}_{4}} & {{f}_{2}}+{{f}_{5}} \\ f_{1}^{*}+f_{3}^{*} & 0 & {{f}_{2}} & {{f}_{4}} \\ f_{4}^{*} & f_{2}^{*} & 0 & {{f}_{1}}+{{f}_{3}} \\ f_{2}^{*}+f_{5}^{*} & f_{4}^{*} & f_{1}^{*}+f_{3}^{*} & 0 \\ \end{array} \right),\end{eqnarray} \tag{ 2 }$$

where

$$\begin{eqnarray}&&\begin{array}{l} {{f}_{1}}=2{{t}_{1}}{{e}^{i\frac{1}{2\sqrt{3}}{{a}_{x}}{{k}_{x}}}}{\rm cos} \frac{1}{2}{{a}_{y}}{{k}_{y}},\quad {{f}_{2}}={{t}_{2}}{{e}^{-i\frac{1}{\sqrt{3}}{{a}_{x}}{{k}_{x}}}},\quad {{f}_{3}}=2{{t}_{3}}{{e}^{-i\frac{5}{2\sqrt{3}}{{a}_{x}}{{k}_{x}}}}{\rm cos} \frac{1}{2}{{a}_{y}}{{k}_{y}}, \\ {{f}_{4}}=4{{t}_{4}}{\rm cos} \frac{\sqrt{3}}{2}{{a}_{x}}{{k}_{x}}{\rm cos} \frac{1}{2}{{a}_{y}}{{k}_{y}},\quad {{f}_{5}}={{t}_{5}}{{e}^{2i\frac{1}{\sqrt{3}}{{a}_{x}}{{k}_{x}}}}, \\ \end{array}\end{eqnarray} \tag{ 3 }$$

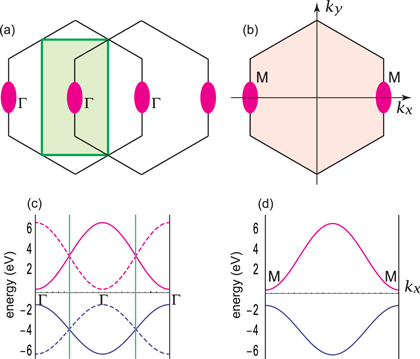
where a_x and a_y are the length of the unit cell into the x and $y$ directions. We show the Brillouin zone and the energy spectrum of the tight-binding model in figures 2(a) and (c), respectively.

Zoom In Zoom Out Reset image size

We are able to reduce the four-band model to the two-band model due to the ${{D}_{2\,h}}$ point group invariance. We focus on a blue point (atom in upper layer) and view other lattice points in the crystal structure (figure 1). We also focus on a red point (atom in lower layer) and view other lattice points. As far as the transfer energy is concerned, the two views are identical. Namely, we may ignore the color of each point. Hence, instead of the unit cell containing four points, it is enough to consider the unit cell containing only two points. This reduction makes our analytical study considerably simple.

The two-band model is given by ${{H}_{2}}={{\sum }_{{\boldsymbol{k}} }}{{c}^{\dagger }}({\boldsymbol{k}} ){{\hat{H}}_{2}}({\boldsymbol{k}} )c({\boldsymbol{k}} )$ with

$$\begin{eqnarray}{{\hat{H}}_{2}}=\left( \begin{array}{ccccccccccccccc} {{f}_{4}} & {{f}_{1}}+{{f}_{2}}+{{f}_{3}}+{{f}_{5}} \\ f_{1}^{*}+f_{2}^{*}+f_{3}^{*}+f_{5}^{*} & {{f}_{4}} \\ \end{array} \right).\end{eqnarray} \tag{ 4 }$$

The rectangular Brillouin zone of the four-band model is constructed by folding the hexagonal Brillouin zone of the two-band model, as illustrated in figure 2(a).

The equivalence between the two models (2) and (4) is verified as follows. We have explicitly shown the energy spectra of the four-band model (2) and the two-band model (4) in figures 2(c) and (d), respectively. It is demonstrated that the energy spectrum of the four-band model is constructed from that of the two-band model: The two bands are precisely common between the two models, while the extra two bands in the four-band model are obtained simply by shifting the two bands of the two-band model, as dictated by the folding of the Brillouin zone.

By diagonalizing the Hamiltonian, the energy spectrum reads

$$\begin{eqnarray}&&E({\boldsymbol{k}} )={{f}_{4}}\pm \left| {{f}_{1}}+{{f}_{2}}+{{f}_{3}}+{{f}_{5}} \right|.\end{eqnarray} \tag{ 5 }$$

The band gap is given by

$$\begin{eqnarray}&&\Delta =4{{t}_{1}}+2{{t}_{2}}+4{{t}_{3}}+2{{t}_{5}}=1.52\;{\rm eV}.\end{eqnarray} \tag{ 6 }$$

The asymmetry between the positive and negative energies arises from the ${{f}_{4}}$ term.

In the vicinity of the $\Gamma$ point, we make a Tayler expansion of f_i in (3) and obtain

$$\begin{eqnarray*}\begin{array}{rcl} {{f}_{1}} & = & {{t}_{1}}\left( 2+\frac{i}{\sqrt{3}}{{a}_{x}}{{k}_{x}}-\frac{1}{12}{{({{a}_{x}}{{k}_{x}})}^{2}}-\frac{1}{4}{{({{a}_{y}}{{k}_{y}})}^{2}} \right), \\ \end{array}\end{eqnarray*}$$

$$\begin{eqnarray}\begin{array}{rcl} {{f}_{2}} & = & {{t}_{2}}\left( 1-\frac{i}{\sqrt{3}}{{a}_{x}}{{k}_{x}}-\frac{1}{6}{{({{a}_{x}}{{k}_{x}})}^{2}} \right), \\ {{f}_{3}} & = & {{t}_{3}}\left( 2-\frac{5i}{\sqrt{3}}{{a}_{x}}{{k}_{x}}-\frac{25}{12}{{({{a}_{x}}{{k}_{x}})}^{2}}-\frac{1}{4}{{({{a}_{y}}{{k}_{y}})}^{2}} \right), \\ {{f}_{4}} & = & {{t}_{4}}\left( 4-\frac{3}{2}{{({{a}_{x}}{{k}_{x}})}^{2}}-\frac{1}{2}{{({{a}_{y}}{{k}_{y}})}^{2}} \right), \\ {{f}_{5}} & = & {{t}_{5}}\left( 1+\frac{2i}{\sqrt{3}}{{a}_{x}}{{k}_{x}}-\frac{2}{3}{{({{a}_{x}}{{k}_{x}})}^{2}} \right). \\ \end{array}\end{eqnarray} \tag{ 7 }$$

The Hamiltonian (4) reads

$$\begin{eqnarray}&&{{\hat{H}}_{2}}={{f}_{4}}+[\varepsilon +\alpha {{({{a}_{x}}{{k}_{x}})}^{2}}+\beta {{({{a}_{y}}{{k}_{y}})}^{2}}]{{\tau }_{x}}+\gamma {{a}_{x}}{{k}_{x}}{{\tau }_{y}},\end{eqnarray} \tag{ 8 }$$

with the Pauli matrices ${\boldsymbol{ \tau }}$, where

$$\begin{eqnarray}&&\begin{array}{l} m=2{{t}_{1}}+{{t}_{2}}+2{{t}_{3}}+{{t}_{5}}=0.76\;{\rm eV},\ \alpha =-\frac{1}{12}{{t}_{1}}-\frac{1}{6}{{t}_{2}}-\frac{25}{12}{{t}_{3}}-\frac{3}{2}{{t}_{4}}-\frac{2}{3}{{t}_{5}}=0.112\;{\rm eV}, \\ \beta =-\frac{1}{4}{{t}_{1}}+\frac{1}{4}{{t}_{3}}+\frac{1}{2}{{t}_{4}}=0.201\;{\rm eV},\ \gamma =\frac{1}{\sqrt{3}}\left( -{{t}_{1}}+{{t}_{2}}+5{{t}_{3}}-2{{t}_{5}} \right)=2.29\;{\rm eV}. \\ \end{array}\end{eqnarray} \tag{ 9 }$$

Hence, the dispersion is linear in the k_y direction, but parabolic in the k_y direction. The energy spectrum is given by

$$\begin{eqnarray}&&E={{f}_{4}}\pm {{E}_{0}},\end{eqnarray} \tag{ 10 }$$

with

$$\begin{eqnarray}&&{{E}_{0}}=\sqrt{\gamma k_{x}^{2}+{{[m+\alpha {{({{a}_{x}}{{k}_{x}})}^{2}}+\beta {{({{a}_{y}}{{k}_{y}})}^{2}}]}^{2}}}.\end{eqnarray} \tag{ 11 }$$

The low-energy Hamiltonian agrees with the previous result [30] with a rotation of the Pauli matrices ${{\tau }_{x}}\mapsto {{\tau }_{z}}$ and ${{\tau }_{y}}\mapsto {{\tau }_{x}}$.

A prominent feature of a phosphorene nanoribbon is the presence of the quasi-flat edge modes isolated from the bulk modes found in figures 3(a) and (b). They are doubly degenerate for a zigzag–zigzag nanoribbon, and nondegenerate for a zigzag-beard nanoribbon, while they are absent in a beard–beard nanoribbon [figure 3(c)].

We explore the mechanism of how such an isolated quasi-flat band emerges in phosphorene. As far as the energy spectrum is concerned, instead of ${{\hat{H}}_{2}}({{k}_{x}},{{k}_{y}})$ as defined by (4), it is enough to analyze the two-band Hamiltonian

$$\begin{eqnarray}&&\hat{H}_{2}^{\prime }({{k}_{x}},{{k}_{y}})={{\hat{H}}_{2}}({{k}_{x}},{{k}_{y}})-{{f}_{4}}({{k}_{x}},{{k}_{y}}).\end{eqnarray} \tag{ 12 }$$

The term ${{f}_{4}}({{k}_{x}},{{k}_{y}})$ only shifts the energy spectrum. The energy spectrum of $\hat{H}_{2}^{\prime }({{k}_{x}},{{k}_{y}})$ is symmetric between the positive and negative energy spectra, as we have noticed in (5). We show the band structures of the three types of nanoribbons in figures 3(d), (e) and (f) for the Hamiltonian $\hat{H}_{2}^{\prime }({{k}_{x}},{{k}_{y}})$, where the quasi-flat edge modes are found to become perfectly flat.

It is a good approximation to set ${{t}_{3}}={{t}_{5}}=0$, since the transfer energies t₁ and t₂ are much larger than the others. Indeed, we have checked numerically that almost no difference is induced by this approximation. The two-band model $\hat{H}_{2}^{\prime }({{k}_{x}},{{k}_{y}})$ is well approximated by the anisotropic honeycomb model,

$$\begin{eqnarray}\hat{H}_{2}^{\prime\prime }=\left( \begin{array}{ccccccccccccccc} 0 & {{f}_{1}}+{{f}_{2}} \\ f_{1}^{*}+f_{2}^{*} & 0 \\ \end{array} \right).\end{eqnarray} \tag{ 13 }$$

This Hamiltonian has been studied in the context of strained graphene and optical lattice [31–34]. The energy spectrum reads

$$\begin{eqnarray}&&E=\sqrt{t_{2}^{2}+4\left( t_{1}^{2}+{{t}_{1}}{{t}_{2}}{\rm cos} \frac{\sqrt{3}}{2}{{a}_{x}}{{k}_{x}} \right){\rm cos} \frac{1}{2}{{a}_{y}}{{k}_{y}}},\end{eqnarray} \tag{ 14 }$$

which implies the existence of two Dirac cones at ${{k}_{x}}=0$ and ${{k}_{y}}={{k}_{{\rm D}}}$ with

$$\begin{eqnarray}&&a{{k}_{{\rm D}}}=2{\rm arctan} (\sqrt{4t_{1}^{2}-t_{2}^{2}}/{{t}_{2}}),\end{eqnarray} \tag{ 15 }$$

for $\left| {{t}_{2}} \right|\lt 2\left| {{t}_{1}} \right|$, where we have set $a={{a}_{y}}$.

We explore the origin of the flat band in the anisotropic honeycomb-lattice model (13). It is instructive to study the change of the band structure of nanoribbon by changing the parameter t₂ continuously, with ${{t}_{1}}$ being fixed. We show the band structure with (a) the zigzag–zigzag edges, (b) the zigzag-beard edges, and (c) the beard–beard edges in figure 4 for typical values of t₁ and t₂.

• (i)  
  We start with the case ${{t}_{2}}=\left| {{t}_{1}} \right|$, where the energy spectrum (14) becomes that of graphene with two Dirac cones at the K and ${{K}^{\prime }}$ points. The perfect flat band connects the K and ${{K}^{\prime }}$ points, that is, it lies for (a) $-\pi \leqslant ak\leqslant -\frac{2}{3}\pi$ and $\frac{2}{3}\pi \leqslant ak\leqslant \pi$; (b) $-\pi \leqslant ak\leqslant \pi$; (c) $-\frac{2}{3}\pi \leqslant ak\leqslant \frac{2}{3}\pi$. It is attached to the bulk band. See figures 4(a)–(c).
• (ii)  
  As we increase t₂ but keep t₁ fixed, the two Dirac points move towards k = 0, as is clear from (15). The flat band is kept be present and connects the two Dirac points. See figures 4 (d)–(f).
• (iii)  
  At $\left| {{t}_{2}} \right|=2\left| {{t}_{1}} \right|$, the two Dirac points merge into one Dirac point at k = 0, as implied by (15). The flat band touches the bulk band at k = 0 for the zigzag–zigzag nanoribbon and the zigzag-beard nanoribbon, but disappears from the beard–beard nanoribbon. See figures 4(g)–(i).
• (iv)  
  For $\left| {{t}_{2}} \right|\gt 2\left| {{t}_{1}} \right|$, the bulk band shifts away from the Fermi level, as follows from (14 ). The flat band is disconnected from the bulk band for the zigzag–zigzag nanoribbon and the zigzag-beard nanoribbon, where it extends over all of the region $-\pi \leqslant k\leqslant \pi$. On the other hand, the edge band becomes a part of the bulk band and disappears from the Fermi level for the beard–beard nanoribbon. See figures 4(j)–(l).

Zoom In Zoom Out Reset image size

The topological origin of the flat band has been discussed in graphene [29]. It is straightforward to apply the reasoning to the anisotropic honeycomb-lattice model (13). We consider one-dimensional (1D) Hamiltonian ${{H}_{k}}({{k}_{x}})$ in the k_x space, which is essentially given by the two-band model (13) at a fixed value of $k\equiv {{k}_{y}}$. We analyze the topological property of this 1D Hamiltonian. Because the k_x space is a circle due to the periodic condition, the homotopy class is ${{\pi }_{1}}({{S}^{1}})=\mathbb{Z}$.

We write the Hamiltonian as

$$\begin{eqnarray}{{H}_{k}}({{k}_{x}})=\left( \begin{array}{ccccccccccccccc} 0 & {{F}_{k}}({{k}_{x}}) \\ F_{k}^{*}({{k}_{x}}) & 0 \\ \end{array} \right).\end{eqnarray} \tag{ 16 }$$

It is important to remark that the gauge degree of freedom is present in this Hamiltonian [35]. Indeed the phase of the term ${{F}_{k}}({{k}_{x}})$ is irrelevant for the energy spectrum of the bulk system. However, this is not the case for the analysis of a nanoribbon, since the way of taking the unit cell is inherent to the type of nanoribbon, as illustrated in figure 5. It is necessary to make a gauge fixing so that the hopping between the two atoms in the unit cell becomes real, namely, t₁ for the zigzag edge and t₂ for the beard edge.

Zoom In Zoom Out Reset image size

For the zigzag edge we thus make the gauge fixing such that

$$\begin{eqnarray*}&&{{F}_{k}}({{k}_{x}})={{e}^{-i(\frac{1}{2\sqrt{3}}{{a}_{x}}{{k}_{x}}+\frac{1}{2}ak)}}({{f}_{1}}+{{f}_{2}})={{t}_{1}}\left( 1+{{e}^{-iak}} \right)+{{t}_{2}}{{e}^{-i\frac{1}{2}(\sqrt{3}{{a}_{x}}{{k}_{x}}-ak)}},\end{eqnarray*}$$

where the parameter k corresponds to the momentum of zigzag nanoribbons. Here, t₁ for the link in the unit cell and ${{e}^{-iak}}{{t}_{1}}$ for the neighboring link [figure 5(a)]. The topological number of the 1D system is given by

$$\begin{eqnarray}&&{{N}_{{\rm wind}}}(k)=\int _{-\pi /a}^{\pi /a}d{{k}_{x}}\;{{\partial }_{{{k}_{x}}}}{\rm log} {{F}_{k}}({{k}_{x}}).\end{eqnarray} \tag{ 17 }$$

By an explicit evaluation, ${{N}_{{\rm wind}}}(k)$ is found to take only two values; ${{N}_{{\rm wind}}}=1$ for $|k|\lt {{k}_{{\rm D}}}$, and ${{N}_{{\rm wind}}}=0$ for $\pi \geqslant |k|\gt {{k}_{{\rm D}}}$. We may interpret this as the winding number as follows. We consider the complex plane for ${{F}_{k}}({{k}_{x}})=|{{F}_{k}}({{k}_{x}})|{\rm exp} [i{{\Theta }_{k}}({{k}_{x}})]$. The quantity ${{N}_{{\rm wind}}}(k)$ counts how many times the complex number ${{F}_{k}}({{k}_{x}})$ winds around the origin as ${{k}_{x}}$ moves from 0 to $2\pi /a$ for a fixed value of k. Note that the origin implies ${{F}_{k}}({{k}_{x}})=0$, where the Hamiltonian is ill defined. We have shown such a loop for typical values of k in figure 5(b), where the horizontal axis is for Re $[{{F}_{k}}({{k}_{x}})]$ and the vertical axis is for Im $[{{F}_{k}}({{k}_{x}})]$,

$$\begin{eqnarray}&&\operatorname{Re}[{{F}_{k}}({{k}_{x}})]={{t}_{1}}(1+{\rm cos} ak)+{{t}_{2}}{\rm cos} \frac{1}{2}\left( \sqrt{3}{{a}_{x}}{{k}_{x}}-ak \right),\end{eqnarray} \tag{ 18a }$$

$$\begin{eqnarray}&&{\rm Im}[{{F}_{k}}({{k}_{x}})]={{t}_{1}}{\rm sin} ak+{{t}_{2}}{\rm sin} \frac{1}{2}\left( \sqrt{3}{{a}_{x}}{{k}_{x}}-ak \right).\end{eqnarray} \tag{ 18b }$$

The loop surrounds the origin and ${{N}_{{\rm wind}}}(k)=1$ when $-\pi \leqslant k\lt -{{k}_{{\rm D}}}$ and ${{k}_{{\rm D}}}\lt k\leqslant \pi$, while it does not and ${{N}_{{\rm wind}}}(k)=0$ when $|k|\lt {{k}_{{\rm D}}}$: The loop touches the origin when $k=\pm {{k}_{{\rm D}}}$. We have demonstrated that the system is topological for $|k|\gt {{k}_{{\rm D}}}$ and trivial for $|k|\lt {{k}_{{\rm D}}}$.

We next appeal to the bulk-edge correspondence to the topological system. When we cut the bulk along the y direction, the 1D system has an edge. Since the edge separates a topological insulator and the trivial state (i.e., the vacuum state), the gap must close at the edge, namely, there must appear a gapless edge mode. The gapless edge mode appears for all $|k|\lt {{k}_{{\rm D}}}$, implying the emergence of a flat band connecting the two Dirac points given by (15).

For the beard edge, we make the gauge fixing such that

$$\begin{eqnarray}&&{{F}_{k}}({{k}_{x}})={{e}^{i\frac{1}{\sqrt{3}}{{a}_{x}}{{k}_{x}}}}({{f}_{1}}+{{f}_{2}})\end{eqnarray} \tag{ 19 }$$

and carry out an analogous argument (see figure 5). We reach at the conclusion that a flat band appears for $|k|\gt {{k}_{{\rm D}}}$ and connects the two Dirac points given by (15) but in an opposite way to the case of the zigzag edge.

We have explained how the flat band appears in the anisotropic honeycomb-lattice model. The flat band corresponds to the quasi-flat band in the original Hamiltonian ${{\hat{H}}_{2}}$.

We construct an analytic form of the wave function at the zero-energy state in the anisotropic honeycomb-lattice model (13) as follows. We label the wave function of the atom on the outer most cite as ψ₁, and that of the atom next to it as ψ₂, and as so on. The total wave function is $\psi =\left\{ {{\psi }_{1}},{{\psi }_{2}},\cdots ,{{\psi }_{N}} \right\}$ if there are N atoms across the nanoribbon. The Hamiltonian is explicitly written as

$$\begin{eqnarray}H=\left( \begin{array}{ccccccccccccccc} 0 & {{t}_{1}}g & 0 & 0 & \cdots \\ {{t}_{1}}{{g}^{*}} & 0 & {{t}_{2}} & 0 & \cdots \\ 0 & {{t}_{2}} & 0 & {{t}_{1}}g & \cdots \\ 0 & 0 & {{t}_{1}}{{g}^{*}} & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \right),\end{eqnarray} \tag{ 20 }$$

with $g=1+{{e}^{-iak}}$. The eigenvalue problem $H\psi =0$ is easily solved [36], yielding ${{\psi }_{2n}}=0$ and ${{\psi }_{2n+1}}={{[{{t}_{1}}(1+{{e}^{iak}})/{{t}_{2}}]}^{n}}{{\psi }_{1}}$. By solving the Hamiltonian matrix recursively from the outer most cite, we obtain the analytic form of the local density of states of the wave function for odd cite j,

$$\begin{eqnarray}&&|\psi (j)|={{\alpha }^{j}}\sqrt{1-{{\alpha }^{2}}},\end{eqnarray} \tag{ 21 }$$

with $\alpha =2|{{t}_{1}}|({\rm cos} \frac{ak}{2})/|{{t}_{2}}|$. The wave function is zero for even cite. It is perfectly localized at the outermost site when $ak=\pi$, and describes the flat band.

We can derive the energy spectrum of the quasi-flat band perturbatively. With the use of this wave function, the energy spectrum ${{E}_{{\rm qf}}}(k)$ of the quasi-flat band is estimated perturbatively by taking the expectation value of the t₄ term as

$$\begin{eqnarray}&&{{E}_{{\rm qf}}}(k)=\mathop{\sum }\limits_{n=0}^{\infty }{{t}_{4}}(1+{{e}^{-iak}})\psi _{n}^{*}{{\psi }_{n+2}}+{{t}_{4}}(1+{{e}^{iak}})\left( \psi _{n+2}^{*}{{\psi }_{n}} \right)=-\frac{4{{t}_{1}}{{t}_{4}}}{{{t}_{2}}}(1+{\rm cos} ak),\end{eqnarray} \tag{ 22 }$$

where $4{{t}_{1}}{{t}_{4}}/{{t}_{2}}=0.14$. On the other hand, we numerically obtain $E(0)=-0.301$ eV. The agreement is excellent.