Abstract
Chiral symmetry, fundamental in the physics of graphene, guarantees the existence of topologically stable doubled Dirac cones and anomalous behaviors of the zero-energy Landau level in magnetic fields. Its crucial role, especially its manifestation in optical responses and many-body physics in graphene, is explained in this paper. We also give an overview of multilayer graphene from the viewpoint of the optical properties and their relation with chiral symmetry.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
While the Dirac cone physics in graphene is forming a new branch of condensed-matter physics, there is an increasing fascination with optical responses in graphene [1–3]. The present paper focuses on how the physics of the massless Dirac cone is related to the optical properties of graphene. There, we stress that the factor that links the two is chiral symmetry. So, the purpose of this paper is to first discuss the significance of chiral symmetry in graphene including many-body interaction and multilayer systems, and then explore optical properties.
So let us start with the Dirac cone, which comes from the symmetry of graphene. The honeycomb lattice structure of this material has two atoms per unit cell, and if we focus on the two π-bands arising from this, the system is effectively described by a traceless hermite Hamiltonian, H(k) = R(k)σ, which is parametrized by R with three real components. This implies that the Dirac cone has a co-dimension of three [4]. Since the momentum in two dimensions is described by two parameters, the Dirac cones do not arise in general, while the symmetry of the graphene at K and K' points gives rise to the Dirac cones. Here one may also attribute the gapless dispersion of graphene to the chiral symmetry of the honeycomb lattice. When the lattice points are classified into two sublattices and the hopping of electrons is only allowed between them, the system is chiral symmetric. Then we can show that the degree of freedom in R is reduced from three to two. This also ensures the topological stability (against various modifications) of the Dirac cones of the chiral symmetric two-dimensional system, since the degeneracy cannot be removed by small but finite modifications as far as the chiral symmetry (or its extension) is respected. A conspicuous feature in graphene and related models is that the Dirac cones appear in pairs (at K and K' points in graphene). This is due to the well-known fermion doubling in chiral-symmetric systems, which is a two-dimensional analogue of the Nielsen–Ninomiya theorem in four-dimensional lattice gauge theory [5, 6]. Many of the physically interesting features of graphene are naturally understood from chiral symmetry. For example, anomalous stability of the n = 0 Landau level against ripples is due to the index theorem for the massless Dirac fermions where a ripple induces a random gauge field but respects the chiral symmetry [7, 8].
In real graphene, chiral symmetry does not rigorously hold. In the standard tight-binding parameters for graphene [9], however, most of the chiral-symmetry-breaking parameters are significantly smaller than the chiral symmetric ones in magnitude. Then the chiral symmetric model is quite useful in discussing the low-energy physics of graphene, especially optical responses, which are one of the main targets of the present paper. Moreover, the chiral symmetry breaking due to small but finite tight-binding parameters causes a gap opening around the zero energy for some types of multilayer graphene. Hence we discuss the optical responses for various types of multilayer graphene from the viewpoint of chiral symmetry. Also, an energy gap opening due to many-body effects around the charge neutrality point is one of the important current topics in graphene. Indeed, the interplay between chiral symmetry and many-body effects is an important issue to be clarified, which we shall address in this paper with a unified description of chiral symmetry.
This paper is organized as follows. In section 2 we shall give a compact and self-contained description of the chiral symmetry on the honeycomb lattice, putting stress on its relevance to the zero-energy modes. The formalism is also applied to a discussion of the many-body physics of graphene. Specifically, a chiral basis for the n = 0 Landau level introduced here has not been described in detail in the existing literature, but is seen to facilitate the formulation of the chiral condensates in strong magnetic fields. The chiral symmetry is also important for optical responses of graphene, as we shall see in section 5. In section 3 we give a detailed description of the chiral condensate on the honeycomb lattice. If the state in a strong magnetic field is assumed to be spin polarized, the chiral condensate, which is gapped and has an exact degeneracy of two, turns out to be one of the possible many-body ground states of graphene at half filling for a model with nearest-neighbor interactions. The chiral condensate is identified to be a Hall insulator from a consideration of a many-body topological (Chern) number. Section 4 describes electronic structures of bilayer graphene and multilayer extensions in zero and strong magnetic fields, where chiral symmetry again plays an important role. Namely, although chiral symmetry is only approximate in multilayer graphene, we can make a description of the electronic structure and properties of multilayer graphene transparent in terms of chiral symmetry and its breakdown. Indeed, the effects of chiral symmetry are probed here from a direct numerical calculation of the Landau levels which are done for much weaker magnetic fields (hence much closer to real situations) than hitherto performed including the situation around the Lifshitz transition of multilayer graphene. The calculation with edges also enables us to confirm the bulk-edge correspondence in multilayer graphene. Section 5 focuses on optical responses of bilayer and trilayer graphene. There, optical Hall conductivity as well as optical longitudinal conductivity are examined numerically. A key topic of interest we discuss there is effects of the trigonal warping and chiral symmetry on the optical responses of graphene. Many-body effects are mentioned as well. The final section gives the conclusion of the paper.
2. Chiral symmetry and chiral basis for the zero modes
Many of the characteristic features of graphene are due to the Dirac cones at K and K' points, which may be attributed to the specific crystal structure of the material but are also attributable to the chiral symmetry of the honeycomb lattice. This, in fact, guarantees the existence of massless Dirac cones. The chiral symmetry is preserved for some types of physical perturbation for graphene such as shear modulation of the crystal, or the ripples that introduce random gauge fields. The chiral symmetry allows us to discuss massless Dirac fermions for these cases from a generic point of view. This is also the case with multilayer graphene systems, where the presence or absence of an energy gap, which also affects optical responses, is governed by the chiral symmetry. Chiral symmetry is also important when discussing many-body states in graphene. With these applications in mind, we present a self-contained formulation of the chiral symmetry for a generic lattice model in this section.
Let us start with the definition of the chiral symmetry for fermions on a lattice. When the lattice is bipartite, that is, all of the lattice points can be divided into two sublattice sites • and ○, the non-interacting Hamiltonian 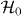 is expressed as a block off-diagonal form,
is expressed as a block off-diagonal form,

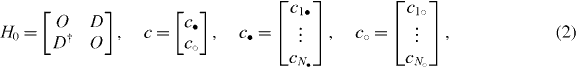
where D is an N• × N○ matrix with N•(N○) being the number of • (○) sites, respectively. We can then introduce the chiral operator Γ,

with Γ2 = IN, N = N• + N○ and Tr Γ = N• − N○. The chiral symmetry, {H,Γ} = 0, implies that if φi is an eigenstate of H with an energy λi, then Γφi is another eigenstate (the 'chiral partner') with an energy −λi.
For N• ⩾ N○ (without loss of generality) the secular equation becomes
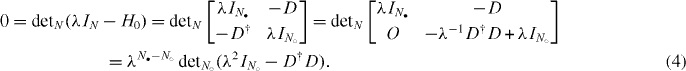
This implies that there are at least N• − N○ zero-energy states. These zero-energy states (zero modes) are determined by the geometrical structure of the lattice. As for a zero-energy state, its chiral partner is degenerated in energy.
When we apply a magnetic field, we have graphene Landau levels. Although we do not reproduce a standard derivation for the Landau levels, we shall focus on the zero-energy Landau level in graphene. Before proceeding, let us mention what we really mean by the zero-energy Landau level. Rigorously speaking, the n = 0 Landau level has energy exactly equal to zero only for massless Dirac fermions in a continuous model. Conversely, if we consider a lattice model such as the honeycomb tight-binding model, the n = 0 Landau level has, in general, a finite width (a kind of Harper's broadening), and the zero-energy condition is only realized in the limit of a weak magnetic field (ϕ → 0 where ϕ is the flux per hexagon). Consequently, in a numerical calculation for the honeycomb lattice model with a finite ϕ, the n = 0 Landau level has a small but finite width. When we want to project the problem onto the n = 0 Landau level, which contains M states, we can define the  -zero modes by collecting those M states that have energies between −
-zero modes by collecting those M states that have energies between − and
and  , where
, where  (>0) is (half) the width of the Landau level. These naturally include the geometrical zero modes discussed above for B = 0.
(>0) is (half) the width of the Landau level. These naturally include the geometrical zero modes discussed above for B = 0.
Now let us take an orthonormalized basis for the  -zero modes which form an
M-dimensional multiplet as ψ = (ψ1,...,ψM) with ψ†iψj = δij, and
-zero modes which form an
M-dimensional multiplet as ψ = (ψ1,...,ψM) with ψ†iψj = δij, and

for every i. This property is inherited by a unitary-transformed ψω = ((ψω)1,...,(ψω)M) = ψω with ω being unitary. It implies that the  -zero modes are U(M) gauge invariant.
-zero modes are U(M) gauge invariant.
Then one can construct a normalized complete multiplet as

where φ is the multiplet of negative-energy states with H0φi = −λiφ, λi >  , while Γφ is the multiplet of chiral partners of φ. The normalization and the orthogonality of all the states are expressed as
, while Γφ is the multiplet of chiral partners of φ. The normalization and the orthogonality of all the states are expressed as
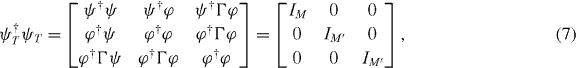
where M' is the dimension of the negative (positive) energy multiplet φ (Γφ). The completeness reads

With this multiplet ψT , H0 is block-diagonalized as

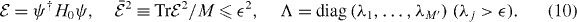
Due to the completeness and orthogonality relations equation (7), we have
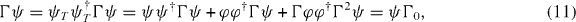

where the M × M dimensional Hermite matrix Γ0 satisfies Γ20 = IM. Its trace is evaluated as
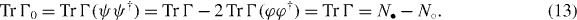
Then Γ0 is diagonalized as

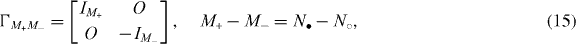
where ωΓ∈U(M) with M+ + M− = M. Now let us define a chiral multiplet ψΓ = ψωΓ that satisfies


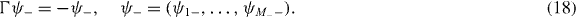
Namely, ψi±'s are eigenstates of Γ as


where ψ• is an N• × M+ matrix and ψ○ an N○ × M− matrix.
3. Electron–electron interaction and chiral condensate in magnetic fields
The substantial advances made recently to improve the quality of graphene allow us to begin discussing the physics of electron–electron interaction in graphene. The low-energy physics in the Dirac cones around the charge neutrality point is the focus of the problem. In particular, since the kinetic energy is quenched in a magnetic field, there can be various possibilities for symmetry breaking in the n = 0 Landau level (with the Landau-level filling ν = 0) [10–15]. Since the n = 0 Landau level is topologically protected by the index theorem, chiral symmetry plays a fundamental role in the electron–electron interaction for the ν = 0 state. If one takes a nearest-neighbor electron–electron interaction for the n = 0 Landau level, the ν = 0 state, for the spin-polarized case, is given by the chiral condensates [16] which are doubly degenerate. In this section, we give a self-contained description of the states, which are gapped many-body states.
3.1. Ground state within the projected subspace
As to the electron–electron interaction, we take the two-body interaction Vijninj between sites 〈ij〉, which can include long-range interactions. Note that
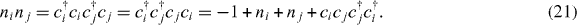
We can express the interaction in an electron–hole symmetric form, at half-filling, as
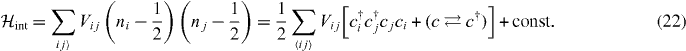
We assume that the electron–electron interaction is sufficiently weak as compared with the Landau gap between the n = 0 Landau level and those for n = ± 1. When the filling factor of the n = 0 LL is ν < 1, the ground state is then given by the configurations of the n = 0 LL states, while the filled states below them can be regarded as a 'Dirac sea'. Since the one-particle spectrum in graphene is given by the  -zero modes with chiral pairs as discussed above, the kinetic energy from the
-zero modes with chiral pairs as discussed above, the kinetic energy from the  -zero modes is negligible, so that the ground state is given perturbatively (i.e. for the interaction energy that is smaller than the Landau gap) as
-zero modes is negligible, so that the ground state is given perturbatively (i.e. for the interaction energy that is smaller than the Landau gap) as
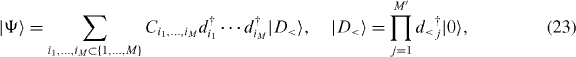
where |D<〉 is the filled Dirac sea (di|D<〉 = 0 for all i's), {i1,...,iM} a subset of the  -zero modes and M is the number of particles. The free-fermion Hamiltonian
-zero modes and M is the number of particles. The free-fermion Hamiltonian 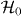 is written as
is written as
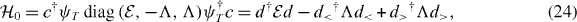
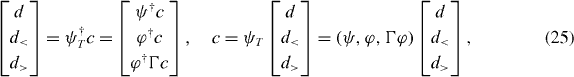
where d† = (d†1,...,dM), d<† = (d<1†,...,d<M'†) and d>† = (d>1†,...,d>M'†) are, respectively, fermion creation operators for the  -zero mode, the negative-energy states and positive ones with {dℓ,d†ℓ'} = δℓℓ', {d<ℓ,d†<ℓ'} = δℓℓ', {d>ℓ,d†>ℓ'} = δℓℓ', etc.
-zero mode, the negative-energy states and positive ones with {dℓ,d†ℓ'} = δℓℓ', {d<ℓ,d†<ℓ'} = δℓℓ', {d>ℓ,d†>ℓ'} = δℓℓ', etc.
3.2. Projected interaction and its symmetry
Now let us take the chiral basis for the  -zero modes to describe the interaction between the particles. We assume that the perturbative ground state within the configuration of the n = 0 Landau level is determined by the projected interaction
-zero modes to describe the interaction between the particles. We assume that the perturbative ground state within the configuration of the n = 0 Landau level is determined by the projected interaction 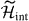 . The projected Hamiltonian is defined as
. The projected Hamiltonian is defined as
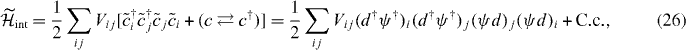
where C.c. is a charge conjugation defined below, and 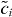 is a projected fermion defined as
is a projected fermion defined as
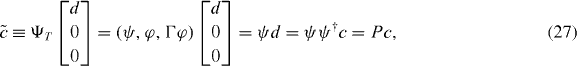
with P = ψψ† = P† being the projection to the  -zero modes. These
-zero modes. These 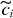 's are not canonical fermion operators, since
's are not canonical fermion operators, since
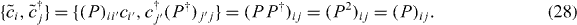
Note that the projected Hamiltonian is clearly positive semi-definite.
3.3. Chiral transformation and charge conjugation
Let us take a chiral basis to define canonical fermions di for the  -zero modes, defined as
-zero modes, defined as
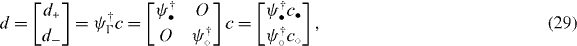


We can define a chiral transformation 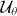 as
as

where the generator of the transformation, the chirality  , is given as
, is given as
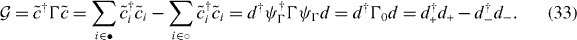
The chiral transformation operates as


Then it is clear that the projected interaction is invariant under the chiral transformation as

For an infinitesimal transformation this implies a conservation law,

Let us next define a charge conjugation which is anti-unitary as

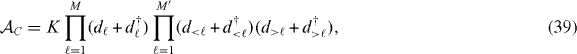
where K is complex-conjugation with K2 = 1. Its operation is, for example,
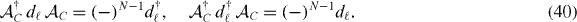
Then the invariance of the interaction Hamiltonian under the charge conjugation,

trivially follows.
3.4. Chiral condensate as a doubly degenerate Hall insulator
In this section, we restrict ourselves to considering a repulsive interaction that only acts between the • and ○ sites. The projected interaction in this case is written as

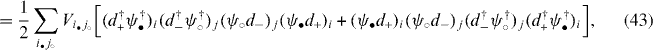
where Vi•j○ > 0. Here we allow any (i.e. including long-ranged) repulsive interactions between the • and ○ sites.
Now we can readily see that the two states

which have maximum and minimum chiralities, respectively, are special, since each of them has vanishing interaction energy with 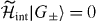 . Namely, |G+〉 has all the dℓ+ states filled with (d†+ψ†•)i|G+〉 = 0. Also, none of the dℓ− states are occupied, so that we have (ψ○d−)j|G+〉 = 0. Since the interaction Hamiltonian
. Namely, |G+〉 has all the dℓ+ states filled with (d†+ψ†•)i|G+〉 = 0. Also, none of the dℓ− states are occupied, so that we have (ψ○d−)j|G+〉 = 0. Since the interaction Hamiltonian 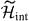 is semi-positive definite, these two states are thus the ground states of
is semi-positive definite, these two states are thus the ground states of 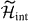 with a degeneracy of two.
with a degeneracy of two.
As to the chiral transformation, we have

where 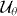 is the chiral operation defined above. This property follows, since |G±〉 are eigenstates of the chirality
is the chiral operation defined above. This property follows, since |G±〉 are eigenstates of the chirality 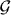 as
as

Thus we have shown that the ground states are the chiral condensates, where the chirality is macroscopic (M± ∼ N).
As to the charge conjugation, it operates as

where |D>〉 is the positive Dirac sea up to the sign.
The Hall conductivity of the doubly degenerate chiral condensates can be calculated with the Niu–Thouless–Wu formula as
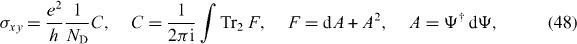
where Ψ = (|G+〉,|G−〉) is the chiral-condensed ground states with the degeneracy of ND = 2.
The doublet, being degenerate, can be mixed, but diagonalization of the chirality  acts to fix the gauge. Here we assume a finite energy gap above the ground state multiplet. Then the Chern number of the doublet becomes well defined, and is given by the sum as
acts to fix the gauge. Here we assume a finite energy gap above the ground state multiplet. Then the Chern number of the doublet becomes well defined, and is given by the sum as

where C± is the Chern number for |G±〉. Further, we can decompose the condensate as

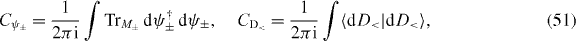
where CD< is the Chern number of the filled Dirac sea. Since the chiral operator Γ is unitary, the Chern number of the positive Dirac sea is the same as that of the negative Dirac sea as
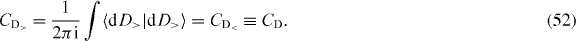
The charge conjugation is anti-unitary, which implies that

and we end up with the total Chern number of the doubly degenerate chiral condensate as
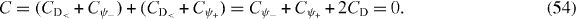
Namely, the exact chiral condensate for the half-filling (i.e. ν = 0) constructed from the chiral doublet for the projected interaction is a Hall insulator with the topological degeneracy of 2. Physical behaviors such as the boundary effects of the edge states and correlation functions are discussed in a recent paper [16].
The discussion here is for spinless fermions. An extension to chiral condensates for spinful cases can be important for the graphene if the state is spin unpolarized [13]. Also, optical responses of the chiral condensates are among the interesting future problems. These will be published elsewhere based on the present formulation.
4. Multilayer graphene and chiral symmetry
Since graphene is considered as a single-layer graphite, investigation of multilayer graphene is important to elaborate the specialty of graphene and also dimensional crossover from two dimensions to three. There is a long history of the studies of graphite, and its electronic structure is well described by the tight-binding model [9]. In view of the chiral symmetry, some of the tight-binding parameters break the chiral symmetry, while others do not. Surprisingly, the ones with chiral symmetry breaking are substantially small compared with the ones respecting chiral symmetry. Then, imposing the chiral symmetry for the studies of multilayer graphene is a good starting point and makes the physical picture of multilayer graphene dramatically simple, which we present in this section. Generically, the chiral symmetry breaking causes gap opening at the zero energy. Optical responses are sensitive to the existence of the gap. Then, some of the spectra of multilayer graphene are well understood from the viewpoint of chiral symmetry breaking. It makes the universal feature of chiral symmetry clear.
4.1. Bilayer and trilayer Hamiltonians
Although the low-energy effective Hamiltonian has been discussed previously [17–19], the chiral symmetric model has several advantages. One is that the discussion of low-energy physics is much clearer since the derivation of the low-energy Hamiltonian is substantially simplified, especially as the behaviors of the wavefunctions are very clearly described. Also, we can treat the tight-binding Hamiltonian with a weak magnetic field directly since the zero energy is special for the chiral symmetric model and the physics near the zero energy, which is our main interest, is accessible by the sparse matrix technique as described below. This is essential to describe the physics of multilayers such as trigonal warping which is only relevant for a very weak magnetic field. The tight-binding model with such a very weak magnetic field is only accessible by using the chiral symmetry and the sparse matrix technique.
Let us start with the Hamiltonian of bilayer graphene in a magnetic field as a simple generalization of the monolayer model [6]. With j = (j1,j2) denoting two-dimensional coordinates, e1,2 the unit translations and φ the total flux per hexagon in units of the flux quantum φ0 = h/e (see figure 1), the Hamiltonian is written as

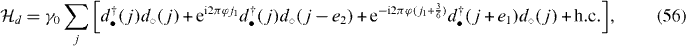


where we have used the Peierls phases to describe the effects of the magnetic field. Then the lattice periodicity is enlarged by the magnetic field. One needs a very large system for the systems with a weak magnetic field. Here 'u(d)' denote up (down) layers, γ0 is the nearest-neighbor hopping within each layer and γ1 is the inter-layer hopping perpendicular to the layer. The hopping γ3, the second largest inter-layer hopping, is along an oblique direction, and causes trigonal deformation of the energy dispersion (trigonal warping) [9] in zero magnetic field. In a finite magnetic field, the hopping acquires Peierls phases appearing in the Hamiltonian above, again due to the oblique directions of the hopping.
Figure 1. Lattice structure of bilayer graphene. Interlayer couplings γ1 and γ3 are denoted by green and yellow bonds, respectively.
Download figure:
Standard imageAs to the trilayer, we have
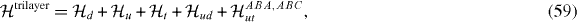

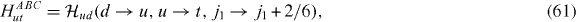

Here we have added 't' (top layer) on top of the d,u (down, up) layers, and ABA (ABC) stands for the trilayer graphene with the ABA (ABC) stacking.
Now let us Fourier-transform dα,uα,tα, first along the e2 direction as

where the momentum is defined as
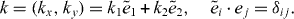
Then we have
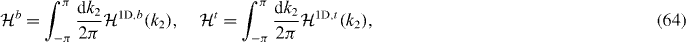

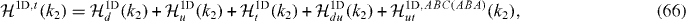
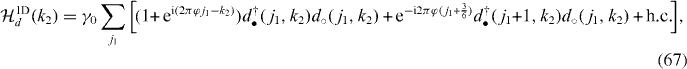


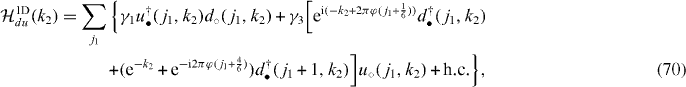
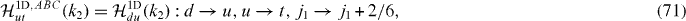

In figure 2, we have shown the spectrum of bilayer graphene on a cylinder. Here the translation symmetry along e2 makes the wave number k2 a good quantum number, so that the dispersion against k2 is depicted. Due to the chiral symmetry, states near the zero energy, which are our focus, are obtained by diagonalizing the sparse matrices D†D or DD†, which are semi-positive definite (see equation (4)) only near the minimum energies. Numerically, it is substantially easy compared with diagonalizing H directly.
Figure 2. Energy spectrum in the region around the n = 0 Landau level in bilayer graphene with zigzag edges and periodic boundaries orthogonal to those (along e2). Here we have a relatively small magnetic field ϕ = 1/500, with γ0 = 1.0 and γ1 = 0.2. The system size for the x directions is 1000. The attached numbers denote the Hall conductivity when EF is in each interval between the Landau levels, which coincide with the number of edge modes (curves traversing different Landau levels).
Download figure:
Standard imageThe 'bulk-edge correspondence', which dictates that bulk topological features such as the quantized Hall conductivity have a one-to-one correspondence to edge properties, allows us to obtain the Hall conductivity of the system by counting the number of edge modes. The numerical results with edges for a weak magnetic field are given in figure 2. Counting the number of branches, the Hall conductances in units of e2/h are given in the figure.
4.2. Zero magnetic field
For zero magnetic field, we can Fourier transform uα,dα,tα along the e1 as

The fully Fourier-transformed bilayer Hamiltonian is

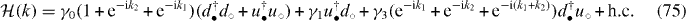


where


For the trilayer, we have

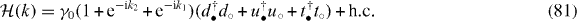
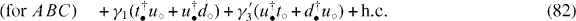
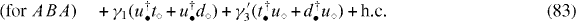
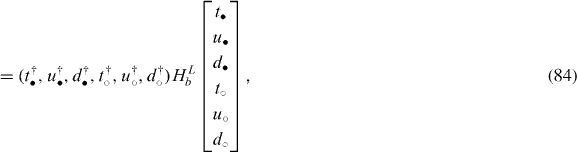

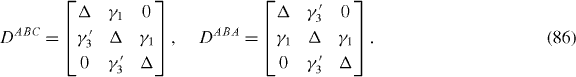
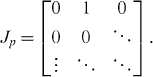
Further, we can extend the above argument to consider the stacked system with a general number (p) of ABC layers. In the present representation, the Hamiltonian simplifies to
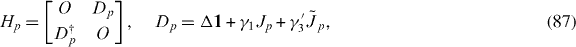
where 1 is a p-dimensional unit matrix and
4.2.1. Low-energy Hamiltonians around K and K'
The Dirac points (K and K' points) for the monolayer graphene are specified by e−ik01 = ω and e−ik02 = ω2, ω3 = 1, ω ≠ 1, at which Δ vanishes along with γ3' → 0. Around the Dirac points we can expand them as
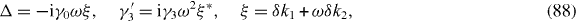
where δki = ki − k0i. As to multilayer graphene, gapless momenta are determined by 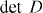 's. For the bilayer, it is given as
's. For the bilayer, it is given as
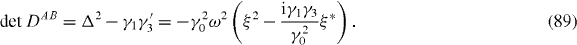
This vanishes at four points, ξ = 0,ξ0,ωξ0,ω2ξ0, where ξ0 = (γ1γ3/γ20)eiπ/6. Namely, each Dirac point proliferates into four.
For the trilayer, it is
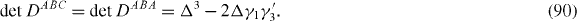
This gives Dirac cones at 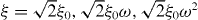 and double zero at ξ = 0. One may discuss the case of p-layers as well.
and double zero at ξ = 0. One may discuss the case of p-layers as well.
The Dirac points in the chiral-symmetric system at E = 0 are specified by 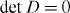 , which determines the gap closing momenta. Since
, which determines the gap closing momenta. Since  is a product of the energies of all branches and the high-energy ones are considered as constants near the gap closing momentum, the low-energy dispersion near E = 0 is given by
is a product of the energies of all branches and the high-energy ones are considered as constants near the gap closing momentum, the low-energy dispersion near E = 0 is given by  . In figure 3, we have shown
. In figure 3, we have shown  and Arg
and Arg 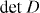 for a finite value of γ3 in the bilayer system. From this plot, we can see that the chiralities of the four Dirac points are +1,−1,−1,−1 or −1,+1,+1,+1. This characterization of the Dirac cones by the phase of
for a finite value of γ3 in the bilayer system. From this plot, we can see that the chiralities of the four Dirac points are +1,−1,−1,−1 or −1,+1,+1,+1. This characterization of the Dirac cones by the phase of 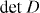 is only possibly using the special form of the chiral symmetric Hamiltonian.
is only possibly using the special form of the chiral symmetric Hamiltonian.
Figure 3. For bilayer graphene in the presence of trigonal warping (γ3 ≠ 0), we show 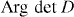 (left panel), contours for
(left panel), contours for 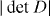 (center) and
(center) and 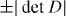 (right). Note that the right panel may look like a band dispersion, but actually it plots
(right). Note that the right panel may look like a band dispersion, but actually it plots 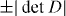 (∝ the band dispersion in fact). Here we take γ0 = 3.1, γ1 = 0.4, γ3 = 0.3.
(∝ the band dispersion in fact). Here we take γ0 = 3.1, γ1 = 0.4, γ3 = 0.3. 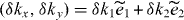 .
.
Download figure:
Standard imageNow let us discuss the low-energy Hamiltonian in the absence of the trigonal warping (γ3 = 0). In the ABC-stacked p-layered graphene (including bilayer), Dp is triangular
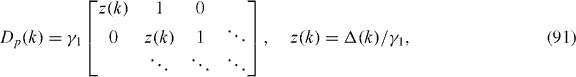

where taking a continuous limit around K and K' points implies that we are assuming |z| ≪ 1. Precisely at the K and K' points, we have D†pDp = γ21diag (0,1,1,...), i.e. there exists only one low-energy mode for D†pDp while the others have γ21. Then the chiral symmetry (i.e. Hp is composed of Dp as the off-diagonal block) implies that Hp has two low-energy modes, ± (k), with
(k), with 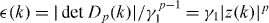 . Here we can take the chiral basis introduced in previous sections to expand the low-energy doublet as
. Here we can take the chiral basis introduced in previous sections to expand the low-energy doublet as
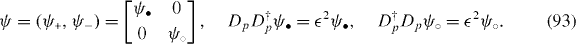
ψ•,○ are asymptotically (|z| ≪ 1) normalized and given as
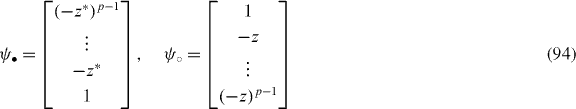
with 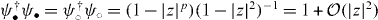 . They are consistent with equation (93) up to the errors arising from the normalization of ψ†•ψ• and ψ†○ψ○. Then projecting out the high-energy sectors, we have an effective Hamiltonian for the low-energy doublet formed by the chiral basis ψ (including the monolayer case) as
. They are consistent with equation (93) up to the errors arising from the normalization of ψ†•ψ• and ψ†○ψ○. Then projecting out the high-energy sectors, we have an effective Hamiltonian for the low-energy doublet formed by the chiral basis ψ (including the monolayer case) as
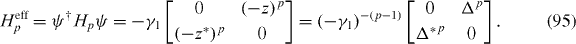
It is given in [19] with a unitary transformation. Here the derivation is substantially simplified with the projection operator exploiting the chiral symmetry.
As to the ABA trilayer, (DABA)†DABA has two low-energy modes around the K and K' points, which implies that the low-energy modes of HABA3 are spanned by a four-dimensional orthonormalized chiral basis as
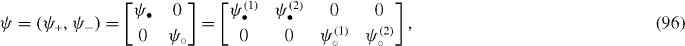

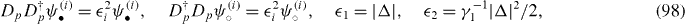
where we have, up to the leading order,
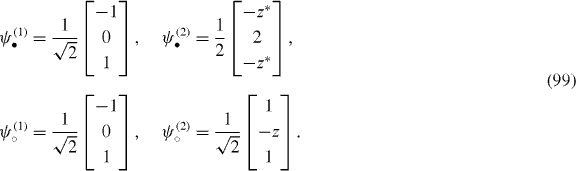
Now we have

and
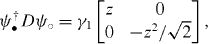
so that we end up with a simple decomposition,
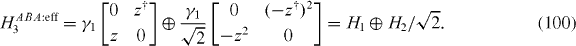
4.2.2. Landau levels
Around the Dirac cones, we can expand the effective Hamiltonian, as in the monolayer case, as
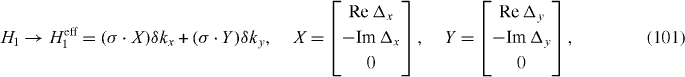
where 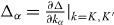 . Then we have
. Then we have

where c2 = |X × Y |/ℏ2 is an effective 'light velocity' and 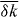 is the averaged momentum near the Dirac cones with
is the averaged momentum near the Dirac cones with 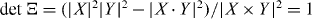 . Note that
. Note that

where χ = sgn Im ΔxΔ*y is the chirality of the Dirac cones.
In a magnetic field, the Hamiltonian HC1 in the continuum limit is obtained by replacing ℏδkα → πα = pα − eAα = −iℏ∂α − eAα where [πx,πy] = iℏeB = i(ℏ/ℓB)2 with 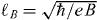 (eB > 0). As to the ABC stacked p-layered graphene (including monolayer and bilayer), the effective continuum Hamiltonian is obtained as the extension of McCann–Fal'ko [17] as
(eB > 0). As to the ABC stacked p-layered graphene (including monolayer and bilayer), the effective continuum Hamiltonian is obtained as the extension of McCann–Fal'ko [17] as
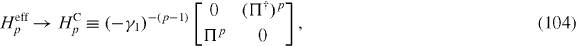

This is another derivation of the pth layer effective Hamiltonian discussed by Koshino–McCann [19] for the chiral symmetric case. Here the commutation relation of Π is given as
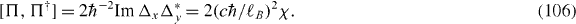
Then one can define a canonical boson operator a ([a,a†] = 1) as

For the positive chirality χ = + 1, one has
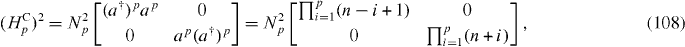
where 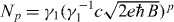 , n = a†a, and
, n = a†a, and
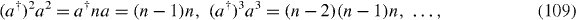

Then we have a series of non-equally spaced Landau levels

The χ = −1 case follows trivially.
4.3. Lifshitz transition in magnetic fields
In this section, let us focus on the Lifshitz transition caused by the trigonal warping term γ3, by directly calculating the energy levels on a honeycomb lattice without using the low-energy effective model [17, 18]. We stress here that our numerical calculations are performed for the tight-binding model on a honeycomb lattice with the Peierls phases for the magnetic field which require diagonalization of large matrices for systems with a weak magnetic field. This becomes only possible by the chiral symmetry using the sparse matrix technique. It is enough to diagonalize the sparse matrix D†D (see equation (4)) near the zero energies. The results are compared with the discussion of the Lifshitz transition using the effective low-energy model in [17, 18]. However, the crossover phenomenon from the lattice model to the low-energy effective Hamiltonian caused by γ1 is only possible by the present direct lattice calculation (see figure 4). The Landau levels of the bilayer graphene as a function of γ1 are shown in figure 4. One can observe the crossover, that is, the γ1 produces bonding–antibonding splitting, so that the low-energy sector is projected out from the high-energy one.
Figure 4. Low-energy Landau levels in the bilayer graphene for the magnetic field ϕ = 1/3000 as a function of γ1 (with γ0 = 1.0 and γ3 = 0 here).
Download figure:
Standard imageFigure 5, on the other hand, displays the Landau levels as a function of the γ3. One can see that the Landau levels at γ3 = 0 are adiabatically connected to two classes of Landau levels at γ3 ≠ 0, which correspond to those of two kinds of four Dirac cones with different Fermi velocities. To observe the phenomenon at the moderate value of the flux, we take an artificially large value for γ1/γ0 = 0.5 in the left panel of figure 5. In the right panel, the same plot for a much smaller, realistic γ1 and the magnetic field is shown. Numerical calculations for such a weak magnetic field become possible only by imposing the chiral symmetry. Then the Lifshitz transition with realistic parameters is clearly demonstrated using the tight-binding model.
Figure 5. The Lifshitz transition caused by γ3 in terms of: (left) the low-energy Landau levels in the bilayer graphene in a magnetic field ϕ = 1/3000 (γ0 = 1.0 and γ1 = 0.5). The red points at γ3 = 0 indicate a sequence 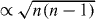 (n = 0,1,2,...). We have also displayed the sequences
(n = 0,1,2,...). We have also displayed the sequences 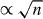 for n = 0,1,2,3 (blue dots) and for n = 1,2,3 (orange) at the largest γ3. They show four Dirac cones after the Lifshitz transition has been classified into two different classes. (Right) The same plot for a realistic case (with γ1 = 0.2 and a flux as small as ϕ = 1/30 000). The bunching of the Landau levels is not clearly seen for the realistic parameters.
for n = 0,1,2,3 (blue dots) and for n = 1,2,3 (orange) at the largest γ3. They show four Dirac cones after the Lifshitz transition has been classified into two different classes. (Right) The same plot for a realistic case (with γ1 = 0.2 and a flux as small as ϕ = 1/30 000). The bunching of the Landau levels is not clearly seen for the realistic parameters.
Download figure:
Standard image5. Optical responses in bilayer and trilayer graphene
In this section, we discuss optical responses in bilayer and trilayer graphene in the quantum Hall regime. In particular, we focus on the effect of the presence or absence of the chiral symmetry. The non-zero chiral index associated with the chiral symmetry of the system, as is the case in bilayer and trilayer graphene, implies the existence of chiral zero modes (n = 0 LLs) in the presence of magnetic fields and the massless bands or bands touching each other at zero energy without magnetic fields. This affects the optical responses associated with n = 0 LLs, since n = 0 LLs are situated at exactly zero energy with chiral symmetry, while they valley-split without chiral symmetry. Here we study the optical longitudinal conductivity σxx(ω), which describes the optical absorption, and the optical Hall conductivity σxy(ω), which is directly related to the Faraday rotation, since the Faraday rotation angle ΘH is proportional to σxy(ω) in the quantum Hall regime as
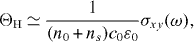
where c0 is the speed of light and n0(ns) is the refractive index of the air (substrate) [20].
The Faraday rotation for monolayer graphene was studied theoretically [21, 22], and has experimentally started to be measured [23]. Further, there is growing interest in the optical properties of bilayer and trilayer graphene, given that their electronic structures are distinct from that of monolayer graphene. As we have seen in section 4, bilayer graphene has two parabolic bands touching at the K and K' points [17, 24]. Trilayer graphene comes with two different types of stacking, ABA and ABC, where the former is described effectively as a mixture of monolayer and bilayer bands, while the latter shows a cubic band as equation (104) with p = 3. If we only consider hopping terms with γ0,γ1 for these multilayers and the chiral symmetry is preserved, the n = 0 LLs are zero energy states and particle–hole symmetric, so that σxx( F,ω),σxy(
F,ω),σxy( F,ω) become even and odd functions with respect to
F,ω) become even and odd functions with respect to  F = 0. If we consider small hopping terms breaking the chiral symmetry, which we discuss in ABA trilayer, the valley splitting of n = 0 LLs gives rise to splitting of optical resonances associated with n = 0 LLs and σxx(
F = 0. If we consider small hopping terms breaking the chiral symmetry, which we discuss in ABA trilayer, the valley splitting of n = 0 LLs gives rise to splitting of optical resonances associated with n = 0 LLs and σxx( F,ω),σxy(
F,ω),σxy( F,ω) are no longer even or odd functions with
F,ω) are no longer even or odd functions with  F = 0.
F = 0.
In order to calculate the optical longitudinal (σxx(ω)) and Hall (σxy(ω)) conductivities, we utilized the Kubo formula
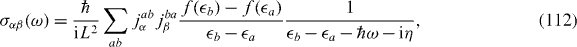
where f(ε) is the Fermi distribution,  a eigenenergies, η a small energy cutoff for a stability of the calculation and jabα the matrix element of the current operator j = ∂H/∂A.
a eigenenergies, η a small energy cutoff for a stability of the calculation and jabα the matrix element of the current operator j = ∂H/∂A.
5.1. Bilayer graphene
We start with the optical conductivities for the bilayer system with γ0,γ1 terms (equation (104) with p = 2). In figures 6(a) and (b), we show optical longitudinal and Hall conductivities (σxx( F,ω),σxy(
F,ω),σxy( F,ω)) plotted against the Fermi energy
F,ω)) plotted against the Fermi energy  F and the frequency ω. Energy and frequency are normalized with the cyclotron frequency ωc = 2v2eB/γ1 for bilayer parabolic bands. If we label LLs with the Landau index n and an electron/hole band index s = ± , the selection rule for bilayer graphene is described with intra-band transitions (n,s) → (n + 1,s) and inter-band transitions (n,−s) → (n + 1,s). For both σxx(
F and the frequency ω. Energy and frequency are normalized with the cyclotron frequency ωc = 2v2eB/γ1 for bilayer parabolic bands. If we label LLs with the Landau index n and an electron/hole band index s = ± , the selection rule for bilayer graphene is described with intra-band transitions (n,s) → (n + 1,s) and inter-band transitions (n,−s) → (n + 1,s). For both σxx( F,ω),σxy(
F,ω),σxy( F,ω), intra-band transitions (n,s) → (n + 1,s) occur around
F,ω), intra-band transitions (n,s) → (n + 1,s) occur around
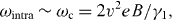
with the Fermi velocity of the Dirac cone v (=c in section 4), since LLs are almost equally spaced, unlike in the monolayer case where LL energy 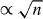 is not equally separated. The inter-band transitions across the band-touching point occur around
is not equally separated. The inter-band transitions across the band-touching point occur around

for large enough n. When both transitions (n,−) → (n + 1,+) and (n + 1,−) → (n,+) are allowed, these contributions for optical conductivities add up for σxx( F,ω) while they cancel out for σxy(
F,ω) while they cancel out for σxy( F,ω) due to the sign of current matrix elements, so that we have inter-band transitions wide in
F,ω) due to the sign of current matrix elements, so that we have inter-band transitions wide in  F for σxx(
F for σxx( F,ω) while they are seen in σxy(
F,ω) while they are seen in σxy( F,ω) only for a region of Fermi energy where one of the transitions is allowed.
F,ω) only for a region of Fermi energy where one of the transitions is allowed.
Figure 6. For the bilayer graphene QHE system with only γ0,γ1 terms, we show (a) optical longitudinal conductivity σxx( F,ω), and (b) optical Hall conductivity σxy(
F,ω), and (b) optical Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and the frequency ω.
F and the frequency ω.
Download figure:
Standard image5.2. ABA trilayer graphene
For ABA stacked trilayer, the effective Hamiltonian around K+/K− points is given by a 6 × 6 matrix (the dimension being 2 sublattices × 3 layers) as [25–28]
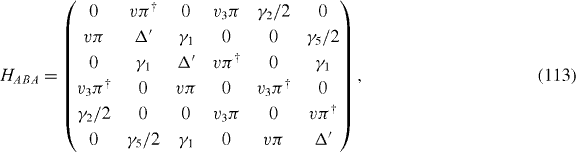
with π = πx + iπy, a velocity v3 associated with γ3 as v3 = vγ3/γ0, Δ' the on-site energy difference between the atoms with and without vertical bond γ1, and γ2 (γ5) the next-nearest interlayer hoppings between A1 and A3 (B1 and B3).
First, we only retain γ0,γ1 terms in equation (113), in which case the Hamiltonian is chiral-symmetric. In figures 7(a) and (b), the optical longitudinal and Hall conductivities σxx( F,ω),σxy(
F,ω),σxy( F,ω) are plotted against the Fermi energy
F,ω) are plotted against the Fermi energy  F and frequency ω. The magnetic field is chosen so that an interlayer hopping energy is γ1/ℏωc = 5, with the monolayer cyclotron energy
F and frequency ω. The magnetic field is chosen so that an interlayer hopping energy is γ1/ℏωc = 5, with the monolayer cyclotron energy 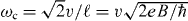 . We can see a monolayer contribution (Dirac cyclotron frequency =ωc) and a bilayer contribution with a cyclotron energy,
. We can see a monolayer contribution (Dirac cyclotron frequency =ωc) and a bilayer contribution with a cyclotron energy, 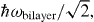 both of which show intra-band and inter-band transitions. For moderate magnetic fields B ∼ 1 T, the cyclotron frequency for the monolayer is much larger than that for the bilayer, ωc ≫ ωbilayer. In this case, σxx is an even function with respect to
both of which show intra-band and inter-band transitions. For moderate magnetic fields B ∼ 1 T, the cyclotron frequency for the monolayer is much larger than that for the bilayer, ωc ≫ ωbilayer. In this case, σxx is an even function with respect to  F = 0, while σxy is odd due to the electron–hole symmetry, a consequence of the chiral symmetry. The jump of σxy at
F = 0, while σxy is odd due to the electron–hole symmetry, a consequence of the chiral symmetry. The jump of σxy at  F = 0 is related to the chiral zero modes.
F = 0 is related to the chiral zero modes.
Figure 7. We show optical responses for ABA-stacked trilayer graphene only with v,γ1 terms (with γ1/ℏωc = 5), which respect the chiral symmetry. (a) Optical longitudinal conductivity σxx( F,ω) and (b) optical Hall conductivity σxy(
F,ω) and (b) optical Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and frequency ω.
F and frequency ω.
Download figure:
Standard imageNow, if we include all the hopping terms in equation (113), the chiral symmetry is broken, and we no longer have the chiral protection for zero modes (three zero-energy LLs). We have then a massive Dirac band plus gapped bilayer bands with energy shifts. As to hopping parameters, we adopt the values for graphite, γ0 = 3.2 eV, γ1 = 0.39 eV, γ3 = 0.32 eV, γ2 = −0.020 eV, γ5 = 0.038 eV, Δ' = 0.050 eV [9, 29].
Figures 8(a) and (b) depict the result for the optical longitudinal σxx( F,ω) and Hall conductivity σxy(
F,ω) and Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and frequency ω for ABA-stacked trilayer graphene, including all the hoppings. We see contributions from monolayer-like Dirac LLs (labeled with M) and those from bilayer LLs (B), both of which exhibit intra-band and inter-band transitions. Since the Dirac cone is massive due to the chiral symmetry breaking and the zero-energy LL for the monolayer band (M0) is situated at the bottom of the conduction band for K+ valley and the top of the valence band for K−, M0 → M(1,+) resonance occurs at an energy lower than M(1,−) → M0 for K+, and vice versa for K− (figure 8(c)). A cancellation of resonances in σxy, due to the opposite signs in current matrices, occurs between M(1,−) → M0 for K+ and M0 → M(1,+) for K− for a region of Fermi energy between M0(K+) and M0(K−), while this is not the case with σxx. For bilayer contributions, satellites appear as
F and frequency ω for ABA-stacked trilayer graphene, including all the hoppings. We see contributions from monolayer-like Dirac LLs (labeled with M) and those from bilayer LLs (B), both of which exhibit intra-band and inter-band transitions. Since the Dirac cone is massive due to the chiral symmetry breaking and the zero-energy LL for the monolayer band (M0) is situated at the bottom of the conduction band for K+ valley and the top of the valence band for K−, M0 → M(1,+) resonance occurs at an energy lower than M(1,−) → M0 for K+, and vice versa for K− (figure 8(c)). A cancellation of resonances in σxy, due to the opposite signs in current matrices, occurs between M(1,−) → M0 for K+ and M0 → M(1,+) for K− for a region of Fermi energy between M0(K+) and M0(K−), while this is not the case with σxx. For bilayer contributions, satellites appear as 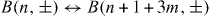 and
and  , since the trigonal warping term mixes n LLs and n + 3 LLs [30, 31]. The resonance frequency for intra-band transition within the conduction band is larger than that within the valence band, which is a consequence of the electron–hole asymmetry in the bilayer bands, triggered by a breaking of the chiral symmetry. A deviation in the cyclotron mass for electron and hole bands prevents complete cancellation between B(n,−) → B(n + 1,+) and B(n + 1,−) → B(n,+) transitions, which results in small inter-band transitions in a wide region of Fermi energy.
, since the trigonal warping term mixes n LLs and n + 3 LLs [30, 31]. The resonance frequency for intra-band transition within the conduction band is larger than that within the valence band, which is a consequence of the electron–hole asymmetry in the bilayer bands, triggered by a breaking of the chiral symmetry. A deviation in the cyclotron mass for electron and hole bands prevents complete cancellation between B(n,−) → B(n + 1,+) and B(n + 1,−) → B(n,+) transitions, which results in small inter-band transitions in a wide region of Fermi energy.
Figure 8. We show optical responses for ABA-stacked trilayer graphene with all the hopping parameters. (a) Optical longitudinal conductivity σxx( F,ω) and (b) optical Hall conductivity σxy(
F,ω) and (b) optical Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and the frequency ω for a magnetic field B = 1 T. (c) A diagram indicating allowed resonances in σxy.
F and the frequency ω for a magnetic field B = 1 T. (c) A diagram indicating allowed resonances in σxy.
Download figure:
Standard image5.3. ABC trilayer graphene
The low-energy effective Hamiltonian of ABC-stacked trilayer graphene in a 2 × 2 matrix equation (104) is a cubic form in the momentum, if we neglect hopping terms but γ0,γ1. For this effective Hamiltonian, LL energy, equation (111) shows a magnetic-field dependence 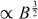 , resulting in a smaller LL spacing compared to the single-layer LL
, resulting in a smaller LL spacing compared to the single-layer LL  and bilayer LL ∝B for weak magnetic fields.
and bilayer LL ∝B for weak magnetic fields.
Now we turn to a result for the optical conductivities in ABC trilayer for an interlayer hopping energy γ1/ℏωc = 5, with monolayer cyclotron frequency 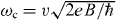 . Figures 9(a) and (b) show the optical longitudinal and Hall conductivity σxy(
. Figures 9(a) and (b) show the optical longitudinal and Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and frequency ω for ABC-stacked trilayer graphene in strong magnetic fields. In contrast to ABA stacking (figure 7), we only see a single sequence of intra-band and inter-band transitions with a much smaller cyclotron energy than ℏωc due to the dependence on magnetic fields
F and frequency ω for ABC-stacked trilayer graphene in strong magnetic fields. In contrast to ABA stacking (figure 7), we only see a single sequence of intra-band and inter-band transitions with a much smaller cyclotron energy than ℏωc due to the dependence on magnetic fields 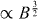 due to the LL energy structure (equation (111) with p = 3). The inter-band transition occurs at ℏω ∼ 2
due to the LL energy structure (equation (111) with p = 3). The inter-band transition occurs at ℏω ∼ 2 F for the same reason as in the bilayer, while the intra-band transition energy grows with increasing LL index n as
F for the same reason as in the bilayer, while the intra-band transition energy grows with increasing LL index n as

which explains why the intra-band resonance energy increases with n in figure 9(a), while it decreases with n in the case of monolayer graphene [22]. We can then predict in general that, for ABC p-layered graphene, the intra-band transition occurs at

and the inter-band transition at ω ∼ 2 F. Thus, we end up with intra-band transition energies that exhibit different behaviors with the Landau index n as
F. Thus, we end up with intra-band transition energies that exhibit different behaviors with the Landau index n as
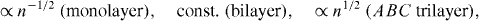
while the inter-band transition energies are qualitatively the same with ∼2 F.
F.
Figure 9. For an ABC-stacked trilayer graphene QHE system (with γ1/ℏωc = 5), we show (a) optical longitudinal conductivity σxx( F,ω), and (b) optical Hall conductivity σxy(
F,ω), and (b) optical Hall conductivity σxy( F,ω) plotted against the Fermi energy
F,ω) plotted against the Fermi energy  F and frequency ω.
F and frequency ω.
Download figure:
Standard imageFinally, let us mention the effects of electron–electron interactions on the optical responses. It is argued that the many-body gap is open for bilayer and trilayer graphene [32, 33]. This many-body gap causes a splitting of n = 0 LL and the optical transitions associated with n = 0 LL would also be split as we have seen in ABA trilayer with all hoppings. Another interesting problem is the effects of the inter-valley plasmon and possible CDW [34], which can cause a similar splitting of optical transitions or low-energy modifications of optical spectra.
6. Conclusion
One of the most intriguing features of graphene is a gapless Dirac dispersion at the charge neutrality point. It can be attributed to the special crystal symmetry of graphene. However, it is better characterized by the chiral symmetry of the honeycomb lattice and its multilayer generalization. It guarantees topological stability of the Dirac cones and the n = 0 Landau level at the zero energy for any small but finite perturbation respecting the chiral symmetry. The chiral symmetry is also important for many important physics of graphene such as many-body effects, electronic structures of multilayer graphene and optical responses. We have described these in detail in the paper.
Strictly speaking, the chiral symmetry is approximate in real graphene; then the chiral symmetry breaking is also useful in characterizing phenomena such as the gap opening in some types of multilayer graphene. In this paper, we have focused on the chiral symmetry and presented a unified and simplified description of the physics of graphene.
Acknowledgments
We thank Mikito Koshino for fruitful discussions. This work was supported in part by Grants-in-Aid for Scientific Research numbers 23340112, 23654128, 24840047 and 23540460 from the JSPS. The computation in this work has been done in part using the facilities of the Supercomputer Center, Institute for Solid State Physics, University of Tokyo.











