Discrete breathers and negative-temperature states

The physics of atomic Bose–Einstein condensates (BEC) has unveiled a large variety of new interesting phenomena that are relevant for atomic physics as well as for quantum optics [1]. For instance, BEC in optical lattices are ideal benchmarks to investigate the role of nonlinearity and spatial discreteness in quantum transport phenomena [2, 3]. The refined experimental techniques now available [4–8] enable investigations and applications of BEC in quantum coherence, quantum control, quantum information processing and the quantum-classical correspondence [9]. In addition, BEC in optical lattices can be considered as the 'atomic analogues' of light propagating in waveguide arrays [10].

The discrete nonlinear Schrödinger equation (DNLSE) is a basic semiclassical model for the study of BEC in optical lattices [11] and light propagating in arrays of optical waveguides [10]. Numerical studies have revealed the important role played by localized solutions, notably discrete breathers [11, 12]. Many aspects of the relationship between breathers and transport properties in BEC have recently been reviewed in [13]. The DNLSE has also been found to exhibit unusual thermodynamic features. A first statistical-mechanics study of the DNLSE identified a region in the parameter space characterized by the spontaneous formation of breathers and conjectured it to correspond to negative-temperature (NT) states [14]. NT states have attracted the curiosity of researchers since the pioneering work in systems of quantum nuclear spins [15]. From a thermodynamic point of view, the presence of NT states implies that the system's entropy is a decreasing function of the internal energy. In a series of recent papers [16–19], Rumpf provided a convincing theoretical argument that excludes the physical occurrence of NT equilibrium states in the DNLSE. In particular, he showed that even in the region of parameter space where breathers form spontaneously via a modulational instability, the DNSLE eventually reaches a maximum entropy (equilibrium) state formed by a background at infinite temperature superposed on a single breather that collects the 'excess' energy. It was also observed that the convergence to the equilibrium state predicted by Rumpf would need transients lasting over astronomical times [20]. Therefore, the question of characterizing DNLSE states over physically accessible time scales remains open.

Here, thanks also to a new algorithm for the measurement of the microcanonical temperature [21], we show that the dynamical evolution attains an NT quasi-stationary regime. The occurrence of long transients is not rare in statistical mechanics: it may be due to coarsening, nucleation, presence of free-energy barriers or the metastability of some modes. Such phenomena manifest themselves as slower-than-exponential relaxation laws. Within physical setups that are close to the DNLSE, a non-exponential relaxation was first found in chains of nonlinear oscillators and shown to originate from the presence of long-lived localized solutions [22]. Slow relaxations have been also found in Heisenberg spin chains and traced back to the existence of two conservation laws [23]. The latter example is particularly instructive, since—like the DNLSE—the equilibrium state can be identified by maximizing the entropy, given the constraints imposed by the conservation laws. Entropy arguments are, however, of little help to investigate the convergence to equilibrium. In order to clarify such features, we have implemented a microcanonical Monte Carlo (MMC) method which, in the so-called weak-coupling limit, has allowed us to identify a first source of 'slowness' in a coarsening phenomenon that follows from a sub-diffusive behaviour of the breather amplitudes. As a result, the density of breathers vanishes in time as t^−α with an exponent α = 0.37 ± 0.04. Direct simulations reveal, however, that the full DNLSE is characterized by even stronger mechanisms inhibiting the diffusion of the breather amplitudes. We are indeed able to show that a broad range of initial conditions (IC) converges towards a well-defined thermodynamic state characterized by an NT and a finite density of breathers. Such a state does not contradict the theoretical arguments of [16, 17], although the dynamical freezing of the high-amplitude breathers slows down the evolution so much as to render the convergence to equilibrium unobservable. Altogether, this phenomenon is reminiscent of ageing in glasses, although a more detailed analysis will be required to frame the analogy on more firm grounds.

Finally, let us comment on two simple strategies to generate quasi-stationary NT states in BEC in optical lattices and in arrays of optical waveguides. The methods are based on the introduction of boundary dissipations and the free expansion of wavepackets initially at equilibrium at a positive temperature, respectively. Both schemes are far simpler than the thermalization methods recently proposed for BEC trapped in lattices which require non-trivial Mott states followed by sweeps across Feshbach resonances to invert the sign of the atomic interaction [24]⁷.

The DNLSE describes the dynamics of BEC in an optical lattice in the mean-field limit [11, 13]. The corresponding Hamiltonian writes

$$\begin{equation} {\cal H} = \sum_j (V |\psi_j|^4 +\epsilon_j |\psi_j|^2) - Q \sum_j (\psi^*_j \psi_{j+1} + \mathrm{c.c.}), \end{equation} \noindent \tag{ 1 }$$

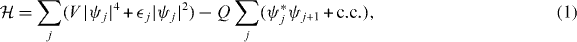
where j = 1,...,N is the index of the lattice site and periodic boundary conditions are assumed, and |ψ_j|² is the number of atoms at site j so that $\sum _j|\psi _j|^2$ is a conserved quantity. V measures the strength of the on-site interaction, Q is the hopping amplitude and _j is the on-site chemical potential. The sign of the first term in the rhs is considered positive, since we refer to the case of a repulsive-atom BEC (or the self-defocusing case for light propagating in waveguides), while the sign of the hopping term is irrelevant due to the symmetry associated with the gauge transformation ψ_j → ψ_je^iπj. In the following, we consider the uniform case _j = const so that this term can be removed in ${\cal H}$ via a suitable rotation of the wave function ψ_j. Complex canonical variables are defined through the Poisson bracket {ψ*_j,ψ_ℓ} = iδ_jℓ/ℏ, while the DNLSE is derived from the Hamilton's equation of motion

$$\begin{equation} \mathrm{i} \hbar \frac{\mathrm{d}\psi_j}{\mathrm{d}t} = \frac{\partial {\cal H}} {\partial \psi^*_j} = 2\,V |\psi_j|^2 \psi_j - Q (\psi_{j-1} + \psi_{j+1}). \end{equation} \tag{ 2 }$$

Since we are interested in dynamical aspects of the DNLSE, it is convenient to rewrite the Hamiltonian (1) in a form that is more profitable for numerical simulations. For this purpose, we introduce the adimensional variables

$$\begin{equation} q_j = \frac{1}{2}\sqrt{\frac{V}{Q}}(\mathrm{e}^{-\mathrm{i} \pi j} \psi_j + \mathrm{e}^{\mathrm{i} \pi j} \psi^*_j), \end{equation} \tag{ 3 }$$

$$\begin{equation} p_j = \frac{1}{2\mathrm{ i}}\sqrt{\frac{V}{Q}}(\mathrm{e}^{-\mathrm{i} \pi j} \psi_j - \mathrm{e}^{\mathrm{i} \pi j} \psi^*_j). \end{equation} \tag{ 4 }$$

Accordingly, after the rescaling $\mathcal H{\to }(V/Q^2)\mathcal H$, we obtain the adimensional Hamiltonian⁸

$$\begin{equation} H(p,q) = \sum_{j} (p_j^2+q_j^2)^2 + 2 \sum_{j}(p_j p_{j_{+1}}+q_j q_{j_{+1}}). \end{equation} \tag{ 5 }$$

The dynamics generated by this Hamiltonian conserves also the quantity $U = \sum _j u_j=\sum _j(p_j^2+q_j^2)$ that amounts to the rescaled number of particles.

The thermodynamic properties of this model are summarized in a phase diagram of energy (h) versus particle (u) density per site [14]. In figure 1, one can identify three regions: (i) a forbidden region R_f that lies below the ground state; (ii) an intermediate positive temperature region R_p; (iii) a region R_n where, according to  [14], NT states are expected.

Zoom In Zoom Out Reset image size

The presence of slow relaxation phenomena in R_n was first noted in [14] by monitoring the probability density of the local amplitudes u_j. The reason was traced back to the presence of breathers (that arise as a result of a modulational instability [23, 25–27]) and attributed to the weakness of their coupling to the background.

We start our analysis by studying the DNLSE for large energy and particle densities, since this allows clarification of the role of entropic constraints in the convergence towards the equilibrium state. In this parameter region, the contribution of the hopping term to the Hamiltonian (5) is negligible and R_n is identified by the condition h/u² > 2 [16, 17] (with our normalizations).

Since the interaction term is negligible, the local phase does not play any role and the system is characterized only by the particle numbers u_j. Nevertheless, the model keeps all the essential features of the original problem. In particular, it is possible to prove that, within R_n, the equilibrium state is characterized by a single breather superposed on an infinite-temperature background [18]. In the absence of an interaction energy, we have investigated the convergence to the equilibrium state by introducing an MMC method with a local stochastic rule that allows us to move on the hyper-surface characterized by a fixed energy and particle number. In this way, the evolution mimics the deterministic dynamics and singles out the role of entropic forces. More specifically, we start by randomly selecting a triplet (j − 1,j,j + 1) of consecutive sites and randomly modify the particle numbers, so as to leave U^s_j = u_j−1 + u_j + u_j+1 and the energy H^s_j = u²_j−1 + u²_j + u²_j+1 constant. As a result, the new configuration must lie along the intersection between a plane (particle-number constraint) and the surface of a sphere (energy constraint), and be restricted to the positive octant (u_j ⩾ 0). Depending on the relative amplitude of H^s_j and U^s_j, this line may be either a full circle or made of three separate arcs. In the former case, we select a point on the circle (assuming uniform probability); in the latter one, we select a point within the same arc as for the IC. Energy and particle numbers are thereby conserved and it is easy to verify that detailed balance is satisfied too. The time scale of the resulting dynamics is 'artificial' since it is not directly connected to that of the full DNLSE model, where the relaxation is determined by the now-missing coupling terms. In this work it is, however, more important to understand the way time scales increase when the thermodynamic limit is approached, rather than their actual values. Furthermore, the relevance of the MMC dynamics relies on the fact it is purely stochastic, so that it allows us to separately identify entropic and dynamical effects (see also section 4).

After having checked that the MMC algorithm yields a fast (i.e. exponential) convergence towards the expected equilibrium state in the T > 0 region, we have performed simulations in R_n. The IC is fixed by assigning a random amplitude u_j (with a flat distribution between 0 and 1) to all sites and by adding B units to a fraction p of randomly chosen sites. We have run a series of detailed simulations for B = 40/3 and p = 1/20 (this IC corresponds to h ≈ 9.89 and u ≈ 1.17, i.e. it lies inside R_n, since it satisfies the condition h/u² > 2). In order to monitor the convergence towards the equilibrium state it is necessary to distinguish between breathers and the background. This can be done by choosing an amplitude threshold η much larger than the typical background fluctuations but sufficiently smaller than the asymptotic breather amplitude. Taking into account that the background is characterized by Poissonian statistics [16, 17] the previous conditions correspond to the inequality

$$\begin{equation} 1 \ll \eta/u < \sqrt{N(h/u^2 -2)}. \end{equation} \tag{ 6 }$$

In our simulation, we have taken η = 10 that is appropriate even for the smallest system size, N = 400, used in the simulations. Figure 2 shows the MMC evolution of the fraction ρ of sites where the amplitude u_j is larger than the chosen threshold for three different system sizes. The three curves nicely overlap and show that, for large time t,⁹ the density of breathers vanishes. Note that in a system of size N, ρ is expected to converge to 1/N, since the equilibrium state is characterized by a single breather. This is nothing but a finite-size effect; it is far more interesting to observe that the overall decay is characterized by a clear power-law behaviour ρ ∼ t^−α, with α = 0.37 ± 0.04, independently of the system size. This suggests that we are in the presence of a coarsening phenomenon, presumably triggered by a subdiffusive process.

Zoom In Zoom Out Reset image size

In order to gain further insight, we plot in figure 3(a) the position of the breathers of amplitude larger than the threshold η. The breathers are basically static, except for a weak mutual attraction that some of them exhibit before disappearing (i.e. before becoming smaller than the assigned threshold η). Since this representation does not provide any information on the way energy is distributed among the existing breathers, we have introduced the function $H^*(j) = \sum _{l=1}^j (u_l^2- \eta ^2)\,\theta \,(u_l^2- \eta ^2)$ (θ being the Heaviside function) representing the sum of the 'excess' energies contained in the breathers: H*(j) is a non-decreasing staircase function of j. In figure 3(b), the dots for any given time t represent the sequence of increasing values taken by H*(j) in correspondence to each breather in the lattice. Accordingly, the horizontal distance between two successive dots amounts to the excess energy of the right breather, so that the abscissa of the rightmost dot is the total excess energy contained in all the breathers. After an initial transient during which the excess energy is almost constant, the breathers perform a sort of Brownian motion in energy space, until they merge and the total excess energy concentrates over a smaller and smaller number of breathers, as expected. Note that the time needed to concentrate the energy in a single breather is much longer than the scale in figure 3 where two breathers are still present after 10⁸ time units.

Zoom In Zoom Out Reset image size

It is intriguing to observe that the measured value of the exponent α (0.37) is relatively close to the critical exponent of another coarsening process, namely that described by the Cahn–Hilliard equation (1/3) [28]. It is, however, unclear whether the closeness is accidental or suggestive of a deeper relationship. We leave the task of identifying such a possible link to future investigations. In any case, from the point of view of the motivations behind the present work, we can conclude that entropic forces are responsible for a progressive slowing down of the convergence to equilibrium in the R_n region.

The MMC study has shown that in the weak-coupling limit, the convergence is characterized by a coarsening process: the fewer the breathers, the weaker their interaction and the slower the convergence process. The uncoupled limit is, however, rather peculiar, as it lacks the hopping mechanism. In the natural case of a finite coupling, we have turned our attention to simulations of the deterministic DNLSE, since effective implementations of MMC rules are not feasible. Figure 4 presents the space–time evolution for a chain of 4096 sites for u = 1 and h = 2.4. To emphasize the breather dynamics, we plot only the lattice points, where the instantaneous amplitude u_j is larger than η = 10. Thanks to a symplectic fourth-order algorithm of the Yoshida type [29], we have simulated the dynamics over time scales much longer than in previous numerical studies. In figure 4 one can see that, like in the MMC simulations, the breathers do not basically move. At variance with the uncoupled case, however, we observe spontaneous birth and death of breathers as in a standard stationary process. This is due to the presence of a finite interaction (hopping) energy: the background can store excess energy in the phase differences of neighbouring sites and this implies that breathers can spontaneously nucleate. In order to better investigate the convergence properties of the dynamics, we have built four different sets of ICs, all with the same energy density and number of particles density, but substantially different macroscopic structures (see the caption of figure 5). First, we have monitored the evolution of the density of breathers ρ (identified by setting η = 10). The average results for N = 4096 are plotted in figure 5(a). At variance with the simulations described in figure 2, the density appears to converge towards a common finite value, i.e. towards a multi-breather stationary state. Moreover, the dotted line corresponding to a simulation with N = 2048 indicates that the asymptotic value of ρ is independent of the system size (and is approximately equal to one breather per thousand sites).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We have also monitored the temperature. In this model, the standard kinetic definition does not apply since the Hamiltonian is not decomposable into kinetic and potential energy. Nevertheless, one can use the microcanonical definition, T⁻¹ = ∂S/∂H, where S is the thermodynamic entropy and the partial derivative must be computed taking into account the existence of two conserved quantities. This task requires long and careful calculations with a final non-local expression [21]. We have preliminarily verified that the definition of [21] works for positive temperatures when applied to the full and to short subchains. The results in R_n are plotted in figure 5(b), where one can see that β ≡ 1/T converges to a common value for all of the four different classes of ICs (either from above or from below), with negligible finite-size effects (once again the dotted curve refers to a chain of half length, N = 2048). Altogether, one can conclude that on the time scales that are numerically accessible (of the order of 10⁷), the dynamics of the DNLSE converges towards a multi-breather state, characterized by a finite density of breathers and a well-defined NT.

In practice, the breathers are prevented from becoming 'too large'. In figure 6, one can indeed see that the quasi-stationary distribution of breather amplitudes is effectively localized below u = 22 and, more importantly, the distribution is basically independent of the system size. This means that there is a dynamical process which 'screens' the high-amplitude region. One can argue that this dynamical effect is due to the low efficiency of the energy transfer among breathers interacting through the background, a manifestation of their intrinsic dynamical stability. As a consequence, the evolution is 'confined' within a region of the phase space that is characterized by an NT. We still expect a final convergence towards the equilibrium state predicted in [16, 17], but the process occurs on such long (unobservable) time scales¹⁰ (further slowed down by coarsening processes) to make it unaccessible. It is nevertheless reasonable to speculate that if the IC contains one or more sufficiently high breathers, the amount of energy that is carried by them is effectively frozen, while the remaining 'excess' energy contributes to the convergence towards the quasi-stationary state. In other words, the density ρ of breathers that is generated starting from sufficiently homogeneous states (such as those used in our simulations) is the maximal density that can be attained for such parameter values. The dependence of the breather density ρ on both energy and particle density is indirectly determined by the effectiveness of the energy transfer mechanisms. One can expect that it increases with h (since the excess energy increases too), while the dependence on u is less clear, since it affects the interaction strength. Altogether, the scenario is reminiscent of spin-glass dynamics, although a more quantitative analysis is necessary to clarify, for example, possible ageing phenomena.

Zoom In Zoom Out Reset image size

NT states can be generated by suitably evolving homogeneous (i.e. positive temperature) states. Two particularly simple mechanisms are: (i) a free expansion within a larger lattice; and (ii) a localized boundary dissipation with removal of mass (and energy) acting at the extrema of the chain [12].

The free-expansion mechanism is summarized by the dot-dashed lines in figure 5. In this case, half of the chain has been prepared in a homogeneous thermalized state in R_p, while the other half is initially empty. The values of h and u on the overall chain are chosen in R_n. By averaging over a dozen IC, we observe that the inverse temperature β converges to a common negative value in both halves of the chain, while the average breather density ρ relaxes to the same value ($\mathcal {O} (10^{-3})$) originating from different classes of IC in R_n. In either BEC in optical lattices or arrays of optical waveguides, this procedure amounts to preparing a standard equilibrium state at T > 0 and leaving it to spread in sufficiently larger lattice structures. This method is much simpler than the experimental schemes described in [24], although relatively large system sizes (e.g. $N \sim \mathcal {O} (10^3)$ for the parameter values in figure 5(a)) might be necessary to observe the spontaneous formation of breathers.

An alternative procedure for observing NT states starting from an IC at positive temperature is to use losses at the ends of the lattice [12, 13]. Average trajectories resulting from the presence of a boundary dissipation in chains of different, but limited, sizes is shown in figure 7. The smoothness of these lines indicates that this process is quite regular and effective. This notwithstanding, we have observed that fluctuations may drive some of the trajectories to an empty state, although this event becomes more and more rare for increasing values of the chain size and the initial energy density. In an experimental setup the feasibility of such a mechanism depends mainly on the possibility of controlling the dissipation procedure.

Zoom In Zoom Out Reset image size

After reaching the region R_n in the phase diagram (u,h), we have turned the localized dissipations off and proceeded to measure the microcanonical temperature. For the three simulations reported in figure 7 for N = 400,200 and 100, we have measured temperatures of −3.4 × 10⁻², −2.2 × 10⁻² and −9.9 × 10⁻², respectively. This demonstrates that the long-lived NT states described here can be experimentally accessible in setups containing a relatively small number of lattice sites. Although the expression for the microcanonic temperature is complicated [21], NT can be measured once the amplitudes and phases of the lattice BEC [30] or of the waveguide array have been recovered.

When considering relatively small numbers of lattice sites, the absolute value of the final temperature depends on the size of the sample. This is demonstrated, for example, by the fact that in figure 7 the final temperature for the simulations with N = 400 is more negative than that with N = 200, while one would have expected the opposite when considering the final values of the energy densities. Although finite-size effects lead to larger fluctuations in the evaluation of the absolute value of the final temperature, the important message here is that the negative character of T should be measurable at the end of out-of-equilibrium processes performed on lattices of relatively small size, thus paving the way for the observation of NT states experimentally.

As a final remark, we observe that much attention has been devoted in the literature to the study of the formation of an intrinsically localized state (ILS) both theoretically [11] and experimentally [10]. The ILS is obtained from an initial Gaussian wavepacket that typically evolves to a single breather state, by releasing part of the initial energy to the lattice in the form of a radiation-like background [13]. In the light of our results, this scenario can be viewed as a first preliminary piece of evidence of the existence of the region at NT, R_n, in the thermodynamic diagram of figure 1. As a matter of fact, one can observe the formation of an ILS only if the initial Gaussian wavepacket is in R_n. If the initial wavepacket starts in R_p, relaxation to a positive-temperature state is observed. The ILS is a close approximation of the equilibrium state in R_n predicted by Rumpf [18], i.e. a background at infinite temperature supporting the excess energy into a single breather. In this respect, the measurement of the phase distribution in the background is a promising tool to infer the temperature in experimental setups: it will be useful to explore to what extent the idea can be turned into a quantitative protocol.

Extremely long-lived states at NT corresponding to a quasi-stationary density of breathers have been identified in the numerical simulations of the DNLSE. The asymptotic convergence to the single-breather equilibrium state occurs on quite long (and practically unattainable) time scales. The reason why breathers play an important role in the attainment of NT states is the existence of a second conservation law which favours energy concentration, while limiting the overall entropy. We do not expect similar scenarios to occur in lattices where breathers appear in models with a single conservation law (see, e.g., [31]). It might, nevertheless, be instructive to investigate the local temperature dynamics in the vicinity of the breathers, even in such cases.

Further insights into the nature of the NT quasi-stationary states have been provided via MMC simulations in the so-called weak-coupling limit. The source of slowness has been identified in a coarsening phenomenon that follows from a sub-diffusive behaviour of the breather amplitudes. The density of breathers decreases in time as t^−α with α remarkably close to the Cahn–Hilliard 1/3 exponent. From a theoretical point of view, we envisage a quantitative theory that relates the slow time scales to the breather amplitudes, their stationary density and the system size so as to establish possible connections with, e.g., ageing phenomena.

All these results indicate the possibility of observing NT states experimentally, in BEC and optical waveguides, as a result of quasi-stationary states yielding peculiar non-equilibrium thermodynamic properties. We have suggested two possible scenarios where quasi-stationary NT states can be realized: free expansion of a positive-temperature state in a larger lattice and the utilization of boundary dissipations. Initial Gaussian wavepackets leading to a single breather ILS may also be used for the realization of maximum entropy states although the measurement of the phase distribution is required in order to establish the infinite-temperature nature of the background.

Finally, it would be worth clarifying to what extent the scenario described here survives when passing to continuous models: some preliminary simulations provide encouraging results, but computationally heavy simulations are required before drawing reliable conclusions. Finally, let us note, en passant, that a richer scenario would presumably arise in higher-dimensional setups, due to the existence of a finite activation energy threshold for the discrete breathers (see the recent review [32]).

RL acknowledges financial support from the Italian MIUR-PRIN project no. 20083C8XFZ and G-LO from the EU Commission FET Open Grant HIDEAS. We acknowledge financial support from EPSRC grant EP/I006826/1. SI and AP thank T Carletti for useful discussions on the implementation of symplectic integrators.