Abstract
We determine the limit of the lowest achievable photoemitted electron temperature, and therefore the maximum achievable electron brightness, from unstructured photoemitting materials producing dense relativistic or nonrelativistic photoelectron beams. The limit is given by electron heating that occurs just after emission into vacuum, and is due to poorly screened Coulomb interactions equivalent to disorder induced heating seen in ultracold neutral plasmas. We first show that traditional analytic methods of Coulomb collisions fail for the calculation of this strongly coupled heating. Instead, we employ an N-body tree algorithm to compute the universal scaling of the disorder induced heating in fully contained bunches, and show it to agree well with a simple model utilizing the tabulated correlated energy of one component plasmas. We also present simulations for beams undergoing Coulomb explosion at the photoemitter, and demonstrate that both the temperature growth and subsequent cooling must be characterized by correlated effects, as well as correlation-frozen dynamics. In either case, the induced temperature is found to be of several meV for typical photoinjector beam densities, a significant fraction of the intrinsic beam temperature of the coldest semiconductor photocathodes. Thus, we expect disorder induced heating to become a major limiting factor in the next generation of photoemission sources delivering dense bunches and employing ultra-cold photoemitters.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Beam brightness is a principle figure of merit for relativistic photoelectron sources for use in high brilliance linear accelerators or for ultrafast electron diffraction (UED) experiments. It is qualitatively defined as the average particle flux per phase space volume. For high brilliance linear accelerators used for x-ray production, the brightness of the x-ray beam is directly determined by that of the electron beam [1]. For UED setups, the brightness of the electron beam is the main beam parameter that determines the resolving power of the instrument [2].
Such electron sources are comprised of a photoemitting material placed in an accelerating gradient, where both direct current and radio frequency accelerating fields are used for various applications. We will restrict our focus in this work to emitters without nano- or micro-scale structure, whose photoemission probability is uniform across the cross sectional area where light illuminates its surface. For either x-ray or electron diffraction experiments, it is often the four dimensional transverse normalized brightness that is most pertinent. For a given beam current I, we can define the 'microbrightness' as the phase space density itself,  , where dV4 = dx dy dpx dpy is the phase space volume element. The normalized total beam brightness can then be defined as a statistical average of the micro-brightness:
, where dV4 = dx dy dpx dpy is the phase space volume element. The normalized total beam brightness can then be defined as a statistical average of the micro-brightness:
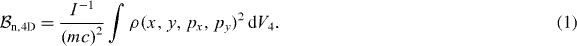
For a bunched beam with some bunch repetition rate f, the average current can be written as Iav = qf, where q is the charge of the bunch. In a previous work [3], it was shown that the maximum achievable beam brightness (either microbrightness or total) can be written as

where Eacc is the accelerating electric field directly at the photocathode, which sets the maximum supportable charge density at the photocathode. For such sources, the minimum divergence is set by kT, the temperature of photoemitted electrons, an intrinsic property of the choice of photoemitter and laser wavelength. In the absence of emitter imperfections such as surface roughness, a nonzero temperature arises fundamentally from the electron momentum spread inside the photoemitting material, and can then be significantly increased due to excess laser energy above the photoemission threshold, as well as electron scattering off of imperfections in the emitter.
As it is one of the two independent parameters of the maximum achievable beam brightness per bunch, the photoemission temperature has been the focus of much work in photoelectron sources. Great progress has been made by those working with negative electron affinity semiconductor photocathodes and those pursuing electron emission from laser-cooled atoms. Several semiconductor photocathode groups have measured photoemission of equivalent temperatures well below kT = 25 meV, or the thermal energy at room temperature. This is achieved either via the cryogenic cooling of the photocathode [4], or via the maintenance of a pristine photoemissive conditions in ultra high vacuum, allowing the low effective mass of conduction electrons to produce an effect equivalent to Snell's law in which the velocity spread of electrons is drastically reduced at the vacuum interface [5]. Furthermore, using laser-cooled atoms which are photoionized, there has been production of electrons at temperatures equivalent to ∼ 1 meV [6].
The number of electrons per bunch varies widely across various applications, with a range approximately between 106 and 109 electrons, which for moderate to high flux applications often corresponds to densities in the range of n0 = 1017 → 1020 m−3. For example, the Cornell energy recover linac injector prototype operates with a charge density of 5 × 1017 m−3 as described in [7], whereas photoguns operating in the blowout regime may have densities higher than 1019 m−3, calculated from the parameters given in [8]. For a near-zero temperature bunch with such high density, we expect some contribution of individual stochastic Coulomb interactions from close encounters just after emission into vacuum to add to the total effective photoemission temperature. In this work, we determine this amount of stochastic heating as a function of beam density and initial temperature, as well as the nature of its evolution in time.
We expect this effect to be most prevalent when the electrostatic potential energy of neighboring particles is comparable to their thermal energy, that is kT ∼ e2/4π 0a, where a is the Wigner–Seitz radius, a = (3/4πn0)1/3. Thus for a given density, we expect the heating to be of the order e2/4π
0a, where a is the Wigner–Seitz radius, a = (3/4πn0)1/3. Thus for a given density, we expect the heating to be of the order e2/4π 0a, and should thus scale with the cubic root of the density, and should be independent of the number of particles in the bunch. For a rough estimate of the importance of the effect, the plasma coupling parameter Γ can be used, defined as the ratio of kT to the average pair interaction potential. It ranges from Γ = e2/4π
0a, and should thus scale with the cubic root of the density, and should be independent of the number of particles in the bunch. For a rough estimate of the importance of the effect, the plasma coupling parameter Γ can be used, defined as the ratio of kT to the average pair interaction potential. It ranges from Γ = e2/4π 0akT = 0.2–2 given an electron temperature of 5 meV, and for the density ranges described above. Thus, for applications requiring a large charge density, we expect this stochastic heating to serve as a hard limit to the lowest attainable electron temperature, and limiting the maximum attainable beam brightness.
0akT = 0.2–2 given an electron temperature of 5 meV, and for the density ranges described above. Thus, for applications requiring a large charge density, we expect this stochastic heating to serve as a hard limit to the lowest attainable electron temperature, and limiting the maximum attainable beam brightness.
2. Failure of analytic models for Coulomb collisions
We will now describe how traditional collisional methods in beam physics, familiar to many accelerator practitioners, fail for the case of a cold dense beam. Readers familiar with the inability of such methods to accurately describe our strongly correlated case can bypass this section. A simple model for a bunch that has just been photoemitted into vacuum is a static, uniform, randomly distributed electron sphere with very small initial temperature kT ∼ 0, in a constant accelerating field. We first draw a sharp distinction between the stochastic heating in question and the effects of space charge, which is the collective, mean field effect of Coulomb repulsion. The space charge approximation, applied in most beam physics calculations, self-consistently calculates the interparticle interaction based on the local single particle beam density, ∇2Φ(r) = en(r)/ 0, where Φ is the total electrostatic potential of a particle at r. This approximation requires that the individual electron interaction is heavily screened, meaning that the Debye screening length
0, where Φ is the total electrostatic potential of a particle at r. This approximation requires that the individual electron interaction is heavily screened, meaning that the Debye screening length  is much larger than the interparticle separation. However, for the lowest temperatures attained in semiconductor photoemission kT ∼ 5 meV [5], and the lowest of the above densities n0 = 1017 m−3, the Debye length is already on the order of the interparticle separation. In this case, the collective field will describe the overall density evolution, but cannot capture the growth of the stochastic component of the velocity.
is much larger than the interparticle separation. However, for the lowest temperatures attained in semiconductor photoemission kT ∼ 5 meV [5], and the lowest of the above densities n0 = 1017 m−3, the Debye length is already on the order of the interparticle separation. In this case, the collective field will describe the overall density evolution, but cannot capture the growth of the stochastic component of the velocity.
The effect of Coulomb interactions in particle beams has been treated analytically in various schemes. Perhaps the most famous is the diffusive Fokker–Planck method [9, 10]. The Fokker–Planck method assumes that the effects of Coulomb collisions can be treated via the calculation of effective velocity diffusion and dynamical friction terms. This approach requires that the shifts in velocity due to Coulomb collisions are small compared to the overall velocity spread of the beam. This assumption is maximally violated for the case of a cold dense beam as described above, in which transverse velocities begin near zero.
Nondiffusive, two-particle methods have also been developed that do not require the assumption of Debye screening. A clear presentation of these is given in [11]. The method applicable over the largest parameter space is the extended two-particle approximation (ETPA), developed by Jansen. This method relies on the calculation of the displacement (either velocity displacement, or position displacement) of a test particle in the presence of a single field particle over some collision time δtc. If we calculate the velocity displacement Δv of a particle pair initially at rest, the ETPA allows the formation of the probability distribution ρ(Δv), by averaging Δv over all possible separations and initial velocities in the beam. Each of these encounters is assumed to be statistically and dynamically independent. The second moment of the velocity distribution 〈Δv2〉 is then a measure of the temperature. We will proceed with a sketch of this calculation to highlight the failure of some of its assumptions in the cold dense beam case.
For two particles initially at rest (i.e. kT ∼ 0) with initial separation ri, using the dimensionless variables  and
and  the equation of motion for their separation is given by
the equation of motion for their separation is given by

This equation is integrable for the function  , which is not analytically invertible, but is trivial to invert numerically to obtain
, which is not analytically invertible, but is trivial to invert numerically to obtain  . With a global choice of δtc, and with a test particle chosen at the origin, we can obtain Δv as a function of ri by replacing the scaling factors. Then, we average over the entire distribution of ri:
. With a global choice of δtc, and with a test particle chosen at the origin, we can obtain Δv as a function of ri by replacing the scaling factors. Then, we average over the entire distribution of ri:
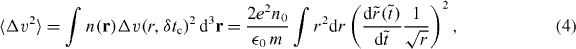
where  is also evaluated at δtc and ri. The velocity kick Δv falls off sufficiently fast with large separation, and the integral measure r2 dr ensures that the averaging does not diverge at small r, and thus we can integrate over all space. Equation (4) is the statistical average of all two particle interactions in a beam during some time δtc.
is also evaluated at δtc and ri. The velocity kick Δv falls off sufficiently fast with large separation, and the integral measure r2 dr ensures that the averaging does not diverge at small r, and thus we can integrate over all space. Equation (4) is the statistical average of all two particle interactions in a beam during some time δtc.
2.1. Unbound trajectories
The expression given in (4) and similar uncorrelated two-particle collision methods fail in the cold dense beam case for various, but interconnected reasons. First, it assumes that each pair-wise interaction is statistically independent from each other. There can be no dynamic correlation between separate pair interactions. However in the cold dense beam case a large contribution to the final temperature can be given by simultaneous three-body (or higher) interactions. The assumption of statistical and dynamical independence allows for the unbound expansion particles with very small initial separation, which are the most pertinent interactions in the cold dense beam case. In a real electron bunch, such electrons would interact with other near neighbors, containing their expansion, and significantly contributing to the bunch heating.
This issue cannot be easily resolved within two particle methods. The reason for this is as follows. From the definition of the scaled coordinates, any choice of δtc has an associated minimum initial separation scale rc∝δt2/3c which that choice of δtc probes. However, since we are assuming that electrons are distributed across all length scales, there is no physical choice of δtc or cutoff minimum separation rc that captures all interactions. For perspective, in other Coulomb collision calculations, this ambiguity is seen the calculation of the so-called 'Coulomb logarithm', defined as  , or the logarithm of the ratio of the maximum to minimum impact parameters over the whole bunch. However, as it appears under the logarithm in such problems, the minimum distance is often not considered to be a sensitive parameter [9].
, or the logarithm of the ratio of the maximum to minimum impact parameters over the whole bunch. However, as it appears under the logarithm in such problems, the minimum distance is often not considered to be a sensitive parameter [9].
In a similar method to the ETPA, in [12] Massey et al calculate the uncorrelated root mean square (rms) fluctuation in the interaction force, and from it they obtain a stochastic energy spread. The authors directly impose a minimum interaction distance which corresponds to those collisions for which half of the potential energy is converted to kinetic energy over a certain time. Collisions with more of a fraction of potential energy release (i.e. smaller separation) are ignored. They readily acknowledge the ambiguity of this choice, and argue that the effect is small for the beams in their study. However, for a cold beam just after photoemission, it is this fast-timescale release of potential energy as close neighbors rearrange that we are interested in calculating. Thus, an average over independent two particle interactions is not sufficient here.
2.2. Scaling with density
Furthermore, even if one does make a choice of δtc based on some other reasoning, the fact that this scheme involves taking a moment of the single particle distribution means one will always find 〈v2〉 ∼ n0, whereas the effect we desire to calculate should have 〈v2〉 ∼ n1/30, argued above. This scaling of the velocity spread with density occurs in the Fokker–Planck method (as shown in [9] in equation (5.243)), in the ETPA (as shown in [11] in equation (5.5.11)), and in the work by Massey (see [12] in equation (19)).
A method that produces the correct scaling with density, but is also flawed, is again given by Jansen in [11]. In what he calls the 'thermodynamic limit', Jansen takes the difference of the total electrostatic potential energy of an initially uniform distribution of charge with no screening, and a final state of a Debye-screened distribution with some kT, and sets this difference equal to the total thermal energy,  . However, instead of using a single particle density, Jansen implicitly uses the two-particle correlated density for Debye screening:
. However, instead of using a single particle density, Jansen implicitly uses the two-particle correlated density for Debye screening:
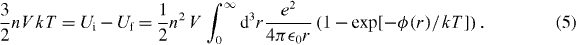
Here Ui and Uf stand for the initial and final potential energy in the system, respectively given by the first and second terms of the integral. ϕ(r) is the interaction potential of two electrons separated by r, and is assumed to have the form:  . The factor
. The factor  is the final two particle correlated density. This equation has a solution of the form
is the final two particle correlated density. This equation has a solution of the form

where α is a dimensionless number determined by numerical solution of the above, α = 0.087 02.5 This number corresponds to a coupling factor at thermodynamic equilibrium of Γeq = 3.53. However, if one evaluates the number of particles in the Debye sphere, one finds  , whereas the Debye approximation requires that the number of particles in the Debye sphere must be large. Thus, we may not apply the Debye/Yukawa form for ϕ(r) nor for the two particle density function used in (5). It is the use of a two particle correlated density function that provides the correct scaling with density, however, it is difficult to analytically compute the correlated density in general. It must be found by some other numerical means [13].
, whereas the Debye approximation requires that the number of particles in the Debye sphere must be large. Thus, we may not apply the Debye/Yukawa form for ϕ(r) nor for the two particle density function used in (5). It is the use of a two particle correlated density function that provides the correct scaling with density, however, it is difficult to analytically compute the correlated density in general. It must be found by some other numerical means [13].
3. Disorder induced heating
The heating associated with the relaxation of a random, near-zero temperature distribution of charges is well known to the ultracold neutral plasma (UNP) community. In such systems, a cold gas is laser ionized, and after a time on the order of  the temperature rises to an equilibrium nonzero value higher than the initial gas temperature. In the traditional plasma physics terminology, this effect is referred to as disorder induced heating (DIH), and the effect is seen for Γ of order unity or larger [14], and we will argue that an exact analogue of this effect is present in practical photoemission.
the temperature rises to an equilibrium nonzero value higher than the initial gas temperature. In the traditional plasma physics terminology, this effect is referred to as disorder induced heating (DIH), and the effect is seen for Γ of order unity or larger [14], and we will argue that an exact analogue of this effect is present in practical photoemission.
DIH has been experimentally observed for the ions in a neutral plasma [15]. In cold neutral plasmas, the electrons equilibrate much faster than the ionic ω−1p, and then serve to screen ion–ion interaction. An expression for the amount of DIH in ions was first given for Yukawa systems (for which electron screening, but not electron–ion recombination, is considered) in [16]. The initial ionic distribution is uncorrelated, and can be defined as the zero energy state. As the ions relax, the ion distribution begins to develop order, and the resulting correlations have an associated binding energy. This correlation binding energy can be calculated from the two particle density function g(r), and is only a function of Γ and the electron screening parameter κ = λ/a:
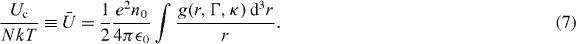
This binding energy is balanced by an increasing ion temperature. Calculating the increase in temperature thus only requires knowledge of  for a given electron screening. Analytic calculation of g(r) for strongly coupled systems is difficult, and alternatively,
for a given electron screening. Analytic calculation of g(r) for strongly coupled systems is difficult, and alternatively,  has been tabulated via molecular dynamics (MD) simulations [16].
has been tabulated via molecular dynamics (MD) simulations [16].
It has been demonstrated that a trapped, charged plasma, such as an electron bunch, is equivalent to the one-component plasma (OCP) model, in which the charges exist in a uniform neutralizing background [17]. The external containing potential allows the initial uncorrelated state to be viewed as zero total energy. As electrons relax, correlations develop, and the presence of a 'Coulomb hole' in g(r) for r < a creates an effective correlation binding energy equal to that of a OCP. In the case of an OCP, there is no second species to provide additional screening, and thus  is only a function of Γ. Owing to this simplification, MD data has been fit to a power series relation for
is only a function of Γ. Owing to this simplification, MD data has been fit to a power series relation for  , where the coefficients are given in [17], a = −0.90, b = 0.590 673, c = −0.265 69. We may now write down the expression for the final coupling Γf, and thus the final equilibrium temperature for a fully confined, initially uncorrelated (
, where the coefficients are given in [17], a = −0.90, b = 0.590 673, c = −0.265 69. We may now write down the expression for the final coupling Γf, and thus the final equilibrium temperature for a fully confined, initially uncorrelated ( ), uniform distribution of charges with initial coupling Γi, analogous to that presented in [16]:
), uniform distribution of charges with initial coupling Γi, analogous to that presented in [16]:

It is important to note the power series relation is quoted only for Γ > 1, however we find that for Γ < 1, the above expression is well approximated by Γi = Γf, or the limit of no DIH, as we expect. The final coupling given in (8) is plotted in figure 1. For an ideal bunch with zero initial temperature, Γi → ∞, (8) can be solved to give Γf ≈ 2.23.
Figure 1. Final coupling Γf versus initial coupling Γi, given by (8) (blue line), with Γf = Γi for Γi → 0 (red, dotted), and Γf = 2.23 for Γi → ∞ (green, dashed). Dots are simulation results of a fully contained, equipartitioned electron sphere, density n0 = 1020 m−3, and initial temperatures between kT = 0.25 and 20 meV. Squares are simulation results for multiple densities, where kTz = 0, and kTx = kTy, and where Γ is calculated from the average of the three directions. Error bars are an estimate of the uncertainty in final temperature determination due to the residual oscillations, as in figure 2.
Download figure:
Standard image High-resolution imagePractical relativistic photoelectron sources contain a number of complicating factors. Inside the emitting material (either a cold gas or crystal), the electron coupling, and thus DIH will be dramatically reduced by the presence of the ionic/nuclear potential, and here we only need to consider DIH developing in vacuum. The beam density during emission will vary in time and with position across the bunch. The temperature associated with DIH should be reached on the order of ω−1p after electron emission into vacuum, which for typical beam densities is on the picosecond scale. On this scale, we can neglect relativistic effects, such as the 1/γ2 damping of the interaction force [9]. The coupling given by Γf = 2.23 ≡ Γeq, for a given local beam density, can then be viewed as the fundamental photoemission temperature limit. We consider the effects of a changing local beam density, as well as the nonrelativistic effects of acceleration during the evolution of DIH below, and we find it to correspond well with the prediction of (8). Rewriting it in terms of practical units, the heating induced in a zero temperature bunch is given by kT(eV) = 1.04 × 10−9(n0 (m−3))1/3. Along with (2), this forms the fundamental photoemission brightness limit.
To test the prediction of (8), we have chosen to use a tree-algorithm electrostatic simulation package, with nonrelativistic, spherical, uniform particle bunches. Traditional particle-in-cell integrators have an intrinsic length scale—the spatial grid on which local fields are calculated. However, tree algorithms lack a spatial grid, and thus are better suited to our initial conditions, where both close interactions and long range correlations are significant. Several plasma tree-algorithms have been developed, see for instance [18], and one has been included in a relativistic particle accelerator code6. However, considering the simplicity of the problem, we elected to directly modify a code originally written for gravitational interaction [19], simply by inverting the sign of the interaction force and changing its scale.
We consider a randomly distributed spherical bunch of 105 particles with uniform density, and vary only the density (1017 → 1020 m−3) and initial Gaussian velocity distribution (kT∈{0.25,20} meV or kT = 0), where we use the definition  , where me is the electron mass and i is a Cartesian coordinate. This definition of temperature subtracts position-correlated motion, as in the bulk flow or expansion of charge, from the total rms velocity distribution width. For a fully contained uniform bunch there is no correlated flow, thus 〈xivi〉 ≈ 0, and the temperature is just a measure of average electron kinetic energy, with no spatial dependence. Bunches are contained in simulation via the application of a radial external force equal and opposite to the SC field.
, where me is the electron mass and i is a Cartesian coordinate. This definition of temperature subtracts position-correlated motion, as in the bulk flow or expansion of charge, from the total rms velocity distribution width. For a fully contained uniform bunch there is no correlated flow, thus 〈xivi〉 ≈ 0, and the temperature is just a measure of average electron kinetic energy, with no spatial dependence. Bunches are contained in simulation via the application of a radial external force equal and opposite to the SC field.
The parameters of the interparticle force calculation are the Barnes–Hut opening angle θ, and the numerical integration time step dt. In any Barnes–Hut simulation, the opening angle θ = s/D is the force calculation accuracy parameter that determines whether an electron in a cubic volume of size s, at a distance D from the test particle is treated individually or lumped together with other electrons in that volume [20]. An opening angle of zero corresponds to a fully point-to-point summation of the interaction force, whereas the large angle θ = 1 corresponds to lumping electrons together in a box as wide as it is distant from the test particle. No effect was seen from a force-softening distance p, such that the force between two particles is f12∝(r12 + p)−2, from p = a/106 up to p = a/100. While p is not exactly equivalent to the rc of two particle methods, the insensitivity of simulation results to this parameter does illustrate the significance of multiple strong interactions for closely spaced particles, which contain their initially rapid expansion. For all simulations presented, we have demonstrated convergence using dt = τ/120, θ = 23°, N = 105.
For an initial distribution with zero temperature, the final temperature for several applicable beam densities is plotted in figure 2. We note that for extremely dense beams, n0 > 1019 m−3, the DIH is comparable to the temperature of photoemission from the coldest semiconductor cathodes kT ∼ 5 meV. Furthermore, we note the oscillation of the electron temperature at 2ωp, which has been measured experimentally in UNP systems [15]. These oscillations last far longer than those seen in UNPs, as the bunch density remains uniform in simulation (rather than evolving into a Gaussian), and there is thus no spatial temperature smearing.
Figure 2. Temperature versus number of plasma periods from treecode simulation using 105 contained electrons, and n0 = 1020 (top curve), 1019, 1018, 1017 m−3 (bottom curve), with zero initial temperature, Γi → ∞. The equilibrium value predicted by (8), Γf ≈ 2.23 is shown (dotted lines).
Download figure:
Standard image High-resolution imageFor bunches with nonzero initial temperature, the amount of additional heating can be calculated in the final coupling, plotted along with the prediction of (8) in figure 1. All simulations here had a constant density n0 = 1020 m−3, with varied initial Maxwellian velocity distribution. The duration of the temperature oscillations visible in figure 2 is reduced with increasing initial temperature, though the exact dependence was not extracted in this study. In practical systems, initial acceleration in a voltage gap V will have cooled any photocathode emission temperature along the acceleration direction by a factor kTi/eV , making kT|| ∼ 0 almost instantaneously in high gradient electron sources, whereas the transverse velocity spread will remain unaffected [9]. Simulations were performed for contained bunches of multiple densities with kTx = kTy ≠ 0 and kTz = 0. Equivalent dynamics to figure 2, as well as agreement with (8) were found if the average of the temperatures in all three directions is used to calculate Γi and Γf, as shown in figure 1. The timescale of equipartition here also depends on kTi and n0, but for the densities considered above and initial temperatures comparable to DIH heating, it was seen that equipartition occurs between τ and 3τ. A bunch instantaneously emitted into a uniform accelerating field will not have the DIH evolution altered, a fact that was also verified in simulation.
Real electron bunches just after emission are very infrequently fully transversely contained in the sense described above, and are not emitted instantaneously. The overall space charge force can double the beam radius on the timescale of ω−1p, and acceleration can significantly lengthen the pulse afterwards. Thus, we must consider the process of DIH in bunches with time dependent density reduction. A system of fully coupled charges will have an equilibrium temperature that decreases as kT∝1/Γeqa, as given above. However, it is well known that system of noninteracting charges expanding under linear forces will have an equilibrium temperature that decreases as kT∝1/a2 [9], as a consequence of rms emittance conservation, which therefore leaves the phase space density or brightness unchanged. During the explosion, the beam is in a highly nonequilibrium state, but our definition of temperature above still applies, where here 〈rvr〉 ≠ 0.
Simulations were performed to determine the temperature as a function of time for a bunch undergoing full Coulomb explosion. Multiple densities were considered, however the previous scaling with n1/30 was seen. Thus, we present only results for n0 = 1020 m−3 in figure 3. The total overall expansion and velocity growth is plotted in the inset, with the prediction of the equation of motion given by Gauss' law (integrated numerically), showing excellent agreement. The temperature shows an initial increase due to DIH at a time of tmax ≈ ω−1p, to a value of kT(t = tmax) = e2/4π 0a(tmax), or a value a(tmax)/a0 ≈ 1.6 times smaller than for a fully contained beam. The bunch continues to expand, attempting to equilibrate to Γeq = 2.23, and the temperature continues to decrease. However, at longer times, the temperature falls as a−2, as in an uncoupled system. Thus, there must be a time at which correlation ceases to grow with decreasing temperature. Such behavior has been noted in the adiabatic expansion of UNPs due to kinetic pressure [21].
0a(tmax), or a value a(tmax)/a0 ≈ 1.6 times smaller than for a fully contained beam. The bunch continues to expand, attempting to equilibrate to Γeq = 2.23, and the temperature continues to decrease. However, at longer times, the temperature falls as a−2, as in an uncoupled system. Thus, there must be a time at which correlation ceases to grow with decreasing temperature. Such behavior has been noted in the adiabatic expansion of UNPs due to kinetic pressure [21].
Figure 3. Rms velocity spread of a spherical bunch undergoing coulomb expansion, treecode data (circles), and prediction of (9) (solid line). The inset shows the overall expansion of the bunch in normalized units, both the prediction of the equation of motion given by Gauss's law, integrated numerically (solid line) and treecode data (dots). Uniform bunches remain uniform, and the normalized bunch size R(τ)/R0 is independent of density.
Download figure:
Standard image High-resolution imageThus, to phenomenologically model the temperature as a function of time, we can factorize the temperature as a product of the correlated growth and the decoupled expansion after correlation ceases. Thus,  , where Tc is the correlated temperature dependence, and the term
, where Tc is the correlated temperature dependence, and the term  describes the expansion of independent particles. Since the growth of the radius is small during the time of DIH, at early times T(t)∝Tc, and later times as T(t)∝a(t)−2 with Tc unchanging or changing slowly. To model Tc, we know that the rate of DIH should dependent on the difference of the current temperature T(t) to the equilibrium temperature at that radius,
describes the expansion of independent particles. Since the growth of the radius is small during the time of DIH, at early times T(t)∝Tc, and later times as T(t)∝a(t)−2 with Tc unchanging or changing slowly. To model Tc, we know that the rate of DIH should dependent on the difference of the current temperature T(t) to the equilibrium temperature at that radius,  . The simplest ansatz one can make is a linear dependence of the DIH temperature growth rate on the temperature difference between the current temperature to the equilibrium temperature:
. The simplest ansatz one can make is a linear dependence of the DIH temperature growth rate on the temperature difference between the current temperature to the equilibrium temperature:
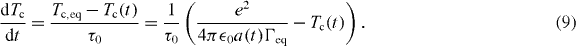
The only free parameter of this model is decoupling time scale τ0, or the time scale when the correlated heating ceases. Integrating this numerically and fitting to the temperature data, we find τ0 = 0.325τ, which is also plotted in figure 3. This time is non-negligibly greater than tmax, and suggests that the bunch is cooled not only via decoupled expansion, but coupled expansion as well just after tmax. We can verify this prediction by looking at the pair correlation as a function of time. This is computed in figure 4, via averaging over 5 × 103 particles randomly selected from the distribution. The development of the 'Coulomb hole' and an accompanying shock profile due to violent repulsion is clearly visible, as has also been seen in UNP simulations [22]. Indeed the correlation ceases to change after a time of approximately τ0 = 0.3τ. Partial confinement effected by linear focusing in the source would yield an altered a(t), and thus a longer τ0, whereas acceleration that lengthens the bunch significantly near the DIH heating timescale would yield a shorter τ0, but in either case the DIH heating timescale should remain unchanged.
Figure 4. Pair correlation function g(r), computed at multiple simulation times for a bunch undergoing coulomb explosion. Both the initial 'shock' profile and the freezing out of correlations despite increasing Γ is visible.
Download figure:
Standard image High-resolution imageThe above case demonstrates that even for practical dense bunches that do not have constant volume, DIH will still play a large role. For a changing beam density, the temperature is well described by (8) until the beam density decreases enough to decouple the interaction at τ0. After τ0 the temperature scaling shifts away from a(t)−1 as given in (8), to the familiar scaling of σ2v∝a(t)−2, as given by emittance/brightness conservation. A more detailed calculation of DIH for practical cases in which the bunch shape is both time and space dependent should involve averaging over a temperature distribution given by (8) and (9) using the local density as determined by space charge tracking.
4. Conclusion
In summary, we have characterized the fundamental temperature limit of photoemission from unstructured emitters caused by DIH of electrons due to poorly screened Coulomb interactions at all length scales, where the analytic two particle models fail. We have shown that the tabulated thermodynamic quantities of one component plasmas are sufficient to explain both fully contained and Coulomb exploding instances of DIH, and have verified two simple relations that describe the temperature evolution. Furthermore, many interesting effects of DIH in UNP, such as temperature oscillation and correlation decoupling, should also be present in such cold beams, yielding the possibility of rich interdisciplinary study.
It is important to note that it may be possible circumvent the above limit with engineered photoemitters that produce electrons in a pre-ordered state, such as has been suggested in metal photocathodes [23], and in cold gas electron sources [24]. The full degree to which the effects of DIH can be mitigated remains an open question. As such structured emitters are arrays of smaller sub-emitters, unless each sub-emitter emits only one electron at a time, the DIH limit applies to each one individually. Furthermore, it may be possible to create beams of higher brightness downstream of the source by emitting a low density beam for which DIH effects are negligible, and employing transverse and longitudinal bunch compression after relativistic acceleration, for which the interparticle interaction force will be relativistically reduced. However, the above brightness limit should hold in the nonrelativistic regime near an unstructured source.
In practical terms, we have shown that the brightness of a next-generation cold electron unstructured photoemission source cannot arbitrarily increase its brightness. Furthermore, given the rapid progress of photocathode temperature reduction, we anticipate such a limit to be approached in the next generation of high brightness electron sources producing intense beams.
Acknowledgments
The authors thank two anonymous reviewers for helpful suggestions that clarified the presentation of the work. The authors also thank Joshua Barnes, the original author of the treecode package modified for use in this work. This work was supported by the National Science Foundation grant no. DGE-0707428, and by the Department of Energy grant no. DE-SC0003965. This work was also supported by the Director, Office of Science, Office of Basic Energy Sciences of the US Department of Energy, under contract numbers DE-AC02-05CH11231, KC0407-LSJNT-I0013 and DE-SC0005713.
Footnotes
- 5
An incorrect value of alpha is quoted for α in [11], which explains the use of the Debye relations, though the final value of λ shows that they are not applicable.
- 6
Pulsar physics, general particle tracer v. 3.10.







