Abstract
The applications of negative index materials (NIM) are currently severely limited by absorption. Subsequent to improvements of metamaterial design, it has been suggested that dense gases of atoms could form NIM with negligible loss. In such gases, the low absorption is facilitated by quantum interference. In this paper, we show that additional gain mechanisms can be used to tune and effectively remove absorption in a dense gas NIM. In our setup, the atoms are coherently prepared by control laser fields, and further driven by a weak incoherent pump field to induce gain. We employ nonlinear optical Bloch equations to analyze the optical response. Metastable neon was identified as a suitable experimental candidate at infrared frequencies to implement a lossless active negative index material.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Over the last few years, tremendous progress has been accomplished in the field of negative refractive index materials [1–6]. To a large extent, this progress was fueled by the ongoing miniaturization and optimization of metamaterials, which are artificial materials made of structures smaller than the wavelength of the probing light [6]. In most cases, however, negative refraction is accompanied by a substantial amount of absorption, especially toward higher frequencies. These losses typically occur since the refractive index becomes negative only close to electromagnetic resonances where the absorption is high. As a result, the relevant figure of merit (FOM), the ratio between the real and the imaginary part of the refractive index FOM = |Re(n)/Im(n)| for high-frequency metamaterials, is currently only of the order of unity [7], restricting most of the possible applications [8–12]. It has been proposed and demonstrated in proof-of-principle experiments to circumvent this limitation by implementing a gain mechanism into the medium [13–15]. Still, it remains challenging to achieve sufficiently large gain coefficients.
As an alternative approach, recently, dense gases of atoms have been proposed to achieve a negative index of refraction without metamaterials [16–19]. In particular, it has been shown that by reducing absorption via interference, negative refraction can be achieved over a certain spectral region with negligible absorption [18, 19]. The achievement of a negative index of refraction is further supported by a cross-coupling that allows to induce a magnetization by the electric field component of the probe field [18–27]. Gases also naturally have a macroscopic extent in all spatial dimensions, unlike high-frequency metamaterials which typically are produced layer by layer on a surface [28].
Here, we explore the possibility of implementing gain mechanisms in atomic gases to achieve a negative index of refraction with tunable absorption. In our setup, a dense gas of atoms is exposed to control laser fields that create coherence between different internal atomic states. Quantum interference effects reduce the absorption in the gas and an additional weak incoherent pumping field is used to render the system completely lossless: Im(n) = 0; or transfer it into an active, amplifying state where Im(n) < 0. As our main result, we show that changing the intensity of the pumping field continuously allows for a controlled transition from a passive to an active state.
The feasibility of our scheme is discussed for the case of a dense gas of metastable neon, where we find negative refraction to be in the infrared range at a wavelength of about λ = 5 μm. We explicitly demonstrate that our main results are robust under the effect of Doppler broadening, which occurs in a thermal gas. The required energy level scheme, depicted in figure 1, however, could be realized also in other solid state systems like doped semiconductors or quantum dot arrays, or with different atomic species, where cold-atom realizations are possible. This would significantly reduce the effect of Doppler broadening.
Figure 1. Five-level scheme with probe field with components Eb, Bb (red) and coupling fields Ea, Ec, Ed (blue) of frequencies ωb, ωa, ωc and ωd, respectively. The electronic states in jL-coupling notation refer to the special case of metastable neon (http://physics.nist.gov/Pubs/AtSpec/ and http://physics.nist.gov/PhysRefData/), with the corresponding wavelengths λb = 5.4 μm, λa = 704 nm, λc = 352 nm and λd = 1.05 μm. The magnetic and electric probe field transitions |1〉–|2〉 (M1) and |3〉–|4〉 (E1) are energetically degenerate up to a small energy gap Δ = 3.33 cm−1 = 100 GHz. An incoherent light field (black) acts as a pump rate r34, r43 between the states |3〉 and |4〉.
Download figure:
Standard imageThe remainder of this paper is structured as follows. In section 2, we explain how to calculate the linear optical response of a dense gas of metastable neon atoms, and show how it allows for a negative index of refraction with tunable absorption. In section 3, we present the results for metastable neon at two different vapor densities. We also provide a detailed discussion on the effect of Doppler broadening on the thermal gas. In section 4, we summarize our results.
2. Linear-response theory of a dense gas of five-level atoms
In this section, we introduce the energy level scheme of the atoms and the role of the applied light fields in achieving a negative refractive index with tunable absorption. Since we are dealing with a rather dense gas, we have to consider nonlinear effects arising from the resonant interaction between close by atoms. This is accomplished within the framework of solving a nonlinear optical Bloch equation.
2.1. Five-level atoms and the role of applied light fields
We consider a gas of five-level atoms with an energy level structure that is shown in figure 1. In the following, we first motivate the chosen model system, and discuss the significance of different coupling fields. A complete definition of the model in terms of the master equation will be given in section 2.3. A specific feature of the scheme is that it contains an electric and a magnetic dipole transition at roughly the same energy  43 ≈
43 ≈  21, where
21, where  ij =
ij =  i −
i −  j, and
j, and  i is the energy of state i. An incoming probe field with frequency ωb ≈
i is the energy of state i. An incoming probe field with frequency ωb ≈  21 therefore couples near-resonantly to the transition |3〉–|4〉 with its electric field component Eb and to the transition |1〉–|2〉 with its magnetic field component Bb.
21 therefore couples near-resonantly to the transition |3〉–|4〉 with its electric field component Eb and to the transition |1〉–|2〉 with its magnetic field component Bb.
Close to the resonance ωb ≈  21 one thus finds that both the electric permittivity Re(
21 one thus finds that both the electric permittivity Re( ) < 0 and the magnetic permeability Re(μ) < 0 become negative. As a result, the refractive index n, which is given by
) < 0 and the magnetic permeability Re(μ) < 0 become negative. As a result, the refractive index n, which is given by 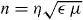 if magneto-electric cross-couplings can be neglected, exhibits a negative real part. Here, η∈{1,−1} determines the branch of the square root function, which is determined by the condition that the imaginary part Im(n) is positive in a passive system, as both Im(
if magneto-electric cross-couplings can be neglected, exhibits a negative real part. Here, η∈{1,−1} determines the branch of the square root function, which is determined by the condition that the imaginary part Im(n) is positive in a passive system, as both Im( ,μ) > 0.
,μ) > 0.
The strength of the magnetic response is weaker than the electric response by a factor of α2, where α = 1/137 is the fine-structure constant. For this reason one requires rather large densities of N ∼ 1017 cm−3 to achieve negative refraction in such an atomic gas. To enhance the magnetic response we apply two (strong) coupling laser fields Ea and Ec which together with the electric probe field component induce the coherence ρ21 = 〈2|ρ|1〉 which drives the magnetic dipole moment of the atom. Here, ρ denotes the density matrix of a single atom. The two fields Ea,c drive transitions between states |1〉–|3〉 and |2〉–|4〉, respectively. We choose the frequencies of both fields to be equal (ωa = ωc) and almost resonant with the transition |1〉–|3〉 [29].
The third coupling laser field Ed, which resonantly couples states |4〉–|5〉, serves a different purpose. It allows shifting electric and magnetic probe field resonances with respect to each other, because it causes an Autler–Townes splitting of the fourth level into two dressed states at  4 →
4 →  4 ± ℏ|Ω54|/2, where Ω54 is the Rabi frequency associated with this coupling laser to be defined later. This is useful for two reasons. First, it allows one to bring electric and magnetic resonances closer to each other, if they are separated in energy in the bare atom. This is a way of circumventing the problem of non-degenerate electric and magnetic probe field transitions [16]. In metastable neon, for example, the two resonances are separated in energy by the bare gap
4 ± ℏ|Ω54|/2, where Ω54 is the Rabi frequency associated with this coupling laser to be defined later. This is useful for two reasons. First, it allows one to bring electric and magnetic resonances closer to each other, if they are separated in energy in the bare atom. This is a way of circumventing the problem of non-degenerate electric and magnetic probe field transitions [16]. In metastable neon, for example, the two resonances are separated in energy by the bare gap
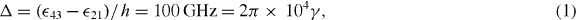
where we have used that γ = 107/(2π)Hz is a typical value for the spontaneous decay rate in neon. In order to close this gap via an induced Stark shift, we consider applying a strong laser field with Ω54 ≈ 104γ. Since neighboring transitions are still detuned at the least by 15Ω54, such large light shifts are feasible without inducing unwanted transitions. We define the resulting effective gap as

It turns out, however, that it is not mandatory to close this gap completely. Due to the large density, the electric permittivity  exhibits a negative real part Re(
exhibits a negative real part Re( ) ≈ −2 already relatively far away from the resonance [30]. More importantly, the states |2〉 and |3〉 are connected by a two-photon transition induced by the fields Ec and Eb, which becomes important only for non-zero effective gap frequencies Δ'.
) ≈ −2 already relatively far away from the resonance [30]. More importantly, the states |2〉 and |3〉 are connected by a two-photon transition induced by the fields Ec and Eb, which becomes important only for non-zero effective gap frequencies Δ'.
This two-photon transition is the motivation to apply an additional incoherent light field which is resonant with the transition |3〉–|4〉. It transfers population between the two levels with rates r34 = r43 = r. In combination with spontaneous emission from |4〉 to |2〉, it effectively pumps population from state |3〉 into state |2〉. As soon as the population of state |2〉 exceeds the one of state |3〉, i.e. for ρ22 > ρ33, the probe field Eb is amplified by means of this two-photon process. It is then more likely for the transition to occur in the direction |2〉 → |3〉 than in the reverse direction. Since this direction involves the emission of a probe field photon, we observe gain in the electric probe field component for ρ22 > ρ33. Choosing equal coupling laser frequencies ωa = ωc ensures that this two-photon resonance is always located at the position of a magnetic probe field resonance close to δ21 = 0. The two-photon virtual intermediate level is separated from state |4〉 by the tunable effective gap Δ' defined in equation (2). For sufficiently large Δ', the two-photon transition will thus be the dominant process around δ21 ≃ 0. This is important, as it allows to obtain gain in the electric probe field component exactly at those frequencies where the magnetic response is strong.
2.2. Linear response and the index of refraction n
We now define the electromagnetic linear response functions and the index of refraction n. As stated above, negative refraction Re(n) < 0 requires that both the electric and the magnetic component of an electromagnetic probe wave couple near-resonantly to the system. We are thus interested in the linear response of the medium to a weak probe field of frequency ωb with electric component Eb and magnetic field component Hb. The electric polarization P and magnetization M induced in the medium at the frequency ωb are given by [20]
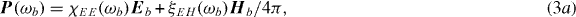
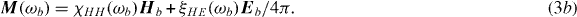
We now bring the vector relations in equations (3) into a simpler scalar form, where the response functions reduce to complex scalars. To this end, we focus on a circularly polarized probe beam that propagates in the z-direction in the following. Its wavevector reads k = nk0ez with k0 = 2π/λb. The electric and magnetic field components are given by

and Hb = ∓ie±1 e−iωbtHb/2 + c.c. with polarization unit vectors that are defined as 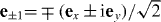 . The two signs indicate the two circular polarizations σ±. The electric polarization then becomes
. The two signs indicate the two circular polarizations σ±. The electric polarization then becomes

with amplitude

The real (imaginary) part of the susceptibility χEE describes the electric response in phase (out of phase) with the incoming probe field. The response from the cross-coupling adds to the electric polarization via ξEH. Accordingly, we derive for the amplitude M of the induced magnetization 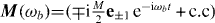 the response relation
the response relation

It is useful to define the electric permittivity ε and the magnetic permeability μ as usual as


 and μ are complex scalars in our situation, since we assume a circularly polarized probe field, where magnetic and electric field components are only phase shifted to each other.
and μ are complex scalars in our situation, since we assume a circularly polarized probe field, where magnetic and electric field components are only phase shifted to each other.We can now calculate the refractive index n, which depends on the probe wave polarization. For circular σ±-polarization, we obtain [19, 20]

As before, η∈{1,−1} determines the branch of the square root function, which we determine as discussed in section 2.1. We note that in our system the chiralities turn out to be negligible compared to the direct response coefficients  and μ. The refractive index is therefore approximately given by
and μ. The refractive index is therefore approximately given by  , and thus is independent of polarization.
, and thus is independent of polarization.
To find the electric polarization P(ωb) and magnetization M(ωb) induced in the atomic gas, we have to calculate the electric and magnetic dipole moments of the atoms at the probe field frequency ωb. The total response of the medium is given by a superposition of the individual responses of the atoms. These are determined by the steady-state density matrix ρ of an atom in the driven laser field configuration of figure 1. Specifically, the steady-state coherences ρ43 and ρ21 govern the induced polarization and magnetization at the probe field frequency as


2.3. Master equation for five-level atoms
We now set up a master equation for the five-level atoms in the laser configuration of figure 1, which allows us to calculate the steady-state density matrix and thus the response of the medium. Since the density of the gas is rather large, we have to take into account nonlinearities arising from a resonant atom–atom interaction.
In the setup of figure 1, the probe field couples to the transition |3〉–|4〉 with its electric field component and to the transition |1〉–|2〉 with its magnetic field component. Coupling fields drive the transitions |1〉–|3〉, |2〉–|4〉 and |4〉–|5〉. Without a probe field, the atom is in a superposition of the states |1〉 and |3〉. In the presence of the probe field, the atom also evolves into the other states. The zero-order subspace {|1〉,|3〉} is also connected to the other states by the incoherent pump field r34.
The time evolution of a single such five-level atom with density matrix ρ is governed by the master equation [31]
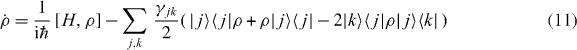
with the system Hamiltonian given by
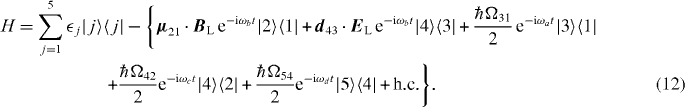
Here,  j is the energy of state |j〉 and the other terms describe the interaction with the laser fields in the long-wavelength and dipole approximations. The fields have frequencies ωn with n∈{a,b,c,d}. The laser detuning on transition |i〉–|j〉 reads
j is the energy of state |j〉 and the other terms describe the interaction with the laser fields in the long-wavelength and dipole approximations. The fields have frequencies ωn with n∈{a,b,c,d}. The laser detuning on transition |i〉–|j〉 reads

with  , where
, where  and
and  ij =
ij =  i −
i −  j, and we have introduced the angular frequencies
j, and we have introduced the angular frequencies






with polarization vector εm (m∈{a,c,d}) give rise to the complex Rabi frequencies



It is important to note that the Hamiltonian equation (12) contains instead of the external probe fields Eb, Hb the actual local fields EL, BL inside the medium. These contain contributions from the surrounding atoms in the medium as described by the polarization P and magnetization M. The corresponding Rabi frequencies are thus defined as


The second part of equation (11) describes spontaneous decay and decoherence arising due to elastic collisions. The decay rate on transition |i〉 → |j〉 is denoted by γij and set to γij = γ if |i〉 → |j〉 is electric dipole allowed (E1) and set to γij = α2γ for metastable E2, M1 transitions, where α = 1/137 is the fine-structure constant. To model elastic collisions, we add an effective dephasing constant γC to the decay rates of the off-diagonal density matrix elements ρjk in equation (11), such that they read

for  . In our numerical calculations, we set γC = γ.
. In our numerical calculations, we set γC = γ.
2.4. Nonlinear optical Bloch equations
As already mentioned, the Hamiltonian equation (12) contains the actual local fields inside the medium, whereas the medium response equation (3) is formulated in terms of the external probe fields Eb, Hb. It turns out that atom densities exceeding N ∼ 1016 cm−3 are required to obtain negative refraction, meaning that many particles are found in a cubic wavelength volume Nλ3b ≫ 1. Then, the local probe fields EL, HL experienced by the atoms may considerably deviate from the externally applied probe fields Eb, Hb in free space, since they contain contributions from neighboring atoms. Therefore, single-atom results for ρ43 and ρ21 cannot describe the system and thus are not shown here.
Different approaches have been proposed in the literature to solve this problem. One approach, which is expected to be valid for moderate densities, consists of expanding the steady-state density matrix elements ρ21 and ρ43 to linear order in the local fields EL, HL to obtain the medium polarization and magnetization. Then, the local and external fields are related by the Lorentz–Lorenz (LL) formulae [30, 32]


Here, we use an alternative method. We relate the local fields via the LL-relations to the external fields already in the Hamiltonian in equation (11). The corrections by the induced polarization P and magnetization M render the master equation nonlinear, since P and M given in equation (10a) itself depend on ρ [33]. Specifically, we obtain the complex Rabi frequencies
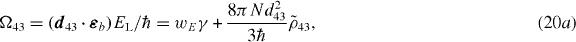

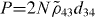 and slowly varying
and slowly varying  as follows from equations (5) and (10a). In the same way, we find that BL = HL = Hb + 4πM/3 with
as follows from equations (5) and (10a). In the same way, we find that BL = HL = Hb + 4πM/3 with  and
and 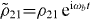 . We have also defined the small and real expansion parameters
. We have also defined the small and real expansion parameters


To find the linear response coefficients χαα and ξαβ (α,β∈{E,H}) introduced in equations (3), we numerically integrate the nonlinear differential equations of motion (11) using a standard Runge–Kutta-like algorithm [35] until the system has reached its steady state. This is done for a number of different electric field amplitudes Eb, holding the magnetic field amplitude Hb fixed. Linear regression of the relevant coherences ρ21,ρ43 as a function of Eb allows to extract the response coefficients χαα and ξαβ as slope mα and y-axis intercept bα from equations (3). We note again that in the case of a circularly polarized probe field, these equations describe scalar relations. In the following, we choose Eb ∼ e−1 and thus Hb ∼ ie−1.
The response functions χEE and ξEH are obtained from the electric polarization
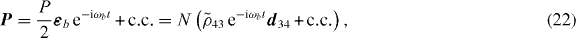
where  is the slowly varying part of the coherence. We find that
is the slowly varying part of the coherence. We find that

and thus
with the small expansion parameters defined in equations (21). Solving the nonlinear master equation (11) for different values of wE keeping wH fixed, we calculate  and thus
and thus

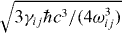 . Analogously, using
. Analogously, using 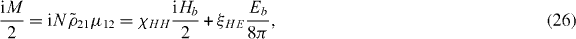
one obtains the response coefficients for the magnetization from 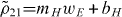 as
as


3. Optical response for different atomic densities
In the following, we present results for two different parameter sets. The main difference is the atomic vapor density, which we choose N1 = 2.55 × 1017 cm−3 in the first and N2 = 5 × 1016 cm−3 in the second set of parameters. We note that the results are invariant under proper rescaling of both density and probe wavelength such that the product Nλ3b remains invariant (see equations (25) and (27)). Here, we set λb = 5 μm, which corresponds to metastable neon, but smaller densities are sufficient in a system with larger λb.
3.1. Larger density N1 = 2.55 × 1017 cm−3
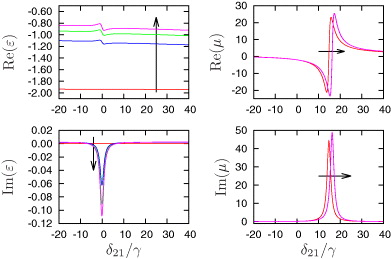
In figure 2, the permittivity  and the permeability μ of the medium are shown as a function of the probe field detuning from the magnetic resonance δ21. The resulting refractive index n can be seen in figure 3. Without incoherent pumping the system is passive and thus ε, μ and n have a positive imaginary part, i.e. the medium absorbs. Whereas absorption is small for the electric response due to local field effects [30], the losses are significant in the magnetic component. The fact that Re(
and the permeability μ of the medium are shown as a function of the probe field detuning from the magnetic resonance δ21. The resulting refractive index n can be seen in figure 3. Without incoherent pumping the system is passive and thus ε, μ and n have a positive imaginary part, i.e. the medium absorbs. Whereas absorption is small for the electric response due to local field effects [30], the losses are significant in the magnetic component. The fact that Re( ) ≈ −2 and the electric losses are small Im(
) ≈ −2 and the electric losses are small Im( ) ∼ 1/N follows directly from the Clausius–Mossotti relation applied to a simple oscillator model [30]. The local-field-induced shift of the magnetic resonance away from δ21 = 0 to positive δ21 can also be qualitatively understood within this approach. We observe power broadening in all response functions due to the nonlinearities that appear in the master equation because of the local fields that include near-dipole–dipole effects (see equations (20)). With gradually increasing the incoherent pumping rate between levels |3〉 and |4〉, we find that the imaginary part of ε around zero detuning turns negative, indicating that the two-photon transition |2〉–|3〉 amplifies the probe field. The magnetic permeability is mostly unaffected by the incoherent field. The real part of n is negative for all the shown detunings. It is worth pointing out that this even includes regions with Re(μ) > 0, where negative refraction can occur since Re(
) ∼ 1/N follows directly from the Clausius–Mossotti relation applied to a simple oscillator model [30]. The local-field-induced shift of the magnetic resonance away from δ21 = 0 to positive δ21 can also be qualitatively understood within this approach. We observe power broadening in all response functions due to the nonlinearities that appear in the master equation because of the local fields that include near-dipole–dipole effects (see equations (20)). With gradually increasing the incoherent pumping rate between levels |3〉 and |4〉, we find that the imaginary part of ε around zero detuning turns negative, indicating that the two-photon transition |2〉–|3〉 amplifies the probe field. The magnetic permeability is mostly unaffected by the incoherent field. The real part of n is negative for all the shown detunings. It is worth pointing out that this even includes regions with Re(μ) > 0, where negative refraction can occur since Re( ) < 0 and absorption is dominant, Im(μ) ≫ Re(μ) [36].
) < 0 and absorption is dominant, Im(μ) ≫ Re(μ) [36].
Figure 2. Electric permittivity ε and magnetic permeability μ as a function of δ21 for different pump rates r1 = 0, r2 = 0.004γ, r3 = 0.0052γ and r4 = 0.006γ between states |3〉 and |4〉. The arrow denotes the direction of increased pumping. Other parameters are set to Ω42 = 5.6γ, Ω31 = 0.0063γ, Δ' = 560γ, δ31 = −0.01γ, δ42 = 0, δ54 = 0, where γ = 107/(2π)Hz is a typical spontaneous decay rate in neon. The probe field wavelength is λb = 5 μm and the density N1 = 2.55 × 1017 cm−3.
Download figure:
Standard imageFigure 3. Refractive index n for different pump rates as a function of δ21 for larger density N1 = 2.55 × 1017 cm−3. Parameters are the same as in figure 2. Arrows indicate the direction of increased pumping. Without pumping, the imaginary part is strictly positive, as expected for a passive system. On increasing the pump rate, the system turns active, and negative refraction is obtained without absorption or even with amplification. The panels on the right-hand side show a magnification of parts of the left-hand side.
Download figure:
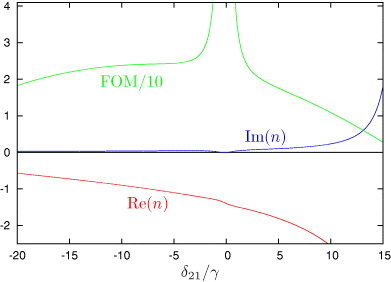
Standard imageIncreasing the pump rate r decreases the absorption over the whole range of displayed probe detunings. Since we can continuously change the pump rate, we can identify the physically correct square root branch of n if we follow the path in the complex plane starting from the root with a positive imaginary part for the passive system. Increasing r thereby continuously decreases Im(n) in a region around δ21 = 0 with a width of a few γ. Finally, for suitable incoherent pump rates, negative refraction occurs without absorption or even with amplification, see figure 4. In this frequency range, the FOM becomes very large due to the vanishing imaginary part. The physical mechanism for the crossover from passive to active can easily be understood by following the path of ε, μ, n2 and n in the complex plane as a function of the pump rate r, see figure 5. Without pumping (step 1), the system is passive and shows absorption. With increasing the pump rate, Im(ε) becomes negative, which compensates for the losses via the magnetic component. Thus, Im(n) decreases and finally vanishes, while Re(n) remains negative. In figure 4, one finds FOM > 10 for a frequency range of more than 30γ. FOM > 50 is achieved over a range of about γ.
Figure 4. Lossless negative refraction for a pump rate of r = 0.0052γ and larger density N1. Other parameters are the same as in figure 2. Shown are Re(n), Im(n) and the FOM = |Re(n)/Im(n)| divided by 10.
Download figure:
Standard imageFigure 5. Paths of ε, μ, n2/2, and  in the complex plane parametrized by the pumping rate r. The detuning is chosen as δ21 = −γ/2. Other parameters are the same as in figure 2. Step 1 corresponds to zero pumping r1, where the system is passive. Thus, the black filled circle is the physical solution and not the pink star, which corresponds to −n. Increasing the pump rate r > 0 continuously, we follow the path indicated by the arrow. At step 2 with an intermediate pump rate, the system is still absorptive. Finally, step 3 shows lossless negative refraction.
in the complex plane parametrized by the pumping rate r. The detuning is chosen as δ21 = −γ/2. Other parameters are the same as in figure 2. Step 1 corresponds to zero pumping r1, where the system is passive. Thus, the black filled circle is the physical solution and not the pink star, which corresponds to −n. Increasing the pump rate r > 0 continuously, we follow the path indicated by the arrow. At step 2 with an intermediate pump rate, the system is still absorptive. Finally, step 3 shows lossless negative refraction.
Download figure:
Standard image3.2. Smaller density N2 = 5 × 1016 cm−3
We now turn to the second set of parameters. The second set is based on a lower density, which, however, is still large compared to the typical densities applied in light propagation through coherently prepared atomic media. Another main difference lies in the much lower effective gap Δ' for the case with lower density. Nevertheless, in both cases the effective gap is large enough to render two-photon processes important.
It can be seen from figure 6 that the permittivity and permeability are qualitatively similar to the ones in figure 2 for larger density. This, in particular, applies also to the dependence on incoherent pumping. Generally, the permittivity shows a stronger dependence on detuning, with a tilted base line, which is due to the lower value of Δ'. Consequently, the index of refraction, shown in figure 7, and the evolution of  ,μ,n2 and n in the complex plane are qualitatively similar to the case with higher density (see figures 3 and 5).
,μ,n2 and n in the complex plane are qualitatively similar to the case with higher density (see figures 3 and 5).
Figure 6. Electric permittivity ε and magnetic permeability μ as a function of δ21 for different pump rates r1 = 0, r2 = 0.032 γ, r3 = 0.063 γ, r4 = 0.083 γ between states |3〉 and |4〉. The arrow denotes the direction of increased pumping. Other parameters are set to Ω42 = γ, Ω31 = 0.01 γ, Δ' = 40 γ, δ31 = 0.05 γ, δ54 = 0, where γ = 107/(2π) Hz is a typical spontaneous decay rate in neon. The probe field wavelength is λb = 5 μm and the density N2 = 5 × 1016 cm−3.
Download figure:
Standard imageFigure 7. Refractive index n for different pump rates as a function of δ21 for lower density N2 = 5 × 1016 cm−3. Parameters are the same as in figure 6. Arrows indicate direction of increased pumping. Without pumping, the imaginary part is strictly positive, as expected for a passive system. On increasing the pump rate, the system becomes active, and negative refraction is obtained without absorption or even with amplification. Right panels zoom into the region around δ21 = 0.
Download figure:
Standard imageNevertheless, quantitatively, the lower density leads to a smaller range of negative refraction with a low absorption and thus a high FOM. Results are shown in figure 8. The detuning range with the imaginary part of n close to zero is about one decay rate γ; the range with the absolute value of the real part exceeding that of the imaginary part (FOM > 1), however, is about 10γ. This is a significantly smaller region than in the high density case. Therefore, as expected, the facilitated implementation due to the lower density comes at the price of a reduced performance in terms of lossless negative refraction.
Figure 8. Lossless negative refraction for a pump rate of r = 0.083 γ and lower density N2. Other parameters are the same as in figure 6. Shown are Re(n), Im(n) and the FOM = |Re(n)/Im(n)| divided by 10.
Download figure:
Standard image3.3. Doppler broadening
Finally, we estimate the effect of Doppler broadening on our results. For this, we use Antoine's equation, logp = A − B/(C + T), where p is the vapor pressure in units of bar, T is the temperature in kelvin, and A = 3.75641, B = 95.599 and C = −1.503 are parameters taken from NIST [37] for neon. We further relate the density N to the pressure and temperature via N = p/(kBT) with kB the Boltzmann constant. From these two relations, we obtain for the larger density N1 = 2.55 × 1017 cm−3 a temperature of T1 = 15.1 K, and for the smaller density N2 = 5 × 1016 cm−3 a temperature of T2 = 13.8 K. Note that these temperatures are slightly below the temperature range (15.9–27 K) given in [37] for the parameters A,B and C.
We assume a Maxwell–Boltzmann velocity distribution of the atoms in the laser propagation direction with the most probable velocity 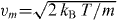 with m the mass of a single atom. The Doppler shift thus leads to an additional detuning ΔD with a Gaussian distribution [38]
with m the mass of a single atom. The Doppler shift thus leads to an additional detuning ΔD with a Gaussian distribution [38]
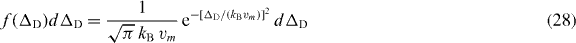
over which we average our medium response coefficients. The full-width at half-maximum of this distribution evaluates to a Doppler width of 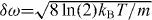 . It should be noted that it is not obvious whether the averaging over the microscopic medium response provides the full picture. For example, modifications to the nonlinear density-dependent local field corrections could arise due to the motion of the atoms. If the probe field transitions for atoms with different velocities are shifted out of resonance relative to each other, the local field at one of the atoms due to the presence of the second atom will be different from the effect of a resonant atom. This could, for example, effectively reduce the density entering the local field corrections for a particular atom to that of mutually resonant atoms moving with similar velocities. Such effects, however, are beyond the scope of this paper.
. It should be noted that it is not obvious whether the averaging over the microscopic medium response provides the full picture. For example, modifications to the nonlinear density-dependent local field corrections could arise due to the motion of the atoms. If the probe field transitions for atoms with different velocities are shifted out of resonance relative to each other, the local field at one of the atoms due to the presence of the second atom will be different from the effect of a resonant atom. This could, for example, effectively reduce the density entering the local field corrections for a particular atom to that of mutually resonant atoms moving with similar velocities. Such effects, however, are beyond the scope of this paper.
In our calculations, we scale all frequencies to the decay rate γ on transition 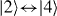 , which is approximately γ = 107/(2π) s−1. We thus take this transition as a reference, and obtain Doppler widths of δω1 ≈ 333γ and δω2 ≈ 318γ for the wavelength λc at the two densities N1 and N2. The Doppler broadenings for laser fields with wavelengths λ other than that of the reference transition are different from δωi by a factor of λc/λ. In particular, the Doppler broadening on the probe transitions is about 15 times smaller, since λb ≈ 15λc. The probe field Doppler width is thus about 21γ.
, which is approximately γ = 107/(2π) s−1. We thus take this transition as a reference, and obtain Doppler widths of δω1 ≈ 333γ and δω2 ≈ 318γ for the wavelength λc at the two densities N1 and N2. The Doppler broadenings for laser fields with wavelengths λ other than that of the reference transition are different from δωi by a factor of λc/λ. In particular, the Doppler broadening on the probe transitions is about 15 times smaller, since λb ≈ 15λc. The probe field Doppler width is thus about 21γ.
As a first step, we Doppler averaged our results in figures 4 and 8. We found that while the Doppler broadening has a detrimental effect on the results, nevertheless even with full Doppler broadening taken into account negative refraction with significant FOM = |Re(n)/Im(n)| is achieved over a broad spectral range. Overall, the modifications of the results due to Doppler broadening are consistent with the estimated probe transition Doppler width of about 21γ. The Doppler broadening has a stronger effect on the results of figure 8 compared with figure 4, since the range of probe field detunings over which negative refraction is observed is lower in this case.
But there are important differences compared with the results without Doppler averaging. Due to the different wavelength on the various transitions, the two-photon resonance between states |2〉 and |3〉 via state |4〉 occurs at different probe field detunings for different atom velocities, such that its effect is reduced in the Doppler averaging. Also, we found that for the parameters of figures 4 and 8, only atoms in a certain velocity range exhibit negative refraction. Thus, the Doppler averaged result contains contributions, both with negative and positive index of refraction. The optimum incoherent pump rates to eliminate absorption depend on the atom velocity as well. Finally, since the linewidth of the dipole-forbidden transition between |1〉 and |3〉 is suppressed by α2, already small Doppler shifts detune the pump field Ω31 strong enough to significantly change the medium response to the electric probe field component. In effect, the Doppler averaged results have a more involved dependence on the various system parameters compared with the non-averaged results, and a straightforward enhancement of the results by incoherent pump fields becomes more challenging with increasing Doppler width.
Nevertheless, we found that the concept of using active media to improve the performance of atomic negative refractive index media can also be applied in Doppler broadened vapors. For this, we replaced the coherent pumping Ω31 by a broadband incoherent pump field between |1〉 and |3〉, such that the electric response becomes less dependent on the Doppler shift. Results are shown in figure 9 for slightly adjusted control field parameters, but with the same density as in figure 4. The two curves (i) show the real part of the index of refraction n (the lower half of the figure) and the FOM divided by 10 (FOM/10, upper half) in the passive medium without Doppler broadening. It can be seen that already in this passive case negative refraction with FOM of more than 20 can be achieved over a spectral range of several γ. The curves (ii) show the corresponding results with full Doppler broadening. Whereas the system still exhibits negative refraction, the maximum FOM is reduced to about eight due to the averaging. But, as shown in curves (iii), rendering the Doppler broadened system active by applying an incoherent pump field between states |3〉 and |4〉 leads to significant enhancement of the FOM, which in this case approaches 100. Interestingly, for the case with Doppler broadening, the FOM and the overall performance are not monotonically improved with increasing the incoherent pump rate. Rather, increasing the pump rate first worsens the results, and only toward slightly higher pump rates it leads to a strong increase in the FOM as shown in figure 9. This more complicated dependence again arises from the averaging of the different results for the various atom velocities.
Figure 9. Effect of Doppler broadening. The curves in the upper half show the FOM = |Re(n)/Im(n)| divided by 10. The curves in the lower half show the real part of the index of refraction. (i) Results without Doppler broadening for the passive system. (ii) Results with Doppler broadening δω1 ≈ 333γ taken into account for the passive system. (iii) The figure shows Doppler broadened results for the active case with an incoherent pump rate r = 0.164γ between states |3〉 and |4〉. The other parameters are Ω42 = 28γ, Δ' = 150 γ, δ54 = 0. The probe field wavelength is λ = 5 μm and the density 2.55 × 1017 cm−3. The coupling field Ω31 has been replaced by an incoherent pump field between |1〉 and |3〉 with rate r13 = 4 × 10−5.
Download figure:
Standard imageOur estimates above apply to a thermal gas vapor, which leads to rather large Doppler widths. Alternative implementations such as in ultracold gases, solid-state quantum optics or with Doppler-free laser configurations in related level structures could lead to significantly lower Doppler widths even at high atom densities. Interestingly, we found that for some parameters, moderate Doppler broadening can even lead to an enhancement of the FOM compared with the case without Doppler broadening. This again points to the rich interplay between incoherent pump, Doppler broadening and medium response, such that independent control over density and Doppler broadening would certainly be desirable. In any case, we can conclude from our analysis that the general concept of significantly improving the performance of a dense gas of atoms as a negative refractive index medium by rendering it active via the application of suitable pump fields proves beneficial also for the Doppler broadened case in thermal vapors.
4. Summary
We have predicted negative refraction with adjustable loss in a dense gas of atoms. A possible experimental realization of our system is a thermal gas of metastable neon atoms, where negative refraction occurs at an infrared wavelength of λ = 5 μm. Employing the transition to an active medium by means of an incoherent pumping field allows to change between a system with positive and negative imaginary parts of the refractive index while keeping the real part of the index of refraction negative. It should be noted, however, that turning the gas into an active medium can render it unstable [39, 40].
One of the main advantages of our setup is that the transition from absorptive to lossless to amplifying is externally tunable by a small incoherent light field. In particular, this allows to study the behavior of a negative refractive medium close to the active-to-passive threshold [13–15]. We have explicitly shown that our main results are robust under the effect of Doppler broadening in a thermal gas of neon. Due to its wide tunability and control, our system is not only interesting from a proof-of-principle point of view, but also promises the enhancement of optical effects which are severely degraded by losses accompanying negative refraction in current metamaterials.
Acknowledgment
The Young Investigator Group of PPO received financial support from the 'Concept for the Future' of the Karlsruhe Institute of Technology within the framework of the German Excellence Initiative.