Abstract
Two-photon resonant photoionization of helium is investigated both experimentally and theoretically. Ground state helium atoms are excited to the 1s4p, 1s5p and 1s6p 1P states by synchrotron radiation and ionized by a synchronized infrared pulsed picosecond laser. The photoelectron angular distributions of the emitted electrons are measured using a velocity map imaging (VMI) spectrometer. The measured asymmetry parameters of the angular distribution allow the phase differences and the ratios of the dipole matrix elements of the 1s s and 1s
s and 1s d channels to be determined. The experimental results agree with the calculated values obtained in a configuration–interaction calculation with a Coulomb–Sturmian basis set. The effects of the radiative decay of the intermediate state and the static electric field of the VMI spectrometer on the measurements are discussed.
d channels to be determined. The experimental results agree with the calculated values obtained in a configuration–interaction calculation with a Coulomb–Sturmian basis set. The effects of the radiative decay of the intermediate state and the static electric field of the VMI spectrometer on the measurements are discussed.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Two-photon ionization via angular momentum aligned intermediate states has proven to be a useful tool for the investigation of the photoionization dynamics of atoms [1]. The reasons for this are multiple and include access to the photoionization dynamics of excited states, as well as the possibility of extracting complete information on the photoionization event [2]. Furthermore, in the case of helium, it is particularly attractive because the relatively simple electronic structure of this two-electron atom makes the process theoretically tractable. In recent years, there has been a revival of interest in two-colour experiments on helium in which the high-lying Rydberg states play an important role. Swoboda et al [3] reported on the effect of the He 1s3p 1P resonance on the phase of the resonant two-photon ionization. Johnsson et al [4] and Holler et al [5] discussed different effects of the attosecond electron wave packet interference due to strong infrared (IR) fields on electronic structure, whereas Ranitovic et al [6] demonstrated the time-dependent transparency of helium to light, which is a consequence of the interaction of the harmonics of the strong IR field with the atom. Unlike the measurements and calculations presented in this work, in all of these cases, the strength of the IR field needs to be taken into account as it cannot simply be considered as a weak perturbation of the system. However, it may be expected that an investigation of the unperturbed electronic structure and its interaction with light may provide an alternative testing ground for theory. Very recently, Ishikawa and Ueda [7] theoretically assessed the effect of the pulse length of the vacuum ultraviolet (VUV) light from a free-electron laser on the angular distributions of electrons emitted in one-colour two-photon single ionization of He. They discussed in detail the effect of the interference between the resonant pathways (via the 1snp 1P states) and the direct non-resonant two-photon absorption.
From an experimental point of view, access to excited states in helium is hampered by the high energy of the Rydberg states; for example, the lowest of the 1Po states, the 1s2p state, lies 21.218 eV above the ground state. Early measurements successfully resolved this problem using electrical discharges to prepare the atoms in the metastable 1s2s singlet and triplet states. These atoms could subsequently be excited and ionized by visible laser light. By a careful calibration of the metastable atom and photon densities it was possible to extract the absolute cross-section for photoionization of atoms in the 1s3p, 1s4p and 1s5p 1P and 3P states for a number of different photon energies [8, 9]. Further progress was not made until the advent of laser high-order harmonic generation (HHG) sources, which allowed sufficiently intense VUV sources to directly photo-excite the He 1snp 1P states from the ground state. The so-formed intermediate states could then be ionized by the fundamental or lower order harmonics of the same laser. This method was first employed to measure the lifetime of the 1s2p singlet state [10] and was subsequently used to measure the energy dependence of the absolute photoionization cross-sections for the n = 2 and 3 members of the 1snp 1P series [11, 12].
However, absolute cross-sections give no information on the phase differences between the outgoing partial waves. In the case of photoionization from an excited 1P state, the dipole selection rules lead to 1s s or 1s
s or 1s d partial waves. By measuring the angular distribution of the ejected photoelectrons, it is possible to infer the relative dipole matrix elements pertaining to continuum partial waves, as well as the phase difference between them. Such measurements provide a more stringent test of theoretical descriptions of the photoionization process than the comparison to the absolute cross-sections. This type of measurement has recently been made for the first time on the helium atom in the 1s3p and 1s4p singlet states by combining pump–probe studies using HHG and low harmonics of a femtosecond Ti:sapphire laser with the photoelectron velocity map imaging (VMI) technique to measure the photoelectron angular distributions (PADs) [13]. In this work, we present the use of different light sources with the same detection technique to investigate a series of the 1snp 1P states (4 ⩽ n ⩽ 6), with the aim of measuring the principal quantum number and energy dependence of the ratio of the transition matrix elements and phase differences. It was previously suggested that such measurements were not possible at the second-generation synchrotron sources even for the lowest 1snp states [11]. Here we show, however, that the passage to the third generation synchrotron in combination with VMI and coincidence methods has allowed us to make these measurements in spite of the strongly falling cross-section of the 1s2 → 1snp transitions with increasing n. Moreover, the continuous tunability of synchrotron radiation makes this approach more versatile than approaches based on HHG sources.
d partial waves. By measuring the angular distribution of the ejected photoelectrons, it is possible to infer the relative dipole matrix elements pertaining to continuum partial waves, as well as the phase difference between them. Such measurements provide a more stringent test of theoretical descriptions of the photoionization process than the comparison to the absolute cross-sections. This type of measurement has recently been made for the first time on the helium atom in the 1s3p and 1s4p singlet states by combining pump–probe studies using HHG and low harmonics of a femtosecond Ti:sapphire laser with the photoelectron velocity map imaging (VMI) technique to measure the photoelectron angular distributions (PADs) [13]. In this work, we present the use of different light sources with the same detection technique to investigate a series of the 1snp 1P states (4 ⩽ n ⩽ 6), with the aim of measuring the principal quantum number and energy dependence of the ratio of the transition matrix elements and phase differences. It was previously suggested that such measurements were not possible at the second-generation synchrotron sources even for the lowest 1snp states [11]. Here we show, however, that the passage to the third generation synchrotron in combination with VMI and coincidence methods has allowed us to make these measurements in spite of the strongly falling cross-section of the 1s2 → 1snp transitions with increasing n. Moreover, the continuous tunability of synchrotron radiation makes this approach more versatile than approaches based on HHG sources.
From a theoretical point of view, the absolute cross-sections for the ionization of the singlet 1snp states with 2 ⩽ n ⩽ 4 have been calculated in the energy range between the threshold and 1 eV above the threshold using close coupling calculations [14, 15]. Chang and Fang [16, 17] have more recently calculated the absolute and partial cross-sections (for the emission of the  s or
s or  d waves) for the 1snp 1P states with 2 ⩽ n ⩽ 5 in a broad range of kinetic energies of the photoelectron using the B-spline configuration interaction (CI) method. Later, a range of methods has been used for the calculation of the phase differences between the
d waves) for the 1snp 1P states with 2 ⩽ n ⩽ 5 in a broad range of kinetic energies of the photoelectron using the B-spline configuration interaction (CI) method. Later, a range of methods has been used for the calculation of the phase differences between the  s and
s and  d partial waves. As will be seen later in the text, the overall phase shift is made up of an analytically calculable Coulomb phase shift and a phase shift due to the short-range potential. The latter shifts have been calculated using a number of methods including the close-coupling method [18], the Harris–Nesbet variation method [19] and the above-mentioned B-spline CI method [16, 17].
d partial waves. As will be seen later in the text, the overall phase shift is made up of an analytically calculable Coulomb phase shift and a phase shift due to the short-range potential. The latter shifts have been calculated using a number of methods including the close-coupling method [18], the Harris–Nesbet variation method [19] and the above-mentioned B-spline CI method [16, 17].
In this paper, we present a theoretical description of the two-photon ionization process and its relationship to the experimentally measured parameters. We compare the results of the theoretical description both to previous calculations and to the new experimental results, which have been obtained by taking advantage of the tunability of the synchrotron source to reach the singlet 1s4p, 1s5p and 1s6p states, combined with the VMI technique to detect the photoelectrons emitted subsequent to absorption of a second photon from an IR laser.
2. Theoretical description
Two-photon ionization by simultaneous irradiation with synchrotron photons (energy ω1, polarization 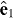 ) and Ti:sapphire laser photons (energy ω2, polarization
) and Ti:sapphire laser photons (energy ω2, polarization 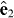 ) proceeds in the following way:
) proceeds in the following way:

where 4 ⩽ n ⩽ 6. The energy of the synchrotron is tuned to match the transition energy to the selected singly excited intermediate 1snp 1P state. The bandwidths of the two sources are much smaller than the energy difference between the 1snp states considered here (i.e. both sources are monochromatic), and the polarization vectors of the synchrotron light and the laser are parallel (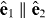 ). The intensities of the two sources are taken to be low enough and the duration of the pulses long enough compared to 1/ω1 and 1/ω2 (see section 3), so that the atom–light interaction can be described by a two-photon transition amplitude. We choose the quantization axis along the direction of
). The intensities of the two sources are taken to be low enough and the duration of the pulses long enough compared to 1/ω1 and 1/ω2 (see section 3), so that the atom–light interaction can be described by a two-photon transition amplitude. We choose the quantization axis along the direction of 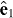 (
(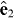 ). Since the electric dipole excitation is dominant, the generalized two-photon differential ionization cross-section [20] is proportional to
). Since the electric dipole excitation is dominant, the generalized two-photon differential ionization cross-section [20] is proportional to
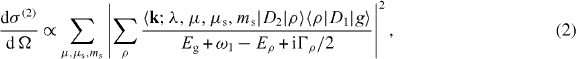
where 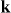 is the wave vector of the ejected electron, λ, μ and μs are the angular momentum of the core electron, its projection on the z-axis and the projection of its spin, respectively, ms is the spin projection of the continuum electron and |g〉 denotes the ground state. The sum over ρ runs over the complete set of states {|ρ〉}. The decay width of the intermediate state |ρ〉 is denoted by Γρ, and D1 and D2 are the dipole operators describing absorption of the synchrotron and the IR photon, respectively. The energy of the incident photons is tuned to match the transition energy to a selected intermediate state |ν〉. In this case, only the dominant term ρ = ν can be considered in the summation over ρ, and the generalized cross-section is approximately proportional to
is the wave vector of the ejected electron, λ, μ and μs are the angular momentum of the core electron, its projection on the z-axis and the projection of its spin, respectively, ms is the spin projection of the continuum electron and |g〉 denotes the ground state. The sum over ρ runs over the complete set of states {|ρ〉}. The decay width of the intermediate state |ρ〉 is denoted by Γρ, and D1 and D2 are the dipole operators describing absorption of the synchrotron and the IR photon, respectively. The energy of the incident photons is tuned to match the transition energy to a selected intermediate state |ν〉. In this case, only the dominant term ρ = ν can be considered in the summation over ρ, and the generalized cross-section is approximately proportional to

where it has been taken into account that ω1 = Eν − Eg.
If the angular momentum of the continuum electron and its projection are denoted by ℓ and m, the resultant momentum (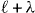 ) and the corresponding projection are denoted by L and M, and the total spin and its projection are given by S and MS, then the partial waves of the final continuum state which are accessible in the present geometry have ℓ = μ = 0, L = ℓ = 0 or L = ℓ = 2, μs = −ms, M = 0 and S = MS = 0. Note that singlet–triplet coupling is not considered in the present formalism, since the singlet and triplet singly excited states with the total angular momentum L ⩽ 2 are only weakly mixed [21]. The relevant matrix elements between the intermediate state and the final state can therefore be written in the following way:
) and the corresponding projection are denoted by L and M, and the total spin and its projection are given by S and MS, then the partial waves of the final continuum state which are accessible in the present geometry have ℓ = μ = 0, L = ℓ = 0 or L = ℓ = 2, μs = −ms, M = 0 and S = MS = 0. Note that singlet–triplet coupling is not considered in the present formalism, since the singlet and triplet singly excited states with the total angular momentum L ⩽ 2 are only weakly mixed [21]. The relevant matrix elements between the intermediate state and the final state can therefore be written in the following way:

where γ stands for (ℓ,λ,L,S),  is the Coulomb phase shift of the partial wave with angular momentum ℓ, the phase shift due to the short-range (non-Coulombic) potential is denoted by πκγ, and
is the Coulomb phase shift of the partial wave with angular momentum ℓ, the phase shift due to the short-range (non-Coulombic) potential is denoted by πκγ, and  = k2/2 is the kinetic energy of the ejected electron. In (4), the Clebsch–Gordan coefficients are written as (...|...), and Yℓm is used for the spherical harmonic functions. From (3) and (4) it follows that the form of the cross-section is
= k2/2 is the kinetic energy of the ejected electron. In (4), the Clebsch–Gordan coefficients are written as (...|...), and Yℓm is used for the spherical harmonic functions. From (3) and (4) it follows that the form of the cross-section is

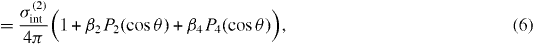
where 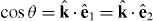 , σ(2)int is the integrated generalized two-photon cross-section and Pq is the Legendre polynomial of order q. The asymmetry parameters can be expressed with the coefficients Aq as β2 = A2/A0 and β4 = A4/A0 [22].
, σ(2)int is the integrated generalized two-photon cross-section and Pq is the Legendre polynomial of order q. The asymmetry parameters can be expressed with the coefficients Aq as β2 = A2/A0 and β4 = A4/A0 [22].
The matrix elements 〈ν|D2| ;γ,0〉 can be transformed further using the Wigner–Eckart theorem and the uncoupling formula [23, 24] (used to uncouple the 'inner' electron part and the 'outer' electron part of the wavefunction) and by considering that the intermediate state is well described within a single configuration approximation. In this case, the asymmetry parameters can be written as:
;γ,0〉 can be transformed further using the Wigner–Eckart theorem and the uncoupling formula [23, 24] (used to uncouple the 'inner' electron part and the 'outer' electron part of the wavefunction) and by considering that the intermediate state is well described within a single configuration approximation. In this case, the asymmetry parameters can be written as:


where 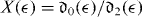 is the ratio of radial integrals
is the ratio of radial integrals

of the s and d partial waves and
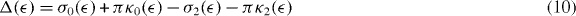
is the total phase difference between these waves. It should be noted that in contrast to the ratio X( ), which depends on the intermediate state |ν〉, the phase difference Δ is the property of the final continuum state alone and is thus independent of the principal quantum number n of the intermediate state. Expressions (7) and (8) have also been obtained by Haber et al [13] and in a slightly different form also by Ishikawa and Ueda [7].
), which depends on the intermediate state |ν〉, the phase difference Δ is the property of the final continuum state alone and is thus independent of the principal quantum number n of the intermediate state. Expressions (7) and (8) have also been obtained by Haber et al [13] and in a slightly different form also by Ishikawa and Ueda [7].
The eigenstate wavefunctions used in the present calculations have been expressed in a basis of real CI coupled two-electron Coulomb–Sturmian functions [25–27]. These square integrable basis functions form a complete set of states, and can be used for the description of both the bound and continuum states. In particular, diagonalization of the Hamiltonian matrix (i.e. the representation of the Hamiltonian operator in the Coulomb–Sturmian basis) for the total angular momentum L and parity (−1)L results in a discrete set of states. If the corresponding energies lie below the first ionization threshold IN=1 = −2 au, these states are associated with the bound atomic states. On the other hand, the states with energies above IN=1 can be interpreted as a representation of the electronic continuum if they are renormalized, so that they correspond to the continuum wavefunctions with delta (energy) normalization [28, 29]. Since for each L only a single continuum channel is open in our case, this can be done conveniently by means of the calculated energies of these states. Diagonalization of the Hamiltonian matrices for L = 0 and 2 results in two sets of states with energies above IN=1, corresponding to the 1s s and 1s
s and 1s d continua. The energies of these discrete states do not coincide, so that the ratio X(
d continua. The energies of these discrete states do not coincide, so that the ratio X( ) is obtained by interpolation of either
) is obtained by interpolation of either 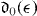 or
or 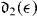 .
.
The calculated ratios X( ) for the intermediate states 1snp, 2 ⩽ n ⩽ 6, are shown in figure 1.
) for the intermediate states 1snp, 2 ⩽ n ⩽ 6, are shown in figure 1.
Figure 1. The calculated ratios X( ) for the 1snp intermediate states for 2 ⩽ n ⩽ 6 (empty circles). The ratios extracted from the partial single-photon ionization cross-sections of unpolarized atoms taken from [16] (Chang & Fang I) are plotted with orange squares. The ratios extracted from the cross-sections for the near-threshold region taken from [17] (Chang & Fang II) are plotted with solid green lines. The inset shows a magnified view of the near-threshold region.
) for the 1snp intermediate states for 2 ⩽ n ⩽ 6 (empty circles). The ratios extracted from the partial single-photon ionization cross-sections of unpolarized atoms taken from [16] (Chang & Fang I) are plotted with orange squares. The ratios extracted from the cross-sections for the near-threshold region taken from [17] (Chang & Fang II) are plotted with solid green lines. The inset shows a magnified view of the near-threshold region.
Download figure:
Standard imageIt has been checked that the values of X( ) just above the ionization threshold match the values obtained by calculating the density of oscillator strength pertaining to the bound 1sn's and 1sn'd states (i.e. for
) just above the ionization threshold match the values obtained by calculating the density of oscillator strength pertaining to the bound 1sn's and 1sn'd states (i.e. for  < 0) and then extrapolating their values across the threshold (
< 0) and then extrapolating their values across the threshold ( > 0). The behaviour just above the threshold has also been analysed by increasing the basis size. The results with larger basis sets have been found to agree with the results obtained with the initial basis set.
> 0). The behaviour just above the threshold has also been analysed by increasing the basis size. The results with larger basis sets have been found to agree with the results obtained with the initial basis set.
In figure 1, we compare our results to the dipole matrix element ratios extracted from the single-photon partial ionization cross-sections of unpolarized helium atoms in the 1snp 1P states (2 ⩽ n ⩽ 5) calculated by Chang and Fang [16, 17]. The ratios have been obtained from the relation

where σu(··· ) denotes the partial ionization cross-sections of an ensemble of unpolarized atoms. This implies a summation over the projections Mν of the 1snp states in addition to the summation over the projections M of the final continuum state in the calculation of σu. The extracted ratios from [16] are in good agreement with the present calculations for  ⩾ 0.5 eV. Closer to the threshold, the extracted values deviate slightly towards higher values compared with our results. However, the results from [17] obtained using the same approach which focus on the near-threshold region (
⩾ 0.5 eV. Closer to the threshold, the extracted values deviate slightly towards higher values compared with our results. However, the results from [17] obtained using the same approach which focus on the near-threshold region ( ≲ 0.11 eV) may be seen to be in excellent agreement with the present calculations.
≲ 0.11 eV) may be seen to be in excellent agreement with the present calculations.
The phase differences between the 1s s and 1s
s and 1s d waves have been obtained in two ways: by fitting a linear function to the energy dependence of the quantum defects κ0 and κ2 of the 1sn's and 1sn'd states and extrapolating across the threshold and by matching the radial part of the continuum wave to the known analytic form in the asymptotic region. Since the photoelectron kinetic energy region we examine here is relatively narrow, the dependence of κ0 and κ2 on
d waves have been obtained in two ways: by fitting a linear function to the energy dependence of the quantum defects κ0 and κ2 of the 1sn's and 1sn'd states and extrapolating across the threshold and by matching the radial part of the continuum wave to the known analytic form in the asymptotic region. Since the photoelectron kinetic energy region we examine here is relatively narrow, the dependence of κ0 and κ2 on  is negligible in comparison with the stronger energy dependence of the Coulomb part of the total shift. Almost identical results have been obtained if, above the threshold, the quantum defect difference κ0 − κ2 has been fixed to a constant value that approximately matches the difference for an arbitrary pair of bound states 1sn's and 1sn'd.
is negligible in comparison with the stronger energy dependence of the Coulomb part of the total shift. Almost identical results have been obtained if, above the threshold, the quantum defect difference κ0 − κ2 has been fixed to a constant value that approximately matches the difference for an arbitrary pair of bound states 1sn's and 1sn'd.
A comment is in place concerning the parametrization from (7) and (8). These relations have been obtained under the assumption that the intermediate state is described well within the single-configuration approximation, which is well justified for the 1snp states, including the lowest members of the series [30]. The use of the uncoupling formula is thus justified and the resulting ratios of the single-electron transition matrix elements are meaningful. Furthermore, since the number of accessible channels is small, the number of independent parameters in (7) and (8) is also small. This is in contrast with a two-photon two-colour photoionization of neon atoms proceeding through the 2p53d states [22], where a larger number of parameters were necessary for the description of the PADs and where it was shown that a simplified treatment neglecting the coupling details of various channel functions resulted in incorrect values of the asymmetry parameters.
3. Experimental setup and data analysis
The experiment was carried out using synchrotron light from the undulator Gas Phase Photoemission beamline of the Italian synchrotron radiation source Elettra [31]. The monochromatized synchrotron light was focused into the interaction region of the VMI spectrometer [32], where it was overlapped with a focused Ti:sapphire laser beam tunable in the range from 600 to 1000 nm [33] (see the schematic outline of the experiment in figure 2). As the individual components of the experiment including the layout of the beamline [31], the coupling of the Ti:sapphire laser with the synchrotron [33] and the VMI spectrometer used [32] have been described in detail in previous publications, we will concentrate here on aspects of inherent importance to the experiments performed and the data analysis methods that have been developed.
Figure 2. Schematic view of the experimental setup. The polarization of the synchrotron light and the polarization of the Ti:sapphire laser (green arrows) are parallel to each other and the beams are counter-propagating. The red spheres represent the expanding electron cloud as it travels towards the position-sensitive detector.
Download figure:
Standard imageThe synchrotron light is tuned to the individual resonances in the energy region between 23.742 and 24.211 eV, where the ground state helium atoms can be excited to the 4 ⩽ n ⩽ 6 members of the He 1snp 1P series. The resulting Rydberg state can then be ionized by the absorption of a photon from a mode-locked Ti:sapphire laser (full width at half maximum (FWHM) 15 ps, repetition rate 83.3 MHz, Tsunami, Spectra Physics). The two linearly polarized light beams are counter-propagating and are focused to the interaction region of the VMI spectrometer with their electric field vectors parallel to the face of the position-sensitive detector of the VMI spectrometer (see figure 2). The repetition rate of the laser is exactly 1/6 times the frequency of the synchrotron source, meaning that the laser pulses can be synchronized to every sixth synchrotron pulse, with one laser pulse every 12 ns compared to synchrotron light pulses every 2 ns [33]. By recording the ring clock in coincidence with the arrival time of the electron on the position-sensitive detector, it has been possible to filter an image corresponding to electrons produced in a time window of 400 ps around the presence of the laser in the interaction zone out of the entire laser pulse-to-pulse window of 12 ns (for further details see [32]). This allows for a significant improvement of the signal-to-noise ratio of the photoelectron image.
The processed images are centred and symmetrized for presentation. At this point, the image is inverted using the pBasex method introduced by Garcia et al [34] in order to recover the original three-dimensional (3D) distribution from the 2D projection recorded in the experiment. The pBasex method works by fitting the analytically known inverse Abel integrals of a set of basis functions (Legendre polynomials for the angular part and Gaussian functions for the radial part) to the 2D image. Further details of the data analysis are given in section 4.1.
Both light sources are sufficiently weak to not induce any multiphoton or intensity-related effects. The laser has an average power of 1 W at near peak gain of the crystal at about 800 nm (1.55 eV), which translates into 12 nJ of energy per pulse. The peak intensity of the IR laser is thus in the range of 106–107 W cm−2 depending on the precise focusing conditions, temporal pulse shape and laser power variations within the focal spot. This leads to the ponderomotive energy (which is a measure of the strength of the field) of Up < 6 × 10−7 eV. The synchrotron source is even weaker from the point of view of the field intensity, with 40 photons per pulse (2 × 1010 photons s−1 at 500 MHz repetition rate), which leads to pulse energies of the order of 10−16 J and thus to negligible ponderomotive energy. Since this is the case and since the duration of the pulses is long enough, so that both fields oscillate many times, the atom–light interaction can be treated perturbatively.
4. Results and discussion
4.1. Experimental two-photon angular distributions of electrons and the comparison to the calculated distributions
The PADs of the electrons emitted following photoionization of the 4 ⩽ n ⩽ 6 members of the He 1snp 1P series have been measured. In order to assess the effect of the principal quantum number of the intermediate state on the angular distribution, the total photon energy ℏω1 + ℏω2 has been kept constant while changing n. Therefore, the kinetic energy of the photoelectron remains constant (0.927 eV), and changes in the photoionization dynamics due to accessing a different point in the continuum could be eliminated. The β2 and β4 asymmetry parameters extracted from the corresponding three VMI images are shown in table 1, where they are compared to the theoretical values.
Table 1. Experimental and theoretical values of β2, β4, X and cosΔ for the two-photon ionization of the He atom proceeding through the 1snp 1P states (4 ⩽ n ⩽ 6). The kinetic energy of the ejected photoelectron is  = 0.927 eV.
= 0.927 eV.
| Experiment | Theory | |||||||
|---|---|---|---|---|---|---|---|---|
| β2 | β4 | X | cos Δ | β2 | β4 | X | cos Δ | |
| 1s4p | 2.95 ± 0.10 | 1.87 ± 0.10 | 0.55 ± 0.05 | −0.96±0.06 | 2.94 | 1.86 | 0.555 | −0.952 |
| 1s5p | 2.93 ± 0.10 | 1.77 ± 0.12 | 0.60 ± 0.06 | −0.94±0.06 | 2.95 | 1.81 | 0.582 | −0.952 |
| 1s6p | 2.76 ± 0.08 | 1.82 ± 0.18 | 0.57 ± 0.10 | −0.86±0.06 | 2.95 | 1.77 | 0.599 | −0.952 |
The second set of data was obtained by accessing the same intermediate state (the 1s5p 1P state) and changing the laser photon energy to probe different parts of the continuum. The electron kinetic energies, as well as β2 and β4 extracted from these images, are presented in table 2. In figure 3, a subset of the VMI images is shown in order to illustrate the data analysis. In particular, a series of images are shown corresponding to the ionization of the 1s5p state with laser photons of energy ℏω2 = 1.469 eV, where (a) shows the raw image, (b) the symmetrized image and (c) the inverted image produced by pBasex. Also shown in figure 3 is the VMI image for ionization of the 1s5p state with photons of energy ℏω2 = 1.772 eV (figure 3(d)) and the kinetic energy distributions extracted from both images (figures 3(e) and (f)). The inversion procedure has been described in detail previously [32, 34]. Additional checks have been performed during the analysis of these images by increasing the even orders of the Legendre polynomials used in the basis sets to q ⩽ 10. In this way, the unphysical parameters β6, β8 and β10 were extracted from the images and confirmed to be zero within the experimental error bars, thus showing that the images are indeed fully described by (6). Furthermore, it was noted that in the case where the β2 and β4 parameters fully describe the PAD, each quadrant of the image contains exactly the same information. To ensure that this is the case once the raw images were centred, each quadrant of the images was analysed independently using the pBasex method and the β2 and β4 parameters were extracted. The resulting values were used as a part of the error analysis and are thus contained within the error bars shown in tables 1 and 2. Other sources of errors, such as background subtraction, errors in the centring and the number of pixels within the PES peak used for β2 and β4 parameter determination were also included in the error analysis.
Figure 3. The velocity map images formed by exciting the ground state atom to the 1s5p 1P state (ℏω1 = 24.046 eV) and ionizing with laser radiation of photon energy (a)–(c) ℏω2 = 1.469 eV (λ = 844.07 nm,  = 0.927 eV) and (d) ℏω2 = 1.772 eV (λ = 699.85 nm,
= 0.927 eV) and (d) ℏω2 = 1.772 eV (λ = 699.85 nm,  = 1.230 eV). Images (a)–(c) are shown to illustrate the image analysis procedure (see the text for details), where image (a) is the raw image, (b) is the symmetrized image and (c) is the inverted image produced by pBasex. The photoelectron spectra extracted from these images using the pBasex inversion are shown in (e) and (f). The origin of the low-energy feature in (d) and (f) is discussed in section 4.2.
= 1.230 eV). Images (a)–(c) are shown to illustrate the image analysis procedure (see the text for details), where image (a) is the raw image, (b) is the symmetrized image and (c) is the inverted image produced by pBasex. The photoelectron spectra extracted from these images using the pBasex inversion are shown in (e) and (f). The origin of the low-energy feature in (d) and (f) is discussed in section 4.2.
Download figure:
Standard imageTable 2. Experimental and theoretical values of β2, β4, X and cos Δ for the two-photon ionization of the He atom proceeding through the 1s5p 1P state. The kinetic energy of the ejected photoelectron is denoted by  .
.
 (eV) (eV) |
Experiment | Theory | ||||||
|---|---|---|---|---|---|---|---|---|
| β2 | β4 | X | cos Δ | β2 | β4 | X | cos Δ | |
| 0.760 | 2.86 ± 0.16 | 1.78 ± 0.18 | 0.60 ± 0.10 | −0.91±0.07 | 2.99 | 1.81 | 0.581 | −0.970 |
| 0.927 | 2.93 ± 0.10 | 1.77 ± 0.12 | 0.60 ± 0.06 | −0.94±0.06 | 2.95 | 1.81 | 0.582 | −0.952 |
| 1.230 | 2.89 ± 0.09 | 1.69 ± 0.15 | 0.65 ± 0.08 | −0.92±0.05 | 2.88 | 1.80 | 0.585 | −0.917 |
The results of the calculations and the ratios and phase differences extracted from the experimental parameters using (7) and (8) are given in table 2 (the dependence of the parameters on the kinetic energy of the photoelectron for the 1s5p intermediate state) and in table 1 (the dependence of the parameters on the principal quantum for a fixed energy of the photoelectron).
The calculated phase differences between the outgoing 1s s and 1s
s and 1s d waves are plotted against the photoelectron energy in figure 4 for energies reaching up to 4.0 eV above the ionization threshold. These values are compared to the parameters extracted from the experimentally determined asymmetry parameters for ionization of the 1s4p, 1s5p and 1s6p states with different laser wavelengths by inverting (7) and (8). In addition to the phase difference determined in this work, also the results of Haber et al [13] for ionization of the 1s3p and 1s4p states, where the outgoing electrons had kinetic energies between 0.04 and 3.14 eV, are shown in figure 4. As mentioned above, the phase difference does not depend on the principal quantum number of the intermediate state as it is a property that is intrinsic to the continuum wavefunctions. Therefore, the phase differences determined from the photoionization of the 1s3p, 1s4p, 1s5p and 1s6p states can all be compared to the same theoretical curve. The results of [13] span a wider energy range than in the present case since different harmonics of the laser were used for the ionization of the intermediate states in [13]. The results of [13] agree very well with the theory. While the values determined in this work also agree quite well, there are some values that do not agree within the errors, in particular the value extracted for the 1s6p state. Possible explanations for this discrepancy are explored in the following subsections.
d waves are plotted against the photoelectron energy in figure 4 for energies reaching up to 4.0 eV above the ionization threshold. These values are compared to the parameters extracted from the experimentally determined asymmetry parameters for ionization of the 1s4p, 1s5p and 1s6p states with different laser wavelengths by inverting (7) and (8). In addition to the phase difference determined in this work, also the results of Haber et al [13] for ionization of the 1s3p and 1s4p states, where the outgoing electrons had kinetic energies between 0.04 and 3.14 eV, are shown in figure 4. As mentioned above, the phase difference does not depend on the principal quantum number of the intermediate state as it is a property that is intrinsic to the continuum wavefunctions. Therefore, the phase differences determined from the photoionization of the 1s3p, 1s4p, 1s5p and 1s6p states can all be compared to the same theoretical curve. The results of [13] span a wider energy range than in the present case since different harmonics of the laser were used for the ionization of the intermediate states in [13]. The results of [13] agree very well with the theory. While the values determined in this work also agree quite well, there are some values that do not agree within the errors, in particular the value extracted for the 1s6p state. Possible explanations for this discrepancy are explored in the following subsections.
Figure 4. Phase difference between the outgoing 1s s and 1s
s and 1s d waves as a function of the kinetic energy
d waves as a function of the kinetic energy  of the photoelectron. The solid line shows the calculated phase difference, the open circles are the present experimentally determined values (see tables 1 and 2) and the filled triangles are the values from [13] (photoionization of atoms in the 1s3p and 1s4p states).
of the photoelectron. The solid line shows the calculated phase difference, the open circles are the present experimentally determined values (see tables 1 and 2) and the filled triangles are the values from [13] (photoionization of atoms in the 1s3p and 1s4p states).
Download figure:
Standard imageThe calculated ratios of radial integrals of the dipole matrix elements to the 1s s and 1s
s and 1s d channels are plotted against photoelectron kinetic energy in figure 5 (see section 2 for details of the calculation). The experimental values extracted in this work for the 1s4p, 1s5p and 1s6p states, as well as those for the 1s3p and 1s4p intermediate states taken from [13], are plotted in the same figure. In contrast to the phase difference, the ratio X does depend on the identity of the intermediate state and, in the energy region experimentally investigated, increases with n. Furthermore, the values of X vary only very slowly with the kinetic energy of the photoelectron in the region under investigation in this work. The calculated values of the ratios fall within the error bars of the values extracted from the measurements in all but one case: for the ratio extracted from the angular distribution following photoionization of the 1s4p state for 0.7 eV electrons (from [13]). However, the error bars of all points are larger than the differences between the ratios pertaining to different intermediate states. Therefore, while the comparison between experiment and theory is consistent, it cannot be concluded that the variation of X as a function of n can be experimentally confirmed.
d channels are plotted against photoelectron kinetic energy in figure 5 (see section 2 for details of the calculation). The experimental values extracted in this work for the 1s4p, 1s5p and 1s6p states, as well as those for the 1s3p and 1s4p intermediate states taken from [13], are plotted in the same figure. In contrast to the phase difference, the ratio X does depend on the identity of the intermediate state and, in the energy region experimentally investigated, increases with n. Furthermore, the values of X vary only very slowly with the kinetic energy of the photoelectron in the region under investigation in this work. The calculated values of the ratios fall within the error bars of the values extracted from the measurements in all but one case: for the ratio extracted from the angular distribution following photoionization of the 1s4p state for 0.7 eV electrons (from [13]). However, the error bars of all points are larger than the differences between the ratios pertaining to different intermediate states. Therefore, while the comparison between experiment and theory is consistent, it cannot be concluded that the variation of X as a function of n can be experimentally confirmed.
Figure 5. The calculated (solid line) and experimentally determined (empty symbols) dependence of the ratio X on the kinetic energy of the photoelectron  . Also shown are the results of Haber et al [13] (filled symbols).
. Also shown are the results of Haber et al [13] (filled symbols).
Download figure:
Standard image4.2. Analysis of the cascade states
Possibly the most surprising feature of the image in figure 3(d) is an inner ring that appears in addition to the outer ring. Each of these rings represents photoelectrons emitted with different kinetic energies, as can be seen from the photoelectron spectra extracted from the images in figures 3(e) and (f). Kinetic energy calibration of the image reveals that this peak corresponds to photoionization of atoms in an excited state with the energy of 22.91 ± 0.03 eV above the ground state. The only accessible state in this energy region lying within the energy uncertainty is the 1s3s 1S state, which can be reached from the 1s5p state by spontaneous decay. An atom in the 1s3s state can be subsequently ionized, i.e. the absorption–spontaneous emission–absorption process is described by:
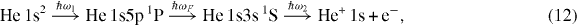
where ℏωF is the energy of the emitted photon. An excited state with the energy which corresponds to the 1s3s state is again observed in the case of ionization of the 1s4p 1P state with laser light of ℏω2 = 1.772 eV. In the 1s4p case, the intensity of the 1s3s peak is 11% of the intensity of the main photoelectron line, while in the 1s5p case, this intensity rises to 13%. Within the present detection limit, ionization signal from no other cascade state has been observed.
Considering that the ionization of the 1s3s 1S state is observed quite clearly, it is somewhat surprising, at first glance, that photoionization signals of the 1s3d 1D and 1s4s 1S states are not observed, even though radiative decay to these states is allowed and they are energetically accessible to ionization by the laser. In order to understand why the apparent asymmetry between the 1s3s, 1s3d and 1s4s states arises, we modify the model which takes into account the pulsed nature of the sources used by Žitnik et al [35].
Upon repetitive pulsed excitation with synchrotron light, the number of atoms Nnℓ in the 1snℓ state displays a periodic oscillation around some equilibrium value with an amplitude which goes to zero when the lifetime of the 1snℓ state τnℓ becomes much longer than the pulse repetition time t0. The number of atoms is given by an infinite series of Gale's functions:

where the functions αp(t) and βp(t) are


and where excitation with a Gaussian pulse of duration 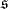 (standard width) has been assumed. The photo-excited 1snℓ state decays to lower-lying 1sn'ℓ' states, which is described by branching ratios Bnℓ,n'ℓ'. Since the lower-lying states have finite lifetimes τn'ℓ', the number of atoms in the 1sn'ℓ' states is described by the following rate equation:
(standard width) has been assumed. The photo-excited 1snℓ state decays to lower-lying 1sn'ℓ' states, which is described by branching ratios Bnℓ,n'ℓ'. Since the lower-lying states have finite lifetimes τn'ℓ', the number of atoms in the 1sn'ℓ' states is described by the following rate equation:

When τn'ℓ' ≫ τnℓ, the relative number of atoms in the 1sn'ℓ' state with respect to the number of atoms in the 1snℓ state may be considerably higher than predicted by the single-atom (single-pulse) branching ratio Bnℓ,n'ℓ' (see figure 6(a)). At times q t0 which coincide with the centres of the synchrotron pulses, the ratio becomes
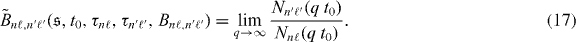
Finally, the relative intensities of the photoelectron peaks at the selected laser wavelength can be estimated from the ratio of the number of atoms in the two intermediate excited states 1snℓ and 1sn'ℓ' if the ratio of the corresponding photoionization cross sections is known:

Care should be taken when calculating the photoionization cross-sections used in (18). In the present case, the σnp cross-sections (i.e. σnℓ for ℓ = 1) include only the contributions from the M = 0 1snp states since these are the states directly accessible by absorption of the synchrotron photon. The cross-sections σn's (σn'ℓ' for ℓ' = 0)—which denote the photoionization cross-sections for the 1sn's states accessible through the radiative decay of the 1snp states—also comprise only the M = 0 component since this is the only possible projection for the total angular momentum L = 0. On the other hand, the 1sn'd states accessible in the radiative decay can have −1 ⩽ M ⩽ 1, so that the σn'd cross-sections include the contributions from all the 1sn'd states with projections |M| ⩽ 1.
Figure 6. (a) The number of atoms N5p and N3s in the excited 1s5p and 1s3s states, respectively, upon excitation of the target with the pulsed synchrotron light (starting at t = 0, with 2 ns repetition time and 0.12 ns pulse width) tuned to the 1s5p state. The effective branching ratio 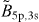 rises with time and stabilizes at a value about an order of magnitude larger than the single atom branching ratio B5p,3s. (b) The total photoionization cross-sections σnp, σn's and σn'd (see text) for linearly polarized laser light (polarization along the z-axis). The experimental laser photon energy ℏω2 = 1.772 eV is marked with a dashed vertical line.
rises with time and stabilizes at a value about an order of magnitude larger than the single atom branching ratio B5p,3s. (b) The total photoionization cross-sections σnp, σn's and σn'd (see text) for linearly polarized laser light (polarization along the z-axis). The experimental laser photon energy ℏω2 = 1.772 eV is marked with a dashed vertical line.
Download figure:
Standard imageInserting the values from table 3, we estimate I3s/I4p = 9.9% and I3s/I5p = 12.8% at ℏω2 = 1.772 eV, close to the reported experimental values (11 and 13%, respectively). This result is not very sensitive to the precise duration of light pulses involved since the pulse repetition time t0 and the lifetimes of the states involved are much longer. According to our simulation, at 1.772 eV laser photon energy, the intensity of the 1s4s ionization signal (at photoelectron kinetic energy  = 858 meV) is expected to be four times lower than the 1s3s ionization signal (at
= 858 meV) is expected to be four times lower than the 1s3s ionization signal (at  = 105 meV) when the synchrotron light is tuned to the 1s5p resonance (table 3). As seen in figure 3(f), such an intensity is just at the detection limit of the present experiment. On the other hand, the 1s3d ionization signal (expected at
= 105 meV) when the synchrotron light is tuned to the 1s5p resonance (table 3). As seen in figure 3(f), such an intensity is just at the detection limit of the present experiment. On the other hand, the 1s3d ionization signal (expected at  = 259 meV) falls below the detection limit—although the photoionization cross-section ratio σ3d/σ5p is similar to σ3s/σ5p (see table 3 and figure 6(b)), the effective branching ratio is much smaller (
= 259 meV) falls below the detection limit—although the photoionization cross-section ratio σ3d/σ5p is similar to σ3s/σ5p (see table 3 and figure 6(b)), the effective branching ratio is much smaller (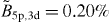 ) because of the relatively short τ3d and the small branching ratio B5p,3d.
) because of the relatively short τ3d and the small branching ratio B5p,3d.
Table 3. Single-atom fluorescence decay branching ratios Bnp,n'ℓ' for the 1snp → 1sn's (n' = 3,4) and 1snp → 1sn'd (n' = 3) spontaneous dipole transitions and the corresponding effective values 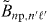 for the ground state photoexcitation to the 1snp states with a pulsed synchrotron light source (pulse repetition time t0 = 2 ns; Gaussian pulse width
for the ground state photoexcitation to the 1snp states with a pulsed synchrotron light source (pulse repetition time t0 = 2 ns; Gaussian pulse width 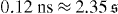 ). Also given is the ratio of the total photoionization cross-sections σn'ℓ'/σnp for photon energy ℏω2 = 1.772 eV (see the text for details).
). Also given is the ratio of the total photoionization cross-sections σn'ℓ'/σnp for photon energy ℏω2 = 1.772 eV (see the text for details).
| n'ℓ' | τn'ℓ' (ns) | 4p (τ4p=3.97 ns) | 5p (τ5p=7.63 ns) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| B4p,n'ℓ' (%) | 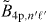 (%) (%) |
σn'ℓ'/σ4p | In'ℓ'/I4p (%) | B5p,n'ℓ' (%) | 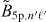 (%) (%) |
σn'ℓ'/σ5p | In'ℓ'/I5p (%) | ||
| 3s | 54.7 | 0.56 | 7.65 | 1.29 | 9.9 | 0.71 | 5.14 | 2.49 | 12.8 |
| 3d | 15.7 | 0.12 | 0.47 | 3.70 | 1.7 | 0.10 | 0.20 | 7.17 | 1.4 |
| 4s | 88.0 | 0.02 | 0.51 | 0.63 | 0.3 | 0.22 | 2.64 | 1.21 | 3.2 |
As has been explained, the 1sn'd states accessible in the spontaneous decay of the 1snp states may have projections of the orbital angular momentum which differ from zero. This 'depolarization' of the target does, in principle, break the cylindrical symmetry of the PADs. However, as can be seen in table 3, the intensity of the 1s3d ionization signal is low, and its influence on the PADs is not observed in the case of the 1s4p and 1s5p intermediate states. Note that for the 1s6p state, no experimental data exist for ℏω2 = 1.772 eV and that the photon energy of 1.303 eV—for which the angular distributions have been recorded—is not sufficient to ionize atoms in the 1s3d states. However, our calculations show that the intensity ratios I4d/I6p and I5d/I6p for ℏω2 = 1.303 eV are of the order of 1%, which is again below the detection limit.
4.3. Effect of a static electric field on the measured photoelectron angular distributions
In a VMI spectrometer, the photoelectrons are generated in a region where a static electric field of typically a few hundreds of volts per cm (in the present case 340 V cm−1) is present. Thus, it is important to consider whether or to what extent this field may modify the measured PADs. In order to examine the effect of this static electric field, we first note that, for the field strengths of interest here, the ground state remains completely unaffected by the field due to the large energy separation from the excited states. Since the field 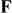 in the interaction region is perpendicular to the polarization of the incident light (
in the interaction region is perpendicular to the polarization of the incident light (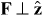 ), it couples field-free states with different projections of the total angular momentum. Using the first-order perturbation theory, the 1snp intermediate state |ν〉 is coupled to the states |ρ〉:
), it couples field-free states with different projections of the total angular momentum. Using the first-order perturbation theory, the 1snp intermediate state |ν〉 is coupled to the states |ρ〉:

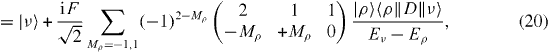
where 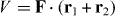 describes the atom–field interaction and 〈ρ∥D∥ν〉 is the reduced dipole matrix element. We have assumed that
describes the atom–field interaction and 〈ρ∥D∥ν〉 is the reduced dipole matrix element. We have assumed that 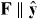 and have taken into account that Mν = 0. To the lowest order in F, the singly excited states coupled to the selected 1snp state are the 1sn'd states. Since the inter-manifold energy separation is relatively large, we consider only the case where n' = n, since we expect this coupling to be strongest.
and have taken into account that Mν = 0. To the lowest order in F, the singly excited states coupled to the selected 1snp state are the 1sn'd states. Since the inter-manifold energy separation is relatively large, we consider only the case where n' = n, since we expect this coupling to be strongest.
The generalized photoionization cross-section is proportional to

where the accessible partial waves are those with λ = μ = 0, S = MS = 0, L = ℓ, ML = m and μs = −ms. This means that in addition to the 1s s and 1s
s and 1s d waves, the 1s
d waves, the 1s p and 1s
p and 1s f waves also become accessible through the admixture of the 1snd state.
f waves also become accessible through the admixture of the 1snd state.
Since the field is perpendicular to the polarization vectors, the angular distribution no longer possesses cylindrical symmetry. As a consequence, the differential cross-section is parametrized as

From the fact that the cross-section is real valued, it follows that 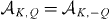 . It is convenient to introduce generalized asymmetry parameters
. It is convenient to introduce generalized asymmetry parameters

so that β2 = β20 and β4 = β40.
The dependence of the calculated magnitudes of the non-zero parameters βKQ on the field strength for the 1s6p 1P intermediate state is shown in figure 7. As can be seen, the coefficients β20 and β40 are about two orders of magnitude larger than the other coefficients for F ∼ 0.34 kV cm−1. This means that the contributions of the higher-order (K > 4) terms, as well as the terms which describe the dependence on the azimuthal angle (Q ≠ 0), lie below the sensitivity of the experiment. Similar results have also been obtained for the 1s4p and 1s5p states. Generally speaking, the influence of the electric field increases with n. However, as shown above, even for the case of the highest n state investigated here, n = 6, the static electric field in the interaction region in this experiment has a negligible effect on the measured PADs.
Figure 7. The magnitudes of the generalized asymmetry parameters βKQ for the 1s6p intermediate state.
Download figure:
Standard image5. Summary and conclusions
The β2 and β4 parameters of the electrons emitted in photoionization of aligned n = 4, 5 and 6 members of the He 1snp 1P series have been measured using a combination of synchrotron and laser radiation. The photoelectron kinetic energy has been varied by changing the wavelength of the ionizing laser light. The experimental parameters which describe the angular distributions of the photoelectrons were related to the phase difference between the 1s s and 1s
s and 1s d partial waves and to the ratio of the radial integrals of the dipole matrix elements connecting the intermediate states to the 1s
d partial waves and to the ratio of the radial integrals of the dipole matrix elements connecting the intermediate states to the 1s s and 1s
s and 1s d continua. These parameters have been evaluated theoretically for the 1snp 1P (2 ⩽ n ⩽ 6) intermediate states. The calculated values of the phase differences and the ratios generally agree well with the experimentally determined values found in this work, although there is an exception for the Δ value extracted from the PAD of the 1s6p state which lies off the calculated phase shift curve even taking into account the errors.
d continua. These parameters have been evaluated theoretically for the 1snp 1P (2 ⩽ n ⩽ 6) intermediate states. The calculated values of the phase differences and the ratios generally agree well with the experimentally determined values found in this work, although there is an exception for the Δ value extracted from the PAD of the 1s6p state which lies off the calculated phase shift curve even taking into account the errors.
Near the ionization threshold, the emission of the 1s d wave dominates, whereas at higher photoelectron energies, the 1s
d wave dominates, whereas at higher photoelectron energies, the 1s s wave becomes more important than close to the threshold. The ratios X may be seen to increase with the principal quantum number n of the intermediate state near the threshold, but converge to a similar value as the photoelectron energy increases. The phase difference is dominated by the Coulomb shift with only a small contribution from the non-Coulomb (scattering) phase shift. Thus, the decrease of Δ with increasing electron kinetic energy in the near-threshold region is mainly due to the change of the Coulomb shift.
s wave becomes more important than close to the threshold. The ratios X may be seen to increase with the principal quantum number n of the intermediate state near the threshold, but converge to a similar value as the photoelectron energy increases. The phase difference is dominated by the Coulomb shift with only a small contribution from the non-Coulomb (scattering) phase shift. Thus, the decrease of Δ with increasing electron kinetic energy in the near-threshold region is mainly due to the change of the Coulomb shift.
It has been shown that the low-energy photoelectron peaks appearing in the photoelectron spectra for the 1s4p and 1s5p intermediate states for the laser energy of 1.772 eV may be attributed to photoionization of atoms in the 1s3s state. This state is formed by population pooling due to radiative decay of the intermediate states. Other accessible states (1s4s and 1s3d in particular) are not observed due to a combination of the radiative decay branching ratios of the intermediate state, the lifetimes of the states formed and the relative photoionization cross-sections, resulting in the electron yield below the detection limit of the present experiment.
Furthermore, the effect of the static electric field of the VMI spectrometer is discussed in detail from a theoretical point of view and is found to have negligible effects on the measured photoelectron distribution for the intermediate states considered here. It is concluded that neither a possible depolarization due to fluorescence decay of the intermediate states nor the static electric field effects are responsible for the discrepancy between theory and experiment for the 1s6p state.
Acknowledgments
This research was partly supported by the Italy–Slovenia joint research project 'Dynamics at nanoscale' and by PRIN 2009W2W4YF and 2009SLKFEX. AM and MŽ acknowledge financial support from the Slovenian Ministry of Education, Science, Culture and Sport (research program no. P1-0112).









