Abstract
Nonlinearity and disorder in discrete systems give rise to fascinating dynamics in various fields of physics. Photonic lattices allow investigation of them in an optical context. The very nature of discrete propagation allows perfect reconstruction of arbitrary initial wave packets by introducing phase shifts to specific lattice sites. We investigate, both numerically and experimentally, the interplay of nonlinearity with this so-called segmentation imaging in the presence of disorder. We find that whereas in the linear regime perfect imaging is achieved for arbitrary amounts of coupling disorder, the onset of nonlinear self-focusing generally destroys imaging. Interestingly, the influence of Anderson localization in strongly disordered lattices renders the imaging significantly more susceptible to nonlinear perturbations.
Export citation and abstract BibTeX RIS
1. Introduction
One of the key tasks in optics is imaging: the faithful reconstruction of the input light distribution at the output of the transmission system. Arrays of evanescently coupled waveguides, so-called photonic lattices [1], offer several possibilities to tackle this challenge in the field of discrete optics. Exploiting the analogy to the ordered structure of crystals, it is possible to mimic self-imaging solid state phenomena such as discrete harmonic oscillation [2], Bloch oscillations [3], dynamic localization [4] and coherent destruction of tunneling [5]. However, this approach relies on imprinting specific external potentials [6] on the otherwise homogeneous system and consequently requires a high accuracy in fabrication. An alternative method makes use of the very nature of discrete propagation. By staggering the phases of adjacent waveguides at half the desired propagation distance, a wave packet's evolution can be reversed, giving rise to a perfect reconstruction of the initial field distribution. This phase shift can be readily introduced by segmentation [7]. Recent investigations have shown that segmentation-based imaging persists for arbitrary amounts of disorder within the lattice, provided that the individual waveguides are identical ('off-diagonal' disorder) [8, 9]. Consequently, segmentation imaging is inherently robust to fabrication tolerances.
A fascinating aspect of disordered systems is Anderson localization [10]. Whereas each eigenmode of a homogeneous lattice spans the entirety of its transverse dimensions, disorder decreases the mean width of the supermodes. Hence, a narrow excitation yields significant occupation in fewer supermodes than it would in the corresponding homogeneous system. Consequently, the diffractive broadening of a launched wave packet is impeded compared to the uniform lattice. Since its discovery over 50 years ago, Anderson localization has been explored in a variety of physical systems [11] and under both on-diagonal [10] and off-diagonal manifestations of disorder [12]. In contrast to higher-dimensional systems, which undergo a transition from ballistic to diffusive transport before finally exhibiting Anderson localization above a certain level of disorder, one-dimensional disordered configurations show localization for any non-zero disorder [12]. Generally, the width of the localized states decreases with the degree of disorder.
Localization of wave packets may also occur due to nonlinear self-focusing. Giving rise to the so-called discrete solitons, the propagation of light in nonlinear photonic lattices has been the focus of intensive research [13–15]. The interplay of nonlinearity and disorder in such systems has been the subject of theoretical [16, 17] as well as experimental [18–20] efforts. More recently, the influence of dimensionality crossover [21] as well as nonlinear interfaces [22] on Anderson localization was investigated.
A particularly fruitful platform for experimental investigations of discrete solitons is provided by femtosecond laser-written [23] arrays of waveguides [24]. Interestingly, linear and nonlinear localization mechanisms may mutually impede each other, as was demonstrated for dynamic localization [25] and solitons in disordered lattices [16].
The question arises as to how the self-imaging property of segmented waveguide arrays is impacted by nonlinear propagation effects and whether disorder may serve to stabilize it by virtue of Anderson localization. In this paper, we investigate this notion for the case of positive Kerr nonlinearity numerically as well as experimentally in laser-written waveguide arrays. We find that self-focusing distorts the imaging in both homogeneous and disordered lattices before tightly localized solitons emerge at high powers. Surprisingly, the presence of localized Anderson modes renders the self-imaging significantly more susceptible to nonlinear perturbations.
2. Numerical investigation
The propagation of light in photonic lattices is governed by a set of coupled differential equations [1] for the modal amplitudes φn in the individual waveguides:
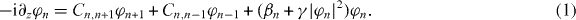
In this so-called discrete nonlinear Schrödinger equation, Ck,ℓ = Cℓ,k are the symmetric coupling coefficients between adjacent waveguides. Finite lattices are described by limiting the waveguide index to a certain range, e.g. n∈[1,N], and consequently C1,0 = CN,N+1 = 0. The propagation constants in the individual waveguides are described by βn, which in the case of identical guides can be removed by transformation into a co-propagating reference frame. The strength of the focusing Kerr nonlinearity is given by the coefficient γ. The total power 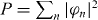 is a conserved quantity of equation (1). To model the evolution of a wave packet, we numerically solve the initial value problem given by the input field distribution φn(0). In the case of segmented arrays we introduced the phase flip at half the propagation distance: φn(L/2) → einπφn(L/2). Disorder was realized by assigning uniformly distributed values to the coupling coefficients
is a conserved quantity of equation (1). To model the evolution of a wave packet, we numerically solve the initial value problem given by the input field distribution φn(0). In the case of segmented arrays we introduced the phase flip at half the propagation distance: φn(L/2) → einπφn(L/2). Disorder was realized by assigning uniformly distributed values to the coupling coefficients ![$C\in [\bar {C}-\sigma ,\bar {C}+\sigma ]$](https://content.cld.iop.org/journals/1367-2630/14/7/073026/revision1/nj431708ieqn2.gif) , where
, where 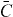 is the mean coupling constant and the width σ of the distribution is a measure of the degree of disorder. Values of
is the mean coupling constant and the width σ of the distribution is a measure of the degree of disorder. Values of ![$\sigma \in [0,0.8\bar{C}]$](https://content.cld.iop.org/journals/1367-2630/14/7/073026/revision1/nj431708ieqn4.gif) were considered to avoid zero (or near-zero) couplings while maintaining the mean value for all distributions.
were considered to avoid zero (or near-zero) couplings while maintaining the mean value for all distributions.
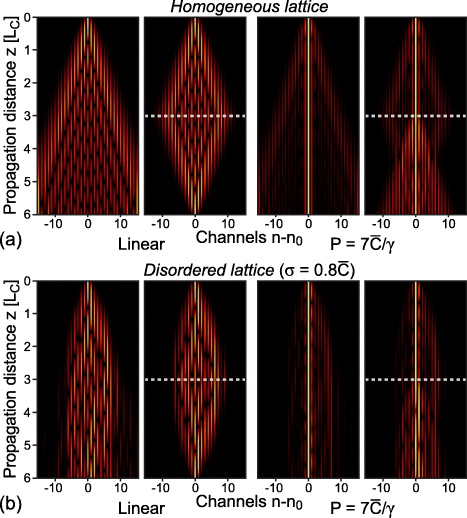
Figure 1(a) illustrates the propagation of light in a homogeneous lattice comprised of N = 31 waveguides over a distance of six coupling lengths 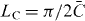 . In the linear regime (P → 0), a single-site excitation of the central channel yields the V-shaped pattern characteristic of discrete diffraction (first panel), whereas the segmented array facilitates self-imaging (second panel). In contrast, an input power of
. In the linear regime (P → 0), a single-site excitation of the central channel yields the V-shaped pattern characteristic of discrete diffraction (first panel), whereas the segmented array facilitates self-imaging (second panel). In contrast, an input power of  is sufficient for exciting a narrowly confined soliton, which emerges after a certain fraction of the light is radiated away as diffractive background (third panel). Interestingly, the soliton essentially shatters as it encounters a phase flip (fourth panel). This effect can be understood by considering that for focusing Kerr nonlinearity (γ > 0), the soliton resides in the semi-infinite gap above the propagation band and exhibits a smooth phase front [15]. Thus, the imposed staggered phase results in substantial amounts of light being radiated into the lattice before the wave packet can reshape itself to conform with the profile of a lower-power soliton. Consequently, the imaging is distorted as soon as the Kerr effect leads to appreciable deviations from the phase distributions in the linear regime.
is sufficient for exciting a narrowly confined soliton, which emerges after a certain fraction of the light is radiated away as diffractive background (third panel). Interestingly, the soliton essentially shatters as it encounters a phase flip (fourth panel). This effect can be understood by considering that for focusing Kerr nonlinearity (γ > 0), the soliton resides in the semi-infinite gap above the propagation band and exhibits a smooth phase front [15]. Thus, the imposed staggered phase results in substantial amounts of light being radiated into the lattice before the wave packet can reshape itself to conform with the profile of a lower-power soliton. Consequently, the imaging is distorted as soon as the Kerr effect leads to appreciable deviations from the phase distributions in the linear regime.
Figure 1. (a) Left to right: simulated linear propagation, segmentation imaging, nonlinear propagation at  and nonlinear delocalization at
and nonlinear delocalization at 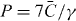 in a homogeneous array of N = 31 waveguides. (b) The corresponding panels for an exemplary realization of a disordered lattice with couplings uniformly distributed across the interval
in a homogeneous array of N = 31 waveguides. (b) The corresponding panels for an exemplary realization of a disordered lattice with couplings uniformly distributed across the interval ![$[\bar {C}-\sigma ,\bar {C}+\sigma ]$](https://content.cld.iop.org/journals/1367-2630/14/7/073026/revision1/nj431708ieqn9.gif) with
with  . In all cases the total propagation length is 6 LC, and segmentations are indicated by dashed lines.
. In all cases the total propagation length is 6 LC, and segmentations are indicated by dashed lines.
Download figure:
Standard imageThe corresponding behavior of light in an exemplary realization of a disordered lattice with 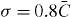 is shown in figure 1(b). The linear propagation patterns clearly illustrate how the transverse transport is inhibited in the regime of Anderson localization (first panel) and that segmentation imaging persists [9] (second panel). Similar to the homogeneous lattice, a tightly confined soliton is excited at
is shown in figure 1(b). The linear propagation patterns clearly illustrate how the transverse transport is inhibited in the regime of Anderson localization (first panel) and that segmentation imaging persists [9] (second panel). Similar to the homogeneous lattice, a tightly confined soliton is excited at  (third panel). Note that the diffractive background also remains Anderson localized in the vicinity of the excited guide. Interestingly, the introduction of the phase flip results in a weaker broadening of the emerging wave packet compared to the linear case (fourth panel).
(third panel). Note that the diffractive background also remains Anderson localized in the vicinity of the excited guide. Interestingly, the introduction of the phase flip results in a weaker broadening of the emerging wave packet compared to the linear case (fourth panel).
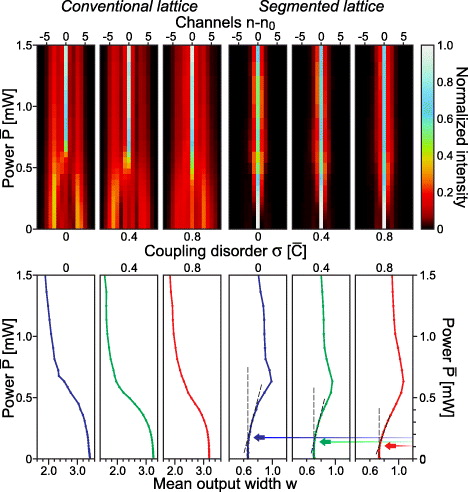
We systematically explore the power dependence of the output mean width

arising from single-site excitations at waveguide n0 in lattices with varying disorder. To ensure statistically meaningful results, we generated sets of R = 100 realizations for each σ and evaluated the averaged intensity patterns after a propagation distance of 6LC. The upper part of figure 2 illustrates how the ensemble-averaged output patterns for the homogeneous lattice as well as intermediate 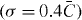 and strong
and strong 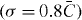 disorder change with increasing power. The initially broad light distribution in the conventional homogeneous lattice contracts abruptly around a normalized input power of
disorder change with increasing power. The initially broad light distribution in the conventional homogeneous lattice contracts abruptly around a normalized input power of 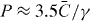 . In contrast, more power is required in the disordered systems to form a tightly localized soliton regardless of the intrinsically narrower spread in the linear regime (left group of panels). Note that despite a more gradual localization behavior, the output pattern in the disordered lattices starts to contract at lower powers. The corresponding behavior in segmented lattices is shown in the right group of panels. Surprisingly, for the disordered systems nonlinear delocalization occurs at lower powers. Furthermore, in the disordered systems substantially higher powers are required to excite solitons, which are sufficiently localized to become impervious to delocalization.
. In contrast, more power is required in the disordered systems to form a tightly localized soliton regardless of the intrinsically narrower spread in the linear regime (left group of panels). Note that despite a more gradual localization behavior, the output pattern in the disordered lattices starts to contract at lower powers. The corresponding behavior in segmented lattices is shown in the right group of panels. Surprisingly, for the disordered systems nonlinear delocalization occurs at lower powers. Furthermore, in the disordered systems substantially higher powers are required to excite solitons, which are sufficiently localized to become impervious to delocalization.
Figure 2. Top: calculated power-dependent mean (100 realizations) output intensity distributions from a conventional lattice after a propagation distance of 6LC for zero, intermediate and high disorder (left group). The corresponding behavior in the segmented lattice (right group). For reasons of visibility, the intensity distributions have been normalized with respect to their maxima of each row. Bottom: dependence of the mean (100 realizations) output intensity distribution's width w after a propagation distance of 6LC on input power P and degree of disorder σ. Left: conventional lattice; right: segmented lattice.
Download figure:
Standard imageThe dependence of the mean output width on power and disorder is shown in the lower part of figure 2 in more detail. Here, w is visualized as a false color plot with blue resembling broad distributions and red a narrow output. The plot for the conventional system (left panel) clearly demonstrates the impact of Anderson localization (i.e. decreasing w for growing disorder at a fixed power) and soliton formation (i.e. decreasing w for growing power at a fixed disorder). Likewise, the nonlinear delocalization in the segmented system (right panel) is apparent. Remarkably, despite the earlier onset of delocalization for higher disorder, Anderson localization allows the ejected light to spread less widely across the lattice for strong disorder, resulting in a lower maximum width.
3. Experimental results
Based on our theoretical results, we expect segmentation imaging in disordered lattices to be more susceptible to nonlinear perturbations. In order to verify our findings, we fabricated conventional as well as segmented photonic lattices with vanishing (σ = 0), intermediate  and strong
and strong 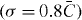 disorder. For each of the two latter cases, ten independent realizations of coupling distributions were examined. The individual coupling coefficients were implemented by adjusting the waveguide separation [26]. In all cases, the sample length of 100 mm corresponded to 1.28LC mean coupling lengths for
disorder. For each of the two latter cases, ten independent realizations of coupling distributions were examined. The individual coupling coefficients were implemented by adjusting the waveguide separation [26]. In all cases, the sample length of 100 mm corresponded to 1.28LC mean coupling lengths for 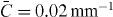 . A Ti:sapphire laser system (Spectra Physics Tsunami/Spitfire), delivering 300 fs pulses with a repetition rate of 1 kHz at a carrier wavelength of λ = 800 nm, was used for single-site excitation. The waveguides were segmented over a distance of 5.2 mm to achieve optimum imaging [7]. We recorded the output intensity distributions arising from injected average powers between
. A Ti:sapphire laser system (Spectra Physics Tsunami/Spitfire), delivering 300 fs pulses with a repetition rate of 1 kHz at a carrier wavelength of λ = 800 nm, was used for single-site excitation. The waveguides were segmented over a distance of 5.2 mm to achieve optimum imaging [7]. We recorded the output intensity distributions arising from injected average powers between  . The upper panel of figure 3 shows the ensemble-averaged output patterns within the conventional (left group) and segmented (right group) lattices. Note that dynamic excitation effects generally prevent complete localization and give rise to a diffractive background even at powers sufficient to suppress coupling at the pulse center [27]. Furthermore, imperfections in the segmented waveguides lead to a non-unity fidelity of imaging even in the linear regime. This effect becomes more visible for higher degrees of disorder as the non-imaged parts of the wave function remain in closer proximity of the initial excitation due to Anderson localization. Despite these limitations, the principal behavior of the system agrees well with the theoretical predictions for continuous wave conditions. While nonlinear localization occurs at lower powers in disordered conventional lattices, nonlinear delocalization is substantially accelerated in the corresponding segmented systems. The widths according to equation (2) of the ensemble-averaged intensity distributions are shown in the lower part of figure 3. The onset of nonlinear delocalization, highlighted by arrows, occurs at
. The upper panel of figure 3 shows the ensemble-averaged output patterns within the conventional (left group) and segmented (right group) lattices. Note that dynamic excitation effects generally prevent complete localization and give rise to a diffractive background even at powers sufficient to suppress coupling at the pulse center [27]. Furthermore, imperfections in the segmented waveguides lead to a non-unity fidelity of imaging even in the linear regime. This effect becomes more visible for higher degrees of disorder as the non-imaged parts of the wave function remain in closer proximity of the initial excitation due to Anderson localization. Despite these limitations, the principal behavior of the system agrees well with the theoretical predictions for continuous wave conditions. While nonlinear localization occurs at lower powers in disordered conventional lattices, nonlinear delocalization is substantially accelerated in the corresponding segmented systems. The widths according to equation (2) of the ensemble-averaged intensity distributions are shown in the lower part of figure 3. The onset of nonlinear delocalization, highlighted by arrows, occurs at 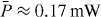 in the uniform case. The presence of disorder decreases this threshold to
in the uniform case. The presence of disorder decreases this threshold to  for
for 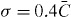 and
and  for
for 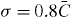 .
.
Figure 3. Top: measured power-dependent mean (ten experimental realizations) output intensity distributions from a conventional lattice after a propagation distance of 1.28LC for zero, intermediate and high disorder (left group). The corresponding behavior in the segmented lattice (right group). For reasons of visibility, the intensity distributions have been normalized with respect to their overall maxima. Bottom: power-dependent width of the mean output intensity. The arrows indicate the onset of delocalization in the segmented lattices.
Download figure:
Standard image4. Interpretation
Nonlinear phase contributions perturb segmentation imaging as light propagation can no longer be described by a superposition of the system's linear eigenmodes. In turn, segmentation introduces a phase distortion which shatters nonlinearly localized wave packets. The general interplay of these two competing mechanisms is valid for uniform as well as disordered lattices. However, a growing degree of disorder increasingly confines the eigenmodes (see exemplary amplitude profiles in figure 4(a)) and hence lowers the number of participating lattice sites. Conversely, the excitation of a single lattice site effectively results in the population of fewer states and thus a narrower maximum spread of the evolving wave packet. Consequently, a given total power induces larger nonlinear phase contributions. In conventional lattices this effect manifests itself as an accelerated onset of wave packet contraction, whereas light in segmented lattices is subject to delocalization at lower powers. From the perspective of individual realizations, this behavior can be understood more intuitively: for a given degree of disorder, light propagating in different realizations undergoes (de-)localization at slightly different powers than in the uniform system. The ensemble average thus leads to a smoothing over transition, which becomes more pronounced with increasing disorder. Moreover, even for an individual eigenstate in a specific disorder realization, the nonlinear contraction may progress more slowly than in the homogeneous case (see figure 4(b)). Consequently, the presence of disorder delays the contraction of the ensemble average at high powers in both conventional and segmented lattices alike.
Figure 4. (a) Linear eigenvalue spectrum of a homogeneous lattice (left) and an exemplary disordered lattice with 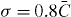 (right) of 15 waveguides each; amplitude profiles corresponding to the highest (flat phased states) and lowest eigenvalues (staggered states), respectively. (b) Nonlinear deformation of the uppermost eigenstates (homogeneous lattice: blue/dashed; disordered: red/solid) at powers P = 2, 3 and
(right) of 15 waveguides each; amplitude profiles corresponding to the highest (flat phased states) and lowest eigenvalues (staggered states), respectively. (b) Nonlinear deformation of the uppermost eigenstates (homogeneous lattice: blue/dashed; disordered: red/solid) at powers P = 2, 3 and  . The corresponding nonlinear eigenvalues are shown in panel (a) as haloed dots above the range of linear eigenvalues.
. The corresponding nonlinear eigenvalues are shown in panel (a) as haloed dots above the range of linear eigenvalues.
Download figure:
Standard imageNote that while Anderson localization relies on the system being invariant along the propagation direction, the segmentation technically breaks this symmetry. However, the phase shift is introduced 'instantaneously', i.e. over a distance much smaller than the coupling length LC. Consequently, the system effectively behaves as z-invariant: the supermodes and their corresponding eigenvalues are the same on all points along the z-axis. The influence of the segmentation then is merely a one-time reshuffling of the occupation levels of the supermodes.
5. Conclusion
In conclusion, we found that Anderson localization renders segmentation imaging in disordered lattices significantly more susceptible to nonlinear perturbations. A systematic study of this phenomenon revealed that while in disordered lattices nonlinear delocalization sets in at lower powers, substantially higher powers are required for overcoming it. Nevertheless, even in strongly disordered photonic lattices, segmentation imaging can withstand a certain amount of nonlinearity. Although our investigations were carried out in the context of photonic lattices, our findings have much wider implications. Discreteness, disorder and nonlinearity can be found in manifold manifestations throughout nature. Likewise, the need to control the evolution of wave packets under these conditions arises in various fields of physics beyond optics, such as quantum mechanics and solid state physics.
Acknowledgments
The authors gratefully acknowledge funding from the German Federal Ministry of Education and Research (ZIK 03Z1HN31 'ultra optics 2015') and the Thuringian Ministry for Education, Science and Culture (research group 'Spacetime', grant no. 11027-514). MH was financially supported by the German National Academy of Sciences Leopoldina (grant no. LPDS 2012-01). UN acknowledges partial support from Programa ICM P10-030-F, Programa de Financiamiento Basal de CONICYT (FB0824/2008) and a CONICYT doctoral fellowship. FD was financed by Graduate Research School OptiMi (B514-10061).