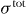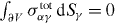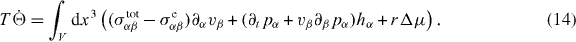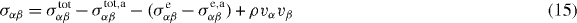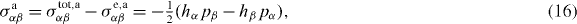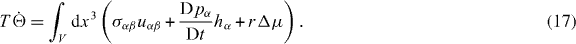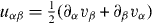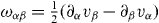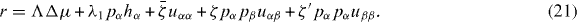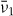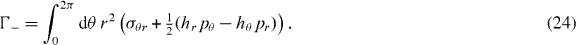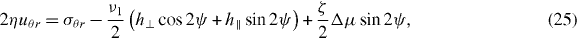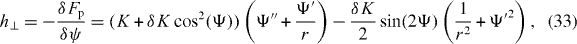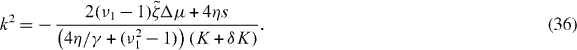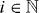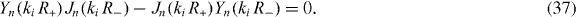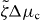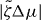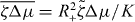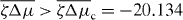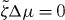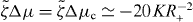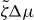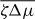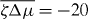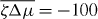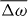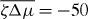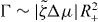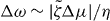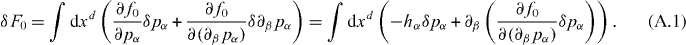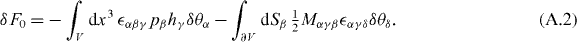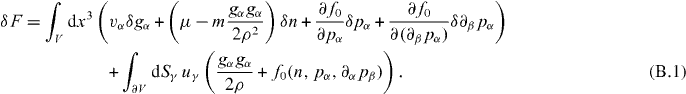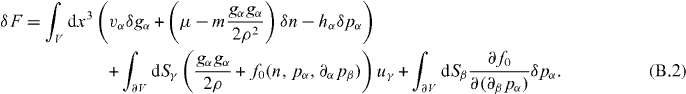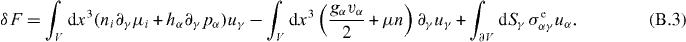The Taylor–Couette motor: spontaneous flows of active polar fluids between two coaxial cylinders

Living matter is internally driven far from thermodynamic equilibrium by active molecular processes such as the action of motor molecules. These motors consume a chemical fuel, adenosinetriphosphate (ATP), to generate directed movements and mechanical work by interacting with structurally polar filaments. In living cells, large numbers of motors and filaments collectively generate dynamic processes such as cell division, cell locomotion and organelle transport in cells. The network of filaments and motors is called the cytoskeleton and provides a key example of an active complex fluid with unconventional material properties. Other examples are suspensions of microswimmers or collections of many cells, for example, in developing tissues.

Active fluids often exhibit long-range nematic or polar order. For example, in crawling cells, cytoskeletal filaments orient typically in the direction of motion. Similarly, the direction of motion of microswimmers defines a polarity vector. Macroscopic polar order emerges when many filaments align or swimmers form swarms [1]. The interplay of actively generated flow fields with the orientation of polar order can render ordered states unstable [2, 3]. Instabilities of active polar fluids can have interesting physical consequences and might also be responsible for observed 'low Reynolds number turbulence' in bacterial suspensions [4]. Furthermore, the polarity dynamics of active fluids could be responsible for physiologically relevant structures such as contractile rings in dividing cells [5–7], flows during cellular wound healing [8] or the reorientation of planar cell polarity in tissues [9].

In the hydrodynamic limit, i.e. on large length and long time scales, the generic properties of visco-elastic active polar gels are described by generic equations. Hydrodynamic modes are the result of conservation laws and of broken continuous symmetries [10]. Hydrodynamic equations can be obtained systematically by first identifying conjugate pairs of thermodynamic fluxes and forces. Constitutive material relations can be expressed by writing all linear coupling terms permitted by symmetry, respecting Onsager reciprocity relations and the signature with respect to time-reversal [11–13]. Note that similar approaches have also been used to describe bird flocks [14], swarms of hydrodynamically interacting swimmers [2], active nematic fluids [15, 16] or active solids [17–19]. Furthermore, an extension to multi-component active fluids has been developed [20].

A large number of instabilities of externally driven flows are known, some of which have been analyzed in remarkable detail [21]. Among the best-studied instabilities are those of a fluid flowing in the interstice between two rotating coaxial cylinders, known as the Taylor–Couette system. In this context, complex fluids such as ferrofluids in the presence of a magnetic field or visco-elastic fluids have also been considered. For the latter, notably, finite-amplitude instabilities of linearly stable states have been found even at low Reynolds numbers if elastic stresses decay sufficiently slowly [22, 23].

Here, we study the flow of an active polar fluid in the Taylor–Couette geometry to highlight some of the interesting rheological properties of active fluids in a setup that might be experimentally accessible. This requires an analysis of the angular momentum flux, which is related to the externally applied torque. In particular, we discuss the role of the Ericksen stress in the torque balance and extend the discussion of the so-called magic spiral [24, 25] to active fluids. Our main result is that an active polar gel in a Taylor–Couette system becomes a rotatory motor which can generate spontaneous rotation against external torques. We distinguish between symmetric motors where motion occurs by spontaneous symmetry breaking and asymmetric motors in which symmetry is broken by boundary conditions. Our analysis is also relevant to biological processes, notably for active flows in the cytoskeleton. Moreover, it might serve as a starting point for the design of biomimetic rotational motors.

This paper is organized as follows. In section 2, we present a derivation of the hydrodynamic equations of active polar fluids, paying particular attention to the conservation of angular momentum. The analysis of the Taylor–Couette motor is presented in section 3. The paper concludes with a discussion of our results in section 4.

We discuss the hydrodynamic equations of an isothermal active polar fluid. Following the logic outlined in [11, 12, 24], we express the conservation laws and introduce the relevant hydrodynamic variables. Based on the conjugate pairs of fluxes and forces in the entropy production, we write the dynamic equations of the system. In the Taylor–Couette geometry discussed here, angular momentum fluxes play an important role and are therefore specifically discussed.

2.1. Conservation laws

In a fluid, the conserved quantities are mass, momentum and angular momentum. Conservation of mass implies that

$$\begin{equation} \partial_t \rho +\partial_\alpha(\rho v_\alpha)=0, \end{equation} \tag{ 1 }$$

where ρ denotes mass density. This equation defines the center of mass velocity v_α. The conservation of momentum is given by

$$\begin{equation} \partial_t g_\alpha-\partial_\beta \sigma^{\mathrm{tot}}_{\alpha\beta}=f^{\mathrm{ext}}_\alpha, \end{equation} \tag{ 2 }$$

where g = ρv is the momentum density. Here, the stress tensor ${\sigma }^{\rm tot}$ denotes the total momentum flux and f^ext denotes the density of external bulk forces. Greek indices take the values 1,...,d, where d is the spatial dimension. Angular momentum conservation is expressed by

$$\begin{equation} \partial_t\ell_{\alpha\beta}- \partial_\gamma M_{\alpha\beta\gamma}^{\mathrm{tot}}=\tau^{\mathrm{ext}}_{\alpha\beta}+r_\alpha f^{\mathrm{ext}}_\beta-r_\beta f^{\mathrm{ext}}_\alpha, \end{equation} \noindent \tag{ 3 }$$

where ℓ_αβ = r_αg_β − r_βg_α is the angular momentum density and τ^ext_αβ is the density of the external bulk torques. The total angular momentum flux M^tot_αβγ has contributions r_ασ^tot_βγ − r_βσ^tot_αγ resulting from momentum fluxes. In complex fluids, however, there exist in general additional contributions M_αβγ to the angular momentum flux that are related to molecular anisotropies:

$$\begin{equation} M_{\alpha\beta\gamma}^{\mathrm{tot}}=M_{\alpha\beta\gamma}+r_\alpha\sigma^{\mathrm{tot}}_{\beta\gamma}- r_\beta\sigma^{\mathrm{tot}}_{\alpha\gamma}. \end{equation} \noindent \tag{ 4 }$$

Here, we are interested in polar fluids with a local polar anisotropy that is described by the polarization vector p. This polarization field is defined as the average of microscopic polarity in small volume elements of the system. For a polar fluid, the expression for the intrinsic angular momentum flux M is given in appendix A. Using the force and torque balance equations (2) and (3), we see that the antisymmetric part of the total stress in general does not vanish and obeys

$$\begin{equation} \sigma_{\alpha\beta}^{\rm{tot,a}}=\textstyle\frac{1}{2}\partial_\gamma M_{\alpha\beta\gamma}+ \textstyle\frac{1}{2} \tau^{\mathrm{ext}}_{\alpha\beta}. \end{equation} \noindent \tag{ 5 }$$

Here σ^tot,a_αβ = (σ^tot_αβ − σ^tot_βα)/2, see also [44]⁵.

We only consider situations where the total external force and torque applied to the system is zero and where external bulk forces and torques vanish, i.e. f^ext_α = 0 and τ^ext_αβ = 0. In this case, external forces σ^tot_αγ dS_γ and torques

$$\begin{equation} \mathrm{d}\Gamma_{\alpha\beta}= \mathrm{d}S_\gamma M^{\rm tot}_{\alpha\beta\gamma} \quad \end{equation} \noindent \tag{ 6 }$$

can still act locally on the boundary ∂V at a surface element dS_γ pointing outward. Vanishing external force and torque imply $\int _{\partial V}\sigma ^{\mathrm {tot}}_{\alpha \gamma }\,\mathrm {d}S_\gamma =0$ and

$$\begin{equation} \int\nolimits_{\partial V}\mathrm{d}\Gamma_{\alpha\beta}= \int\nolimits_{\partial V} \mathrm{d}S_\gamma M^{\rm tot}_{\alpha\beta\gamma}=0. \end{equation} \noindent \tag{ 7 }$$

Note that even if the total flux M^tot_αβγ vanishes at the boundary, the contributions due to M_αβγ and σ^tot_αβ can be non-zero according to equation (4).

2.2. Free energy and hydrostatic stress

We consider a fluid that is locally in thermal equilibrium, but globally evolves in time. Local equilibrium implies that the free energy density f is well defined. We write the free energy density as

$$\begin{equation} f=\frac{g_\alpha g_\alpha}{2\rho}+f_0(n,p_\alpha,\partial_\alpha p_\beta). \end{equation} \tag{ 8 }$$

The first term is the kinetic energy of center-of-mass motion. The second term is the free energy density in the local rest frame. Here, n = ρ/m is the particle density and m denotes the molecular mass. We define the field h_α = −δF/δp_α conjugate to the polarization field, and the chemical potential μ = ∂f₀/∂n, conjugate to the particle density. The total free energy is given by $F=\int d^dx f$.

The hydrostatic or Ericksen stress,

$$\begin{equation} \sigma_{\alpha\beta}^{\mathrm{e}}= (f_0-\mu n)\delta_{\alpha\beta}- \frac{\partial f_0}{\partial(\partial_\beta p_\gamma)}\partial_\alpha p_\gamma, \end{equation} \noindent \tag{ 9 }$$

can be obtained by considering variations of the free energy as shown in appendix B and is a generalization for anisotropic fluids of the hydrostatic pressure. Exploiting the translation invariance of the system, we obtain the Gibbs–Duhem relation, which links the intensive thermodynamic variables,

$$\begin{equation} \partial_\beta\sigma_{\alpha\beta}^{\mathrm{e}}=-n\partial_\alpha\mu-h_\gamma\partial_\alpha p_\gamma. \end{equation} \noindent \tag{ 10 }$$

The hydrostatic stress tensor has an antisymmetric component,

$$\begin{equation} \sigma_{\alpha\beta}^{\mathrm{e,a}}=\textstyle\frac{1}{2}(h_\alpha p_\beta-h_\beta p_\alpha)+\frac{1}{2}\partial_\gamma M_{\alpha\beta\gamma}. \end{equation} \noindent \tag{ 11 }$$

This equation is a consequence of the rotational invariance of f₀.

In equilibrium, when h_α = 0 and σ^tot_αβ = σ^e_αβ, equation (11) becomes a special case of equation (5). Note that even though M_αβγ and σ^tot_αβ do not necessarily vanish at equilibrium, the total angular momentum flux M^tot_αβγ must be zero if external forces and torques are absent. This implies that

$$\begin{equation} 0=M_{\alpha\beta\gamma}+r_\alpha \sigma^{\rm e}_{\beta\gamma}-r_\beta \sigma^{\rm e}_{\alpha\gamma} . \end{equation} \noindent \tag{ 12 }$$

Consequently, the torques due to polarization field and due to the Ericksen stress cancel each other. This fact is illustrated by the so-called magic spiral [24, 25].

2.3. Entropy production and constitutive equations

Starting from an expression for the rate of entropy production, we identify thermodynamic forces and the conjugate thermodynamic fluxes and express constitutive relations between these fluxes and forces. The rate of entropy production $\dot \Theta$ for an isothermal system [11] can be written as

$$\begin{equation} T\dot\Theta=-\skew3\dot{F}+\dot W+J_{\mathrm{F}}. \end{equation} \noindent \tag{ 13 }$$

Here T denotes the temperature, the dots indicate time-derivatives and J_F denotes changes in free energy due to fluxes at the boundary. Moreover, W denotes the work exerted by external forces and torques. Using the conservation laws, we can evaluate ${\skew3\dot{F}}$ and find the entropy production rate,

$$\begin{equation} T\dot\Theta=\int\nolimits_V \mathrm{d}x^3\left((\sigma^{\mathrm{tot}}_{\alpha\beta}-\sigma^{\mathrm{e}}_{\alpha\beta}) \partial_\alpha v_{\beta} +(\partial_t p_\alpha+v_\beta\partial_\beta p_\alpha) h_\alpha +r\Delta\mu \right). \end{equation} \noindent \tag{ 14 }$$

Here, we have assumed that the system is driven by a chemical reaction of a fuel which is provided everywhere at constant concentration by a reservoir. In the biological context this fuel is ATP, which is hydrolyzed to adenosinediphosphate (ADP) and inorganic phosphate P. The chemical free energy transduced per fuel molecule Δμ = μ_ATP − μ_ADP − μ_P is the difference of the chemical potentials of ATP and its hydrolysis products. The reaction rate describing the number of fuel molecules hydrolyzed per unit time is denoted by r. Therefore, the rate of entropy production due to ATP hydrolysis is rΔμ/T.

We separate ${\sigma }^{\rm tot}-{\sigma }^{\rm e}$ into a symmetric part

$$\begin{equation} \mathsf{\sigma}_{\alpha\beta}=\sigma_{\alpha\beta}^{\rm{tot}}-\sigma_{\alpha\beta}^{\rm{tot,a}} -(\sigma_{\alpha\beta}^{\rm{e}}-\sigma_{\alpha\beta}^{\rm{e,a}})+\rho v_\alpha v_\beta \end{equation} \noindent \tag{ 15 }$$

and an antisymmetric part

$$\begin{equation} \sigma^{\rm {a}}_{\alpha\beta}=\sigma^{\rm {tot,a}}_{\alpha\beta}-\sigma^{\rm {e,a}}_{\alpha\beta}=-\textstyle\frac{1}{2}(h_\alpha p_\beta-h_\beta p_\alpha), \end{equation} \noindent \tag{ 16 }$$

where equations (5) and (11) have been used. Note that equation (16) differs from the expression given for σ^a_αβ in [13] by an overall sign. Equation (14) then becomes

$$\begin{equation} T\dot\Theta=\int\nolimits_V \mathrm{d}x^3\left(\sigma_{\alpha\beta} u_{\alpha\beta} +\frac{{\rm D} p_\alpha}{{\rm D} t}h_\alpha +r\Delta\mu \right). \end{equation} \noindent \tag{ 17 }$$

Here $u_{\alpha \beta }=\frac {1}{2}(\partial _\alpha v_\beta +\partial _\beta v_\alpha )$ are the components of the strain rate tensor, while the convected co-rotational derivative of the polarization vector is given by

$$\begin{equation} \frac{{\rm D} p_\alpha}{{\rm D} t} =\partial_t p_\alpha+v_\gamma \partial_\gamma p_\alpha +\omega_{\alpha\beta}p_\beta, \end{equation} \noindent \tag{ 18 }$$

where $\omega _{\alpha \beta }=\frac {1}{2}(\partial _\alpha v_\beta -\partial _\beta v_\alpha )$ is the vorticity of the velocity field.

From equation (17) we thus identify the thermodynamic fluxes σ_αβ, Dp_α/Dt and r as well as the respective corresponding thermodynamic forces u_αβ, h_α and Δμ. Expanding the fluxes in terms of the forces, respecting the symmetries of the system and Onsager's reciprocity principle, we obtain the generic constitutive equations of the active polar fluid [13]:

$$\begin{equation} \fl 2\eta u_{\alpha\beta}=\sigma_{\alpha\beta}-\frac{\nu_1}{2}(p_\alpha h_\beta+p_\beta h_\alpha)-\bar\nu_1p_\gamma h_\gamma \delta_{\alpha\beta}+\bar\zeta\delta_{\alpha\beta}\Delta\mu + \zeta p_\alpha p_\beta\Delta\mu + \zeta' p_\gamma p_\gamma\delta_{\alpha\beta}\Delta\mu, \end{equation} \tag{ 19 }$$

$$\begin{equation} \frac{{\rm D} p_\alpha}{{\rm D}t}=\frac{1}{\gamma}h_\alpha +\lambda_1p_\alpha\Delta\mu - \nu_1 p_\beta u_{\alpha\beta}-\bar\nu_1u_{\beta\beta}p_\alpha, \end{equation} \tag{ 20 }$$

$$\begin{equation} r=\Lambda\Delta\mu+\lambda_1p_\alpha h_\alpha +\bar\zeta u_{\alpha\alpha}+\zeta p_\alpha p_\beta u_{\alpha\beta}+\zeta' p_\alpha p_\alpha u_{\beta\beta}. \end{equation} \noindent \tag{ 21 }$$

The viscosities η and γ denote the resistance of the fluid to internal rearrangements. The coefficients ν₁, $\bar \nu _1$ capture the coupling of the polar distortion field to flows. Finally, the coefficients denoted by ζ, $\bar \zeta$, ζ' describe the active stresses. Positive active stresses are called expansive, while negative active stresses are called contractile. The values of these phenomenological constants either need to be measured or can be derived by coarse-graining microscopic theories [26–30].

The equations of motion of the system are given by the continuity equations (1) and (2) and by equation (20) for the time evolution of p. Using equations (11) and (5) and the Gibbs–Duhem relation (10), the force balance becomes

$$\begin{equation} \partial_t g_\alpha = \partial_\beta\left(\sigma_{\alpha\beta}-\rho v_\alpha v_\beta -\textstyle\frac{1}{2}(h_\alpha p_\beta-h_\beta p_\alpha )\right)-n\partial_\alpha\mu-h_\gamma\partial_\alpha p_\gamma. \end{equation} \tag{ 22 }$$

We now discuss the flows of an active polar fluid in the Taylor–Couette geometry at low Reynolds number. The fluid is confined to the space between two impermeable concentric cylinders of radii R₊ and R₋, as shown in figure 1(a). We will discuss situations where the two cylinders are either stationary or rotate relative to each other at a rate Δω. At low Reynolds number we can choose to keep the inner cylinder fixed without loss of generality. The rotation rate of the outer cylinder then equals Δω. We only consider cases that are invariant with respect to rotations around and translations along the cylinders' long axes. Furthermore, the fluid is incompressible, which together with translational and rotational invariance imposes v_r = 0. We only consider cases where the vector p is confined to the r–θ-plane. Furthermore, since the magnitude of p is not a hydrodynamic variable, we only consider the orientation dynamics of the polarity vector. The orientational dynamics is captured by choosing p² = 1. Therefore, the polarity p can be expressed in terms of the polarization angle ψ such that p_r = cos ψ and p_θ = sin ψ, see figure 1(b).

Zoom In Zoom Out Reset image size

One can apply torques Γ₊ and Γ₋ per unit axial length on the outer and the inner cylinder surfaces, respectively, such that the total torque on the surface vanishes, Γ₊ + Γ₋ = 0. Using equation (6),

$$\begin{equation} \Gamma_{-} = -\int\nolimits_0^{2\pi} \mathrm{d}\theta\,r M^{\mathrm{tot}}_{\theta rr}(r,\theta), \end{equation} \noindent \tag{ 23 }$$

which is independent of r for R₋ ⩽ r ⩽ R₊ because of angular momentum conservation. Using equations (4) and (16), this implies that

$$\begin{equation} \Gamma_-=\int_0^{2\pi} \mathrm{d}\theta\,r^2 \left(\sigma_{\theta r}+\textstyle\frac{1}{2}(h_r p_\theta-h_\theta p_r)\right). \end{equation} \tag{ 24 }$$

3.1. Equation of motion and boundary conditions

We now present the equations of motion governing the system in polar coordinates. The only non-vanishing component of the strain rate tensor is u_θr. From equation (19) we obtain

$$\begin{equation} 2\eta u_{\theta r}=\sigma_{\theta r}-\frac{\nu_1}{2}\left(h_\perp\cos 2\psi +h_\parallel\sin 2\psi\right)+\frac{\zeta}{2}\Delta\mu\sin 2\psi, \end{equation} \noindent \tag{ 25 }$$

where h_∥ = h·p and h_⊥ = h_rp_θ − h_θp_r. Projecting equation (20) onto the directions parallel and perpendicular to the polarization vector yields

$$\begin{equation} \frac{1}{\gamma}h_\parallel = \nu_1u_{\theta r} \sin 2\psi-\lambda_1\Delta\mu, \end{equation} \tag{ 26 }$$

$$\begin{equation} \partial_t\psi = \frac{1}{\gamma}h_\perp-u_{\theta r}(\nu_1\cos{2\psi}-1). \end{equation} \tag{ 27 }$$

The parallel component of the distortion field h_∥ = p·h acts as a Lagrange multiplier to impose the constraint p² = 1. The perpendicular component h_⊥ is the torque exerted by the polarization field and is given by the expression h_⊥ = −δF/δψ. The force balance equation (22) becomes

$$\begin{equation} \partial_r \left(\sigma_{\theta r}+\frac{h_\perp}{2}\right)+\frac{ 2\sigma_{\theta r}}{r}+\frac{h_\perp}{r}=0, \end{equation} \noindent \tag{ 28 }$$

where we have neglected inertial terms. Integration of equation (28) yields

$$\begin{equation} \sigma_{\theta r}=\frac{\Gamma_-}{2\pi r^2}-\frac{1}{2}h_\bot, \end{equation} \noindent \tag{ 29 }$$

where the integration constant Γ₋ is the torque applied to the inner cylinder as can be seen by comparing equations (29) and (24). Combining equations (25)–(27) and (29) we obtain the equation of motion for the polarization field:

$$\begin{equation} \fl \partial_t\psi=\left[\frac{1}{\gamma}+\frac{(\nu_1^2\cos^2 2\psi-1)}{4\eta+\nu_1^2\gamma(\sin 2\psi)^2}\right]h_\perp- \left(\tilde\zeta\!\Delta\mu\sin 2\psi+\frac{\Gamma_-}{2\pi r^2}\right)\frac{\nu_1\cos 2\psi-1}{2\eta+\frac{\nu_1^2\gamma}{2}(\sin 2\psi)^2}, \end{equation} \noindent \tag{ 30 }$$

where $\tilde \zeta =\frac {1}{2}(\zeta +\gamma \nu _1\lambda _1)$. For a given polarity field ψ(r), we can determine the flow field v_θ by integrating equation (25).

The boundary conditions that we consider are the following. We prescribe the polarization angle at both cylinder surfaces, ψ(R₋) = ψ(R₊) = ψ₀. We impose no-slip boundary conditions for the velocity of the fluid at both cylinders. At the fixed inner cylinder, this implies v_θ(R₋) = 0, at the outer cylinder v_θ(R₊) = ΔωR₊. With u_θr = (r/2)∂_r(v_θ/r), the rotation rate Δω reads

$$\begin{equation} \Delta\omega=\int_{R_-}^{R_+}\mathrm{d}r\frac{2u_{\theta r}}{r}. \end{equation} \noindent \tag{ 31 }$$

At the outer cylinder we have the choice of two ensembles: (i) prescribed torque Γ₊ = −Γ₋ or (ii) prescribed rotation rate Δω. We will discuss both cases.

3.2. Equilibrium steady states

In equilibrium, all thermodynamic fluxes and forces vanish. In particular, h_⊥ = 0 and Δμ = 0. In addition, equilibrium requires that Γ₋ = 0 and that no movements occur, v_θ = 0. The polarization field ψ of an equilibrium steady state is obtained by solving the equation h_⊥ = 0, with the specified boundary conditions. Choosing the standard Landau–de Gennes form for the free energy of the polarization field,

$$\begin{equation} F_{\mathrm{p}}=2\pi\int \mathrm{d}r\;r\left\{\frac{K}{2}\left(\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}r\cos\psi\right)^2+\frac{K+\delta K}{2}\left(\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}r}r\sin\psi\right)^2\right\}, \end{equation} \tag{ 32 }$$

we have

$$\begin{equation} h_\perp=-\frac{\delta F_{\mathrm{p}}}{\delta\psi}=(K+\delta K \cos^2(\Psi)) \left(\Psi''+\frac{\Psi'}{r}\right)- \frac{\delta K}{2}\sin(2\Psi)\left(\frac{1}{r^2}+{\Psi'} ^2\right), \end{equation} \tag{ 33 }$$

where primes indicate derivatives with respect to r. In this expression K is the splay elastic modulus and K + δK is the bend elastic modulus. If the boundary conditions are chosen accordingly, equilibrium steady states with a constant ψ(r) = ψ₀ exist for certain values of ψ₀. These special solutions are 'asters' with ψ₀ = 0 or π and 'vortices' with ψ₀ = ± π/2.

3.3. Non-equilibrium steady states

We now discuss how the equilibrium situation is changed as Δμ becomes non-zero. We start by analyzing the stability of the symmetric aster and vortex states with boundary condition (i) and a prescribed torque Γ₋ = 0.

3.3.1. No external torque at the outer surface

We write ψ(r,t) = ψ₀ + δψ(r,t) with δψ = 0 at both boundaries. The time evolution described by equations (30) can be linearized around a steady state with ψ = ψ₀. For aster solutions, i.e. ψ₀ = 0, we find that

$$\begin{eqnarray} &&\fl \partial_t \delta\psi(r,t) = (K+\delta K)\left(\frac{1}{\gamma}+\frac{\nu_1^2-1}{4\eta}\right)\left( \delta\psi''(r,t)+\frac{\delta\psi'(r,t)}{r}\right)\nonumber\\ &&-\,\delta K\left(\frac{1}{\gamma}+\frac{\nu_1^2-1}{4\eta}\right)\frac{\delta\psi(r,t)}{r^2}-\tilde \zeta\! \Delta \mu\frac{\nu_1-1}{\eta}\delta\psi(r,t). \end{eqnarray} \tag{ 34 }$$

Using the separation ansatz δψ(r,t) = δψ(r)e^st, we can solve for δψ(r)

$$\begin{equation} \delta \psi ( r ) = C_1 J_n(k \, r ) +C_2 Y_n(k \,r ), \end{equation} \noindent \tag{ 35 }$$

where J_n and Y_n are Bessel functions of the first kind with n² = δK/(K + δK) and

$$\begin{equation} k ^{2} = -\,\frac{2(\nu_1-1)\tilde\zeta\!\Delta\mu+4\eta s}{\left(4\eta/\gamma+(\nu_1^2-1)\right)( K+{\delta K})}. \end{equation} \noindent \tag{ 36 }$$

Asters are stable if the real parts of all growth exponents s are negative. The possible values k_i of k with $i \in \mathbb{N}$ are restricted by the boundary conditions δψ(R₋) = δψ(R₊) = 0. Explicitly, the values k_i satisfy the equation

$$\begin{equation} Y_n (k_i R_+) J_n(k_i R_-)-J_n (k_i R_+) Y_n(k_i R_-) =0 . \end{equation} \tag{ 37 }$$

We find that k²_i and the corresponding values of s are real and we order these values such that k²₁ < k²₂ < ··· < k²_i < ···. By setting s = 0 in equation (36), we can thus determine a critical value $\tilde \zeta\! \Delta \mu _{\mathrm {c}}$ for the activity, such that asters are unstable if $\tilde \zeta\! \Delta \mu <\tilde \zeta\! \Delta \mu _{\mathrm {c}}$. Explicitly,

$$\begin{equation} \tilde \zeta\!\Delta \mu_{\mathrm{c}}=-k_1^2\frac {\left( 4\eta+\gamma(\nu_1^2-1) \right)}{2\gamma (\nu_1-1)} \left( K+{\delta K} \right). \end{equation} \tag{ 38 }$$

Following the same logic it is also possible to determine the stability of vortices. We find that the activity threshold for the stability of vortices is

$$\begin{equation} \tilde\zeta\!\Delta \mu_{\mathrm{c}}=-l_1^2\frac {\left( 4\eta +\gamma(\nu_1^2-1) \right)}{2\gamma (\nu_1+1)}K . \end{equation} \tag{ 39 }$$

The values l_i satisfy Y_m(l_iR₊)J_m(l_iR₋) − J_m(l_iR₊)Y_m(l_iR₋) = 0 with m² = −δK/K and we order their values such that l²₁ < l²₂ < ··· < l²_i < ···. The limit R₋ → 0 corresponds to point defects that were studied in [13]. Note that our results differ slightly since the sign of the antisymmetric part of the deviatory stress was chosen incorrectly in [13].

The steady states of equation (30) beyond the instability can be obtained numerically by a shoot-and-match algorithm. In these states, the fluid flows spontaneously and the outer cylinder rotates. We present the bifurcation diagram of the Taylor–Couette motor for Γ₋ = 0 and vortex boundary conditions, ψ₀ = ± π/2, in figure 2. The sense of rotation of the outer cylinder is determined by spontaneous symmetry breaking. Therefore, two stable branches exist in the bifurcation diagram. We have explicitly determined the linear stability of these and all following states numerically. Moving further away from the bifurcation point, additional unstable steady states appear. These states correspond to l²₂ and present an additional node for ψ(r). Further unstable steady states corresponding to l²_i with i > 2 exist for yet larger values of $|\tilde \zeta\! \Delta\mu|$ and the number of nodes of the corresponding ψ(r) is i − 1.

Zoom In Zoom Out Reset image size

3.3.2. The stalled system

The emergence of spontaneous rotations indicates that the system can act as a rotatory motor. Its stall torque is determined by setting Δω = 0. To investigate the stability of the corresponding steady state, we employ again equation (30), but now Γ₋ depends on time. Its value is determined by simultaneously solving equation (25) for v_θ and imposing v_θ(R₊) = 0. For the stationary vortex solution with ψ₀ = ± π/2, we again find an instability at a critical value ζΔμ_c at which spontaneous flows occur, as is shown in the bifurcation diagram figure 3. As in the case Γ₋ = 0, the direction of the flow depends on the initial conditions via spontaneous symmetry breaking. In contrast to the case considered above, the solutions with Δω = 0 are characterized by non-vanishing torques Γ₋.

Zoom In Zoom Out Reset image size

3.4. The relation between the rotation rate and applied torque

We determine the relation between applied torque Γ₋ and rotation rate Δω by numerically solving for the stationary solutions of equations (25) and (27). In the passive case $\tilde \zeta\! \Delta \mu =0$, the rotation rate Δω is always proportional to the torque Δω∝Γ₋ and vanishes for Γ₋ = 0. Our results for finite $\tilde \zeta\! \Delta \mu$ are displayed in figure 4. For a sufficiently small $\tilde \zeta\! \Delta \mu$, the rotation rate Δω increases monotonically as a function of Γ₋, see figure 4(a). For $\tilde \zeta\! \Delta \mu = \tilde \zeta\! \Delta \mu _{\mathrm {c}}\simeq -20 K\!R_+^{-2}$, a critical point appears. Beyond this point, three solutions coexist for $\tilde \zeta\! \Delta \mu \lesssim -20K\!R_+^{-2}$, two of which are stable (solid lines) and one is unstable (dashed line); see figure 4(b). As a consequence, the rotation rate exhibits discontinuous changes as a function of torque and hysteresis occurs. If $\tilde \zeta\! \Delta \mu$ is decreased further, a more complex set of branches of unstable steady states emerges, see figures 4(c) and (d). In all cases there are two stable branches and a regime of hysteresis. Note that the stable branches always have positive slope, while the slope of unstable branches can have either sign. This relation between torque and rotation rate is very similar to the properties of the force–velocity relation of symmetric collections of molecular motors [31, 32].

Zoom In Zoom Out Reset image size

3.5. Variation of the boundary conditions of the polarization field

Changing the polarization angle ψ₀ at the boundaries leads in general to a non-symmetric motor, which has a spontaneous rotation rate even in the absence of a torque. In figure 5, we show the steady state rotation rate Δω for Γ₋ = 0 as a function of ψ₀ for different values of the active stress. This figure shows that the system rotates spontaneously except for ψ₀ = 0 (aster) and ψ₀ = π/2 (vortex). As the magnitude of the active stress is increased, unstable branches appear and the rotation rate exhibits discontinuous changes and hysteresis. The vortex becomes unstable for lower values of the active stress than the aster, see figure 5(b). Figure 5(c) reveals the subsequent emergence of additional unstable branches as well as the instability of the aster.

Zoom In Zoom Out Reset image size

In summary, we analyzed the dynamics of an active polar fluid confined in the Taylor–Couette geometry between two coaxial cylinders. We found that similar to active polar fluids confined to a straight channel [3], the active stress can induce spontaneous flows. The circular flow in the Taylor–Couette system drives a rotation of the outer cylinder relative to the inner cylinder even in the absence of an externally applied torque. If the polarization angle at the boundary is either parallel or perpendicular to the cylinder wall, relative motion between the two cylinders occurs by spontaneous symmetry breaking if the contractile active stress exceeds a critical value. Beyond this instability two steady states with opposite rotation rates coexist. For any other boundary condition imposed on the polarization, rotation in the absence of torque occurs for non-zero active stress. Here, we have restricted our analysis to states that are invariant with respect to rotations around and translations along the cylinder axis. Since we know that in the passive system rotationally symmetric states are stable for sufficiently low Reynolds numbers, we expect that the rotationally symmetric active steady states discussed above are stable for small enough active stresses. Additional instabilities to those discussed here could therefore occur at higher values of active stresses. Notably, active analogues of Taylor vortices, which break rotational and translational invariance, might exist.

The classical Taylor–Couette system displays a large variety of flow patterns, including turbulent flow for very large Reynolds numbers. It will be interesting to see which of these structures can be generated in the low Reynolds number regime by active stresses. In particular, flow patterns that break the axial and rotational symmetries we imposed in this study should be analyzed. In view of 'low Reynolds number turbulence' observed in bacterial suspensions [4], one might also be interested in investigating the possibility of spatiotemporal chaos in the Taylor–Couette motor. Considering the finite relaxation time of elastic stresses exhibited by a number of active gels, the system might also be capable of spontaneously generating oscillations. Consequently, the classical system of two rotating coaxial cylinders is a promising geometry to study also experimentally the rich dynamic behavior of active gels.

If an external torque is applied between the two cylinders, the system behaves as a rotary motor that can perform mechanical work. In the special cases where the polarization is parallel or perpendicular to the boundary, this motor only works beyond the instability and can act in both senses of rotation. We find dynamic transitions between states of different rotation rates and hysteresis. These behaviors are very similar to those found for collections of symmetric coupled molecular motors where motion occurs via spontaneous symmetry breaking [31, 32]. The behaviors of the Taylor–Couette motor for other choices of boundary conditions can be compared to those found for asymmetric collections of motors. Indeed, as already described for collective motors we find here dynamic transitions between states of different rotation rates at finite applied torques. Coupling to a rotational spring would thus lead to spontaneous oscillations [33–35]. Due to the possible appearance of additional unstable states, such oscillations may exist only in a finite range of active stresses.

The Taylor–Couette motor described in this paper could be realized experimentally using actin gels with myosin motors in small Taylor–Couette rheometers. We will now estimate the orders of magnitude of the quantities characterizing the system's dynamics. First, we note that the active stress together with the elastic constant K, which has the dimension of a force, see equation (32), introduce a length scale ξ = (K/ζΔμ)^1/2, see also [3]. The instability criterion derived above can be expressed in terms of this length scale: for ξ ≪ R₊ − R₋ spontaneous motion occurs in a symmetric system. The critical active stress beyond which spontaneous motion occurs is thus of the order of K/R²₊ for which ξ ≃ R₊ − R₋. In passive systems, the value of K has been estimated using dimensional analysis, as K ∼ U/a where U and a are a characteristic interaction energy and length, respectively [24]. Using U = 10 pN nm and a = 1 nm implies a value of K of the order of several pN, which is consistent with estimates provided by Odijk for semi-flexible polymers [36]. In an actin gel, the stiffness K could result from the action of motor molecules and therefore be larger. For example, estimating K by the typical stress exerted by myosin mini-filaments on an actin filament in the network suggests values of several tens of pN. The active stress generated by the actin cytoskeleton has been estimated to be up to ζΔμ ≃ 10³ Pa [37], which would correspond to ξ ≃ 1 μm.

In a Taylor–Couette system with an outer radius R₊ = 5 mm and an inner radius R₋ = 1 mm, the critical active stress would be of the order of 10⁻⁶ Pa and thus the system should start to rotate even at very small active stresses. The order of magnitude of the stall torque can be obtained from $\Gamma \sim |\tilde \zeta\! \Delta \mu |R_+^2$, see equation (24) and figure 3. Using again R₊ ≃ 5 mm and ζΔμ ≃ 10³ Pa, we estimate a stall torque per unit length Γ ≃ 25 × 10⁻³ N. To estimate the corresponding rotation rate Δω ∼ u_rθ, we note that it scales as $\Delta \omega \sim |\tilde \zeta\! \Delta \mu |/\eta$, see equations (31) and (25) and figure 2. The viscosity η of an actin gel can be estimated as η ≃ Eτ, where E is the gel elastic modulus and τ denotes the characteristic visco-elastic relaxation time. The elastic modulus of a passive actin gel scales as E ≃ k_BTL_pλ⁻⁴, where L_p is the persistence length of actin filaments and λ is the mesh size of the gel. For k_BT ≃ 4 pN nm, L_p ≃ 17 μm and λ ≃ 100 nm [38], we estimate that E ≃ 10³ Pa, which is consistent with measurements for actin gels under various conditions [39–41]. Using τ ≃ 30 s [42], we obtain η ≃ 10⁴ Pa s. For ζΔμ ≃ 10³ Pa, we estimate a rotation rate of about Δω ≃ 0.1 s⁻¹.

The Taylor–Couette motor could be realized at small scales with radii of several μm using microfabrication techniques [43]. This leads to a stall torque of the order of several nN and since the rotation rate is rather insensitive to the system size again to rotation rates of the order of 0.1 s⁻¹. Note that when the system size approaches the mesh site of the acto-myosin gel, the hydrodynamic limit will no longer provide an accurate approximation. Note also that a symmetric system would only rotate if the characteristic length ξ is smaller than the system size. However, even in micrometer-sized systems, we expect many of the general features and the scaling relations to still hold. Thus, the Taylor–Couette motor described here is a promising candidate for the construction of artificial rotational micromotors.

To find the torque exerted by the polarization field, we write down the variation of the free energy $F_0=\int \mathrm {d}x^d f_0(n,p_\alpha ,\partial _\beta p_\alpha )$ due to changes in p_α,

$$\begin{equation} \fl \delta F_0=\int \mathrm{d}x^d \left(\frac{\partial f_0}{\partial p_\alpha}\delta p_\alpha+\frac{\partial f_0}{\partial( \partial_\beta p_\alpha)}\delta \partial_\beta p_\alpha \right) = \int \mathrm{d}x^d \left(-h_\alpha\delta p_\alpha + \partial_\beta \left(\frac{\partial f_0}{\partial( \partial_\beta p_\alpha)}\delta p_\alpha\right)\right). \end{equation} \noindent \tag{ A.1 }$$

Under infinitesimal rotations defined by the pseudovector δθ_α, with δp_α = _αβγδθ_βp_γ we have

$$\begin{equation} \delta F_0 =-\int\nolimits_V \mathrm{d}x^3\,\epsilon_{\alpha\beta\gamma}p_\beta h_\gamma \delta\theta_\alpha- \int\nolimits_{\partial V} \mathrm{d}S_\beta\,\textstyle\frac{1}{2}M_{\alpha\gamma\beta}\epsilon_{\alpha\gamma\delta}\delta\theta_\delta. \end{equation} \tag{ A.2 }$$

From these expressions, we identify the angular momentum density flux carried by the polarization field as

$$\begin{equation} M_{\alpha\beta\gamma}=\frac{\partial f_0}{\partial (\partial_\gamma p_\beta)}p_\alpha-\frac{\partial f_0}{\partial (\partial_\gamma p_\alpha)}p_\beta. \end{equation} \tag{ A.3 }$$

To obtain the Ericksen stress we consider a general variation of the free energy of a volume V of a fluid,

$$\begin{eqnarray} &&\fl \delta F=\int\nolimits_V \mathrm{d}x^3\left(v_\alpha\delta g_\alpha +\left(\mu-m \frac{g_\alpha g_\alpha}{2\rho^2}\right)\delta n+\frac{\partial f_0}{\partial p_\alpha}\delta p_\alpha+ \frac{\partial f_0}{\partial (\partial_\beta p_\alpha)}\delta\partial_\beta p_\alpha\right)\nonumber\\ &&+\int\nolimits_{\partial V} \mathrm{d}S_\gamma\,u_\gamma\left(\frac{g_\alpha g_\alpha}{2\rho}+f_0(n,p_\alpha,\partial_\alpha p_\beta)\right). \end{eqnarray} \noindent \tag{ B.1 }$$

The first term describes variations in the bulk of the volume, while the second captures variations of the volume surface with u denoting the corresponding infinitesimal displacements. Using Gauss' theorem we obtain

$$\begin{eqnarray} &&\fl \delta F = \int\nolimits_V \mathrm{d}x^3\left(v_\alpha\delta g_\alpha +\left(\mu-m\frac{g_\alpha g_\alpha}{2\rho^2}\right)\delta n-h_\alpha\delta p_\alpha\right)\nonumber\\ &&+\int\nolimits_{\partial V} \mathrm{d}S_\gamma\left(\frac{g_\alpha g_\alpha}{2\rho}+f_0(n,p_\alpha,\partial_\alpha p_\beta)\right) u_\gamma+\int\nolimits_{\partial V} \mathrm{d}S_\beta \frac{\partial f_0}{\partial(\partial_\beta p_\alpha)}\delta p_\alpha. \end{eqnarray} \noindent \tag{ B.2 }$$

The dependence of the free energy on derivatives of the polarization field thus generates an additional surface term. Displacing the hydrodynamic fields by the deformation field u, δg_α = −u_γ∂_γg_α, δp_α = −u_γ∂_γp_α and δn = −u_γ∂_γn, yields

$$\begin{equation} \fl \delta F=\int\nolimits_V \mathrm{d}x^3 (n_i\partial_\gamma\mu_i+h_\alpha\partial_\gamma p_\alpha)u_\gamma-\int\nolimits_V \mathrm{d}x^3\left(\frac{g_\alpha v_\alpha}{2}+\mu n \right)\partial_\gamma u_\gamma+\int\nolimits_{\partial V} \mathrm{d}S_\gamma\,\sigma_{\alpha\gamma}^{\mathrm{e}}u_\alpha. \end{equation} \noindent \tag{ B.3 }$$

Here, we identify the Ericksen stress from the surface term, leading to the expression given in equation (9). Let us remark that the Gibbs–Duhem relation is automatically satisfied if u = const, as can be deduced from equation (B.2).

Now, from equation (9) we deduce that rotation invariance implies that σ^e_αβ = 0 for a uniform rotation around the origin of angle θ; that is, δg_α = −u_γ∂_γg_α + _αβγθ_βg_γ, δp_α = −u_γ∂_γp_α + _αβγθ_βp_γ, δn_i = −u_γ∂_γn_i and u_α = _αβγθ_βr_γ. This leads to equation (11).