Abstract
It has recently been shown that in every spatial dimension there exist precisely five distinct classes of topological insulators or superconductors. Within a given class, the different topological sectors can be distinguished, depending on the case, by a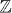 
or a 
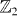topological invariant. This is an exhaustive classification. Here we construct representatives of topological insulators and superconductors for all five classes and in arbitrary spatial dimension d, in terms of Dirac Hamiltonians. Using these representatives we demonstrate how topological insulators (superconductors) in different dimensions and different classes can be related via 'dimensional reduction' by compactifying one or more spatial dimensions (in 'Kaluza–Klein'-like fashion). For 
-topological insulators (superconductors) this proceeds by descending by one dimension at a time into a different class. The 
-topological insulators (superconductors), on the other hand, are shown to be lower-dimensional descendants of parent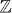 
-topological insulators in the same class, from which they inherit their topological properties. The eightfold periodicity in dimension d that exists for topological insulators (superconductors) with Hamiltonians satisfying at least one reality condition (arising from time-reversal or charge-conjugation/particle–hole symmetries) is a reflection of the eightfold periodicity of the spinor representations of the orthogonal groups SO(N) (a form of Bott periodicity). Furthermore, we derive for general spatial dimensions a relation between the topological invariant that characterizes topological insulators and superconductors with chiral symmetry (i.e., the winding number) and the Chern–Simons invariant. For lower-dimensional cases, this formula relates the winding number to the electric polarization (d=1 spatial dimensions) or to the magnetoelectric polarizability (d=3 spatial dimensions). Finally, we also discuss topological field theories describing the spacetime theory of linear responses in topological insulators (superconductors) and study how the presence of inversion symmetry modifies the classification of topological insulators (superconductors).
GENERAL SCIENTIFIC SUMMARY Introduction and background. A topological insulator is an insulator that has exotic metallic states on its boundary when placed next to vacuum. Similarly, a topological superconductor is a fully gapped superconductor that has delocalized Andreev surface states. These conducting boundaries are due to topological invariants, which cannot change as long as a the bulk gap remains finite. Both topological insulators and superconductors can be classified within an elegant mathematical framework, which can be viewed, in a sense, as an extension of Bloch's band theory. The result of this exhaustive classification scheme is that in every spatial dimension there exist precisely five distinct classes of topological insulators or superconductors (see figure 1).
Main results. We show how topological insulators and superconductors in different dimensions and different classes can be related via dimensional reduction procedures by compactifying one or more spatial dimensions, in 'Kaluza–Klein'-like fashion. For some of the lower dimensional cases, the topological invariants are shown to be related to the electric polarization or to the magnetoelectric polarizability. Furthermore, we elaborate on the intimate links between the fields of topological insulators, Anderson localization physics, and K-theory.
Wider implications. An important outcome of the classification scheme of figure 1 is the prediction of new topological phases of matter. Notable examples are superfluid 3He B, and the time-reversal invariant topological singlet superconductor. Finding experimental realizations of these new types of topological insulator and superconductor would be an outstanding achievement. These novel topological phases might be relevant for technological innovation, for example in the field of spin-based electronic devices or in the field of topological quantum computation.
Figure. Ten-fold way of topological insulators and superconductors. The ten symmetry classes are defined in terms of the presence or absence of time-reversal symmetry, 
, particle-hole symmetry, 
, and chiral symmetry, 
. The presence and absence of symmetries is denoted by '±1' and '0', respectively, with '+1' or '−1' specifying whether the antiunitary operator implementing the symmetry at the level of the single-particle Hamiltonian squares to '+1' or '-1'. The symbols 
and 
indicate that the topologically distinct phases within a given symmetry class of topological insulators (superconductors) are characterized by an integer invariant 
, or a quantity, respectively. The topological classifications show a regular pattern as a function of symmetry class and spatial dimension.