Abstract
The nucleon microscopic optical potential is obtained by calculating the mass operator of the one-particle Green function with an effective Skyrme interaction. The real and imaginary part potentials for finite nuclei are given by applying a local density approximation as usual, while the spin–orbit potential is further amended by using the Skyrme–Hartree–Fock approach and relativistic mean field results. The new variants of Skyrme interaction parameters are found by simultaneously fitting the characteristics of nuclear matter, the binding energy, charge radius and single-particle energy levels of double closed shell nuclei, the neutron induced reaction cross sections and polarization data. These data include the total cross sections, nonelastic sections, elastic scattering angular distributions and analyzing powers for the target mass range 24 ⩽ A ⩽ 209 with incident neutron energies below 100 MeV. Further, the Landau parameters are considered to describe the properties of an excited state. The obtained variants of Skyrme forces are used to predict the neutron–actinide reactions with incident energies below 100 MeV. It is found that the calculations can give a satisfactory description of the experimental data. Analogous calculations by the new Skyrme forces are performed to predict the proton induced reactions, which also yield reasonable results.
Export citation and abstract BibTeX RIS
1. Introduction
The optical model [1] is one of the most important theoretical models in nuclear reaction theory, which makes a strong impact on many branches of nuclear physics. The key point of the optical model is the optical potential. The phenomenological optical potential (POP) is obtained by adjusting its parameters to minimize the deviation between the calculated results and the existing nuclear reaction experimental data; it can well reproduce the experimental data of nuclei around the beta-stable line. However, it is hard to reliably predict the data for the nuclei far-away from beta-stable line since it lacks the microscopic basis in theory. The generation of a microscopic optical potential (MOP) is based on the nucleon–nucleon interaction, which has great significance in many branches of nuclear physics, especially for the reaction from unstable nuclei. So, the derivation of an optical potential from more basic theory is one of the most important problems in nuclear theory, which has both theoretical and practical significance.
From the view of the many-body theory, the nucleon MOP can be identified with the mass operator of the one-particle Green function [2, 3]. This identification makes it possible to utilize the many-body theory technique to obtain a MOP without free parameters. A nucleon–nucleus optical potential based on the realistic nuclear force is built from the Brueckner–Hartree–Fock (BHF) theory and the nuclear-matter approach by Jeukenne, Lejeune and Mahaux (JLM) [4]. This is an important progress of the MOP theory and many good results were obtained through JLM model, but a satisfactory agreement cannot be achieved between the calculated results and the experimental data in certain energy or nucleus region. So, energy dependent phenomenological normalization factors are added to improve the agreement, which is called the semimicroscopic nucleon–nucleus optical model [5]. Recently, the BHF approach with three-body force was proposed to study the MOP [6, 7] and calculate the proton–nucleus elastic scattering with the help of the phenomenological three-body force and some renormalization factors [8]. Meanwhile, the relativistic MOP are studied in the Dirac–Bruecner–Hartree–Fock (DBHF) approach based on the realistic nuclear force [9–11]. As the DBHF calculation in nuclear matter is divergent at very low density, the microscopic calculation results cannot be obtained below half normal density (0.08 fm−3), especially for the spin–orbit potential whose contribution mainly appears in the nuclear surface. Up to now, we have not found a MOP approach based on the realistic nuclear force that can give good agreement between the calculation and experimental data in a wide energy and nucleus region without the help of the phenomenological potential or normalization factors. Thus, these approaches cannot unifiedly describe the properties of the nuclear mater, nuclear structure and nuclear reaction. Obviously, the prediction by the existing MOP of the realistic nuclear force is somewhat inconvincible. Another kind of MOP is based on the effective nuclear force [12]. Although it has much less theoretical basis compared with the realistic nuclear force MOP, some weakness of the realistic nuclear force MOP can be extently overcome in the effective nuclear force MOP. All calculation results are obtained by adjusting the effective nuclear force parameters and have no need of the phenomenological potential or normalization factors. The properties of the nuclear mater, nuclear structure and nuclear reaction can be unifiedly described in the effective nuclear force MOP approach. Therefore, it has some prediction abilities in certain energy and nucleus regions. Furthermore, an effort has been made to get the effective nuclear force parameters based on the realistic force [13], which will also prompt us to simultaneously concern the MOP theories based on the realistic and effective forces in future work.
In 1979, Bernard and Giai [14] first gave out the method considering the nuclear reaction data in the nuclear structure approach by Skyrme force MOP. Another method describing the nuclear reaction data with Skyrme forces [15, 16] was in the nuclear-matter approach [4, 17]. Since the Skyrme interactions can be viewed as effective G matrices in the Hartree–Fock (HF) calculations [19, 20], the first-order mass operator represents the real part of the optical potential; the imaginary part of the second-order mass operator is considered as the imaginary part of the optical potential. The optical potential for the finite nuclei is usually given by the local density approximation (LDA) [21]. The complex particle MOP has been obtained with this approach [18]. In this article, we further amend the spin–orbit potential for the finite nuclei by the Skyrme–Hartree–Fock (SHF) approach and the relativistic mean field results.
There are many sets of Skyrme interactions at present, most of which are quite successful in calculating the ground-state properties of nuclei. As is known to all, different Skyrme interactions give more or less reasonable results for HF calculations but yield quite different results for excited states [22–25]. Vauherin and Brink [19] gave two sets of Skyrme force parameters by fitting the characteristics of nuclear matter and the nuclear ground-state in the HF method. Then, another four sets of Skyrme force parameters [26] were given out by a similar method. The standard Skyrme force parameters SKa and SKb [27] obtained from mass formula were also based on the experimental data of the nuclear ground-state properties. Subsequently, several sets of standard Skyrme force parameters were obtained by fitting the characteristics of nuclear matter, nuclear ground-states and excited states simultaneously. The Skyrme interactions SkM [28] and SGI [22] accounted for the measurement of the giant monopole resonances and the properties of nuclear matter. The Sly4∼7 [29] described the spectroscopic properties of nuclei from the β-stability line to the drip lines and other exotic phenomena, such as super- or hyper-deformation. The LNS [13] fitted the nucleon effective masses and the Landau parameters. The LNS1 and LNS2 were also given in [23]. The GS1∼GS6 [30] added the density-dependent S-wave term t4 and the spin exchange parameter x4 to self-consistently describe the ground and excited state properties. All these Skyrme interactions were achieved from the characteristics of the nuclear-matter saturation properties and the ground-state properties of nuclei. A simultaneous description for the properties of nuclear ground-states and excited states with Skyrme interaction is an important progress of effective Skyrme forces.
In addition, we have obtained the MOP of finite nuclei for different incident particles with certain versions of the Skyrme interactions [15, 16, 18]. It shows that the potential depth, shape and relative contributions of the surface and volume parts, as well as the energy dependence, are all similar to those of the corresponding incident particles POP and those based on the realistic nucleon–nucleon interaction for certain energy regions. Some predicted results, such as the total and nonelastic cross sections and angular distributions of elastic scattering, are also in agreement with the experimental data in some energies and nuclei regions. Considering them as a whole, the real and imaginary parts of GS2 are the most approximate to those of the POP, while the SKa and SKb are the second. However, the GS2 has more terms (t4 and x4) than the standard Skyrme force. Recently, Pilipenko et al also gave two sets of Skyrme force parameters: SkOP1 and SkOP2 [31]. This was the first achievement of the Skyrme interaction parameters, which was simultaneously based on the experimental data of nuclear structure and nuclear reaction. By considering the experimental data of elastic scattering angular distributions and analyzing powers, the results could reasonably describe the case of neutron energies up to 15 MeV. Furthermore, the real part of the optical potential including the rearrangement potential was derived by the research on the specific finite nuclides.
Therefore, we hope to find some new variants of the standard Skyrme forces by means of modifying their parameters. They can satisfactorily describe not only the nuclear-matter saturation properties and the finite nuclei ground-state properties, but also the characteristic of a nuclear reaction. For this purpose, some new Skyrme interaction parameters are found by simultaneously fitting the characteristics of the nuclear matter, binding energy, charge radius, the single-particle energy levels of the target nucleus, the neutron induced reaction cross sections and polarization data, including total cross sections, nonelastic cross sections, elastic scattering angular distributions; further, by analyzing powers for the target mass range 24 ⩽ A ⩽ 209 with incident neutron energies below 100 MeV. Then, the proton induced and nucleon-actinide reactions with incident nucleon energies below 100 MeV are predicted using the obtained Skyrme interaction parameters.
The paper is organized as follows: section 2 presents the nucleon MOP with the standard Skyrme interaction. Some expressions on the nuclear-matter properties are given in section 3. Section 4 describes the fitting procedure and gives two new sets of Skyrme force parameters. Section 5 presents and discusses the HF results. The results of the projectile nucleon reaction data are analyzed in section 6. Finally, concluding remarks are demonstrated in section 7.
2. Nucleon microscopic optical potential with standard Skyrme interaction
The standard Skyrme force is only a two-body effective interaction described by a density- and momentum-dependent delta function. It has the following form:

where 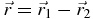 and
and  are the relative and center-of-mass radius vectors of two nucleons,
are the relative and center-of-mass radius vectors of two nucleons, 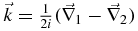 acting on the right and its Hermitian conjugate operator
acting on the right and its Hermitian conjugate operator 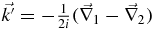 acting on the left, which are the operators of the momentum of the nucleon relative motion in the initial and final states, respectively; Pσ is the spin exchange operator and
acting on the left, which are the operators of the momentum of the nucleon relative motion in the initial and final states, respectively; Pσ is the spin exchange operator and  is the Pauli spin matrix. The t0, t1, t2, t3, x0, x1, x2, x3, α, W0 are the parameters of Skyrme force.
is the Pauli spin matrix. The t0, t1, t2, t3, x0, x1, x2, x3, α, W0 are the parameters of Skyrme force.
2.1. Nuclear-matter approach
The Hamiltonian composed of two-body interactions can be written as

where


H0 is the single-particle Hamiltonian, H1 is the residual interaction and Ui is the mean field of the single particle.
The optical potential can be identified with the mass operator Mα, α of the one-particle Green function (Mα, β = 〈α∣M∣β〉, α and β being the final and initial states of the incident nucleon, respectively) by perturbation theory up to the Feynman diagrams of the second order.
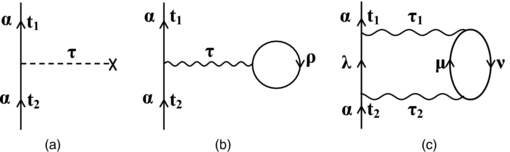
Figure 1 shows the first- and second-order Feynman diagrams of the one-particle Green functions. The dashed line in figure 1(a) represents the mean field. Figure 1(b) corresponds to the contributions by two-body interactions. Figure 1(c) is the second-order Feynman diagram of the one-particle Green functions. We choose the first-order mass operator 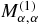 as the mean HF potential. The HF mean field Uα, α is expressed as
as the mean HF potential. The HF mean field Uα, α is expressed as

where nρ are the occupation numbers of the ρ state nucleon with energies ερ and Vαρ, αρ as the matrix elements of the two-body nucleon–nucleon interaction. The second-order mass operator is presented as

where the ε is the corresponding energies for different particles, the η is an infinitesimal and the two-body interaction matrix elements is

We use the nuclear-matter approach to simplify the calculation. In the nuclear matter, the wave function of nucleon α is just the plane wave function.
Figure 1. The first and second-order Feynman diagrams of the one-particle Green functions.
Download figure:
Standard image High-resolution imageThe real part of nucleon MOP is obtained with the first-order mass operator based on equation (5)

where the summation conditions ⩽F represent below the Fermi surface and the τα is the nucleon of a given sort (τα = n, p).
The second-order diagrams are the lowest order diagrams which contribute to the imaginary part of a MOP. That means

The formula for the principle value integral is expressed as

Putting equation (1) into equation (8), the real part of the nucleon MOP is obtained as follows:

where 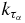 is the Fermi momentum of the nucleon τα. From the expression above, we can see that the W0 term of the Skyrme force has no contribution to the real part of the nucleon MOP. Then the nucleon effective mass m* can be obtained as follows:
is the Fermi momentum of the nucleon τα. From the expression above, we can see that the W0 term of the Skyrme force has no contribution to the real part of the nucleon MOP. Then the nucleon effective mass m* can be obtained as follows:

where 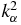 is given by
is given by

and  and M are the mass of the nucleon τα and the target nucleus, respectively. EL is the energy of the incident nucleon in the laboratory frame. The Coulomb potential VC in nuclear matter is expressed as
and M are the mass of the nucleon τα and the target nucleus, respectively. EL is the energy of the incident nucleon in the laboratory frame. The Coulomb potential VC in nuclear matter is expressed as 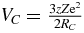 . Then we have
. Then we have

The expression shows that the real part of the nucleon MOP has a linear relation with EL and is isospin dependent. Putting equation (1) into equation (9) and using the following formulas:


the imaginary part of the nucleon MOP is obtained as follows:

where
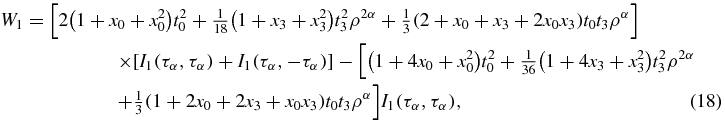

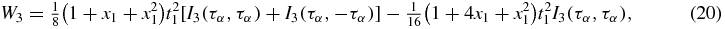

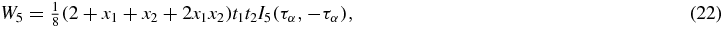



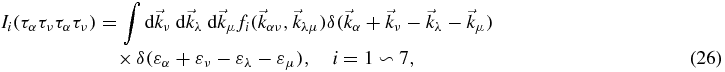

In the integrals mentioned above, the condition ν ⩽ F and α, λ, μ > F must be satisfied. 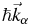 is the incident nucleon momentum. For asymmetric nuclear matter, the integrals for equation (26) are provided in [16].
is the incident nucleon momentum. For asymmetric nuclear matter, the integrals for equation (26) are provided in [16].
The simplest way to obtain a MOP for a finite nucleus is to use the LDA. The SHF method can only give the densities of double closed shell nuclei. If the considered nuclei are more in the SHF method, the adjustable pairing force parameters must be added. As in the previous papers [4, 15, 16], the used nuclear densities are now expressed by Negele's empirical formula [21]
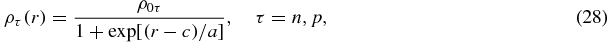
where


2.2. Nuclear structure approach
The SHF equation for double closed shell spherical nuclei is expressed as

where α = {nljτ}, uα(r) is the radial part of the wave function and the subscript τ refers to the neutron (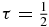 ) or the proton (
) or the proton ( ). The central and spin–orbit potential Uτ(r) and
). The central and spin–orbit potential Uτ(r) and 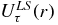 are given by
are given by

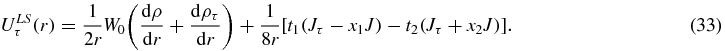
The effective mass is defined by

where ρτ, Tτ and 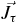 are the density, the kinetic energy density and the spin–current density for the neutron or proton and UC(r) is the Coulomb potential.
are the density, the kinetic energy density and the spin–current density for the neutron or proton and UC(r) is the Coulomb potential.
In equations (31)–(34), only the occupied states of an A-particle system enter into the determination of self-consistent potential Uτ(r) and effective mass 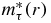 . In the framework of the HF approximation, the excitation of an (A + 1) particle system corresponds to the unoccupied states of the A-particle system. So, calculating the nucleon scattering of energy E from the target nucleus has to firstly solve the HF equations for the occupied states in the target nucleus to find the functions Uτ(r) and
. In the framework of the HF approximation, the excitation of an (A + 1) particle system corresponds to the unoccupied states of the A-particle system. So, calculating the nucleon scattering of energy E from the target nucleus has to firstly solve the HF equations for the occupied states in the target nucleus to find the functions Uτ(r) and 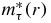 , then we should solve equation (31) with the eigenvalue eα replaced by the continuous variable E.
, then we should solve equation (31) with the eigenvalue eα replaced by the continuous variable E.
Simultaneously, the nucleon effective mass of the bound states takes effect in the nuclear interior, while the impact is in the nuclear exterior for the normal nucleon mass of the scattering states. So, a transformation of the wave function is introduced [32]

then the bound states equation (31) can be transformed into the following scattering states equation:
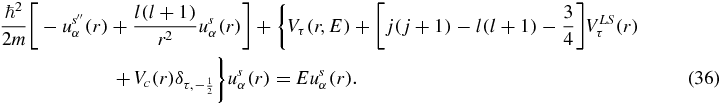
This is the usual Schrodinger equation of scattering radial wave function 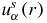 . In this equation, the real part of the energy dependent equivalent local central potential reads as
. In this equation, the real part of the energy dependent equivalent local central potential reads as

The real part of the spin–orbit potential becomes

The Coulomb potential is changed to

In the derivation, the whole energy dependent term 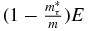 is put into the central potential; actually, it is also reasonable considering the spin–orbit and Coulomb potential are energy dependent. Moreover, since the Coulomb potential has the main contribution in the outside of the nucleus when the r approaches infinity, it can be taken as Vc(r) ≈ Uc(r). The spin–orbit potential has the main contribution in the surface region of the nucleus where
is put into the central potential; actually, it is also reasonable considering the spin–orbit and Coulomb potential are energy dependent. Moreover, since the Coulomb potential has the main contribution in the outside of the nucleus when the r approaches infinity, it can be taken as Vc(r) ≈ Uc(r). The spin–orbit potential has the main contribution in the surface region of the nucleus where  ; therefore, the coefficient
; therefore, the coefficient 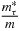 in equation (38) and considering the energy dependence, are needed for the spin–orbit potential. In [15, 16] taking
in equation (38) and considering the energy dependence, are needed for the spin–orbit potential. In [15, 16] taking 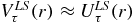 is not suitable. The numerical results of the spin–orbit potential equation (33) show that the contribution produced by the central force involving Jτ(r) is much smaller than directly arising from the two-body spin–orbit force W0. So the real part of the spin–orbit potential for finite nuclei can be reduced to
is not suitable. The numerical results of the spin–orbit potential equation (33) show that the contribution produced by the central force involving Jτ(r) is much smaller than directly arising from the two-body spin–orbit force W0. So the real part of the spin–orbit potential for finite nuclei can be reduced to

where λ = 0.00178 MeV−1 is obtained by fitting the relativistic nucleon optical potential [33]. In the calculation of ρ(r), ρτ(r) and 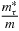 take the calculation results in the nuclear-matter approach. The imaginary part of spin–orbit potential
take the calculation results in the nuclear-matter approach. The imaginary part of spin–orbit potential 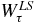 below 100 MeV is usually very small and is omitted here.
below 100 MeV is usually very small and is omitted here.
3. Formulations of the nuclear-matter properties and the Landau parameters
The energy per nucleon E/A, the incompressibility K in symmetric nuclear matter, the symmetry energy Esym, the slope L(ρ0) of nuclear-matter symmetry energy at saturation density and the Landau parameters 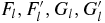 (l = 0, 1) are expressed with Skyrme force parameters t0, t1, t2, t3, x0, x1, x2, x3, α as follows [24, 29, 34]:
(l = 0, 1) are expressed with Skyrme force parameters t0, t1, t2, t3, x0, x1, x2, x3, α as follows [24, 29, 34]:




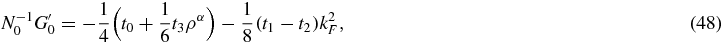




where 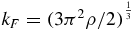 and N0 = 2m*kF/(π2ℏ2).
and N0 = 2m*kF/(π2ℏ2).
4. Determination of Skyrme force parameters
We have chosen a procedure [35] to automatically search for the modified Skyrme force parameters, which may give a satisfactory description of the experimental data including total cross sections, nonelastic cross sections, elastic scattering angular distributions and analyzing powers for certain energy regions. Simultaneously, they can also make allowance for conditions, ensuring an acceptable description of some nuclear matter and finite nuclei characteristics.
In the procedure, the adjustable Skyrme force parameter is performed automatically to minimize a chi-square quantity χ2, which represents the deviation of calculated results from experimental values. We regard χ2 as the function of adjustable parameters. In order to minimize the modified χ2 value, the adjustable parameters are constantly changing along the direction in which the χ2 decreases fastest; each parameter step length can be adjusted respectively and automatically. The total χ2 is defined as

where the right term of each equation orderly represents the χ2 contributions of different quantities, including the total average nuclear reaction, the characteristics of nuclear matter, the binding energy, the charge radius and the single-particle energy levels. W is the relative weight of each controlled quantity in the process of adjustment and the relative weight of the nuclear reaction is 1.0. Firstly, these quantities controlling the nuclear-matter characteristics have no experimental data; there are some empirical values and the range of some quantities have been universally accepted. So, we choose the binding energy per nucleon E/A, the symmetry energy Esym, the incompressibility K, the effective nucleon mass m*/m, the equilibrium density ρ0 and the Fermi momentum kF as the controlled quantities to make a constraint for the nuclear-matter characteristics. The ui respectively represents each controlled quantity. The kF, ρ0 and E/A have definite values and the according error Δui is smaller, while the Δui of K, m*/m, Esym is somewhat larger. The weight WNM is 0.036 for SkC or SkD in the process of adjustment. Secondly, the ΔE and Δr are the experimental error of the binding energy and the charge radius in the third and fourth terms. In this work, the 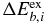 is taken as 0.02 MeV for 15 considered doubly closed shell nuclei, which means that the relative error is about 0.25%. The weight WBE is 0.75 and 1.35 for SkC and SkD respectively. Furthermore, the average value of the real experimental
is taken as 0.02 MeV for 15 considered doubly closed shell nuclei, which means that the relative error is about 0.25%. The weight WBE is 0.75 and 1.35 for SkC and SkD respectively. Furthermore, the average value of the real experimental 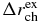 for 15 nuclei is 0.0025 fm [36], which means the relative error is less than 0.1%. The precision is so high that it is difficult to get for multiple nuclei. So we take the
for 15 nuclei is 0.0025 fm [36], which means the relative error is less than 0.1%. The precision is so high that it is difficult to get for multiple nuclei. So we take the 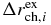 to be 0.03 fm for all nuclei, which means the relative error is about 1.0%. The weight WRC is 1.29 and 1.89 for SkC and SkD respectively. Finally, the EL, i, j is the jth single-particle energy level position for the ith nucleus. NL, i is the energy level number for the ith nucleus. fi is the weight factor. In our work, the 16O, 40, 48Ca, 90Zr and 208Pb are selected and
to be 0.03 fm for all nuclei, which means the relative error is about 1.0%. The weight WRC is 1.29 and 1.89 for SkC and SkD respectively. Finally, the EL, i, j is the jth single-particle energy level position for the ith nucleus. NL, i is the energy level number for the ith nucleus. fi is the weight factor. In our work, the 16O, 40, 48Ca, 90Zr and 208Pb are selected and  is taken as 1.0 MeV for all considered nuclei. Because the number of the energy level of 208Pb is more, the weight f of 208Pb is given as 2 and the rest is taken as 1. The weight WNL is taken as 1.0 for SkC or SkD.
is taken as 1.0 MeV for all considered nuclei. Because the number of the energy level of 208Pb is more, the weight f of 208Pb is given as 2 and the rest is taken as 1. The weight WNL is taken as 1.0 for SkC or SkD.
As the controlled characteristics of a nuclear reaction, we choose the total cross sections, nonelastic cross sections, elastic scattering angular distributions and analyzing powers. We firstly obtain the chi-square for each target, then the average value of the total chi-square for all targets is obtained. The 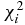 for each target at all energy points, here i and j respectively indicate each target nucleus and energy point, is defined as follows
for each target at all energy points, here i and j respectively indicate each target nucleus and energy point, is defined as follows

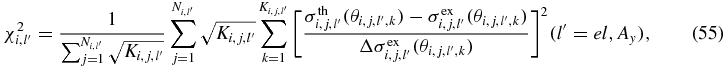
where Ni, l are the energy point numbers of the experimental total cross sections (or nonelastic cross sections). 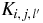 are the angle numbers of the experimental elastic scattering angular distributions (or analyzing powers). The superscripts th and ex represent the theoretically calculated value and the experimental value respectively. σi, l(j) are the total cross sections (or nonelastic cross sections), as well as
are the angle numbers of the experimental elastic scattering angular distributions (or analyzing powers). The superscripts th and ex represent the theoretically calculated value and the experimental value respectively. σi, l(j) are the total cross sections (or nonelastic cross sections), as well as 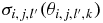 the elastic scattering angular distributions (or analyzing powers) for the kth outgoing angle. Δσ is the experimental error of the corresponding data. For the total cross sections, the evaluated data and average experimental error are used. The average value of the total nuclear reaction chi-square
the elastic scattering angular distributions (or analyzing powers) for the kth outgoing angle. Δσ is the experimental error of the corresponding data. For the total cross sections, the evaluated data and average experimental error are used. The average value of the total nuclear reaction chi-square 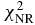 is
is
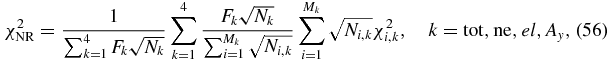
where Mk is the number of targets for reaction k. Ni, k are the energy point numbers of each target nucleus for reaction k. For every type of observable quantity, Nk are total energy point numbers of all targets for reaction k. Fk is the weight factor for tot, ne, el, Ay and respectively taken as 1, 1, 2, 2, which is the reason that the elastic scattering angular distributions (or analyzing powers) have more experimental data of angles for each energy point.
On the basis of the obtained MOP and using the previously described optimization procedure, we have carried out analyses of some selected nuclear reaction experimental data to search the modified Skyrme forces. As a result, the total cross sections, nonelastic cross sections, elastic scattering angular distributions and analyzing powers in the target mass range 24 ⩽ A ⩽ 209 with incident energies below 100 MeV are used in the fits. These experimental data include all of those used by the global POP, called the Koning–Delaroche (KD) potential [37], and some new experimental data with incident neutron energies below 100 MeV. They are all from the electronic nuclear data tables at www-nds.iaea.org/exfor/exfor.htm. The variation of parameters is performed starting from some initial values for well-known Skyrme forces, the starting variants being chosen as effective forces SKa.
As a result, the obtained two new sets of the Skyrme force parameters SkC and SkD are shown in table 1. Simultaneously, the main characteristics of the nuclear matter are also compared between the obtained parameters and other different Skyrme force parameters. We present the comparison of the main nuclear-matter characteristics between the obtained two new sets of the Skyrme force and some frequently used Skyrme forces in table 2. The obtained equilibrium density ρ0, the energy per nucleon E/A, the effective nucleon mass m*/m and symmetry energy Esym are in reasonable agreement with the empirical saturation point (0.16 fm−3, −16.0 MeV, 0.6, 32.0 MeV). The density slopes L(ρ0) are also predicted for SkC, SkD and the other Skyrme forces in table 2. The results of predictions are in the reasonable range [38]. Moreover, the Landau parameters  (l = 0, 1) are given using the obtained Skyrme forces to self-consistently describe the ground and excited state properties. The calculated results are shown in figure 2 together with other Skyrme force parameters obtained by the self-consistent HF+RPA approach, which can give the reasonable results.
(l = 0, 1) are given using the obtained Skyrme forces to self-consistently describe the ground and excited state properties. The calculated results are shown in figure 2 together with other Skyrme force parameters obtained by the self-consistent HF+RPA approach, which can give the reasonable results.
Figure 2. Comparison of Landau parameters using different Skyrme forces.
Download figure:
Standard image High-resolution imageThe χ2 in the nuclear reaction are compared among the different Skyrme forces, which are SkC, SkD, GS2, SKa, SGI, Sly4, SkOP1, SkOP2 and LNS. These results are based on the experimental data of total cross sections, nonelastic cross sections, elastic angular distributions and analyzing powers. They cover the range in the mass number 24 ⩽ A ⩽ 209 with incident neutron energies below 100 MeV. Simultaneously, these results from global neutron POP KD are also given. They are all listed in table 3. It is obvious that the chi-square of the total average nuclear reaction (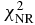 ) for SkC is closer to that for KD than the others. The chi-square of nonelastic cross sections (
) for SkC is closer to that for KD than the others. The chi-square of nonelastic cross sections (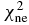 ) and analyzing powers (
) and analyzing powers (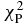 ) for GS2 are closer to that for KD than SkC, while the chi-square of total cross sections (
) for GS2 are closer to that for KD than SkC, while the chi-square of total cross sections (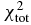 ) is converse. Since the type of Skyrme force GS2 including t4 and x4 terms is not popular, the Skyrme force SkC is more useful than GS2. The
) is converse. Since the type of Skyrme force GS2 including t4 and x4 terms is not popular, the Skyrme force SkC is more useful than GS2. The 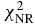 for SkD is slightly larger than that for SkC and GS2, while it is smaller than that for SKa. For SkOP1 and SkOP2, the
for SkD is slightly larger than that for SkC and GS2, while it is smaller than that for SKa. For SkOP1 and SkOP2, the 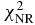 in the energy range up to 100 MeV are both much larger than that for Ska.
in the energy range up to 100 MeV are both much larger than that for Ska.
5. The calculations of HF ground-state properties
In this section, we discuss the results of HF calculations for finite nuclei with the obtained SkC and SkD. Since the SHF equation is solved self-consistently by the usual iteration procedure with the initial wave functions from the Woods–Saxon potential, the nuclear ground-state properties are obtained by the SHF method, such as the density distributions, single-particle energies, binding energies and charge radii, etc. The neutron and proton density distributions in 208Pb are calculated by SkC and SkD, and are shown in figure 3 compared with those for the well-known effective force Sly4.
Figure 3. Calculated neutron, proton and mass density distributions using SkC, SkD and Sly4 for 208Pb.
Download figure:
Standard image High-resolution imageIn figure 4, the relative deviations ΔEb = (Eb, th − Eb, ex)/Eb, ex and Δrch = (rch, th − rch, ex)/rch, ex of the theoretical values for binding energies and charge radii from their experimental data [36, 39] are presented, which are obtained for a number of nuclei from the self-consistent HF calculations with SkC, SkD, SKa and Sly4. It shows that the SkD calculation results reproduce the experimental data with an accuracy of not worse than 1.0%, except for 16O, where the SkD and Sly4 discrepancies of charge radius are 1.6% and 2.3%, respectively. For SkC, the discrepancy of charge radii is a little larger than that of SKa and Sly4, while it is reasonable in the binding energies.
Figure 4. Calculated relative deviations of charge radii (upper panel) and energies per nucleon (lower panel) using SkC, SkD, Sly4 and SKa for the selected nuclei.
Download figure:
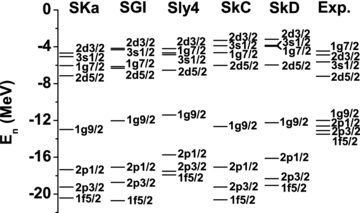
Standard image High-resolution imageThe HF single-particle energy—the eigenvalue of equation (31)—is the removal energy of the particle, provided that the wave functions of the residual particles or density remain unchanged. The neutron and proton single-particle energy levels near the Fermi surface for 16O, 40, 48Ca, 90Zr and 208Pb are calculated with the obtained Skyrme force SkC and SkD. These results are compared with experimental values [19] and those of the other Skyrme interactions. Figures 5 and 6 show these calculated results by SKa, SGI, Sly4, SkC and SkD for 90Zr and compare with experimental data. It is obvious that the energy levels order is right and the neutron energy levels with SkC and SkD have less density than the experimental removal energies, which may be due to the omitted dispersive contribution from the imaginary part of optical potential [24]. Comparing with those of the other Skyrme interactions, the proton energy levels with SkC and SkD are closer to the experimental values.
Figure 5. Comparison of the calculated neutron single-particle energy levels near the Fermi surface using various Skyrme forces with the experimental data [19] for 90Zr.
Download figure:
Standard image High-resolution imageFigure 6. The same as figure 6, but with proton single-particle energy levels [19].
Download figure:
Standard image High-resolution imageFurthermore, the average deviation of binding energies, charge radii and single-particle energy levels near the Fermi surface for different Skyrme forces are presented in table 4. It shows that the found Skyrme force SkC or SkD can reasonably describe the main nuclear structure characteristics for some doubly closed shell nuclei and the SkD is better. Compared with the Sly4, the SkD has the same descriptive power for binding energies and charge radii, moreover, it is a little better for single-particle energy levels and much better for nuclear reaction data. The SkC can also satisfactorily describe binding energies and single-particle energy levels near the Fermi surface, although the average deviation of charge radii are slightly larger than that for some Skyrme forces. In addition, the total average nuclear reaction chi-square with the SkC is 30.39, which is also improved from other well-known effective forces. So, the presented Skyrme forces SkC and SkD are both reasonably unified on describing the nuclear properties.
6. The calculations and analysis of the projectile nucleon reaction data
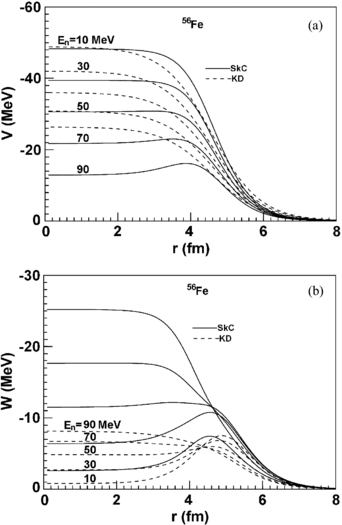
The achieved MOP of finite nuclei by the LDA are analyzed. The radial dependence of the real and imaginary parts of MOP with SkC are compared with those of KD potential for 56Fe at incident neutron energies 10, 30, 50, 70 and 90 MeV, which are presented in figure 7. It is observed that the shapes of curve are similar between them. The absolute value of the real part decreases with increasing radius and incident energy; the dominant contribution of the imaginary part changes from the surface absorption to the volume absorption as the incident energy increases. The values of the corresponding real parts of the MOP are slightly different at the different neutron energies, while there are great differences between them for imaginary parts. The imaginary parts of the MOP are obviously deeper than those of the KD potential, especially for high energy. The analogous results are acquired with SkD.
Figure 7. Radial dependence of neutron MOP with SkC (solid line) and the global neutron POP KD (dash line) for 56Fe. (a) the real part; (b) the imaginary part.
Download figure:
Standard image High-resolution imageThe obtained Skyrme forces SkC and SkD can describe the nuclear ground-state properties, as well as reproduce the nuclear reaction data. The neutron total cross sections, nonelastic cross sections, elastic scattering angular distributions and analyzing power are calculated using the SkC and SkD in the mass range of target nuclei 24 ⩽ A ⩽ 209 with incident energies below 100 MeV. These calculations are systematically compared with experimental data and those results from the neutron global POP KD.
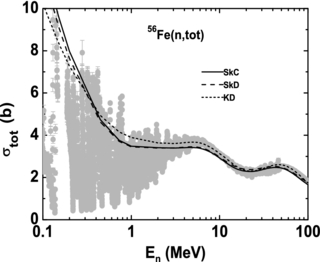
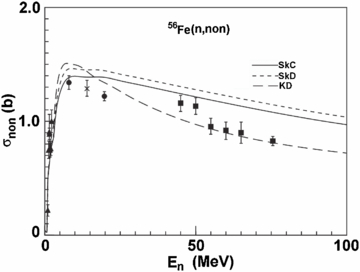
Comparisons of neutron total cross sections calculated results with the experimental data [40, 41] for 56Fe are shown in figure 8. For the light nuclei experimental data of neutron total cross sections, narrow and broad resonances with large amplitudes appear in the hundreds of keV to a few MeV range, which is just the shaded area in figure 8; the MOP is only expected to provide smooth average results in this region. Extently realized is that the shape of predicted neutron total cross sections deviates from the experimental data points between 100 KeV and 3 MeV. At energies above 3 MeV, we get the usual agreement with data; the deviation of our calculations from the experiment are on average within 5% for 56Fe.
Figure 8. Comparison of the calculated total cross sections using SkC (solid line), SkD (dashed line) and KD (short-dashed line) with experimental data (shaded area) [40, 41] for the n + 56Fe reaction.
Download figure:
Standard image High-resolution imageFor most targets, there are only the experimental data of neutron nonelastic cross sections below 40 MeV. New experimental data [42] are given for the natural nuclides natSi, natFe, natZr and natPb between 40 and 80 MeV in 2002. As shown in figure 9, the curve shapes of calculated neutron nonelastic cross sections with SkC and SkD are similar with experimental data [42–45] for 56Fe. The calculated nonelastic cross sections with SkC are in reasonable agreement with the experimental data with incident neutron energy below 50 MeV for 56Fe, while the calculated magnitudes are larger than experimental data for higher energies.
Figure 9. Comparison of the calculated nonelastic cross sections using SkC (solid line), SkD (dashed line) and KD (short-dashed line) with experimental data (symbols) [42–45] for the n + 56Fe reaction.
Download figure:
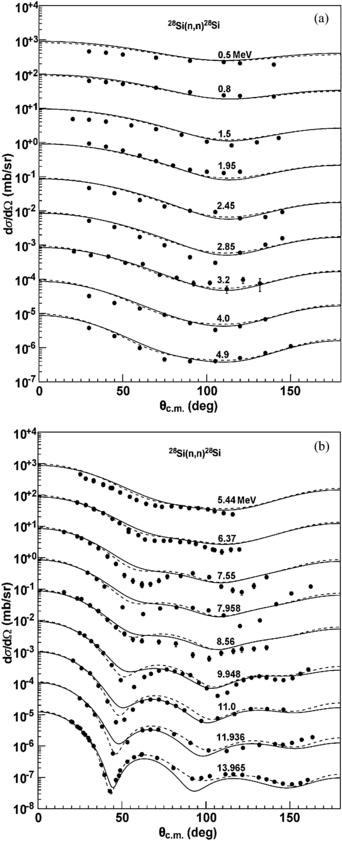
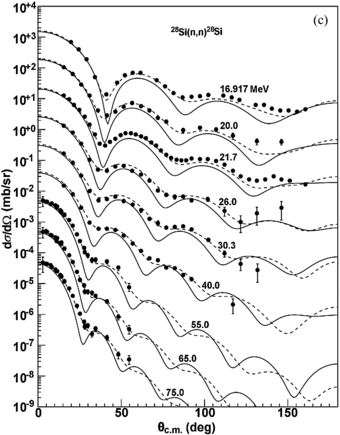
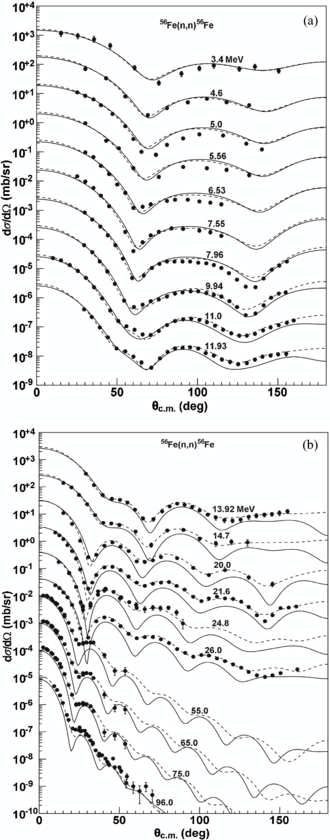
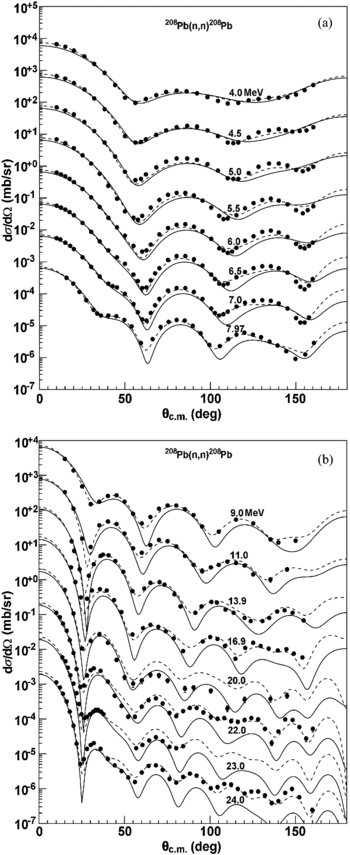
Standard image High-resolution imageThe neutron elastic scattering angular distributions are calculated by SkC and SkD for different targets (from 24Mg to 208Pb) and compared with those results of the global POP KD. The comparisons of SkC results with experimental data and those of KD are only given in the paper. Figure 10 presents these calculated results for 28Si at incident neutron energies from 0.5 to 75.0 MeV together with the experimental data [46–55]. For the SkC, reasonable agreements are obtained except for incident neutron energy 20.0 MeV above 130°, where the calculated results are smaller than experimental data and their curve shapes are similar to the experimental data. Similar results are presented for targets 24Mg and 27Al. Those results are well described for 31P and 32S. The neutron elastic scattering angular distributions for 56Fe at incident energies from 3.4 to 96.0 MeV are given in figure 11; the calculated results are in reasonable agreement with experimental data [55–62]. Similar results are presented for 52Cr, 55Mn, 54Fe, 58, 60Ni, 63, 65Cu, 80Se and 88Sr. The results of SkC are in good agreement with the experimental data for 96, 98, 100Mo, 103Rh, 106Pd, 107Ag, 114Cd, 115In, 120Sn, 123Sb and 141Pr. The reasonable agreements are obtained below 13.9 MeV for 206, 208Pb and 209Bi. There is a slight underestimation at the other energies above 70° for the SkC, but the curve shapes of our results are similar to the experimental data. Figure 12 shows the comparisons of SkC and KD results with the experimental data [54, 55, 63–70] for 208Pb.
Download figure:
Standard image High-resolution imageFigure 10. Calculated elastic scattering angular distributions using SkC (solid line) and KD (dashed line) compared with experimental data (symbols) [46–55] for the n + 28Si reaction. The results are offset by factors of 10.
Download figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageTable 1. The obtained Skyrme force parameters.
| SkC | SkD | |
|---|---|---|
| t0 (MeV fm3) | −1353.099 | −1577.398 |
| t1 (MeV fm5) | 594.171 | 631.477 |
| t2 (MeV fm5) | −61.613 | −58.655 |
| t3 (MeV fm3 + 3α) | 5810.413 | 7099.157 |
| x0 | 0.0320 | 0.0579 |
| x1 | 0.0401 | 0.129 |
| x2 | −0.608 | −0.350 |
| x3 | 0.0276 | −0.234 |
| α | 0.446 | 0.331 |
| W0 (MeV fm5) | 130.0 | 146.707 |
Table 2. The main nuclear-matter characteristics of different Skyrme forces.
| SkC | SkD | SKa | GS2 | SGI | Sly4 | SkOP1 | SkOP2 | LNS | |
|---|---|---|---|---|---|---|---|---|---|
| kF (fm−1) | 1.340 | 1.312 | 1.320 | 1.330 | 1.317 | 1.332 | 1.343 | 1.330 | 1.372 |
| ρ0 (fm−3) | 0.162 | 0.153 | 0.155 | 0.159 | 0.154 | 0.160 | 0.164 | 0.159 | 0.175 |
| E/A (MeV) | −16.088 | −15.948 | −15.996 | −16.018 | −15.898 | −15.977 | −16.107 | −16.113 | −15.319 |
| K (MeV) | 285.021 | 267.154 | 263.202 | 300.000 | 261.80 | 229.954 | 227.259 | 251.320 | 210.815 |
| m*/m | 0.557 | 0.564 | 0.608 | 0.600 | 0.608 | 0.695 | 0.733 | 0.759 | 0.826 |
| Esym (MeV) | 30.814 | 34.910 | 32.910 | 25.959 | 28.328 | 32.003 | 28.254 | 28.964 | 33.426 |
| L(ρ0) | 64.570 | 78.147 | 74.623 | 30.261 | 63.864 | 45.956 | 33.018 | 50.786 | 61.451 |
Table 3. The χ2 of all considered quantities with different Skyrme forces and KD for targets of 24 ⩽ A ⩽ 209 with incident neutron energies below 100 MeV. They are total cross sections 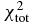 , nonelastic cross sections
, nonelastic cross sections 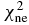 , elastic scattering angular distributions
, elastic scattering angular distributions 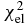 , analyzing powers
, analyzing powers 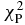 and total average nuclear reaction
and total average nuclear reaction 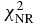 , respectively.
, respectively.
| Force | 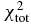 |
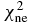 |
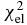 |
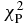 |
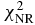 |
|---|---|---|---|---|---|
| KD | 2.89 | 3.73 | 16.03 | 20.21 | 10.77 |
| SkC | 14.48 | 23.76 | 39.19 | 50.16 | 30.39 |
| SkD | 11.92 | 34.87 | 45.62 | 60.54 | 34.83 |
| GS2 | 20.44 | 13.50 | 40.60 | 42.90 | 31.31 |
| SKa | 11.58 | 43.02 | 60.18 | 50.01 | 42.42 |
| SGI | 12.41 | 50.22 | 70.42 | 45.57 | 48.44 |
| Sly4 | 40.29 | 147.04 | 139.28 | 61.70 | 104.49 |
| SkOP1 | 39.09 | 101.31 | 190.01 | 110.98 | 127.72 |
| SkOP2 | 34.54 | 72.15 | 184.45 | 98.93 | 119.31 |
| LNS | 39.61 | 112.21 | 190.27 | 80.92 | 127.38 |
Table 4. The average deviation for binding energies, charge radii and single-particle energy levels near the Fermi surface with different Skyrme forces.
| Force | 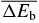 (%) (%) |
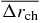 (%) (%) |
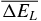 (MeV) (MeV) |
|---|---|---|---|
| SkC | 0.889 | 1.552 | 2.23 |
| SkD | 0.459 | 0.382 | 2.11 |
| SKa | 0.893 | 0.327 | 2.23 |
| SGI | 2.474 | 0.287 | 2.31 |
| Sly4 | 0.368 | 0.397 | 3.18 |
| SkOP1 | 0.893 | 0.574 | 3.43 |
| SkOP2 | 0.980 | 0.412 | 3.66 |
| LNS | 4.121 | 2.486 | 3.58 |
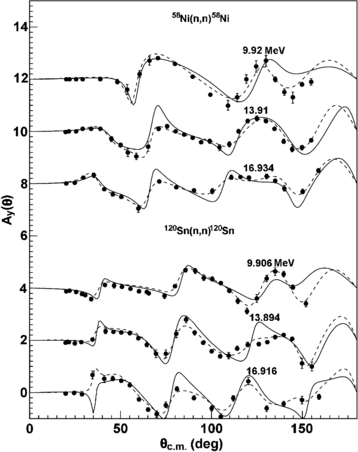
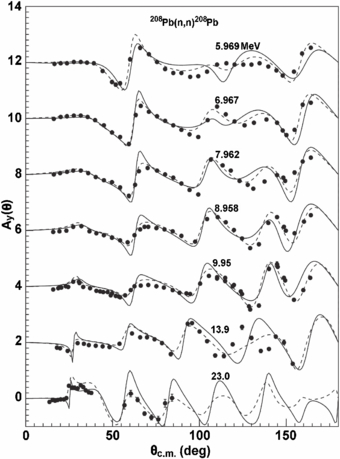
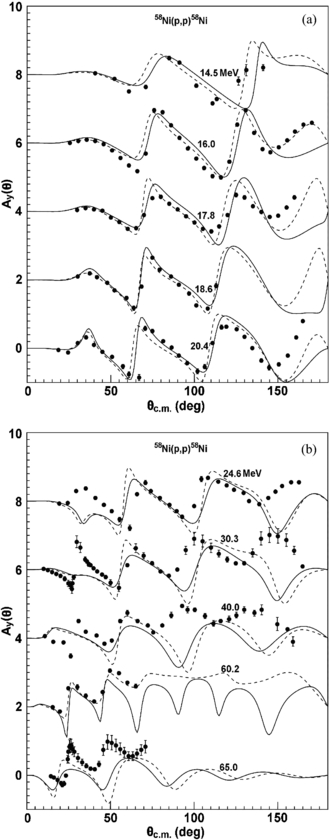
For calculations of the elastic scattering differential cross sections, we carry out the calculations of analyzing power Ay(θ) for different targets and incident energies. The analyzing power Ay(θ) for 58Ni, 120Sn and 208Pb are plotted in figures 13 and 14. Obviously, the agreements of theoretical curves with experimental data [65, 67, 68, 71, 72] are also satisfactory.
Figure 13. Calculated analyzing powers using SkC (solid line) and KD (dashed line) compared with experimental data (symbols) [71, 72] for the n + 58Ni and 120Sn reaction. The curves and data points at the bottom represent true values, while the others are added by 2.0.
Download figure:
Standard image High-resolution imageDownload figure:
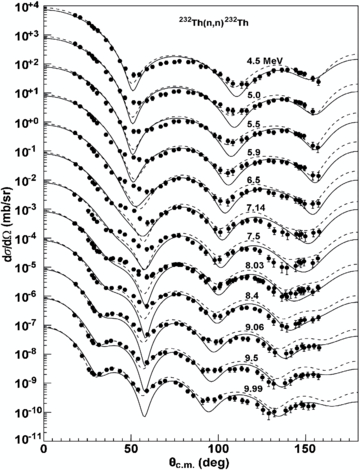
Standard image High-resolution imageThe nuclear reaction data for A = 23 and 209 < A ⩽ 239 are predicted at an incident neutron energy below 100 MeV. Since the discrepancy is not too great between the spherical nuclei and common actinide nucleus, the largest deformation parameter is about 0.2 for the common actinide nucleus. Furthermore, we applied the spherical symmetry model to deformed actinides and good results were obtained [73]. So, the nuclear reaction data for actinide nucleus 232Th, 235, 238U and 239Pu are predicted to be in this range. Some incident neutron experimental data [74] including the elastic and inelastic scattering angular distributions were given for 232Th. In figure 15, the largest deviations seem to occur for the first minimum, the reason for which is that the inelastic scattering is not included in the calculations. Similar results are obtained for 235; 238U and 239Pu.
Figure 15. Comparison of the predicted elastic scattering angular distributions using SkC (solid line) and KD (dashed line) with experimental data (symbols) [74] for the n + 232Th reaction. The results are offset by factors of 10.
Download figure:
Standard image High-resolution imageBesides, the reaction cross sections, elastic scattering angular distributions and analyzing powers for the projectile proton are also predicted with the obtained Skyrme force parameters SkC and SkD.
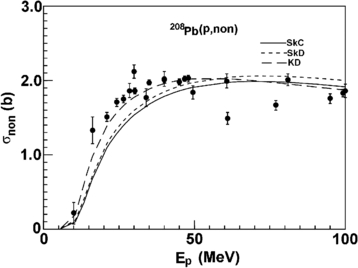
The proton reaction cross sections for different targets (from 23Na to 239Pu) are calculated using the obtained Skyrme force parameters SkC and SkD. These calculated results are compared with those of the proton global POP KD. Most experimental data of reaction cross sections are taken from [75]; the recent experimental data from [76] is also included. There are few experimental data of the proton reaction cross sections below 100 MeV for actinide nuclei 232Th and 238U. The comparisons of the calculated results with experimental data [75, 76] for 208Pb are shown in figure 16. The results of SkC and SkD underestimate the reaction cross section below about 35 MeV for 208Pb, but the curve shapes of our results are similar to the experimental data. The results of SkC and SkD are agreement with the experimental data for the higher energies.
Figure 16. Comparison of the predicted nonelastic cross sections using SkC (solid line), SkD (dashed line) and KD (short-dashed line) with experimental data (symbols) [75, 76] for the p + 208Pb reaction.
Download figure:
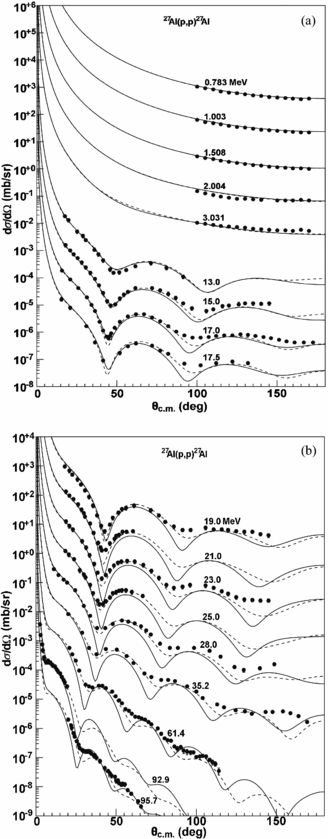
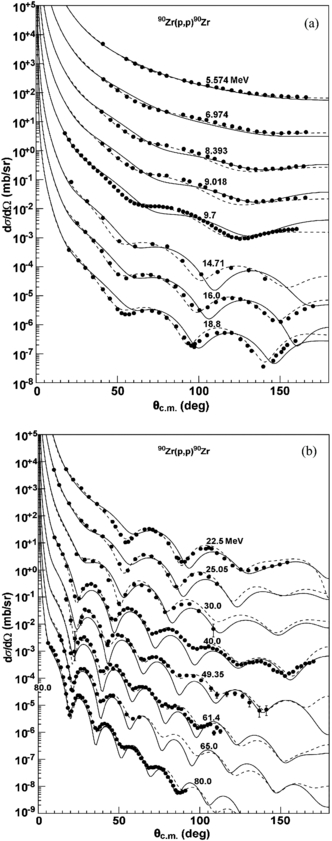
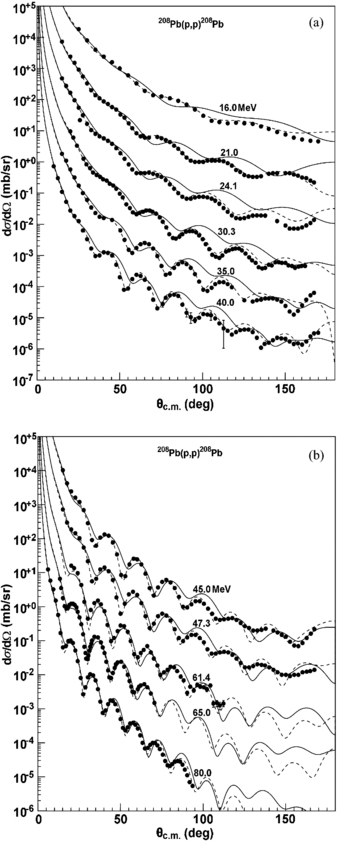
Standard image High-resolution imageThe calculated proton elastic scattering angular distributions using SkC and the proton global POP KD are compared with the experimental data for different targets. Figure 17 shows the comparisons of the SkC results with the experimental data [77–83] for 27Al at incident proton energies from 0.783 to 95.7 MeV. Reasonable agreements between the SkC results and the experimental data are obtained, except for incident proton energy 23.0 MeV above 130°, where the SkC results are smaller than the experimental data and the curve shapes of our results are similar to the experimental data. The SkC results are good in agreement with the experimental data [82, 84–93] for 90Zr. These results are presented in figure 18. For 208Pb, the comparisons of the SkC results with the experimental data [82, 84, 86–88, 94, 95] are plotted in figure 19. It is observed that reasonable agreements are obtained above 40 MeV. There is a slight underestimation at the other energies above 80°, but the curve shapes of our results are similar to the experimental data. The elastic scattering angular distributions for actinide nucleus 232Th are also compared with the experimental data [83, 86, 96] at incident proton energies from 16.0 to 94.7 MeV, as shown in figure 20. The SkC results are a little larger than experimental data above 80° between 16.0 and 26.0 MeV.
Figure 17. Comparison of the predicted elastic scattering angular distributions using SkC (solid line) and KD (dashed line) with experimental data (symbols) [77–83] for the p + 72Al reaction. The results are offset by factors of 10.
Download figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageThe proton analyzing powers are calculated with the obtained Skyrme forces SkC and SkD for some targets. In most cases, better or acceptable agreements are obtained between our predictions and the experimental data. Comparisons of the SkC results with the experimental data [84, 86, 97–103] and those of KD for 58Ni are plotted in figure 21. For 58Ni, an overall good description of the analyzing power data is given between 14.4 and 20.4 MeV, although the extreme is not completely reached as the incident proton energy increases.
Figure 21. Comparison of the predicted analyzing powers using SkC (solid line) and KD (dashed line) with experimental data (symbols) [84, 86, 97–103] for the p + 58Ni reaction. The curves and data points at the bottom represent true values, while the others are added by 2.0.
Download figure:
Standard image High-resolution image7. Conclusion
The nucleon MOP is given by the standard Skyrme force through the Green function method and the nucleon optical potential for finite nuclei is obtained by the LDA. The spin–orbit potential has also been further amended by the SHF approach and the relativistic mean field results. Using the given nucleon MOP, two new sets of Skyrme interaction parameters are achieved by simultaneously fitting the characteristics of nuclear matter, the finite nuclei, the neutron induced reaction cross sections and polarization data, including total cross sections, nonelastic cross sections, elastic scattering angular distributions and analyzing powers in the target mass range 24 ⩽ A ⩽ 209 with incident neutron energies below 100 MeV. Moreover, the proton induced and nucleon-actinide reactions (from 23Na to 239Pu) with incident nucleon energies below 100 MeV are also predicted by the obtained Skyrme interaction parameters and the reasonable calculated results are given. Although some calculation results are not good and need to be improved in the future, the more experimental data are considered, the larger the predictive power of the obtained Skyrme force parameters will become. So, the Skyrme interaction parameter SkC and SkD including ten parameters can be used to predict those data for the stable or unstable target in the mass range 23 ⩽ A ⩽ 239 with incident nucleon energies below 100 MeV. Simultaneously, these results prove that, along with the success of the SHF method in the description of ground state properties, the application of the Skyrme interaction for describing some quantities in the nuclear reaction in terms of the optical model leads to promising results. This gives us reasons to hope for constructing potentials of the shell and optical models in a unified approach based on Skyrme forces. Up to now, the Skyrme force parameters have been achieved by simultaneously fitting some characteristics of nuclear structure and nuclear reaction, which is a direction to study the Skyrme force.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (grant no 11175260) and National Basic Research Program of China (973 Program, grant no 2007CB209903).