Abstract
A superconductor-semiconducting nanowire-superconductor heterostructure in the presence of spin–orbit coupling and magnetic field can support a supercurrent even in the absence of phase difference between the superconducting electrodes. We investigate this phenomenon—the anomalous Josephson effect—employing a model capable of describing many bands in the normal region. We discuss the geometrical and symmetry conditions required to have a finite anomalous supercurrent, and in particular we show that this phenomenon is enhanced when the Fermi level is located close to a band opening in the normal region.
Export citation and abstract BibTeX RIS
1. Introduction
Hybrid nanostructures, combining superconducting and semiconducting elements, hold promise for novel functionalities, and their transport properties are attracting increased attention and intense experimental and theoretical effort. A two-dimensional electron gas trapped in a semiconductor heterostructure, and contacted with superconductors, provides an archetypical superconductor/normal metal/superconductor (SNS) system [1]. Semiconducting quantum dots [2] or semiconducting nanowires [3–5] can be contacted with superconductors. These devices allow for the gating of the semiconductor with increased control of its carrier density [6]. In this respect, hybrid structures including ferromagnetic barriers offer another exciting arena on its own [7, 8] and are of the utmost relevance for spintronics [9, 10]. Recently, there has been a burst of activity regarding hybrid heterostructures involving semiconductors with strong spin–orbit (SO) interaction, as SO can also be a tremendous tool for controlling spin transport. It has been established that SO is at the origin of a topological non-trivial order in topological insulator materials respecting time reversal symmetry [11–14]. Semiconducting nanowires, with SO interaction, Zeeman spin splitting induced by a longitudinal magnetic field, and superconductivity, can be described in terms of a chain of spinless fermions. It has been shown that zero energy neutral excitations (Majorana bound states) localize at the end of the nanowire, when the system is driven to the topological non-trivial state [15–18]. As Majorana bound states can become a valuable tool in future quantum information devices [19], it is becoming more and more essential nowadays to characterize the superconducting proximity in quasi one-dimensional SNS structures with SO and Zeeman spin splitting both in the topologically trivial phase and in the non-trivial one.
Here we consider a semiconductor nanowire with both Rashba and Dresselhaus SO coupling, forming a quasi one-dimensional wire, contacted with conventional s-wave singlet pairing superconductors. We assume that the normal region is much shorter than the superconducting coherence length ξ (short junction limit), so that the superconducting coherence is fully established across the SNS structure. In the short junction limit, the Josephson current is carried by the Andreev bound states, belonging to the discrete subgap energy spectrum [20].
The anomalous Josephson effect (AJE), consists of a non-zero Josephson current Ia flowing with zero phase difference between the superconducting order parameters of the contact superconductors, φ = 0. This implies that the zero current ground state is located at a phase difference φ0 ≠ {0, π} (in some of the literature these junctions are named φ0-junctions [21]). The situation under consideration here is different from the case of Josephson junctions with a strong negative second harmonic [22]. For these junctions the ground state is located at a phase difference determined by the minimum of the Josephson energy, which depends on the relative strength of the first and the second harmonic.
The AJE was initially predicted for unconventional superconductors [23–28]. Several possibilities for the normal region have been addressed: a magnetic normal metal [21, 29–33], a one-dimensional quantum wire, a quantum dot [34, 35], a multichannel system with a barrier or a quantum point contact [36, 37], and a semiconducting nanowire [38, 39]. Anomalies of the Josephson current have also been predicted in the presence of Coulomb interactions and SOI for a wire [40, 41] or a quantum dot [35] contacted with conventional s-wave superconductors.
We show that Ia is maximum when the system's parameters are away from highly symmetrical points (i.e. pure Rashba, pure Dresselhaus, or equal strength of Rashba and Dresselhaus SO interaction). Moreover, while studying the dependence of Ia on the location of the chemical potential EF, we find an enhancement of Ia when EF is close to the opening of a new channel in the normal region. Similar threshold effects are not new in scattering theory, even in the absence of spin effects [42].
This paper is organized as follows: in section 2 we review the relation between the Josephson current and the scattering matrix of the normal region. In section 3 we show how to compute the scattering matrix as a function of the chemical potential, the spin–orbit coupling and the Zeeman field. In section 4 we discuss our results, we summarize in section 5.
2. Andreev states and current calculation
We consider a quasi 1D nanowire between two conventional s-wave superconductors. In our model the nanowire is in the region
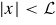 , while the left (right) superconductor is in the region
, while the left (right) superconductor is in the region
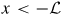
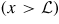 . We assume that the SO interaction and the magnetic field are only present in the nanowire region. Recent advances in the fabrication of nanowires of InAs and InSb have made materials with a large g-factor and a strong spin–orbit (SO) interaction available. A topological phase with Majorana fermions as boundary excitations could appear when the SO interaction was present in the leads [43]. By contrast, we assume no SO interaction in the leads as we want to focus on the non-topological phase, which has been poorly addressed in the literature. Moreover, due to a large g factor in the semiconducting region, a strong Zeeman spin splitting can be recovered, even for weak values of the magnetic field which, in turn, does not affect the superconductors and is accordingly neglected in the leads. Moreover, we disregard the orbital effect of the magnetic field, which we take perpendicular to the plane containing the nanowire and the top surface of the leads.
. We assume that the SO interaction and the magnetic field are only present in the nanowire region. Recent advances in the fabrication of nanowires of InAs and InSb have made materials with a large g-factor and a strong spin–orbit (SO) interaction available. A topological phase with Majorana fermions as boundary excitations could appear when the SO interaction was present in the leads [43]. By contrast, we assume no SO interaction in the leads as we want to focus on the non-topological phase, which has been poorly addressed in the literature. Moreover, due to a large g factor in the semiconducting region, a strong Zeeman spin splitting can be recovered, even for weak values of the magnetic field which, in turn, does not affect the superconductors and is accordingly neglected in the leads. Moreover, we disregard the orbital effect of the magnetic field, which we take perpendicular to the plane containing the nanowire and the top surface of the leads.
We look for solutions of the Bogoliubov–de Gennes equations:
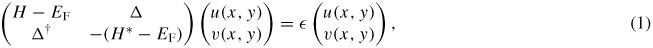
where  measures the energy with respect to the Fermi level EF, while u(x, y) and v(x, y) are, respectively, the electron and hole spinors in the Nambu representation. Notice that the spin structure is not explicit at this level. The even parity pairing potential is taken to be:
measures the energy with respect to the Fermi level EF, while u(x, y) and v(x, y) are, respectively, the electron and hole spinors in the Nambu representation. Notice that the spin structure is not explicit at this level. The even parity pairing potential is taken to be:

with
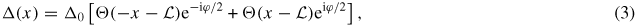
and we take a symmetric phase difference φ between the two superconductors. Θ(x) is the Heaviside step function.
For the sake of generality we assume that both Rashba and Dresselhaus SO interactions are present5. We notice that in conventional InAs/InSb nanowires the Rashba term is in general much larger than the Dresselhaus one. However, in our calculation we also explore a region of parameters where the two interactions have comparable strength, which is achievable in (In,Ga)As quantum wells [44]. We assume a harmonic confining potential in the y directions, so that electrons propagate along the the x direction. The choice of a harmonic confining potential is particularly convenient when expressing the matrix elements of the SO interaction [45, 46]6. The Hamiltonian reads:

where
![$\alpha(x)=\alpha[\Theta(x+\mathcal{L})-\Theta(x-\mathcal{L})]$](https://content.cld.iop.org/journals/0953-8984/27/20/205301/revision1/cm512494ieqn004.gif) and
and
![$\beta(x)=\beta[\Theta(x+\mathcal{L})- \Theta(x-\mathcal{L})]$](https://content.cld.iop.org/journals/0953-8984/27/20/205301/revision1/cm512494ieqn005.gif) are, respectively, the strength of the Rashba and Dresselhaus component of the SO interaction. An important ingredient in equation (4) is given by the δ-like scattering centers, with strength δa and δb different from each other. This point is crucial, here, as such an asymmetry between left and right contact is fundamental in determining the anomalous Josephson effect, as we will discuss in the following. Finally, B is the applied magnetic field, while the last term in equation (4) is necessary to preserve the hermicity of the Hamiltonian operator in case of a position-dependent SO interaction strength. Due to the presence of the transverse confinement potential, it is natural to employ a scattering approach to the problem. Indeed, in the superconducting leads one can define transverse modes, so that the electron wave functions in the x-direction are characterized by a band and a spin index.
are, respectively, the strength of the Rashba and Dresselhaus component of the SO interaction. An important ingredient in equation (4) is given by the δ-like scattering centers, with strength δa and δb different from each other. This point is crucial, here, as such an asymmetry between left and right contact is fundamental in determining the anomalous Josephson effect, as we will discuss in the following. Finally, B is the applied magnetic field, while the last term in equation (4) is necessary to preserve the hermicity of the Hamiltonian operator in case of a position-dependent SO interaction strength. Due to the presence of the transverse confinement potential, it is natural to employ a scattering approach to the problem. Indeed, in the superconducting leads one can define transverse modes, so that the electron wave functions in the x-direction are characterized by a band and a spin index.
The spectrum of equation (1) consists of a finite set of bound states (Andreev levels) with energy | | < Δ0, and a continuum of states with |
| < Δ0, and a continuum of states with | | > Δ0. The current can be obtained from the ground state energy Egs(φ) at zero temperature by the thermodynamic relation
| > Δ0. The current can be obtained from the ground state energy Egs(φ) at zero temperature by the thermodynamic relation

In the short junction limit only the subgap Andreev states contribute to the Josephson current (in the long-junction limit, one can use the technique developed in [47, 48] to exactly account for contributions from all the states, to leading order in the inverse junction length). Thus, one obtains

In equation (6) 'n' labels the Andreev states, the primed sum means that only negative energy (occupied) Andreev states are considered. Notice that a factor of 2 differences with the usual relation is found in the literature because the spin degeneracy is lifted here. Before we move further in our analysis it is useful to note, as put forward in [38, 49], how the symmetry of equations (1) can rule out the anomalous Josephson effect. Denoting with
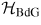 the matrix in equation (1), in the absence of a magnetic field, the time reversal operator
the matrix in equation (1), in the absence of a magnetic field, the time reversal operator
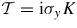 (with K the complex conjugation operator) induces a self-duality
(with K the complex conjugation operator) induces a self-duality
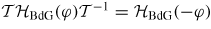 , so that, if
, so that, if
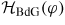 has an allowed energy eigenvalue En,
has an allowed energy eigenvalue En,
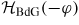 will have the same eigenvalue. In this case the anomalous Josephson effect is ruled out. Similarly, when there is no SO interaction, one obtains
will have the same eigenvalue. In this case the anomalous Josephson effect is ruled out. Similarly, when there is no SO interaction, one obtains
 , which again implies no anomalous Josephson effect. The previous considerations are general, not depending on the details of the Hamiltonian describing the nanowire (explicit form of the confinement potential, presence of disorder, etc). We notice that for our specific model, even in the presence of SO interaction and magnetic field along the z direction, when δa = δb the operator
, which again implies no anomalous Josephson effect. The previous considerations are general, not depending on the details of the Hamiltonian describing the nanowire (explicit form of the confinement potential, presence of disorder, etc). We notice that for our specific model, even in the presence of SO interaction and magnetic field along the z direction, when δa = δb the operator
 (with Π the parity operator) also gives
(with Π the parity operator) also gives
 ; for this reason, in order to recover the anomalous Josephson effect, in this article we always assume asymmetric delta potentials at the interfaces between normal and superconducting regions.
; for this reason, in order to recover the anomalous Josephson effect, in this article we always assume asymmetric delta potentials at the interfaces between normal and superconducting regions.
The calculation of the Andreev states in a quasi one-dimensional system can be conveniently done using a scattering matrix approach [20]. We assume that for energies below the superconducting gap Δ0 at the interface between the normal and the superconducting regions only intra-channel Andreev scattering takes place where a hole (electron) with spin σ is reflected as an electron (hole) with spin −σ. Accordingly, these processes are encoded in the relations

and the Andreev scattering matrix is defined as:

with
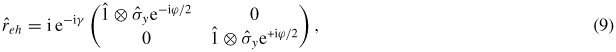
and
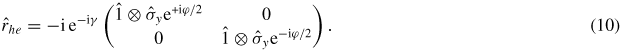
In equation (10)
 is the identity matrix in the channel space, the
is the identity matrix in the channel space, the
 Pauli matrix acts in the spin space and γ = arccos(
Pauli matrix acts in the spin space and γ = arccos( /Δ). In the normal region Andreev scattering processes are not allowed, which allows us to write
/Δ). In the normal region Andreev scattering processes are not allowed, which allows us to write

The energy of the Andreev bound states is determined by the following equation [50]:

In the short-junction limit one can disregard the energy dependence of the scattering matrix and take
 . Therefore, in order to solve equation (12), one has to calculate the scattering matrix of the normal region at the Fermi energy. We carry on this task in the next section.
. Therefore, in order to solve equation (12), one has to calculate the scattering matrix of the normal region at the Fermi energy. We carry on this task in the next section.
3. Model and calculation of the scattering matrix S
In this section we evaluate the scattering matrix S of the normal region as a function of the Fermi energy. We address the case of one open channel (with two spin orientations). However, our method is easily generalized to two or more open channels.
As a first step, we solve the Schroedinger equation within the L-lead
 and the R-lead
and the R-lead
 (assuming no superconductivity), as well as in the central region SO with spin–orbit interaction
(assuming no superconductivity), as well as in the central region SO with spin–orbit interaction
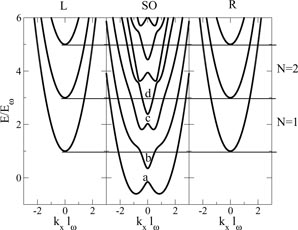
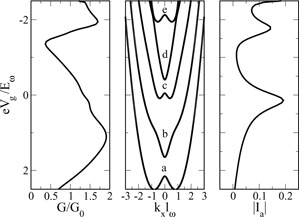
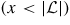 (see figures 1 and 2). Therefore, we derive the scattering matrix by matching the solutions at the interfaces between the three regions. In figure 2 we plot the band structure in these three regions (parameters in the caption). One can notice that the band structure is strongly influenced by the presence of the spin–orbit coupling and, interestingly enough, depending on the position of the Fermi level, the number of open channels of the leads and the central region can be different.
(see figures 1 and 2). Therefore, we derive the scattering matrix by matching the solutions at the interfaces between the three regions. In figure 2 we plot the band structure in these three regions (parameters in the caption). One can notice that the band structure is strongly influenced by the presence of the spin–orbit coupling and, interestingly enough, depending on the position of the Fermi level, the number of open channels of the leads and the central region can be different.
Figure 1. Electron and hole incoming states in the (ai) are scattered into outgoing states (bi) by a nanowire region described by the scattering matrix Se/h. Andreev scattering at NS interfaces where electron (hole) states are scattered into hole (electron) states is described by the Andreev scattering matrix SA.
Download figure:
Standard image High-resolution imageFigure 2. Here we show the band structure obtained by numerically diagonalizing the Hamiltonian of Equation (4), we define Eω = ℏω/2 and
 . In this figure we use the following paramenters: mζ lω/ℏ2 = 0.9, θ = π/8, gμBB/Eω = 0.6 and the number of transverse bands l = 5.
. In this figure we use the following paramenters: mζ lω/ℏ2 = 0.9, θ = π/8, gμBB/Eω = 0.6 and the number of transverse bands l = 5.
Download figure:
Standard image High-resolution imageTo obtain a reliable approximation for the eigenfunctions and eigenvectors in the SO region, we exactly diagonalize the Hamiltonian on the basis of the wave functions {eiκxχm(y)φσ}, with {χm(y)} being the eigenfunctions of the harmonic oscillator and φσ the eigenfunctions of σz, by considering a finite number l of transverse modes {χm(y)}, m ∈ {1, ..., l}. The above basis functions are eigenfunctions in the right-hand (left) region R (L).
Such an approximation is indeed expected to provide a good description of the scattering dynamics of the system at energies small compared to the energy of the last transverse mode considered. In our calculation we find that the low-energy properties of our system are well described if we truncate the basis at l = 5.
Therefore, the problem is now reduced to finding the eigenvalues and the eigenfunction of the corresponding 2l × 2l-dimensional Hamiltonian matrix
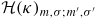 . For a given energy E the allowed κi are the solution of
. For a given energy E the allowed κi are the solution of

For each value of the energy we have κi(i = 1, .., 4l) solutions, and the generic eigenfunction is:
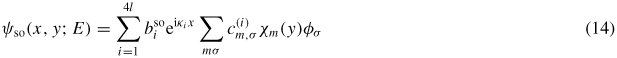
where the coefficients
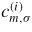 have to be determined numerically (the coefficients
have to be determined numerically (the coefficients
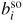 are determined by imposing the matching conditions listed below). We note, with reference to figure 2, that the number of real {κi} in the SO region may vary according to the value of the Fermi energy. As we will show later, changing the number of real {κi} without affecting the number of propagating channels in the leads, greatly affects the conductance of the system when it is in the normal state, and in turn the Josephson current when the leads are superconducting.
are determined by imposing the matching conditions listed below). We note, with reference to figure 2, that the number of real {κi} in the SO region may vary according to the value of the Fermi energy. As we will show later, changing the number of real {κi} without affecting the number of propagating channels in the leads, greatly affects the conductance of the system when it is in the normal state, and in turn the Josephson current when the leads are superconducting.
As we consider one open transport channel in the leads with two spin orientations, the scattering matrix Se introduced in the previous section is given by:

with

and similarly for rR, tRL and tLR.
In order to obtain the total S-matrix, one has to compute all the reflection and transmission coefficients, by matching the wave function in equation (14) with the one in the leads for any possible choice of scattering boundary conditions. For instance, let us consider explicitly the case of a spin-up particle incoming from the left-hand side. In this case the wave functions within L and R are respectively given by:


with k1 = [2m(E − ℏω/2)]1/2/ℏ and ki = [2m(ℏω(i + 1/2) − E)]1/2/ℏ for {i = 2, ..., l}.
The wave function at
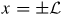 must be continuous, its derivative with respect to x must be, in general, discontinuous to account for the non-perfect transparency at the interfaces and the SO interaction (see equation (4)). Projecting the equations corresponding to the matching conditions onto the basis states χm(y)φσ(m = 1, ..., l; σ = ↑, ↓) we obtain the following set of equations:
must be continuous, its derivative with respect to x must be, in general, discontinuous to account for the non-perfect transparency at the interfaces and the SO interaction (see equation (4)). Projecting the equations corresponding to the matching conditions onto the basis states χm(y)φσ(m = 1, ..., l; σ = ↑, ↓) we obtain the following set of equations:




Therefore, we have a set of 8l equations which we solve numerically to determine the corresponding S matrix elements elements. Repeating the calculation for each possible incoming channel we construct the complete scattering matrix Se as a function of the energy E, which we set to EF in the following as we are interested only in on-shell scattering matrices.
4. Results and discussion
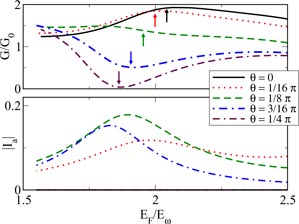
In this section we use the scattering matrix of the normal region to derive the Andreev spectrum using equation (12), from which we eventually derive the Josephson current as a function of the phase difference between the two superconductors. We study the Josephson current at φ = 0, i.e. the anomalous Josephson current Ia, as a function of the Fermi energy. To gain more information, we also show the normal conductance G = G0Tr t†t (with G0 = e2/h) of the corresponding normal system in the same range of values of the Fermi energy. As we will show in detail below, the AJE is accompanied by a change in the normal conductance in correspondence of the opening of a new transport channel in the nanowire region.
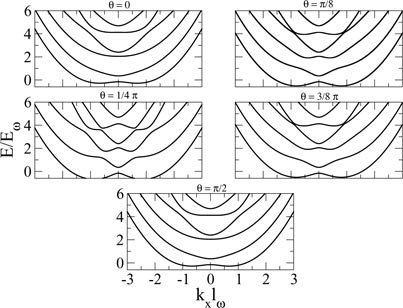
In figure 3 the band structure is reported, with an increasing ratio between the strength α of the Rashba and the strength β of the Dresselhaus term. We parametrize them as α = ζ cos (θ) and β = ζ sin (θ). Energies are plotted in units of Eω = ℏω/2. We notice that the Hamiltonian (4) satisfies the relation UH(θ)U−1 = H(π/2 − θ) with U = exp{iπ σz/4}K; this implies that the normal conductance satisfies G(θ) = G(π/2 − θ), and explains the band structure illustrated in figure 3. In figure 4 in the top and bottom panel we plot the normal conductance and the anomalous Josephson current, respectively, for different values of the angle θ from 0 to π/4. The operator U acting on the Bogoliubov–de Gennes Hamiltonian induces the relation
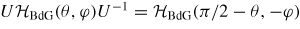 , thus the Josephson current must obey the following constraint I(θ, φ) = −I(π/2 − θ, −φ). We have Ia(θ) = −Ia(π/2 − θ), in particular the anomalous Josephson current is zero for θ = π/4. Besides, for θ = π/4 we find that the anomalous Josephson current is also zero for θ = 0 (pure Rashba) and θ = π (pure Dresselhaus).
, thus the Josephson current must obey the following constraint I(θ, φ) = −I(π/2 − θ, −φ). We have Ia(θ) = −Ia(π/2 − θ), in particular the anomalous Josephson current is zero for θ = π/4. Besides, for θ = π/4 we find that the anomalous Josephson current is also zero for θ = 0 (pure Rashba) and θ = π (pure Dresselhaus).
Figure 3. Here we show the band structure of the nanowire for several values of the angle θ. We take the strength of the SO interaction mζ lω/ℏ2 = 0.9 and the transverse magnetic field gμBB/Eω = 0.6.
Download figure:
Standard image High-resolution imageFigure 4. In panel (a) we show the total normal conductance in the absence of superconductivity as a function of the chemical potential for several values of θ. The arrows indicate the position of the bottom of the band in the nanowire region. In panel (b) we show the Josephson current at φ = 0 also as function of the chemical potential for several values of θ. Note that for θ = 0, π/4, π/2 the Josephson current at φ = 0 is always zero (see main text). The Hamiltonian parameters are the same as in figure 2. The length of the junction is
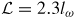 , and the strength of the delta-barriers are 2 m lωδa/ℏ2 = 0.2, 2mlωδb/ℏ2 = −0.8
, and the strength of the delta-barriers are 2 m lωδa/ℏ2 = 0.2, 2mlωδb/ℏ2 = −0.8
Download figure:
Standard image High-resolution imageFor θ = 0 the above statement can be understood as follows: even in the presence of delta barriers which breaks inversion symmetry in the x direction the operator O1 = RyK acting on the Bogoliubov–de Gennes Hamiltonian gives
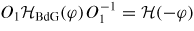 , hence Ia = 0. For the θ = π/2 case, the operator O2 = RyKσz acting on the Bogoliubov-de Gennes Hamiltonian gives
, hence Ia = 0. For the θ = π/2 case, the operator O2 = RyKσz acting on the Bogoliubov-de Gennes Hamiltonian gives
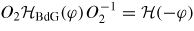 , and again Ia = 0.
, and again Ia = 0.
For intermediate values of θ(θ≠{0, π/4, π/2}) we do find an anomalous Josephson effect. Let us consider as an example θ = π/8 (see figure 4). As the chemical potential makes the band c accessible the conductance decreases but, most importantly, the anomalous Josephson current is maximum. The latter effect is independent of the particular choice of θ.
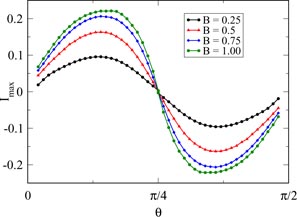
To characterize the dependence of the anomalous Josephson current on the magnetic field and on the angle θ, we introduce the quantity Imax as the maximum anomalous current Ia in the interval from EF = 1.5 Eω to EF = 2.5 Eω (see figure 5). Such a range is sufficient to explore the opening of the band c for all the values of θ and B considered here. We find that for a fixed value of θ the absolute value of Imax is enhanced by the magnetic field and that for a fixed value of the magnetic field the largest value of Imax (in absolute value) is found for θ ≃ π/8.
Figure 5. In this figure we show the maximum anomalous Josephson current Imax (see main text) obtained spanning the energy range EF = 1.5Eω to EF = 2.5Eω as a function of the angle θ for several values of the magnetic field in units of Eω/gμB.
Download figure:
Standard image High-resolution imageOur study is limited to the case N = 1 so that only one band (twice spin degenerate) is open in the leads. In order to address the effect of the nanowire's higher bands, keeping the Fermi energy constant, we introduce a gate in the normal region. We modify the Hamiltonian of equation (4) as H → H + e Vg. In figure 6 we set the value of the Fermi energy to EF = 2Eω and study the normal conductance and the anomalous Josephson current as a function of the gate potential Vg. We find that the anomalous Josephson current exhibits a similar behavior as found before for the case of band c (see figure 4); indeed, it is maximum when the bottom of band e is energetically accessible (see figure 6). One might speculate that no anomalous Josephson is found at the opening of bands b and d because both spin polarizations are fully contributing to the transport; unforunately, such a simple picture is not correct as either spin polarization (and helicity) are not good quantum numbers in the nanowire region. Note that this approach, albeit instructive, is not equivalent to changing the Fermi energy in the leads.
Figure 6. In this figure the Fermi energy is set to EF = 2Eω and we consider a rigid shift of the bands of the nanowire region by applying a gate potential Vg. θ = π/8 and the remaining parameters are the same as in figure 2. We plot the normal conductance and the Josephson current at φ = 0.
Download figure:
Standard image High-resolution imageAs a last remark we would like to stress that in our setup the magnetic field is perpendicular to the plane containing the nanowire. If one would change the orientation of the magnetic field with respect to the nanowire plane one may find the angle θ which maximizes the anomalous Josephson effect to be different from π/4. Note that with an in-plane magnetic field (not considered here) we should observe AJE even with pure Rashba or pure Dresselhaus spin–orbit interaction.
5. Conclusions
We have studied the dc Josephson effect in a superconductor/nanowire/superconductor junction. The nanowire has a strong spin–orbit interaction of Rashba and Dresselhaus type; moreover, a perpendicular Zeeman field is applied. We include a finite number of channels in the calculation. Although our approach can be extended to a generic number N of open channels in the leads, we have discussed in detail the case of a N = 1, but allowing the number of open channels in the normal region region to be larger than 1. We have found that a necessary condition for the anomalous Josephson effect (in our specific setup: i.e. with a perpendicular magnetic field) is the simultaneous presence of Rashba and Dresselhaus spin–orbit interaction, together with an asymmetric choice of the barriers at the interfaces between normal and superconductiong regions. This condition may seem to be restrictive, but it is completely satisfied in actual experiments. Indeed, for a small number of impurities in the system we expect these to mimic the role of the delta potentials in our model, hence giving rise to the AJE. On the other hand, as this number increases we should move towards a self-averaging regime where the reflection symmetry is restored and the AJE suppressed.
Most important for our results, we observe that, because of the spin–orbit interaction the electronic band structure of the nanowire region being lowered with respect to the one in the leads, by carefully tuning the Fermi level, so as to remain in the N = 1 case, we find that the anomalous Josephson effect is maximum in correspondence with the opening of a new band in the nanowire region. We do expect this phenomenology to also be found in the case N > 1; this will be object of further investigation. It is important to stress that the condition found here for the anomalous Josephson effect, namely the opening of a new band in the normal region, is different to that found for instance in [39, 40], where it can be ascribed to the asymmetry of the 1D electronic spectrum due to the coupling of transverse bands by the spin–orbit interaction.
Acknowledgments
We acknowledge the enlightening discussions with P W Brouwer, V Marigliano Ramaglia, Yu V Nazarov, F Trani, and T Yokoyama. The financial support from FIRB 2012 Projects 'HybridNanoDev' (Grant No. RBFR1236VV) is gratefully acknowledged.
Footnotes
- 5
The same system can be addressed with pure Rashba SO or Dresselhaus SO, but allowing for a magnetic field with an in-plane component.
- 6
Another possible choice would be using a hard wall confinement [46]. There are, of course, quantitative changes, in particular for the excited states, however we are interested in the low energy physics, where the splitting of the lateral sub-bands are almost comparable within the two models.