Abstract
Low-temperature dc-magnetization, ac electrical resistivity and specific heat measurements were performed on single crystals of the intermetallic compound β-IrSn4. The compound crystallizes in the tetragonal MoSn4-type structure (space group I41/acd) and exhibits superconductivity below Tc = 0.9 ± 0.05 K. Further, the magnitude of the ratios ΔCp/(γnkBTc) = 1.29, 2Δ/(kBTc) = 3.55 and of the electron–phonon coupling  imply that superconductivity in β-IrSn4 can be ascribed to a s-wave weak coupling regime. We determined crucial thermodynamic characteristics of the superconducting state. It turned out that depending on the assumption of either a spherical or non-spherical Fermi surface, the superconductivity can be ascribed to either a type-I and type-II/1 or type-II in clean limit, respectively. However, the behavior of the upper critical field and the anisotropic crystalline structure of the studied compound provide strong support to the type-II superconductivity. In the normal state the resistivity exhibits a prominent quadratic temperature dependence, which together with a large Kadowaki–Woods ratio and with the enhanced effective mass indicate that the electrons in β-IrSn4 are strongly correlated.
imply that superconductivity in β-IrSn4 can be ascribed to a s-wave weak coupling regime. We determined crucial thermodynamic characteristics of the superconducting state. It turned out that depending on the assumption of either a spherical or non-spherical Fermi surface, the superconductivity can be ascribed to either a type-I and type-II/1 or type-II in clean limit, respectively. However, the behavior of the upper critical field and the anisotropic crystalline structure of the studied compound provide strong support to the type-II superconductivity. In the normal state the resistivity exhibits a prominent quadratic temperature dependence, which together with a large Kadowaki–Woods ratio and with the enhanced effective mass indicate that the electrons in β-IrSn4 are strongly correlated.
Export citation and abstract BibTeX RIS
1. Introduction
Among various subjects of condensed matter physics, superconductivity has been attracting much attention. Interest at present mainly concerns the search for superconductors with high critical temperatures or establishing the proper mechanisms of Cooper pairing in so-called unconventional superconductors. The theme of the type-I BCS superconductivity is generally considered to be less interesting. This is owing to the fact that the type-I superconductivity occurs mostly in simple elemental metals or metalloids and the mechanism underlying the superconductivity is basically the well-known electron–phonon interaction. Curiously, type-I superconductivity has recently been found in several binary and ternary compounds, for instance, YbSb2 [1, 2], TaSi2 [3], (Sc,Lu)Ga3 [4], LaPd2Ge2 [5], LaRh2Si2 [6], (Lu,Y,La)Pd2Si2 [6] and LaRhSi3 [7]. These discoveries have not only broken the exclusive association between type-I superconductivity and elemental metals, but have encouraged further investigation of type-I superconductivity, since a field-dependent anisotropic order parameter in the superconducting state has been considered for LaRhSi3 [7].
Intermetallic IrSn4 binary crystallizes in three modifications; the low-temperature form, so-called α-IrSn4, adopts the trigonal IrGe4-type structure (space group P3121) [8], the high-temperature form, β-IrSn4 has the tetragonal MoSn4-type structure (space group I41/acd) [9], and the high-pressure form, HP-IrSn4, possesses the orthorhombic PtSn4-type structure (space group Ccca) [10, 11]. The structures of the two latter modifications stand in close relation to each other. To the best of our knowledge, only α-IrSn4 was reported to be a Pauli paramagnet and non-superconducting down to 2 K [8], whereas none of physical properties of β-IrSn4 and HP-IrSn4 have been reported yet.
In this work, we present magnetization, electrical resistivity and specific heat measurements on single crystals of intermetallic compound β-IrSn4, which becomes superconducting with a transition temperature Tc of 0.9 ± 0.05 K. Although the zero-field data characterize β-IrSn4 well as a s-wave weakly coupled type-I superconductor in a dirty limit, from an estimation of some thermodynamic parameters we arrive at a conclusion that superconductivity in β-IrSn4 can be ascribed to a type-II superconductor in a clean limit with an assumption of a non-spherical Fermi surface.
2. Single crystal growth and crystallographic characterization
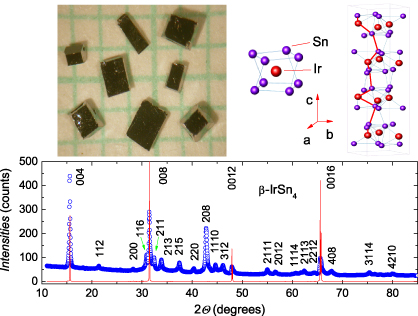
Single crystals of β-IrSn4 were grown by the self-flux method. A mixture of high-quality elemental metals Ir (purity 99.99%) and Sn (at. 99.999%) with the atomic ratio Ir:Sn = 1:80 was placed in an alumina crucible, sealed in an evacuated quartz ampule, and heated up to 900 °C. After cooling down to 600 °C at a rate of 5 °C h−1, the furnace was turned off and the quartz ampule was slowly cooled down to 300 °C within 3 h. Then, liquid Sn flux was decanted and the excess of Sn was removed by etching in HCl. Single crystals were obtained in the form of regular geometric shapes (see the left upper panel of figure 1).
Figure 1. Left upper panel shows a photograph of grown single crystals. Right upper graph shows the square antiprism formed by eight Sn atoms with the central Ir atom and the schematic crystal structure of β-IrSn4. The thick line joining atoms indicates the shortest interatomic distances. The bottom panel is the powder x-ray diffraction pattern (small circle symbols) compared to a single crystal diffraction pattern (solid line) obtained using an x-ray beam perpendicular to the 00l plane.
Download figure:
Standard imageX-ray powder diffraction of powdered small crystals and single crystal diffraction of a crystal were performed at room temperature using a X'Pert PRO x-ray diffractometer with monochromatized Cu Kα radiation. Since powdered small crystals possess texture, lattice parameters were calculated from the positions of the Bragg peaks only. Two alternative models of the crystal structure were considered, i.e., the tetragonal MoSn4-type structure and the orthorhombic PtSn4-type structure. Our analysis indicated that all the observed Bragg lines on the x-ray diffraction patterns could be indexed on the basis of the tetragonal MoSn4-type structure with the lattice parameters a = 0.6308(2) nm and c = 2.2739(4) nm (see the bottom panel of figure 1). The lattice parameters of our sample are in good agreement with those previously reported (a = 0.6309 nm and c = 2.2770 nm) [9]. The single crystal diffraction pattern (solid line) shows only 00l reflections, indicating that the crystallographic c-axis is perpendicular to the widest surface of the crystals.
Taking into account the atomic positions of Ir(8b) and Sn(32g) [9], we show the crystal structure of β-IrSn44 in the right upper panel of figure 1. In this tetragonal MoSn4-type structure, the Ir atoms are coordinated by eight Sn atoms. The eight Sn atoms form a square antiprism, which together with other antiprisms establish infinite layers. Further, the structure can be described as a stacking of four layers of IrSn8 antiprisms. The atoms are arranged in the sequence, 4Sn–Ir–4Sn...4Sn–Ir–4Sn...4Sn–Ir–4Sn...4Sn–Ir–4Sn along the c-direction. The minimum interatomic distances within layers are dSn–Sn = 0.309 and dIr–Ir = 0.446 nm. Because of a large dIr–Ir, the direct Ir–Ir interactions are almost excluded. Thus, the closer Sn–Sn contacts are favorable for an in-plane charge-carrier flow within the Sn layers. However, we recognize that interatomic distances dIr–Sn = 0.275 nm and dSn–Sn = 0.296 nm between layers are even shorter than these within the plane. This means that dominant charge carriers would take a path ...Ir–Sn–Sn–Ir–Sn–Sn–Ir... along the shortest interatomic distances, i.e., the chain along the c-axis. In considering the origins of the physical behavior discussed below, the fact that the Ir and Sn atoms in the unit cell are nearest neighbors may suggest overlap of the Sn sp-orbitals with Ir d-orbitals as mostly responsible for the electron transport properties in β-IrSn4.
3. Physical properties
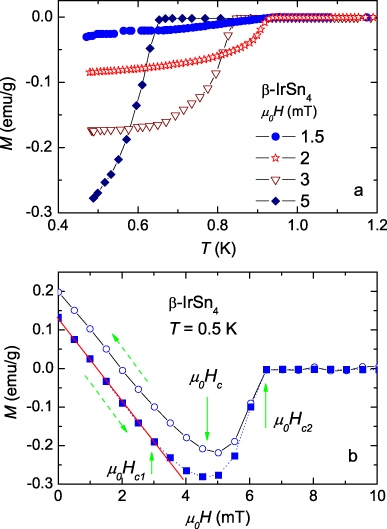
Dc-magnetization measurement was carried out using a commercial SQUID magnetometer (Quantum Design MPMS-XL) with an iQuantum 3He outfit. For the measurement, several single crystals were glued together to get a specimen of 18 mg. In figure 2(a) we present the temperature dependence of the magnetization M(T) collected at several magnetic fields. The data at 1.5 mT reveal a large diamagnetic signal below Tc(1.5 mT) = 0.95 K, indicating a superconducting transition. It is interesting to note that the onset of the superconductivity in 2 mT occurs at the same Tc as in 1.5 mT. With further increasing fields, Tc shifts down to lower temperatures, the diamagnetic signal at 0.45 K becomes stronger and simultaneously the transition becomes sharper. The latter finding may suggest that superconductivity becomes more homogeneous with magnetic fields. Figure 2(b) shows the isothermal magnetization measured at a temperature around 0.5 K. The hysteresis of the magnetization in the superconducting state resembles the behavior of both type-I and type-II superconductors with comparable coherence lengths and penetration depths. If β-IrSn4 is a type-I superconductor then the departure from the discontinuous jump transition at the critical field can be ascribed to a strong pinning of domain walls in the intermediate state or to an unaccounted demagnetization factor. In this case, the thermodynamic critical field μ0Hc can be estimated to be approximately 4.7 mT. If β-IrSn4 is considered as a type-II superconductor then one can estimate the lower critical field μ0Hc1 and the upper critical field μ0Hc2. μ0Hc1 = 3 mT, if is defined as the field where the deviation of the M(H) curve from linearity in the Meissner state sets in, while μ0Hc2 = 6.5 mT at 0.5 K, determined as the intersection between linear interpolations of the magnetization in the superconducting and normal states. The positions of the critical fields are denoted by solid arrows in figure 2(b). Above μ0Hc2 = 6.5 mT or in the normal state the studied compound behaves like a Pauli paramagnet.
Figure 2. (a) Zero-field cooled dc-magnetization at several magnetic fields as a function of temperature. (b) Isotherms measured at 0.5 K. The dashed arrows indicate the sweeping direction of the applied magnetic fields. The solid arrows denote the critical fields μ0Hc1,μ0Hc and μ0Hc2.
Download figure:
Standard imageElectrical resistivity was measured using a conventional four-probe ac-technique with an in-plane current of 0.5 mA and frequency of 37 Hz. The gold wires for electrical contracts were attached to samples using silver paste. The two measured samples have dimensions of 0.36 × 1.68 × 0.18 mm3, 1.2 × 0.74 × 0.1 mm3, respectively. The measurements were carried out using a Quantum Design physical property measurement system (PPMS) with a 3He cooler. Several selected magnetic fields up to 10 mT were applied parallel to the c-axis. The experimental data obtained on the two samples were reproducible. The typical value of the remnant field is less than 0.5 mT when decreasing the field from 10 mT in the oscillating mode. For measurements in fields below 2 mT, the bias field was further removed to get a lower remnant field, below 0.2 mT, before cooling the sample from room temperature. The strength of the remnant fields was controlled by an Applied Physics Systems Fluxgate Model 150–6325 magnetometer.
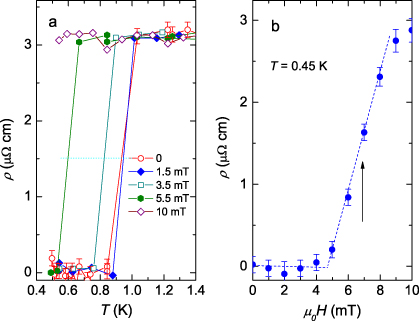
Low-temperature data shown in the upper inset of figure 3(a) indicate that the resistivity starts to drop abruptly at 1 K and arrives at zero value at 0.84 K. The critical temperature, Tc, defined as a middle point of the superconducting transition, and the transition width, ΔTc = Tc(90%) − Tc(10%), are determined to be 0.93 K and 0.15 K, respectively. Upon increasing the magnetic fields, the superconducting transition shifts to lower temperatures and even a small field of 10 mT is sufficient to reduce the Tc to less than 0.5 K. From the field dependence of the resistivity we have determined the upper critical field. At 0.45 K μ0Hc2 = 6.8 mT (see figure 3(b)), which is in good agreement with the value obtained from the magnetization measurements.
Figure 3. (a) Field-dependent electrical resistivity of β-IrSn4 around the superconducting phase transition. The dotted line indicates the middle point of the transition. (b) Field dependence of the resistivity at 0.45 K. The arrow denotes the midpoint of the transition and is taken as an upper critical field.
Download figure:
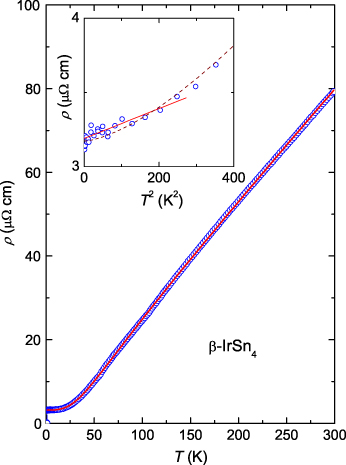
Standard imageIn figure 4 we show the electrical resistivity of β-IrSn4 in the temperature range 0.35–300 K. The temperature dependence of ρ(T) indicates that this intermetallic is a good metal. At room temperature the resistivity amounts to 80 μΩ cm and decreases to approximately 3 μΩ cm at 1 K. A large residual resistivity ratio RRR = 27, sharp superconducting transition and small residual resistivity value manifest the good sample quality and negligible scattering by defects and impurities. The resistivity just above Tc follows a quadratic temperature dependence ρ(T) = ρ0 + AT2, as shown in the inset of figure 4 by the solid line. By fitting this formula to the data between 1 and 15 K we obtained the residual resistivity of ρ0 = 3.2 μΩ cm and the coefficient A = 0.9 × 10−3 μΩ cm K−2. It is apparent that the A-coefficient is greatly enhanced, as compared to those observed for transition metals with A of the order of magnitude of 10−5 μΩ cm K−2 [12]. The observation of the ρ ∝ T2 dependence and a relatively large A coefficient are symptomatic of strong electron–electron interactions in the Fermi-liquid state of β-IrSn4. At higher temperatures, a curvature of the resistivity suggests to analyze it in terms of the Bloch–Grüneisen relation [13]. We fitted the experimental data to equation (1) and found that the residual resistivity ρ0 = 3.17 μΩ cm, the coefficient k = 112 μΩ cm, the Debye temperature ΘD = 216 K and the exponent n = 3. The observed value n = 3 and a good agreement between theory and the experimental data up to room temperature implies a significant s–d band scattering.

Figure 4. Temperature dependence of the resistivity of β-IrSn4 (circle symbols) with a Bloch–Grüuneisen–Mott fit (solid line). The inset shows the resistivity versus T2 with a solid line representing the T2 fit and dashed line denoting the Bloch–Grüuneisen–Mott fit.
Download figure:
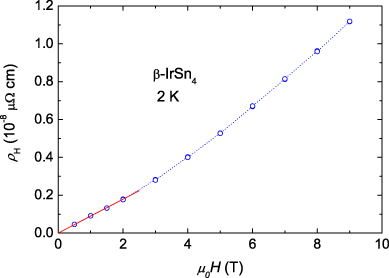
Standard imageThe Hall effect was measured on one of the samples used in the resistivity measurements. We utilized a Quantum Design Horizontal Rotator in a Quantum Design PPMS platform to rotate the sample from 0° to 180°. The Hall resistivity data, determined as 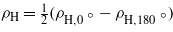 , were collected at 2 K and in fields up to 9 T using a conventional four-probe ac-technique with an in-plane current of 0.5 mA and frequency of 37 Hz. Figure 5 depicts the experimental Hall resistivity. The data show that ρH is linearly proportional to μ0H up to 2 T. At high fields, ρH deviates from the initial linear dependence. The reason for the nonlinear ρH(H) behavior is not ascertained as yet. One suspects that it may arise from a new contribution associated with spin–orbit coupling, which is negligible in a low-field regime but becomes perceptible in high fields. Alternatively, one can consider the observed field dependence of the Hall resistivity as due to competing contributions of two carrier types with different densities and mobilities. In the low-field limit, the Hall coefficient is dominated by the ordinary term R0 and can be estimated by R0 = ρH/(μ0H) = 8.95 × 10−10 m3 C−1. In the simple one-band approximation, the ratio 1/(R0e), where e is the elementary charge, may be interpreted as an effective charge-carrier concentration. We estimated the number of carriers, n = 1/(R0e) = 6.98 × 1027 m−3. Because the Hall coefficient is positive at all fields measured, it implies that the charge carriers are predominantly hole-like. The Hall ordinary term R0 can be combined with the resistivity data to obtain the Hall mobility μH and Hall mean free path lH. From the equations μH = R0/ρ and
, were collected at 2 K and in fields up to 9 T using a conventional four-probe ac-technique with an in-plane current of 0.5 mA and frequency of 37 Hz. Figure 5 depicts the experimental Hall resistivity. The data show that ρH is linearly proportional to μ0H up to 2 T. At high fields, ρH deviates from the initial linear dependence. The reason for the nonlinear ρH(H) behavior is not ascertained as yet. One suspects that it may arise from a new contribution associated with spin–orbit coupling, which is negligible in a low-field regime but becomes perceptible in high fields. Alternatively, one can consider the observed field dependence of the Hall resistivity as due to competing contributions of two carrier types with different densities and mobilities. In the low-field limit, the Hall coefficient is dominated by the ordinary term R0 and can be estimated by R0 = ρH/(μ0H) = 8.95 × 10−10 m3 C−1. In the simple one-band approximation, the ratio 1/(R0e), where e is the elementary charge, may be interpreted as an effective charge-carrier concentration. We estimated the number of carriers, n = 1/(R0e) = 6.98 × 1027 m−3. Because the Hall coefficient is positive at all fields measured, it implies that the charge carriers are predominantly hole-like. The Hall ordinary term R0 can be combined with the resistivity data to obtain the Hall mobility μH and Hall mean free path lH. From the equations μH = R0/ρ and 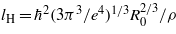 we estimated μH = 280 cm2 V−1 s−1 and lH = 109 nm, respectively.
we estimated μH = 280 cm2 V−1 s−1 and lH = 109 nm, respectively.
Figure 5. Field dependence of the Hall resistivity of β-IrSn4 at 2 K. Solid line represents a linear fit of the Hall resistivity in the low-field regime.
Download figure:
Standard imageThe specific heat was measured by the thermal relaxation method on a sample of ∼1 mg. The specific heat measurements were done using the same setup and experimental conditions as the electrical resistivity. We carried out careful calibration of the calorimeter and measurement of addenda before the proper measurements were done. The zero-field specific heat of β-IrSn4 divided by temperature, Cp/T, versus T2 is depicted in figure 6(a). The normal state specific heat follows the standard law for metals Cp = γnT + βT3, where γn and β are the normal state electronic heat and phonon specific heat coefficients, respectively. A linear fit of the data to Cp/T = γn + βT2 yields γn = 5.2 ± 0.2 mJ mol−1 K−2 and β = 0.91 ± 0.15 mJ mol−1 K−4. Knowing the β value, we can determine the Debye temperature: ΘD = (12π4rR/5β)1/3 = 221 ± 8 K, in a good agreement with the value ΘD deduced from the resistivity data (where r = 5 is the number of atoms per formula unit and R is the gas constant). In order to get some information on the strength of the electron–phonon coupling we estimate the average electron–phonon coupling constant  using the McMillan equation [14]:
using the McMillan equation [14]:
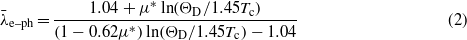
where μ* is the Coulomb pseudopotential, usually assumed to be between 0.1 and 0.15 [14, 15]. For μ* = 0.15,ΘD = 221 K and Tc ≈ 0.9 K, equation (2) yields  , suggestive of a weak electron–phonon coupling in β-IrSn4.
, suggestive of a weak electron–phonon coupling in β-IrSn4.
Figure 6. (a) Specific heat of β-IrSn4 divided by temperature Cp/T as a function of temperature squared in zero magnetic field. The solid line indicates the linear behavior in Cp/T = γn + βT2. The dashed line is a guide for the eye. (b) The electronic specific heat on a logarithmic scale as a function of 1/T. The solid line presents the exponential function given by the BCS theory Cel(T) = AγnTcexp(−Δ0/kBT), with A = 12.8 and Δ0/kB = 1.51 K.
Download figure:
Standard imageThe bulk nature of superconductivity in β-IrSn4 is evidenced by a clear peak in the Cp(T)/T dependence. The critical temperature Tc = 0.85 K, taken as the middle point of the ΔCp(T)/T jump, agrees fairly with that deduced from the resistivity. We determined the ratio ΔCp/γnTc = 1.29, which is noticeably smaller than 1.43 given by the BCS theory for weakly coupled superconductors. In figure 6(b) we show the ln(Cel(T)) versus 1/T dependence, where Cel(T) = ΔCp(T) = Cp(T) − βT3 is the electronic specific heat. It is clear that in the superconducting state Cel(T) follows a single-gapped BCS-like function Cel(T) = AγnTcexp(−Δ0/kBT). For the temperature range 0.4–0.7 K we obtained an energy gap Δ0/kB = 1.51 K, corresponding to 2Δ0/kBTc = 3.55 and parameter A = 12.8. The two latter values are comparable to those of weak coupling BCS superconductors: 3.52 and 8.5, respectively. This and the value of the ratio ΔCp/γnTc consistently imply that β-IrSn4 is a weak coupled superconductor.
The plot of Cp(T)/T measured in various magnetic fields up to 7 mT is shown in figure 7. The main points to note from this figure are the following: first, the specific heat jump ΔCp/Tc in small magnetic fields, namely in 1, 1.5 and 2 mT, is larger than that in zero-field. The observed field dependence of ΔCp/Tc means that the transition order changes from the second order in zero-field to the first order in applied magnetic fields. A similar behavior has been observed in the type-I superconductors (Sc,Lu)Ga3 [4] and LaRhSi3 [7], thus strongly supporting a type-I superconductivity in β-IrSn4. Second, perhaps most surprisingly, the critical temperature increases a little, up to 0.94 K, on the application of a field of 1.5 mT. The same Tc value was obtained from the Cp-data at 2 mT. Because the used field strength is much larger than the remnant field (<0.5 mT), the measurement artifact can be excluded. Moreover, the values of the critical temperature Tc are reproduced in independent measurements of specific heat and magnetization on different samples. Therefore, it is most likely that the slight enhancement of Tc upon application of the magnetic fields is an intrinsic property of the studied samples.
Figure 7. The specific heat divided by temperature Cp(T)/T in various magnetic fields plotted versus temperature squared.
Download figure:
Standard imageIn figure 8(a) we show the effect of applied magnetic fields on the Sommerfeld ratio Cp(H)/T at 0.4 K. Apparently, Cp(H)/T is not linear in field. Similarly to the case of LaRhSi3 [7] one describes the field dependence of the Cp(H)/T data by the exponential function Cp(H)/T = γ(0.4 K) + A × exp(−H*/H), where γ(0.4 K),A and μ0H* are fitting parameters. The best fit for data collected in magnetic fields below 7 mT gives γ(0.4 K) = 3.9 mJ mol−1 K−2,A = 15.8 mJ mol−1 K−2 and μ0H* = 9.5 mT. The exponential field dependence of Cp(H)/T in the tetragonal superconducting LaRhSi3 has been attributed to a change in the superconducting gap, which is isotropic in zero-field but becomes anisotropic in applied magnetic fields [7]. Since a similar nonlinearity of Cp(H)/T is observed in LaRhSi3 and β-IrSn4, one may think that the effect reported for β-IrSn4 can be explained in the same frame as has been used for LaRhSi3. However, because our specific heat data were collected on single crystals, i.e. for μ0H ∥ c-axis, our data should reflect the field dependence of the superconducting gap along one direction only, thus contradict the anisotropic model of the superconducting gap. To unravel the strong field dependence of Cp(H)/T in β-IrSn4, we propose to consider Cp(H)/T in two field ranges: below 2.5 mT, where Cp(H)/T is independent of magnetic fields, and in the field range 2.5–6 mT, where Cp(H)/T follows magnetic fields linearly. These two field regimes correspond approximately to those below μ0Hc1, and between μ0Hc1 and μ0Hc2, respectively. We note that for a standard BCS superconductor with a single isotropic energy gap, Cp(H)/T should increase linearly in magnetic fields, until the flux lines start to overlap. Such a linear field dependence of Cp(H)/T is found for applied fields larger than the lower critical field, when the non-superconducting density of states develops with an increasing number of flux lines. Obviously, in fields smaller than μ0Hc1 ∼ 3 mT,Cp(H)/T should be practically independent of fields since the magnetic flux penetrating into the material is only in a very thin layer of the surface and the contribution of the non-superconducting density of states to the total density at the Fermi level is negligible.
Figure 8. (a) Field dependence of the Sommerfeld ratio Cp(H)/T at 0.4 K. The dotted line is a fit to exp(−H*/H) with μ0H* = 9.5 mT. The solid lines express the behavior of Cp(H)/T in two magnetic field regimes: below μ0Hc1, and between μ0Hc1 and μ0Hc2. (b) Temperature dependence of the critical field Hc(T) determined from measurements of the specific heat (open circles), magnetization (closed stars) and electrical resistivity (bullets) under applied magnetic fields and that calculated from free-energy considerations of specific heat data at zero-field (closed squares) and 1.5 mT (open squares). The dashed line represents the theoretical WHH model with Tc0 = 1.14 K and μ0dHc2/dT =− 9.83 mT K−1 while the dashed–dotted line is a guide to the eye.
Download figure:
Standard imageFrom our measurements of magnetization, electrical resistivity and specific heat we deduced the critical fields μ0Hc2(T). The resulting H–T phase diagram is shown in figure 8(b). In this figure we compare also the temperature dependences of the thermodynamic critical fields μ0Hc(T) calculated from the Cp-data at 0 and 1.5 mT. The theoretical μ0Hc(T) values have been obtained by integrating the difference of specific heats between the superconducting (s) and normal (n) state and integrating the difference of the specific heats divided by temperature according to the formulas:
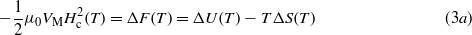
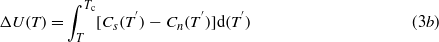
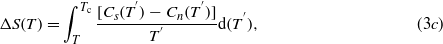
where ΔU(T) is the internal energy difference and ΔS(T) is the entropy difference. Using the relation  , the values γn = 5.2 × 10−3 J mol−1 K−2,VM = 68.24 × 10−6 m3 mol−1 and Δ0 = 1.51 K we obtained μ0Hc(0) = 5.76 mT at 0 K. This value is denoted by a solid diamond in figure 8(b). Clearly, there is an essential deviation of the experimental μ0Hc2(T) data from the thermodynamic field deduced from the entropy balance. This behavior indicates that β-IrSn4 should be a type-II superconductor in magnetic fields. A comparison of the calculated thermodynamic critical fields at 0 and 1.5 mT indicates that the temperature dependence of μ0Hc(T) is sensitive to applied magnetic fields.
, the values γn = 5.2 × 10−3 J mol−1 K−2,VM = 68.24 × 10−6 m3 mol−1 and Δ0 = 1.51 K we obtained μ0Hc(0) = 5.76 mT at 0 K. This value is denoted by a solid diamond in figure 8(b). Clearly, there is an essential deviation of the experimental μ0Hc2(T) data from the thermodynamic field deduced from the entropy balance. This behavior indicates that β-IrSn4 should be a type-II superconductor in magnetic fields. A comparison of the calculated thermodynamic critical fields at 0 and 1.5 mT indicates that the temperature dependence of μ0Hc(T) is sensitive to applied magnetic fields.
A remarkable finding of our measurements is that Tc(Hc2) = 0.85 K at zero field attains its maximum value of 0.94 K in fields 1.5 and 2 mT. This behavior resembles the situation found for EuxSn1−xMo6S8 [16], λ-(BETS)2FeCl4 [17], URhGe [18] and Eu(Fe0.81Co0.18)2 As2 [19], namely superconductivity can be induced or the critical temperature can be increased by the application of suitable magnetic fields. The analogy between β-IrSn4 and the mentioned superconductors is not obvious because the observed effect in β-IrSn4 occurs just below μ0Hc1 and is rather obscure. Therefore, further investigations will be required in order to establish the proper mechanism of the unusual Tc(H) dependence observed in β-IrSn4.
Another aspect worth considering is the almost linear behavior of Hc2(Tc) above 2 mT. In fact, a fit of the conventional relation Hc2(T) = Hc2(0)[1 − (T/Tc(0))n] to the experimental data gives the critical field Hc2(0) = 9.55 mT, critical temperature Tc(0) = 1.13 K and exponent n = 1.25. The latter value is significantly reduced in respect to n = 2 expected from the BCS theory.
We calculated the upper critical field using the model developed by Werthamer et al [20] (WHH model) for a type-II superconductor. Taking the slope of μ0Hc2(T) in the temperature range 0.63–0.94 K, dμ0Hc2(T)/dT =− 9.83 mT K−1, and the orbital-limiting field relation ![${\mu }_{0}{H}_{\mathrm{c}2}^{\mathrm{orb}}=0.7 3{T}_{\mathrm{c}}(0)[-\mathrm{d}{\mu }_{0}{H}_{\mathrm{c}2}(T)/\mathrm{d}T]_{{T}_{\mathrm{c}}}$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn272.gif) for a clean limit superconductor, we obtain
for a clean limit superconductor, we obtain 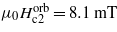 for Tc(0) = 1.13 K. It appears that all observed values of the critical fields are small and certainly indicate the absence of the Pauli limiting field μ0Hp = 1.86Tc, which is of the order of ∼2 T. In order to support the dominant orbital-pair breaking effect we determined the value of the Maki parameter [20, 21],
for Tc(0) = 1.13 K. It appears that all observed values of the critical fields are small and certainly indicate the absence of the Pauli limiting field μ0Hp = 1.86Tc, which is of the order of ∼2 T. In order to support the dominant orbital-pair breaking effect we determined the value of the Maki parameter [20, 21], 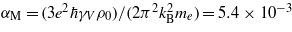 . In the formula, γV = 76.2 J m−3 K−2 is the electronic specific heat coefficient per volume and me is the electron mass. On the other hand, from the relation αM = 0.528 × [−dHc2(T)/dT]Tc [20, 21], with dHc2(T)/dT in the units of T K−1, the value of the Maki parameter is ≈5.2 × 10−3, i.e., very close to the above value.
. In the formula, γV = 76.2 J m−3 K−2 is the electronic specific heat coefficient per volume and me is the electron mass. On the other hand, from the relation αM = 0.528 × [−dHc2(T)/dT]Tc [20, 21], with dHc2(T)/dT in the units of T K−1, the value of the Maki parameter is ≈5.2 × 10−3, i.e., very close to the above value.
It is of considerable interest to estimate some thermodynamic parameters characterizing the superconducting state. First, we calculated the Fermi wavenumber kF = (3π2ns)1/3 = 4.65 × 109 m−1, where the superconducting carrier density ns = 3.39 × 1027 m−3 is a half of the total electron density n and e is the elementary charge. Then, we determined the effective mass 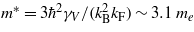 . The London penetration depth λL(0) = 162 nm can be obtained from the formula:
. The London penetration depth λL(0) = 162 nm can be obtained from the formula:  , where c is the speed of light. On the other hand, using the BCS relation for the coherence length ξ0 = 0.18ħυF/kBTc, we obtained ξ0 = 261 nm, where υF = ħkF/m* = 1.71 × 105 m s−1 is the Fermi velocity. The obtained ratio
, where c is the speed of light. On the other hand, using the BCS relation for the coherence length ξ0 = 0.18ħυF/kBTc, we obtained ξ0 = 261 nm, where υF = ħkF/m* = 1.71 × 105 m s−1 is the Fermi velocity. The obtained ratio 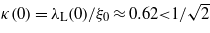 suggests ascribing the superconductivity in β-IrSn4 to either a type-I or to a type-II/1 in the classification of Auer and Ullmaier [22]. Further, using the formulas given by Orlando et al [23], we can estimate the BCS coherence length
suggests ascribing the superconductivity in β-IrSn4 to either a type-I or to a type-II/1 in the classification of Auer and Ullmaier [22]. Further, using the formulas given by Orlando et al [23], we can estimate the BCS coherence length ![${\xi }_{0}=7.9 5\times 1{0}^{-1 7}{n}_{s}^{2/3}S/{S}_{\mathrm{F}}/[{\gamma }_{V}{T}_{\mathrm{c}}]$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn297.gif) and London penetration depth
and London penetration depth ![${\lambda }_{\mathrm{L}}(0)=1.3 3\times {1 0}^{8}{\gamma }_{V}^{1/2}/[{n}_{s}^{2/3}S/{S}_{\mathrm{F}}]$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn298.gif) . In this estimation, uncertainties may appear due to the unknown ratio of the Fermi surface of the superconducting electrons, S, to the surface of the free electrons SF,S/SF. Therefore, we will consider two extreme cases, namely assuming a spherical Fermi surface (S/SF = 1) or non-spherical Fermi surface (e.g. S/SF = 0.35). The first assumption yields ξ0 = 262 nm,λL = 163 nm, whereas with the latter one we obtain ξ0 = 92 nm,λL = 465 nm. Correspondingly, the electronic mean free path
. In this estimation, uncertainties may appear due to the unknown ratio of the Fermi surface of the superconducting electrons, S, to the surface of the free electrons SF,S/SF. Therefore, we will consider two extreme cases, namely assuming a spherical Fermi surface (S/SF = 1) or non-spherical Fermi surface (e.g. S/SF = 0.35). The first assumption yields ξ0 = 262 nm,λL = 163 nm, whereas with the latter one we obtain ξ0 = 92 nm,λL = 465 nm. Correspondingly, the electronic mean free path ![${l}_{e}=1.2 7\times {1 0}^{4}/[{\rho }_{0}{n}_{s}^{2/3}(S/{S}_{\mathrm{F}})]$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn305.gif) amounts to 521 or 1489 nm, respectively. Because le is always larger than ξ0, the superconductivity in β-IrSn4 is certainly in the clean limit. The estimation leads to an interesting conclusion that if the Fermi surface is spherical then κ = 0.62, so supporting type-I and type-II/1 superconductivity in β-IrSn4. Conversely, if the Fermi surface is non-spherical, κ takes a value of 5, implying that the superconductivity is of type-II.
amounts to 521 or 1489 nm, respectively. Because le is always larger than ξ0, the superconductivity in β-IrSn4 is certainly in the clean limit. The estimation leads to an interesting conclusion that if the Fermi surface is spherical then κ = 0.62, so supporting type-I and type-II/1 superconductivity in β-IrSn4. Conversely, if the Fermi surface is non-spherical, κ takes a value of 5, implying that the superconductivity is of type-II.
In the clean limit, the Ginzburg–Landau coherence length ξGL and Ginzburg–Landau parameter κGL can be estimated using the respective relations ![${\xi }_{\mathrm{GL}}=5.8 7\times 1{0}^{-1 7}/[{n}_{s}^{2/3}(S/{S}_{\mathrm{F}})]$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn314.gif) and
and ![${\kappa }_{\mathrm{GL}}=1.6\times {1 0}^{2 4}{T}_{\mathrm{c}}{\gamma }_{V}/[{n}_{s}^{2/3}(S/{S}_{\mathrm{F}})]^{2}$](https://content.cld.iop.org/journals/0953-8984/25/15/155701/revision1/cm458697ieqn315.gif) [23]. We obtained ξGL and κGL values of 68 nm and 4.9, respectively, and the resulting Ginzburg–Landau penetration depth is λGL = κGLξGL = 327 nm. Also, a method of estimation of ξGL is based on the knowledge of the upper critical field. Assuming
[23]. We obtained ξGL and κGL values of 68 nm and 4.9, respectively, and the resulting Ginzburg–Landau penetration depth is λGL = κGLξGL = 327 nm. Also, a method of estimation of ξGL is based on the knowledge of the upper critical field. Assuming 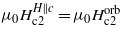 , an anisotropic value of the Ginzburg–Landau coherence length ξab, which is related to
, an anisotropic value of the Ginzburg–Landau coherence length ξab, which is related to 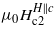 by the relation
by the relation 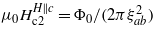 , where Φ0 is the flux quantum. For
, where Φ0 is the flux quantum. For 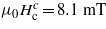 this results as ξab = 206 nm.
this results as ξab = 206 nm.
4. Discussion and conclusions
The first picture which emerges from our measurements on single crystals of β-IrSn4 is that this binary intermetallic compound becomes superconducting below 0.9 ± 0.05 K. The zero-field data listed in table 1 are in accordance with the conventional s-wave singlet pairing mechanism and would also provide a hint of either the type-I or type-II/1 superconductivity with a weak electron–phonon coupling.
Table 1.
Thermodynamic parameters of the superconductor β-IrSn4: critical temperature Tc, critical field μ0Hc0(0), electron–phonon coupling constant 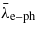 , Maki parameter αM, electronic heat coefficient γn, lattice heat coefficient β, specific heat jump ΔCp/γnTc, superconducting energy gap ratio 2Δ0/kBTc, Fermi wavevector kF, effective masses of superconducting carriers m*.
, Maki parameter αM, electronic heat coefficient γn, lattice heat coefficient β, specific heat jump ΔCp/γnTc, superconducting energy gap ratio 2Δ0/kBTc, Fermi wavevector kF, effective masses of superconducting carriers m*.
| Tc (K) | 0.9 ± 0.05 |
| μ0Hc0(0) (mT) | 5.8 ± 0.1 |
| αM | 5.3 × 10−3 |
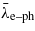
|
0.5 ± 0.05 |
| γn (mJ mol−1 K−2) | 5.2 ± 0.2 |
| β (mJ mol−1 K−4) | 0.91 ± 0.15 |
| ΔCp/γnTc | 1.3 ± 0.1 |
| 2Δ0/kBTc | 3.55 ± 0.05 |
| kF (×109 m−1) | 4.7 ± 0.5 |
| m* (me) | 3.1 ± 0.3 |
In order to get insight into the physics underlying the superconductivity in β-IrSn4 we can discuss several factors which would be involved in the Cooper pairing mechanism: (i) anisotropy of the Fermi surface and (ii) electron correlations. First of all, on account of the fact that β-IrSn4 crystallizes in the tetragonal MoSn4-type structure, an anisotropy of the Fermi surface is expected. Moreover, the assumption of a non-spherical Fermi surface leads to a deduction of the type-II superconductivity, which coincides with the observation of the upper critical field μ0Hc2. To examine the electron correlation factor, a determination of the Kadowaki–Wood ratio, RKW, [24, 25] is useful. Using the electronic heat coefficient γn = 5.2 mJ mol−1 K−2 and the T2-resistivity coefficient A = 0.9 × 10−3 μΩ cm, the RKW is estimated to 3.3 × 10−5 μΩ cm/(mJ mol−1 K)−2. This value is essentially larger than the value of 1 × 10−5 μ Ω cm/(mJ mol−1K)−2 commonly found for many correlated electron systems. Thus, we are dealing with the fact that both RKW and the effective mass of ∼3 me are enhanced in β-IrSn4. This implies that the electron correlation effect, presumably due to an overlap of Sn sp-orbitals with Ir d-orbitals, would have an impact on the Cooper pairing mechanism.
Finally, an interesting outcome is obtained from comparison of the studied compound with the intermetallic compound AuSn4, which was previously reported to undergo a superconducting transition at Tc = 2.4 K [26, 27]. The latter compound has been shown to have an orthorhombic PdSn4 structure with the noncentrosymmetric space group Aba2 [28]. Aside from the different crystallographic structures, the intermetallic β-IrSn4 and AuSn4 compounds differ in the number of d-electrons. So, the microscopic mechanisms of the electron pairing in these superconductors may be quite different.
To summarize, we have grown single crystals of intermetallic compound β-IrSn4, crystallizing in the tetragonal MoSn4-type structure. We have measured low-temperature magnetic, electrical resistivity and specific heat properties of the compound. We found a superconducting transition Tc(0T) = 0.9 ± 0.05 K and an upper critical magnetic field μ0Hc2(0) ∼ 8 mT. We have determined basic thermodynamic parameters characterizing the superconducting state, such as the specific heat jump at Tc,ΔCp(Tc)/γnTc, electron–phonon coupling constant, λe–ph, coherence length ξ, Fermi wavevector kF, effective mass m*, magnetic penetration depth λ, and Ginzburg–Landau parameter κ. The determined parameters are gathered in tables 1 and 2. The analysis of the experimental data allows us to characterize β-IrSn4 as either a type-I as well as type-II/1 or a type-II clean limit superconductor, depending on assumption of a spherical or non-spherical Fermi surface, respectively. We favor the assumption of a non-spherical Fermi surface, since β-IrSn4 crystallizes in the tetragonal MoSn4-type structure. Moreover, the behavior of the upper critical field data indicates that a type-II superconductivity is realized in β-IrSn4 and this interpretation does not contradict the unusual phenomena observed, including the nonlinear field dependence of the Sommerfeld coefficient and a jump in the critical magnetic field around the critical temperature, since all these anomalies may occur in the vicinity of the lower critical field μ0Hc1. In the light of the observation of superconductivity on the border between the type-II and type-I in β-IrSn4, the physical properties of this intermetallic compound are interesting and demand further investigation.
Table 2. Comparison of the coherence length ξ0, London penetration depth λL, electron mean free path le, Ginzburg–Landau coherence length ξGL, Ginzburg–Landau penetration depth λGL and Ginzburg–Landau parameter κGL, estimated from the BCS theory for the spherical (S/SF = 1) and non-spherical Fermi surface (S/SF = 0.35).
| Parameters | BCS model | S/SF = 1 | S/SF = 0.35 |
|---|---|---|---|
| ξ0 (nm) | 262 ± 5 | 262 ± 5 | 92 ± 3 |
| λL (nm) | 162 ± 5 | 163 ± 5 | 465 ± 10 |
| le (nm) | — | 521 ± 10 | 1489 ± 20 |
| κ | 0.62 ± 0.05 | 0.62 ± 0.05 | 5 ± 0.5 |
| ξGL (nm) | — | 193 ± 5 | 68 ± 2 |
| λGL (nm) | — | 115 ± 5 | 333 ± 10 |
| κGL | — | 0.6 ± 0.05 | 4.9 ± 0.5 |
Acknowledgment
The authors acknowledge for the financial support from the project 2011/01/B/ST3/04553 of the National Science Centre of Poland.