Abstract
A general approach to equilibrium and oscillations in a turbulent Bose–Einstein condensate, valid in the mean-field approximation, is proposed. Two different wave equations, describing the quasi-static equilibrium and the elementary excitations of the medium are derived. In particular, it is shown that a modified Thomas–Fermi equilibrium can be defined in the presence of an arbitrary spectrum of oscillations.
The oscillating modes are also determined using Bogoliubov–de Gennes (BdG) equations, valid in different geometrical configurations, such as infinite, cylindrical and toroidal. The case of a non-homogenous density is considered, which includes the modified equilibrium profiles. A general form of dispersion relation for the elementary excitations is derived. Twisted phonons, carrying a finite amount of angular momentum, are shown to be a particular class of BdG modes. They were previously derived from fluid equations. Nonlinear analysis also shows that envelope dark solitons can exist, and correspond to a rarefaction of twisted phonons.
Export citation and abstract BibTeX RIS
1. Introduction
Turbulence is an important and fascinating topic in both classical and quantum fluids. This includes superfluid helium [1] and Bose–Einstein condensates (BEC) of low density alkaline gases, where turbulence has been studied in recent experiments [2]. From observation and simulations [3], it emerges the view that a turbulent condensate includes vortices and phonon oscillations.
Vortices have been observed in [4, 5], and the corresponding quantum theory was explored by a large number of authors [6, 7]. Large vortices of the size of the condensate, reminding those observed in [4], have also been theoretically described as Rossby waves, similar to those occurring in planet atmospheres [8]. Vortex condensates are known to organize in Abrikosov lattices, which have normal modes of oscillation called Tkachenko modes [9, 10]. These modes have been first observed by [11]. A more general class of lattice oscillations, associated with Rossby–Tkachenco modes, has also been considered [12].
Phonons are elementary excitations in the medium, and it is commonly believed that they cannot carry any angular momentum in uniform condensates. However, recent work has shown that twisted phonons, with angular momentum, can exist in a non-rotating and unbounded condensate [13]. Similar concepts have also been proposed, such as twisted phonons in classical fluids [14, 15].
Here we propose a general approach to oscillating BEC, where the mutual influence of quasi-static Thomas–Fermi (TF) equilibrium, vortices and elementary excitations of the turbulent spectrum is considered. The term turbulence is sometimes misleading as it can refer to different physical situations. Alternatively, we could talk about excited condensates, but this could also be misleading. Here we call turbulent a condensate where many different oscillations coexist. And we focus on a steady state turbulence, where the instabilities have saturated and the amplitude of the oscillations is nearly constant.
The spectrum of oscillations is assumed arbitrary, and described by a superposition of Bogoliubov–de Gennes (BdG) modes, in different geometrical configurations. BdG modes can be seen as generalized elementary oscillations of the condensate, which reduce to the simple phonons in a uniform medium.
The cases of cylindrical and toroidal media with arbitrary density profiles will be considered. The following questions will be addressed: (a) what are the changes introduced by turbulence on the quasi-static density profiles; (b) what are the changes introduced by such modified profiles on the basic BdG modes; (c) can these BdG modes include the case of twisted phonons, previously derived with a fluid model?
The structure of the paper is the following. In section 2, we start from the Gross–Pitaevskii (GP) equation, which efficiently describes the behavior of BECs in the mean-field approximation, and derive two different equations for the fast and quasi-static wavefunction components. These will be the basic equations of our model. In this introductory section it will be also shown that, for steady state turbulence, a modified TF equilibrium will eventually emerge, where the condensate density will adjust, in order to keep the unperturbed value of the chemical potential. Modified vortex solutions can also be derived.
In section 3, we successively consider the BdG solutions for an infinite BEC, and for cylindrical and toroidal configurations with uniform density. We first consider phonon beams with a beam waist much smaller than the transverse dimensions of the condensate, therefore justifying the infinite medium assumption and the neglect of boundary conditions. We show that the resulting modes are described by Laguerre–Gauss (LG) orthogonal functions and possess angular momentum. These are the expected twisted phonons, previously described using quantum fluid equations [13]. The cylindrical case is formally very similar, apart from the fact that the transverse boundary conditions are included, and a Fourier–Bessel (FB) decomposition is used instead. As for the toroidal case, it can be reduced to a periodic cylinder, if the major radius of the torus is much larger than the minor radius, which is relevant for experiments.
In section 4, we consider the case of a non-homogenous BEC, under quite general density profile conditions. Modified BdG modes will be derived, extending the results of the previous section. A general form of dispersion relation is obtained, which includes the effects of both the non-uniformity of the medium and the BdG mode configuration. Finally, in section 5, we consider nonlinear mode solutions and show that dark envelope solitons can occur for LG and FB modes. This is a new kind of soliton solution, which are not to be confused with the well known (non-envelope) dark solitons [12]. The present work confirms and generalizes our previous work based on a fluid description [13]. Finally, in section 6, we state some conclusions.
2. Basic description
We start with the GP equation, describing the behavior of a condensate in the mean field approximation, using the standard notation, as

Here,  is the collective wavefunction of the condensed matter,
is the collective wavefunction of the condensed matter, 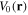 is the confining potential, and g is the coupling parameter associated with binary atomic collisions in the low energy limit. We assume that this equation is satisfied by a generic solution of the form
is the confining potential, and g is the coupling parameter associated with binary atomic collisions in the low energy limit. We assume that this equation is satisfied by a generic solution of the form

where  describes the static equilibrium profile,
describes the static equilibrium profile, 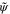 is a superposition of BdG modes to be specified later, and μ is the chemical potential. Replacing this in equation (1), and taking a time average over a period much longer than the typical BdG mode period, such that
is a superposition of BdG modes to be specified later, and μ is the chemical potential. Replacing this in equation (1), and taking a time average over a period much longer than the typical BdG mode period, such that  , we obtain
, we obtain
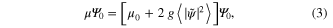
where 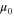 is determined by the unperturbed GP equation
is determined by the unperturbed GP equation

The chemical potential μ introduced in equation (3) is clearly distinct from the unperturbed chemical potential,  , which is defined for a condensate in equilibrium and in the absence of oscillations [6]. On the other hand,
, which is defined for a condensate in equilibrium and in the absence of oscillations [6]. On the other hand,  is the density profile. Assuming that equation (3) is satisfied, we can then use equation (1) to establish an evolution equation for the turbulent part of the wavefunction, of the form
is the density profile. Assuming that equation (3) is satisfied, we can then use equation (1) to establish an evolution equation for the turbulent part of the wavefunction, of the form
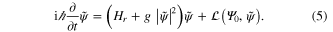
We can see that this equation strongly resembles the initial GP equation (1), but with a different Hamiltonian Hr, instead of H0, and an additional term 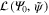 , describing the interaction between the slow and the oscillating parts of the wavefunction. They are defined as
, describing the interaction between the slow and the oscillating parts of the wavefunction. They are defined as

Equations (2) and (5) will be used as the starting point of our present work.
Before discussing the different BdG modes which are the basic elements of the turbulent spectrum, let us consider the modified equilibrium. For that purpose, we assume an arbitrary spectrum of oscillations, leading to an average density perturbation  . We can assume that a modified TF equilibrium will eventually be established, such that
. We can assume that a modified TF equilibrium will eventually be established, such that
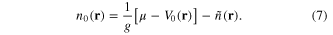
This equality is obtained by neglecting the kinetic term of the Hamiltonian H0, as usual. By assuming a radial potential shape  , where
, where  is the frequency of the harmonic trap, and taking the plausible assumption that turbulence is absent at the boundary r = a, where
is the frequency of the harmonic trap, and taking the plausible assumption that turbulence is absent at the boundary r = a, where  (as assumed in figure 1), we conclude that
(as assumed in figure 1), we conclude that 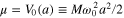 . This contrast with the unperturbed value
. This contrast with the unperturbed value 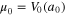 , where a0 is the radius of the condensate in the absence of turbulence. We notice that, due to the existence of a spectrum of oscillations, the size of the condensate increases,
, where a0 is the radius of the condensate in the absence of turbulence. We notice that, due to the existence of a spectrum of oscillations, the size of the condensate increases,  . Integration over the BEC volume, assuming that the total number of condensed atoms is the same, leads to
. Integration over the BEC volume, assuming that the total number of condensed atoms is the same, leads to
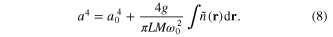
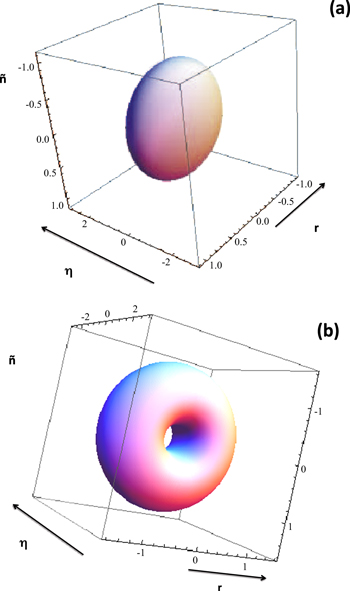
This expression is valid for a cylindrical BEC with length L. The resulting modified density profile is illustrated in figure 1, for the cylindrical case in the presence of two BdG modes (these modes will be described below). In this figure we compare the dynamically renormalized profile with the unperturbed profile, as it would occur in a cylindrical nonuniform condensate. The observed static undulations of the density profile, the reduction of its maximum value  , and the increase of radial dimension are due to the existence of oscillations.
, and the increase of radial dimension are due to the existence of oscillations.
Figure 1. Modified TF equilibrium profile for a cylindrical condensate, where two BdG modes as those of equation (24), with  and
and  and amplitudes equal to 0.1 of the unperturbed density. The unperturbed TF profile is also shown.
and amplitudes equal to 0.1 of the unperturbed density. The unperturbed TF profile is also shown.
Download figure:
Standard image High-resolution imageFrom the above discussion we can also conclude that the vortex equation for a modified TF equilibrium, will reduce to the usual form  , where μ is now replacing
, where μ is now replacing  . No changes in the local structure of the vortex solutions will therefore be expected, except for the fact that vortices will exist on a modified density profile.
. No changes in the local structure of the vortex solutions will therefore be expected, except for the fact that vortices will exist on a modified density profile.
3. Modes in uniform BEC
We now focus on the BdG modes, starting with the simple case of a uniform BEC, where the unperturbed density n0 is assumed constant. The discussion of the elementary excitations of a BEC can be done by linearizing equation (5) with respect to the perturbation associated with a given turbulence mode  . We then get
. We then get

For a mode with frequency ω, we can assume a solution of the form
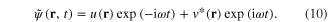
Replacing this in equation (9), we obtain the two equalities
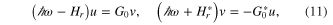
where we have used  . These are the so-called BdG equations for the condensate. At this point we assume a solution satisfying the equations
. These are the so-called BdG equations for the condensate. At this point we assume a solution satisfying the equations  , where k is a wavenumber, to be specified. The kinetic operator inside Hr is then reduced to
, where k is a wavenumber, to be specified. The kinetic operator inside Hr is then reduced to  , and the two equations in (10) become purely algebraic, and can be written in matricial form as
, and the two equations in (10) become purely algebraic, and can be written in matricial form as  , with
, with

Solution of this matrix equation implies that  , which can be written as
, which can be written as
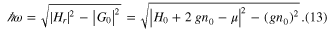
Ignoring the confining potential  , and assuming that the chemical potential is
, and assuming that the chemical potential is  , this reduces to the well known dispersion relation [6]
, this reduces to the well known dispersion relation [6]
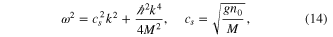
where cs is the Bogoliubov sound velocity. In order to understand the generality of this dispersion relation, we consider the case of twisted phonons [13] where, instead of a plane wave, we have a wave beam propagating along the z-axis, as  . Here,
. Here,  and
and  are slowly varying amplitudes, such that
are slowly varying amplitudes, such that  and
and  . They satisfy the two paraxial equations
. They satisfy the two paraxial equations

Solutions of these equations are well known, and can be written as a superposition of LG modes [16]
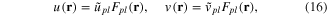
where  and
and  are constant amplitudes, and
are constant amplitudes, and  are LG functions of the form
are LG functions of the form

Here, Cpl are normalization constants, Lpl are the associated Laguerre polynomials, and  , where the wave beam waist
, where the wave beam waist  slowly varies along the z-axis. It is well known that, choosing appropriate normalization constants, these LG functions satisfy the orthogonality relations
slowly varies along the z-axis. It is well known that, choosing appropriate normalization constants, these LG functions satisfy the orthogonality relations

Such solutions correspond to twisted phonons, carrying a finite amount of angular momentum, as first derived in [13] by using the quantum fluid equations. These modes are re-derived here, as a special example of BdG modes. They correspond to phonons with a beam waist much shorter than the size of the condensate.
Let us now consider the opposite situation, where the wave structure occupies the whole size of the condensate, and the finite boundaries play a significant role. For this purpose, we consider a condensate with a homogeneous cylindrical shape, with radius a. In this case, we can assume solutions of the form

We then obtain differential equations for  and
and  of the form
of the form

with  , and a similar equation for
, and a similar equation for  . The solutions are Bessel functions of order l, such that
. The solutions are Bessel functions of order l, such that

with constant amplitudes  and
and  . Noting that the wave amplitudes vanish at the boundary r = a, we have to choose the perpendicular wavenumber
. Noting that the wave amplitudes vanish at the boundary r = a, we have to choose the perpendicular wavenumber  such that
such that  , and
, and  , where
, where  are the zeros of the Bessel function Jl. It can easily be shown that the solutions for these new BdG modes, valid for a cylindrical configuration, satisfy orthogonality relations similar to equation (18), of the form
are the zeros of the Bessel function Jl. It can easily be shown that the solutions for these new BdG modes, valid for a cylindrical configuration, satisfy orthogonality relations similar to equation (18), of the form
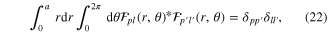
where we have defined the new orthogonal FB functions
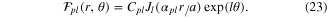
The new normalization constant is  . Finally, it should be noticed that these cylindrical BdG solutions can easily be adapted to a toroidal configuration, if the large radius of the torus R, is much larger than the minor radius a. We can then describe the torus as a periodic cylinder, with
. Finally, it should be noticed that these cylindrical BdG solutions can easily be adapted to a toroidal configuration, if the large radius of the torus R, is much larger than the minor radius a. We can then describe the torus as a periodic cylinder, with  , where ϕ is toroidal angle. For the resulting toroidal BdG modes, the above cylindrical solutions stay valid, but only discrete values of the parallel wavenumber are considered, such that
, where ϕ is toroidal angle. For the resulting toroidal BdG modes, the above cylindrical solutions stay valid, but only discrete values of the parallel wavenumber are considered, such that  , where the integer m is the toroidal mode number.
, where the integer m is the toroidal mode number.
4. Modes in non-uniform BEC
Let us now generalize the above description for the case of a non-uniform condensate. We assume that the condensate density is slowly varying (and eventually periodic) along the z-axis. The transverse density profile,  is assumed arbitrary and not necessarily cylindrically symmetric. Instead of the above simple assumption, stated in equation (10), we now use a generic mode decomposition of the form
is assumed arbitrary and not necessarily cylindrically symmetric. Instead of the above simple assumption, stated in equation (10), we now use a generic mode decomposition of the form

where the subscript k represents here the set of mode numbers,  , where
, where  for LG modes,
for LG modes,  for cylindrical modes, or
for cylindrical modes, or  for toroidal modes. Using the modified TF equilibrium of equation (7), such that
for toroidal modes. Using the modified TF equilibrium of equation (7), such that  , we can get from the linearized wave equation (9) the following pair of BdG equations, for each k mode
, we can get from the linearized wave equation (9) the following pair of BdG equations, for each k mode

At this point we should notice that, each of these k modes satisfy an equation of the form  and
and  . Using the relevant orthogonality conditions (18) or (22), and after integration over
. Using the relevant orthogonality conditions (18) or (22), and after integration over  , we obtain the following result
, we obtain the following result

where we have defined
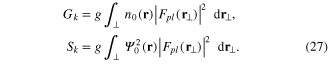
Here, these quantities can slowly vary along z, and the integration over  extends from r = 0 to r = R, for the cylindrical case, or from r = 0 to infinity for LG modes. These new equations (26) can be re-written in matrix form
extends from r = 0 to r = R, for the cylindrical case, or from r = 0 to infinity for LG modes. These new equations (26) can be re-written in matrix form  , with
, with
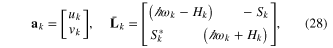
where we have defined  . This leads to the general dispersion relation of BdG in a non-uniform medium, of the form
. This leads to the general dispersion relation of BdG in a non-uniform medium, of the form
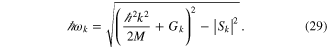
From here, we obtain
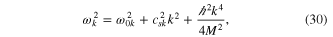
where the cut-off frequency  , and the modified Bogoliubov sound velocitycsk, are defined by
, and the modified Bogoliubov sound velocitycsk, are defined by

This is a generalization of the dispersion relation equation (14) to a non-uniform medium. At this point, it should be notice that, in the definition of Sk of equation (27), we can write  . This means that Sk only differs from Gk because of the phase factor
. This means that Sk only differs from Gk because of the phase factor  inside the integrand. If this phase is assumed constant, we will have
inside the integrand. If this phase is assumed constant, we will have  , and the cut-off frequency
, and the cut-off frequency  will vanish. However, this is not necessarily true. It will depend on the solutions of the average wave equation (3).
will vanish. However, this is not necessarily true. It will depend on the solutions of the average wave equation (3).
We conclude that, in general, the BdG modes show a cut-off frequency and a modified sound velocity, which both depend on the shape of the condensate density, and on the shape of the BdG mode. Both quantities will also eventually depend on z, if the condensate density is supposed to vary slowly along the axis of propagation. In this case, the total mode wavenumber k will slowly adapt to the local axial conditions, for a fixed mode frequency. On the other hand, the transverse shape of the equilibrium density can be assumed as arbitrary.
5. Envelope solitons
Let us now consider a nonlinear mode analysis. For that purpose, we use a single mode solution, with frequency  , of the form
, of the form
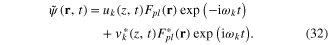
Replacing this in the nonlinear wave equation, equation (5), and neglecting the terms describing second and third harmonics evolving as  and
and  , we obtain the following expressions
, we obtain the following expressions
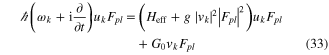
and
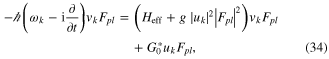
where we have used the auxiliary quantity

We now assume that the mode amplitudes depend on z, according to  , where the new amplitudes also depend on z and t. This means that the nabla-square operator inside the Hamiltonian Hr can be replaced by
, where the new amplitudes also depend on z and t. This means that the nabla-square operator inside the Hamiltonian Hr can be replaced by

with a similar equation for vk. Notice that, with an appropriate choice of orthogonal functions Fpl, these expressions are valid for LG modes, (if we assume  ), as well as for cylindrical Bessel modes with radius a (if we assume
), as well as for cylindrical Bessel modes with radius a (if we assume  and
and  , with
, with  ). The toroidal configuration with major radius
). The toroidal configuration with major radius  , can also be described by the same type of cylindrical Bessel modes, if in addition we use discrete values for the axial wavenumber
, can also be described by the same type of cylindrical Bessel modes, if in addition we use discrete values for the axial wavenumber  , as discussed above.
, as discussed above.
Taking this into account, multiplying equation (33) by  , and integrating over the transverse space variables, we obtain the nonlinear BdG relations
, and integrating over the transverse space variables, we obtain the nonlinear BdG relations

Here, we have used the nonlinear Hamiltonian operator
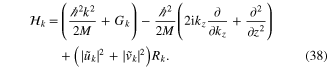
We recognize in the first two terms under brackets the linear Hamiltonian Hk, appearing in equation (28). The quantities Gk and Sk are defined as in the previous section, and we have added a new quantity

At this point, we should use symmetry arguments, and assume  , as an additional and necessary condition. Assuming that the linear dispersion relation for the generic BdG modes, as given by equations (29)–(31), is still satisfied, we can then reduce the system of coupled equations (37) to the following nonlinear evolution
, as an additional and necessary condition. Assuming that the linear dispersion relation for the generic BdG modes, as given by equations (29)–(31), is still satisfied, we can then reduce the system of coupled equations (37) to the following nonlinear evolution

where the vector  is defined by
is defined by ![${\bf u}=\left[ {{\tilde{u}}_{k}},{{\tilde{v}}_{k}} \right]$](https://content.cld.iop.org/journals/0953-4075/48/6/065302/revision1/jpb509864ieqn83.gif) . It is now convenient to use a transformation of variables, from
. It is now convenient to use a transformation of variables, from  to the non-dimensional variables
to the non-dimensional variables  , as defined by
, as defined by

This transforms equation (40) into the form
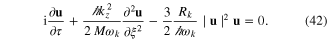
This is a defocusing nonlinear Shrödinger equation, which can be rewritten in a more appropriate form by rescaling the space variable ξ and the mode amplitude  , as
, as
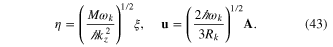
We are then led to the final standard form

It is well known that such an equation satisfies dark soliton solutions, given by
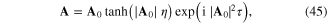
where the constant vector  determines the soliton amplitude. Such solutions describe nonlinear BdG modes in a non-uniform medium, and correspond to twisted phonons propagating in a non-uniform BEC. They generalize similar envelope soliton solutions [13], previously derived from a quantum fluid description. The present approach is, not only more general because it applies for non-uniform condensates, but also more exact in the sense that the GP wave equation is used, instead of the fluid approximation. Furthermore, these new solutions were built over a modified TF equilibrium profile, which is attained in the presence of an arbitrary broadband spectrum of oscillations, assumed with constant amplitudes, as described in section 2. The density perturbations associated with these dark envelope solitons, as given by
determines the soliton amplitude. Such solutions describe nonlinear BdG modes in a non-uniform medium, and correspond to twisted phonons propagating in a non-uniform BEC. They generalize similar envelope soliton solutions [13], previously derived from a quantum fluid description. The present approach is, not only more general because it applies for non-uniform condensates, but also more exact in the sense that the GP wave equation is used, instead of the fluid approximation. Furthermore, these new solutions were built over a modified TF equilibrium profile, which is attained in the presence of an arbitrary broadband spectrum of oscillations, assumed with constant amplitudes, as described in section 2. The density perturbations associated with these dark envelope solitons, as given by  , are illustrated in figure 2.
, are illustrated in figure 2.
Figure 2. Shape of dark envelop solitons in the axial and radial directions, for: (a) the Gaussian mode  , and (b) the twisted LG mode
, and (b) the twisted LG mode  .
.
Download figure:
Standard image High-resolution image6. Conclusions
A general approach to turbulence in BEC was proposed in this work. Starting from the GP equation, which adequately describes the condensate in the mean-field approximation, we have derived two different equations describing the steady state and the elementary excitations in a BEC. We have shown that the TF equilibrium, as well as the vortex structure, can be modified due to the existence of a background spectrum of oscillations.
On the other hand, we have derived a general dispersion relation for BdG modes valid in different geometries, which takes into account the modified quasi-static equilibria. We have explicitly discussed the cases of infinite and finite condensates, with or without homogeneous density. We have shown that the twisted phonons considered by us in a recent publication [13] are indeed BdG modes, defined in the paraxial approximation. The cases of cylindrical and toroidal condensates were considered. Finally, we have studied the nonlinear BdG solutions, and shown that envelope dark solitons exist for modes satisfying the phonon dispersion relation. These soliton solutions confirm and generalize our previous results on twisted nonlinear waves.
The possible existence of global oscillations, such as breathing and surface modes, was not considered here. Such modes, are known in both condensed and non-condensed gas [17, 18], and can also play a role in the turbulent medium. They could be treated as a natural extension of the present work. We have also ignored transient phenomena, and have focused our attention on nearly steady state oscillations. An important problem would be the influence of the BdG mode spectrum on stability and growth of vortices [19], as well as the exchange of energy and angular momentum between these structures and the elementary excitations. This will left to a future publication. Another important extension of the present approach concerns coupling with a non-condensed background gas, where modified gap solitons, similar to those found in [20], could eventually be observed. Finally, the present work suggests that a quasi-particle description of the BEC spectrum of oscillations is possible, where the vortex structures and equilibria can be defined on a background of a quasi-particle gas. This can be seen as analogue to the well known two-fluids approach to superfluidity, and could contribute to the understanding of finite temperature effects in a Bose gas [21].
Acknowledgments
We would like to thank the Brazilian research funding agencies CNPq and FAPESP, for financial support.