Abstract
Based on the drift-diffusion equations, the behaviour of electrons, ions and fine particles in fine particle plasmas is analysed both analytically and numerically. The cylindrical symmetry of the system is assumed and the cases of up to two species (sizes) of fine particles are considered. It is shown that, in the domain where fine particles exist, the charge neutrality is satisfied to a much higher accuracy, so that the electrostatic potential and the electron distribution are almost flat, and the change in the negative charges due to fine particles is compensated by the ion distribution. This occurs when the charge density of particles multiplied by their charge number exceeds the electron and ion charge densities, and is analytically attributed to the participation of fine particles to the screening of the space charge. The condition for the formation of void at the centre is obtained and the behaviour of particle distribution for parameters around the condition is observed. In the case of two species, the possibility is shown that smaller particles are distributed inside of the domain of larger particles and, when the larger ones form a void, it is filled with smaller ones, the enhanced charge neutrality being recovered.
Export citation and abstract BibTeX RIS
I. Introduction
Fine particle (dusty) plasmas, mixtures of plasma and fine (dust) particles, have played a very important role in investigating the basic properties of charged particle systems and their possible applications [1–3]. In order to clarify the behaviour of fine particles in plasmas, it is desirable to have plasmas with simple geometry and characteristics as much as possible. The plasmas generated in long uniform cylinders may be one of strongest candidates in the sense that we can assume cylindrical symmetry around the axis and uniformity along the axis.
The positive column plasma in a long discharge tube is an example of this kind of plasma. For fine particles which are to be added to this plasma, however, the effect of gravity is significant: When the symmetry axis of the discharge is parallel to the gravity, the uniformity along the axis will be lost and, when the axis is perpendicular to the gravity, the azimuthal isotropy around the axis will be lost. In this context, the fine particle plasma under the condition of microgravity is expected to provide us with an almost ideal system with both the cylindrical symmetry and the axial uniformity. In the project called PK-4, experiments in such an apparatus are in progress on the International Space Station (ISS) [4]. Our purpose is to clarify the basic properties of fine particle plasmas in the stationary state with cylindrical symmetry and axial uniformity.
Here, we consider a system composed of weakly ionised plasma (electrons and ions) and fine particles with no average motion (flow) along the axis and, as is usually observed in experiments, with different temperatures of the components. We assume that the neutral gas is uniform and without flow. The charge density of the fine particles is assumed to be, at most, of the order of a few to a few tens % of the total negative charges, and therefore the properties of the discharge are not drastically changed by the existence of fine particles. A typical example may be the room temperature Ar plasma of 10– , in a cylindrical apparatus of radius around 1–2 cm, with the plasma (electrons and ions) density 108–
, in a cylindrical apparatus of radius around 1–2 cm, with the plasma (electrons and ions) density 108–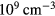 , the fine particle density 104–
, the fine particle density 104– , the electron temperature 1–3 eV/
, the electron temperature 1–3 eV/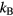 , and the ion and particle temperature around 300 K (room temperature).
, and the ion and particle temperature around 300 K (room temperature).
We assume that the plasma is generated in proportion to the electron density and lost to the wall of the discharge tube and the surface of the fine particles, the former loss being larger. For example, a dc electric discharge is used and the the flow of fine particles along the axis is prevented by the polarity switching with the frequency around 1 kHz [5] (the electrons and ions follow this alternating electric field while the field is averaged to zero for fine particles).
In experiments using the PK-3 Plus apparatus on the ISS under microgravity, a central space called a 'void' was observed inside the fine particle cloud where there exist no fine particles [6]. The formation of this void is considered to be due to the ion drag force on the fine particles [7]. We here take into account the ion drag force on the fine particles and derive the condition for the formation of voids in cylindrical systems. In addition, we consider the cases with fine particles of up to two species (sizes) and show that smaller particles are located inside the domain of larger particles and, when larger particles form a void around the axis, smaller ones tend to fill it.
We analyse the behaviour of fine particles on the basis of self-consistent solutions of drift-diffusion equations [8] and the Poisson's equation, both analytically and numerically. By expanding the solution with respect to the radial coordinate, we derive some interesting effects coming from the very existence of fine particles: In the domain where we have an appreciable charge density of fine particles, the charge neutrality is satisfied with much higher accuracy compared with the case of no particles, the electrostatic potential and the electron density are almost flat, and the ion density is increased so as to compensate the negative contribution of the particles to the charge density. We show that the origin of this behaviour is the participation of the fine particles in the (macroscopic) screening of the space charge and what matters is not the charge density but the charge density multiplied further by the charge number of fine particles. Being proportional to the square of the charge number, which is as large as 103–104, the existence of fine particles strongly enhances the charge neutrality giving accompanying effects, even if the charge density is far less than a few tens of %. We also show that these characteristics derived analytically are confirmed by numerical analysis of the equations.
In section II, basic equations for densities, for the generation and loss of plasma, and for the ion drag force are given. In section III, the behaviour of solutions without fine particles are described. In section IV, the solutions are expanded with respect to the radius and their behaviour is analysed. Section V is devoted to the numerical treatment of basic equations: examples of the results are given in comparison with the analytic ones and the condition for the void formation is given. The discussions and conclusions are given in sections VI and VII, respectively.
II. Basic equations and the general properties of stationary solutions with cylindrical symmetry
The typical parameters of our interest are rather common in experiments of fine particle plasmas and conditions with various collisions have been discussed; for example, in [2]. The ion mean free path (due to ion-neutral collisions) is much smaller than the radius of the apparatus of around 1–2 cm. The particle-neutral collision gives the momentum exchange rate around 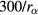 [μm] s−1 at 50 Pa (equation (48) in [2],
[μm] s−1 at 50 Pa (equation (48) in [2], 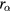 is the particle radius) and, with their thermal velocity around
is the particle radius) and, with their thermal velocity around ![$0.1/{{\left({{r}_{\alpha}}\left[\mu \text{m}\right]\right)}^{3/2}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn007.gif) cm s−1, the particles experience frequent collisions when moving at 0.1 cm. As for the electrons, the mean free path (due to electron-neutral collisions) at 50 Pa is ∼0.5 cm, which is smaller (but not much smaller) than the apparatus radius. We expect the effect of the relatively large electron mean free path is small in the ambipolar diffusion controlled by ions: since the diffusion coefficient of electrons is much larger than that of ions, the effects of the generation/loss of plasma has a small effect on the electron density, which is approximately given by the Boltzmann distribution under the self-consistent potential. The drift-diffusion approach has been applied, for example, to analyse fine particle plasmas of a few cm in Ar typically at 40 Pa [8]. It is to be noted that, in order to discuss the mutual correlation between fine particles (for example, lattice-like structures), it is necessary to take into account the fluctuations from the average distribution [9]. This analysis, however, is beyond the scope of this work and we also apply the drift-diffusion equation for fine particles.
cm s−1, the particles experience frequent collisions when moving at 0.1 cm. As for the electrons, the mean free path (due to electron-neutral collisions) at 50 Pa is ∼0.5 cm, which is smaller (but not much smaller) than the apparatus radius. We expect the effect of the relatively large electron mean free path is small in the ambipolar diffusion controlled by ions: since the diffusion coefficient of electrons is much larger than that of ions, the effects of the generation/loss of plasma has a small effect on the electron density, which is approximately given by the Boltzmann distribution under the self-consistent potential. The drift-diffusion approach has been applied, for example, to analyse fine particle plasmas of a few cm in Ar typically at 40 Pa [8]. It is to be noted that, in order to discuss the mutual correlation between fine particles (for example, lattice-like structures), it is necessary to take into account the fluctuations from the average distribution [9]. This analysis, however, is beyond the scope of this work and we also apply the drift-diffusion equation for fine particles.
II.A. Drift-diffusion equations
Our system is composed of electrons, ions and fine particles (simply 'particles' in what follows). We denote the physical quantities of these components by suffixes 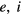 , and α, respectively, α being the species of the particles. For densities
, and α, respectively, α being the species of the particles. For densities  and flux densities
and flux densities  , we have the equations of continuity in the general form,
, we have the equations of continuity in the general form,
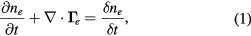
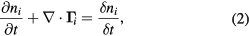
and
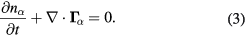
On the right-hand sides, 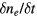 and
and 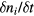 express the generation of electrons and ions by the ionisation and their loss from the system, respectively. In this article, we consider only the stationary case where
express the generation of electrons and ions by the ionisation and their loss from the system, respectively. In this article, we consider only the stationary case where 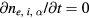 .
.
We assume that flux densities are expressed by diffusion coefficients 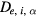 and mobilities
and mobilities  in the forms,
in the forms,
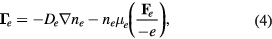
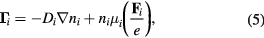
and
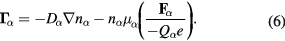
Here −e, e, 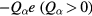 and
and 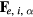 are the charges and the forces for an electron, an ion and a particle of species α, respectively. We also assume that the diffusion coefficients and mobilities are related by Einstein relations as
are the charges and the forces for an electron, an ion and a particle of species α, respectively. We also assume that the diffusion coefficients and mobilities are related by Einstein relations as
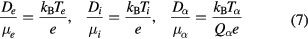
with the temperature of the corresponding components, 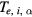 . Note that, since we have no generation/loss of particles, the stationary state of our system depends, within the drift-diffusion approximation, only on
. Note that, since we have no generation/loss of particles, the stationary state of our system depends, within the drift-diffusion approximation, only on 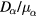 and we need not specify
and we need not specify 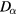 nor
nor 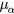 when
when 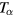 is given.
is given.
The electric field 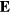 is related to the net charge density by the Poisson's equation
is related to the net charge density by the Poisson's equation

The force acting on a particle of species α is given by
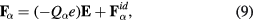
where the first term is due to the electric field 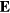 and the second term is the ion drag force. The force on an ion is given by
and the second term is the ion drag force. The force on an ion is given by
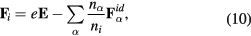
where the second term is the reaction of 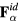 in (9). The force on an electron is written as
in (9). The force on an electron is written as

The ion drag force has been investigated extensively for usual positive ions, as in our system [2, 10–12] and also for negative ions [13]. It is along the direction of the average ion flow  and here we estimate the magnitude by the expression [10] (see appendix
and here we estimate the magnitude by the expression [10] (see appendix
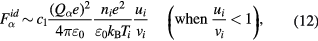
where

and 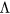 is the generalised Coulomb logarithm
is the generalised Coulomb logarithm
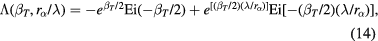
 being the exponential integral (
being the exponential integral (![${{\beta}_{T}}\sim \left[|{{Q}_{\alpha}}|{{e}^{2}}/4\pi {{\varepsilon}_{0}}{{k}_{\text{B}}}{{T}_{i}}\right]/$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn029.gif)
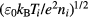 as defined in appendix
as defined in appendix  (mi is the ion mass) and we have
(mi is the ion mass) and we have 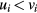 in all cases shown below: the particles are distributed near the symmetry axis and they do not approach the domain near the wall, where we have the opposite condition
in all cases shown below: the particles are distributed near the symmetry axis and they do not approach the domain near the wall, where we have the opposite condition  . We also note that the average ion flux
. We also note that the average ion flux  is given by
is given by
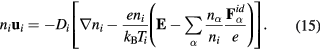
II.B. Generation and loss of plasma and charging of fine particles
We assume that the axial electric field maintains the discharge. This field induces a discharge current composed mainly of electrons, and they eventually have the temperature of the order of a few electron volts. These electrons are considered to generate the plasma (electrons and ions) by the impact ionisation, and the generation rate is proportional to the neutral atom density and the electron density; the proportionality constant is dependent on the electron temperature [14]. We regard factors other than the electron density as uniform, and express the rate per volume by  with the coefficient cg, which is constant in the system (we assume uniform neutral gas density).
with the coefficient cg, which is constant in the system (we assume uniform neutral gas density).
We assume that the plasma is lost by recombination after diffusing onto the outer boundary of the system (wall) or the surface of fine particles, neglecting the recombination in the bulk of the plasma. The charge of the particle α, 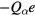 , is determined by the balance between the ion current
, is determined by the balance between the ion current  and the electron current
and the electron current 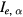 onto the surface of particle α,
onto the surface of particle α,

or explicitly,
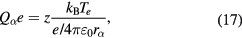
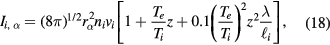
and
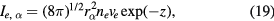
where  is the particle radius and ve is the the electron thermal velocity defined by
is the particle radius and ve is the the electron thermal velocity defined by  (me is the electron mass). In (18), the effect of ion-neutral collisions is expressed by the third term in square brackets (| |) [15] where
(me is the electron mass). In (18), the effect of ion-neutral collisions is expressed by the third term in square brackets (| |) [15] where 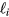 is the ion mean free path and λ is the screening length defined by
is the ion mean free path and λ is the screening length defined by

ki and ke being the ion and electron Debye wave numbers, respectively,
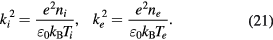
Since we assume 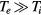 ,
, 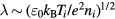 . Denoting the balanced current
. Denoting the balanced current 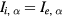 by
by  , we have
, we have 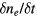 and
and 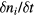 in (1) and (2) as
in (1) and (2) as
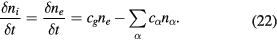
II.C. Stationary solutions with cylindrical symmetry
We assume that our system is stationary and cylindrically symmetric. In this case, 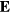 ,
, 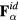 , and
, and 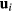 has only the radial component E,
has only the radial component E, 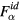 , and ui, respectively, and we define the ratio of the magnitudes of the ion drag force to the electric field force for a particle α,
, and ui, respectively, and we define the ratio of the magnitudes of the ion drag force to the electric field force for a particle α,  , by
, by

In terms of s = R2 where R is the radius, equations (1)–(6) and (8) reduce to
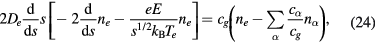

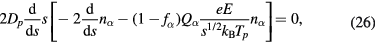
and
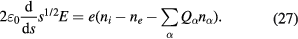
These equations, together with (16) and (17), determine ne, ni, 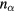 ,
, 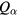 , and E. Equation (15) reduces to
, and E. Equation (15) reduces to
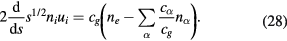
Noting that the densities and E/s1/2 are finite at s = 0, we integrate both sides of these equations with respect to s and introduce  defined, respectively, by
defined, respectively, by
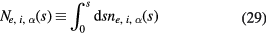
to have the equations as shown in appendix
III. Solutions without fine particles
Without fine particles,  in (24)–(28). Eliminating E from (24) and (25) and noting that
in (24)–(28). Eliminating E from (24) and (25) and noting that 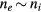 and
and 
 , we have the well-known simple ambipolar diffusion equation for the plasma density [16]
, we have the well-known simple ambipolar diffusion equation for the plasma density [16]
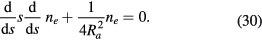
Here the characteristic scale length Ra is related to the ambipolar diffusion coefficient Da
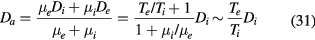
via

From the boundary condition of the finiteness of ne(R = 0),  are given by the solution of (30) as
are given by the solution of (30) as
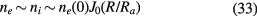
and we have the potential, along with the other functions shown in appendix
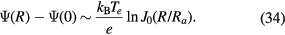
The discharge tube radius corresponds to the first zero of  at R = 2.40 Ra. We assume that the outer radius of the system (the discharge tube radius) Rw is related to Ra by
at R = 2.40 Ra. We assume that the outer radius of the system (the discharge tube radius) Rw is related to Ra by 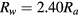 , also in the case with particles.
, also in the case with particles.
The charge density around the centre normalised by ene(0) is given by
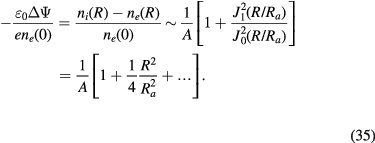
Here the parameter 1/A is defined by
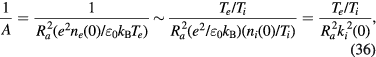
ki(0) being the ion Debye wave number at R = 0. Usually ki (and also ke) is much larger than the inverse of the system size represented by Ra and we have

The space charge is thus controlled by the Debye length and the quasi-charge-neutrality (relative to ene(0)) is satisfied to the order 1/A. In section IV.A, we discuss the screening of the space charge on a more general ground.
We here emphasise that, although the usual Debye wave number appears in the factor controlling the charge neutrality, we are not applying the Debye theory for the screening of the point charge. The drift-diffusion approach describes only the average distributions in the continuum limit: in order to treat the screening of point charges as is done in the Debye theory, however, we have to take into account the fluctuations from the average (in other word, the effect of discreteness) [9].
In the case where ions have the charge Ze, 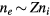 and
and  . Eliminating E similarly from (24) and (25), we have
. Eliminating E similarly from (24) and (25), we have

instead of (30) and therefore
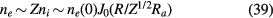
and
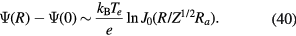
The normalised charge density is then given by
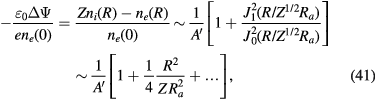
where
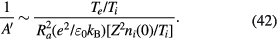
Comparing 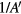 with 1/A in (36), the charge neutrality is satisfied to an enhanced extent inversely proportional to
with 1/A in (36), the charge neutrality is satisfied to an enhanced extent inversely proportional to 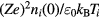 .
.
IV. Behaviour of solutions near the axis: enhanced charge neutrality, flat potential and flat electron distribution
We here discuss the behaviour of the solutions of the drift-diffusion equations mainly in the case of single particle species α. We expand the solution of equations (24)–(27) around the axis with respect to s = R2 and obtain
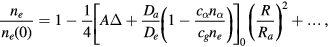
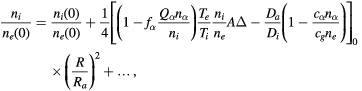

and
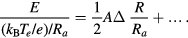
Here the suffix 0 expresses the value at R = 0 and 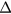 is the normalised charge density at R = 0,
is the normalised charge density at R = 0,
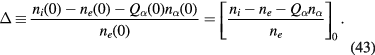
Near the axis, we have the charge density normalised by ene(0) as
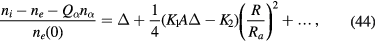
where
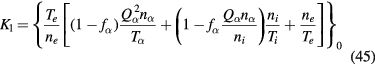
and1

When the value of 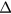 is appropriately chosen for a given value of
is appropriately chosen for a given value of 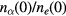 , we have densities vanishing at the outer boundary of the system; otherwise, the (absolute) values of densities diverge with the increase in s = R2 (see also numerical procedures described in section V.A). Since
, we have densities vanishing at the outer boundary of the system; otherwise, the (absolute) values of densities diverge with the increase in s = R2 (see also numerical procedures described in section V.A). Since 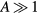 , the normalised charge density
, the normalised charge density 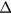 is much smaller than unity, as in the case without particles, and we expend
is much smaller than unity, as in the case without particles, and we expend  with respect to 1/A in the form
with respect to 1/A in the form
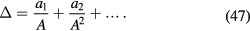
In order for the right-hand side of (44) not to diverge and to be of the order of 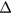 , we have to satisfy a condition for a1,
, we have to satisfy a condition for a1,
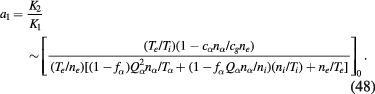
As a result, the charge density is given by
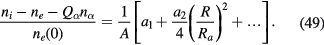
When  , (48) reduces to the case of no particles (35) or
, (48) reduces to the case of no particles (35) or 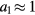 and
and
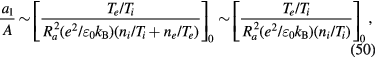
as they should.
In the case of multiple species of particles, K1 and K2 take the form
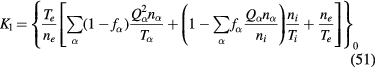
and
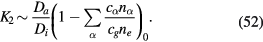
IV.A. Case of weak ion drag
Let us first consider the case where the effect of the ion drag force (expressed by 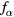 ) can be neglected and K1 reduces to
) can be neglected and K1 reduces to  . We then have
. We then have
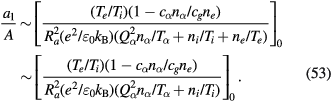
Here, in the denominator, fine particles also contribute to the factor

in contrast to the case without particles (36), where the factor reduces to 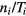 (equation (53) includes the latter case with
(equation (53) includes the latter case with 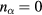 ).
).
We assume that the charge density of the fine particles is less than a few tens % of the total negative charges. However, since 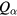 is usually as large as 103–104, we expect the inequality holds (at R = 0)
is usually as large as 103–104, we expect the inequality holds (at R = 0)
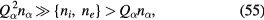
unless  is very small. Then the first terms in () of (54) and in [ ] of K1 are dominant (
is very small. Then the first terms in () of (54) and in [ ] of K1 are dominant (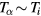 ) and a1 become much smaller than unity (the value without fine particles);
) and a1 become much smaller than unity (the value without fine particles);
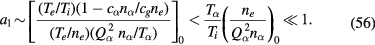
The densities around the axis are thus given by
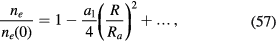
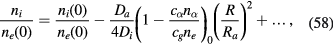
and
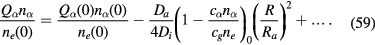
For ne, the coefficient of 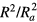 is much smaller than unity and also than those for ni and
is much smaller than unity and also than those for ni and 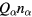 , the latter two being the same and giving charge densities compensating each other. From (44), we see that the charge neutrality near the axis is satisfied to much higher accuracy than the case without particles, where
, the latter two being the same and giving charge densities compensating each other. From (44), we see that the charge neutrality near the axis is satisfied to much higher accuracy than the case without particles, where  .
.
When (55) is satisfied, the behaviour of the solutions near the axis is thus characterised by (a) much enhanced charge neutrality and almost flat potential, (b) almost flat electron density and (c) almost compensating (parallel) the charge densities of the ions and particles. As shown in (53) and (54), they are the result of the participation of the particles in the screening of the space charge. These will also be confirmed by the numerical solutions in section V.C. Though the above analysis is for the case of cylindrical symmetry, we may qualitatively apply the conclusions to the general case where we have appreciable amount of fine particle charges in the sense of (55). It should be noted that the dependency on the square of the charge number also appeared in (42) in the case without particles.
We emphasise again that (53) describes the behaviour of the space charge around the axis based on the expansion of solutions of the drift-diffusion equations (24)–(27). Although (54) takes the form of the Debye wave number squared when multiplied by 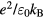 , the usual Debye theory for the screening of point charge is not applied, as in the case without particles (36) and (42).
, the usual Debye theory for the screening of point charge is not applied, as in the case without particles (36) and (42).
IV.B. Linear density of fine particles and central density and distribution radius
In the experiments, one of controllable parameters may be the linear density of the fine particles along the axis Nz. We now relate Nz to the central density and the radius of distribution. From (59), we have the approximate radius of particle distribution R0
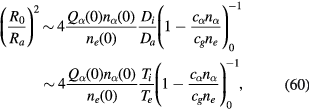
which is small compared with Ra,  . This estimation will be compared with the numerical solutions in section V, and shown to be in reasonable agreement. (The factor
. This estimation will be compared with the numerical solutions in section V, and shown to be in reasonable agreement. (The factor ![${{\left[1-{{c}_{\alpha}}{{n}_{\alpha}}(0)/{{c}_{g}}{{n}_{e}}(0)\right]}^{-1}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn092.gif) could be much larger than unity, but in the examples given there,
could be much larger than unity, but in the examples given there, 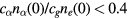 .) Then we have
.) Then we have
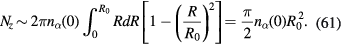
In terms of Nz, we have
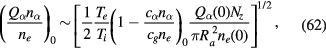
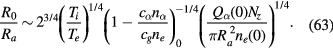
These expressions determine the shape of the particle distribution when the linear density Nz is given. The central density and the distribution radius increase in proportion to 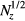 and
and  , respectively.
, respectively.
IV.C. Effects of ion drag force and void formation condition
Let us now consider the effects of the ion drag force on the particles and discuss the condition for the formation of voids in cylindrical systems. We first assume that we have fine particles of one species α.
According to (48), the distributions have the same characteristics, (57)–(59) and therefore (a), (b) and (c), as far as we have the inequality at R = 0
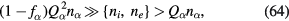
even if 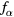 increases and approaches unity. The characteristics really change when (at R = 0)
increases and approaches unity. The characteristics really change when (at R = 0)
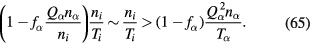
Then a1 reduces to the value without particles
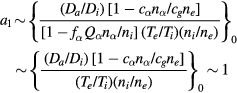
and we have
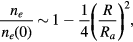
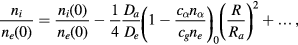
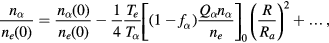
where (by (65))
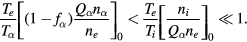
Thus, the electron distribution reduces to the case of no particles and the charge density distributions of the particles and ions are still parallel (compensating), both being nearly flat (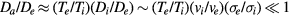 , ve being the electron thermal velocity and
, ve being the electron thermal velocity and 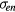 and
and 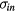 , the electron and the ion-neutral collision cross sections).
, the electron and the ion-neutral collision cross sections).
When 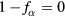 , the particle distribution becomes flat. We expect this occurs at R = 0 first (with respect to parameters): in order to have
, the particle distribution becomes flat. We expect this occurs at R = 0 first (with respect to parameters): in order to have  first at some finite values of
first at some finite values of 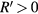 , we have to satisfy two apparently independent conditions at
, we have to satisfy two apparently independent conditions at 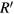 ,
, 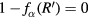 and
and ![${{\left[\text{d}{{f}_{\alpha}}(R)/\text{d}R\right]}_{{{R}^{\prime}}}}=0$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn105.gif) and this is not realistic.
and this is not realistic.
With a further increase in 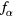 ,
, 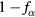 becomes negative. However, K1 cannot be negative: a negative K1 gives a1 < 0 and therefore E < 0, the inward electric field, which makes
becomes negative. However, K1 cannot be negative: a negative K1 gives a1 < 0 and therefore E < 0, the inward electric field, which makes 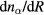 and
and 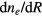 positive and
positive and  negative, causing the increase in
negative, causing the increase in 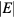 with the radius and its divergence. In order for K1 to be still positive,
with the radius and its divergence. In order for K1 to be still positive, 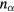 should satisfy (at R = 0)
should satisfy (at R = 0)
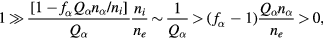
because  is 103–104. This indicates that
is 103–104. This indicates that  is almost zero (formation of a void), except for the case where
is almost zero (formation of a void), except for the case where 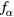 is very close to unity. Thus, the void formation condition is approximately given by
is very close to unity. Thus, the void formation condition is approximately given by
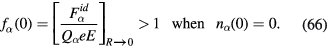
We note that this condition is naturally expected from the competition between the confining electric force and the ion drag force.
By (12) for 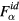 and noting
and noting  , we can rewrite the condition (66) into the form
, we can rewrite the condition (66) into the form

where the critical value 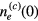 is determined by
is determined by
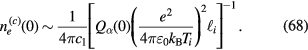
On the right-hand side, c1,  and
and  depend on parameters including ne as in (14), (17), and
depend on parameters including ne as in (14), (17), and

( is the ion-neutral gas collision frequency and nn, pn, and Tn are the neutral gas number density, pressure and temperature, respectively). Using the interpolation for
is the ion-neutral gas collision frequency and nn, pn, and Tn are the neutral gas number density, pressure and temperature, respectively). Using the interpolation for 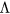 , (A.3) in appendix
, (A.3) in appendix 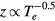 , we have the parameter dependency of
, we have the parameter dependency of 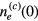 from (68) in the form
from (68) in the form
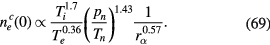
This will be compared with the results of the numerical analysis in section V.D.
IV.D. Fine particles of two species and a void-like structure
It should be noted that when 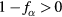 is satisfied by all species, (48) leads to features (a), (b) and (c), even in the case of multiple species of particles. We now consider the case of two species of particles, α and β, with radii
is satisfied by all species, (48) leads to features (a), (b) and (c), even in the case of multiple species of particles. We now consider the case of two species of particles, α and β, with radii 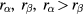 , and therefore
, and therefore  . When
. When 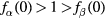 , we have a distribution of particles β in the void formed by particles α. The reason is as follows. Without particles β, particles α have a distribution with a void at the centre, as determined by the one-species case. Since the solutions in the void reduce to the ones without particles, we may apply, at least around the centre, the case of one species to the distribution of particles β. We thus have a structure where smaller particles distribute inside the void of larger particles. Details of the structure are difficult to have analytically and are left to the numerical treatment of the drift-diffusion equations in section V.E. As a distribution of the species α, there is a void at the centre. However, being different from the simple void, this void is filled with smaller fine particles of species β.
, we have a distribution of particles β in the void formed by particles α. The reason is as follows. Without particles β, particles α have a distribution with a void at the centre, as determined by the one-species case. Since the solutions in the void reduce to the ones without particles, we may apply, at least around the centre, the case of one species to the distribution of particles β. We thus have a structure where smaller particles distribute inside the void of larger particles. Details of the structure are difficult to have analytically and are left to the numerical treatment of the drift-diffusion equations in section V.E. As a distribution of the species α, there is a void at the centre. However, being different from the simple void, this void is filled with smaller fine particles of species β.
V. Numerical analyses
V.A. Values of the parameters and the method of the numerical solution
In numerical analyses, it is necessary to specify some parameters of the system. We assume the gas is Ar. The adopted values of the basic parameters and the corresponding values of the typical characteristic parameters are listed in tables 1 and 2, respectively. The radii 0.5 and 1 μm are within the applicability of (12)–(14) and are included in the range of particle size in experiments by PK-4.
Table 1. Basic parameters.
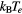 |
3 eV, 1 eV |
|---|---|
| Ti | 300 K |
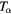 |
300 K |
| ne(R = 0) | 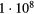  |
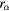 |
0.5 μm, 1 μm |
| Rw | 1.5 cm |
| pn | 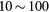 Pa Pa |
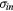 |
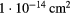 |
 |
 |
Table 2. Typical values of the characteristic parameters (for Te-dependent ones, the left and right values being for Te = 3 eV and Te = 1 eV, respectively).
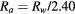 |
0.624 cm |
|---|---|
![$1/{{k}_{e}}(0)={{\left[{{\varepsilon}_{0}}{{k}_{\text{B}}}{{T}_{e}}/{{n}_{e}}(0){{e}^{2}}\right]}^{1/2}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn140.gif) |
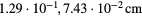 |
![$1/{{k}_{i}}(0)\approx {{\left[{{\varepsilon}_{0}}{{k}_{\text{B}}}{{T}_{i}}/{{n}_{e}}(0){{e}^{2}}\right]}^{1/2}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn142.gif) |
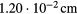 |
![$\lambda (0)={{\left[{{k}_{e}}{{(0)}^{2}}+{{k}_{i}}{{(0)}^{2}}\right]}^{-1/2}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn144.gif) |
 |
![$A=\left({{T}_{i}}/{{T}_{e}}\right){{\left[{{k}_{i}}(0){{R}_{a}}\right]}^{2}}$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn146.gif) |
23.5, 70.4 |
We numerically solve (24)–(27) introducing 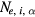 , as described in appendix
, as described in appendix  . We adjust
. We adjust 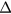 so as to have asymptotically vanishing densities near the wall: starting integration with inappropriate values of
so as to have asymptotically vanishing densities near the wall: starting integration with inappropriate values of 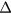 leads to a divergence of densities before reaching the wall. The solutions are quite sensitive to
leads to a divergence of densities before reaching the wall. The solutions are quite sensitive to 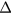 and numerical computations with very high accuracy are necessary.
and numerical computations with very high accuracy are necessary.
V.B. Solutions without fine particles
Examples of the set of solutions without fine particles are shown in figure 1 and compared with the analytical values obtained by the ambipolar diffusion equation, (33), (34) and (35). Starting from the quasi-neutral domain around the centre, the positive space charge increases with the radius, connecting to the domain of the sheath near the outer boundary. We observe that the known solutions given in section III are reproduced for R < Ra. It should be noted that, in our approach described in section II, the densities near the wall are not intended to be accurate, similar to the description by the ambiploar diffusion equation (30). In this sense, the comparison of our numerical result with the analytical one in section III has a physical meaning only within the domain R < Ra, both being inaccurate otherwise. We observe, however, that, our numerical solution gives a gradual increase in the space charge smoothly connecting to the domain of the sheath, in contrast to the diverging of the space charge given by the extrapolation of the analytic solution (35).
Figure 1. Electron and ion densities normalised by ne(0) (top), the electrostatic potential normalised by 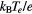 (middle), and the net charge density normalised by ne(0) (bottom) without fine particles. The broken lines are the results of the ambipolar diffusion equation (30).
(middle), and the net charge density normalised by ne(0) (bottom) without fine particles. The broken lines are the results of the ambipolar diffusion equation (30).
Download figure:
Standard image High-resolution imageIn principle, a separate treatment is necessary for detailed analyses of the domain of the sheath. However, since our interest is mainly in the behaviour of the fine particles and the plasma around the axis and not in the domain of the sheath, we may adopt our approach for our purpose. We also emphasise that Rw is an outer boundary extrapolated from the domain described by the ambipolar diffusion equation and, in all the cases analysed in what follows, the domain of the particles' existence is limited well within Rw. Therefore, this separate treatment is not expected to be influenced by the existence of particles in our examples.
Based on the equations for the velocity-moments of the distribution functions, we can approximately describe the average ion and electron velocities as functions of radius including the sheath domain near the wall [14]. In figure 2, we show the ratio of the ion drift velocity u to the ion sound velocity cs, obtained by moment equations in the cases of Te = 1 eV and 3 eV with Ti = 300 K. This ratio is larger for higher electron temperatures and increases with the radius, starting from 0 and reaching unity around the edge of the sheath; for Te = 3 eV, 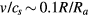 in R/Ra < 0.5. In our results shown below, the radius of the particle distribution is mostly well within 0.5 Ra, except for the case of and near the void formation, where it is of the order of 0.5 Ra. Although the ion thermal velocity is smaller than the ion sound velocity by the factor
in R/Ra < 0.5. In our results shown below, the radius of the particle distribution is mostly well within 0.5 Ra, except for the case of and near the void formation, where it is of the order of 0.5 Ra. Although the ion thermal velocity is smaller than the ion sound velocity by the factor 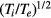 , the ratio of the ion drift velocity to the ion thermal velocity is less than 0.5 in R/Ra < 0.5. This may partly justify our approach, where the ion flux is described by the diffusion coefficients and mobilities, as in (4) and (5).
, the ratio of the ion drift velocity to the ion thermal velocity is less than 0.5 in R/Ra < 0.5. This may partly justify our approach, where the ion flux is described by the diffusion coefficients and mobilities, as in (4) and (5).
Figure 2. Electron and ion densities normalised by ne(0) and the ratio of the ion drift velocity to the ion sound velocity (left) and electrostatic potential normalised by  (right), both obtained by the moment equations.
(right), both obtained by the moment equations.
Download figure:
Standard image High-resolution imageIn section III we assumed that the outer boundary of the plasma is related to the radius of the apparatus Rw by  based on the behaviour of the solution of (30). Since the electron density nearly vanishes at
based on the behaviour of the solution of (30). Since the electron density nearly vanishes at  in figure 2, it might seem more appropriate to assume
in figure 2, it might seem more appropriate to assume 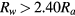 . On the other hand, the decrease in the potential of the solution of (30) in figure 1 is closer to the result of the moment equation, especially for Te = 3 eV. Therefore, we still adopt
. On the other hand, the decrease in the potential of the solution of (30) in figure 1 is closer to the result of the moment equation, especially for Te = 3 eV. Therefore, we still adopt 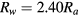 in this article keeping in mind that, if we should take
in this article keeping in mind that, if we should take 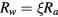 with
with 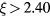 , the parameter Rw given in table 1 should be regarded as
, the parameter Rw given in table 1 should be regarded as  cm.
cm.
V.C. Fine particles of one species
Typical examples of densities in the case of fine particles of one species at Te = 1 eV and Te = 3 eV are shown in figure 3, where the potential and the net charge density are also shown. The radius of the particle distribution increases with the increase in the central particle density  . In these results, we observe the features (a), (b) and (c) as described in section IV.A.
. In these results, we observe the features (a), (b) and (c) as described in section IV.A.
Figure 3. Ion, electron and fine particle densities normalised by ne(0) (top), the electrostatic potential normalised by  (middle), and the net charge density normalised by ne(0) (bottom), for
(middle), and the net charge density normalised by ne(0) (bottom), for  at Te = 1 eV, and
at Te = 1 eV, and 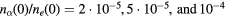 at Te = 3 eV. The broken lines are the values without fine particles,
at Te = 3 eV. The broken lines are the values without fine particles, 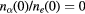 . With the increase in the central density, the domain of enhanced charge neutrality becomes wider, accompanying peak structures of positive overshooting.
. With the increase in the central density, the domain of enhanced charge neutrality becomes wider, accompanying peak structures of positive overshooting.
Download figure:
Standard image High-resolution imageIn the bottom panels in figure 3, we see that the charge neutrality is largely enhanced only in the domain where particles exist and it returns to values without fine particles outside that domain. In the domain of the particles' existence, the electrostatic potential and electron distribution become almost flat, and the charge density of the ions and the (absolute value of) the particle charge density are almost parallel, in accordance with the enhanced charge neutrality.
At the radius where the particle density vanishes, the drop in the ion density is slower than particles, and we have overshooting in the net positive charge density. While the potential is almost flat in the domain of the particles' existence, the potential changes at the edge of particle distribution. There, the decay of the particle density is sharper than that of the electrons or ions due to large charges on the particles, causing the overshooting of the positive charge.
The radius of particle distribution is compared with the estimation (60) in table 3. We observe that they are in good agreement, (60) overestimating the radius only slightly in most cases. We also show the ratio of the plasma loss onto the surface of particles 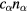 to the plasma generation
to the plasma generation 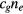 at the centre. Although the loss increases with the increase in the particle density, it is still less than half even when the central charge density of particles is about 20% of the electrons. The rest of the generated plasma is transported to the wall by the ambipolar diffusion.
at the centre. Although the loss increases with the increase in the particle density, it is still less than half even when the central charge density of particles is about 20% of the electrons. The rest of the generated plasma is transported to the wall by the ambipolar diffusion.
Table 3. Distribution radius and the ratio  (
(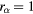 μm).
μm).
 (eV) (eV) |
 |
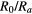 |
 by (60) by (60) |
 |
|---|---|---|---|---|
| 1 | 0.19 | 0.17 | 0.18 | 0.36 |
| 1 | 0.097 | 0.10 | 0.11 | 0.18 |
| 1 | 0.049 | 0.07 | 0.075 | 0.090 |
| 3 | 0.17 | 0.075 | 0.086 | 0.19 |
| 3 | 0.088 | 0.045 | 0.058 | 0.095 |
| 3 | 0.035 | 0.015 | 0.036 | 0.038 |
V.D. Formation of a void
With the increase in ne(0), the particle distribution increases its radius and becomes flatter, as shown by the examples in figure 4. The corresponding behaviour of the potential and the net charge density is also shown.
Figure 4. Increase in the radius of the particle distribution at  cm−3. The critical value for the formation of void
cm−3. The critical value for the formation of void 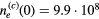 cm−3. The particle density is
cm−3. The particle density is 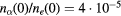 .
.
Download figure:
Standard image High-resolution imageWhen ne(0) exceeds some critical value 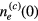 , the particle density increases with R, even starting from a very small value at R = 0: This signals the appearance of the void at the centre. The critical value
, the particle density increases with R, even starting from a very small value at R = 0: This signals the appearance of the void at the centre. The critical value  for the void formation decreases either by the increase in the particle radius
for the void formation decreases either by the increase in the particle radius 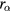 , the increase in the electron temperature Te or the decrease in the neutral gas pressure pn. On the right-hand side of (67) in section IV.B, the increase in
, the increase in the electron temperature Te or the decrease in the neutral gas pressure pn. On the right-hand side of (67) in section IV.B, the increase in 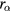 or Te gives the increase for
or Te gives the increase for  , and the decrease in pn gives the increase in
, and the decrease in pn gives the increase in  , all giving the decrease in
, all giving the decrease in 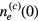 . We have analysed the domain
. We have analysed the domain ![$0.5<{{r}_{\alpha}}\left[\mu \text{m}\right]<1$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn187.gif) ,
, ![$10<{{p}_{n}}\left[\text{Pa}\right]<100$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn188.gif) , and
, and ![$1<{{T}_{e}}\left[\text{eV}\right]<3$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn189.gif) , and the results are plotted in figure 5. The dependency on
, and the results are plotted in figure 5. The dependency on 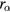 , Te, and pn is approximately expressed by
, Te, and pn is approximately expressed by
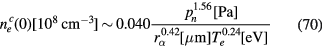
to within a few %. Although the above dependence on parameters is not exactly the same but consistent with our expectation (69), the latter being obtained using approximate interpolations for the parameter-dependence of 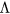 and z. The main point of our results may be that, when
and z. The main point of our results may be that, when 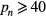 Pa, the critical density at the centre is sufficiently larger than 109 cm−3 and rapidly increases with the increase in pn.
Pa, the critical density at the centre is sufficiently larger than 109 cm−3 and rapidly increases with the increase in pn.
Figure 5. Void formation condition. A void appears when the parameters are in the domain above the lines. The dotted lines are (70). (Those for (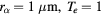 eV) and (
eV) and (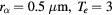 eV) are almost identical.)
eV) are almost identical.)
Download figure:
Standard image High-resolution imageExamples of the distributions, the potential and the net charge density with the void are shown in figure 6 in the cases where ne(0) slightly exceeds the critical value 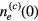 for Te = 3 eV and
for Te = 3 eV and  μm. Starting from very small values, the particle charge density reaches the maximum and decays with a further increase in R. In the domain of the void, we observe the increase in the net charge density or the weakened charge neutrality: This confirms that the enhanced charge neutrality (feature (a) in section IV.A) is due to the existence of the particles, as described there. (Since (B.4) indicates that
μm. Starting from very small values, the particle charge density reaches the maximum and decays with a further increase in R. In the domain of the void, we observe the increase in the net charge density or the weakened charge neutrality: This confirms that the enhanced charge neutrality (feature (a) in section IV.A) is due to the existence of the particles, as described there. (Since (B.4) indicates that 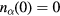 means
means 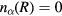 everywhere, we have to start with some finite but very small values for
everywhere, we have to start with some finite but very small values for 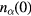 . The solutions, however, are not so sensitive as the starting value
. The solutions, however, are not so sensitive as the starting value 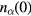 . The results shown here are obtained by assuming
. The results shown here are obtained by assuming 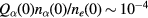 and the behaviour of the solutions is almost the same, at least when the starting value is changed within factor 2.)
and the behaviour of the solutions is almost the same, at least when the starting value is changed within factor 2.)
Figure 6. The distributions, potential and net charge density with void for 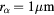 .
.
Download figure:
Standard image High-resolution imageV.E. Distribution of fine particles of two species
Here, we consider the case where we have particles of two species or two radii. The void formation condition depends on the radius of the particles 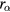 through the charge on a particle
through the charge on a particle 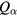 , which is approximately proportional to
, which is approximately proportional to 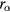 and through the coefficient c1.
and through the coefficient c1.
When larger particles satisfy the no-void condition, the smaller particles are automatically under the same condition. Examples of distributions in this case are shown in figure 7. Even if 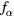 is smaller for smaller particles, it does not necessarily mean that the arithmetic sum of the inward electric force and the outward ion drag is larger for smaller particles. The results of the numerical analysis shown here indicate that the smaller particles are located inside the larger particles and, with R, the density of the smaller particles decays fast and is taken over by the larger particles. Since we also have features (a), (b) and (c) in multicomponent cases, the total charge density of the particles is kept almost constant. As a result, the addition of smaller particles (which only distribute very near to the axis) induces a higher density of larger particles in the domain where no smaller particles exist: this can be clearly seen in the lower figures in figure 7, where the density of the larger particles at the centre is kept constant.
is smaller for smaller particles, it does not necessarily mean that the arithmetic sum of the inward electric force and the outward ion drag is larger for smaller particles. The results of the numerical analysis shown here indicate that the smaller particles are located inside the larger particles and, with R, the density of the smaller particles decays fast and is taken over by the larger particles. Since we also have features (a), (b) and (c) in multicomponent cases, the total charge density of the particles is kept almost constant. As a result, the addition of smaller particles (which only distribute very near to the axis) induces a higher density of larger particles in the domain where no smaller particles exist: this can be clearly seen in the lower figures in figure 7, where the density of the larger particles at the centre is kept constant.
Figure 7. Changes in distributions (left), the potential (centre), and the net charge density (right) due to the addition of the particles of 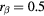 μm from the distribution of the particles of
μm from the distribution of the particles of 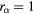 μm without a void for
μm without a void for 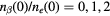 , and
, and 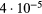 . The distribution for
. The distribution for  is shown in figure 4.
is shown in figure 4.
Download figure:
Standard image High-resolution imageWhen the larger particles are under the void condition, the smaller particles are with either the void condition or the no-void condition. Here, we consider the latter case. An example of the distributions, the potential and the net charge density is shown in figure 8. Without the smaller particles, the larger particles form a void at the centre, as shown in figure 6. When we have both larger and smaller particles, the smaller ones distribute around the centre as if to fill the void of the larger particles. As shown in figure 8, due to the existence of smaller particles, the charge neutrality becomes satisfied to a higher accuracy in the domain very near to the centre, which is originally in the void of the larger particles. We also notice that the takeover of the particle charge density by the larger particles is not so smooth as the case shown in figure 7, as indicated by the overshooting of the positive charge density.
Figure 8. Behaviour of distributions (left), the potential (middle), and the net charge density (right), when the particles of  μm are added to the void-forming particles of
μm are added to the void-forming particles of  μm.
μm.  .
.
Download figure:
Standard image High-resolution imageVI. Discussions
The behaviour of the fine particles in the glow discharge positive column has been investigated based on drift-diffusion equations by several authors [17, 18]. The flat distribution of fine particles with a tail has been assumed [17] and then self-consistency has been achieved [18]. In these investigations, the density of fine particles is rather high, so that the charge density of fine particles is comparable with that of ions and electrons and the generation of plasma is balanced with the loss to the surface of fine particles. The enhancement of the charge neutrality has been shown, but the physical origin of this phenomenon is left undiscussed.
In this paper, we have considered the cases with a gradually increased density of fine particles, staring from the well-known electron and ion distributions without fine particles described by the ambipolar diffusion theory, and thereby clarified the effects of fine particles on the charge neutrality. We have analytically shown their physical origin, enabling the results to apply qualitatively to systems which are not cylindrically symmetric. We have also shown that the condition required for this behaviour is (55) which is weaker by the factor  than the one on the simple charge density of fine particles. We have also taken into account the effect of the ion drag force, which has a strong effect on the distribution of fine particles and obtained the condition for the formation of voids.
than the one on the simple charge density of fine particles. We have also taken into account the effect of the ion drag force, which has a strong effect on the distribution of fine particles and obtained the condition for the formation of voids.
We have assumed that electrons, ions and fine particles have temperatures which are constant throughout the system. In principle, their temperatures are determined self-consistently by the flow of energy between the system and the environment (the excitation for plasma production) and between three components of the system, and becomes position dependent.
Among the three temperatures, the electron temperature plays the most important role. In this article, we have shown the numerical results with electron temperatures of 1 and 3  and indicated that the analytically derived features (such as enhanced charge neutrality) are confirmed for the electron temperatures around these values. Although not position-dependent nor self-consistent, we consider our results to be useful to understand the fundamental nature of fine particle plasma within the drift-diffusion approach.
and indicated that the analytically derived features (such as enhanced charge neutrality) are confirmed for the electron temperatures around these values. Although not position-dependent nor self-consistent, we consider our results to be useful to understand the fundamental nature of fine particle plasma within the drift-diffusion approach.
It is known that, for some effects, the deviation of the distribution function of electrons from the Maxwellian plays an important role. In this article, however, we have focused on the variety of behaviour of fine particle systems within the analytical and numerical treatment of simple drift-diffusion equations, expecting the results could be useful as a basis for taking those effects into account.
We have also neglected the effect of the discreteness of the particles, which is responsible for the shell or lattice-like structures of fine particles in the system with cylindrical as well as the spherical symmetry [19–23]. We have shown that, even without discreteness, the behaviour of fine particles has a rich variety [24]2.
In the numerical simulations of void formation in the configuration of the PK-3 Plus apparatus, which has hosted many successful experiments under microgravity, the densities of the constituent components were also monitored in the cloud of fine particles [25]. The characteristics shown here might have appeared, but the void and its periphery have been the main target of investigation. With a simpler geometry and also with simple assumptions about temperature, here we have clarified the behaviour of the components in the cloud of fine particles.
The observation of lattice-like structures of fine particles in glow discharges [26] and fine particles in positive-column glow discharges have been experimentally investigated mainly from the viewpoint of strong coupling effects (mutual correlation) and the macroscopic characteristics of discharge [17, 27, 28]. Although circular cross sections of clouds have been often observed, these experiments on the ground have not realised the cylindrical symmetry of the apparatus, and direct comparisons with our results seem to be difficult. We expect the results of on-going experiments under microgravity will become available in the near future.
VII. Conclusions
Based on the drift-diffusion equations, we have obtained the distribution of electrons, ions and fine particles both analytically and numerically. We have assumed the cylindrical symmetry of the system and considered the cases of up to two species of fine particles.
In the case of particles of one species, we have shown that the charge neutrality is satisfied to a much higher accuracy, the electrostatic potential and the electron distribution are almost flat, and the change in the negative charges due to fine particles is compensated by the ion distribution. This occurs in the domain of appreciable charge density of the particles in the sense that the particle charge density multiplied by the charge number is much larger than the electron and ion charge densities. It is analytically derived that this comes from the participation of particles to the screening of the space charge. We have also obtained the condition for the formation of a void at the centre and have shown the behaviour of the particle distribution with parameters near this condition. In the case of two species of particles, we have shown that smaller particles are distributed inside larger particles and, when larger ones form a void, they fill the inside of the void.
We expect that the behaviour of the distributions of electrons, ions and particles shown here is not critically dependent on the assumed symmetry of the system and the knowledge obtained within the drift-diffusion equations may be useful as a basis for further analyses with effects which are outside of these equations. The PK-4 project on the International Space Station (ISS) is in progress, and microgravity experiments are planned in the near future. The apparatus has cylindrical symmetry and comparisons of particle distributions will be interesting, especially in the case of two particle species.
Acknowledgments
The author would like to thank members of the JAXA Working Group especially Drs K Takahashi and S Adachi for fruitful discussions, Professor G Morfill, Drs H Thomas, M Thoma, and M Pustylnik of Max Plank Institute for Extraterrestrial Physics for the useful information of PK-4, and the ISS Science Project Office of JAXA for partly supporting this work.
Appendix A.: Ion drag force
The ion drag force depends on the parameter characterising the ion–particle coupling 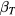 ,
,

and the ratio 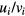 (the thermal Mach number): in our numerical analysis,
(the thermal Mach number): in our numerical analysis,  is of the order of unity and
is of the order of unity and 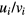 is less than unity. The ion drag force is determined by the momentum transfer from ions to fine particles via absorption and scattering. Theoretical treatments hitherto taken are based on either the ion–particle binary collision [10] or the linear kinetic method which regards the plasma including ions as a dielectric medium [11, 12]. The former approach taking into account both absorption and scattering gives
is less than unity. The ion drag force is determined by the momentum transfer from ions to fine particles via absorption and scattering. Theoretical treatments hitherto taken are based on either the ion–particle binary collision [10] or the linear kinetic method which regards the plasma including ions as a dielectric medium [11, 12]. The former approach taking into account both absorption and scattering gives
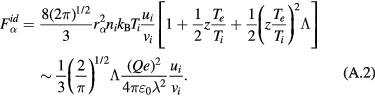
Here 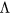 is given by (14). When
is given by (14). When 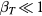 , (A.2) coincides with the result of the kinetic approach and, compared with the numerical calculations, is shown to be applicable for
, (A.2) coincides with the result of the kinetic approach and, compared with the numerical calculations, is shown to be applicable for 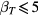 . The generalised Coulomb logarithm (14) has been used in numerical simulations with particles with a larger radius [8]. We note that, while the effect of the ion-neutral collisions is taken into account in the kinetic approach [11, 12], they are neglected in (A.2). We nevertheless adopt (A.2) for two reasons. The estimation of the collisional effect for
. The generalised Coulomb logarithm (14) has been used in numerical simulations with particles with a larger radius [8]. We note that, while the effect of the ion-neutral collisions is taken into account in the kinetic approach [11, 12], they are neglected in (A.2). We nevertheless adopt (A.2) for two reasons. The estimation of the collisional effect for  seems to be unavailable. When
seems to be unavailable. When 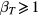 , the impact parameter for the closest approach less than λ (and therefore large angle scattering) becomes considerably larger than λ (the range of potential) by a factor
, the impact parameter for the closest approach less than λ (and therefore large angle scattering) becomes considerably larger than λ (the range of potential) by a factor 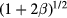 even without collisions [10] and we may expect a relatively small increase in the effective impact parameter by collisions. The expression (A.2) is also applied in the analysis of particle charging with the collisional effect [15], with a discussion estimating the effect of the collisions to be small.
even without collisions [10] and we may expect a relatively small increase in the effective impact parameter by collisions. The expression (A.2) is also applied in the analysis of particle charging with the collisional effect [15], with a discussion estimating the effect of the collisions to be small.
We find that, in our domain of interest 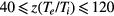 and
and 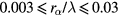 , the values are reproduced by the interpolation formula
, the values are reproduced by the interpolation formula
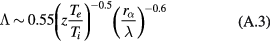
within relative errors of a few %.
Appendix B.: Equations in terms of  and normalisation
and normalisation
Introducing  , we have
, we have
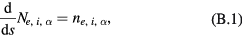
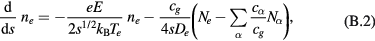
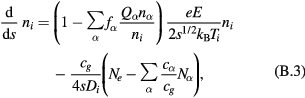
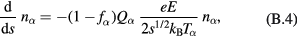
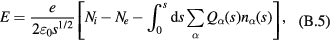
and
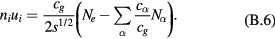
We define the normalised quantities by
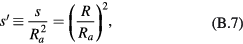
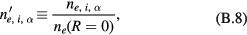
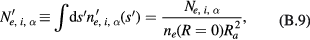
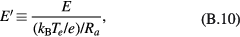

and
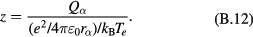
The equations to be solved take the forms
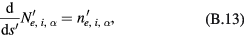
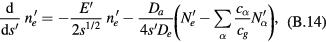
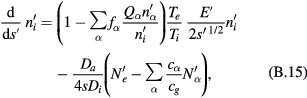
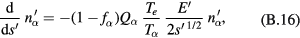
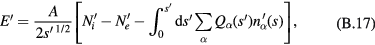
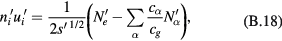
and
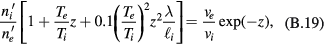
where
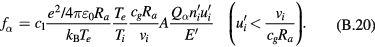
Noting 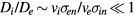 ,
, 
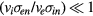 ,
,  ,
, 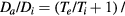
 , and
, and 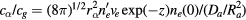 , we have values of coefficients in these equations. (The estimation
, we have values of coefficients in these equations. (The estimation  is used only for small factors
is used only for small factors 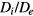 and
and 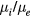 .) The normalised potential
.) The normalised potential 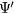 is defined by
is defined by
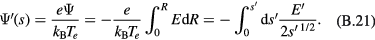
Appendix C.: Solutions without fine particles
Footnotes
- 1
In K2, we note
 and also neglect the contribution from the change of
and also neglect the contribution from the change of  in comparison with
in comparison with  , evaluating as
, evaluating as ![${{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{\text{d}{{Q}_{\alpha}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{\partial {{Q}_{\alpha}}}{\partial {{n}_{i}}}\frac{\text{d}{{n}_{i}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{{{Q}_{\alpha}}}{{{n}_{i}}}\frac{\text{d}{{n}_{i}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{Q}_{\alpha}}{{n}_{\alpha}}}{{{n}_{e}}}\frac{\text{d}\left[{{n}_{i}}/{{n}_{e}}(0)\right]}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}.$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=)
- 2
A part of preliminary result has been given in [24].










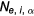




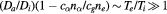
![${{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{\text{d}{{Q}_{\alpha}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{\partial {{Q}_{\alpha}}}{\partial {{n}_{i}}}\frac{\text{d}{{n}_{i}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{n}_{\alpha}}}{{{n}_{e}}}\frac{{{Q}_{\alpha}}}{{{n}_{i}}}\frac{\text{d}{{n}_{i}}}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}\sim {{\left\{\frac{{{Q}_{\alpha}}{{n}_{\alpha}}}{{{n}_{e}}}\frac{\text{d}\left[{{n}_{i}}/{{n}_{e}}(0)\right]}{\text{d}\left(s/R_{a}^{2}\right)}\right\}}_{0}}.$](https://content.cld.iop.org/journals/0741-3335/58/4/045010/revision1/ppcfaa0fd3ieqn071.gif)