Abstract
Magneto-inertial fusion (MIF) is an approach for thermonuclear fusion. It consists in applying a strong magnetic field to the inertial-fusion plasma, with the role of the magnetic field being to limit the diffusion of the formed plasma during the impact of an intense laser pulse with a target containing the thermonuclear fuel, as well as the confinement alpha particles produced by the fusion reaction. This allows the reduction of energy loss and improves compression conditions. In this paper we are interested in the study of the electron-ion inverse bremsstrahlung absorption (IBA) of the laser energy in magnetized plasma in the MIF frame. In addition, we apply the derived formula to calculate the absorption in magnetic fusion plasma heated by microwave. We use the Fokker-Planck-Maxwell theory to calculate the IBA explicitly in magnetized plasma. Scaling laws for IBA in MIF plasma and for magnetic confinement plasma are established. The numerical treatment of the model equations shows the influence of the magnetic field and the polarization of the wave on the absorption.
Export citation and abstract BibTeX RIS
Introduction
Magneto-inertial fusion (MIF) [1–6] is an approach to fusion which combines aspects of magnetic confinement fusion (MCF) [7,8] and inertial confinement fusion (ICF) [9,10]. In the first aspect, a dense 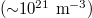 , high temperature
, high temperature  plasma is stored in a given volume under the influence of a magnetic field pressure countermining the plasma pressure. The second aspect is based on heating the thermonuclear fuel to a high temperature for a period of time comparable to the characteristic time scale of the hydrodynamic expansion of the plasma using powerful sources of energy (laser, heavy ions beam...).
plasma is stored in a given volume under the influence of a magnetic field pressure countermining the plasma pressure. The second aspect is based on heating the thermonuclear fuel to a high temperature for a period of time comparable to the characteristic time scale of the hydrodynamic expansion of the plasma using powerful sources of energy (laser, heavy ions beam...).
The main ideas of the MIF have been known for nearly four decades [2,3]. The concept of this approach involves applying a strong magnetic field to the inertial fusion target and freezing the magnetic flux in the hot spot or embedding the magnetic flux in a target plasma bounded by a conducting shell, called a liner, serving as a magnetic flux conserver [3]. In a manner similar to conventional inertial fusion, the hot spot or the conducting shell (liner) is imploded and the magnetic flux is compressed with it, and thus the intensity of the magnetic field is increased. During compression of the plasma, the thermal diffusivity is significantly reduced by the intense applied magnetic field, and therefore the plasma is easily heated to thermonuclear-fusion temperatures. In addition, the very high magnetic field, formed in the hot spot or in the fusion plasma, traps the alpha particles, produced by the thermonuclear reaction, which permits to boost the alpha energy disposition in the fusion plasma.
The energy absorption has a greater significance in fusion experiments as it directly contributes to the plasma heating in order to achieved the Lawson criteria [11,12].
In the laser fusion plasma, the absorption is achieved by several mechanisms including inverse bremsstrahlung absorption (IBA) [13–16], resonance absorption [17,18] and anomalous absorption [19].
The most important absorption mechanism in the laser MIF experiments is the IBA, in which the radiation is absorbed by electrons when they scatter off the Coulomb field of ions. In the magnetic fusion devices, the electromagnetic energy can be absorbed by the cyclotron resonance mechanism. The non-linear anomalous absorption mechanism, which will be the object of a future publication, has not been taken into account in this work.
In this paper we are interested in the study of the IBA of laser energy by magnetized plasma in the MIF frame through a theoretical development, and we use the derived formula to calculate the absorption in magnetic fusion (MF) plasma heated by microwave.
This paper is organized as follows. The equations of the l-th component of the high- and low-frequency electronic distribution function expanded on the spherical harmonics, are calculated from the Fokker-Planck equation in the presence of a magnetic field [20]. In the next section, the absorption is explicitly calculated using the results of the previous section. Then, scaling laws are given for the IBA in laser MIF and in MF plasma heated by microwave [21]. Finally, an interpretation and conclusion of the obtained results are given.
Electron velocities distribution in magnetized laser fusion plasma
In order to formulate the propagation of a laser pulse through magnetized collisional plasma in the non-relativistic regime, we consider an inhomogeneous plasma heated by a circularly polarized laser wave in the presence of an axial magnetic field. It is judicious to use the Fokker-Planck equation to describe magnetized collisional plasma. Following the notation of Braginskii [22], the electrons Fokker-Planck equation (FP) is presented as

where 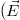 ,
, 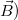 denotes the laser electromagnetic field,
denotes the laser electromagnetic field,  is the applied magnetic field along the wave propagation, f, e and me
are the electron distribution function, the electron charge and the electron mass, respectively.
is the applied magnetic field along the wave propagation, f, e and me
are the electron distribution function, the electron charge and the electron mass, respectively.
The right-hand side of eq. (1) represents the Landau electron-ion collision operator [23]:

where  , with Z being the ion charge number, ne
is the electron density,
, with Z being the ion charge number, ne
is the electron density, 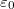 is the electric permittivity of free space, and
is the electric permittivity of free space, and 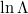 is the Coulomb logarithm.
is the Coulomb logarithm.
We have neglected the electron-electron collision term for high-order order anisotropic components of the distribution function 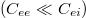 , which corresponds to the Lorentz-plasma approximation (high Z limit).
, which corresponds to the Lorentz-plasma approximation (high Z limit).
In this paper we consider a parallel circularly polarized laser wave propagating in the direction of an applied magnetic field (z) and oscillating in the perpendicular plane. Usually, this geometry is used in MIF experiments [19,24,25]:


and

where 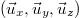 are the unit vectors and ω is the laser wave frequency.
are the unit vectors and ω is the laser wave frequency.
The distribution function is supposed to be constituted of two contributions: a fast oscillation distribution, f(h), which follows the laser wave time variation, 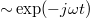 , and a quasi-static distribution, f(s), which has a slow variation as the plasma hydrodynamic parameters [25–28], hence:
, and a quasi-static distribution, f(s), which has a slow variation as the plasma hydrodynamic parameters [25–28], hence:

Note that the indices (s) and (h) respectively refer to the low and high frequency time scales, and will be used throughout this work.
Substituting eqs. (3)–(6) into eq. (1) and separating the time scale orders, we obtain a system of two coupled equations, the high-frequency kinetic equation and a quasi-static kinetic equation:
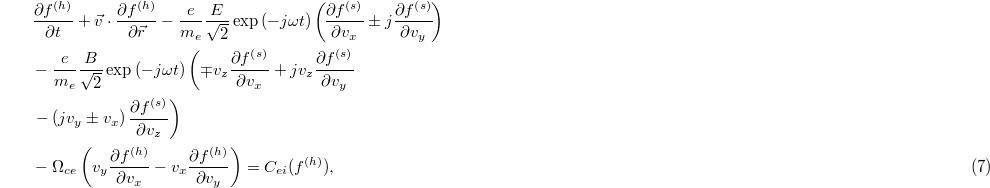
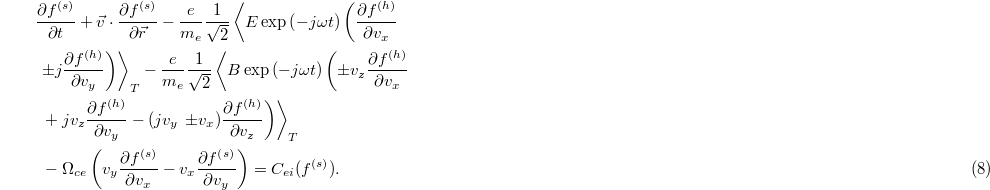
The symbol 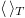 in eqs. (8) denotes the average over the laser wave cycle time
in eqs. (8) denotes the average over the laser wave cycle time  and
and  is the electronic cyclotron frequency.
is the electronic cyclotron frequency.
The two coupled equations (7) and (8) constitute the basic equations in the present work.
We introduce the spherical coordinates  , which are justified by the fact that the Landau collision operator only affects the angular part of the function and has the spherical harmonics as own functions [25].
, which are justified by the fact that the Landau collision operator only affects the angular part of the function and has the spherical harmonics as own functions [25].

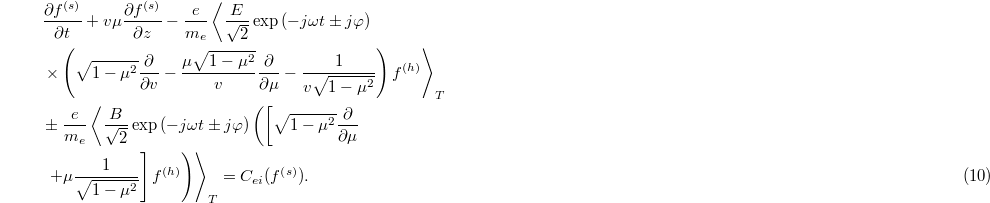
Equations (9) and (10) imply that f(h) is proportional to 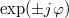 and f(s) is independent of φ. This allows us to expand f(h) using associated Legendre polynomials
and f(s) is independent of φ. This allows us to expand f(h) using associated Legendre polynomials 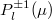 and f(s) using Legendre polynomials
and f(s) using Legendre polynomials 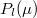 [29,30], thus
[29,30], thus


From eq. (9), and using recurrence relations between Pl
and 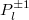 , the expression for the l-th component of f(h) is given by
, the expression for the l-th component of f(h) is given by

Additionally, the l-th component of 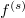 is given by
is given by
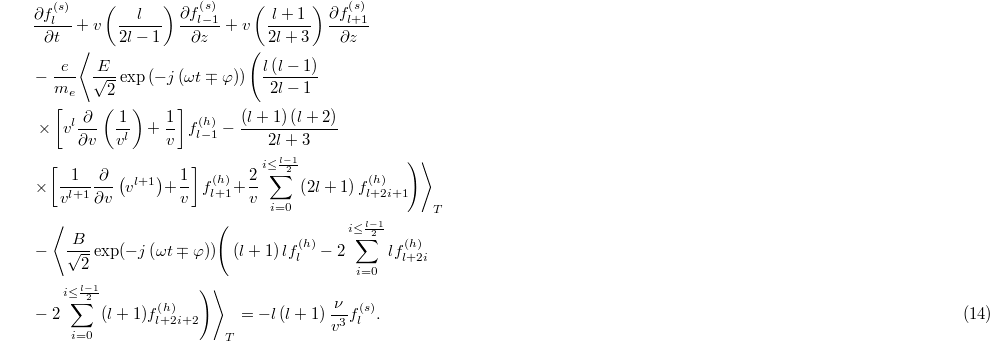
The set of equations (13) and (14) allows us to compute all components of the distribution function for magnetized plasma heated by a laser pulse. These equations actually provide us with more information on the plasma than eq. (23) of ref. [25], by including the magnetic field, and give more information than eq. (4) of ref. [26], by including the higher anisotropic distribution. Note that at the zeroth order, we recover, for the isotropic distribution function, eq. (4) of ref. [26]. By ignoring the distortion term in this equation the solution is Maxwellian and it is a super Maxwellian [25] by taking into account the distortion of the isotropic distribution (Langdon effect).
Electron-ion inverse bremsstrahlung absorption
The time-average power dissipated per unit volume by the electron-ion inverse bremsstrahlung mechanism is [26]

where 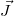 is the current density defined by the electronic distribution, f, which takes into account the laser field, the applied magnetic field and the electron-ion collisions, so
is the current density defined by the electronic distribution, f, which takes into account the laser field, the applied magnetic field and the electron-ion collisions, so

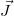 contains a quasi static part,
contains a quasi static part,  , and a high-frequency part,
, and a high-frequency part, 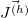 , which oscillates at the laser frequency, ω, thus
, which oscillates at the laser frequency, ω, thus

The contribution of the static component vanishes since it averages to zero on the laser cycle time, and thus we are only left with the contribution of the high-frequency distribution. Using eqs. (13)–(17), the absorption Γ can be expressed as follows:

where 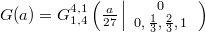 is the Meijer function [29] with argument
is the Meijer function [29] with argument 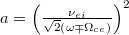 .
.
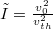 is a normalized laser intensity, with
is a normalized laser intensity, with 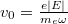 being the peak oscillating-electron velocity in the (hf) laser electric field,
being the peak oscillating-electron velocity in the (hf) laser electric field, 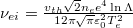 is the electron-ion collision frequency,
is the electron-ion collision frequency, 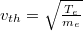 is the electron-thermal velocity, whereas Te
is the electron temperature.
is the electron-thermal velocity, whereas Te
is the electron temperature.
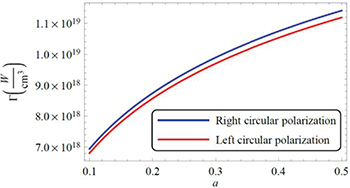
We present in fig. 1 the absorption as a function of a for typical parameters of plasmas and laser pulse.
Fig. 1: Plot of Γ as a function of a. The blue and red lines, respectively, correspond to the right and left circular polarizations. The typical parameters of plasmas, laser pulse and the applied magnetic field, respectively, are 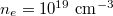 ,
, 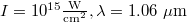 and
and 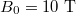 .
.
Download figure:
Standard imageScaling laws
In this section we derive the scaling law for the 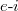 inverse bremsstrahlung in magnetized laser-fusion plasma and magnetically confined plasma heated by an electromagnetic wave which corresponds to the microwave heating.
inverse bremsstrahlung in magnetized laser-fusion plasma and magnetically confined plasma heated by an electromagnetic wave which corresponds to the microwave heating.
Magnetized laser-fusion plasma
The fusion plasma is created by an intense laser pulse. Consequently, the plasma parameters are given by the laser field parameters. In ref. [31] the temperature of the corona is deduced by calculating the energy balance in the critical layer, where the plasma frequency, 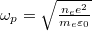 , is equal to the laser frequency
, is equal to the laser frequency 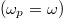 .
.
The critical density, nc , is directly given by the laser wavelength, thus

The electron temperature, Te , is given by the laser wavelength λ and the absorbed laser intensity Ia , as

Here, 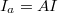 is the absorbed laser intensity, with I being the laser pulse intensity expressed by W/cm2, and A is the absorption coefficient. In the case of total absorption, we can consider that
is the absorbed laser intensity, with I being the laser pulse intensity expressed by W/cm2, and A is the absorption coefficient. In the case of total absorption, we can consider that 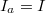 and A = 1.
and A = 1.
The critical density nc
, the laser wavelength λ and the electron temperature Te
in the critical layer are respectively expressed by cm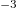 , μm and keV.
, μm and keV.
Using eqs. (18), (19) and (20) the absorption for laser MIF plasma can be expressed as

where Γ, λ, I and B0 are respectively expressed by  , μm,
, μm, 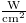 and T.
and T.
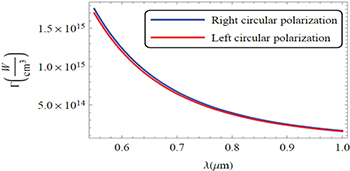
We illustrate in fig. 2 the absorption as a function of the laser wavelength using the typical parameters for laser intensity 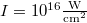 and applied magnetic field
and applied magnetic field 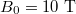 .
.
Fig. 2: Plot of Γ as a function of the laser wavelength λ. The blue and red lines, respectively, correspond to the right and left circular polarizations. The parameters of laser and the applied magnetic field are 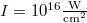 and
and 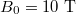 .
.
Download figure:
Standard imageThis figure shows that absorption decreases with the laser wavelengths, which can be interpreted by the decrease of the critical density as the laser wavelength increases 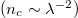 and therefore the decrease in collision frequency
and therefore the decrease in collision frequency 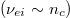 , which is implied by the decrease in absorption Γ.
, which is implied by the decrease in absorption Γ.
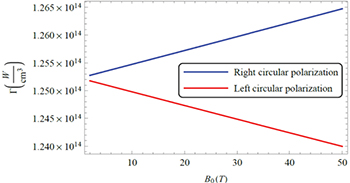
We show in fig. 3 the effect of the applied magnetic field B0 on the absorption Γ.
Fig. 3: Plot of Γ as a function of the applied magnetic field B0. The blue and red lines, respectively, correspond to the right and left circular polarizations. The parameters of laser are 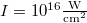 and
and 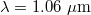 .
.
Download figure:
Standard imageWe see from fig. 3 the effect of the applied magnetic field B0 on the absorption Γ in the game of 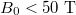 . This figure shows that the IB absorption is slowly increasing with B0, which is explained by the fact that in the case of parallel circularly polarized laser wave, the direction of electron motion due to laser field is the same as the direction of cyclotron motion due to the magnetic field, so the pulsation of the electrons increases (
. This figure shows that the IB absorption is slowly increasing with B0, which is explained by the fact that in the case of parallel circularly polarized laser wave, the direction of electron motion due to laser field is the same as the direction of cyclotron motion due to the magnetic field, so the pulsation of the electrons increases (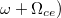 . These results increase in the absorption.
. These results increase in the absorption.
Magnetic confinement plasma
In magnetic fusion devices, high-power microwave sources (e.g., a MW gyrotron [32]) are used to heat electrons or ions via electron cyclotron resonance [4–5] or ion cyclotron resonance. Microwave heating is one of the main modes that are used to heat thermonuclear plasma to temperatures of the order of keV. Absorption is mainly due to resonance of the ions or electrons with the cyclotron frequency. The radiofrequency wave can also be absorbed by the inverse bremsstrahlung mechanism [33,34].
Electromagnetic waves in the microwave range at higher frequencies (100 to 300 GHz) are used to heat the plasma in MC devices. For the absorption by the resonance mechanism, we use waves in resonance with electron cyclotron, 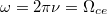 , where ν is the frequency of injected microwave.
, where ν is the frequency of injected microwave.
In this case, the electron-ion IBA scaling law can be directly obtained from eq. (18) as follows:
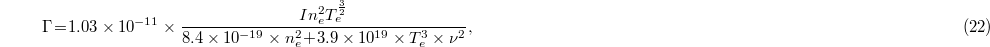
where Γ, ne
, I, Te
and ν are respectively expressed by 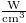 , cm
, cm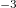 ,
, 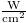 , keV and GHz.
, keV and GHz.
This equation expresses the absorption value in terms of injected microwave frequency, electronic density, electronic temperature and injected microwave intensity. Here we represent the effect of each parameter on absorption.
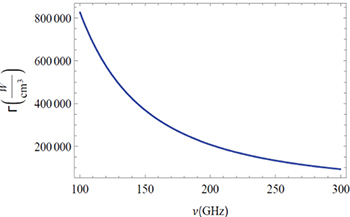
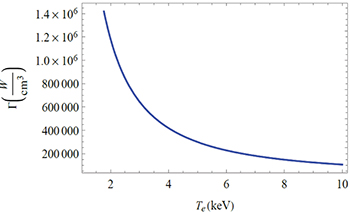
We show in fig. 4 the absorption profile Γ as a function of the injected microwave frequency.
Fig. 4: Plot of Γ as a function of the injected microwave frequency. The typical parameters of plasma and microwave, are, respectively, 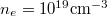 ,
, 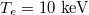 and
and 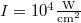 .
.
Download figure:
Standard imageFrom this figure we conclude that absorption is important for small values of the microwave frequency.
The effect of the second parameter is illustrated in fig. 5, using the typical parameters: 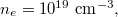
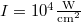 and
and  [32].
[32].
Fig. 5: Plot of Γ as a function of electron temperature for the typical parameters 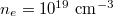 ,
, 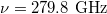 and
and 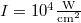 .
.
Download figure:
Standard imageWe conclude via fig. 5 that the absorption is important for low values of the electronic temperature, the physical reason of this effect is the fact that the electron-ion collisions are more frequent as long as the plasma is cold 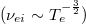 and consequently the IB absorption is more efficient.
and consequently the IB absorption is more efficient.
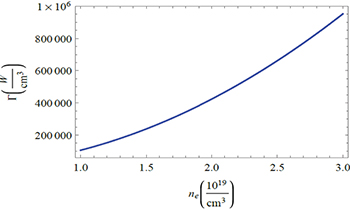
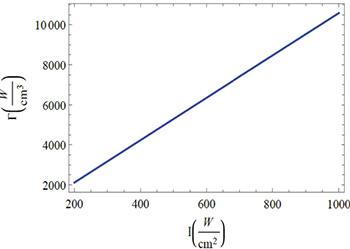
We show in figs. 6 and 7 the absorption profile Γ as a function of electronic density and intensity of the microwave.
Fig. 6: Plot of Γ as a function of the electron density of the plasma. The typical parameters of microwave and plasma, are, respectively,  ,
,  and
and 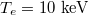 .
.
Download figure:
Standard imageFig. 7: Plot of Γ as a function of the injected microwave intensity. The typical parameters are 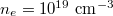 ,
, 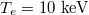 and
and 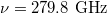 .
.
Download figure:
Standard imageThe absorption is large for high values of the electron density, and therefore the heating of the plasma is very effective for high densities, the physical reason of this effect is the fact that the electron-ion collisions are more frequent as long as the plasma is dense  and consequently the IB absorption is more efficient.
and consequently the IB absorption is more efficient.
Figure 7 shows that the absorption is large for high values of the microwave intensity, and therefore the heating of the plasma is very effective for high intensities. It is obvious that, by increasing the microwave intensity, the total absorption coefficient is increased. As we know, the main absorption mechanism of the microwave energy is the electron or ion cyclotron resonance absorption but the inverse bremsstrahlung absorption can also contribute to the energy transfer.
Discussion and conclusion
In this paper we studied the e-i inverse bremsstrahlung absorption for a magnetized plasma in the frame of the MIF. We explicitly calculated the absorption as a function of the laser pulse parameter. We have shown that the magnetic field affects the absorption and that its effect depends on the polarization direction. We found that the absorption is actually slightly larger for the right polarization and is slightly smaller for the left polarization (figs. 1–3). We derived useful scaling laws for IBA in a magnetized inertial fusion plasma and for magnetically confined plasma, heated by radiofrequency electromagnetic waves. In this study we restricted ourselves to the linear approach of IBA. The non-linear effect due to the higher anisotropy of the distribution function and the distortion of the isotropic distribution (Langdon effect), which can reduce significantly the absorption, has not been taken into account in this paper. This study allows us to optimize the laser pulse parameters in order to obtain an efficient absorption.
Acknowledgments
This work is supported by the General Direction of Scientific Research and Technology Development of Algeria (DGRSDT). The authors thank the General Director Mr. Aourag Hafidh for his support. One of the authors, AS, wishes to thank the head of the Algerain Authority of Atomic Energy (COMENA) for the delegation to the 28th IAEA Fusion Energy Conference, where part of this work will be presented.