Abstract
In this work we study the plasmon-polariton spectra in one-dimensional photonic crystals based on the Fibonacci, Thue-Morse and double-period sequences, where we have graphene at the interface of one of the constituent building blocks (A = SiO2/graphene, B = SiO2). The dispersion relations for each quasicrystal are numerically calculated by using a transfer-matrix approach. The spectra of these structures are shown to be fractals (for the bulk bands distribution), obeying a power law in a particular frequency region and these are induced specifically by the quasiperiodic ordering in the unit cells of each system studied. We also report a strong dependence of the width of the bulk bands on the wave vector for this particular frequency region, whereas for large wave vectors the fractal properties in these spectra are absent.
Export citation and abstract BibTeX RIS
Introduction
Fractals have been one of the most fascinating areas of research over the last forty years [1]. Nowadays, we have studies and applications of fractals in many different areas, like condensed-matter physics [2], engineering [3,4], metamaterials [5], and biology [6]. Specifically, their quantum effects were recently studied including transport [7], optical [8] and plasmonic [9] properties of regular fractal structures (Sierpinski carpet and gasket), and their power-law energy level spacing distributions [10]. However, there exists a very special one-dimensional system that exhibits fractal spectra as one of its main characteristics: the so-called 1D quasiperiodic system. Interest in such systems started with the discovery of quasiperiodic crystalline (or quasicrystalline) alloys in 1982 by Shechtman et al. [11]. It emerged that quasicrystals corresponded to an intermediate system between ordered and random systems, like amorphous materials. Today quasicrystals are well recognized as a natural extension of the notion of a crystal to structures with quasiperiodic (QP), instead of periodic, arrangements of atoms [12,13]. A more recent updated definition of quasicrystals with dimensionality n (n = 1, 2 or 3) is that they can also be defined as a projection of a periodic structure in a higher-dimensional space mD, where m > n [14]. Quasicrystals, therefore, represent a special class of deterministic aperiodic structures, exhibiting fractal properties in their spectra [15], with a distinct appearance for each chain [16], even for different excitations [17–19].
The pioneering work of Merlin et al. [20] on one-dimensional quasicrystals (1D-QC) structures, called quasiperiodic superlattices, has become the standard. We may define two distinct building blocks, each of which carries the necessary physical information, and then they are arranged according to a particular sequence. For example, they can be described in terms of a series of generations that obey the relation of particular recursion. In this work, we consider the building blocks A as silica (SiO2) with graphene in one of its interfaces, and the building blocks B are composed only by silica. Our choice here is intentional for a study of the quasiperiodicity induced by the graphene sheets in their plasmon-polariton spectra. A previous work on Fibonacci 1D-QC [21] with graphene at all interfaces focussed only on the band distribution and transmission spectra induced by the quasiperiodic organization of the dielectric layers at normal and oblique incidence. It is well known [18,19,22] that our type of choice illustrates more clearly the fractal nature in the spectra. On the other hand, the fractal, that was introduced by Mandelbrot [23] to characterize geometrical figures that are not defined in the Euclidian geometry, exhibits very interesting properties that can appear in diverse fields ranging from DNA [24] to the edges of Saturn's rings [25].
Graphene is a 2D material that consists of a flat sheet of carbon atoms, arranged in a hexagonal lattice and forming a monoatomic layer [26]. Its very special electronic structure reveals an exotic "zero bandgap" and it exhibits semiconductor properties when doped [27]. Also, in doped graphene we should have collective excitations such as plasmons, and plasmon-polaritons [28] with interesting optical characteristics in a similar way to surface plasmons on metal surfaces [29]. These interesting properties make graphene ideal for the study of metamaterials in the infrared and terahertz regions [30]. These optical properties of graphene give us several applications in photonics [31] and plasmonics [32].
Polaritons are mixed excitations of a photon (light) and a crystal excitation. In 1D dielectric photonic crystals (PCs) we can use Maxwell's equations to study these modes at long wavelengths (typically wave vectors below 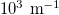 [22,33]). In this limit the electric and magnetic fields may extend beyond the boundaries of a PC. These fields couple with the excitations in the neighbouring (as well as the same) layers in a PC. Through Bloch's theorem, we can understand that these collective excitations characterize the PC. Specifically, if we have a 2D electron gas at interfaces in these systems, the collective modes are plasmon-polaritons. They are described by a Bloch wave number Q for the direction normal to the interfaces. The propagation of a polariton mode corresponds to Q lying within a new Brillouin zone associated with the PC periodicity,
[22,33]). In this limit the electric and magnetic fields may extend beyond the boundaries of a PC. These fields couple with the excitations in the neighbouring (as well as the same) layers in a PC. Through Bloch's theorem, we can understand that these collective excitations characterize the PC. Specifically, if we have a 2D electron gas at interfaces in these systems, the collective modes are plasmon-polaritons. They are described by a Bloch wave number Q for the direction normal to the interfaces. The propagation of a polariton mode corresponds to Q lying within a new Brillouin zone associated with the PC periodicity, 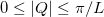 , where L is the unit cell size of the PC. For completeness, we will study here the surface modes of a semi-infinite PC (formed by truncating an infinite PC by an external surface). The reduction of symmetry can lead to the appearance of so-called surface polaritons.
, where L is the unit cell size of the PC. For completeness, we will study here the surface modes of a semi-infinite PC (formed by truncating an infinite PC by an external surface). The reduction of symmetry can lead to the appearance of so-called surface polaritons.
The development of graphene-based devices in the terahertz regime is currently attractive following the discovery that the surface plasmon polaritons supported by graphene sheets can be tuned in the terahertz regime by adjusting the external gate voltage or chemical doping. Recently, the production of terahertz (THz) radiation by a relatively low-energy electron beam directed onto the top of graphene layers was recently proposed as a new THz source (for a review see [34]). In this approach, surface plasmon polaritons with resonance frequencies in the THz range can be excited by an incident beam of moving electrons with speeds of less than 10 percent of the light speed. In this context, the present work can give insights into this new emerging field called graphene plasmonics.
Specifically we study the plasmon-polariton spectra in 1D photonic crystals generated by the Fibonacci, Thue-Morse and double-period sequences, where we have graphene at the interface of one of the constituents of its building blocks. This work is organized as follows. In the next section we present the general theory of plasmon-polaritons for dielectric or semiconductor multilayers with graphene sheets in the interfaces, and we apply this theory to our present case, showing the transfer matrix for each 1D-QC structure. Then we show the numerical results, illustrating the important role of the graphene sheets in the fractal spectra, and also we contrast it with other studies about the Fibonacci case. Finally we present the conclusions of this work.
Theory
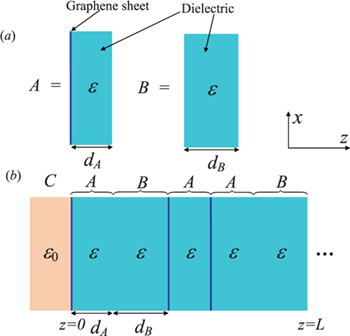
We consider a 1D-QC with building blocks A and B juxtaposed in a fashion that is determined according to a chosen quasiperiodic sequence to form a layered structure. The individual building blocks A and B are layers of a dielectric material (chosen as SiO2 with dielectric constant  ) having thicknesses dA and dB, respectively, as in fig. 1(a). One interface of building block A is taken to have a monolayer of graphene (with thickness negligible compared with dA), whereas B has no graphene layer.
) having thicknesses dA and dB, respectively, as in fig. 1(a). One interface of building block A is taken to have a monolayer of graphene (with thickness negligible compared with dA), whereas B has no graphene layer.
Fig. 1: (a) The A and B building blocks considered here, taken as SiO2, with 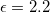 , and
, and 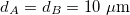 . (b) The layered geometry illustrated for the third-generation Fibonacci sequence (ABAAB) showing graphene sheets at some interfaces. In the case of a semi-infinite array with a surface at z = 0 the external medium is denoted as C.
. (b) The layered geometry illustrated for the third-generation Fibonacci sequence (ABAAB) showing graphene sheets at some interfaces. In the case of a semi-infinite array with a surface at z = 0 the external medium is denoted as C.
Download figure:
Standard imageThe graphene monolayers can be modelled as having a frequency-dependent optical conductivity, which includes both the intraband 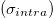 and interband
and interband 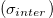 contributions (see [35] and references therein). The interband contribution plays the leading role around the absorption limit,
contributions (see [35] and references therein). The interband contribution plays the leading role around the absorption limit, 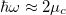 , while the intraband contribution is important at low frequencies compared with
, while the intraband contribution is important at low frequencies compared with 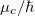 , giving a competing effect. Here, we are considering the form taken by the optical conductivity in the THz regime [36].
, giving a competing effect. Here, we are considering the form taken by the optical conductivity in the THz regime [36].
Following [37] we consider a periodic alternation of unit cells, where the arrangement of A and B layers are chosen to correspond to a quasiperiodic sequence, which may be either Fibonacci, Thue-Morse or double-period. For example, in fig. 1(b) we show the third-generation Fibonacci sequence. Initially, we consider an infinitely extended structure, for which Bloch's theorem is applicable, and then the effects of an external surface are introduced. Only p-polarization will be considered here, since the effects of the graphene are more evident in this case [38].
Dispersion relations: general multilayer
In order to obtain the plasmon-polariton bulk modes of the infinite PC, we utilise Maxwell's equations within each dielectric medium. For the transverse magnetic modes (TM or p-polarization) within medium A (or B) of the m-th layer, the electric field component is

where 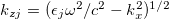 with kx being the in-plane component of the wave vector (parallel to the x-y plane), ω is the angular frequency,
with kx being the in-plane component of the wave vector (parallel to the x-y plane), ω is the angular frequency, 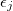 is the dielectric function in medium j and c is the velocity of the light in vacuum. The constants
is the dielectric function in medium j and c is the velocity of the light in vacuum. The constants 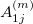 and
and 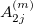 (
(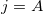 or B;
or B; 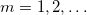 ) are amplitudes for forward- and backward-travelling waves, respectively. Using
) are amplitudes for forward- and backward-travelling waves, respectively. Using 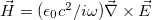 , the corresponding magnetic-field component in medium A ( or B) can be calculated. We consider the magnetic permeability
, the corresponding magnetic-field component in medium A ( or B) can be calculated. We consider the magnetic permeability 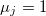 in each medium. Also we have used
in each medium. Also we have used 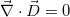 to relate the amplitudes of the electric and magnetic fields.
to relate the amplitudes of the electric and magnetic fields.
By applying the electromagnetic boundary conditions, requiring the continuity of the tangential component of the electric field and the discontinuity of the magnetic field to be equal to the current density 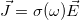 , at the interfaces
, at the interfaces 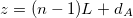 and z = nL, we can relate the electromagnetic fields for cell n to those for cell n + 1. After re-expressing the amplitudes in terms of those for index n (recall that m labels the individual layers, while n labels the unit cells), we obtain
and z = nL, we can relate the electromagnetic fields for cell n to those for cell n + 1. After re-expressing the amplitudes in terms of those for index n (recall that m labels the individual layers, while n labels the unit cells), we obtain

where 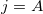 or B, depending on the quasiperiodic sequence. For the periodic case this matrix is simply given by
or B, depending on the quasiperiodic sequence. For the periodic case this matrix is simply given by 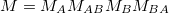 , with
, with 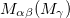 corresponding to the electromagnetic propagation across the interface
corresponding to the electromagnetic propagation across the interface 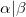 (across the medium γ), where
(across the medium γ), where 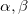 and γ denote A or B. These matrices are [35]
and γ denote A or B. These matrices are [35]


with 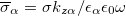 . Although the quasiperiodic structures have no translational symmetry, we use the periodicity of the unit cell through the application of Bloch's theorem. We consider that this model describes the quasiperiodicity when the number of generation goes to infinity (called the thermodynamic limit [39]). Therefore, the implicit dispersion relation for the bulk plasmon-polariton modes is (see, e.g., [22,33,39])
. Although the quasiperiodic structures have no translational symmetry, we use the periodicity of the unit cell through the application of Bloch's theorem. We consider that this model describes the quasiperiodicity when the number of generation goes to infinity (called the thermodynamic limit [39]). Therefore, the implicit dispersion relation for the bulk plasmon-polariton modes is (see, e.g., [22,33,39])

where M is a unimodular matrix and Tr denotes the trace.
For the surface modes we consider a semi-infinite PC with the geometry as in fig. 1(b). The region z < 0 is assumed to be a dielectric medium C with electric field

where 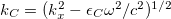 . The previous electromagnetic boundary conditions apply at
. The previous electromagnetic boundary conditions apply at 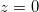 . For simplicity, we assume
. For simplicity, we assume  so that kC takes only real and positive values. The localized surface plasmon-polaritons correspond to decaying solutions for the amplitudes of the electromagnetic fields with respect to the distance from the surface plane
so that kC takes only real and positive values. The localized surface plasmon-polaritons correspond to decaying solutions for the amplitudes of the electromagnetic fields with respect to the distance from the surface plane 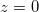 . Therefore, we can find the implicit dispersion relation for the surface modes [22,35] as
. Therefore, we can find the implicit dispersion relation for the surface modes [22,35] as

where 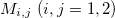 are the elements of the matrix M defined in eq. (2), and
are the elements of the matrix M defined in eq. (2), and 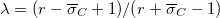 is a surface-dependent parameter. We have defined the ratio
is a surface-dependent parameter. We have defined the ratio 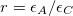 , with
, with  ). Also, here we choose
). Also, here we choose 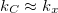 , only in the surface case, following [40].
, only in the surface case, following [40].
Dispersion relations: one-dimensional quasicrystals
We now apply the above formalism to the bulk and surface plasmon-polaritons in aperiodic (Fibonacci, Thue-Morse, and double-period) structures. First the Fibonacci structure can be constructed by juxtaposing the two building blocks A and B so that the n-th generation is given by the interactive rule 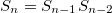 , for
, for 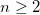 , with
, with 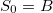 and
and 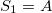 . Also, it can be constructed by applying the inflation rules
. Also, it can be constructed by applying the inflation rules 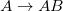 and
and 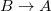 for each generation, starting with A. The Fibonacci generations are
for each generation, starting with A. The Fibonacci generations are 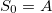 ,
, 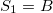 ,
, 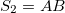 ,
, 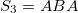 , etc. The number of the building blocks increases according to the Fibonacci number,
, etc. The number of the building blocks increases according to the Fibonacci number, 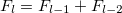 (with
(with  ). The transfer matrices are
). The transfer matrices are
a) for 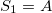 and
and 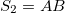

b) for 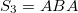

c) for any higher generation 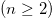

Knowing the initial transfer matrices 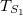 and
and 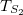 , we can determine the transfer matrix of any generation. Another way to obtain the same result (for bulk modes) is through a study of the trace map of
, we can determine the transfer matrix of any generation. Another way to obtain the same result (for bulk modes) is through a study of the trace map of 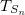 [41].
[41].
The Thue-Morse sequence at the n-th stage is defined by 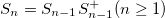 , where
, where 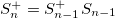 , with
, with  and
and 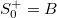 . Alternatively we can employ the transformations steps
. Alternatively we can employ the transformations steps 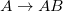 ,
, 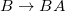 . The number of building blocks increases as
. The number of building blocks increases as 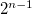 . The first stages for Thue-Morse generations are
. The first stages for Thue-Morse generations are 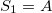 ,
, 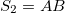 ,
, 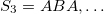 , and the transfer matrices for each generation can be calculated by induction using
, and the transfer matrices for each generation can be calculated by induction using
a) for 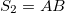

where

b) for 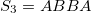

where 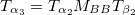 and
and 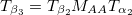 ;
;
c) for any generation 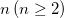

with

and

We can define a similar rule for the double-period sequence, where the n-th stages are found from the recursion relations 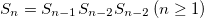 , with
, with 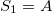 and
and 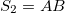 . Alternatively the transformation rules
. Alternatively the transformation rules 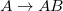 ,
, 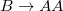 can be applied. The double-period generations are
can be applied. The double-period generations are 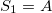 ,
, 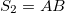 ,
, 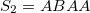 , etc. The number of building blocks for this sequence increase like
, etc. The number of building blocks for this sequence increase like  . The transfer matrix for the 2nd generation
. The transfer matrix for the 2nd generation  is found in the same way as in the Fibonacci case, i.e.,
is found in the same way as in the Fibonacci case, i.e.,
a) for 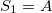 and
and 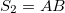

b) for 3rd generation we have

c) for any generation 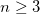

Numerical results
We present numerical examples to illustrate the results for the plasmon-polariton spectra that can propagate in the quasiperiodic structures described in the last section. We consider the dielectric media in building blocks A and B to be 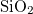 with
with 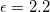 appropriate for THz frequencies [42]. Also we choose the temperature
appropriate for THz frequencies [42]. Also we choose the temperature  and
and 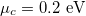 for the graphene sheets [35]. We ignore the role of absorption since it is typically small in SiO2 for other distinct crystalline forms and composition [43] in the temperature and frequencies of interest in this work. The other physical parameters used here are
for the graphene sheets [35]. We ignore the role of absorption since it is typically small in SiO2 for other distinct crystalline forms and composition [43] in the temperature and frequencies of interest in this work. The other physical parameters used here are 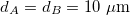 . We consider medium C to be vacuum
. We consider medium C to be vacuum  . All the frequencies encountered here are in the THz range. We should comment that the use of the transfer-matrix method (TMM) is computationally more efficient for our purpose than the use of more accurate methods such as the Finite Element Method or Boundary Element Method, where it would be necessary to access large-scale computational facilities, like clusters, etc. By using TMM we can employ a simple personal computer.
. All the frequencies encountered here are in the THz range. We should comment that the use of the transfer-matrix method (TMM) is computationally more efficient for our purpose than the use of more accurate methods such as the Finite Element Method or Boundary Element Method, where it would be necessary to access large-scale computational facilities, like clusters, etc. By using TMM we can employ a simple personal computer.
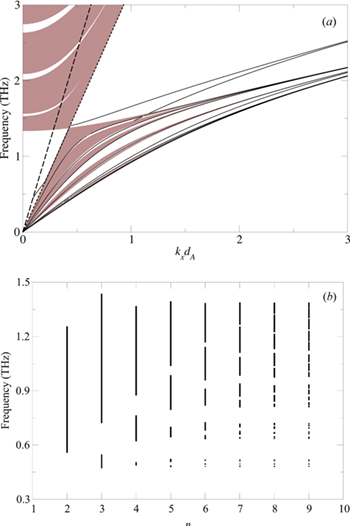
The plasmon-polariton spectra for the quasiperiodic Fibonacci, Thue-Morse, and double-period PCs are presented in figs. 2(a) and 4(a), respectively. Here the surface modes are represented by the black lines, while the bulk bands are characterized by the shaded areas, which are bounded by the conditions 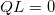 and
and 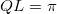 (at which the cosine factor in eq. (5) is
(at which the cosine factor in eq. (5) is  ). The results presented in those figures are in accordance with those found in the literature for the periodic case, including the so-called graphene-induced gap [35], for normal incidence
). The results presented in those figures are in accordance with those found in the literature for the periodic case, including the so-called graphene-induced gap [35], for normal incidence 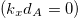 . The surface modes lie outside the bulk bands, subject to the constraint
. The surface modes lie outside the bulk bands, subject to the constraint 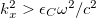 . This means that any surface mode in these plots lies to the right of the vacuum light line (VLL) given by
. This means that any surface mode in these plots lies to the right of the vacuum light line (VLL) given by 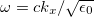 . For reference, we also show the dielectric light line (DLL) for the PC given by
. For reference, we also show the dielectric light line (DLL) for the PC given by 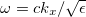 .
.
Fig. 2: (a) Plasmon-polariton bulk and surface dispersion relation for the quasiperiodic 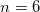 Fibonacci 1D-QC. The straight lines VLL and DLL represent the vacuum (dashed line) and the dielectric (dotted line) light lines, respectively. (b) Distribution of bandwidths for the plasmon-polaritons as a function of the Fibonacci generation number n.
Fibonacci 1D-QC. The straight lines VLL and DLL represent the vacuum (dashed line) and the dielectric (dotted line) light lines, respectively. (b) Distribution of bandwidths for the plasmon-polaritons as a function of the Fibonacci generation number n.
Download figure:
Standard imageIn fig. 2(a) for the spectrum for the 6th Fibonacci generation we have 8 building blocks A and 5 building blocks B. We can note two well-defined regions for the bulk plasmon-polariton spectrum, for frequencies above and below 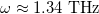 . For ω below about 1.34 THz and for
. For ω below about 1.34 THz and for 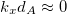 there is a large gap, sometimes called the graphene-induced gap [44,45], which extends out to the DLL of SiO2. For kxdA values to the right of the DLL we have many bulk bands which start at the origin and eventually merge into three narrow bands that will join in a straight line with a constant group velocity for high values of kxdA (not shown here). We can infer that these bands are induced by the graphene sheets at interfaces in building blocks A. In fact, the effect of the optical conductivity is expected to be stronger at low frequencies [36]. Therefore, for frequencies greater than
there is a large gap, sometimes called the graphene-induced gap [44,45], which extends out to the DLL of SiO2. For kxdA values to the right of the DLL we have many bulk bands which start at the origin and eventually merge into three narrow bands that will join in a straight line with a constant group velocity for high values of kxdA (not shown here). We can infer that these bands are induced by the graphene sheets at interfaces in building blocks A. In fact, the effect of the optical conductivity is expected to be stronger at low frequencies [36]. Therefore, for frequencies greater than 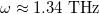 and wave vectors kxdA to the left of the DLL, we have only the quasiperiodic effects induced by the dielectric layers (except for a shift in all spectra, when compared with [22,33,46,47]), which is well known (see [48] to compare with the normal incidence case).
and wave vectors kxdA to the left of the DLL, we have only the quasiperiodic effects induced by the dielectric layers (except for a shift in all spectra, when compared with [22,33,46,47]), which is well known (see [48] to compare with the normal incidence case).
We see (to the right of the DLL) that the number of bulk bands is equal to the number of building blocks A and to the Fibonacci number 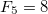 . It is a general property that this number is always equal to the Fibonacci number of the n –1 generation. Also in this region, there are 12 surface modes in total. There is one between the VLL and DLL, and the others are at the right of DLL between the bulk bands, except for one close to
. It is a general property that this number is always equal to the Fibonacci number of the n –1 generation. Also in this region, there are 12 surface modes in total. There is one between the VLL and DLL, and the others are at the right of DLL between the bulk bands, except for one close to 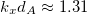 and
and  that has a very interesting behaviour. This mode starts at
that has a very interesting behaviour. This mode starts at 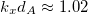 and
and 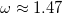 and "crosses" its adjacent surface and bulk modes. For higher values kxdA it merges with another surface branch. The crossing (or anti-crossing) effects between surfaces modes have been a subject of intense studies over decades (for a review see [49]). It has been shown that in crossing effects we have one or several modes coexisting at the same frequency and wave vector. Moreover, their dispersion curves appear to be closely spaced, just as in our case. At the point(s) of their convergence the curve(s) can intersect, merge with each other or split apart [50], i.e., the waves modes are either not coupled or the coupling is negligible. The anti-crossing effect that can appear in the system that we are studying is related to there being significant coupling between the modes, resulting in the modes type transformation and/or energy exchange between the waves. Such modes can appear between waves of the same or different nature, and, in particular, a "mixing" between surface, guided and bulk modes can occur [51]. The effect can appear in metallic thin films, where specifically it is linked with the strong coupling between surfaces modes rather like two coupled harmonic oscillators [49]. We can infer here that we have an anti-crossing effect and it is related with the quasiperiodic organization of the Fibonacci (or other) sequence in the PC. In other words, the Fibonacci sequence will cause a strong coupling between electromagnetic fields of the plasmon-polariton surface modes (mainly due to building blocks A), in such a way that we have a strong coupling in a specific point,
and "crosses" its adjacent surface and bulk modes. For higher values kxdA it merges with another surface branch. The crossing (or anti-crossing) effects between surfaces modes have been a subject of intense studies over decades (for a review see [49]). It has been shown that in crossing effects we have one or several modes coexisting at the same frequency and wave vector. Moreover, their dispersion curves appear to be closely spaced, just as in our case. At the point(s) of their convergence the curve(s) can intersect, merge with each other or split apart [50], i.e., the waves modes are either not coupled or the coupling is negligible. The anti-crossing effect that can appear in the system that we are studying is related to there being significant coupling between the modes, resulting in the modes type transformation and/or energy exchange between the waves. Such modes can appear between waves of the same or different nature, and, in particular, a "mixing" between surface, guided and bulk modes can occur [51]. The effect can appear in metallic thin films, where specifically it is linked with the strong coupling between surfaces modes rather like two coupled harmonic oscillators [49]. We can infer here that we have an anti-crossing effect and it is related with the quasiperiodic organization of the Fibonacci (or other) sequence in the PC. In other words, the Fibonacci sequence will cause a strong coupling between electromagnetic fields of the plasmon-polariton surface modes (mainly due to building blocks A), in such a way that we have a strong coupling in a specific point, 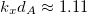 and
and  , in the dispersion relation for n = 6.
, in the dispersion relation for n = 6.
The distribution of the bandwidths for Fibonacci PCs is shown up to the 9th generation (a unit cell with 55 A and 34 B building blocks) in fig. 2(b), for 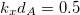 . One can observe that the forbidden and allowed frequencies are a function of the generation number n. As expected, for large n, the allowed band distribution gets narrower, with the behaviour becoming like a guided mode (sometimes called a localized mode) for large n. It forms the famous Cantor set (or Cantor dust) in this limit (also found in [17–19]). In fact, the total width of the total width of the allowed frequency bands goes down as a power law
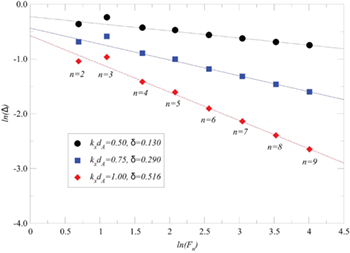
. One can observe that the forbidden and allowed frequencies are a function of the generation number n. As expected, for large n, the allowed band distribution gets narrower, with the behaviour becoming like a guided mode (sometimes called a localized mode) for large n. It forms the famous Cantor set (or Cantor dust) in this limit (also found in [17–19]). In fact, the total width of the total width of the allowed frequency bands goes down as a power law 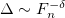 , where Fn is the Fibonacci number and the exponent δ is a function of the in-plane wave vector kxdA as we can see in fig. 3. Here we show a log-log plot indicating the power laws for three different values of kxdA, namely 0.5, 0.75 and 1.0.
, where Fn is the Fibonacci number and the exponent δ is a function of the in-plane wave vector kxdA as we can see in fig. 3. Here we show a log-log plot indicating the power laws for three different values of kxdA, namely 0.5, 0.75 and 1.0.
Fig. 3: Log-log plot of the total width of the allowed regions Δ as a function of the Fibonacci number Fn.
Download figure:
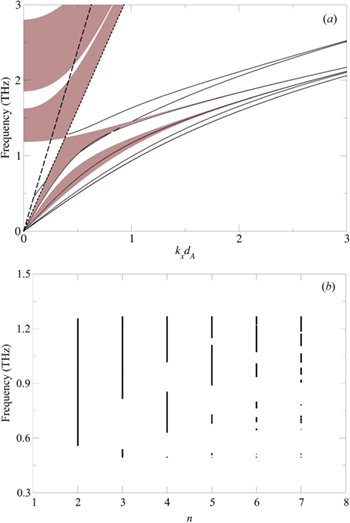
Standard imageThe Thue-Morse quasiperiodic 4th generation is shown in fig. 4(a). Here, as previously, we have two well-defined regions for the plasmon-polariton spectrum. For the region to the right of the DLL, the number of bulk bands increases as 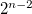 , which is the number of building blocks A. For wave vectors kxdA at the right of the DLL there are bands which start at the origin and merge into three narrow bands (guided modes), that will join in a straight line with a constant group velocity for high values of kxdA (not shown here). The surface modes lie between the bulk bands and, as in the previous case, we have also the anti-crossing surfaces modes at
, which is the number of building blocks A. For wave vectors kxdA at the right of the DLL there are bands which start at the origin and merge into three narrow bands (guided modes), that will join in a straight line with a constant group velocity for high values of kxdA (not shown here). The surface modes lie between the bulk bands and, as in the previous case, we have also the anti-crossing surfaces modes at 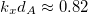 and
and  . Again, this is induced by the quasiperiodic organization of the graphene sheets. The bandwidth distribution, forming the so-called Cantor set when the generation number goes to infinity, is presented in fig. 4(b), for
. Again, this is induced by the quasiperiodic organization of the graphene sheets. The bandwidth distribution, forming the so-called Cantor set when the generation number goes to infinity, is presented in fig. 4(b), for 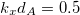 . We go up to the 7th generation, which means a unit cell with
. We go up to the 7th generation, which means a unit cell with 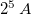 and B building blocks. The total allowed bandwidth Δ has power law as
and B building blocks. The total allowed bandwidth Δ has power law as 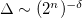 , where δ depends on the wave vector kxdA (like in fig. 3), but for δ vs. 2n, where we now find
, where δ depends on the wave vector kxdA (like in fig. 3), but for δ vs. 2n, where we now find 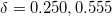 , and 1.067 for the same value of kxdA shown in fig. 3.
, and 1.067 for the same value of kxdA shown in fig. 3.
Fig. 4: (a) As in fig. 2, but for Thue-Morse 1D-QC. The straight lines VLL and DLL represent the vacuum light line (dashed line) and the dielectric light line (dotted line), respectively. (b) Distribution of bandwidths for the plasmon-polaritons as a function of the generation number n.
Download figure:
Standard imageFinally, the plasmon-polariton spectrum was studied for the double-period quasiperiodic structures up to the 4th generation (not shown here due to the similarity to the Thue-Morse case). We have found also two well-defined regions for the plasmon-polariton spectrum. For the surface modes we may identify two anti-crossing effects, and we do not find a surface mode between the VLL and DLL, as previously. For the forbidden and allowed regions we have a similar behaviour to the previous case in fig. 3(b), including the scaling 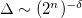 , where again the exponent δ is a function of the wave vector kxdA.
, where again the exponent δ is a function of the wave vector kxdA.
Conclusions
In this work we have presented a general theory for the propagation of plasmon-polaritons in 1Q-PC with graphene sheets in one of the building blocks. The spectra are illustrated in figs. 2 and 4. We have studied physical properties related to the quasiperiodicity of the systems and their self-similarity behaviour, whose fractality can be described by the power laws (see fig. 3 and the text). Also, we presented a discussion for the bulk and surfaces modes for low frequencies. We stress here the interesting properties (mainly in surfaces modes) that arise when we considered the quasiperiodicity induced by the graphene (figs. 2(a) and 4(a)). The localization (the decrease of the bandwidths when the sequence order tends to infinity) of the spectra is expressed by the distribution of their bandwidths shown in figs. 2(b) and 4(b).
The main experimental techniques to probe these results are inelastic (Raman) light scattering and Attenuated Total Reflection (ATR) of the light. In Raman scattering a grating spectrometer is used to detect the scattered light with a typical shift between 0.6 a 500 meV in the frequency of the scattered light [52]. This makes this technique highly suited to probe the plasmon-polariton spectra. Further, the ATR spectroscopy is simpler to implement, but there is less precision in detecting the modes. The structures proposed here can be experimentally fabricated, following [53] where the authors obtained a graphene-based 1D photonic crystal, as confirmed by Raman spectra and optical image of CVD, and demonstrated the excitation of surface modes using a prism coupling technique. Also, Zhang et al. [54] presented an approach to synthesize a high-quality single layer of graphene on a SiO2 substrate using Cu-vapor–assisted chemical vapor deposition. On the other hand, one should mention that another way to probe the self-similarity and fractal spectra of these aperiodic structures in 2D is to consider dark-field scattering spectroscopy to investigate the scattering properties of two-dimensional plasmonic lattices based on the aperiodic sequences presented here (for a review see [55,56]).
Acknowledgments
MSV thanks the Department of Physics and Astronomy at the University of Western Ontario for hospitality during his sabbatical as visiting professor. This study was financed in part by the Coordenação de Aperfeioamento de Pessoal de Nível Superior (CAPES) of Brasil (Finance Code 88881.172293/2018-01) and the Natural Sciences and Engineering Research Council (NSERC) of Canada (grant RGPIN-2017-04429).