Abstract
Dense filamentous brush-like structures are present in many biological interfacial systems (e.g., glycocalyx layer in blood vessels) to control their surface properties. Such structures can regulate the softness of a surface and modify fluid flow. In this letter, we propose a theoretical model which predicts quantitatively flow-induced deformation of a dense brush of stiff polymers or filaments, whose persistence length is larger or comparable to their contour length. The model is validated by detailed mesoscopic simulations and characterizes different contributions to brush deformation including hydrodynamic friction due to flow and steric excluded-volume interactions between grafted filaments. This theoretical model can be used to describe the effect of a stiff-polymer brush on fluid flow and to aid in the quantification of experiments.
Export citation and abstract BibTeX RIS
Introduction
Polymer brushes have been subject to enormous interest in the last several decades due to their importance in various technological and biological systems [1–3]. However, the main focus of most experimental, theoretical, and simulation studies has been on the behavior of brushes consisting of grafted flexible polymers (i.e., with negligible flexural stiffness on the length of a polymer). Brushes with stiff chains, whose persistence length is larger or comparable to the contour length, have received limited attention to date, in spite of their frequent presence in many biophysical systems. Dense filamentous brush-like structures often serve as structural elements in the human body with the examples of lubricating aggrecan brushes in joints [4], endothelial glycocalyx layer in blood vessels [5,6], periciliary layer of lung airway [7], and hair cells in the inner ear mediating the sense of hearing and balance [8,9]. Better understanding of their non-equilibrium behavior, for instance their response to flow, will lead to insights into the functionality of the respective structures and the effects of pathological alterations. Technologically, brushes with stiff grafted elements, such as cantilevered micro- and nano-rod arrays [10] or high-density brushes [11], can be used in nanofluidic devices [12] or in the context of functionalized surfaces [13].
Equilibrium properties of stiff-polymer brushes have been investigated in a few simulation [14–16] and theoretical [16–18] studies predicting the brush height. In silico compression tests of dense semiflexible-polymer brushes [19,20] have shown that such brushes might be much softer mechanically than the brushes made out of flexible polymers making them useful in micro-flow applications. As an example, the response of a glycocalyx layer in blood vessels to fluid flow has been studied in simulations [21] predicting a flow-rate–dependent increase in the flow resistance. Recently, a mean-field approach [22] has been developed to describe the flow-induced deformation of grafted semiflexible polymers. In this theory, the steric interactions between polymers have been neglected limiting the model's applicability to the deformation of a single grafted polymer.
In this letter, we develop a theoretical model which is able to describe quantitatively the flow-induced deformation of a dense stiff-polymer brush and its effect on flow. The model is applicable to the brushes where individual grafted polymers or filaments possess a persistence length which is larger or comparable to their total contour length. To validate this model we perform corresponding mesoscopic simulations for a wide range of conditions including polymer elasticity, grafting density, and flow rate. The model allows us to identify the importance of different contributions to brush deformation such as hydrodynamic friction due to flow and steric excluded-volume interactions between polymers. This model can be employed for the quantification of experiments in biological settings and for the development of brush interfaces with specific surface properties. It can be also used to describe the behavior of a stiff-polymer brush in flow, where explicit brush modeling is difficult or unfeasible.
Simulations
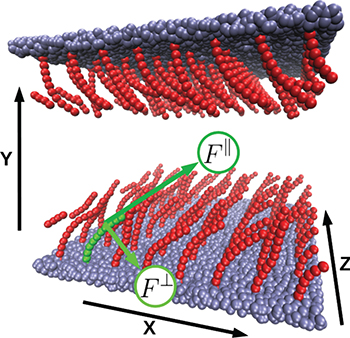
To illustrate the system of interest, fig. 1 presents the simulation setup, where a slit-like geometry with a height D is employed. Both the top and bottom walls are covered by stiff polymers grafted on the square lattice with a constant 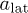 . The polymers are built up from N = 11 bonded beads with a diameter
. The polymers are built up from N = 11 bonded beads with a diameter  and the potential energy given by
and the potential energy given by

where ks is the spring constant,  is the distance between the beads i and i + 1, EI is the bending rigidity,
is the distance between the beads i and i + 1, EI is the bending rigidity, 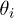 is the angle between two consecutive springs, and
is the angle between two consecutive springs, and  . The polymers are stiffly anchored at the surface by fixing the bead i = 1 at the surface and the bead i = 0 inside the surface. To prevent overlap between beads, the purely repulsive, shifted, and truncated at
. The polymers are stiffly anchored at the surface by fixing the bead i = 1 at the surface and the bead i = 0 inside the surface. To prevent overlap between beads, the purely repulsive, shifted, and truncated at 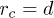 Lennard-Jones (LJ) potential [23] is introduced with the parameters
Lennard-Jones (LJ) potential [23] is introduced with the parameters 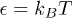 and
and 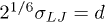 , where kBT is the thermal energy unit.
, where kBT is the thermal energy unit.
Fig. 1: (Colour on-line) Snapshot of a SDPD simulation system with shear flow in the x-direction. Stiff polymers are grafted on both walls. The fluid particles are not shown.
Download figure:
Standard imageTo model the fluid flow, we employ the smoothed dissipative particle dynamics (SDPD) method [24] using a density of 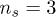 for both fluid and wall particles. Interactions of the fluid particles with the polymer beads are mediated by friction forces. Shear flow is generated by moving one of the walls with a constant velocity. The Poiseuille flow is driven by an external force fq which acts on each fluid particle in the x-direction. This corresponds to a pressure drop
for both fluid and wall particles. Interactions of the fluid particles with the polymer beads are mediated by friction forces. Shear flow is generated by moving one of the walls with a constant velocity. The Poiseuille flow is driven by an external force fq which acts on each fluid particle in the x-direction. This corresponds to a pressure drop 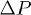 along the slit length lx such that
along the slit length lx such that 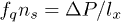 .
.
To characterize the simulated systems we use several dimensionless parameters such as the bending rigidity of the grafted polymers,

grafting density  , and non-dimensional shear rate,
, and non-dimensional shear rate,

Here, 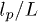 is the ratio of polymer persistence and contour lengths, η is the fluid's viscosity, and
is the ratio of polymer persistence and contour lengths, η is the fluid's viscosity, and  is the shear rate on top of a brush. The effective brush height h is calculated using the first moment of the polymer-bead density profile similar to that in ref. [21],
is the shear rate on top of a brush. The effective brush height h is calculated using the first moment of the polymer-bead density profile similar to that in ref. [21],

To verify our simulation model, we compare in fig. 2 the SDPD results with previous simulations of grafted semiflexible polymers in shear flow using the Brownian-dynamics and lattice-Boltzmann methods [22]. The SDPD results of this work are in excellent agreement with the previous simulations of similar brush systems [22]. In addition, we have also tested whether the type of shear flow (e.g., Couette or Poiseuille) over a brush may have a considerable effect. Figure 2 shows that brush deformation appears to be nearly independent of the flow applied and can be well characterized by 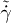 . To span a wide range of conditions, we have simulated systems with grafting densities σ in the range from 0.01 to 1 (which corresponds to SC close packing), polymer elasticities
. To span a wide range of conditions, we have simulated systems with grafting densities σ in the range from 0.01 to 1 (which corresponds to SC close packing), polymer elasticities  between 10 and 100, and shear rates
between 10 and 100, and shear rates  between 101 and 106. Note that the grafted polymers are relatively stiff with
between 101 and 106. Note that the grafted polymers are relatively stiff with 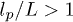 , and, therefore, entropic conformational changes such as polymer coiling can be practically neglected. The corresponding Reynolds numbers
, and, therefore, entropic conformational changes such as polymer coiling can be practically neglected. The corresponding Reynolds numbers  , with v being the velocity at the brush top, have been kept between
, with v being the velocity at the brush top, have been kept between 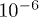 and
and  to ensure no inertial effects. Monitoring of bond lengths has shown that no significant extension
to ensure no inertial effects. Monitoring of bond lengths has shown that no significant extension 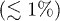 of polymers has been present, and thus, polymer stretching can be neglected.
of polymers has been present, and thus, polymer stretching can be neglected.
Fig. 2: (Colour on-line) Comparison of different simulation methods. Relative polymer brush height  as a function of non-dimensional shear rate
as a function of non-dimensional shear rate 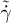 from Brownian-dynamics and lattice-Boltzmann simulations [22] and the SDPD simulations of this work.
from Brownian-dynamics and lattice-Boltzmann simulations [22] and the SDPD simulations of this work.
Download figure:
Standard imageTheory
Our mean-field approach to describe the behavior of stiff polymer brushes in shear flow assumes identical deformation for all polymers. Thus, we consider a single polymer as an elastic cantilever which is subject to a hydrodynamic drag force due to fluid flow and steric interactions due to its neighboring polymers in the lattice. The polymer deformation is described by its internal curve-linear coordinate ![$s \in[0,L]$](https://content.cld.iop.org/journals/0295-5075/109/6/68001/revision1/epl16963ieqn25.gif) and the angle
and the angle 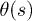 between the y-axis and a local tangent line at s. The correspondence of internal coordinates to the Cartesian coordinates is simply done as
between the y-axis and a local tangent line at s. The correspondence of internal coordinates to the Cartesian coordinates is simply done as 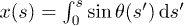 and
and 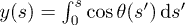 .
.
The torque balance for a circular rod [25], where external forces 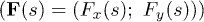 are counteracted by the rods's elastic resistance, leads to
are counteracted by the rods's elastic resistance, leads to

where  is the position on a rod at s such that
is the position on a rod at s such that 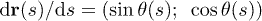 . This equation formulated in terms of the local angle
. This equation formulated in terms of the local angle 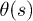 reduces to
reduces to
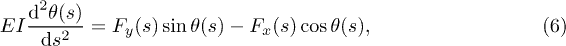
with the boundary conditions of 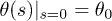 at the grafted surface and
at the grafted surface and 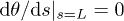 at the free end.
at the free end.  characterizes the grafting angle between the polymer beam and the surface's normal and can generally be a constant or a function of stress applied to the beam. However, in the current study we investigate perpendicular grafting of stiff filaments to a surface with
characterizes the grafting angle between the polymer beam and the surface's normal and can generally be a constant or a function of stress applied to the beam. However, in the current study we investigate perpendicular grafting of stiff filaments to a surface with 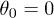 .
.
The force 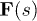 consists of two contributions: i) drag force
consists of two contributions: i) drag force 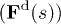 from fluid flow and ii) a force due to excluded-volume interactions
from fluid flow and ii) a force due to excluded-volume interactions 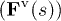 , and thus,
, and thus, 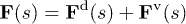 . Note that beam stretching is neglected. The force at a position s can be found as an integral over local force density
. Note that beam stretching is neglected. The force at a position s can be found as an integral over local force density 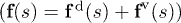 such that
such that

The force density of the drag force exerted on a stiff polymer is given by

where 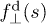 and
and 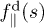 are the corresponding normal and parallel components of the force density with the convention that
are the corresponding normal and parallel components of the force density with the convention that 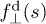 is directed with the x-axis and down to the wall (see fig. 1), while
is directed with the x-axis and down to the wall (see fig. 1), while 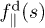 has a tangential direction toward the increase of the s-coordinate.
has a tangential direction toward the increase of the s-coordinate. 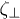 and
and 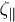 are the normal and tangential components of the friction coefficient per unit length,
are the normal and tangential components of the friction coefficient per unit length, 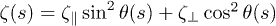 , and
, and 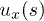 is the local flow velocity and
is the local flow velocity and 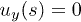 . The friction coefficients are approximated using the slender body theory [26] for a thin cylinder similar to that in ref. [27],
. The friction coefficients are approximated using the slender body theory [26] for a thin cylinder similar to that in ref. [27],
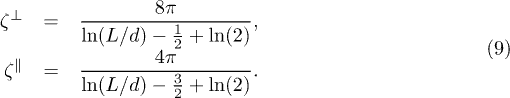
Note that these friction coefficients describe a drag on an isolated rod. If we neglect hydrodynamic interactions, the drag force on a polymer can be described using a single friction coefficient 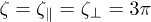 as in ref. [22]. In this case, the force density
as in ref. [22]. In this case, the force density 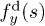 vanishes. The differences in model predictions using these two limiting cases for the friction coefficients will be discussed further in text.
vanishes. The differences in model predictions using these two limiting cases for the friction coefficients will be discussed further in text.
The local velocity 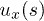 depends on hydrodynamic penetration into the brush [28] and is described by the Brinkman equation [29] for flow in porous media as
depends on hydrodynamic penetration into the brush [28] and is described by the Brinkman equation [29] for flow in porous media as

The same equation has been also used in the theory by Kim et al. [22]. Boundary conditions for eq. (10) are 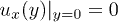 and
and 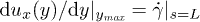 . Equation (10) in internal coordinates becomes
. Equation (10) in internal coordinates becomes

with 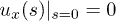 and
and 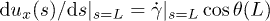 being boundary conditions.
being boundary conditions.
To introduce the steric interactions between the filaments, we discretize the beam into 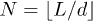 spheres similar to the polymer representation in simulations, where the symbol
spheres similar to the polymer representation in simulations, where the symbol 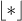 denotes the integer floor function. Since identical deformation of all polymers is assumed, only steric interactions in the plane of beam deformation need to be considered. Therefore, the calculation of volume exclusion interactions includes only the two neighbors surrounding a beam in the flow direction. Finally, the force density
denotes the integer floor function. Since identical deformation of all polymers is assumed, only steric interactions in the plane of beam deformation need to be considered. Therefore, the calculation of volume exclusion interactions includes only the two neighbors surrounding a beam in the flow direction. Finally, the force density 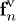 on a sphere
on a sphere ![$n\in [0,\ldots,N-1]$](https://content.cld.iop.org/journals/0295-5075/109/6/68001/revision1/epl16963ieqn61.gif) in a discretized beam due to excluded-volume interactions is computed by a sum over all spheres j of neighboring polymers within the plane of beam deformation as
in a discretized beam due to excluded-volume interactions is computed by a sum over all spheres j of neighboring polymers within the plane of beam deformation as

where 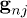 is the force between spheres n and j approximated by a simple repulsive force,
is the force between spheres n and j approximated by a simple repulsive force,

where 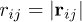 , and
, and  and α are parameters controlling the softness of inter-bead interactions. This force definition appears to be very robust, and the results are hardly affected by
and α are parameters controlling the softness of inter-bead interactions. This force definition appears to be very robust, and the results are hardly affected by 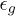 and α, if
and α, if 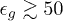 and
and 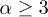 , since the interactions become hard enough. Thus, in order to have a larger time step for a numerical solver, we use
, since the interactions become hard enough. Thus, in order to have a larger time step for a numerical solver, we use 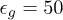 and
and 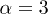 in the theoretical model, while in simulations the employed LJ potential is harder. The volume exclusion force
in the theoretical model, while in simulations the employed LJ potential is harder. The volume exclusion force 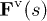 is calculated through the integral in eq. (7), whose discrete representation is given by
is calculated through the integral in eq. (7), whose discrete representation is given by
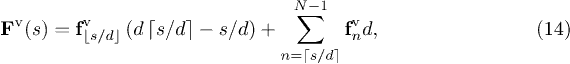
where the symbol 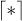 denotes the integer ceiling function.
denotes the integer ceiling function.
Direct numerical solving of eq. (6) appeared to be difficult for high grafting densities and shear rates, i.e. in the regime where excluded-volume interactions dominate. Therefore, we substituted eq. (6) with its time-dependent version given by
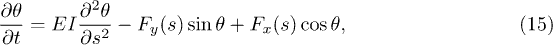
where θ becomes a function of s and time t. Finally, eqs. (15) and (11) are solved numerically for a given set of parameters (elasticity, grafting density, and shear rate on top of a brush) using the following iterative procedure. i) Initially, we guess a beam configuration and the polymer is discretized into 102 elements. Then, eq. (11) is solved using a boundary value problem (BVP) solver for ordinary differential equations [30] in order to obtain the velocity profile. ii) At this step, the calculation of the hydrodynamic drag force 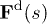 and the volume-exclusion interaction force
and the volume-exclusion interaction force 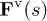 is performed following eqs. (8) and (14), respectively. iii) As a next step, eq. (15) is integrated using the DuFort-Frankel scheme [31], and the resulting configuration is taken as an initial guess for a new cycle. This iteration is repeated until the convergence condition
is performed following eqs. (8) and (14), respectively. iii) As a next step, eq. (15) is integrated using the DuFort-Frankel scheme [31], and the resulting configuration is taken as an initial guess for a new cycle. This iteration is repeated until the convergence condition 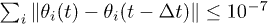 is satisfied, where
is satisfied, where  is the time step.
is the time step.
Results and discussion
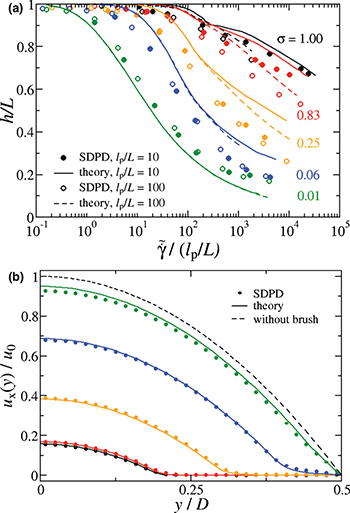
Figure 3(a) presents our main result, the relative brush height as a function of the shear rate on top of the brush normalized by the bending rigidity of the polymers for the case of two friction coefficients from eq. (9). The predictions of our theoretical model are in good quantitative agreement with the corresponding SDPD simulations for two different bending rigidities of 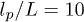 and 100. Brush deformation for different elasticities of the grafted polymers shows a universal behavior with respect to the polymer bending rigidity, if polymers are stiff enough with
and 100. Brush deformation for different elasticities of the grafted polymers shows a universal behavior with respect to the polymer bending rigidity, if polymers are stiff enough with 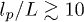 . Clearly, the theory is expected to fail when EI/L becomes smaller or comparable to kBT (or if
. Clearly, the theory is expected to fail when EI/L becomes smaller or comparable to kBT (or if 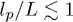 ) or when the grafted polymers can be considered rather flexible. In this case entropic effects have to be necessarily included, which is out of the scope of this work.
) or when the grafted polymers can be considered rather flexible. In this case entropic effects have to be necessarily included, which is out of the scope of this work.
Fig. 3: (Colour on-line) (a) Relative brush height as a function of the shear rate on top of a brush normalized by polymer elasticity from SDPD simulations and the theoretical model for different grafting densities. Two bending rigidities of 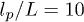 and 100 are considered. (b) Normalized velocity profiles for pressure-driven flow in a micro-channel with walls functionalized with stiff polymers. The dots represent data from simulations and the solid lines refer to the theory for grafting densities (from top to bottom)
and 100 are considered. (b) Normalized velocity profiles for pressure-driven flow in a micro-channel with walls functionalized with stiff polymers. The dots represent data from simulations and the solid lines refer to the theory for grafting densities (from top to bottom) 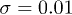 , 0.06, 0.25, 0.83 and 1.0. The dashed line shows the velocity profile for an unperturbed Poiseuille flow and the same pressure gradient.
, 0.06, 0.25, 0.83 and 1.0. The dashed line shows the velocity profile for an unperturbed Poiseuille flow and the same pressure gradient.
Download figure:
Standard imageSome deviations between theoretical predictions and simulations are observed at high grafting densities 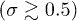 and flow rates due to a better packing of deformed stiff polymers. Remember that the theory assumes identical deformation for all fibers such that possible deformation in the flow vorticity direction (z-axis) is not considered. Thus, the theory overpredicts the effect of excluded-volume interactions, which can be seen in fig. 3(a) for
and flow rates due to a better packing of deformed stiff polymers. Remember that the theory assumes identical deformation for all fibers such that possible deformation in the flow vorticity direction (z-axis) is not considered. Thus, the theory overpredicts the effect of excluded-volume interactions, which can be seen in fig. 3(a) for 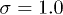 where the theory estimates a larger brush height in comparison to that obtained in simulations. The curve for
where the theory estimates a larger brush height in comparison to that obtained in simulations. The curve for 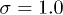 also nicely illustrates the onset of excluded-volume effects with respect to shear rate by a significant change in the slope of brush height occurring at approximately
also nicely illustrates the onset of excluded-volume effects with respect to shear rate by a significant change in the slope of brush height occurring at approximately 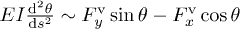 . Thus, at large shear rates the brush height is mainly determined by the excluded-volume interactions.
. Thus, at large shear rates the brush height is mainly determined by the excluded-volume interactions.
To further support the validity of the theoretical model, we present the correspondence of fluid velocities in fig. 3(b). An excellent agreement of theoretical and simulated velocity profiles indicates that the approximation using the Brinkman equation (eq. (11)) properly captures the frictional effect of the brush on fluid flow for a wide range of grafting densities. However, we need to mention that at the lowest grafting density studied  , the Brinkman equation overestimates the influence of the brush on flow. Therefore, in this single case we simply assumed a constant shear rate
, the Brinkman equation overestimates the influence of the brush on flow. Therefore, in this single case we simply assumed a constant shear rate  within the brush, which matches very well the simulated velocity profile, as shown in fig. 3(b).
within the brush, which matches very well the simulated velocity profile, as shown in fig. 3(b).
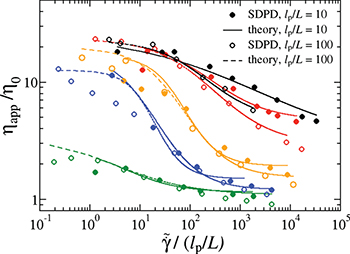
The model predictions in fig. 3 correspond to the case of two friction coefficients from eq. (9), which were derived for a single isolated rod [26]. Thus, they are expected to provide a reasonable approximation for the friction on filaments at low grafting densities. As the grafting density is increased, hydrodynamic interactions are expected to get screened leading to the loss of hydrodynamic correlations between different segments of a polymer. In this case, a single friction coefficient 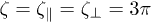 can be assumed. Figure 4 presents the comparison of model predictions using the two different choices of friction coefficients for various grafting densities and
can be assumed. Figure 4 presents the comparison of model predictions using the two different choices of friction coefficients for various grafting densities and 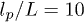 . As expected, the friction coefficient of
. As expected, the friction coefficient of 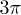 leads to an overestimation of the applied drag for low grafting densities, and the other choice (eq. (9)) appears to be better. At high grafting densities, the difference in model predictions using different friction coefficients nearly vanishes, even though the choice of
leads to an overestimation of the applied drag for low grafting densities, and the other choice (eq. (9)) appears to be better. At high grafting densities, the difference in model predictions using different friction coefficients nearly vanishes, even though the choice of 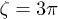 has been expected to be the best. This indicates that at high grafting densities the brush height is mainly determined by the excluded-volume interactions and moderate changes in the applied friction play a secondary role.
has been expected to be the best. This indicates that at high grafting densities the brush height is mainly determined by the excluded-volume interactions and moderate changes in the applied friction play a secondary role.
Fig. 4: (Colour on-line) Comparison of the relative brush height for different choices of the friction coefficients in the theoretical model. Solid lines correspond to the case of two friction coefficients from eq. (9), while the dashed lines represent model predictions for 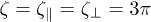 . The data are shown for grafting densities
. The data are shown for grafting densities 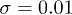 , 0.25, and 0.83 and
, 0.25, and 0.83 and 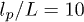 .
.
Download figure:
Standard imageThe effect of stiff-polymer brush on the fluid flow can be characterized by an increase of the flow resistance due to the presence of a brush. Figure 5 shows that the relative apparent viscosity, the ratio of the apparent viscosity (obtained by fitting the Poiseuille law to the resulting flow rate) to the fluid viscosity, might strongly increase if a brush is hardly deformed, and becomes smaller as the brush gets bent by the flow. Qualitatively, this effect can be understood by a change in an effective channel diameter. The flow-induced brush deformation can be used for a flow control in microfluidics and is directly related to an increase in blood flow resistance in small vessels whose surface is covered by glycocalyx having a brush-like structure [5,6]. In vivo experiments on blood flow resistance [32] reveal a much higher resistance in small vessels  in comparison to in vitro experiments in glass tubes [33]. This effect is mainly attributed to the glycocalyx layer at vessel walls [34], and the theoretical model of this work can provide its quantitative description.
in comparison to in vitro experiments in glass tubes [33]. This effect is mainly attributed to the glycocalyx layer at vessel walls [34], and the theoretical model of this work can provide its quantitative description.
Fig. 5: (Colour on-line) Relative apparent viscosity as a function of the shear rate on top of the brush scaled by elasticity. The dots and circles represent data from simulations and the solid and dashed lines refer to the theory for grafting densities (from top to bottom) 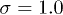 , 0.83, 0.25, 0.06 and 0.01.
, 0.83, 0.25, 0.06 and 0.01.
Download figure:
Standard imageConclusion
In conclusion, the presented theoretical model is able to predict quantitatively the flow-induced deformation of a brush of stiff polymers or filaments and its effect on fluid flow. The model quantifies the relative contributions of fluid friction, polymer bending resistance, and steric excluded-volume interactions between polymers. In comparison to the analytic mean-field approach by Kim et al. [22], the presented theoretical model significantly extends the range of model applicability to high grafting densities of stiff polymers and strong deformations under flow. In particular, the current model explicitly includes the effect of excluded-volume interactions between different polymers. We expect that this model will be used for the quantification of biological and technological experiments with stiff brush-like structures, and can be extended to include direct mechanical deformations due to external forces (e.g., brush-cell interactions).
Acknowledgments
We would like to thank M. Deng and G. E. Karniadakis for useful discussions. We also gratefully acknowledge the computing time granted on the supercomputer JUROPA at Jülich Supercomputing Centre (JSC). DAF acknowledges funding by the Alexander von Humboldt Foundation.