Abstract
We report an observation of the spontaneous liquefaction of glass beads immersed in water and compacted by external isotropic stress. We show that during compression, loose granular samples exhibit a series of sudden rearrangements accompanied by a transient overpressure of interstitial fluid. Ultimately, spontaneous liquefaction with large deformation of the sample is observed. By contrast, denser samples do not show a liquefaction by maintaining its shape integrity. We then discuss the potential mechanisms which could explain this unexpected liquefaction.
Export citation and abstract BibTeX RIS
Introduction
Liquefaction of immersed granular media as observed in geophysical situations is manifested by a loss of shearing resistance that results in catastrophic consequences. The most impressive example is certainly buildings sinking into the soil during an earthquake event. Even liquefaction is sometimes proposed as the triggering mechanism of earthquake [1]. Qualitatively, from the mechanical point of view, liquefaction of a granular packing immersed into water may be explained by a loss of contact of the grains. The grains float and are free to move and the medium behaves like a suspension that cannot support a heavy object. If U denotes the pressure in the interstitial water (pore pressure) and σ the confining pressure of the medium (external total stress), then liquefaction is synonymous to the vanishing of the effective stress 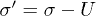 interpreted as the contact stress between grains formulated by Terzaghi [2]. Up to now, liquefaction has been observed in laboratory almost exclusively for totally saturated and loose granular materials (contracting) compressed by external anisotropic stress when the internal fluid is undrained [3]. For a contracting granular soil under undrained condition (null volumetric variation), an increase of external stress in one direction, say
interpreted as the contact stress between grains formulated by Terzaghi [2]. Up to now, liquefaction has been observed in laboratory almost exclusively for totally saturated and loose granular materials (contracting) compressed by external anisotropic stress when the internal fluid is undrained [3]. For a contracting granular soil under undrained condition (null volumetric variation), an increase of external stress in one direction, say  , implies an increase of pore pressure
, implies an increase of pore pressure 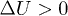 . But in other directions for which the external stress does not vary,
. But in other directions for which the external stress does not vary, 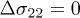 , this variation of internal pore pressure is compensated by a negative variation of effective stress,
, this variation of internal pore pressure is compensated by a negative variation of effective stress, 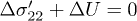 (Terzaghi) which ultimately leads to liquefaction. In nature, the shearing force can be imposed either by monotonic loading (e.g. static overload by man-made construction on soil) or cyclic loading (e.g. dynamic earthquake event) [4]. However, if the pore pressure is maintained constant,
(Terzaghi) which ultimately leads to liquefaction. In nature, the shearing force can be imposed either by monotonic loading (e.g. static overload by man-made construction on soil) or cyclic loading (e.g. dynamic earthquake event) [4]. However, if the pore pressure is maintained constant, 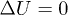 (drained condition), an excess of external stress
(drained condition), an excess of external stress 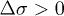 cannot give a reduction of effective stress. This is why liquefaction is a priori not possible when compacting in drained condition. We will show in this letter that this assessment does not always apply.
cannot give a reduction of effective stress. This is why liquefaction is a priori not possible when compacting in drained condition. We will show in this letter that this assessment does not always apply.
In the present work, we report that spontaneous compaction and ultimately liquefaction can be induced by isotropic compression in drained condition, i.e. with no excess pore pressure, on a fully saturated loose model granular assembly. Two basic ingredients are required to perform this simple and conceptually improbable experiment: a loose state of monodispersed model granular material and an initial structural anisotropic state. The isotropic external stress induces an anisotropic deformation of the sample leading to an internal rearrangement of the grain structure. Sometimes, catastrophic events arrive and cause a transient excess pore pressure. Although the internal fluid is nominally maintained at a constant pressure, the short-lived excess pore pressure may reach the effective stress in which case liquefaction is observed.
Experimental setup
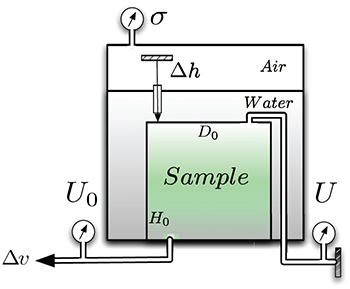
The experiment shown in fig. 1 consists in an isotropic drained compression of a short cylindrical granular sample inside a triaxial cell. The granular sample made of monodisperse and spherical soda lime glass beads (Sil-glass by CVP) of 0.723 mm mean diameter has very loose porosity, is fully saturated and was placed inside a triaxial cell at controlled pressure σ. The sample was enclosed inside a cylindrical and open-ended latex membrane of 0.3 mm thickness.
Fig. 1: (Color online) Sketch of the experimental setup for isotropic compression of a short cylindrical granular sample inside a triaxial cell.
Download figure:
Standard imageDuring compression, the water volume 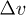 expelled from or moving into the sample was measured (Wykeham Farrance, WF17038) and the global volumetric strain deduced from
expelled from or moving into the sample was measured (Wykeham Farrance, WF17038) and the global volumetric strain deduced from 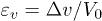 , where V0 is the initial sample volume. The axial displacement
, where V0 is the initial sample volume. The axial displacement 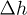 was measured by a linear variable differential transformer sensor (Chauvin Arnoux, L20) mounted directly on the top platen. The global axial strain is estimated from
was measured by a linear variable differential transformer sensor (Chauvin Arnoux, L20) mounted directly on the top platen. The global axial strain is estimated from  with H0 the initial height. The back pressure U0 needed for a full saturation was applied at the bottom of the sample. The pore-water pressure U was recorded by a transducer (Kistler, MD20) outside the triaxial cell using a very thick plastic tube connected to the top cap of the granular sample, at a distance of about 60 cm. In static condition,
with H0 the initial height. The back pressure U0 needed for a full saturation was applied at the bottom of the sample. The pore-water pressure U was recorded by a transducer (Kistler, MD20) outside the triaxial cell using a very thick plastic tube connected to the top cap of the granular sample, at a distance of about 60 cm. In static condition, 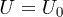 is the homogeneous pore pressure. A synchronized acquisition system (HP3566A) was used to collect the data from different sensors.
is the homogeneous pore pressure. A synchronized acquisition system (HP3566A) was used to collect the data from different sensors.
The sample, 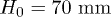 in height and
in height and  in diameter, was prepared using a modified moist tamping and under compaction method [5,6]. Predetermined quantities of moist glass beads, mixed with 2% of distilled water in weight, were placed and gently compacted in five layers of prescribed thickness using a flat-bottom circular stainless-steel tamper 20 mm in diameter. To obtain a fully saturated state, we used the CO2 method [7] with de-aired distilled water, and a constant back pressure U0 of up to 200 kPa was applied. Prior to each experiment, we increased the net total stress
in diameter, was prepared using a modified moist tamping and under compaction method [5,6]. Predetermined quantities of moist glass beads, mixed with 2% of distilled water in weight, were placed and gently compacted in five layers of prescribed thickness using a flat-bottom circular stainless-steel tamper 20 mm in diameter. To obtain a fully saturated state, we used the CO2 method [7] with de-aired distilled water, and a constant back pressure U0 of up to 200 kPa was applied. Prior to each experiment, we increased the net total stress  and measured the excess pore pressure
and measured the excess pore pressure  in undrained condition. The resulting Skempton's coefficient
in undrained condition. The resulting Skempton's coefficient 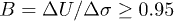 indicates a fully saturated sample [8]. The solid fraction
indicates a fully saturated sample [8]. The solid fraction  defined as the volume of solids of the granular sample to the total volume at confining pressure of 30 kPa was carefully evaluated from the water content obtained at the end of the isotropic compression [9], and also from the usual procedure of measuring the sample dimensions during different fabrication stages. To avoid possible wearing effects, only virgin glass beads were used.
defined as the volume of solids of the granular sample to the total volume at confining pressure of 30 kPa was carefully evaluated from the water content obtained at the end of the isotropic compression [9], and also from the usual procedure of measuring the sample dimensions during different fabrication stages. To avoid possible wearing effects, only virgin glass beads were used.
During the isotropic drained compression test, σ was manually imposed using compressed air and slowly increased while keeping 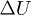 below 4–5 kPa to respect the requirement of full drainage.
below 4–5 kPa to respect the requirement of full drainage.
Results
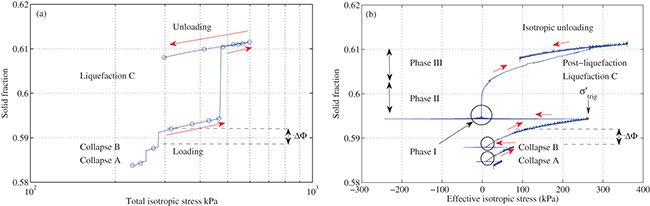
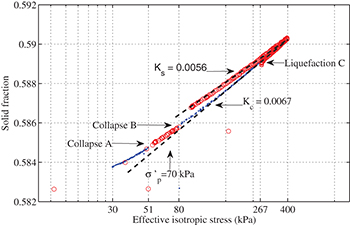
A typical compressibility of very loose model granular materials is shown in fig. 2(a) which represents the evolution of solid fraction 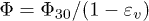 vs. total stress σ. Under imposed external stress, granular media such as sand, exhibit a continuous increase of density [3]. But in our experiments, instead of the expected smooth and continuous compaction, large unexpected drops in Φ can be seen. Between two events, the normal continuous increase of solid fraction is observed during the loading phase. No drop in Φ has been noticed in unloading.
vs. total stress σ. Under imposed external stress, granular media such as sand, exhibit a continuous increase of density [3]. But in our experiments, instead of the expected smooth and continuous compaction, large unexpected drops in Φ can be seen. Between two events, the normal continuous increase of solid fraction is observed during the loading phase. No drop in Φ has been noticed in unloading.
Fig. 2: (Color online) (a) Solid fraction vs. total isotropic stress. (b) Solid fraction vs. effective isotropic stress. Spontaneous collapses and liquefaction under isotropic compression from 30 to 400 kPa with 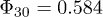 .
.
Download figure:
Standard imageHowever, the compressibility of the granular skeleton is revealed by introducing the effective stress 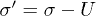 in fig. 2(b), with U the actual measured pore pressure. The drops A, B, C occur successively at effective stress
in fig. 2(b), with U the actual measured pore pressure. The drops A, B, C occur successively at effective stress 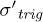 of 51, 80 and 267 kPa, respectively. Each event consists in a sudden and simultaneous compressive volumetric strain (compaction), together with a reduction of
of 51, 80 and 267 kPa, respectively. Each event consists in a sudden and simultaneous compressive volumetric strain (compaction), together with a reduction of 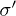 due to a sudden surge of
due to a sudden surge of 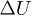 , followed by a gradual recover of
, followed by a gradual recover of 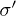 .
.
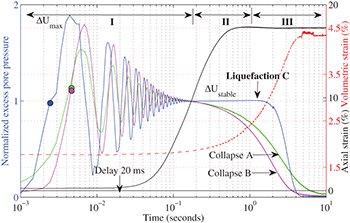
The complete individual time evolution of 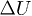 for the three events,
for the three events, 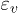 and
and 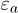 only for event C is plotted in fig. 3. The excess pore pressure
only for event C is plotted in fig. 3. The excess pore pressure 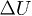 was normalized by the brief stable value
was normalized by the brief stable value 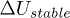 between the oscillations and the return to equilibrium
between the oscillations and the return to equilibrium 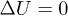 . The time origin is shifted to the beginning of the transient phase
. The time origin is shifted to the beginning of the transient phase 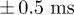 , which is the current time resolution.
, which is the current time resolution.
Fig. 3: (Color online) Three phases of pore water pressure development. I: fast and transient development, II: constant stable (liquefaction) value and III: dissipation (post-liquefaction). The axial strain (black) and volumetric strain (red) refer to the liquefaction event. Referred liquefaction levels (solid circles) are indicated.
Download figure:
Standard imageThe evolution of 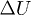 can be decomposed in three phases. First a fast transient phase I (hollow circle in fig. 2(b)) occurred within 200 ms at constant volume and constant axial strain.
can be decomposed in three phases. First a fast transient phase I (hollow circle in fig. 2(b)) occurred within 200 ms at constant volume and constant axial strain. 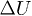 vibrates like an oscillating underdamped system with a dominant frequency of 110 Hz (fig. 3). The rising time to the first peak
vibrates like an oscillating underdamped system with a dominant frequency of 110 Hz (fig. 3). The rising time to the first peak 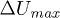 is within 5 ms, followed by relatively fast decay to stabilizing
is within 5 ms, followed by relatively fast decay to stabilizing 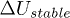 . Then an intermediate second phase II happened only for event C. It is chacracterized by a large increase of volumetric compaction (fig. 2(b)) and axial contraction (fig. 3) at constant
. Then an intermediate second phase II happened only for event C. It is chacracterized by a large increase of volumetric compaction (fig. 2(b)) and axial contraction (fig. 3) at constant 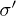 and at stabilizing value of
and at stabilizing value of 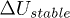 of the excess pore pressure. Finally a third and longest phase III in which
of the excess pore pressure. Finally a third and longest phase III in which 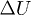 returns to the initial equilibrium
returns to the initial equilibrium 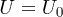 at nearly constant axial strain. During the transient phase I of all collapses, the sample briefly experiences negative values of
at nearly constant axial strain. During the transient phase I of all collapses, the sample briefly experiences negative values of 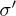 . The solid circles indicate the null effective stress levels. Nevertheless, the duration of this phase was not long enough to sustain a liquefaction state except for event C.
. The solid circles indicate the null effective stress levels. Nevertheless, the duration of this phase was not long enough to sustain a liquefaction state except for event C.
The small increase of Φ for the first two events A and B did not compromise the cylindrical form of the specimen and permits the continuation of isotropic compression; hence, these events are terms as local collapses. In contrast, the last event C destroyed it with a much larger volumetric compaction, and the granular sample collapsed instantaneously onto the pedestal base of the triaxial cell in a spontaneous liquefaction or global collapse with a very large axial strain. For completeness, the isotropic compression was continued until 400 kPa for the post-liquefaction stage and the isotropic unloading afterwards to 100 kPa.
To check that the transient vibration is not an artifact of the measurement system, a dynamic pore pressure sensor (PCB S112A21) having high resonant frequency (250 kHz) was used together with the static one. No difference was detected. Since the pore pressure transducer is on the other side of the porous bronze disk of the top cap and far from the possibly triggering source inside the sample, the actual value of these sharp peaks is likely a minimum estimate.
The time evolution of 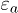 for the catastrophic event C in fig. 3 reveals a fast axial contraction, after a small delay of about 20 ms with respect to
for the catastrophic event C in fig. 3 reveals a fast axial contraction, after a small delay of about 20 ms with respect to  , up to 17.60% from 0.27% within only 0.5 second. This vertical compression indicates an axial strain rate
, up to 17.60% from 0.27% within only 0.5 second. This vertical compression indicates an axial strain rate 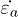 of about 35%/s, much faster than the usual constant
of about 35%/s, much faster than the usual constant 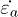 of 0.0048%/s in triaxial drained compression experiment on sand. It clearly indicates a dynamic regime of the liquefaction phenomenon happening within less than one second. Note that half of the axial contraction already happens during the transient phase I of 200 ms, essentially under undrained conditions of
of 0.0048%/s in triaxial drained compression experiment on sand. It clearly indicates a dynamic regime of the liquefaction phenomenon happening within less than one second. Note that half of the axial contraction already happens during the transient phase I of 200 ms, essentially under undrained conditions of 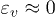 .
.
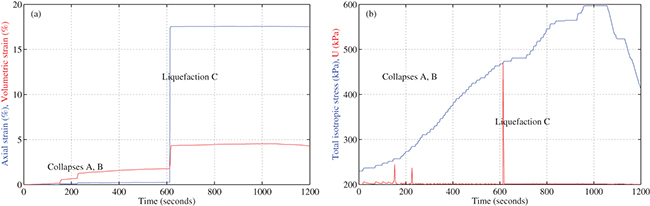
The volumetric strain indicates an overall compaction of only 2.56% during liquefaction, with a larger initial time delay and its development is far behind that of axial strain, both in terms of time evolution and magnitude. Figure 4 shows the complete evolution of U, σ, 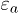 and
and  for the total test duration. Manual control of total stress results in stepwise linear loading and unloading. The three events are shown here with a sudden and simultaneous drop of
for the total test duration. Manual control of total stress results in stepwise linear loading and unloading. The three events are shown here with a sudden and simultaneous drop of 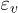 and
and 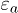 at the beginning of each event. The three narrow and surprisingly very sharp peaks of U are clearly related to these events, despite the drainage system with porous bronze disk embedded in the end plates, and indicate a quite fast dissipation. The last peak, well above 400 kPa, was much larger than the two previous ones of about only 250 kPa and presumably responsible for the observed catastrophic liquefaction with a very large run-away
at the beginning of each event. The three narrow and surprisingly very sharp peaks of U are clearly related to these events, despite the drainage system with porous bronze disk embedded in the end plates, and indicate a quite fast dissipation. The last peak, well above 400 kPa, was much larger than the two previous ones of about only 250 kPa and presumably responsible for the observed catastrophic liquefaction with a very large run-away 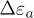 of more than 17% and a sudden volumetric compaction of 2.5% in less than one second.
of more than 17% and a sudden volumetric compaction of 2.5% in less than one second.
Fig. 4: (Color online) Time evolution of (a) axial strain  and volumetric strain
and volumetric strain  , (b) total isotropic stress σ and pore pressure U under isotropic compression from 230 to 600 kPa of total stress.
, (b) total isotropic stress σ and pore pressure U under isotropic compression from 230 to 600 kPa of total stress.
Download figure:
Standard imageCompressibility and anisotropy
In fig. 5, the three loading phases preceding the collapse event (30–51 kPa before event A, 51–80 kPa before B and 80–267 kPa before C) are retrieved and artificially shifting downwards at  by
by 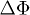 from fig. 2 to form a continuous curve. For clarity, phases I and II are removed. The post-liquefaction and the isotropic unloading phases also appear. This construction reveals a hypothetical mechanical behaviour conforming to the usual isotropic compressibility of loose sand materials without unloading under fully drained conditions [10], or powders in uniaxial compression [11]. The compressibility behaviour can be approximated by two superimposed straight dashed lines in fig. 5 representing the normal compression line and the unloading-reloading line. The initial slope of the curve is usually lower but has the same value as the unloading line. The intersection point of these two lines defines the precompression stress
from fig. 2 to form a continuous curve. For clarity, phases I and II are removed. The post-liquefaction and the isotropic unloading phases also appear. This construction reveals a hypothetical mechanical behaviour conforming to the usual isotropic compressibility of loose sand materials without unloading under fully drained conditions [10], or powders in uniaxial compression [11]. The compressibility behaviour can be approximated by two superimposed straight dashed lines in fig. 5 representing the normal compression line and the unloading-reloading line. The initial slope of the curve is usually lower but has the same value as the unloading line. The intersection point of these two lines defines the precompression stress 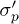 as a reminder of the past maximum effective stress.
as a reminder of the past maximum effective stress.
Fig. 5: (Color online) Compressibility parameters under isotropic compression, upon ignoring the void ratio reduction due to collapses and liquefaction. Alternate colors indicate successive sections of isotropic loading and unloading.
Download figure:
Standard imageSome macroscopic compressibility parameters can be identified: a compression index 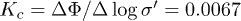 of the loading line, a swelling index
of the loading line, a swelling index 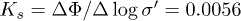 of the unloading line, and a precompression stress
of the unloading line, and a precompression stress 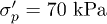 which results from the under-compaction method. Loosely bound glass beads have a particular nearly elastic behaviour with
which results from the under-compaction method. Loosely bound glass beads have a particular nearly elastic behaviour with 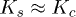 , in contrast with real granular materials [10] where
, in contrast with real granular materials [10] where 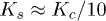 . This observation confirms the quasi-reversibility behaviour for model granular materials numerically obtained in [12], however, without the unexpected collapses and liquefaction.
. This observation confirms the quasi-reversibility behaviour for model granular materials numerically obtained in [12], however, without the unexpected collapses and liquefaction.
Furthermore, the measurements of 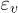 and
and 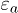 during each segment preceding a local collapse have been systematically exploited to estimate the incremental anisotropy coefficient
during each segment preceding a local collapse have been systematically exploited to estimate the incremental anisotropy coefficient 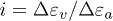 . The typical value obtained before the last collapse is of about 16, indicating a highly anisotropic structure, contrasting sharply the isotropic structure
. The typical value obtained before the last collapse is of about 16, indicating a highly anisotropic structure, contrasting sharply the isotropic structure 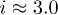 for loose laboratory sands (i.e. Hostun or Toyoura) created by the same moist-tamping procedure [13]. We deduce that this structural anisotropy can be a primary key element in fostering the observed liquefaction.
for loose laboratory sands (i.e. Hostun or Toyoura) created by the same moist-tamping procedure [13]. We deduce that this structural anisotropy can be a primary key element in fostering the observed liquefaction.
Random liquefaction and instabilities
The occurrence of triggering stress 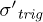 is randomly distributed over a wide range. In the studied range from 30 to 500 kPa, it can be as small as 33 kPa without any preceding local collapses, or as large as 497 kPa with numerous preceding local collapses or precursors. In all tested samples, no more than 4 local collapses were observed before the final liquefaction.
is randomly distributed over a wide range. In the studied range from 30 to 500 kPa, it can be as small as 33 kPa without any preceding local collapses, or as large as 497 kPa with numerous preceding local collapses or precursors. In all tested samples, no more than 4 local collapses were observed before the final liquefaction.
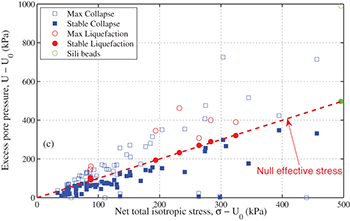
Figure 6 shows the measured transient 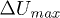 and
and 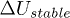 vs.
vs. 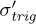 for all events.
for all events. 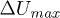 (hollow symbols) is largely and briefly located above the diagonal red line representing the state of null effective stress where the excess pore pressure
(hollow symbols) is largely and briefly located above the diagonal red line representing the state of null effective stress where the excess pore pressure 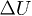 equals the net total stress
equals the net total stress 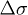 . It can be speculated that most often the brief duration of
. It can be speculated that most often the brief duration of 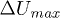 in the range of 200 ms is enough to initiate local liquefaction but not enough to maintain its development and to propagate onto the whole sample. The stabilized values
in the range of 200 ms is enough to initiate local liquefaction but not enough to maintain its development and to propagate onto the whole sample. The stabilized values 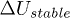 (solid symbols) for all local collapses (square) are below or near this line; but those of the largest events (circle) are precisely on this line for a more lengthy time of at least one second. During this long time (phase II), the effective stress is null which is enough to develop and sustain liquefaction to the overall sample.
(solid symbols) for all local collapses (square) are below or near this line; but those of the largest events (circle) are precisely on this line for a more lengthy time of at least one second. During this long time (phase II), the effective stress is null which is enough to develop and sustain liquefaction to the overall sample.
Fig. 6: (Color online) Effects of 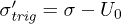 on the excess pore pressure in isotropic collapses and liquefaction. Hollow symbols indicate the maximum value
on the excess pore pressure in isotropic collapses and liquefaction. Hollow symbols indicate the maximum value 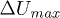 (phase I) and solid symbols the stabilized value
(phase I) and solid symbols the stabilized value  (phase II).
(phase II).
Download figure:
Standard imageA practical consequence is the impossibility to control the solid fraction increase under isotropic compression of very loose and moist-tamped model granular materials, due to the random occurrence of the dynamic instabilities, unless mastering the triggering mechanisms.
Threshold fabric solid fraction
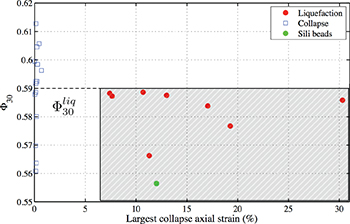
By repeating the experiments with samples of various solid fractions at the fabrication state, hence indirectly 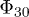 , fig. 7 shows the total disappearance of full liquefaction, characterized by a sudden large axial contraction
, fig. 7 shows the total disappearance of full liquefaction, characterized by a sudden large axial contraction 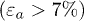 , of denser samples above a threshold solid fraction which can be narrowed down to
, of denser samples above a threshold solid fraction which can be narrowed down to 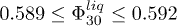 . This threshold solid fraction
. This threshold solid fraction  represents the transitional behaviour from full liquefaction (global collase) in isotropic compression to non-liquefaction with the presence of local collapses. It can be related to another known threshold solid fraction
represents the transitional behaviour from full liquefaction (global collase) in isotropic compression to non-liquefaction with the presence of local collapses. It can be related to another known threshold solid fraction 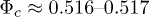 , guaranteeing a liquefaction-free behaviour during subsequent undrained shearing for very loose Toyoura sand [9,14].
, guaranteeing a liquefaction-free behaviour during subsequent undrained shearing for very loose Toyoura sand [9,14]. 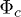 represents the transition from liquefaction behaviour in undrained shearing to non-liquefaction behaviour characterized by the steady state of deformation [15]. However, local collapses can still be observed in isotropic loading.
represents the transition from liquefaction behaviour in undrained shearing to non-liquefaction behaviour characterized by the steady state of deformation [15]. However, local collapses can still be observed in isotropic loading.
Fig. 7: (Color online) Identification of the threshold solid fraction 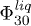 indicating a total disappearance of liquefaction on denser samples.
indicating a total disappearance of liquefaction on denser samples.
Download figure:
Standard imageRepeatability and other materials
Despite a large number of tests on soda lime glass beads, only 8 samples have liquefied out of more than 80 experiments. However, all tests presented instabilities. Although being rare, isotropic liquefaction has been repeatedly and consistently observed in two years of work experience.
Liquefaction has also been observed with other glass beads of different chemical composition and different industrial fabrication processes (Sili beads by Sigmund-Lindner). These beads have a more symmetrical distribution in size than CVP and centered on smaller mean diameter of 0.675 mm. They are also less rounded. The results are shown in green symbols in figs. 6 and 7.
Macropore hypothesis
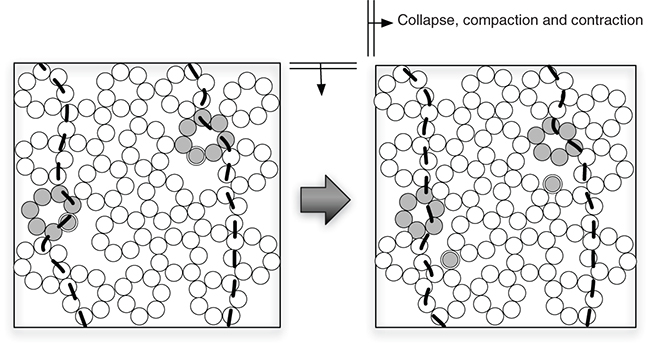
Very loose glass bead samples created by moist tamping technique tend to have more irregular microstructures with the presence of macropores (cell of approximately fixed size constituted by aggregated grains surrounding a large pore), based on direct microscopic observations [16] on Hostun sand using the same fabrication technique. It is well known that the applied external forces were transmitted through the interparticle contact force network within granular media [17]. We speculate that under external isotropic pressure, the induced strain can be strongly anisotropic due to the initial structural anisotropy of the sample 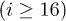 despite the observed quasi-elastic behaviour. The force chains (thick dashed lines in fig. 8 (left)) are therefore deformed and such fragile and anisotropic structures can be broken. The resulting ejection of one or more grains of the metastable honeycombed structures in fig. 8 (right) might be the mechanism responsible for the collapse phase. The incompressibility of the pore water and the spherical grain shape probably facilitate the failures of already fragile contact chain forces and this ejection. The remaining grains still form a new metastable structure and the ejected grains in the fully saturated media transmit the ejecting force into the pore fluid, hence briefly raise the pore pressure to
despite the observed quasi-elastic behaviour. The force chains (thick dashed lines in fig. 8 (left)) are therefore deformed and such fragile and anisotropic structures can be broken. The resulting ejection of one or more grains of the metastable honeycombed structures in fig. 8 (right) might be the mechanism responsible for the collapse phase. The incompressibility of the pore water and the spherical grain shape probably facilitate the failures of already fragile contact chain forces and this ejection. The remaining grains still form a new metastable structure and the ejected grains in the fully saturated media transmit the ejecting force into the pore fluid, hence briefly raise the pore pressure to 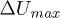 and reduced later to
and reduced later to 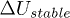 . Consequently, this very fast and strong build-up of
. Consequently, this very fast and strong build-up of 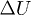 reduces the effective stress and favors the instability, without triggering it. The rapid structural rearrangement can lead to a fast and irreversible volumetric compaction and axial contraction [18]. The local or global failure of the anisotropic contact network would explain the larger magnitudes of the collapse during the slip phase of the stick-slip phenomenon in saturated samples [19], compared to dry ones [20,21] in triaxial experiments; and the spontaneity of slip events in the experimental [22–24], or theoretical perspective [25].
reduces the effective stress and favors the instability, without triggering it. The rapid structural rearrangement can lead to a fast and irreversible volumetric compaction and axial contraction [18]. The local or global failure of the anisotropic contact network would explain the larger magnitudes of the collapse during the slip phase of the stick-slip phenomenon in saturated samples [19], compared to dry ones [20,21] in triaxial experiments; and the spontaneity of slip events in the experimental [22–24], or theoretical perspective [25].
Fig. 8: Macropore hypothesis for loose model granular assembly.
Download figure:
Standard imageIt is worth noting that in all these experiments, no doublet of welded grains was found in binocular microscopy after testing.
Conclusions
We reported the spontaneous liquefaction under isotropic drained compression of model granular materials and reveal some mechanisms underlying the diffuse instability phenomenon, usually hidden or partially developed in sands. The unexpected behaviour can offer some new insights into the complexity of granular matter; however to fully characterize the material response, one needs to understand how the excess pore pressure is initiated, propagated, maintained and ultimately causes liquefaction. The observed collapsible behaviour is currently difficult to predict within the framework of classical soil mechanics. It also represents a challenge for discrete element modelling where the solid-fluid interaction, the dynamic character of liquefaction as well as the creation of very loose granular assembly are still not fully implemented.
Acknowledgments
We wish to thank Julien Scheibert for fruitful discussions.