Abstract
We study a generic two-state model for an assembly of molecular motors which is described by means of a pair of integro-partial differential equations and leads to oscillatory motion in the presence of an elastic coupling to its environment. We discuss a reduction of the system to a minimal set of three ordinary differential equations that successfully capture the complex nonlinear dynamics of the full system. In the limit of high mobility and large elastic modulus, we report on the emergence of subharmonics in the power spectrum of the oscillations. This provides a rationale for the unexplained observation of secondary peaks in a minimal actomyosin system in vitro (Plaçais P.-Y. et al., Phys. Rev. Lett. 103, (2009) 158102), showing that the phenomenon is robust and genuine.
Export citation and abstract BibTeX RIS
Molecular motors are force generators which can produce mechanical oscillations at the cellular scale and play a central role in muscle contraction and cell motility [1,2]. Insect fibrilar muscles of wasps and bees are known to exhibit a wing thrust which is asynchronous to the activating nervous impulses [3,4]. Skinned skeletal and cardiac muscle fibers have also been shown to exhibit spontaneous oscillations in vitro under various conditions [5,6]. Other nonmuscular examples are the periodic motion of cilia and flagella used for cell motility [7,8] and the amplification of weak stimuli via oscillatory instabilities of mechanosensory hair bundles [9,10]. Early models proposed to understand such systems were grounded on experimental evidences of muscle contraction [11–13] and were subsequently generalized to the study of eukaryotic flagella [14,15]. Two main approaches have been used to study instabilities in motor assemblies: two-state "crossbridge" and "stiff motor" models, which can be considered as two different limits of a more general description that considers the motor-filament interaction and the stiffness of the motors [16,17]. In both cases, oscillations are obtained for nonmonotonic velocity-force relationships in the presence of an elastic element. In this work, we study a generic model for the collective dynamics of molecular motors which generates spontaneous oscillations via a Hopf bifurcation [18,19], and successfully explained many experimental results on biological oscillating systems driven by molecular motors [10,20–22]. We show that the pair of integro-partial differential equations studied in ref. [18] can be reduced to a set of three ordinary differential equations which capture the main dynamics of the system and exhibit rich nonlinear behaviour. The robustness of this reduced description is validated through direct comparison with the full system of integro-partial differential equations. Finally, we compare our results with experimental oscillations of a minimal actomyosin system in vitro [22] and show that the unexplained secondary peaks observed in the power spectrum can be understood in the limit of high mobility and large elastic modulus as subharmonics resulting from nonlinearities in the system.
We consider a collection of N molecular motors which are rigidly attached to a common backbone filament as sketched in fig. 1. Motor heads can be found in two possible conformational states  subject to a l-periodic potential
subject to a l-periodic potential 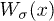 . Depending on whether they are bound to or unbound from the filament, motors feel the potentials W1,W2, respectively. The backbone is coupled to a spring of elastic modulus KN, where K is the elastic modulus per motor. Motors can detach or attach with l-periodic rates
. Depending on whether they are bound to or unbound from the filament, motors feel the potentials W1,W2, respectively. The backbone is coupled to a spring of elastic modulus KN, where K is the elastic modulus per motor. Motors can detach or attach with l-periodic rates  ,
, 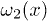 , respectively. In order to obtain spontaneous oscillations, detailed balance must be broken through the addition of localized "active sites" in the minima of the potential W1. We can account for this effect by introducing an l-periodic function
, respectively. In order to obtain spontaneous oscillations, detailed balance must be broken through the addition of localized "active sites" in the minima of the potential W1. We can account for this effect by introducing an l-periodic function 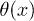 which is proportional to the adenosine triphosphate (ATP) hydrolysis rate:
which is proportional to the adenosine triphosphate (ATP) hydrolysis rate:

where  . The first term on the right side of eq. (1) accounts for thermally driven excitations while the second term describes ATP-hydrolysis–driven excitations. Motors are spaced uniformly with distance q incommensurate to l. We define the probability density of finding a motor in state σ as
. The first term on the right side of eq. (1) accounts for thermally driven excitations while the second term describes ATP-hydrolysis–driven excitations. Motors are spaced uniformly with distance q incommensurate to l. We define the probability density of finding a motor in state σ as  and the backbone position as X(t). For simplicity, we will work in the limit of a large number of motors, where we can assume the total motor density distribution to be uniform and therefore
and the backbone position as X(t). For simplicity, we will work in the limit of a large number of motors, where we can assume the total motor density distribution to be uniform and therefore 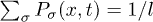 . Switching to the cyclic coordinate
. Switching to the cyclic coordinate 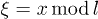 , the dynamics of the system reads [18]
, the dynamics of the system reads [18]
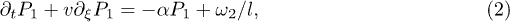

where 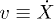 is the backbone velocity, λ is the friction coefficient of the medium,
is the backbone velocity, λ is the friction coefficient of the medium, 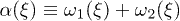 and
and  is the active force generated per motor. Since P1 and P2 are constrained, we focus on the dynamics of one probability distribution (e.g. P1). Equation (2) describes the dynamics of the probability density P1 while eq. (3) accounts for force balance in the system. Following the work in ref. [23], we decompose
is the active force generated per motor. Since P1 and P2 are constrained, we focus on the dynamics of one probability distribution (e.g. P1). Equation (2) describes the dynamics of the probability density P1 while eq. (3) accounts for force balance in the system. Following the work in ref. [23], we decompose 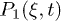 as an infinite sum of modes
as an infinite sum of modes  and
and  :
:
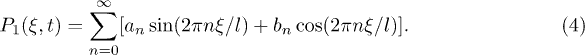
Since the functions  are periodic, they can be generally described in terms of Fourier series. We will consider the simplest approximation by keeping only the first Fourier mode and defining
are periodic, they can be generally described in terms of Fourier series. We will consider the simplest approximation by keeping only the first Fourier mode and defining  . We choose a symmetric sinusoidal potential
. We choose a symmetric sinusoidal potential 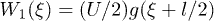 , where U is the amplitude of the potential. We also take α to be constant, such that the sum of the transition rates is independent of the spatial coordinate ξ. This approximation is convenient when the transition rates are almost uniform. The transition rates are given by
, where U is the amplitude of the potential. We also take α to be constant, such that the sum of the transition rates is independent of the spatial coordinate ξ. This approximation is convenient when the transition rates are almost uniform. The transition rates are given by

where 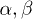 are unknown rates. Without loss of generality, we assume W2 to be constant in the detached state. Since biological motors work far from equilibrium,
are unknown rates. Without loss of generality, we assume W2 to be constant in the detached state. Since biological motors work far from equilibrium, 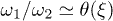 , and thus
, and thus

where  is a dimensionless ATP hydrolysis amplitude and
is a dimensionless ATP hydrolysis amplitude and 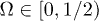 . Using the orthogonality of the Fourier modes, the active force per motor is simply given by
. Using the orthogonality of the Fourier modes, the active force per motor is simply given by 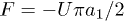 . Hence, we obtain an infinite set of ordinary differential equations for the modes
. Hence, we obtain an infinite set of ordinary differential equations for the modes 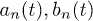 ,
,  and X(t). Remarkably, for constant α, the modes
and X(t). Remarkably, for constant α, the modes  and X(t) are formally decoupled, that is, they evolve independently from the rest (b0 and an, bn for n > 1). The last choice of
and X(t) are formally decoupled, that is, they evolve independently from the rest (b0 and an, bn for n > 1). The last choice of 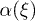 is known as the constant rate approximation [23]. The evolution of b0 is also decoupled from the rest and relaxes exponentially to its steady-state value. Nondimensionalizing with respect to the length scale l, time scale
is known as the constant rate approximation [23]. The evolution of b0 is also decoupled from the rest and relaxes exponentially to its steady-state value. Nondimensionalizing with respect to the length scale l, time scale  and force density
and force density  , the dimensionless governing equations read
, the dimensionless governing equations read

and for n > 1

where Ω plays the role of the control parameter, 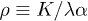 sets the damping rate of oscillations and
sets the damping rate of oscillations and  is an effective mobility. It is interesting to remark that a similar decoupling occurs for the Markus-Lorenz waterwheel equations [24,25] which share some similarities with eqs. (2) and (3). It is noteworthy that all nonlinear terms depend inversely on the friction λ, which plays a major role on the nonlinear nature of the system. Defining the dimensionless active force per motor as
is an effective mobility. It is interesting to remark that a similar decoupling occurs for the Markus-Lorenz waterwheel equations [24,25] which share some similarities with eqs. (2) and (3). It is noteworthy that all nonlinear terms depend inversely on the friction λ, which plays a major role on the nonlinear nature of the system. Defining the dimensionless active force per motor as 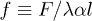 we notice that f is proportional to the first asymmetric mode through
we notice that f is proportional to the first asymmetric mode through 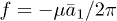 . The system has the symmetry
. The system has the symmetry  , given that
, given that  is symmetric. Furthermore, the backbone position
is symmetric. Furthermore, the backbone position 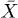 far from the initial value is uniquely given by the evolution of f, from (7):
far from the initial value is uniquely given by the evolution of f, from (7):

where  is the time-lag. Hence,
is the time-lag. Hence, 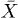 represents the memory of f, i.e. its exponentially weighted past evolution. Through a suitable linear change of variables
represents the memory of f, i.e. its exponentially weighted past evolution. Through a suitable linear change of variables  the set of equations (7) can be rewritten as
the set of equations (7) can be rewritten as

where x describes the position of an overdamped particle in an effective system under a forcing term  . Now the previous symmetry condition is manifested as
. Now the previous symmetry condition is manifested as 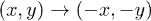 . The dynamics of y and z is the same as in the Lorenz model (for the particular choice of
. The dynamics of y and z is the same as in the Lorenz model (for the particular choice of 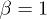 in ref. [26]); however the first equation in (10) is different. The system has a single fixed point at the origin. A linear stability analysis around this point gives one negative eigenvalue −1 and two complex conjugated eigenvalues
in ref. [26]); however the first equation in (10) is different. The system has a single fixed point at the origin. A linear stability analysis around this point gives one negative eigenvalue −1 and two complex conjugated eigenvalues  , where
, where  ,
,  .
. 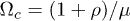 is defined as the critical value of Ω where a Hopf bifurcation takes place, i.e. when
is defined as the critical value of Ω where a Hopf bifurcation takes place, i.e. when  . In view of the similarities between (10) and the Lorenz equations, we investigated the possibility of chaos in the system. We considered the attractor shown in fig. 2, where nearby trajectories tend to locally diverge when found in the two spirals and to locally converge when switching between spirals. The computation of the Lyapunov characteristic exponents for the attractor in fig. 2 was studied numerically by using a Mathematica package [27] based on the algorithms presented in refs. [28,29]. The maximum Lyapunov exponent
. In view of the similarities between (10) and the Lorenz equations, we investigated the possibility of chaos in the system. We considered the attractor shown in fig. 2, where nearby trajectories tend to locally diverge when found in the two spirals and to locally converge when switching between spirals. The computation of the Lyapunov characteristic exponents for the attractor in fig. 2 was studied numerically by using a Mathematica package [27] based on the algorithms presented in refs. [28,29]. The maximum Lyapunov exponent  was found to be nearly zero and the remainder exponents were
was found to be nearly zero and the remainder exponents were  , indicating that the limit set is a periodic orbit and consistently with the system being dissipative. In conclusion, no clear signs of chaotic behaviour were found in the system. Despite the similarities between (10) and the Lorenz equations, the different terms in the first equation of (10) crucially affect the dynamics of the system. Interestingly, as we will discuss next, the system can generally exhibit subharmonic oscillations. Hereinafter, we will focus on the dynamics of
, indicating that the limit set is a periodic orbit and consistently with the system being dissipative. In conclusion, no clear signs of chaotic behaviour were found in the system. Despite the similarities between (10) and the Lorenz equations, the different terms in the first equation of (10) crucially affect the dynamics of the system. Interestingly, as we will discuss next, the system can generally exhibit subharmonic oscillations. Hereinafter, we will focus on the dynamics of  rather than x to allow a physical interpretation compatible with empirical observations.
rather than x to allow a physical interpretation compatible with empirical observations.
Fig. 1: (Color online) Schematic description of the two-state ratchet model of molecular motors coupled to an elastic element. Motors are rigidly attached to a common backbone (blue) and equally spaced with a distance q incommensurable to the filament periodicity l. Motors detach and attach to the polar filament with rates  , respectively, feeling a periodic potential
, respectively, feeling a periodic potential 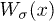 which depends on the state of the motor
which depends on the state of the motor  . Localized active sites are described through the function
. Localized active sites are described through the function  which breaks detailed balance in the system. Finally, the backbone is coupled to a spring of elastic modulus KN.
which breaks detailed balance in the system. Finally, the backbone is coupled to a spring of elastic modulus KN.
Download figure:
Standard imageFig. 2: (Color online) Complex periodic orbit for 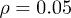 ,
, 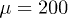 and
and 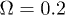 by solving (10). We notice that the attractor fulfills the symmetry
by solving (10). We notice that the attractor fulfills the symmetry 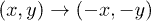 .
.
Download figure:
Standard imageWe choose the model parameters consistent with the minimal actomyosin system in ref. [22] which was shown to be successfully described by the two-state model in ref. [18]. Typical values of KN are found in the range of 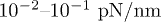 and the number of motors are
and the number of motors are 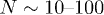 , which gives
, which gives  , while the friction coefficient is found to be
, while the friction coefficient is found to be  [18,22,30]. We take
[18,22,30]. We take 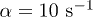 and choose Ω much larger than the critical value. By considering
and choose Ω much larger than the critical value. By considering 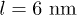 ,
, 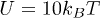 we find
we find 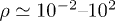 and
and 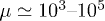 . Therefore, while the dimensionless damping rate ρ is found to be around the characteristic rate of the system (i.e.
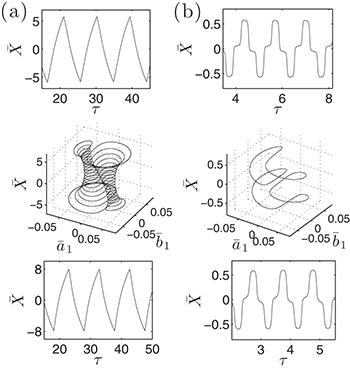
. Therefore, while the dimensionless damping rate ρ is found to be around the characteristic rate of the system (i.e. 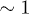 ), the mobility μ is specially high, thus the system works in a regime where nonlinearities are particularly important. In fig. 3 we study two characteristic types of nonlinear oscillations by solving the reduced system (7) (top row) and the complete system (eqs. (2) and (3)) (bottom row) for two different set of parameters corresponding to small (fig. 3(a)) and large (fig. 3(b)) elastic modulus. Numerical solutions for the complete system are carried out taking
), the mobility μ is specially high, thus the system works in a regime where nonlinearities are particularly important. In fig. 3 we study two characteristic types of nonlinear oscillations by solving the reduced system (7) (top row) and the complete system (eqs. (2) and (3)) (bottom row) for two different set of parameters corresponding to small (fig. 3(a)) and large (fig. 3(b)) elastic modulus. Numerical solutions for the complete system are carried out taking 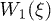 as a symmetric saw-tooth potential of amplitude U, a constant value for W2, a sinusoidal form of the hydrolysis amplitude modulation
as a symmetric saw-tooth potential of amplitude U, a constant value for W2, a sinusoidal form of the hydrolysis amplitude modulation 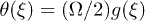 and a constant attachment rate
and a constant attachment rate  . The case (a) corresponds to
. The case (a) corresponds to  cusp-like oscillations with peak-to-peak amplitude of
cusp-like oscillations with peak-to-peak amplitude of  . On the other hand, case (b) corresponds to
. On the other hand, case (b) corresponds to  oscillations with peak-to-peak amplitude of
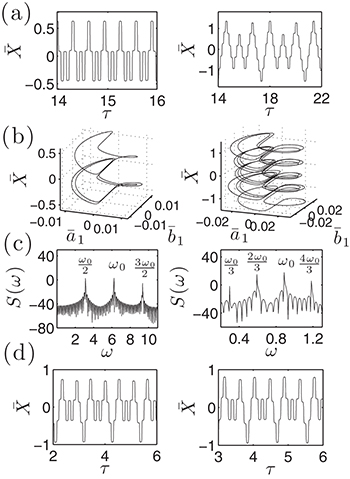
oscillations with peak-to-peak amplitude of 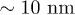 . Notice that despite of using a different set of functions to solve the reduced and the complete system, the shape of the oscillations is very similar. Both cases qualitatively agree with the observed amplitude and frequency measurements reported for spontaneous oscillations in ref. [22]. In fig. 4, subharmonic oscillations are shown by solving (7) (fig. 4(a), (b), (c) and (d) (left)) and the complete system (fig. 4(d) (right)). The periodic movement of the backbone is characterized by the formation of one (fig. 4(c) (left)) or two (fig. 4(c) (right)) subharmonics, where
. Notice that despite of using a different set of functions to solve the reduced and the complete system, the shape of the oscillations is very similar. Both cases qualitatively agree with the observed amplitude and frequency measurements reported for spontaneous oscillations in ref. [22]. In fig. 4, subharmonic oscillations are shown by solving (7) (fig. 4(a), (b), (c) and (d) (left)) and the complete system (fig. 4(d) (right)). The periodic movement of the backbone is characterized by the formation of one (fig. 4(c) (left)) or two (fig. 4(c) (right)) subharmonics, where  is the fundamental frequency of the signal. Remarkably, similar results where found experimentally in ref. [22] for large optical trap stiffness where the fundamental frequency was 2.2 Hz and a clear subharmonic peak at approximately
is the fundamental frequency of the signal. Remarkably, similar results where found experimentally in ref. [22] for large optical trap stiffness where the fundamental frequency was 2.2 Hz and a clear subharmonic peak at approximately 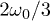 was observed. Although it was argued that molecular details of the actomyosin interaction could be the reason for this effect, we find that for high mobility values μ and in the limit of large elastic modulus (i.e.
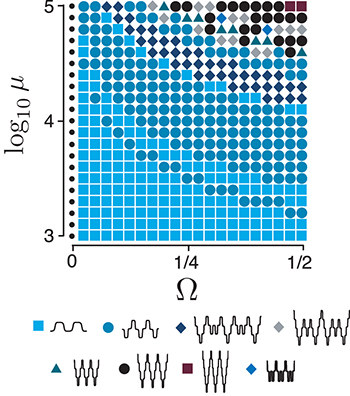
was observed. Although it was argued that molecular details of the actomyosin interaction could be the reason for this effect, we find that for high mobility values μ and in the limit of large elastic modulus (i.e.  ), the system is expected generally to exhibit periodic motion with two subharmonics and less frequently with only one, as shown in figs. 5 and 6. We identify eight types of staircase-shaped oscillations, which exemplify the complex bifurcation scenario. The final steady state of the system is sensitive to the initial conditions as shown in fig. 6, where different basins of attraction are identified. Two types of oscillations exhibit two subharmonics (dark-blue and grey diamonds) and one type exhibits a single subharmonic (light-blue diamonds). It is worth noting that subharmonic oscillations lose the symmetry property
), the system is expected generally to exhibit periodic motion with two subharmonics and less frequently with only one, as shown in figs. 5 and 6. We identify eight types of staircase-shaped oscillations, which exemplify the complex bifurcation scenario. The final steady state of the system is sensitive to the initial conditions as shown in fig. 6, where different basins of attraction are identified. Two types of oscillations exhibit two subharmonics (dark-blue and grey diamonds) and one type exhibits a single subharmonic (light-blue diamonds). It is worth noting that subharmonic oscillations lose the symmetry property 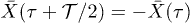 , where
, where  is the fundamental period of the signal. This property is fulfilled for oscillations in fig. 3 since W1 is symmetric; however this can be lost for asymmetric W1 [18]. In this case, a novel symmetry breaking property emerges dynamically due to subharmonic bifurcations of the system. Additionally, the time average of the backbone position in the steady state
is the fundamental period of the signal. This property is fulfilled for oscillations in fig. 3 since W1 is symmetric; however this can be lost for asymmetric W1 [18]. In this case, a novel symmetry breaking property emerges dynamically due to subharmonic bifurcations of the system. Additionally, the time average of the backbone position in the steady state  is different from zero for subharmonic oscillations and introduces an overall shift, as shown in figs. 4(a) and (d). The latter reflects asymmetries on the time the backbone spends for positive and negative displacements.
is different from zero for subharmonic oscillations and introduces an overall shift, as shown in figs. 4(a) and (d). The latter reflects asymmetries on the time the backbone spends for positive and negative displacements.
Fig. 3: Backbone movement (top) and the corresponding phase-space trajectory (middle) by solving the reduced system (7) and backbone movement solving the complete system (eqs. (2) and (3)) with a saw-tooth potential of amplitude U, a constant value of W2, a sinusoidal form of 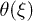 and a constant attachment rate
and a constant attachment rate  (bottom). (a)
(bottom). (a) 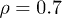 and
and  .
. 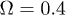 (top, middle) and
(top, middle) and  ,
,  and
and 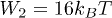 (bottom). (b) The same for
(bottom). (b) The same for  and
and 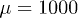 .
.  is the dimensionless time.
is the dimensionless time.
Download figure:
Standard imageFig. 4: Subharmonic oscillations. (a) Backbone time evolution by solving the reduced system for 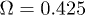 ,
, 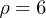 ,
,  with
with 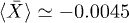 (left) and
(left) and  ,
, 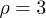 ,
,  with
with  (right). (b), (c): phase-space trajectories and power spectra
(right). (b), (c): phase-space trajectories and power spectra 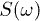 in dB for the trajectories in (a), respectively. (d) Backbone time evolution by solving the reduced system for
in dB for the trajectories in (a), respectively. (d) Backbone time evolution by solving the reduced system for  ,
,  and
and  with
with  (left) and by solving the complete system with the same set of functions as in fig. 3, for
(left) and by solving the complete system with the same set of functions as in fig. 3, for 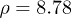 ,
, 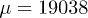 ,
, 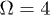 ,
,  and
and 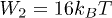 (right).
(right).
Download figure:
Standard imageFig. 5: (Color online) Different types of oscillations in the 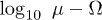 parameter space for
parameter space for 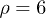 and the initial condition
and the initial condition  by solving the reduced system. We identify eight types of oscillations in this particular case. Each symbol in the parameter space corresponds to a type of oscillation for a choice of
by solving the reduced system. We identify eight types of oscillations in this particular case. Each symbol in the parameter space corresponds to a type of oscillation for a choice of  . Subharmonic oscillations (diamonds) are found with two subharmonics (dark-blue and grey diamonds) and occasionally with a single subharmonic (light-blue diamonds). Dots indicate no oscillations.
. Subharmonic oscillations (diamonds) are found with two subharmonics (dark-blue and grey diamonds) and occasionally with a single subharmonic (light-blue diamonds). Dots indicate no oscillations.
Download figure:
Standard imageFig. 6: (Color online) Different domains of attraction by varying the initial conditions  and
and  and fixing
and fixing  , for
, for 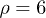 ,
, 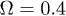 and
and 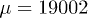 by solving the reduced system. The symbol and color code is the same as in fig. 5, and empty symbols denote the same type of oscillation with
by solving the reduced system. The symbol and color code is the same as in fig. 5, and empty symbols denote the same type of oscillation with  .
.
Download figure:
Standard imageIn this work we have studied in detail a minimal three-variable description for the spontaneous oscillations of collective molecular motors, based on a generic two-state model coupled to an elastic spring. We find that this reduced description captures the dynamics of the full system, which, in turn, unveils different types of nonlinear oscillations which can generally exhibit one or two subharmonics in the limit of large elastic modulus and high mobility. Although the reduced description is only exact for a specific set of functions, direct numerical simulations indicate that the dynamics captured by the reduced system is generic and thus shared by other sets of functions, in particular concerning the occurrence of the referred subharmonic bifurcations. This suggests that a general three-dimensional reduction is inherent to the system, although in general, the corresponding set of variables may not coincide with the explicit ones used in our case. In addition, we found that the importance of nonlinearities is enhanced for smaller friction, a regime that is relevant for myosin motors in vitro. The emergence of two subharmonics on the spectrum of the backbone signal for large elastic modulus is in remarkable accordance with similar subharmonic peaks observed experimentally in analogous conditions [22]. It is worth stressing that the experiments are subject to strong noise sources, mainly due to the stochastic nature of myosin binding kinetics. This fact is likely to modify in a nontrivial way the amplitude and shape of the subharmonic peaks, by inducing transitions between the different oscillatory regimes, and presumably decreasing the time spent in the subharmonic oscillations in favor of the fundamental frequency oscillations. Furthermore, the studied model is not expected to yield an accurate description of the physical system at molecular level, since the precise forms of the potentials and transition rates are essentially unknown. Nevertheless, the mere fact that the subharmonic peaks are observable under the experimental conditions constitutes by itself a strong evidence of the robustness of this phenomenon. Other types of complex nonlinear behavior of molecular motor assemblies have also been reported in the literature for spontaneous sarcomere dynamics [31]. In that case, the assumptions of the model accounted for different physical ingredients and led to notably different nonlinear dynamics, including excitable behaviour and a Ruelle-Takens route to chaos.
The results presented here suggest that hydrodynamic friction could be tuned in biological systems in order to suppress undesired multifrequency oscillations. For example, mechanosensory hair bundles are self-tuned close to a Hopf bifurcation in order to obtain a nonlinear amplification gain [10]. Thus, it is essential for hair cells to have a characteristic frequency at which they are most sensitive. Likewise, flagellated organisms, such as spermetozoa, rely on the propagation of harmonic bending waves along the flagellum to achieve locomotion [32], and thus high motor mobility could slow down their motion and lead to uncoordinated bending waves. Finally, we hope that our results will stimulate future empirical tests on minimal in vitro systems to further scrutinize the role of nonlinearities in molecular-motor–driven oscillations.
Acknowledgments
We acknowledge the support under Projects No. FIS2010-21924-C02-02 and No. 2009-SGR-014. DO acknowledges a FPU grant from de Spanish Government. HG is an Oxford University Hooke Fellowship Holder and is supported by Award KUK-C1-013-04 from King Abdulah University of Science and Technology.