Abstract
We unveil a remarkable connection between the sine-Gordon quantum field theory and the Kardar-Parisi-Zhang (KPZ) growth equation. We find that the non-relativistic limit of the two-point correlation function of the sine-Gordon theory is related to the generating function of the height distribution of the KPZ field with droplet initial conditions, i.e. the directed polymer free energy with two endpoints fixed. As shown recently, the latter can be expressed as a Fredholm determinant which in the large-time separation limit converges to the GUE Tracy-Widom cumulative distribution. Possible applications and extensions are discussed.
Export citation and abstract BibTeX RIS
The sine-Gordon (sG) model and its cousin, the sinh-Gordon (shG) model, are paradigmatic integrable quantum field theories with countless applications in condensed-matter physics (see, e.g., [1] as a review). A lot is known in particular about their spectra in terms of many-particle scattering states and about matrix elements of local operators, the so-called form factors [2,3]. This allowed very striking predictions for experimentally relevant systems (such as spin chains and ladders [1]) which, in the scaling limit, are described by these massive field theories. While the shG model contains only a single type of particle of mass M, the excitation spectrum of the sG model exhibits solitons as well as "breathers" Bm that can be viewed as bound states of m "particles" or, alternatively, as soliton-antisoliton bound states. The two models are also related by an analytic continuation of the coupling constant.
As a recent experimentally relevant application, the non-relativistic limit (NRL) of the shG model was considered in ref. [4], where it was shown that in a double scaling limit (i.e. taking a NRL while taking the shG coupling to zero) the Lieb-Liniger (LL) model [5] is recovered with repulsive interactions. This procedure allowed the analytic calculation of some previously unknown local expectation values [4,6]. Taking the same double scaling limit of the sG model instead gives the Lieb-Liniger (LL) model [5] with attractive interactions, and indeed it is known that the scattering phases of the two models do coincide [7]. However, this procedure has not yet been explored to obtain expectation values of measurable observables.
In an a priori completely different context, there has been much progress in finding exact solutions to the 1D Kardar-Parisi-Zhang (KPZ) equation [8–22]. Some of these approaches used the mapping onto the directed polymer (DP) model, and from there, using the replica method, onto the LL model of bosons with attractive interactions [23]. These bosons form bound states called strings in the large system size limit [24], and summation over these string states has allowed for the calculation of the probability distribution function (PDF) of the KPZ height field for various initial conditions [9,10,13,15,16]. Some of these predictions have been tested experimentally [25].
The aim of this paper is to unveil a connection between the KPZ or DP models and the NRL of the sG quantum field theory which arises because, as we mentioned above, in the NRL the sG model reproduces the attractive LL model. While m, characterizing the breathers, is a bounded integer for sG, it becomes unbounded in the NRL and reproduces the bound states of the LL model, the so-called string states. Working out the details, we show that the connection is remarkably simple and, in particular, we find that the two-point correlation function of exponential fields (vertex operators) in the sG model encodes the information of the PDF of the height field in KPZ.
KPZ equation and Lieb-Liniger model
Let us recall some facts about the KPZ equation in one space dimension. It describes the stochastic growth of an interface of height 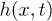 , as a function of time as
, as a function of time as

in dimensionless units, in the presence of white noise 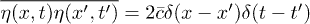 . Here we focus on the so-called droplet, or sharp-wedge, initial condition, where
. Here we focus on the so-called droplet, or sharp-wedge, initial condition, where  with
with 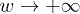 . The height field
. The height field 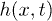 can be written as
can be written as  where Z is the partition sum of a fixed endpoint DP, i.e. paths in the x,t plane with endpoints fixed at (0,0) and
where Z is the partition sum of a fixed endpoint DP, i.e. paths in the x,t plane with endpoints fixed at (0,0) and  , directed along the time direction. In the KPZ context one introduces the generating function
, directed along the time direction. In the KPZ context one introduces the generating function

which is a series representation for the Laplace transform  of the PDF of Z. In the large time limit the (one-point) fluctuations of
of the PDF of Z. In the large time limit the (one-point) fluctuations of  are expected to grow as
are expected to grow as  .
.
To study this limit it is convenient to write  where
where  and
and  is an O(1) random variable. We also define
is an O(1) random variable. We also define  , since then
, since then 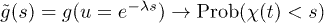 for
for  , hence the generating function
, hence the generating function  is directly the cumulative distribution function (CDF) of the height. The important finding of refs. [9,10] is that
is directly the cumulative distribution function (CDF) of the height. The important finding of refs. [9,10] is that  can be expressed as a Fredholm determinant at all times (see below) and that it converges for large time to
can be expressed as a Fredholm determinant at all times (see below) and that it converges for large time to  , the Gaussian Unitary Ensemble (GUE) Tracy-Widom CDF [26]. These results were obtained exploiting the property that the moments
, the Gaussian Unitary Ensemble (GUE) Tracy-Widom CDF [26]. These results were obtained exploiting the property that the moments  can be written as the diagonal propagator of an n-particle Bose gas with the Hamiltonian
can be written as the diagonal propagator of an n-particle Bose gas with the Hamiltonian
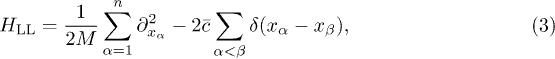
i.e. the attractive LL model which is integrable via the Bethe ansatz [27]. More precisely,  reads
reads
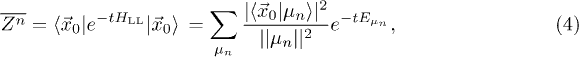
where  are the n-boson eigenstates of
are the n-boson eigenstates of  with eigenenergies
with eigenenergies  ,
,  , so
, so 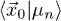 is the real space wave function evaluated at coinciding particle positions in x0. Evaluating this sum over Bethe states in the infinite system size limit is not trivial and was performed in refs. [9,10]. Here we show that the same sum can be retrieved rather simply, directly in the infinite system limit, from known results in the sG field theory, without the need to manipulate Bethe states. Besides its interest for the LL physics, it also raises hope that other interesting quantities in KPZ could be calculated using the sG model.
is the real space wave function evaluated at coinciding particle positions in x0. Evaluating this sum over Bethe states in the infinite system size limit is not trivial and was performed in refs. [9,10]. Here we show that the same sum can be retrieved rather simply, directly in the infinite system limit, from known results in the sG field theory, without the need to manipulate Bethe states. Besides its interest for the LL physics, it also raises hope that other interesting quantities in KPZ could be calculated using the sG model.
Sine-Gordon model
The sG model is a relativistically invariant integrable quantum field theory in  dimension defined by the Euclidean (imaginary-time) Lagrangian density
dimension defined by the Euclidean (imaginary-time) Lagrangian density
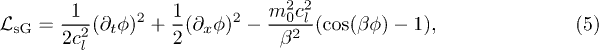
where  is a real scalar field, cl is the speed of light, m0 the bare mass, β the coupling constant, and we set
is a real scalar field, cl is the speed of light, m0 the bare mass, β the coupling constant, and we set  . The renormalized (physical) coupling constant and mass are
. The renormalized (physical) coupling constant and mass are


The spectrum of the theory contains several kinds of particles. The "fundamental" one is called 1-breather which has relativistic dispersion relation with energy and momentum,
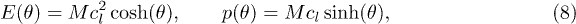
where θ is the rapidity. The spectrum also contains solitons as well as m-breathers which are bound states of particles. We will need below the dispersion relation of the m-breather. Its total energy and momentum as a function of its center-of-mass rapidity θ can be obtained by introducing 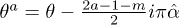 and writing
and writing

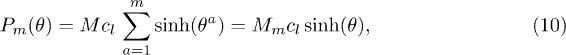
leading to the same dispersion relation as for 1-breathers but with a different mass Mm [28],

Note that the particle content m of the breather is bounded in the relativistic sG model, namely  . Due to its integrability, the sG model supports diffractionless factorized scattering and the exact 2-particle S-matrix is known [3,29]. Based on this, matrix elements of exponential vertex operators between scattering states, i.e. form factors have been computed exactly [2,30,31].
. Due to its integrability, the sG model supports diffractionless factorized scattering and the exact 2-particle S-matrix is known [3,29]. Based on this, matrix elements of exponential vertex operators between scattering states, i.e. form factors have been computed exactly [2,30,31].
Double non-relativistic limit and LL model
Here we are interested in the (double) NRL defined as [4]
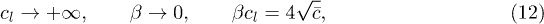
with  fixed and finite. Hence the renormalized coupling tends to zero as
fixed and finite. Hence the renormalized coupling tends to zero as

In this limit the dispersion relation of the particles becomes non-relativistic as

where λ is the usual (non-relativistic) rapidity, i.e. the quasi-momentum. Importantly, this double limit establishes a connection between the exact S-matrices and the form factors of the two models. At the level of the fields the correspondence can be written in the double limit as
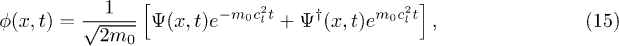
where ϕ is the sG field and  creates a non-relativistic particle (i.e. the LL boson). Plugging (15) into (5) leads, upon expansion and neglecting highly oscillating terms, to the non-linear Schrödinger Hamiltonian
creates a non-relativistic particle (i.e. the LL boson). Plugging (15) into (5) leads, upon expansion and neglecting highly oscillating terms, to the non-linear Schrödinger Hamiltonian
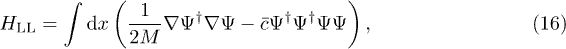
which is the second quantized form of the attractive LL Hamiltonian (3). This limit procedure was first shown for the shG model in ref. [4], leading to the repulsive LL model with interaction parameter  . Here the same method shows that
. Here the same method shows that  emerges as the coupling constant of the attractive LL model. In fact, at the level of the single-particle states a lot can be deduced by analytical continuation from shG to sG
emerges as the coupling constant of the attractive LL model. In fact, at the level of the single-particle states a lot can be deduced by analytical continuation from shG to sG  . This technique was used to study a highly excited gas-like state of the attractive LL model, the super Tonks-Girardeau gas [32]. However, the many-particle states in general are quite different in the repulsive
. This technique was used to study a highly excited gas-like state of the attractive LL model, the super Tonks-Girardeau gas [32]. However, the many-particle states in general are quite different in the repulsive  and attractive
and attractive  cases. Consider the energy of the sG m-breather (9)–(11) in the double NRL:
cases. Consider the energy of the sG m-breather (9)–(11) in the double NRL:

while the momentum is  , where we have scaled
, where we have scaled  and neglected terms
and neglected terms  . Apart from the rest energy, these are exactly the total energies and momenta of the m-string states of the LL model in the limit of infinite system size [24]. The correspondence goes further and indeed also the scattering phases coincide, as pointed out in [7]. Finally, in the NRL the mass of the solitons/antisolitons
. Apart from the rest energy, these are exactly the total energies and momenta of the m-string states of the LL model in the limit of infinite system size [24]. The correspondence goes further and indeed also the scattering phases coincide, as pointed out in [7]. Finally, in the NRL the mass of the solitons/antisolitons  [3] diverges, hence they disappear from the spectrum and we can neglect them. We are then left with an infinite number of breather modes as
[3] diverges, hence they disappear from the spectrum and we can neglect them. We are then left with an infinite number of breather modes as  corresponding to the LL strings. The form factors of the LL model can also be obtained through the NRL from the breather form factors of the sG model, paralleling the calculation for the shG model [4,33]. In the remainder of the paper we will set
corresponding to the LL strings. The form factors of the LL model can also be obtained through the NRL from the breather form factors of the sG model, paralleling the calculation for the shG model [4,33]. In the remainder of the paper we will set  by a choice of units, as customary in the LL model.
by a choice of units, as customary in the LL model.
From sG correlations to the KPZ/DP model
Let us consider the two-point correlator of the exponential field in the Euclidean sG model (i.e. in imaginary time),

as well as the reduced correlation1

which is defined to equal unity at  . Here and below we denote the vacuum expectation value of the exponential field, as
. Here and below we denote the vacuum expectation value of the exponential field, as  .
.
The Lehmann formula [1–3] expresses quite generally such a ground-state expectation value (here in the vacuum) in terms of the form factors of the excitations of the theory. At this stage we do not yet consider the NRL but, for simplicity, we ignore the solitons states (which will be justified only in that limit). It thus takes the form of a sum over states with arbitrary number ns of breathers

where each breather of type mj has rapidity  and particle content mj.
and particle content mj.
The form factors of the breathers can be obtained from those of the particles  . Hence let us start with the particle states, i.e. we temporarily restrict to
. Hence let us start with the particle states, i.e. we temporarily restrict to  in (20). Their form factors are known in sG [34] and can be obtained from the shG ones [35] via analytical continuation to imaginary coupling as
in (20). Their form factors are known in sG [34] and can be obtained from the shG ones [35] via analytical continuation to imaginary coupling as

where  . Here we introduced the matrix (with
. Here we introduced the matrix (with  )
)
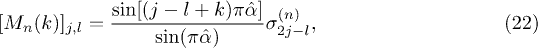
for  , where
, where  is the j-th elementary symmetric polynomial of the variables
is the j-th elementary symmetric polynomial of the variables  , and
, and  . The minimal form factor is given by
. The minimal form factor is given by
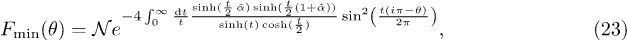
where  . The minimal form factor satisfies the exact relation [35]
. The minimal form factor satisfies the exact relation [35]

We now carefully take the (double) non-relativistic limit of the form factors. To obtain a non-trivial limit we need to let k → ∞ while  with
with  fixed and finite. We also scale the rapidities as
fixed and finite. We also scale the rapidities as  (we recall
(we recall  ). Given that
). Given that  as
as  , using eq. (24) we have in the NRL
, using eq. (24) we have in the NRL

The most complicated term in the form factor (21) is 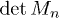 which immensely simplifies in the NRL because one can neglect the
which immensely simplifies in the NRL because one can neglect the  in the matrix Mn to get
in the matrix Mn to get

and  in the NRL. Finally, in the NRL we also have the simple relation
in the NRL. Finally, in the NRL we also have the simple relation

All these relations lead for the most complicated parts of the form factor to the remarkably simple limit

Plugging this in (20) and taking into account the Jacobian of the variable change from θ's to p's, we find for the  contribution
contribution
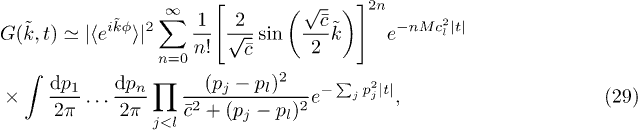
which is a sum of positive contributions, as it should, since it comes from the Lehmann formula.
Let us now generalize the derivation to arbitrary m-breather states. Fusion relations relate the form factors of breathers to the ones of n particles Fn as follows. Let us recall that the rapidities can be written as  . Then, recalling
. Then, recalling  , we have [34]
, we have [34]
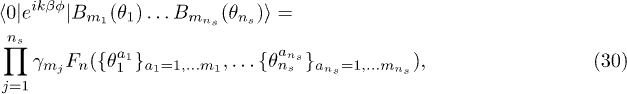
where the NRL of  given in [34] is
given in [34] is

Note that ![$\theta_j^a \to \frac{\pi \hat \alpha}{\bar c} [p_j - \frac{i \bar c}{2} (2 a - 1- m_j) ]$](https://content.cld.iop.org/journals/0295-5075/107/1/10011/revision1/epl16381ieqn71.gif) which coincide with the string rapidities [24].
which coincide with the string rapidities [24].
In taking the NRL of the form factor Fn, only the term with  changes compared to the previous case, leading to
changes compared to the previous case, leading to

where
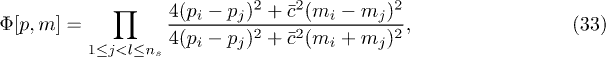
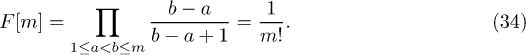
Putting everything together we finally obtain

Now we can compare this with the expression for the moments of the partition sum in the KPZ/DP problem. The calculation of the averaged moments (4) was performed in ref. [9] and found to take exactly the same expression as above (compare with eq. (9) of ref. [9]). Hence we find that the reduced correlation can be written as

showing that there is a relation between the two-point correlation in sG and the moments in the KPZ/DP problem. Furthermore, the sG correlation takes the same form as the KPZ/DP generating function, hence one can also write

where ![$u= - [\frac{2}{\sqrt{\bar c} } \sin( \frac{\sqrt{\bar c}}{2} \tilde k ) ]^2 e^{- M c_l^2 t}$](https://content.cld.iop.org/journals/0295-5075/107/1/10011/revision1/epl16381ieqn73.gif) . Interestingly, by analytic continuation
. Interestingly, by analytic continuation  one also finds
one also finds
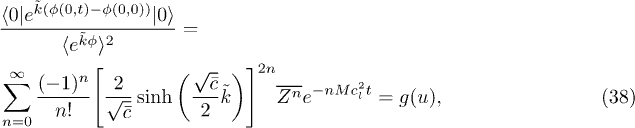
where now ![$u = [\frac{2}{\sqrt{\bar c} } \sinh( \frac{\sqrt{\bar c}}{2} \tilde k )]^2 e^{- M c_l^2 t }$](https://content.cld.iop.org/journals/0295-5075/107/1/10011/revision1/epl16381ieqn75.gif) is a positive number, thereby making the connection closer. Since the KPZ generating function obeys
is a positive number, thereby making the connection closer. Since the KPZ generating function obeys  , it implies that both sides of the above equation are now positive numbers in the interval [0, 1], increasing with
, it implies that both sides of the above equation are now positive numbers in the interval [0, 1], increasing with  . Note that although the operator in the left-hand side of eq. (38) may not be formally defined in the sG field theory, in the Euclidean version it takes the meaning of a canonical statistical mechanics average, with a discretization and regularization at small and large scale (as one would do in a numerical simulation). While the two correlations in eq. (38) may be singular as the regularizations are removed, their ratio should be a well-defined number in the interval [0, 1].
. Note that although the operator in the left-hand side of eq. (38) may not be formally defined in the sG field theory, in the Euclidean version it takes the meaning of a canonical statistical mechanics average, with a discretization and regularization at small and large scale (as one would do in a numerical simulation). While the two correlations in eq. (38) may be singular as the regularizations are removed, their ratio should be a well-defined number in the interval [0, 1].
Having shown that the NRL of the sG correlation contains information about the PDF of the KPZ field, we can ask whether a tighter physical connection exists. Let us recall the expression of the generating function as a Fredholm determinant (FD) obtained in [9]:

where P0 is the projector on  and the kernel can be written as
and the kernel can be written as
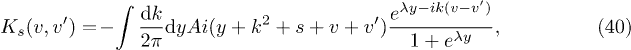
where  was defined above. Let us also recall that at large time this generating function
was defined above. Let us also recall that at large time this generating function  converges to
converges to  , the GUE Tracy-Widom CDF [26]. So it is interesting that this FD contains the information about the precise time dependence of the coefficients of each power of
, the GUE Tracy-Widom CDF [26]. So it is interesting that this FD contains the information about the precise time dependence of the coefficients of each power of  in the decay of the sG correlation function, these coefficients being proportional to the KPZ/DP moments
in the decay of the sG correlation function, these coefficients being proportional to the KPZ/DP moments  . Note, however, that because of these fast-decaying exponentials, there is no point-wise convergence as
. Note, however, that because of these fast-decaying exponentials, there is no point-wise convergence as  in (36) and (38) and, at this stage, there is no direct correspondence between a sG observable and KPZ generating function. An outstanding question is thus how far this correspondence can be pushed and whether one can construct sG observables with an even closer relation to KPZ. Note that it has been known for a long time that the KPZ equation provides an effective description of the driven, overdamped dynamics of the sG model [36]. However, it remains to be understood whether this bears any connection to the present situation.
in (36) and (38) and, at this stage, there is no direct correspondence between a sG observable and KPZ generating function. An outstanding question is thus how far this correspondence can be pushed and whether one can construct sG observables with an even closer relation to KPZ. Note that it has been known for a long time that the KPZ equation provides an effective description of the driven, overdamped dynamics of the sG model [36]. However, it remains to be understood whether this bears any connection to the present situation.
One last interesting point relates to the so-called moment problem in the continuum KPZ/DP problem, i.e. to the fact that the growth of the integer moments  as a function of m at fixed t is too rapid (i.e.
as a function of m at fixed t is too rapid (i.e.  ) to guarantee a unique solution for the PDF for
) to guarantee a unique solution for the PDF for  . While this is still an open question in the mathematics community, it is usually circumvented by resorting to discrete models (such as TASEP, see, e.g., [11]) which do reproduce continuum KPZ in some limit and do not suffer from the same problem. We point out here that the relativistic sG theory can provide yet another interesting regularization of the moment problem because the number of breather types
. While this is still an open question in the mathematics community, it is usually circumvented by resorting to discrete models (such as TASEP, see, e.g., [11]) which do reproduce continuum KPZ in some limit and do not suffer from the same problem. We point out here that the relativistic sG theory can provide yet another interesting regularization of the moment problem because the number of breather types  is bounded until the NRL is taken.
is bounded until the NRL is taken.
Overlaps and propagators in the LL model
One can ask more precisely how can the sG theory retrieve more detailed information about the attractive LL model hereby helping solve KPZ problems. For example, a related fundamental quantity (both for the LL model and the KPZ growth) is the overlap
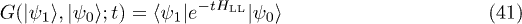
between more general initial  and final states
and final states  . Examples are i) KPZ with flat initial condition, which requires the overlap with an initial uniform state and whose solution was obtained in [13]; ii) the imaginary-time propagator for arbitrary positions [37,38]. Here we have shown that in the NRL the diagonal propagator can be retrieved as2
. Examples are i) KPZ with flat initial condition, which requires the overlap with an initial uniform state and whose solution was obtained in [13]; ii) the imaginary-time propagator for arbitrary positions [37,38]. Here we have shown that in the NRL the diagonal propagator can be retrieved as2
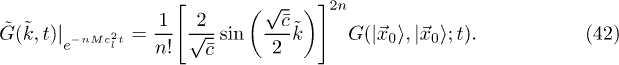
It would be interesting to obtain more general overlaps via this sG correspondence which we leave for future investigations.
Relation (42) can be understood in the following way. The diagonal propagator,  can be extracted from the NRL of the sG correlator
can be extracted from the NRL of the sG correlator 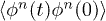 where the operator
where the operator  can be obtained naively from the n-th order of the series expansion of
can be obtained naively from the n-th order of the series expansion of  in powers of k. However, it turns out that the
in powers of k. However, it turns out that the  operator obtained in this way has non-zero matrix elements between states having any number of particles. These form factors survive in the NRL meaning that in the limit one cannot recover the
operator obtained in this way has non-zero matrix elements between states having any number of particles. These form factors survive in the NRL meaning that in the limit one cannot recover the  operator. It turns out that certain linear combinations of different powers of ϕ lead to
operator. It turns out that certain linear combinations of different powers of ϕ lead to  in the NRL. Quite interestingly, these combinations in terms of k give just the sine factor in eq. (42), so this formula, quite miraculously, automatically takes care of this operator mixing.
in the NRL. Quite interestingly, these combinations in terms of k give just the sine factor in eq. (42), so this formula, quite miraculously, automatically takes care of this operator mixing.
Conclusion
In this paper we have shown another method to calculate the PDF for the KPZ growth equation with the narrow-wedge initial condition exploiting the NRL limit of sG field theory. The obtained result fully agrees with previous derivations [9–12]. On the one hand, this result is a useful check of our new method and of present and previous results; on the other hand, this new correspondence raises the hope that it can be used to obtain yet unknown observables for the KPZ growth equation, as well as to provide a new interesting regularization of the problem.
Acknowledgments
MK thanks Gábor Takács for useful discussions. PC acknowledges the ERC for financial support under Starting Grant 279391 EDEQS. MK acknowledges financial support from the Marie Curie IIF Grant PIIF-GA-2012- 330076. PLD acknowledges the hospitality of the Dipartimento di Fisica dell'Università di Pisa where much of this work was completed.
Footnotes
- 1
In our normalization indeed
 and taking the ratio (18) is superfluous. However, this ratio is independent of normalizations and conventions and the results for this quantity are fully general.
and taking the ratio (18) is superfluous. However, this ratio is independent of normalizations and conventions and the results for this quantity are fully general. - 2









