Abstract
We study the dynamical fidelity 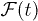 and the Loschmidt echo
and the Loschmidt echo 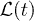 , following a periodic driving of the transverse magnetic field of a quantum Ising chain (back and forth across the quantum critical point) by calculating the overlap between the initial ground state and the state reached after n periods τ. We show that
, following a periodic driving of the transverse magnetic field of a quantum Ising chain (back and forth across the quantum critical point) by calculating the overlap between the initial ground state and the state reached after n periods τ. We show that ![$[\log{\mathcal F}(n\tau)]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn3.gif) (the logarithm of the fidelity per site) reaches a steady value in the asymptotic limit
(the logarithm of the fidelity per site) reaches a steady value in the asymptotic limit  , and we derive an exact analytical expression for this quantity. Remarkably, the steady-state value of
, and we derive an exact analytical expression for this quantity. Remarkably, the steady-state value of ![$[\log{\mathcal F}(n\tau\to \infty)]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn5.gif) shows memory of non-trivial phase information which is instead hidden in the case of thermodynamic quantities; this conclusion, moreover, is not restricted to 1-dimensional models.
shows memory of non-trivial phase information which is instead hidden in the case of thermodynamic quantities; this conclusion, moreover, is not restricted to 1-dimensional models.
Export citation and abstract BibTeX RIS
The dynamical evolution of closed quantum systems has been recently upgraded from a rather academic question to a very intense field of research, due to many experimental advances, notably cold-atom systems [1] and femtosecond resolved spectroscopies [2]. Many studies, in particular, have focused on different non-equilibrium issues, particularly when the quantum system is driven out of equilibrium either by a sudden quench or by a slow adiabatic change of the Hamiltonian (the so-called quantum annealing alias adiabatic quantum computation [3–7]). In parallel, there have been numerous studies on the so-called Kibble-Zurek scaling [8–13] of the defect density generated in the final state reached by driving a system across a quantum critical point (QCP) [14]: For reviews, see refs. [15–17]. Many works have also explored the connection between quantum phase transitions, quantum information [18] and quantum critical dynamics [15]. Two important measures which show distinct behaviour close to a QCP happen to be the Loschmidt echo [19,20] and the ground-state quantum fidelity [21]. Especially the former has been studied extensively in recent years in connection to the dynamics of decoherence [22–24], and the work statistics [25,26].
Considerably less studied is the case of a time-periodic driving, in which a closed quantum system is periodically driven back and forth across a QCP [27,28]. Very recently, it has been argued that periodically driven closed quantum systems possessing an absolutely continuous Floquet spectrum are likely to display a "periodic steady state" [29,30], i.e., a periodic long-time dynamics for most physical observables, an effect that has been explicitly demonstrated for an Ising chain with a periodically driven transverse field.
In this paper we consider the Loschmidt echo [19,20,31] upon a periodic driving of a closed quantum system. The Loschmidt echo [31] is defined as
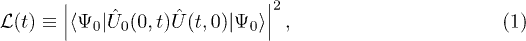
where 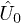 and
and 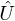 are unitary evolution operators associated to two different Hamiltonians
are unitary evolution operators associated to two different Hamiltonians  and
and 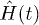 , and
, and 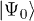 is some initial state. In the particular case in which
is some initial state. In the particular case in which 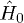 is time independent and
is time independent and 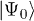 is its ground state, then the Loschmidt echo is equivalently expressed as
is its ground state, then the Loschmidt echo is equivalently expressed as
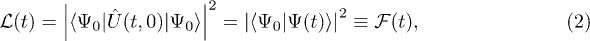
where the right-hand side might be viewed as a dynamical fidelity, i.e., the squared overlap between the initial state and the time-evolved state 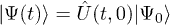 , alias the return probability to the initial state
, alias the return probability to the initial state 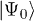 , or the amplitude P0 of the zero-work delta peak,
, or the amplitude P0 of the zero-work delta peak, 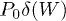 , in the work distribution P(W) [25,26]. We stress that this is different from the conventional ground-state fidelity [21]
, in the work distribution P(W) [25,26]. We stress that this is different from the conventional ground-state fidelity [21] 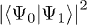 ,
, 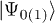 being the ground-states of the Hamiltonian with two different sets of parameters: If the system repeatedly crosses a QCP during the evolution, the defects generated in the process manifest themselves in the dynamical fidelity
being the ground-states of the Hamiltonian with two different sets of parameters: If the system repeatedly crosses a QCP during the evolution, the defects generated in the process manifest themselves in the dynamical fidelity 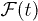 .
.
The key question we will address is whether 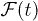 , while not being a standard thermodynamical observable, would still tend to reach a large-t steady-state value [29] when the Hamiltonian
, while not being a standard thermodynamical observable, would still tend to reach a large-t steady-state value [29] when the Hamiltonian 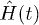 is time-periodic,
is time-periodic, 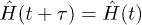 . We will show here that the answer is positive for the explicit case we have studied in detail, i.e., a periodically driven quantum Ising chain, and we believe that this result extends to all the cases in which a periodic steady state is found for ordinary observables [29]. Moreover, and this is the key result of our study, the off-diagonal matrix elements whose long-time average is responsible for the periodic steady state of thermodynamical observables play here, for the dynamical fidelity, an important role: the correct long-time result, for which we derive an exact analytical expression, does not follow from a decohered density matrix [12].
. We will show here that the answer is positive for the explicit case we have studied in detail, i.e., a periodically driven quantum Ising chain, and we believe that this result extends to all the cases in which a periodic steady state is found for ordinary observables [29]. Moreover, and this is the key result of our study, the off-diagonal matrix elements whose long-time average is responsible for the periodic steady state of thermodynamical observables play here, for the dynamical fidelity, an important role: the correct long-time result, for which we derive an exact analytical expression, does not follow from a decohered density matrix [12].
In the following, we will concentrate on a simple model where quasi-analytic information can be extracted on the quantities of interest, namely the quantum Ising chain in transverse field. The Hamiltonian of the system is
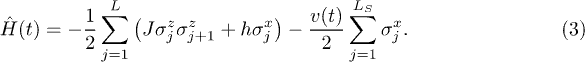
Here, the 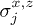 are spin-(1/2) Pauli matrices at site j for a chain of length L with periodic boundary conditions (PBC)
are spin-(1/2) Pauli matrices at site j for a chain of length L with periodic boundary conditions (PBC) 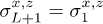 , and J is the standard longitudinal Ising coupling (
, and J is the standard longitudinal Ising coupling (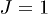 in the following). As for the transverse field terms, involving
in the following). As for the transverse field terms, involving 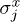 , we allow a uniform piece, h, as well as a time-dependent one, v(t), acting only on a subchain of length LS. We will take the time-dependent term v(t) to be periodic, with a single harmonic, i.e.,
, we allow a uniform piece, h, as well as a time-dependent one, v(t), acting only on a subchain of length LS. We will take the time-dependent term v(t) to be periodic, with a single harmonic, i.e., 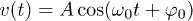 . In the equilibrium case with a homogeneous transverse field (i.e., A = 0) the model has two (mutually dual) gapped phases, a ferromagnetic one
. In the equilibrium case with a homogeneous transverse field (i.e., A = 0) the model has two (mutually dual) gapped phases, a ferromagnetic one 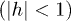 , and a quantum paramagnetic one
, and a quantum paramagnetic one 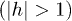 separated by QCPs at
separated by QCPs at 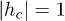 at zero temperature. When A > 0, the transverse field starts to oscillate periodically at t = 0 around the uniform value h, in a region of size LS. In the following we will concentrate on the case in which
at zero temperature. When A > 0, the transverse field starts to oscillate periodically at t = 0 around the uniform value h, in a region of size LS. In the following we will concentrate on the case in which 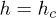 (i.e., we perturb around the critical Ising Hamiltonian) and
(i.e., we perturb around the critical Ising Hamiltonian) and 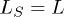 (i.e., the periodic driving acts on the whole chain) for which translational invariance can be exploited. The translationally non-invariant case can be dealt with using similar techniques, as explained in refs. [29,30]. Several questions can be addressed when LS < L, in particular the expected markedly different behaviour of the case in which
(i.e., the periodic driving acts on the whole chain) for which translational invariance can be exploited. The translationally non-invariant case can be dealt with using similar techniques, as explained in refs. [29,30]. Several questions can be addressed when LS < L, in particular the expected markedly different behaviour of the case in which 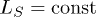 as
as 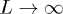 (perturbing a finite region inside a very large system, which will act as "reservoir"), from the case in which
(perturbing a finite region inside a very large system, which will act as "reservoir"), from the case in which 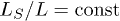 as
as 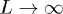 (perturbing an extensive region). The case of a single-site driving,
(perturbing an extensive region). The case of a single-site driving, 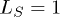 , is evidently connected with previous decoherence studies, usually concerned about sudden quench cases [32]. Also, there exist questions regarding the statistics of the work [25,26] performed during the driving. These issues will be treated in the future, while here we focus on the case
, is evidently connected with previous decoherence studies, usually concerned about sudden quench cases [32]. Also, there exist questions regarding the statistics of the work [25,26] performed during the driving. These issues will be treated in the future, while here we focus on the case 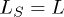 ,
, 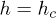 , A = 1 and
, A = 1 and 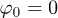 .
.
We shall now proceed to discuss what happens when a periodic driving is performed for a certain number n of periods 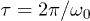 , by looking at the echo/fidelity stroboscopically at time
, by looking at the echo/fidelity stroboscopically at time 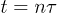 , in a wide range of frequencies
, in a wide range of frequencies 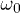 . Quan and Zurek [33] have performed a similar study following a linear quenching of the transverse field, forward and backward, crossing the critical point twice and studying the interference of the phases thus accumulated in the wave function, as reflected in the fidelity. With a periodic driving scheme we can study the dynamical fidelity following successive passages through the QCP and explore its behaviour as a function of n for the entire range of the driving frequency
. Quan and Zurek [33] have performed a similar study following a linear quenching of the transverse field, forward and backward, crossing the critical point twice and studying the interference of the phases thus accumulated in the wave function, as reflected in the fidelity. With a periodic driving scheme we can study the dynamical fidelity following successive passages through the QCP and explore its behaviour as a function of n for the entire range of the driving frequency 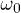 , including the extreme adiabatic
, including the extreme adiabatic 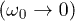 and high-frequency
and high-frequency 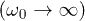 limits. As we shall discuss below, in the limit
limits. As we shall discuss below, in the limit 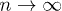 , coherence effects show up prominently for small frequencies, whereas in the opposite limit
, coherence effects show up prominently for small frequencies, whereas in the opposite limit 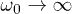 there is a sort of partial loss of coherence, though the dynamics remains fully coherent.
there is a sort of partial loss of coherence, though the dynamics remains fully coherent.
By going to Jordan-Wigner spinless fermions [34] and transforming to k-space, one can rewrite 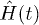 as a sum of two-level systems (see refs. [13,29,30] for details). Using the basis states
as a sum of two-level systems (see refs. [13,29,30] for details). Using the basis states 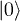 and
and 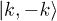 for each mode k, where
for each mode k, where 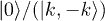 denotes state with no (two) fermion(s), respectively, the two-level Hamiltonian could be cast into the form
denotes state with no (two) fermion(s), respectively, the two-level Hamiltonian could be cast into the form 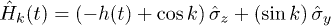 with
with 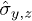 being standard Pauli matrices and
being standard Pauli matrices and 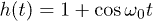 . The state of the system can hence be factorized as
. The state of the system can hence be factorized as 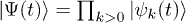 with
with 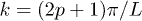 and
and 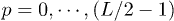 , as appropriate for fermionic antiperiodic boundary conditions (we assume L to be a multiple of 4). Moreover, using the Floquet theory [35,36] we can re-express each k-th component of the state
, as appropriate for fermionic antiperiodic boundary conditions (we assume L to be a multiple of 4). Moreover, using the Floquet theory [35,36] we can re-express each k-th component of the state 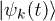 as [29]
as [29]
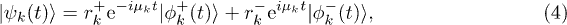
where 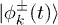 are the (time-periodic) Floquet modes and
are the (time-periodic) Floquet modes and 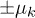 the corresponding Floquet quasi-energies, while the overlap factors
the corresponding Floquet quasi-energies, while the overlap factors 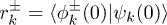 carry information about the initial state. Since
carry information about the initial state. Since 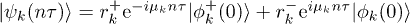 , one readily arrives at the following expression for the fidelity after n complete oscillations of the driving field:
, one readily arrives at the following expression for the fidelity after n complete oscillations of the driving field:

where 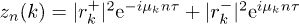 . For very large L, transforming the sum over k into an integral, one easily establishes that
. For very large L, transforming the sum over k into an integral, one easily establishes that 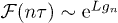 , where the logarithm of the fidelity (per site) is well defined for L → ∞ and given by
, where the logarithm of the fidelity (per site) is well defined for L → ∞ and given by
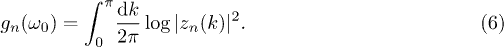
All the Floquet-related quantities appearing in 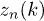 (the overlaps
(the overlaps 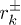 and the quasi-energies
and the quasi-energies 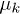 ) are functions of the driving frequency
) are functions of the driving frequency 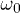 , a dependence that we have explicitly indicated only in
, a dependence that we have explicitly indicated only in 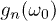 . For n = 0,
. For n = 0, 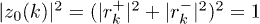 , hence
, hence 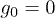 and
and 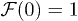 , as expected. For n > 0,
, as expected. For n > 0, 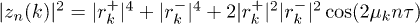 and the phase factors related to the Floquet quasi-energies
and the phase factors related to the Floquet quasi-energies 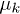 will play a role.
will play a role.
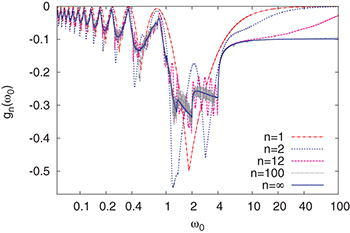
Figure 1 shows the behaviour of 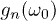 vs. the driving frequency
vs. the driving frequency 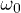 for a few values of n. Here n = 1 corresponds to a single oscillation of the field, i.e., a sweep across the QCP at
for a few values of n. Here n = 1 corresponds to a single oscillation of the field, i.e., a sweep across the QCP at 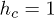 , already showing clear interference effects between the two Kibble-Zurek crossings (back and forth) of the QCP. On the other hand, the case n = 2 shows more marked interference effects, while n = 12, and even more so n = 100, display a quite rich structure of peaks and dips as a function of
, already showing clear interference effects between the two Kibble-Zurek crossings (back and forth) of the QCP. On the other hand, the case n = 2 shows more marked interference effects, while n = 12, and even more so n = 100, display a quite rich structure of peaks and dips as a function of 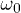 for
for 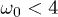 . (The value 4 marks, in our units, the upper limit of the natural frequencies of the unperturbed critical Ising model.) We notice, on the contrary, a rather smooth behaviour for
. (The value 4 marks, in our units, the upper limit of the natural frequencies of the unperturbed critical Ising model.) We notice, on the contrary, a rather smooth behaviour for 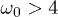 , with
, with 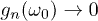 for
for 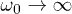 : the larger the value of n, the larger the typical
: the larger the value of n, the larger the typical 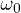 beyond which
beyond which 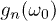 rises towards 0. Indeed, the limit
rises towards 0. Indeed, the limit 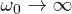 , for fixed finite n, involves a kind of fast driving regime in which the system "does not follow" the extremely fast oscillations of the field and "sees" the average Hamiltonian. This is not hard to justify from eqs. (5), (6): In the limit
, for fixed finite n, involves a kind of fast driving regime in which the system "does not follow" the extremely fast oscillations of the field and "sees" the average Hamiltonian. This is not hard to justify from eqs. (5), (6): In the limit 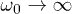 , the Floquet quasi-energies
, the Floquet quasi-energies 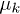 tend towards the unperturbed eigenvalues
tend towards the unperturbed eigenvalues 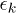 of the critical Ising model around which we are perturbing; since in that limit
of the critical Ising model around which we are perturbing; since in that limit 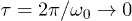 , the phase factors
, the phase factors 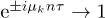 for every finite n, and therefore
for every finite n, and therefore 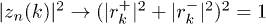 , which makes
, which makes 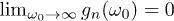 . On the contrary, the behaviour for
. On the contrary, the behaviour for  is highly structured, with peaks and dips at various frequencies
is highly structured, with peaks and dips at various frequencies 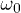 . Notably, for the small values of
. Notably, for the small values of 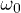 , there are sharp peaks where
, there are sharp peaks where 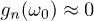 at all frequencies for which
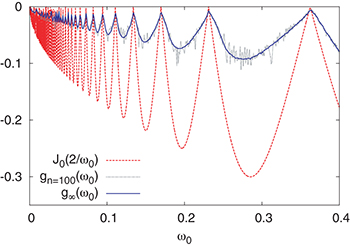
at all frequencies for which 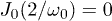 , where J0 is the zeroth-order Bessel function; this is a quite common finding in this field, related to the phenomenon of "coherent destruction of tunnelling" [36,37]. We will address this point later, see fig. 2 and the accompanying discussion.
, where J0 is the zeroth-order Bessel function; this is a quite common finding in this field, related to the phenomenon of "coherent destruction of tunnelling" [36,37]. We will address this point later, see fig. 2 and the accompanying discussion.
Fig. 1: (Colour on-line) ![$g_n=[\log{\mathcal F (n\tau)}]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn75.gif) , the logarithm of the fidelity per site, as a function of the frequency
, the logarithm of the fidelity per site, as a function of the frequency 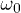 of the driving field
of the driving field 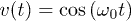 for
for 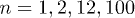 . The value of
. The value of 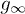 , eq. (10), is also shown. Notice how, for any n finite,
, eq. (10), is also shown. Notice how, for any n finite, 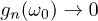 for
for 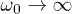 (for n = 100 such a rise towards 0 is visible right before
(for n = 100 such a rise towards 0 is visible right before 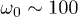 ).
).
Download figure:
Standard imageFig. 2: (Colour on-line) Detail of the low-frequency region, showing that the peaks of 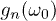 (where
(where 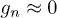 , but finite) closely match with the zeros of
, but finite) closely match with the zeros of 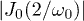 for small
for small 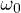 , all the way to the limit
, all the way to the limit 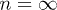 . (The very small-
. (The very small-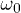 region suffers from numerical accuracy in sampling of the data.)
region suffers from numerical accuracy in sampling of the data.)
Download figure:
Standard imageAn obvious question arising from the inspection of fig. 1 concerns what happens as 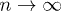 : will gn tend towards some definite limit, and if so, how can we calculate it? This question has to do with whether the system will effectively "synchronize" with the driving, i.e., if the stroboscopic observation of
: will gn tend towards some definite limit, and if so, how can we calculate it? This question has to do with whether the system will effectively "synchronize" with the driving, i.e., if the stroboscopic observation of 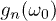 will reveal a steady state reached for
will reveal a steady state reached for 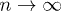 . The issue of reaching a "periodic steady state" when a closed quantum system is periodically driven has been raised and analyzed in detail, precisely for the model we are considering, in ref. [29]. There, it was shown that extensive physical quantities —like the energy density, the density of defects generated, and the transverse magnetization— will indeed reach a periodic steady state predicted by the diagonal elements in the Floquet expansion, while off-diagonal terms will lead to a vanishing contribution for
. The issue of reaching a "periodic steady state" when a closed quantum system is periodically driven has been raised and analyzed in detail, precisely for the model we are considering, in ref. [29]. There, it was shown that extensive physical quantities —like the energy density, the density of defects generated, and the transverse magnetization— will indeed reach a periodic steady state predicted by the diagonal elements in the Floquet expansion, while off-diagonal terms will lead to a vanishing contribution for 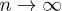 , due to destructive interference effects associated to the widely oscillating phase factors
, due to destructive interference effects associated to the widely oscillating phase factors 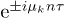 when integrated over all momentum modes: mathematically, this is a consequence of the Riemann-Lebesgue lemma predicting the vanishing, at large times, of Fourier transforms of sufficiently regular spectral densities. This can be rephrased by saying that the pure-state
when integrated over all momentum modes: mathematically, this is a consequence of the Riemann-Lebesgue lemma predicting the vanishing, at large times, of Fourier transforms of sufficiently regular spectral densities. This can be rephrased by saying that the pure-state 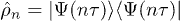 can be effectively replaced, when calculating the average of most extensive physical quantities, with its decohered part [12]. In the Floquet basis, we would express this as follows:
can be effectively replaced, when calculating the average of most extensive physical quantities, with its decohered part [12]. In the Floquet basis, we would express this as follows:
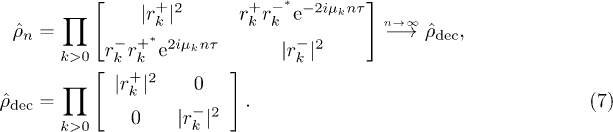
For the fidelity, however, the highly oscillating phase factors due to the off-diagonal terms play a trickier and more important role. To better appreciate this, let us rewrite gn as
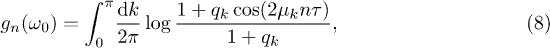
where ![$q_k\equiv2|r_k^+|^2|r_k^-|^2/(|r_k^+|^4 + |r_k^-|^4)\in [0,1]$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn118.gif) . For very large n, the
. For very large n, the 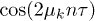 term oscillates rapidly as k runs over the BZ, and one would be tempted to conclude that
term oscillates rapidly as k runs over the BZ, and one would be tempted to conclude that 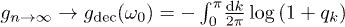 , which is the result predicted by taking
, which is the result predicted by taking ![$g_{\text{dec}}= [\log{\langle \Psi(0) | \hat{\rho}_{\text{dec}} | \Psi(0) \rangle}]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn121.gif) . This conclusion, however, would be swift and wrong. We could indeed write, using
. This conclusion, however, would be swift and wrong. We could indeed write, using 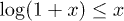 , that
, that
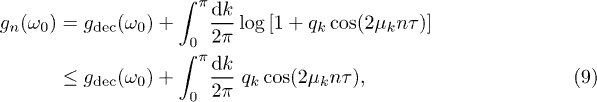
where the integral on the right-hand side of the second expression tends to 0 for n → ∞ (by the Riemann-Lebesgue lemma), but this does not allow us to conclude that  . The analysis of this limit is rather intricate in the general case. For
. The analysis of this limit is rather intricate in the general case. For  , however, things are much simpler, because qk reaches its maximum value,
, however, things are much simpler, because qk reaches its maximum value,  , only at k = 0, where definitely
, only at k = 0, where definitely 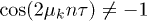 and hence there are no convergence issues in the expansion of the
and hence there are no convergence issues in the expansion of the ![$\log[1+q_k \cos(2\mu_{k}n\tau)]$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn127.gif) . By expanding
. By expanding ![$\log[1+q_k \cos(2\mu_{k}n\tau)]$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn128.gif) , one can show that there are
, one can show that there are 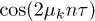 -related terms that survive when
-related terms that survive when 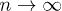 , originating from all even power terms of the expansion, for the simple reason that
, originating from all even power terms of the expansion, for the simple reason that 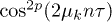 (with p integer) does not average to zero even if n is very large and the oscillations are very fast. For
(with p integer) does not average to zero even if n is very large and the oscillations are very fast. For 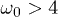 we can derive the following closed analytical expression for
we can derive the following closed analytical expression for 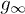 which, quite amusingly, fits our numerical data perfectly well even for
which, quite amusingly, fits our numerical data perfectly well even for 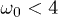 :
:
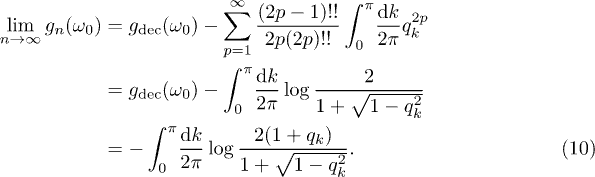
Observe that, for large 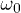 , neither the qk nor the Floquet states on which they depend show a dependence on
, neither the qk nor the Floquet states on which they depend show a dependence on 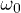 . This is a sign of the fast driving regime: when the driving is fast, the system is not able to follow the oscillations of the field and "sees" the average Hamiltonian. This leads to the high-frequency plateau visible in fig. 1.
. This is a sign of the fast driving regime: when the driving is fast, the system is not able to follow the oscillations of the field and "sees" the average Hamiltonian. This leads to the high-frequency plateau visible in fig. 1.
Even in the regime  , the overall structure of
, the overall structure of 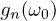 for small/intermediate n is perfectly predicted by the analytical expression in eq. (10). In the small-
for small/intermediate n is perfectly predicted by the analytical expression in eq. (10). In the small-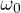 regime, there are peaks of
regime, there are peaks of 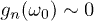 (small but finite negative values, really) at all the frequencies for which
(small but finite negative values, really) at all the frequencies for which 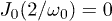 . This result can be understood by looking at the modes close to the critical one at k = 0, for which
. This result can be understood by looking at the modes close to the critical one at k = 0, for which 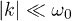 . Investigating the reduced two-level Hamiltonian in this limit (with a bias energy between the two states, appearing in the diagonal terms of the reduced Hamiltonian,
. Investigating the reduced two-level Hamiltonian in this limit (with a bias energy between the two states, appearing in the diagonal terms of the reduced Hamiltonian, 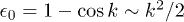 for
for 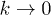 , and the off-diagonal term
, and the off-diagonal term 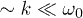 ), and assuming that the system is initially (at t = 0) in the state
), and assuming that the system is initially (at t = 0) in the state 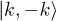 , the squared amplitude of the state
, the squared amplitude of the state 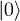 at time t can be shown to be given by
at time t can be shown to be given by ![$\sin^2[tkJ_0(\frac{2}{\omega_0})]$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn148.gif) (see eq. (7) of ref. [38]). Therefore, a coherent destruction of tunneling [36,37] occurs for those values of
(see eq. (7) of ref. [38]). Therefore, a coherent destruction of tunneling [36,37] occurs for those values of 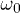 for which
for which 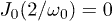 : the system sticks to its initial state, resulting in the peaks shown in fig. 2. The regime
: the system sticks to its initial state, resulting in the peaks shown in fig. 2. The regime 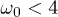 also shows clear dips occurring for
also shows clear dips occurring for 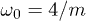 with
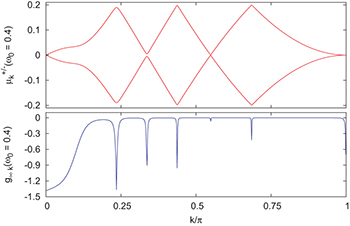
with 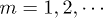 , due to quasi-degeneracies in the Floquet spectrum [29]. As shown in fig. 3, the integrand of
, due to quasi-degeneracies in the Floquet spectrum [29]. As shown in fig. 3, the integrand of 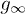 , for instance, when analyzed vs. k, shows clear negative sharp features at all k-points where the Floquet quasi-energies
, for instance, when analyzed vs. k, shows clear negative sharp features at all k-points where the Floquet quasi-energies 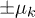 become quasi-degenerate, either at 0 or at
become quasi-degenerate, either at 0 or at 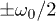 : these negative sharp features, in particular their crossing of the
: these negative sharp features, in particular their crossing of the 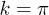 boundary at certain frequencies, are in the end responsible for the sharp dips observed in
boundary at certain frequencies, are in the end responsible for the sharp dips observed in 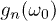 .
.
Fig. 3: (Colour on-line) The integrand of 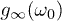 in eq. (10) (lower panel) vs. k for
in eq. (10) (lower panel) vs. k for 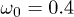 , together with the Floquet quasi-energies
, together with the Floquet quasi-energies 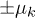 (upper panel). The sharp negative features produce dips in
(upper panel). The sharp negative features produce dips in 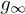 (and gn, not shown) at
(and gn, not shown) at 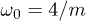 with
with 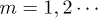 (here m = 10), when a resonance at
(here m = 10), when a resonance at 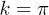 is about to enter/leave the
is about to enter/leave the ![$k\in[0,\pi]$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn166.gif) integration region.
integration region.
Download figure:
Standard imageA crucial question is how much of this phenomenology depends on the one-dimensional nature of our system, and on the fact that the present model is integrable. It is difficult to firmly assess the role of integrability, since non-integrable systems are very difficult to tackle: as argued in ref. [29], we believe, however, that the crucial ingredient is —rather than integrability— an absolutely continuous Floquet spectrum. Concerning the issue of dimensionality, it is simple to provide examples in higher dimensions where the same results can be found. Consider, for instance, a two-dimensional massive Dirac Hamiltonian ![$\hat{H}_D = \int \! \text{d}\textbf{x} \; \widehat{\Psi}^{\dagger}(\textbf{x}) [ m \hat{\sigma}_z -i\hbar v_F (\hat{\sigma}_x \partial_x + \hat{\sigma}_y \partial_y ) ] \widehat{\Psi}(\textbf{x})$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn174.gif) , where
, where 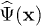 is a two-component spinor field operator describing, for instance, the effective low-energy degrees of freedom for electrons on a graphene lattice with unequal sublattice potentials around a single Dirac point with Fermi velocity vF [39]. Variations of this model are ubiquitous in the field of topological insulators [40,41]. The model has also been considered in the context of the ground-state fidelity and Loschmidt echo in ref. [42]. It shows a quantum phase transition when the mass m is tuned to zero. In momentum space, the Hamiltonian can be written as
is a two-component spinor field operator describing, for instance, the effective low-energy degrees of freedom for electrons on a graphene lattice with unequal sublattice potentials around a single Dirac point with Fermi velocity vF [39]. Variations of this model are ubiquitous in the field of topological insulators [40,41]. The model has also been considered in the context of the ground-state fidelity and Loschmidt echo in ref. [42]. It shows a quantum phase transition when the mass m is tuned to zero. In momentum space, the Hamiltonian can be written as
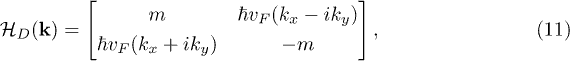
with a momentum cutoff of 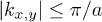 . Suppose the mass m is periodically driven across the QCP,
. Suppose the mass m is periodically driven across the QCP, 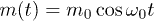 . The dynamical fidelity
. The dynamical fidelity 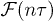 can then be calculated by factorizing the state in terms of two-component spinor wave functions
can then be calculated by factorizing the state in terms of two-component spinor wave functions 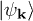 for each momentum, obtaining a result entirely similar to eq. (8), i.e.
for each momentum, obtaining a result entirely similar to eq. (8), i.e.
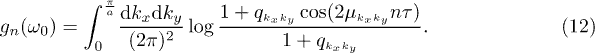
From this relationship, following an identical line of arguments, one can show that gn indeed saturates, in the limit 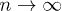 , to the analog of the analytic formula
, to the analog of the analytic formula 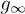 in eq. (10). An instance of this convergence is presented in fig. 4, where we show gn vs. n evaluated numerically for the Dirac model in eq. (11) when
in eq. (10). An instance of this convergence is presented in fig. 4, where we show gn vs. n evaluated numerically for the Dirac model in eq. (11) when 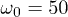 . We see that gn indeed saturates to a steady-state value
. We see that gn indeed saturates to a steady-state value 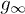 which is definitely below the value of
which is definitely below the value of 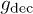 obtained from the decohered density matrix. This picture holds true for all the frequencies we have checked, showing that also in this 2-dimensional case the asymptotic dynamical fidelity retains phase information which is lost in the thermodynamical observables.
obtained from the decohered density matrix. This picture holds true for all the frequencies we have checked, showing that also in this 2-dimensional case the asymptotic dynamical fidelity retains phase information which is lost in the thermodynamical observables.
In conclusion, we have studied the dynamical fidelity 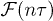 of a quantum Ising chain following an n-period sinusoidal driving of the transverse field across the QCP. We addressed the question of whether
of a quantum Ising chain following an n-period sinusoidal driving of the transverse field across the QCP. We addressed the question of whether ![$g_n=[\log{\mathcal F(n\tau)}]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn186.gif) saturates to a well-defined limit for large n, when the system reaches a periodic steady state as manifested in extensive thermodynamic quantities [29]. The answer is not really obvious: the presence of the logarithm in the expression of gn forbids a direct application of the Riemann-Lebesgue lemma and complicates the situation. Our results confirm that indeed gn saturates to a steady value, and we were able to derive an exact expression for
saturates to a well-defined limit for large n, when the system reaches a periodic steady state as manifested in extensive thermodynamic quantities [29]. The answer is not really obvious: the presence of the logarithm in the expression of gn forbids a direct application of the Riemann-Lebesgue lemma and complicates the situation. Our results confirm that indeed gn saturates to a steady value, and we were able to derive an exact expression for 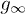 which appears to work perfectly well for all values of
which appears to work perfectly well for all values of 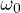 , yielding very detailed information on the exact position of peaks and dips of gn even at intermediate values of n. However, the surprising result of our analysis is that
, yielding very detailed information on the exact position of peaks and dips of gn even at intermediate values of n. However, the surprising result of our analysis is that  cannot be derived from the fully decohered mixed-state density matrix,
cannot be derived from the fully decohered mixed-state density matrix, 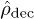 , where all phase information contained in the off-diagonal matrix elements is "effectively" lost, as instead possible for the thermodynamic quantities. Indeed, we have shown that gn (and
, where all phase information contained in the off-diagonal matrix elements is "effectively" lost, as instead possible for the thermodynamic quantities. Indeed, we have shown that gn (and 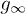 ) is always strictly smaller than the result derived from
) is always strictly smaller than the result derived from 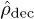 . In the high-frequency region
. In the high-frequency region 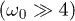 , we find that
, we find that 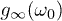 saturates to a finite negative value independent of
saturates to a finite negative value independent of 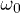 showing that the system is unable to follow the oscillations of a too fast driving. With the example of a Dirac Hamiltonian in two dimensions, we have also shown that our main results are not limited to one-dimensional models.
showing that the system is unable to follow the oscillations of a too fast driving. With the example of a Dirac Hamiltonian in two dimensions, we have also shown that our main results are not limited to one-dimensional models.
Fig. 4: (Colour on-line) ![$g_n=[\log{\mathcal F (n\tau)}]/L$](https://content.cld.iop.org/journals/0295-5075/106/6/67003/revision1/epl16328ieqn167.gif) , the logarithm of the fidelity per site, for a two-dimensional massive Dirac Hamiltonian (11) with a periodic mass driving
, the logarithm of the fidelity per site, for a two-dimensional massive Dirac Hamiltonian (11) with a periodic mass driving 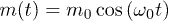 vs. n, for frequency
vs. n, for frequency 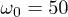 . The numerical calculation has been performed by discetizing the Brillouin zone momenta as
. The numerical calculation has been performed by discetizing the Brillouin zone momenta as 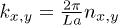 with L = 1000 and
with L = 1000 and 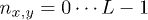 . Observe that gn quickly saturates to the analytical limit
. Observe that gn quickly saturates to the analytical limit 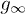 for n → ∞, well below the value
for n → ∞, well below the value 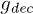 obtained by using the decohered density matrix.
obtained by using the decohered density matrix.
Download figure:
Standard imageAcknowledgments
We acknowledge discussions with A. Silva, R. Fazio, M. Fabrizio, P. Smacchia, and E. Tosatti. Research at SISSA was supported by MIUR, through PRIN-20087NX9Y7, by SNSF, through SINERGIA Project CRSII2 136287 1, by the EU-Japan Project LEMSUPER, and by the EU FP7 under grant agreement No. 280555. AD and SS acknowledge Abdus Salam ICTP, Trieste, where the initial part of the work was done. SS acknowledges CSIR, New Delhi, for financial assistance.