Abstract
Anticorrelation is observed when laser and pseudothermal light beams are incident to the two input ports of a Hong-Ou-Mandel interferometer, respectively. The spatial second-order interference pattern of laser and pseudothermal light beams is reported. A temporal Hong-Ou-Mandel dip is observed when these two detectors are in symmetrical positions. The experimental results can be interpreted by the two-photon interference theory.
Export citation and abstract BibTeX RIS
Introduction
Ever since the second-order interference of light was first observed by Hanbury Brown and Twiss (HBT) in 1956 [1], it has been an important tool to study the properties of light [2]. The second-order interference of light has been studied with photons emitted by different kinds of sources, such as entangled photon pair sources [3], two independent single-photon sources [4–6], laser and single-photon sources [7], laser and quantum down-converted lights [8], two lasers [9–11], two thermal sources [12–17], etc. Many interesting results were obtained from those studies. For instance, Hong et al. were able to measure the time separation between two photons with time resolution millions of times shorter than the resolution of the detector and the electronics [3,18]. Bennett et al. observed a Hong-Ou-Mandel (HOM) dip by feeding photons emitted by a single-photon source and laser light into the two input ports of a HOM interferometer, respectively [7]. The second-order interference of photons coming from laser and thermal light beams seems to have not been studied, in which anticorrelation can be observed, too. In this paper, we will experimentally study the second-order interference of laser and pseudothermal light beams in a HOM interferometer, where anticorrelation and temporal HOM dip are observed when these two detectors are in symmetrical positions.
Two-photon anticorrelation is defined as the two-photon coincidence count probability is less than the accidental two-photon coincidence count probability, which is equal to the product of these two single-photon probabilities [19]. It is convenient to employ the normalized second-order coherence function or the degree of second-order coherence [20],
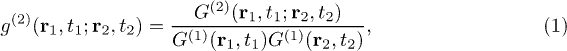
to discuss the second-order correlation of light. Where 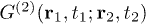 is the second-order coherence function at space-time coordinates
is the second-order coherence function at space-time coordinates 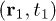 and
and 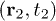 .
.  and
and 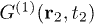 are the first-order coherence functions at
are the first-order coherence functions at 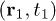 and
and 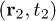 , respectively [21]. When
, respectively [21]. When 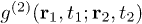 is greater than 1, the photon detection events at
is greater than 1, the photon detection events at 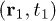 and
and 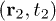 are correlated. When
are correlated. When 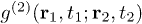 is equal to 1, these events are independent. When
is equal to 1, these events are independent. When 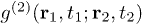 is less than 1, these events are anticorrelated. In our experiments, we are able to observe anticorrelation when these two photon detection events are at the same space-time coordinate in a HOM interferometer, which can be expressed as
is less than 1, these events are anticorrelated. In our experiments, we are able to observe anticorrelation when these two photon detection events are at the same space-time coordinate in a HOM interferometer, which can be expressed as 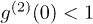 [20].
[20].
The remaining part of this paper is organized as follows. The experiments are introduced in the next section and the theoretical explanation of the experimental results is given in the third section. In the fourth section, we will discuss why anticorrelation is observed in our experiments and how to employ two-photon interference theory to interpret other similar second-order interference experiments. The last section summarizes our conclusions.
Experiments
The experimental setup is shown in fig. 1. A single-mode continuous wave laser with central wavelength at 780 nm and frequency bandwidth of 200 kHz is divided into two equal portions by a nonpolarized beam splitter (BS1). One beam is incident to a rotating ground glass (RG) after passing through a convex lens (L1) to simulate thermal light [12]. The other beam is expanded by another identical lens (L2) to ensure that the intensity of the laser beam is approximately constant across the measurement range. The focus lengths of L1 and L2 are both 50 mm. The distance between L1 and RG is 83 mm. The distances between the lens and detector planes all equal 825 mm. Two single-mode fibers are coupled to D1 and D2 (PerkinElmer, SPCM-AQRH-14-FC) to collect light, respectively. The two-photon coincidence counts are measured by a two-photon coincidence counting system (Becker & Hickl GmbH, SPC630), which is not shown in the figure.
Fig. 1: (Colour on-line) Experimental setup for the second-order interference of laser and pseudothermal light beams in a HOM interferometer. Laser: single-mode continuous wave laser. BS: 50: 50 nonpolarized beam splitter. M: mirror. L: lens. RG: rotating ground glass. D: detector coupled with a single-mode fiber.
Download figure:
Standard imageThe measured normalized second-order coherence functions of laser and pseudothermal light beams in a HOM interferometer are shown by the hollow squares in fig. 2(b), where there is a periodic modulation. 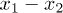 is the transverse relative position of these two detectors and
is the transverse relative position of these two detectors and 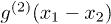 is the normalized second-order coherence function when these two detectors are at x1 and x2, respectively. The red line is the theoretical fitting of the experimental results by employing eq. (4). All the experimental results in fig. 2 are measured by scanning the transverse position of D1 while keeping the position of D2 fixed. The measurement time for each dot is 120 s. The temporal second-order coherence length of the pseudothermal light is
is the normalized second-order coherence function when these two detectors are at x1 and x2, respectively. The red line is the theoretical fitting of the experimental results by employing eq. (4). All the experimental results in fig. 2 are measured by scanning the transverse position of D1 while keeping the position of D2 fixed. The measurement time for each dot is 120 s. The temporal second-order coherence length of the pseudothermal light is 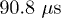 and the two-photon coincidence time window is 12.2 ns. The core diameter of the collecting single-mode fiber is
and the two-photon coincidence time window is 12.2 ns. The core diameter of the collecting single-mode fiber is 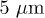 , which is much less than the pseudothermal light spatial second-order coherence length, 1.37 mm. The intensities of the laser and pseudothermal light beams at the two input ports of the HOM interferometer are set to be equal. Anticorrelation is observed in fig. 2(b) when these two photon detection events are at the same space-time coordinate.
, which is much less than the pseudothermal light spatial second-order coherence length, 1.37 mm. The intensities of the laser and pseudothermal light beams at the two input ports of the HOM interferometer are set to be equal. Anticorrelation is observed in fig. 2(b) when these two photon detection events are at the same space-time coordinate.
Fig. 2: (Colour on-line) Spatial second-order interference pattern of laser and pseudothermal light beams. 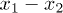 is the transverse relative position of these two detectors and
is the transverse relative position of these two detectors and  is the normalized second-order coherence function when these two detectors are at x1 and x2, respectively. The red circles and black squares in (a) are the measured normalized second-order coherence functions of pseudothermal and laser light beams in a HBT interferometer, respectively. The empty squares in (b) represent the measured normalized second-order coherence function of laser and pseudothermal light beams with equal intensities in a HOM interferometer. See text for details.
is the normalized second-order coherence function when these two detectors are at x1 and x2, respectively. The red circles and black squares in (a) are the measured normalized second-order coherence functions of pseudothermal and laser light beams in a HBT interferometer, respectively. The empty squares in (b) represent the measured normalized second-order coherence function of laser and pseudothermal light beams with equal intensities in a HOM interferometer. See text for details.
Download figure:
Standard imageIn order to confirm that anticorrelation is observed when these two detectors are in symmetrical positions 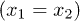 , we have measured the spatial second-order coherence function of pseudothermal light by blocking the laser light in our experiments. It is well known that the second-order coherence function of thermal light in a HBT interferometer will get its maximum when these two detectors are in symmetrical positions [1]. Comparing the second-order coherence function in fig. 2(b) with the one of pseudothermal light in fig. 2(a), which is shown by the black line, two-photon anticorrelation in fig. 2(b) is observed when these two detectors are in symmetrical positions. We also measure the spatial second-order coherence function of laser light in a HBT interferometer, which is shown by the black squares in fig. 2(a). The measurements confirm that the photon detection events of single-mode continuous wave laser in a HBT interferometer are independent [21].
, we have measured the spatial second-order coherence function of pseudothermal light by blocking the laser light in our experiments. It is well known that the second-order coherence function of thermal light in a HBT interferometer will get its maximum when these two detectors are in symmetrical positions [1]. Comparing the second-order coherence function in fig. 2(b) with the one of pseudothermal light in fig. 2(a), which is shown by the black line, two-photon anticorrelation in fig. 2(b) is observed when these two detectors are in symmetrical positions. We also measure the spatial second-order coherence function of laser light in a HBT interferometer, which is shown by the black squares in fig. 2(a). The measurements confirm that the photon detection events of single-mode continuous wave laser in a HBT interferometer are independent [21].
In order to study how 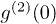 changes with the ratio between the intensities of thermal and total light beams, we also measure
changes with the ratio between the intensities of thermal and total light beams, we also measure 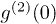 when the laser and pseudothermal light beams have different intensities. The experimental parameters are the same as the ones above except that the temporal second-order coherence length is shortened to be 86.2 ns by putting a ground glass before the rotating ground glass to enlarge the size of the input light beam on the rotating ground glass. The results are shown in fig. 3, where Pt is the ratio between the intensities of thermal and total light beams. The red curve is the theoretical fitting of the experimental results by employing eq. (5), where only the last constant is changeable in the fitting process. The value of the measured
when the laser and pseudothermal light beams have different intensities. The experimental parameters are the same as the ones above except that the temporal second-order coherence length is shortened to be 86.2 ns by putting a ground glass before the rotating ground glass to enlarge the size of the input light beam on the rotating ground glass. The results are shown in fig. 3, where Pt is the ratio between the intensities of thermal and total light beams. The red curve is the theoretical fitting of the experimental results by employing eq. (5), where only the last constant is changeable in the fitting process. The value of the measured 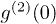 changes between 0.74 and 1.99 as the ratio changes, which means that these photon detection events can be correlated, independent or anticorrelated in different situations.
changes between 0.74 and 1.99 as the ratio changes, which means that these photon detection events can be correlated, independent or anticorrelated in different situations.
Fig. 3: (Colour on-line) Anticorrelation. 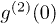 is the normalized second-order coherence function when these two single-photon detection events are at the same space-time coordinate in a HOM interferometer. Pt is the ratio between the intensities of the thermal and total light beams. The red line is the theoretical curve of
is the normalized second-order coherence function when these two single-photon detection events are at the same space-time coordinate in a HOM interferometer. Pt is the ratio between the intensities of the thermal and total light beams. The red line is the theoretical curve of 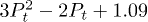 . See text for details.
. See text for details.
Download figure:
Standard imageFigure 4 shows that the two-photon coincidence counts vary with the time difference of these two photon detection events when 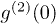 gets its minimum in fig. 3. CC is the two-photon coincidence count for 270 s and
gets its minimum in fig. 3. CC is the two-photon coincidence count for 270 s and 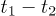 is the time difference between these two single-photon detection events within a two-photon coincidence count. The two-photon coincidence count gets its minimum when t1 equals t2. As the value of
is the time difference between these two single-photon detection events within a two-photon coincidence count. The two-photon coincidence count gets its minimum when t1 equals t2. As the value of 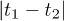 increases, the coincidence count increases and finally becomes a constant when the time difference exceeds the second-order temporal coherence length of pseudothermal light.
increases, the coincidence count increases and finally becomes a constant when the time difference exceeds the second-order temporal coherence length of pseudothermal light.
Fig. 4: (Colour on-line) Temporal HOM dip. CC is the two-photon coincidence count for 270 s and 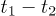 is the time difference between these two photon detection events within a two-photon coincidence count. When t1 equals t2, CC gets its minimum. As the time difference increases, CC increases and finally becomes a constant.
is the time difference between these two photon detection events within a two-photon coincidence count. When t1 equals t2, CC gets its minimum. As the time difference increases, CC increases and finally becomes a constant.
Download figure:
Standard imageTheoretical explanations
Both classical and quantum theories can be employed to interpret our experimental results [21,22]. We will employ the two-photon interference theory to interpret our experiments, for light is intrinsically quantum mechanical and the quantum theory is valid for both classical and nonclassical light [23]. If the same method is employed to interpret the same experiment with classical and nonclassical light, one may obtain a unified interpretation, which might be helpful to understand the physics behind.
There are three different ways for two photons to trigger a two-photon coincidence count in fig. 1. The first way is when both photons come from pseudothermal light. The second way is when both photons come from laser light. The last way is when a photon comes from pseudothermal light and the other photon comes from laser light. The second-order coherence function in fig. 1 can be expressed as [24]
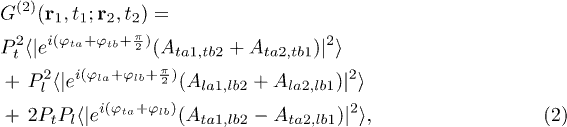
where Pt and Pl (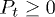 ,
, 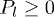 , and
, and 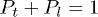 ) are the probabilities of the detected photon coming from pseudothermal and laser light beams, respectively. It is worth noting that Pt also equals the ratio between the intensities of pseudothermal and total light beams in our experiments.
) are the probabilities of the detected photon coming from pseudothermal and laser light beams, respectively. It is worth noting that Pt also equals the ratio between the intensities of pseudothermal and total light beams in our experiments. 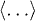 means ensemble average.
means ensemble average.  and
and 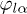 are the initial phase of photon α (
are the initial phase of photon α ( , and b) coming from pseudothermal and laser light beams, respectively. Ata1,lb2 is the two-photon probability amplitude that photon a coming from thermal light travels to detector 1 and photon b coming from laser light travels to detector 2, which is equal to the product of two single-photon probability amplitudes [24].
, and b) coming from pseudothermal and laser light beams, respectively. Ata1,lb2 is the two-photon probability amplitude that photon a coming from thermal light travels to detector 1 and photon b coming from laser light travels to detector 2, which is equal to the product of two single-photon probability amplitudes [24]. 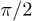 is the phase difference of one photon reflected by a beam splitter comparing to the transmitted one [20]. The minus sign in the last term of eq. (2) is due to the π phase difference between these two different two-photon probability amplitudes, which is the same as for entangled photon pairs in a HOM interferometer [3,18]. The destructive two-photon interference, at least from the quantum-mechanical point of view, is the reason why there is anticorrelation in a HOM interferometer.
is the phase difference of one photon reflected by a beam splitter comparing to the transmitted one [20]. The minus sign in the last term of eq. (2) is due to the π phase difference between these two different two-photon probability amplitudes, which is the same as for entangled photon pairs in a HOM interferometer [3,18]. The destructive two-photon interference, at least from the quantum-mechanical point of view, is the reason why there is anticorrelation in a HOM interferometer.
With similar calculations as those in refs. [17,25,26], it is straightforward to calculate the normalized spatial second-order coherence function as
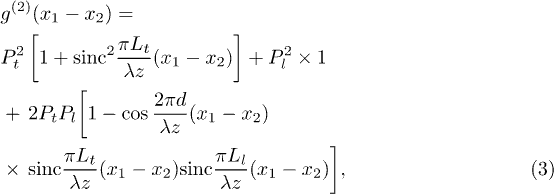
where the temporal part has been ignored and the one-dimension case is considered for simplicity. Lt is the diameter of the pseudothermal light source and Ll is the diameter of the laser light in the same plane as the pseudothermal light source. λ is the central wavelength of the laser. z is the distance between the source and the detector planes. d is the transverse distance between the midpoints of the pseudothermal light source and the image of the laser light source in the ground glass plane by BS2. The first term on the right-hand side of eq. (3) corresponds to two photons both coming from pseudothermal light. Pt2 is the probability and the left part of this term is a typical second-order spatial coherence function of thermal light. The second term corresponds to both photons coming from laser light. It is expressed like this since 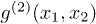 always equals 1 for single-mode continuous wave laser in a HBT interferometer. The third term corresponds to one photon which comes from laser light and to the other one that comes from pseudothermal light. There is a cosine modulation of the second-order coherence function, which is a result of the second-order interference between laser and pseudothermal light.
always equals 1 for single-mode continuous wave laser in a HBT interferometer. The third term corresponds to one photon which comes from laser light and to the other one that comes from pseudothermal light. There is a cosine modulation of the second-order coherence function, which is a result of the second-order interference between laser and pseudothermal light.
Lt equals Ll in our experiments, for the distances between the lens and detection planes are all the same. When the intensities of these two beams are equal, eq. (3) can be simplified as
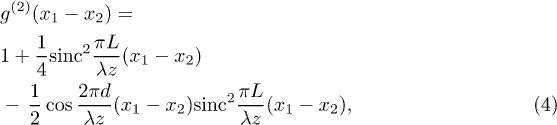
where L equals Lt and Ll, respectively. 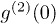 equals 0.75 in eq. (4), which is less than 1. It is worth emphasizing that no observable first-order interference pattern exists in the single-detector counting rate of either D1 or D2. The relative phases between the laser light field and the scattered sub-fields are randomly distributed in the detection planes since the rotating ground glass introduces random phases to each scattered sub-field. The laser and the pseudothermal light beams are first-order incoherent [27].
equals 0.75 in eq. (4), which is less than 1. It is worth emphasizing that no observable first-order interference pattern exists in the single-detector counting rate of either D1 or D2. The relative phases between the laser light field and the scattered sub-fields are randomly distributed in the detection planes since the rotating ground glass introduces random phases to each scattered sub-field. The laser and the pseudothermal light beams are first-order incoherent [27].
We can further calculate how  changes with the ratio between the intensities of pseudothermal and total light beams. Substituting
changes with the ratio between the intensities of pseudothermal and total light beams. Substituting  and
and 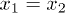 into eq. (3), it is straightforward to have
into eq. (3), it is straightforward to have

When Pt equals 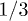 ,
, 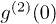 gets its minimum,
gets its minimum, 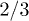 , which is less than 1.
, which is less than 1.
Discussions
It is interesting to find that the spatial second-order interference pattern of laser and pseudothermal light beams in fig. 2(b) is similar to the one of two pseudothermal light beams in a HOM interferometer in ref. [17]. Both the second-order coherence functions get their minimums when these two detectors are in symmetrical positions, respectively. However, there is an important difference between these two experiments. It is predicted [28] and experimentally verified [17,29] that 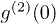 equals 1 for two thermal light beams in a HOM interferometer. This conclusion is true no matter what the ratio between the intensities of these two input thermal light beams is, while in the case of laser and pseudothermal light in a HOM interferometer,
equals 1 for two thermal light beams in a HOM interferometer. This conclusion is true no matter what the ratio between the intensities of these two input thermal light beams is, while in the case of laser and pseudothermal light in a HOM interferometer, 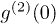 can get the value in the domain of [2/3, 2). Based on eq. (5),
can get the value in the domain of [2/3, 2). Based on eq. (5), 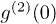 is less than 1 and the photon detection events are anticorrelated when Pt is in the region of (0, 2/3). When Pt equals 2/3,
is less than 1 and the photon detection events are anticorrelated when Pt is in the region of (0, 2/3). When Pt equals 2/3, 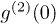 equals 1 and these events are independent. When Pt is in the region of (2/3, 1),
equals 1 and these events are independent. When Pt is in the region of (2/3, 1), 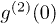 is greater than 1 and these events are correlated. The reasons why the observed results are different for these two similar experiments are as follows. Based on the calculations above, anticorrelation can be interpreted as resulting from two-photon destructive interference, which is shown by the last term of eq. (2). Anticorrelation exists in both the experiments with laser and pseudothermal light and the experiments with pseudothermal and pseudothermal light [17]. However, anticorrelation is only part of the measured second-order coherence functions in both cases. The other terms are accounting for the reasons why anticorrelation is observed in the former experiments, while anticorrelation cannot be not observed in the latter experiments.
is greater than 1 and these events are correlated. The reasons why the observed results are different for these two similar experiments are as follows. Based on the calculations above, anticorrelation can be interpreted as resulting from two-photon destructive interference, which is shown by the last term of eq. (2). Anticorrelation exists in both the experiments with laser and pseudothermal light and the experiments with pseudothermal and pseudothermal light [17]. However, anticorrelation is only part of the measured second-order coherence functions in both cases. The other terms are accounting for the reasons why anticorrelation is observed in the former experiments, while anticorrelation cannot be not observed in the latter experiments. 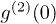 's equal 1 and 2 for laser and thermal light in the HBT interferometer, respectively. In the laser and pseudothermal light case, the contribution of correlation can be less than the contribution of anticorrelation, thus
's equal 1 and 2 for laser and thermal light in the HBT interferometer, respectively. In the laser and pseudothermal light case, the contribution of correlation can be less than the contribution of anticorrelation, thus 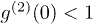 can be observed. While in the case of pseudothermal and pseudothermal light, the correlation contribution has the same magnitude as the anticorrelation contribution, no matter what the ratio between the intensities of these two light beams is [17]. The final observed result is always
can be observed. While in the case of pseudothermal and pseudothermal light, the correlation contribution has the same magnitude as the anticorrelation contribution, no matter what the ratio between the intensities of these two light beams is [17]. The final observed result is always 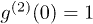 .
.
The same theory can be employed to interpret the HOM dip with entangled photon pairs [3]. If one entangled photon pair is incident to a HOM interferometer, there is only one photon at each input port of the interferometer [18]. Only the last term of eq. (2) will contribute to the measured second-order coherence function. Hence the visibility of the HOM dip with entangled photon pairs can be as high as 100%. However, it is usually impossible to ensure that there is only one entangled photon pair in the interferometer at one time in experiments. The measured visibility will be less than 100%. In the case of classical light in a HOM interferomter, it is impossible to make sure that there is only one photon at each input port in linear optics, such as the one in our experiments. All the terms in eq. (2) will contribute and the visibility of the HOM dip with classical light cannot exceed 50% [30]. However, if a special two-photon coincidence counting system is employed, it is possible that only the last term of eq. (2) contributes even in the case of classical light. For instance, Kaltenbaek et al. observed a high-visibility 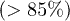 HOM dip with chirped pulses as the input. Their two-photon coincidence counting system is based on sum-frequency generation. Combining the properties of chirped pulse and sum-frequency generation, two photons coming from the same pulse will not trigger a two-photon coincidence count in their experiments. Only one photon from each pulse will trigger a two-photon coincidence count in the sum-frequency generation system. Hence, only the last term of eq. (2) contributes in their experiments and, of course, the visibility of their HOM dip can exceed 50%.
HOM dip with chirped pulses as the input. Their two-photon coincidence counting system is based on sum-frequency generation. Combining the properties of chirped pulse and sum-frequency generation, two photons coming from the same pulse will not trigger a two-photon coincidence count in their experiments. Only one photon from each pulse will trigger a two-photon coincidence count in the sum-frequency generation system. Hence, only the last term of eq. (2) contributes in their experiments and, of course, the visibility of their HOM dip can exceed 50%.
There is one more thing we would like to point out. Although we have observed 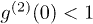 and
and 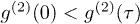 (
(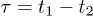 and
and 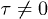 ) in our experiments, this does not mean that we have observed sub-Possion distribution or photon antibunching. Sub-Possion distribution and photon antibunching are defined as
) in our experiments, this does not mean that we have observed sub-Possion distribution or photon antibunching. Sub-Possion distribution and photon antibunching are defined as 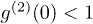 and
and 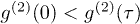 in the HBT interferometer, respectively [20]. These two effects can only be observed with nonclassical light.
in the HBT interferometer, respectively [20]. These two effects can only be observed with nonclassical light.  and
and 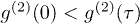 observed in our experiments are in the HOM interferometer. These two interferometers are different. Therefore, the experimental results in our experiments do not satisfy the definition of sub-Possion distribution or photon antibunching.
observed in our experiments are in the HOM interferometer. These two interferometers are different. Therefore, the experimental results in our experiments do not satisfy the definition of sub-Possion distribution or photon antibunching.
Conclusions
In conclusion, we have observed the spatial second-order interference pattern of laser and pseudothermal light beams in a HOM interferometer, in which, anticorrelation is observed when these two detectors are in symmetrical positions. Furthermore, a temporal HOM dip is also observed when these two detectors are in the symmetrical positions. The theoretical interpretations based on the two-photon interference theory agree with the experimental results. Anticorrelation with laser and pseudothermal light in a HOM interferometer can be interpreted by the destructive two-photon interference, which is the same as the interpretation of anticorrelation with entangled photon pairs in a HOM interferometer.
Acknowledgments
This project is supported by Doctoral Fund of Ministry of Education of China (No. 20130201120013), the 111 Project of China (No. B14040), International Science & Technology Cooperation Program of China (No. 2010DFR50480), and the Fundamental Research Funds for the Central Universities.









