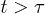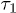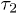Abstract
Inspired by recent bacterial chromosome experiments in narrow channels, we simulate the expansion (and internal) dynamics of a self-avoiding polymer under cylindrical confinement. The chain is trapped in a piston, compressed up to 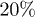 of its equilibrium length, and released unidirectionally from the right end of the piston. Our results suggest that the chain initially expands like a concentrated hard-sphere system, enters a subdiffusive regime at an intermediate time, and eventually relaxes globally to its equilibrium size. Using our results, we test a few theoretical models (e.g., a Flory-type approach), in which the blob-blob or monomer-monomer interaction determines "expansion forces," clarifying their applicability. Our results can be used for exploring further the polymer aspect of bacterial chromosomes.
of its equilibrium length, and released unidirectionally from the right end of the piston. Our results suggest that the chain initially expands like a concentrated hard-sphere system, enters a subdiffusive regime at an intermediate time, and eventually relaxes globally to its equilibrium size. Using our results, we test a few theoretical models (e.g., a Flory-type approach), in which the blob-blob or monomer-monomer interaction determines "expansion forces," clarifying their applicability. Our results can be used for exploring further the polymer aspect of bacterial chromosomes.
Export citation and abstract BibTeX RIS
Introduction
There has been growing interest in understanding single chain molecules (e.g., bacterial chromosomes) in confined or cell-like spaces [1–6]. At the heart of much progress with single molecules is the technical advance for manipulating and visualizing them [1–6]. This enables us to probe quantitatively their static and dynamical properties, which might otherwise remain suspect. For instance, by observing the free expansion of initially compressed chains in a cylindrical pore, one can measure chain relaxation times and effective spring constants [5,6]. In a biological context, such an effort has been useful for clarifying the role of cross-linking proteins in determining the elasticity and spatial organization of bacterial chromosomes as well as for identifying molecular forces required for chain compaction in the cell [5].
Coarse-grained polymer models have often been entertained in the literature as fitting models for chain-expansion or force-compression data [5–7]. In particular, a "renormalized Flory approach", originally proposed for confined polymers with self-avoidance [7–9], has been used to interpret bacterial chromosome experiments [5]. While it is expected to capture correctly the global or long-time behavior of confined molecules, its applicability especially outside the long-time range remains to be tested more systematically. On the other hand, an earlier study suggests that as the chain continues to be compressed, it enters a few distinct scaling regimes: the linearly ordered, semidilute, and concentrated regimes [7]. How this equilibrium picture fits into chain expansion dynamics is unclear and merits consideration. Furthermore, polymer dynamics often reflects the interplay between internal modes, which relax at different rates [10,11]. It will be useful to clarify its significance in the expansion and internal dynamics of a confined chain (see ref. [12] and references therein for its nontrivial effect on looping dynamics). To what extent will the bacterial chromosome in a narrow channel behave as a confined polymer? A better understanding of the latter system is desirable to further explore the polymer aspect of the chromosome beyond what has been observed recently [5].
Using molecular-dynamics (MD) simulations, we study the expansion and internal dynamics of a self-avoiding polymer, consisting of N monomers in a cylindrical pore of diameter D. In the first set of simulations, the chain is capped by a piston and compressed up to 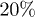 of its equilibrium value. One of the piston wall (the one on the right) is removed suddenly and the chain is then allowed to expand and relax, as illustrated in fig. 1. (This is to mimic the experimental setting for chromosome expansion from lysed cells in a recent work [5]1
.) In the second set of simulations, we let the confined chain relax freely from its uncompressed conformation.
of its equilibrium value. One of the piston wall (the one on the right) is removed suddenly and the chain is then allowed to expand and relax, as illustrated in fig. 1. (This is to mimic the experimental setting for chromosome expansion from lysed cells in a recent work [5]1
.) In the second set of simulations, we let the confined chain relax freely from its uncompressed conformation.
Fig. 1: (a) Equilibrium blob picture of a polymer confined in a cylindrical space: a linear array of blobs of size 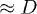 each, as illustrated in green. The farthermost distance or the length of the enveloping tube (the red dashed line) can be chosen as the chain size. Panel (a) is reproduced from [8] by permission of the Royal Society of Chemistry. (b) As the chain is compressed with a piston, it breaks up into smaller blobs of size ξ each (see the top illustration in (b)), resembling a semidilute
each, as illustrated in green. The farthermost distance or the length of the enveloping tube (the red dashed line) can be chosen as the chain size. Panel (a) is reproduced from [8] by permission of the Royal Society of Chemistry. (b) As the chain is compressed with a piston, it breaks up into smaller blobs of size ξ each (see the top illustration in (b)), resembling a semidilute  or concentrated polymer solution
or concentrated polymer solution 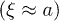 (for the latter, the notion of blobs becomes irrelevant). The chain is then allowed to expand, by removing the piston on the right, similarly to the experimental setting for chromosome expansion [5]. How this equilibrium picture is reflected in chain expansion dynamics is unclear yet.
(for the latter, the notion of blobs becomes irrelevant). The chain is then allowed to expand, by removing the piston on the right, similarly to the experimental setting for chromosome expansion [5]. How this equilibrium picture is reflected in chain expansion dynamics is unclear yet.
Download figure:
Standard imageLet L(t) be the chain size as a function of time t and L0 its equilibrium or relaxed value (i.e., 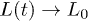 as
as 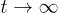 ), as shown in fig. 1(a). Note that L(t) and L0 are not uniquely defined (see ref. [13] and references therein). The end-to-end distance is often used in theoretical considerations (see for instance ref. [7]). A recent study, however, suggests that the unfavorable effect of finite-chain lengths can be corrected by using as L(t) the farthermost distance or the length of an imaginary "enveloping tube" (the red dashed line in fig. 1(a)) [13]. Also this quantity is relevant to ring polymers, e.g., bacterial chromosomes (see ref. [13] for details). This quantity is thus chosen as the chain size.
), as shown in fig. 1(a). Note that L(t) and L0 are not uniquely defined (see ref. [13] and references therein). The end-to-end distance is often used in theoretical considerations (see for instance ref. [7]). A recent study, however, suggests that the unfavorable effect of finite-chain lengths can be corrected by using as L(t) the farthermost distance or the length of an imaginary "enveloping tube" (the red dashed line in fig. 1(a)) [13]. Also this quantity is relevant to ring polymers, e.g., bacterial chromosomes (see ref. [13] for details). This quantity is thus chosen as the chain size.
We find that the chain initially expands like a corresponding hard-sphere system released from a concentrated state ("explosive"), undergoes subdiffusive expansion at the intermediate time range, and eventually enters an exponential-relaxation regime beyond the global relaxation time τ. The emergence of the subdiffusive regime is delayed by the initial explosive expansion. In fig. 1, the onset time for the subdiffusive regime is denoted as 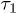 .
.
On the other hand, for the initially compressed case, right-end proximate segments and the center of mass (CM) undergo hard-sphere-like and subdiffusive motion for short time and intermediate time scales, respectively; they eventually enter the diffusive regime at 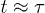 . The dynamics of the left-end segment resembles that of chain segments for the uncompressed case. Our result suggest that chain segments in the initially compressed case enter the subdiffusive and diffusive regimes in a sequential matter: left-end proximate ones first and right-end proximate ones later.
. The dynamics of the left-end segment resembles that of chain segments for the uncompressed case. Our result suggest that chain segments in the initially compressed case enter the subdiffusive and diffusive regimes in a sequential matter: left-end proximate ones first and right-end proximate ones later.
Molecular-dynamics simulations
In our molecular dynamics, we use the "bead-spring model" of a polymer chain: beads, connected by the finitely extensible non-linear elastic (FENE) potential, interact with each other through the fully repulsive Weeks-Chandler-Anderson (WCA) potential [14]. If r be the center-to-center distance between beads, the WCA potential is given by
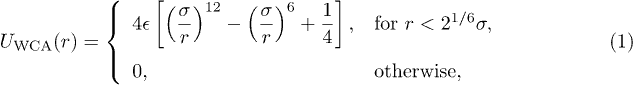
where  and σ represent the strength and range of the WCA potential, respectively. Accordingly, the bead or monomer size
and σ represent the strength and range of the WCA potential, respectively. Accordingly, the bead or monomer size  . On the other hand, the FENE potential is described by [15,16]
. On the other hand, the FENE potential is described by [15,16]

where 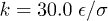 and
and 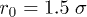 .
.
The confining cylinder is made up of "imaginary" beads of size σ, interacting with beads through WCA potential given in eq. (1).
We simulate the polymer system described above using the simulation package LAMMPS [17]. The equation of motion for beads is integrated using the velocity Verlet algorithm in a discrete time space with a time step 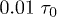 , where
, where  (m is the bead mass). At the same time, the system is kept at a constant temperature
(m is the bead mass). At the same time, the system is kept at a constant temperature 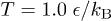 via a Langevin thermostat with a few choices of the damping constant
via a Langevin thermostat with a few choices of the damping constant 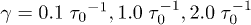 (see refs. [8,9] and references therein). Here and below,
(see refs. [8,9] and references therein). Here and below, 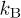 is the Boltzmann constant and T the temperature. On the other hand, in our simulations, we do not include long-range hydrodynamic interactions.
is the Boltzmann constant and T the temperature. On the other hand, in our simulations, we do not include long-range hydrodynamic interactions.
As discussed earlier, we carried out two sets of simulations, depending on whether the chain was initially compressed or not. In both cases, to get reliable chain statistics, we performed 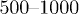 independent simulations over which ensemble averages were obtained. As a result, the error bars are smaller than the thickness of lines or the size of symbols used to represent the results.
independent simulations over which ensemble averages were obtained. As a result, the error bars are smaller than the thickness of lines or the size of symbols used to represent the results.
Theoretical models
According to the blob scaling picture [10,18] (see ref. [13] for a quantitative basis for blobs), a self-avoiding chain trapped in a cylinder of width D is a linear string of blobs of size  each [13], as described in fig. 1(a), where the blobs are illustrated in green. This results in the equilibrium size
each [13], as described in fig. 1(a), where the blobs are illustrated in green. This results in the equilibrium size 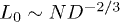 and the effective spring constant
and the effective spring constant  (recall N is the number of monomers) [7,13,18]. In this work, all lengths are measured in units of the monomer size
(recall N is the number of monomers) [7,13,18]. In this work, all lengths are measured in units of the monomer size 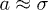 , unless otherwise stated. As the chain is compressed with a piston, it breaks up into smaller blobs (see the top illustration in fig. 1(b)); it enters the semidilute
, unless otherwise stated. As the chain is compressed with a piston, it breaks up into smaller blobs (see the top illustration in fig. 1(b)); it enters the semidilute  and concentrated
and concentrated 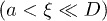 regimes [7]. (Note that these inequalities can be satisfied only for sufficiently large D and N.) The extent to which this feature is reflected in chain dynamics is, however, unclear yet. Nevertheless, it is expected that the initial expansion of a much compressed chain will be dominated by excluded-volume effects; chain connectivity will not play a significant role. As the blobs grow in size while the chain expands, the nature of the expansion force will change, affecting the dynamics. Eventually, the chain enters a (quasi) one-dimensional Rouse regime, in which relaxed blobs behave as subunits of the chain, as illustrated in fig. 1(b)(iii) [13]. The interaction between neighboring blobs will determine chain dynamics. We thus expect subdiffusive and exponentially-relaxing regime to emerge.
regimes [7]. (Note that these inequalities can be satisfied only for sufficiently large D and N.) The extent to which this feature is reflected in chain dynamics is, however, unclear yet. Nevertheless, it is expected that the initial expansion of a much compressed chain will be dominated by excluded-volume effects; chain connectivity will not play a significant role. As the blobs grow in size while the chain expands, the nature of the expansion force will change, affecting the dynamics. Eventually, the chain enters a (quasi) one-dimensional Rouse regime, in which relaxed blobs behave as subunits of the chain, as illustrated in fig. 1(b)(iii) [13]. The interaction between neighboring blobs will determine chain dynamics. We thus expect subdiffusive and exponentially-relaxing regime to emerge.
Before presenting our simulation results, we first recall a few theoretical models for chain expansion, which are based on a "single-particle" picture. Let f be the chain deformation force and 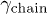 the chain friction coefficient. If
the chain friction coefficient. If 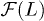 is the confinement-deformation free energy,
is the confinement-deformation free energy,  . Within this picture, the equation of motion for L(t) is
. Within this picture, the equation of motion for L(t) is

This can be solved subject to the initial condition:  [6]. Here and below, the subscript i refers to the initial compressed state. In an "immobile" solvent (in the absence of hydrodynamic interactions),
[6]. Here and below, the subscript i refers to the initial compressed state. In an "immobile" solvent (in the absence of hydrodynamic interactions),  is independent of D. On the other hand, in a mobile solvent,
is independent of D. On the other hand, in a mobile solvent, 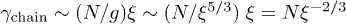 [18,19], where
[18,19], where  is the number of monomers per blob [10].
is the number of monomers per blob [10].
An explicit form of f relies on the physical picture, within which it is obtained. For instance, a Flory-type approach [6,7] leads to the following force-deformation relation:

where 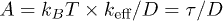 . If combined with eq. (3), this produces
. If combined with eq. (3), this produces
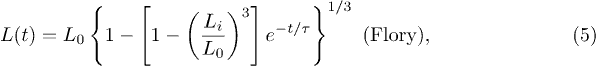
where  (
(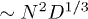 in an immobile solvent [7,13]). For
in an immobile solvent [7,13]). For 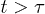 , this implies
, this implies  .
.
It is tempting to improve this mean-field result by mapping the compressed chain onto an equivalent semidilute polymer solution [7] (see ref. [20] for the unconfined case)2 . Then the confinement-compression free energy is given by
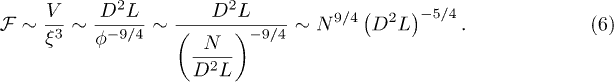
With 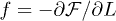 , this leads to the following solution:
, this leads to the following solution:
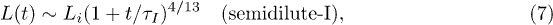
where 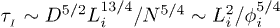 .
.
So far, hydrodynamic interactions have been ignored. Within the blob scaling picture, their effects can be taken into account by assigning a friction 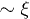 to each blob. The underlying physical picture is that the hydrodynamic interaction is screened beyond ξ [10,11,18,19]. In other words, we consider ξ as the hydrodynamic screening length
to each blob. The underlying physical picture is that the hydrodynamic interaction is screened beyond ξ [10,11,18,19]. In other words, we consider ξ as the hydrodynamic screening length 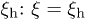 . The total chain friction is then
. The total chain friction is then 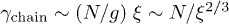 . As a result, we find
. As a result, we find
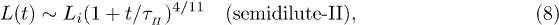
where 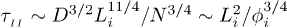 . The exponent here is somewhat larger than in eq. (7) and
. The exponent here is somewhat larger than in eq. (7) and 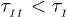 . This means that the chain expands faster in a mobile solvent, thanks to the hydrodynamic effect, as expected.
. This means that the chain expands faster in a mobile solvent, thanks to the hydrodynamic effect, as expected.
Despite seeming plausibility, these models need to be tested. In particular, the use of equilibrium forces (e.g., f in eq. (4)) in the description of chain dynamics is questionable. A related point is that the one-particle picture as assumed in eq. (3) is valid for large t, when internal modes have relaxed [10–12]. (This picture is often referred to as a "local-equilibrium" approach in the sense that all modes but the global-deformation mode have relaxed.)
Results and discussions
In an effort to present a clear dynamical picture of a confined chain, we carried out MD simulations, following the procedure outlined in the previous section. A chain consisting of N monomers trapped inside a cylindrical space of diameter D is compressed up to 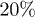 of its equilibrium length
of its equilibrium length 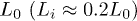 ; it is then allowed to relax from the right end (see fig. 1(b)).
; it is then allowed to relax from the right end (see fig. 1(b)).
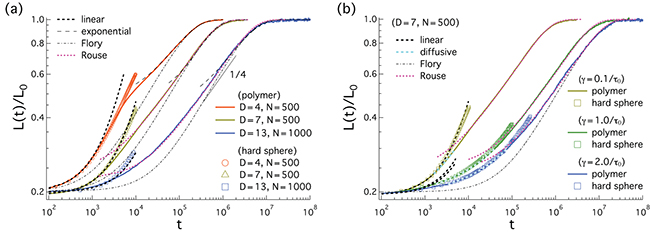
Figure 2 shows our results for L(t), the farthermost distance, obtained with a few choices of N and 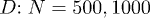 and
and 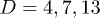 . For (a), we used
. For (a), we used 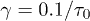 and compared a few larger γ values in (b) to extract a common feature of chain dynamics. Superimposed in fig. 2(a), (b) are our results for the corresponding hard-sphere system initially compressed up to Li, in which beads interact with the WCA potential only3
. Three regimes are identified in (a): i) "explosion" (hard-sphere–like expansion) for
and compared a few larger γ values in (b) to extract a common feature of chain dynamics. Superimposed in fig. 2(a), (b) are our results for the corresponding hard-sphere system initially compressed up to Li, in which beads interact with the WCA potential only3
. Three regimes are identified in (a): i) "explosion" (hard-sphere–like expansion) for 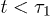 , ii) subdiffusion for the intermediate time range
, ii) subdiffusion for the intermediate time range 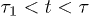 , and iii) global relaxation for
, and iii) global relaxation for  . The explosive motion is initially linear with time (ballistic) but crosses over to diffusion. If
. The explosive motion is initially linear with time (ballistic) but crosses over to diffusion. If 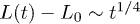 in the subdiffusive regime,
in the subdiffusive regime, 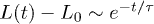 in the global (single-exponential) relaxation regime described by dashed lines. (See refs. [8,9] for actual computations of τ.) It is worth noting that the general trend observed in (a) persists for larger γ values as shown in (b). The main difference is that the linear or ballistic regime is narrower for larger γ.
in the global (single-exponential) relaxation regime described by dashed lines. (See refs. [8,9] for actual computations of τ.) It is worth noting that the general trend observed in (a) persists for larger γ values as shown in (b). The main difference is that the linear or ballistic regime is narrower for larger γ.
Fig. 2: Chain dynamics under confinement. (a) Three regimes are identified to characterize L(t), especially for 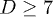 , as also illustrated in fig. 1(b). i) For small t, the chain expands like a corresponding hard-sphere system released from a concentrated state ("explosive"), initially ballistically and diffusively later (see (b)). ii) For intermediate t,
, as also illustrated in fig. 1(b). i) For small t, the chain expands like a corresponding hard-sphere system released from a concentrated state ("explosive"), initially ballistically and diffusively later (see (b)). ii) For intermediate t, 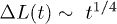 (subdiffusive). iii) For large t,
(subdiffusive). iii) For large t, 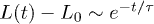 , and the chain relaxes globally (single-exponentially) from its initial conformation. Similarly, the Flory model works well in this regime. For too small D, i.e., D = 4, however, the subdiffusive regime appears to be missing. Our Rouse model (the dashed lines in magenta) fits the expansion data surprisingly well outside regime i). (b) All the regimes shown in (a) are realized for larger damping constants (e.g.,
, and the chain relaxes globally (single-exponentially) from its initial conformation. Similarly, the Flory model works well in this regime. For too small D, i.e., D = 4, however, the subdiffusive regime appears to be missing. Our Rouse model (the dashed lines in magenta) fits the expansion data surprisingly well outside regime i). (b) All the regimes shown in (a) are realized for larger damping constants (e.g., 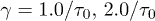 ). The main difference is that for larger γ the emergence of a diffusive sub-regime within the (hard-sphere–like) explosive regime is more obvious.
). The main difference is that for larger γ the emergence of a diffusive sub-regime within the (hard-sphere–like) explosive regime is more obvious.
Download figure:
Standard imageNote that the exponent 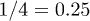 for regime ii) is somewhat close to the exponent
for regime ii) is somewhat close to the exponent 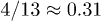 in eq. (7). We believe that this is a coincidence, since the underlying physical picture is obviously different (see below for details). Also, the Flory model in eq. (5) (the dot-dashed line in fig. 2(a)) works well in the global-relaxation regime but deviates noticeably from the data in the other regimes. This clarifies the limitation of equilibrium pictures in describing chain dynamics.
in eq. (7). We believe that this is a coincidence, since the underlying physical picture is obviously different (see below for details). Also, the Flory model in eq. (5) (the dot-dashed line in fig. 2(a)) works well in the global-relaxation regime but deviates noticeably from the data in the other regimes. This clarifies the limitation of equilibrium pictures in describing chain dynamics.
For the D = 4 case in fig. 2(a), the agreement between the polymer and hard-sphere systems persists even outside the initial explosive regime, up to 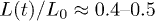 . This also explains why the subdiffusive regime is missing (or too narrow) in the this case. Based on this comparison, the emergence of the explosive regime can then be attributed to a stored energy in the initial concentrated or compressed system.
. This also explains why the subdiffusive regime is missing (or too narrow) in the this case. Based on this comparison, the emergence of the explosive regime can then be attributed to a stored energy in the initial concentrated or compressed system.
Following up on ref. [18], we propose a fitting model for the subdiffusive and global relaxation regimes by mapping the confined chain onto an equivalent one-dimensional Rouse chain. Chain statistics outside ξ is not influenced by self-avoidance, since this effect is screened beyond ξ. Furthermore, each blob relaxes much faster than the whole chain, and thus one can treat blobs as "already relaxed" subunits of the chain. This suggests that the confined chain with self-avoidance can map onto an effective Rouse chain. The free energy of such blob deformations in the Hookean limit, as illustrated in fig. 1(b) (the bottom one or the second one from the bottom4 ), is given by [18]
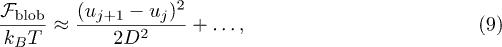
where 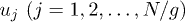 is the position of the i-th blob. The squared chain-size fluctuation
is the position of the i-th blob. The squared chain-size fluctuation ![$\Delta L^2(t) = \bigl< \left[L(t)-L(0)\right]^2\bigr>$](https://content.cld.iop.org/journals/0295-5075/104/6/68003/revision1/epl15962ieqn65.gif) can be expressed as a sum over relaxation modes (see ref. [12] and references therein). If normalized at
can be expressed as a sum over relaxation modes (see ref. [12] and references therein). If normalized at  , it is given by
, it is given by
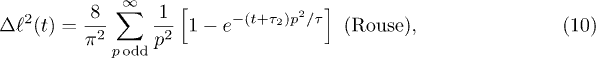
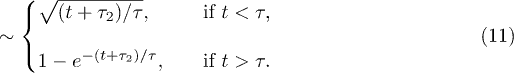
Here, 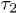 is introduced to "reset" the initial time for free relaxations outside the explosive regime. This is necessary since the Rouse model does not capture the initial explosive forces the chain experiences. These results clearly show the expected crossover between the subdiffusive and global-relaxation regimes. They also highlight the significance of internal modes in determining chain dynamics in the intermediate time range, which are suppressed in a one-particle approach (e.g., eq. (7))5
.
is introduced to "reset" the initial time for free relaxations outside the explosive regime. This is necessary since the Rouse model does not capture the initial explosive forces the chain experiences. These results clearly show the expected crossover between the subdiffusive and global-relaxation regimes. They also highlight the significance of internal modes in determining chain dynamics in the intermediate time range, which are suppressed in a one-particle approach (e.g., eq. (7))5
.
We have fitted the large-D data to 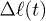 in eq. (10) with
in eq. (10) with 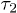 (τ as well) as a fitting parameter (see the dashed lines in magenta). The excellent agreement between our data and theory for
(τ as well) as a fitting parameter (see the dashed lines in magenta). The excellent agreement between our data and theory for 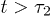 approves eq. (10) as a valid fitting model for chain expansion outside the explosive regime. Even when
approves eq. (10) as a valid fitting model for chain expansion outside the explosive regime. Even when 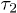 was set to zero, eq. (10) fit the data in a much wider range than the simple exponential fit does (the data not shown)6
.
was set to zero, eq. (10) fit the data in a much wider range than the simple exponential fit does (the data not shown)6
.
It proves useful to examine the dynamics of individual segments as well as the center of mass (CM) of a confined chain. During the sudden expansion of the chain, its different sections will experience different forces and deformations, possibly entering the regimes at different times. This effort will provide additional information, which is hidden in our results for L(t). Let 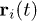 be the position of monomer i at time t. Here, we introduce its mean squared displacement (MSD) defined as an average over several neighboring monomers:
be the position of monomer i at time t. Here, we introduce its mean squared displacement (MSD) defined as an average over several neighboring monomers: ![$g_i(t)=\frac{1}{10}\sum_{j=i-5}^{i+4} \left\langle[\textbf{r}_j (t)-\textbf{r}_j(0)]^2 \right\rangle$](https://content.cld.iop.org/journals/0295-5075/104/6/68003/revision1/epl15962ieqn76.gif) , where 〈...〉 is an ensemble average, i.e., an average over many independent simulations. Note that this procedure is merely to improve statistics as also done in ref. [22]. Similarly, the CM is given by
, where 〈...〉 is an ensemble average, i.e., an average over many independent simulations. Note that this procedure is merely to improve statistics as also done in ref. [22]. Similarly, the CM is given by ![$g_\text{CM}(t)=\frac{1}{N}\sum_{j=1}^{N} \left\langle[\textbf{r}_j (t)-\textbf{r}_j(0)]^2 \right\rangle$](https://content.cld.iop.org/journals/0295-5075/104/6/68003/revision1/epl15962ieqn77.gif) .
.
Figure 3 shows our MSD results for the initially compressed (lines or lines with symbols) and uncompressed cases (symbols) for 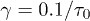 . (From fig. 2(b), it is expected that this choice will not limit the applicability of these results; it alters the relative width of different regimes.) For the former case
. (From fig. 2(b), it is expected that this choice will not limit the applicability of these results; it alters the relative width of different regimes.) For the former case 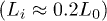 , the internal dynamics of the central and right-end monomers as well as the the dynamics of CM are initially explosive, subdiffusive in the intermediate-time range, and diffusive in the long-time range. (The slopes of fitting curves are designated by numbers.) The emergence of the last two regimes is somewhat delayed for right-end proximate segments, compared to that for the left-chain end, because of their initial explosive motion. As a result, chain segments enter the subdiffusive and diffusive regimes in a sequential manner: left-end proximate ones first and right-end proximate ones later. Also the motion of CM and the central monomer appears to be a bit more complex than that of the left-end or right-end monomer. We attribute this to the internal arrangement of chain segments somewhere in the middle during chain expansion/relaxation.
, the internal dynamics of the central and right-end monomers as well as the the dynamics of CM are initially explosive, subdiffusive in the intermediate-time range, and diffusive in the long-time range. (The slopes of fitting curves are designated by numbers.) The emergence of the last two regimes is somewhat delayed for right-end proximate segments, compared to that for the left-chain end, because of their initial explosive motion. As a result, chain segments enter the subdiffusive and diffusive regimes in a sequential manner: left-end proximate ones first and right-end proximate ones later. Also the motion of CM and the central monomer appears to be a bit more complex than that of the left-end or right-end monomer. We attribute this to the internal arrangement of chain segments somewhere in the middle during chain expansion/relaxation.
Fig. 3: Dynamics of internal segments and the center of mass (CM) for the initially compressed and uncompressed case. The internal dynamics of the central and right end as well as the the dynamics of CM are hard-sphere–like or explosive, subdiffusive, and diffusive in the short-time, intermediate-time, and long-time range, respectively, if the chain is initially compressed. (The slopes of fitting curves are shown.) The emergence of the latter two regimes is delayed, compared to that for the left chain end, because of their initial explosive motion. Also the motion of CM and the central monomer looks a bit more complex than that of a chain end, since it reflects the internal arrangement of chain segments during chain expansion/relaxation. Also included are our results for a freely relaxing chain. The central monomer initially undergoes subdiffusion and enters the diffusive regime at 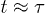 . This crossover time appears to coincide with that for the left end dynamics in the compressed case.
. This crossover time appears to coincide with that for the left end dynamics in the compressed case.
Download figure:
Standard imageIf initially uncompressed, the confined chain shows simpler dynamics (see squares and circles in fig. 3). Similarly to what we expect from a free chain, the CM of such a chain undergoes diffusive motion for the entire time range; the central monomer initially undergoes subdiffusion and enters the diffusive regime at 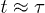 . These results confirm earlier numerical results [22] and are consistent with the Rouse chain analogy described in eq. (9)7
. This crossover time appears to coincide with that for the left-end dynamics in the compressed case.
. These results confirm earlier numerical results [22] and are consistent with the Rouse chain analogy described in eq. (9)7
. This crossover time appears to coincide with that for the left-end dynamics in the compressed case.
While the emergence of the subdiffusive and exponential relaxation regimes is obvious based on the analogy with a one-dimensional Rouse chain (see eqs. (10) and (11)), the seeming absence of the semidilute analogue (see eq. (7)) deserves discussion. One possibility is that in our simulation D is not large enough for this regime to be realized. On the other hand, as D increases, the range of N required to be in the blob-scaling limit increases rapidly. The dynamic blob-scaling limit for moderate D values 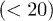 has only recently been reached in numerical studies [13]. Similarly to the Flory approach in eq. (4), however, the semidilute analogue may have a limited applicability in dynamics considerations, since it is based on an equilibrium picture. Furthermore, the reduced one-particle approach, as assumed in eq. (3) (thus in this approach as well), is valid for
has only recently been reached in numerical studies [13]. Similarly to the Flory approach in eq. (4), however, the semidilute analogue may have a limited applicability in dynamics considerations, since it is based on an equilibrium picture. Furthermore, the reduced one-particle approach, as assumed in eq. (3) (thus in this approach as well), is valid for 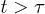 . As a result, the semidilute analogue will work for
. As a result, the semidilute analogue will work for 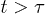 . However, this is also the condition under which
. However, this is also the condition under which 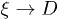 . This explains why such a regime is not realized in our results presented in fig. 2. This also implies that this regime in a mobile solvent (see eq. (8)) may suffer a similar fate, especially when D is not asymptotically large or in the parameter space that is computationally accessible.
. This explains why such a regime is not realized in our results presented in fig. 2. This also implies that this regime in a mobile solvent (see eq. (8)) may suffer a similar fate, especially when D is not asymptotically large or in the parameter space that is computationally accessible.
Our discussion above implies that the effect of hydrodynamic interactions will be felt mainly in the subdiffusive and global-relaxation regimes captured in fig. 2. In the global relaxation regime, this effect can be taken into account by considering 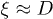 as the hydrodynamic screening length
as the hydrodynamic screening length 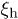 [9,18]. How this effect will modify chain dynamics in the subdiffusive regime is less obvious and will be left for future work.
[9,18]. How this effect will modify chain dynamics in the subdiffusive regime is less obvious and will be left for future work.
Conclusions
Measurements of chain expansion under cylindrical confinement are effective means of probing the physical properties of chain molecules (e.g., bacterial chromosomes) and for clarifying how confinement influences them [5]. Such efforts will also be beneficial for unravelling the way they interact and segregate in a cell-like confined space, because of the relationship between single-chain properties and their segregation [23]. Our results presented here not only test existing models but also show how expansion data should be fitted. If the Flory model works well for the long-time limit  , the semidilute analogue (in the presence or absence of hydrodynamic interactions) will not be easily realized, especially in computationally accessible parameter ranges. The latter model may be relevant to the intermediate-time range but in this case the chain has not relaxed yet. This limits the applicability of this model based on an equilibrium picture.
, the semidilute analogue (in the presence or absence of hydrodynamic interactions) will not be easily realized, especially in computationally accessible parameter ranges. The latter model may be relevant to the intermediate-time range but in this case the chain has not relaxed yet. This limits the applicability of this model based on an equilibrium picture.
It will be instructive to fit experimental data to our results. Along this line, in recent experiments, E. coli chromosomes released from lysed cells were allowed to expand in narrow channels [5]. Similarly to what we observed here, the resulting raw data for chromosome expansion indicate the existence of a few dynamic regimes [5,24]. However, more comprehensive efforts under controlled conditions will be needed to draw a definite conclusion and to further illuminate the polymer aspect of the chromosome beyond recent observations.
Acknowledgments
This work was supported by the collaborative research contract funded by Korea Institute of Science and Technology Information (KISTI) and NSERC (Canada) (B-YH) as well as by the NRF grant funded by the Korean Government (NRF-2012R1A1A2007488 (YJ) and NRF-2011-0011550 (MH)). We benefited from useful discussion with S. Jun and J. Kim.
Footnotes
- 1
See movies S1 and S2 in ref. [5]. On physics grounds, this setting is not expected to introduce any artifact. We rather note that the expected subdiffisive regimes shows up more clearly this way.
- 2
- 3
For this comparison, we rescaled the time for hard-sphere expansion by some constant. Note that this will not change the physics of the hard-sphere system qualitatively.
- 4
A direct comparison is obscured by the non-uniformity of the expanding chain in fig. 1(b). But the "Hookean chain" is closer to the bottom illustration, which is described to be relevant for
 . It is worth mentioning that the time here is measured with reference to the initial state right before chain expansion. When we map the expanding chain onto a Rouse chain, we need to reset the reference time so that this picture is applicable for
. It is worth mentioning that the time here is measured with reference to the initial state right before chain expansion. When we map the expanding chain onto a Rouse chain, we need to reset the reference time so that this picture is applicable for  .
. - 5
The two time scales,
 and
and  , are related to each other in some complicated way. But we will not further explore the relationship here. Crossover times are loosely defined and establishing a relationship between such quantities will not add new insight.
, are related to each other in some complicated way. But we will not further explore the relationship here. Crossover times are loosely defined and establishing a relationship between such quantities will not add new insight. - 6
For too small D, i.e., D = 4, however, the separation of length scales in terms of ξ becomes more arbitray, and the notion of blobs as assumed in the blob approach breaks down; so does the Rouse chain analogy. This is consistent with our earlier view that for small D the confined chain resembles a hard sphere system for wide parameter ranges, shrinking the subdiffusive regime (see fig. 2(a)).
- 7