Abstract
Many biopolymers like proteins, RNA, single-stranded DNA form secondary structures, namely helices and loops. These polymers often get transported from one compartment of the cell to another through narrow protein channels. Motivated by recent experimental results on translocation of polymers through channels and helix-coil transition inside the channel, we have constructed a two-dimensional toy model to study how secondary structures influence such processes. Through a Langevin dynamics simulation we investigated the statistics of translocation as well as how channel width, force and temperature affect the helix-coil transition inside a channel. Our results are in qualitative agreement with experimental data.
Export citation and abstract BibTeX RIS
Transportation of biopolymers inside a cell, from cytoplasm to various compartments and vice versa takes place through protein channels of nanometre scale. For example, RNA translocates between nucleus and cytoplasm through a nuclear pore complex, a virus injects its DNA into a bacteria through a nanopore, various proteins translocate across biological membranes [1] through nanochannels. The durations of these translocation events indirectly control the time scales of various cellular processes in which RNA, DNA or proteins participate. By actively controlling the translocation events the channels ensure the availability of the right reactants at the right places. Because of their biological importance, polymer translocation has been a very active area of research [1–3] since last two decades. Kansianowicz et al. [4] discovered that the electric field can drive single-stranded DNA, which is charged, through an  channel. This led to many in vitro experiments where translocation of polymers through different types of channels has been studied under different experimental conditions, e.g., temperature, applied field [5,6] etc. Channels across biological membranes are typically formed by pore-forming transmembrane proteins or protein complexes and henceforth we will use the terms channel and pore synonymously.
channel. This led to many in vitro experiments where translocation of polymers through different types of channels has been studied under different experimental conditions, e.g., temperature, applied field [5,6] etc. Channels across biological membranes are typically formed by pore-forming transmembrane proteins or protein complexes and henceforth we will use the terms channel and pore synonymously.
Theoretically, translocation of flexible polymers through narrow channels has been addressed using the freely jointed chain (FJC) model by various groups [7–10]. These studies were based on diffusion of a FJC across a free-energy barrier posed by the constriction of the channel. In parallel, simulation studies have probed the effects of polymer length, pulling force [11], molecular crowding [1–3], confinement [12] and fluctuating channel width [13] etc., on translocation of FJC polymers. These studies are important since translocation inside a cell occurs in a crowded, confined and dynamic environment.
Experiments [5,6] on translocation of polynucleotides through protein channels (e.g., 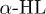 ) found that the translocation time is very sensitive to the polynucleotide sequence. It was conjectured that this might be either due to the interaction between the polynucleotides and the protein (i.e., polymer-channel interaction) or due to formation of secondary structure in certain polynucleotides. While Luo et al. [14,15] have shown that interaction between a simple FJC polymer and the channel does affect the translocation, here we focus on how secondary structure formation (mainly helix) in poly(dA) or poly(A) affects the translocation process. These helical structures, which result from a stacking interaction among the A-bases, render a larger cross-sectional area to the chain compared to that of simple coil-like FJCs, e.g., wild-type ssDNA or RNA. Consequently, poly(dA)/poly(A) behaves as a semiflexible polymer which is modeled by a worm-like chain (WLC). Meller et al. [5] and Akenson et al. [6] found that polynucleotides that can form secondary structures translocate slowly compared to the polynucleotides that cannot. Recent experiments on poly(A) by Lin et al. [12] have shown that poly(A) can form helical segments inside the channel and there it fluctuates between helix and coil states. The effect of varying flexibility along a polymer, namely, a mixture of rod and coil segments, on translocation has recently been studied by Hendrick et al. [16]. But the effect of finite semiflexibility, originating from helical segments and furthermore dynamical inter convertibility between coil and semiflexible segments, on translocation has not been explored yet. We propose a model towards this. The model also allows us to probe the fluctuations between helix and coil states inside the channel, in particular, we study how various parameters like external force and channel width control the kinetics.
) found that the translocation time is very sensitive to the polynucleotide sequence. It was conjectured that this might be either due to the interaction between the polynucleotides and the protein (i.e., polymer-channel interaction) or due to formation of secondary structure in certain polynucleotides. While Luo et al. [14,15] have shown that interaction between a simple FJC polymer and the channel does affect the translocation, here we focus on how secondary structure formation (mainly helix) in poly(dA) or poly(A) affects the translocation process. These helical structures, which result from a stacking interaction among the A-bases, render a larger cross-sectional area to the chain compared to that of simple coil-like FJCs, e.g., wild-type ssDNA or RNA. Consequently, poly(dA)/poly(A) behaves as a semiflexible polymer which is modeled by a worm-like chain (WLC). Meller et al. [5] and Akenson et al. [6] found that polynucleotides that can form secondary structures translocate slowly compared to the polynucleotides that cannot. Recent experiments on poly(A) by Lin et al. [12] have shown that poly(A) can form helical segments inside the channel and there it fluctuates between helix and coil states. The effect of varying flexibility along a polymer, namely, a mixture of rod and coil segments, on translocation has recently been studied by Hendrick et al. [16]. But the effect of finite semiflexibility, originating from helical segments and furthermore dynamical inter convertibility between coil and semiflexible segments, on translocation has not been explored yet. We propose a model towards this. The model also allows us to probe the fluctuations between helix and coil states inside the channel, in particular, we study how various parameters like external force and channel width control the kinetics.
Model
We model the backbone of the polymer as a bead-spring chain in two dimensions (2D) where nearest-neighbour beads are bound to each other through a FENE spring potential, given by  . Here r is the inter-bead distance, k the spring constant and R0 the maximum extension of the spring. The excluded-volume effect between non–nearest-neighbor beads is implemented using a Lennard-Jones (LJ) potential
. Here r is the inter-bead distance, k the spring constant and R0 the maximum extension of the spring. The excluded-volume effect between non–nearest-neighbor beads is implemented using a Lennard-Jones (LJ) potential 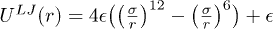 . Here σ is the diameter of the bead and
. Here σ is the diameter of the bead and  the strength of the potential. The LJ potential is truncated such that it is non-zero only when
the strength of the potential. The LJ potential is truncated such that it is non-zero only when 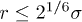 , i.e., in the repulsive regime of the potential.
, i.e., in the repulsive regime of the potential.
We have modeled the helical segments of the polymer as zigzag conformations (see fig. 1). This is done by attaching an attractive FENE spring between the monomers which are next-nearest neighbours. These FENE springs have a different spring constant,  , than that of the nearest-neighbour FENE springs
, than that of the nearest-neighbour FENE springs  . Practically
. Practically 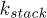 controls the strength of the stacking interaction between the bases. We impose a cutoff distance,
controls the strength of the stacking interaction between the bases. We impose a cutoff distance,  , on this attractive FENE spring potential such that stacking (and consequently the local helical structure) is broken when the next–nearest-neighbor distance
, on this attractive FENE spring potential such that stacking (and consequently the local helical structure) is broken when the next–nearest-neighbor distance  . We simplistically model the channel wall as an array of monomers of diameter σ having a hardcore repulsive interaction with the polymer beads. This is implemented via the repulsive part of a LJ potential with a cutoff of
. We simplistically model the channel wall as an array of monomers of diameter σ having a hardcore repulsive interaction with the polymer beads. This is implemented via the repulsive part of a LJ potential with a cutoff of  and strength
and strength  . In reality the channel-polymer interaction is perhaps much more complicated which can affect both the time scale of translocation as well as the helix-coil fluctuation kinetics inside the channel.
. In reality the channel-polymer interaction is perhaps much more complicated which can affect both the time scale of translocation as well as the helix-coil fluctuation kinetics inside the channel.
Fig. 1: (Color online) Model of a polymer with helical and coil regions.
Download figure:
Standard imageIn experiments, the direction of translocation is fixed by creating a constant electric field inside the channel and choosing a charged polymer. This amounts to a constant force 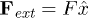 per bead, which are inside the channel at a given time. Langevin equations of motion of the polymer beads are given by
per bead, which are inside the channel at a given time. Langevin equations of motion of the polymer beads are given by  , where
, where  is the position of the i-th bead, m its mass, Γ the friction coefficient and
is the position of the i-th bead, m its mass, Γ the friction coefficient and  is a Gaussian random noise characterised by
is a Gaussian random noise characterised by  and
and 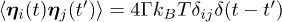 . The Langevin equation is solved numerically by the Verlet algorithm.
. The Langevin equation is solved numerically by the Verlet algorithm.
In our simulation, we used  , σ and m as the units of energy, length and mass, which give the unit of time as
, σ and m as the units of energy, length and mass, which give the unit of time as  . The dimensionless parameters used in our simulation are k = 30,
. The dimensionless parameters used in our simulation are k = 30, 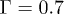 ,
, 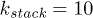 ,
,  ,
,  ,
, 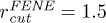 and
and  . The time step used was
. The time step used was  .
.
Our choice of parameters, especially  and
and  , leads to a stacking enthalpy of
, leads to a stacking enthalpy of 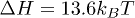 and the resulting force-extension (FX) curve shows a plateau at approximately 18 pN force, see fig. 2. This corresponds to a helix-coil transition as the stacking bonds break beyond certain stretch. This is close to the experimental FX curve of poly(dA) stretching [17,18], despite the fact that our 2D toy model underestimates entropy and also do not have cooperativity among the bases. We note that experimental estimates of stacking enthalpy of poly(dA) lies between 5kBT and 13.3kBT (see refs. [19,20] and references in [20]).
and the resulting force-extension (FX) curve shows a plateau at approximately 18 pN force, see fig. 2. This corresponds to a helix-coil transition as the stacking bonds break beyond certain stretch. This is close to the experimental FX curve of poly(dA) stretching [17,18], despite the fact that our 2D toy model underestimates entropy and also do not have cooperativity among the bases. We note that experimental estimates of stacking enthalpy of poly(dA) lies between 5kBT and 13.3kBT (see refs. [19,20] and references in [20]).
Fig. 2: (Color online) Force-extension plots of our model poly(dA) chain of length N = 21, for three different stacking interaction strengths  . The higher the value of
. The higher the value of  the higher is the plateau.
the higher is the plateau.
Download figure:
Standard imageIn our model the cross-sectional width of the helix can change due to the stretching in the stacked spring. The width (expressed in non-dimensional units) can vary from 1.66 to 1.86 approximately. The width is 1.86 for the relaxed helix, while 1.66 corresponds to the maximally stretched state beyond which the stacking bond breaks. Support for such a stretched helical state comes from MD simulation of ssDNA [21], in particular poly(dA), where it was shown that the average angle between the base and the backbone of a nucleotide changes inside a constricted channel and the resulting alignment of bases leads to the elongation of the ssDNA helix (see fig. 6 in ref. [21]). Further, MD simulation of dsDNA [22] translocation also revealed that dsDNA can stretch before unzipping. Now we discuss the simulation results obtained from our model and compare them with experiments.
Kinetics of the helix-coil transition inside a channel
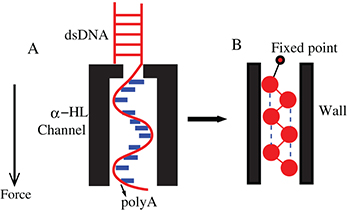
Lin et al. [12] have shown that poly(A) can fluctuate between helix and coil states inside an α-HL channel. In this experiment a poly(A) strand was effectively trapped inside the channel (see fig. 3(B)) by subjecting it to two counter-acting forces. An electric field was applied which tended to push out the poly(A) strand from the channel but this movement was countered by attaching a duplex strand, which cannot pass through the channel, to the poly(A). This amounted to effectively fixing the poly(A)-duplex junction at the opening of the channel. Now, as the segments of the poly(A) strand fluctuate between helix and coil states, the ion current through the channel also fluctuates, approximately between two values, showing the signature of a two-state system. The two states correspond to open and blocked states of the channel and, given that the channel width is comparable to the diameter of the poly(A) helix, it is reasonable to assume that the channel gets blocked even when a part of the poly(A) strand gets into the helical state, i.e. only one bottleneck along the channel is sufficient to stop the current. Henceforth we will use open and blocked states of the channel synonymously with the helical and coil states, respectively, of the poly(A), although the helical state does not imply that all the stacking bonds in the strand are intact. The durations of the current signals in the open  and blocked
and blocked 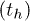 states separately show exponential distributions
states separately show exponential distributions  and
and 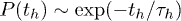 . Note that the exponential nature of
. Note that the exponential nature of 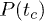 does not dictate that
does not dictate that 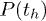 has to be exponential too. For example, one can imagine a situation when th is constant while tc is exponentially distributed.
has to be exponential too. For example, one can imagine a situation when th is constant while tc is exponentially distributed.
Fig. 3: (Color online) (A) shows a ssDNA trapped inside the channel due to the attached duplex strand at one end. (B) shows how the trapping is mimicked in our model.
Download figure:
Standard imageTo mimic this situation we constrain one end of a poly(A) chain by connecting it to a fixed point through a harmonic spring, see fig. 3(B). The width of the channel is W, its length is L and the number of monomers in the polymer chain is N. We perform a Langevin dynamics simulation of this system. To make correspondence with the current measurement in the experiment, we assumed that in a given configuration at least two consecutive stacking springs have to be intact (i.e., in the helical state) in order for the channel to be blocked, otherwise the channel is open. Our results do not change qualitatively if the minimum number of consecutively stacked springs  required to block the current is changed to one, three or four, for example. Only the lifetime of the blocked state reduces when Nh is raised.
required to block the current is changed to one, three or four, for example. Only the lifetime of the blocked state reduces when Nh is raised.
In our Langevin dynamics simulation, starting with a random configuration and excluding the initial transients, the system evolved for 106 time steps during which tc and th were recorded. One thousand such runs, with differing initial configurations, were used to compute the distributions  and
and  .
.
We assume the fluctuation between the coil and helical states as a dichotomous Markov process: 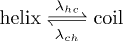 , where
, where 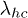 and
and  are the transition rates from closed to open and reverse, respectively. The persistence probability of the helical state, i.e., no transition occurs from the helix to the coil state till time t, can be shown to be proportional to
are the transition rates from closed to open and reverse, respectively. The persistence probability of the helical state, i.e., no transition occurs from the helix to the coil state till time t, can be shown to be proportional to 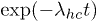 and, conversely, the persistence of the coil state is proportional to
and, conversely, the persistence of the coil state is proportional to 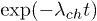 . From the probability of no transition, the characteristic lifetime or mean residence time of the helix and coil state are given by
. From the probability of no transition, the characteristic lifetime or mean residence time of the helix and coil state are given by 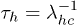 and
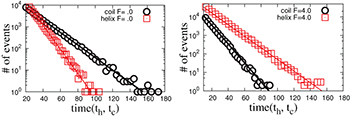
and 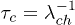 , respectively. A numerical simulation based on our model indeed shows exponential distributions of th and tc, in qualitative agreement with the experimental finding of Lin et al. [12], see fig. 4.
, respectively. A numerical simulation based on our model indeed shows exponential distributions of th and tc, in qualitative agreement with the experimental finding of Lin et al. [12], see fig. 4.
Fig. 4: (Color online) Probability distributions (not normalized) of the life times  of the helical and the coil states, for
of the helical and the coil states, for  and for two different forces F = 5 (A) and F = 4 (B).
and for two different forces F = 5 (A) and F = 4 (B).
Download figure:
Standard imageEffect of external force, channel width and temperature on th and tc
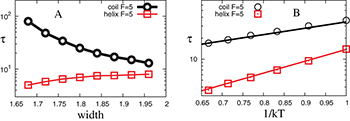
Typically in translocation experiments the channel width is kept fixed, for example, at 2.2 nm in ref. [12], which is comparable to the cross-sectional diameter of a poly(dA) helix (2.1 nm). But the observation made by MD simulation [21] that narrower channels can elongate a poly(dA), has implication for the fluctuation kinetics of the helix-coil transition as we show now. In a wider channel (as in ref. [12]) the poly(A) helix will be in a relaxed state, but if the width of the channel is decreased, the cross-section of the helix will change due to the stretching of the stacking bonds. We varied the channel width in our simulation and found that the distributions of th and tc still remain exponential (fig. 5) although the exponents change. In addition to reducing the channel width there are at least two different ways of stretching the helix: a) by increasing the applied electric field and b) by raising the temperature. While a reduced channel width affects all the monomers equally by suppressing the helix width and locally extending all the stacking bonds, the electric field acts like a body force on all the monomers. Therefore unlike a stretching force that acts at one end of a linear chain and creates uniform tension (at equilibrium) in all the springs, the electrostatic body force generates a tension gradient along the chain. The stacking bonds on the left experience higher tension and therefore break more easily, if the electric force is directed towards the right. Higher temperature, on the other hand, increases the length fluctuations of all the stacking bonds and reduce their lifetime.
Fig. 5: (Color online) (A) Characteristic lifetimes 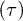 extracted from the exponential distributions
extracted from the exponential distributions  in fig. 4 are shown as a function of the channel width. (B) Lifetime
in fig. 4 are shown as a function of the channel width. (B) Lifetime 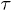 vs. temperature at different widths, at fixed force
vs. temperature at different widths, at fixed force 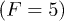 and width
and width  .
.
Download figure:
Standard imageWe will now discuss the feasibility of constructing a free-energy–based framework for understanding the above effects. In terms of the free-energy barriers, the transition rates can be approximated as  and
and 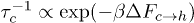 , where
, where 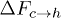 and
and 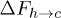 are free-energy barriers for
are free-energy barriers for 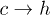 and
and  transitions, respectively. Experimental data on the temperature variation of
transitions, respectively. Experimental data on the temperature variation of 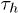 and
and  , from ref. [12], show that
, from ref. [12], show that  although
although 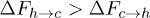 , where
, where 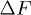 is computed from the slopes of the Arrhenius plots. This implies, from the transition rate formula
is computed from the slopes of the Arrhenius plots. This implies, from the transition rate formula 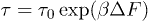 , that the attempt frequency
, that the attempt frequency  is higher for the
is higher for the  transition. Data from ref. [12] also show that as voltage is increased (in the range 120–160 mV)
transition. Data from ref. [12] also show that as voltage is increased (in the range 120–160 mV)  decreases, while
decreases, while  remains constant. Numerical results from our model gives the same qualitative trends for
remains constant. Numerical results from our model gives the same qualitative trends for 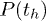 and
and  , and consequently for
, and consequently for 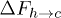 and
and 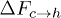 , at force values F = 5 and higher. Our simulation shows that when F is reduced the order reverses, i.e.,
, at force values F = 5 and higher. Our simulation shows that when F is reduced the order reverses, i.e.,  , see fig. 4. This indicates that as the force is reduced the increase in the barrier height
, see fig. 4. This indicates that as the force is reduced the increase in the barrier height 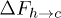 dominates over the effect of the attempt frequency, which can be assumed to be independent of the force. We will now analyse the situation in terms of the breakage probability of a single stacking bond.
dominates over the effect of the attempt frequency, which can be assumed to be independent of the force. We will now analyse the situation in terms of the breakage probability of a single stacking bond.
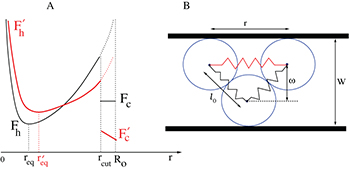
We propose a free-energy landscape like the one shown in fig. 6, where the equilibrium bond length of the stacking bond is req. In the absence of force the free energy  , where
, where 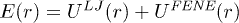 for
for 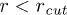 (stacked) and zero beyond
(stacked) and zero beyond 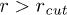 . For the unstacked coil state
. For the unstacked coil state  and we assume the entropies Sh and Sc to be independent of r. When V0 > 0 the beads, of charge q each, experience constant force
and we assume the entropies Sh and Sc to be independent of r. When V0 > 0 the beads, of charge q each, experience constant force 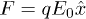 , where
, where  . Thus the total electrostatic energy is
. Thus the total electrostatic energy is 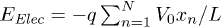 , where
, where 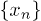 are the x-coordinates of the beads inside the channel. Although the total energy depends on the actual configuration
are the x-coordinates of the beads inside the channel. Although the total energy depends on the actual configuration  , we can approximate
, we can approximate 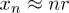 , ignoring the small undulations the chain may have inside a narrow channel. This results in
, ignoring the small undulations the chain may have inside a narrow channel. This results in 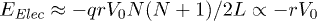 . The electrostatic energy therefore tilts the free-energy landscape towards the coil side and consequently
. The electrostatic energy therefore tilts the free-energy landscape towards the coil side and consequently 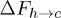 decreases and
decreases and  increases. The experimental data [12] indeed show that the barrier for
increases. The experimental data [12] indeed show that the barrier for  transition slowly decreases with V0, but the barrier for
transition slowly decreases with V0, but the barrier for 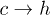 transition remains almost constant. This discrepancy probably arises from our assumption that the entropies are independent of r. Simulation data from our model do not show any significant change of the barrier heights for either of the
transition remains almost constant. This discrepancy probably arises from our assumption that the entropies are independent of r. Simulation data from our model do not show any significant change of the barrier heights for either of the 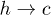 and
and 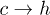 transitions (data not shown) as V0 is changed.
transitions (data not shown) as V0 is changed.
Fig. 6: (Color online) (A) Free-energy landscape F(r) of a stacking bond as a function of the separation between the beads (shown in (B)). When subjected to force the stacking bond extends and can break at 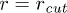 . However r can reach a maximum up to
. However r can reach a maximum up to  which is the new equilibrium position. Note that the nearest-neighbor bonds along the polymer backbone do not stretch significantly. The subscripts h,c implies helical and coil, respectively. The landscape changes from
which is the new equilibrium position. Note that the nearest-neighbor bonds along the polymer backbone do not stretch significantly. The subscripts h,c implies helical and coil, respectively. The landscape changes from 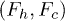 to
to 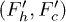 (bold lines) when the electrostatic force F is applied through the potential V0 inside the channel. At zero potential the free-energy barriers
(bold lines) when the electrostatic force F is applied through the potential V0 inside the channel. At zero potential the free-energy barriers 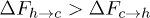 . At V0 > 0, the electrostatic energy which is proportional to
. At V0 > 0, the electrostatic energy which is proportional to  tilts the free-energy landscape towards higher r and as a result
tilts the free-energy landscape towards higher r and as a result  decreases. (B) Constrained configuration of the beads at a fixed channel width W, lesser than the relaxed diameter of the ssDNA helix.
decreases. (B) Constrained configuration of the beads at a fixed channel width W, lesser than the relaxed diameter of the ssDNA helix.
Download figure:
Standard imageFigure 5(A) shows that  in our simulation slowly decreases as the width of the channel is reduced. This can be understood by estimating the barrier for the
in our simulation slowly decreases as the width of the channel is reduced. This can be understood by estimating the barrier for the 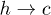 transition:
transition: 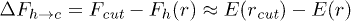 . Using the expression for E(r),
. Using the expression for E(r),
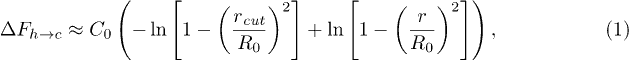
where  . Now the length of the stretched stacking bond r can be obtained from the geometric constraint
. Now the length of the stretched stacking bond r can be obtained from the geometric constraint 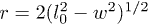 (see fig. 6(B)), where l0 is the length of the covalent bond along the polymer backbone and
(see fig. 6(B)), where l0 is the length of the covalent bond along the polymer backbone and  is the width of the channel. Here we assumed that the covalent bonds do not stretch significantly since they are relatively much stronger than the stacking bonds. Using
is the width of the channel. Here we assumed that the covalent bonds do not stretch significantly since they are relatively much stronger than the stacking bonds. Using 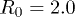 and
and  we get
we get ![$\Delta F_{h\rightarrow c}= C_0\big (\ln[(1-l_0^2) + w^2] - \ln[7/16] \big )$](https://content.cld.iop.org/journals/0295-5075/104/1/18007/revision1/epl15810ieqn112.gif) . Further, using the values
. Further, using the values 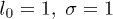 and the relation
and the relation  we get,
we get, ![$\ln \tau_h\propto \beta \ln [\frac{4}{\sqrt 7}(W-1)]$](https://content.cld.iop.org/journals/0295-5075/104/1/18007/revision1/epl15810ieqn115.gif) . This explains the slow rise of
. This explains the slow rise of  with the width of the channel, in fig. 5. For the coil-to-helix transition the effect of the width is just the opposite: at a smaller width as the stacking bond becomes more unstable the coil state becomes more stable.
with the width of the channel, in fig. 5. For the coil-to-helix transition the effect of the width is just the opposite: at a smaller width as the stacking bond becomes more unstable the coil state becomes more stable.
Figure 5(B) shows the effect of temperature on  and
and  at a fixed channel width and force. The Arrhenius nature of the plots corroborates our analysis involving free-energy barriers. The linearity of
at a fixed channel width and force. The Arrhenius nature of the plots corroborates our analysis involving free-energy barriers. The linearity of 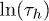 with β is consistent with the formula
with β is consistent with the formula ![$\ln (\tau_h)\propto \beta \ln [\frac{4}{\sqrt 7}(W-1)]$](https://content.cld.iop.org/journals/0295-5075/104/1/18007/revision1/epl15810ieqn120.gif) estimated above.
estimated above.
Note that 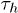 increases with β more steeply than
increases with β more steeply than  , indicating that the free-energy barrier for the helix-to-coil transition is higher than that for the coil-to-helix transition. This feature as well as the Arrhenius nature of the
, indicating that the free-energy barrier for the helix-to-coil transition is higher than that for the coil-to-helix transition. This feature as well as the Arrhenius nature of the  curves are consistent with experimental results [12]. Also note that in fig. 5(B)
curves are consistent with experimental results [12]. Also note that in fig. 5(B)  converge at low temperature, while
converge at low temperature, while  remains lower than
remains lower than 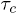 in the selected range of temperatures. This is also consistent with the experiments [12] where only a narrow temperature range
in the selected range of temperatures. This is also consistent with the experiments [12] where only a narrow temperature range 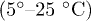 was used.
was used.
Effect of a secondary structure on translocation
As mentioned before, poly(dA) which forms a secondary helical structure takes longer time to translocate than poly(dC) which does not form helical structures [5]. The simulation of our model reproduces this feature, see fig. 7. In the remaining section, poly(dA) and poly(dC) will be representative for polymers with and without secondary helical structures, respectively. Furthermore poly(dA) and poly(dC) will be described by WLC and FJC, respectively. The time interval between the entry of the first bead (see fig. 8) and exit of the last bead from the channel is defined as the translocation time 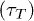 . We used N = 30, and two different channel lengths L = 5 and 10 (results not shown here) showing the same qualitative trends. In the figure, for W > 1.8, poly(dC) takes longer time to translocate than poly(dA). However for W < 1.8 poly(dC) translocates faster, which we will explain later.
. We used N = 30, and two different channel lengths L = 5 and 10 (results not shown here) showing the same qualitative trends. In the figure, for W > 1.8, poly(dC) takes longer time to translocate than poly(dA). However for W < 1.8 poly(dC) translocates faster, which we will explain later.
Fig. 7: (Color online) Dependence of translocation  on the channel width, for poly(dA) and poly(dC) translocating through a "simple" channel of constant width.
on the channel width, for poly(dA) and poly(dC) translocating through a "simple" channel of constant width.
Download figure:
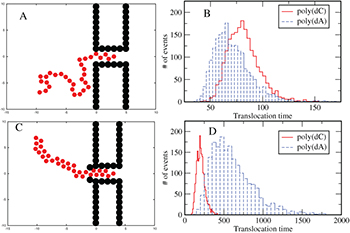
Standard imageFig. 8: (Color online) (A) A FJC translocating through a channel of constant width. (B) Distribution of 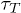 for case (A). (C) A poly(dA) translocating through an α-HL channel with a narrow opening. (D) Distribution of
for case (A). (C) A poly(dA) translocating through an α-HL channel with a narrow opening. (D) Distribution of  for case (C). The distributions were produced from 2000 translocation events each.
for case (C). The distributions were produced from 2000 translocation events each.
Download figure:
Standard imageWhen the channel width is greater than the relaxed diameter of the poly(dA) helix, then coil/FJC takes more time than WLC because the entropic barrier for the entry into the channel is higher for FJC. For both FJC and WLC, if they are inside a narrow channel, their entropies are nearly the same. For WLC there is approximately no change in enthalpy whether it is inside or outside the channel while FJC has no enthalpy anyway. So the free-energy barrier for the entry into the channel is solely determined by the loss of entropy and therefore WLC has a lower free-energy barrier for the entry as compared to FJC (see also ref. [16]).
But when the channel width is narrower than the width of the relaxed helix of the WLC then the stacking bonds have to stretch in order to enter the channel. This requires a rise in the enthalpy  . We show below that as the width decreases
. We show below that as the width decreases  increases. The time taken by the chain to climb up this extra energy approximately scales as
increases. The time taken by the chain to climb up this extra energy approximately scales as 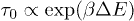 . If we assume that the entry into the channel is the rate limiting step for the translocation process, then
. If we assume that the entry into the channel is the rate limiting step for the translocation process, then  also rises at a smaller width. We can estimate
also rises at a smaller width. We can estimate  as follows:
as follows:
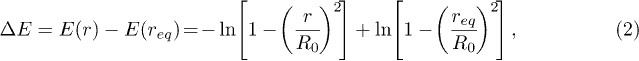
and using  we get
we get ![$\ln \tau_0\propto \beta \ln [\frac{0.83}{W-1}]$](https://content.cld.iop.org/journals/0295-5075/104/1/18007/revision1/epl15810ieqn138.gif) . This is valid till
. This is valid till  , where
, where  . This implies
. This implies 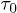 increases as W is reduced, making the energy barrier for the entry into the channel higher at smaller W. When W < 1.66 (corresponding to
increases as W is reduced, making the energy barrier for the entry into the channel higher at smaller W. When W < 1.66 (corresponding to 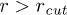 ) then the entry into the channel requires that the stacking bond has to be broken. Then poly(dA) is in helical conformation outside the channel and breaks down into a FJC inside the channel. Beyond
) then the entry into the channel requires that the stacking bond has to be broken. Then poly(dA) is in helical conformation outside the channel and breaks down into a FJC inside the channel. Beyond  the entry barrier does not increase further beyond the limiting value
the entry barrier does not increase further beyond the limiting value 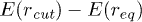 and therefore the translocation time does not change significantly. For FJC, as the width of the channel goes down, the entropy of the chain inside the channel reduces, therefore producing a bigger free-energy barrier for the entry and consequently the
and therefore the translocation time does not change significantly. For FJC, as the width of the channel goes down, the entropy of the chain inside the channel reduces, therefore producing a bigger free-energy barrier for the entry and consequently the 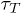 for FJC also goes up (see fig. 7).
for FJC also goes up (see fig. 7).
Such a channel width-dependent translocation time, for polymers that can form a secondary structure, gives rise to an unexpected behavior when the channel width varies along its length. For a simple pore of uniform width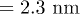 (greater than the helix diameter
(greater than the helix diameter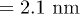 of poly(dA)), poly(dA) takes lesser time than poly(dC) to translocate (see fig. 8(A), (B)). On the other hand, for the α-HL pore [23] which has a narrow opening with diameter
of poly(dA)), poly(dA) takes lesser time than poly(dC) to translocate (see fig. 8(A), (B)). On the other hand, for the α-HL pore [23] which has a narrow opening with diameter (compared to the rest the of the channel with diameter
(compared to the rest the of the channel with diameter ), poly(dA) takes longer time than poly(dC) or poly(C) [5,6]. The simulation of our model with these pore geometries (shown in fig. 8(A), (C)) reproduces similar distributions of
), poly(dA) takes longer time than poly(dC) or poly(C) [5,6]. The simulation of our model with these pore geometries (shown in fig. 8(A), (C)) reproduces similar distributions of  as observed in experiments. From the distributions it is clear that the most probable translocation time for poly(dC) is smaller than poly(dA) in the case of an α-HL pore (fig. 8(D)) since the stacking bond in poly(dA) needs to be broken at the entry of the channel. However, it can reform inside the channel. For fig. 8 we used N = 30 and L = 5. The distribution in fig. 8(D) is consistent with the distributions obtained by Meller et al. [5]. We have also checked that the tails of the histograms can be fitted with exponentials.
as observed in experiments. From the distributions it is clear that the most probable translocation time for poly(dC) is smaller than poly(dA) in the case of an α-HL pore (fig. 8(D)) since the stacking bond in poly(dA) needs to be broken at the entry of the channel. However, it can reform inside the channel. For fig. 8 we used N = 30 and L = 5. The distribution in fig. 8(D) is consistent with the distributions obtained by Meller et al. [5]. We have also checked that the tails of the histograms can be fitted with exponentials.
Conclusion
We have proposed an effective bead-spring model for a polymer that can form a secondary structure. This model qualitatively reproduces many experimental results like the force-extension and tanslocation of poly(dA) through narrow channels. It also qualitatively reproduces the kinetics of the helix-coil transition of poly(A) inside the channel as observed in experiments [12]. Although a channel width-dependent experimental study is not available in the literature, we could reproduce the experimental results on the effect of a non-uniform channel width affecting the translocation of poly(dA) and poly(dC). However a more involved 3D model is needed to match the experimental results quantitatively.