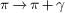Abstract
Pion and kaon decay, π → μ + νμ, K → μ + νμ, into muons and GeV neutrinos is investigated with regard to a possible superluminal neutrino speed. Photonic Cherenkov emission by superluminal high-energy charges is shown to be forbidden by causality violation. A proper causality interpretation of decay processes outside the lightcone involving superluminal particles requires an absolute spacetime conception based on a distinguished frame of reference (aether frame). The universal reference frame is physically manifested as the rest frame of the cosmic microwave background (CMB) radiation. The propagation of particles and radiation modes in the CMB rest frame is determined by dispersive wave equations coupled to isotropic permeability tensors. The decay of ∼50 GeV pions and ∼85 GeV kaons generating the CERN neutrino beam to Gran Sasso (CNGS) is analyzed in this context. Causality constraints on the group velocity of the ∼17 GeV muon neutrinos produced in the decay are derived and compared to recent experimental bounds on the neutrino speed.
Export citation and abstract BibTeX RIS
Introduction
We investigate pion and kaon decay into muons and muon neutrinos, which is the source of the CNGS neutrino beam [1]. This is motivated by upper bounds on a superluminal neutrino velocity recently established by the OPERA [2,3], BOREXINO [4], LVD [5] and ICARUS [6] experiments. Outside the lightcone, a proper causality interpretation of decay processes requires an absolute spacetime conception, as the time order of spacelike connections established by superluminal signals can be overturned in the rest frames of the interacting subluminal constituents [7,8]. The absolute spacetime, the aether, is manifested by dispersive permeability tensors, which affect the wave propagation of particles and radiation modes, in particular their group velocity. The permeability tensors are isotropic in a distinguished frame of reference defined by vanishing temperature dipole anisotropy of the CMB [9–12]. The coupling of Dirac and gauge fields to frequency-dependent permeability tensors has been explained in [13,14]. Here, we focus on specific decay and emission processes outside the lightcone.
We study the decays π → μ + νμ and K → μ + νμ as well as the hypothetical Cherenkov emission of photons by superluminal charges [15–17]. Susceptibility functions are introduced, which allow to treat sub- and superluminal group velocities on equal footing and to develop the decay kinematics irrespectively of whether the particles and radiation quanta are sub- or superluminal. We obtain causality constraints on the group velocities in the CMB rest frame to be satisfied in addition to energy-momentum conservation. In the high-energy limit, these causality conditions can be made explicit as linear inequalities for the frequency-dependent susceptibility functions of the respective particles. These conditions are always met if all constituents of the interaction are subluminal, but they prohibit the often invoked [16, 17] photonic Cherenkov radiation by superluminal charges.
Dispersive two-particle decay in a permeable spacetime: energy-momentum conservation, refractive indices and susceptibility functions
We focus on pion and kaon decay as well as on Cherenkov radiation, but the formalism developed is applicable to two-particle decay in general. We start with energy-momentum conservation in the CMB rest frame (aether frame), ωin = ωout + ων, kin = kout + kν, where (ωin,kin ) denote the energy and momentum variables of the incoming pion or kaon, and (ωout,kout ) the variables of the muon (or the outgoing pion in the case of Cherenkov radiation π → π + γ). The frequency and wave vector of the neutrino (or photon) are denoted by (ων,kν ). The outgoing momenta are split into longitudinal and transversal components,
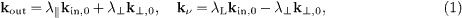
so that kin,0 k⊥,0 = 0. Subscript zeros denote unit vectors, kin = kin (ωin )kin,0, kout = kout (ωout )kout,0, kν = kν(ων)kν,0, where the wave numbers are determined by dispersion relations. We square kout and kν in (1), λ∥2 + λ⊥2 = kout2 (ωout ), λL2 + λ⊥2 = kν 2 (ων ), and substitute ωout = ωin - ων into kout (ωout ). Subtracting these two equations, factorizing, and using momentum conservation λL + λ∥ = kin (ωin ), we obtain

We factorize the wave numbers of the in- and outgoing particles and the neutrino (or photon),

where the refractive indices nin,out,ν read [8]
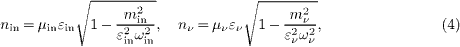
and analogously for nout. The permeabilities (εin (ωin), μin (ωin )), (εout (ωout ),μout (ωout )) and (εν (ων ),μν (ων )) are positive functions of the indicated variables, defining isotropic permeability tensors hin,out,ν,αβ in the CMB rest frame [14],

and analogously for the tensors houtα β (ωout ) and hν α β (ων ). The subscript ν labels the neutrino or photon variables, and is not to be confused with a tensor index. The dispersion relations are derived from Klein-Gordon equations such as (hinα β ∂α ∂β - min2 )ψin = 0, obtained by squaring the Dirac equation of the respective particle [8]. We find hinα β kin,αkin,β + min2 = 0, hν α β kν,α kν,β + mν 2 = 0, and similarly for kout,α, where kin,α = ( - ωin,kin), kout,α = ( - ωout,kout ) and kν ,α = ( - ων ,kν ) are the 4-momenta of the in- and outgoing particles and the neutrino.
In high-energy interactions, where the speed of the sub- and superluminal particles is close to the speed of light, it is efficient to define susceptibility functions for each particle species, in analogy to dielectrics, which serve as expansion parameters. The electric and magnetic susceptibilities of the incoming particle are denoted by χe,in = εin - 1 and χm,in = μin - 1, and analogously for the out-state. The neutrino (or photonic) susceptibilities are χe,ν(ων ) = εν - 1 and χm,ν(ων ) = μν - 1. We expand the neutrino (photon) refractive index nν (ων ) in linear order in χe,ν, χm,ν and mν 2 /ων 2, cf. (4), and analogously the refractive indices of the in- and out-states. This triple Taylor expansion is possible if the velocities of all particles involved are close to the speed of light, so that the permeability tensors (5) are close to the Minkowski metric ηα β = diag( - 1,1,1,1), with electric and magnetic susceptibilities close to zero. In the case of pion and kaon decay, the squared mass/energy ratios in the GeV region are small as well, ensuring refractive indices close to 1 and thus small index variations
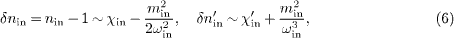
and analogously δnout and δ nν. Here, we expanded in linear order in the enumerated parameters, and defined the shortcut χin = χe,in + χm,in, and analogously for χout and χν. (That is, nin in (6) is linearized in χe,in, χm,in and min2 /ωin2.) The index variations δ nin,out,ν and susceptibilities χin,out,ν can have either sign, being small parameters close to zero like the squared mass/energy ratios. If not indicated otherwise, the energy dependence of the susceptibility functions is χin (ωin), χν (ων ), and χout (ωout ), and similarly for δ nin,out,ν. The primes on δn'in,out,ν denote frequency derivatives; δn'in in (6) stands for (δ nin)' taken at ωin.
We substitute the wave numbers (3) and ωout = ωin - ων into the longitudinal momentum coefficients (2),
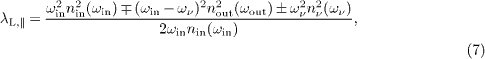
where the upper sign refers to λL. The squared transversal coefficient λ⊥2 in (2) is the product of (ων nν (ων ) ±λL ). We expand (7) in linear order in the index variations δ nin,out,ν, cf. (6),
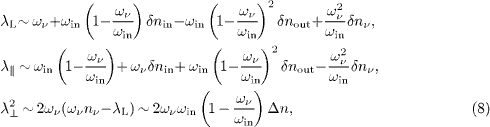
where Δ n denotes the refractive-index increment
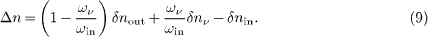
The only approximation in (8) and (9) is linearization in the index variations δ nin,out,ν. The condition λ⊥2 > 0 thus means Δ n > 0. All three frequencies in ωout = ωin - ων are positive, and positivity of the index increment Δ n in (9) is a necessary condition for momentum conservation, cf. (8).
Decay angles and group velocities in the CMB rest frame
To find the decay (or emission) angles, we write the wave vectors (1) as, cf. (3) and (6),
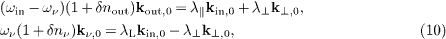
and multiply these identities by kin,0, using kin,0 k⊥,0 = 0. Defining the decay angles by cos θout = kin,0 kout,0 and cos θν = kin,0 kν ,0, we obtain

with the longitudinal momentum coefficients λ∥ and λL in (8) and the refractive-index increment Δ n in (9). The only approximation in (11) is systematic linearization in the index variations δ nin,out,ν, cf. (6) and (9). Expanding the cosines, we find the decay angles

The ratio θν /θout does not depend on the refractive indices, and the angle between the wave vectors kout,0 and kν ,0 of the outgoing particles is θν + θout ∼θout ωin /ων. Thus,
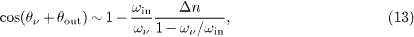
with cos (θν + θout ) = kout,0 kν ,0.
The particle velocities are group velocities obtained as reciprocal frequency derivative of the wave number (3): 1/υν = nν + ων n'ν, where 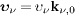 , cf. after (1), and analogously for υin,out. We parametrize the absolute values υin,out,ν with nin,out,ν = 1 + δ nin,out,ν, cf. (6), and expand in linear order,
, cf. after (1), and analogously for υin,out. We parametrize the absolute values υin,out,ν with nin,out,ν = 1 + δ nin,out,ν, cf. (6), and expand in linear order,

The scalar products of the group velocities linearized in the index variations read

where, cf. (9),

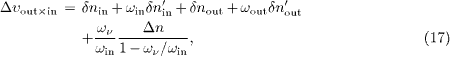
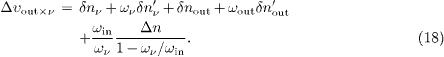
The causality constraints are  , where the subscript i labels the subluminal velocities and j the superluminal ones in the aether frame [7]. These kinematic constraints are thus tantamount to positivity of the respective increments Δυi × j of the velocity products in (16)–(18). For instance, if the pion velocity υin is superluminal and the muon velocity υout subluminal, the pion trajectory appears time inverted in the proper time of the muon if
, where the subscript i labels the subluminal velocities and j the superluminal ones in the aether frame [7]. These kinematic constraints are thus tantamount to positivity of the respective increments Δυi × j of the velocity products in (16)–(18). For instance, if the pion velocity υin is superluminal and the muon velocity υout subluminal, the pion trajectory appears time inverted in the proper time of the muon if 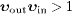 . In this case, the pion reemerges during the muon's proper lifetime, which is causality violating, as the pion was annihilated by decay at the time the muon was created. The velocity constraints
. In this case, the pion reemerges during the muon's proper lifetime, which is causality violating, as the pion was annihilated by decay at the time the muon was created. The velocity constraints 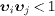 in the aether frame are necessary and sufficient to exclude causality violating time inversions in the rest frames of the subluminal particles. The velocities refer to asymptotic in- and out-states of the interacting particles and radiation modes. The inertial frames and proper times of subluminal in- and out-states are linked by Lorentz boosts to the aether frame [8], which is the universal frame of reference, manifested as the homogeneous and isotropic CMB rest frame [18].
in the aether frame are necessary and sufficient to exclude causality violating time inversions in the rest frames of the subluminal particles. The velocities refer to asymptotic in- and out-states of the interacting particles and radiation modes. The inertial frames and proper times of subluminal in- and out-states are linked by Lorentz boosts to the aether frame [8], which is the universal frame of reference, manifested as the homogeneous and isotropic CMB rest frame [18].
Causality conditions on the susceptibility functions of the aether
We parametrize the velocity increments Δυi × j in (16)–(18) with the susceptibility functions (6), starting with
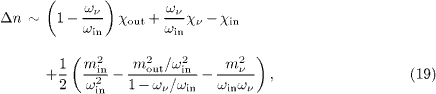
where we invoked energy conservation ωout = ωin (1 - ων /ωin ). We find
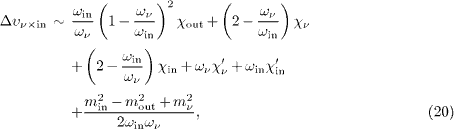
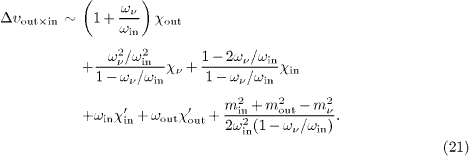
As a consistency check, we may interchange the indices ν ↔out in (20), and use ωout = ωin - ων to recover (21). Similarly, cf. (18),
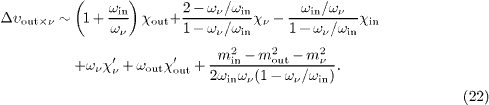
By interchanging ν↔in, we recover (21).
For instance, the decay of a superluminal pion, π → μ + νμ, into a subluminal muon and a superluminal neutrino requires two kinematic causality conditions, Δυout× in > 0 and Δυout×ν > 0. The third condition, Δυν × in > 0, need not be satisfied, as both the outgoing neutrino and the incoming pion are superluminal, so that neither of them admits a rest frame where a time inversion could occur. All causality conditions refer to group velocities in the CMB rest frame. The third condition for this decay is Δ n > 0 in (19), required by momentum conservation, cf. (8). In brief, the causality condition Δυi × j > 0 has to be satisfied in the aether frame if one of the indices labels a superluminal particle or radiation mode and the other a subluminal one. If this condition is violated, the trajectory of the superluminal particle is time inverted in the rest frame of the subluminal particle, so that absorption happens prior to emission in the proper time of the subluminal particle.
Pion decay π → μ + νμ generating the CNGS beam: constraints on the neutrino velocity
The mass squares in the refractive indices (6) of pion and muon read min2 = mπ 2 ≈ 0.0195 GeV2 and mout2 = mμ 2 ≈ 0.0112 GeV2 [19]. A neutrino mass of below 2 eV [20] in the neutrino refractive index is negligible in the GeV range, mν 2 ≈ 0, cf. (4) and (6). As for the CNGS neutrino beam, the energy of the incoming pions is about ωin ≈ 50 GeV [1], and the average energy of the neutrinos ων ≈ 17 GeV [2–6]. The neutrino refractive index (6) is nν (ων ) = 1 + δ nν, with δ nν = nν - 1 ∼ χν. The frequency derivatives of the susceptibilities are put to zero, χ 'ν ,in,out ≈ 0. The pion refractive index is parametrized by δ nin ∼χin - min2 /(2ωin2 ), with derivative δ n'in ∼ min2 /ωin3, cf. (6), and analogously for the outgoing muon, δ nout ∼χout - mout2 /(2ωout2 ), and δ n'out ∼ mout2 /ωout3, taken at ωout = ωin - ων ≈ 33 GeV. The refractive-index increment (19) gives the constraint
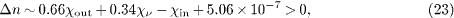
required by energy-momentum conservation. The causality conditions for this decay are obtained from the velocity increments (20)–(22), with χ 'ν ,in,out ≈ 0 and mν 2 ≈ 0:
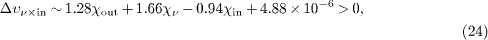
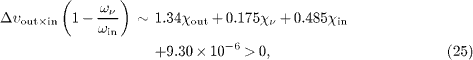
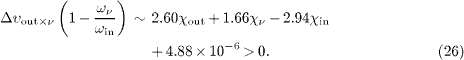
The susceptibilities refer to different frequencies, χout (ωout ), χν (ων ) and χin (ωin ), and the frequency variation is neglected, assuming vanishing derivatives at the respective energies. The neutrino group velocity and refractive index read, cf. (6) and (14),

and analogously for the pionic and muonic group velocities υin,out and their refractive indices nin,out. The susceptibilities χν ,in,out are close to zero and can have either sign, and the same holds true for υν ,in,out - 1 and 1 - nν ,in,out in (27). In deriving (27), we used (ω nν )' = 1/υν. We also put χ 'ν ,in,out ≈ 0 and mν 2 ≈ 0 as in (23)–(26), so that 1 - nν ∼υν - 1 ∼ - χν. A neutrino index nν < 1 or a negative susceptibility is thus tantamount to a superluminal neutrino speed υν > 1. The pion and muon velocities are related to their susceptibilities by υin - 1 ∼ - 3.90 × 10 - 6 - χin and υout - 1 ∼ - 5.14 × 10 - 6 - χout.
The OPERA Collaboration derived the bound υν - 1 = (2.7 ± 6.5) × 10 - 6 on the neutrino velocity, based on ∼15200 events collected in 2009–2011 [2]. BOREXINO obtained υν - 1 = 2.7 ± 5.4 × 10 - 6 in the Oct./Nov. 2011 run, and 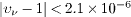 in May 2012 [4]. The OPERA upper bounds inferred from the May 2012 data are υν - 1 < 2.3 × 10 - 6 and
in May 2012 [4]. The OPERA upper bounds inferred from the May 2012 data are υν - 1 < 2.3 × 10 - 6 and 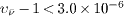 for antineutrinos [3]. The LVD experiment obtained
for antineutrinos [3]. The LVD experiment obtained 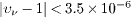 [5], and the ICARUS bound from the May 2012 run is
[5], and the ICARUS bound from the May 2012 run is 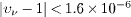 [6]. All bounds refer to an averaged neutrino energy of 17 GeV in the CNGS beam. The OPERA bound from the 2009–2011 data [2] is based on a much larger sample than the other experiments (<100 events). The current MINOS estimate, υν − 1 = 6 ±13 ×10−6 [21], is in line with the quoted CNGS results; all these experiments report a positive neutrino excess velocity with an error bound safely consistent with the speed of light.
[6]. All bounds refer to an averaged neutrino energy of 17 GeV in the CNGS beam. The OPERA bound from the 2009–2011 data [2] is based on a much larger sample than the other experiments (<100 events). The current MINOS estimate, υν − 1 = 6 ±13 ×10−6 [21], is in line with the quoted CNGS results; all these experiments report a positive neutrino excess velocity with an error bound safely consistent with the speed of light.
Given the low relative speed υr ≈ 1.2 × 10 - 3 of the Solar system barycenter in the CMB rest frame [11,12], we can use the linearized addition law for velocities, υCMB - 1 = (υν - 1)(1 + O(υr )), where υCMB is the neutrino speed in the CMB rest frame and υν the speed measured in the baseline frame (rest frame of source and detector) [8]. Hence, υCMB - 1 ∼ υν - 1 ∼ 1 - nν, cf. after (27).
In the following, we assume that the incoming pion and the outgoing muon are subluminal, and the neutrino is superluminal. Furthermore, we assume that pion and muon have similar susceptibilities, so that we can equate χin ≈χout ≈χ in the energy-momentum and causality conditions (23)–(26). (We will later drop this assumption, cf. after (30).) The velocity condition on pion and muon is 1 - υin,out > 0, which gives the bound - 3.90 × 10 - 6 <χ, cf. the estimates stated after (27). Since the neutrino is superluminal, we have χν < 0. The energy-momentum constraint (23) combined with the velocity condition gives
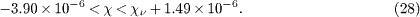
The causality conditions (24) and (26) read

which can only be satisfied if χν > - 2.94 × 10 - 6. In fact, for (28) to be consistent with (29), an even stronger lower bound on χν is required, χν > - 2.694 × 10 - 6. The causality condition (25) does not apply, as the pion as well as the muon are subluminal, cf. after (22). If χν ≈ - 2.694 × 10 - 6, we find the unique solution χ ≈ - 1.204 × 10 - 6. (At the opposite edge χν ≈ 0 of the allowed χν interval, the admissible χ range is given by (28).) As we have put χin ≈χout ≈χ, we find the pion and muon velocities 1 - υin ∼ 2.7 × 10 - 6 and 1 - υout ∼ 3.9 × 10 - 6, respectively. The neutrino excess velocity is υν - 1 ∼ - χν ∼ 2.7 × 10 - 6, which coincides with the quoted OPERA and BOREXINO 2011 upper bounds [2,4].
We return to the basic energy-momentum and causality conditions (23), (24) and (26), substitute χν ≈ - 2.7 × 10 - 6, and drop the assumption of equal pion and muon susceptibilities χin ≈χout to obtain
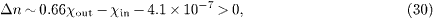
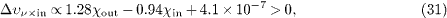

Adding the first to the second and third of these inequalities, we find χin <χout and χin < 0.83χout, the latter is weaker and can be ignored if we consider negative susceptibilities χin,out < 0. The constraints (30)–(32) thus reduce to χin < 0.66χout - 4.1 × 10 - 7 and χin <χout for χin,out in the range - 3.90 × 10 - 6 <χin < 0 and - 5.14 × 10 - 6 <χout < 0. The latter two lower bounds on the pion and muon susceptibilities are required by a subluminal particle velocity, cf. after (27). These constraints are based on the neutrino susceptibility χν ≈ - 2.7 × 10 - 6; a possible solution is χin ≈χout ≈ - 1.2 × 10 - 6 as discussed after (29).
Kaon decay K → μ + νμ and superluminal muon neutrinos
The reasoning is analogous to that of pion decay, cf. (30)–(32). The pionic mass square is replaced by the kaon mass, min2 = mK2 ≈ 0.244 GeV2 [19], and the energy of the incoming kaon is ωin ≈ 85 GeV [1], so that ωout = ωin - ων ≈ 68 GeV for the outgoing muon. The group velocities of kaon and muon are calculated as in (27), 1 - υin ∼ 1.7 × 10 - 5 + χin, and 1 - υout ∼ 1.2 × 10 - 6 + χout. The energy-momentum and causality constraints (19), (20) and (22) read
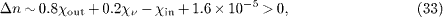
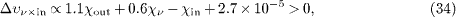
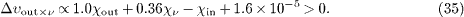
These conditions can readily be satisfied with a neutrino susceptibility in the interval 0 >χν > - 2.7 × 10 - 6, since in this case the χν terms are negligible; χν ≈ - 2.7 × 10 - 6 is the neutrino susceptibility defined by the quoted OPERA [2] and BOREXINO [4] upper bounds on the neutrino excess velocity. Subluminal kaon and muon velocities require the constraints - 1.7 × 10 - 5 <χin and - 1.2 × 10 - 6 <χout. Conditions (33)–(35) are satisfied by negative susceptibilities χin,out subject to these velocity bounds. We do not assume χin ≈χout, as the kaon and muon mass squares substantially differ. χout (ωout ) refers to a muon energy of ωout ≈ 68 GeV, as compared to 33 GeV in the case of pion decay. The neutrino susceptibility χν (ων ) is taken at a neutrino energy of 17 GeV in both cases.
Causality violation prohibiting photon emission  by superluminal high-energy charges
by superluminal high-energy charges
In this section, the subscript index ν labels photon variables. The outgoing photon with frequency ων has zero rest mass mν 2 = 0 and a refractive index nν - 1 = δ nν ∼χν, cf. (6). We assume a nearly constant photon susceptibility χν ⩾ 0, χ 'ν ≈ 0, so that the photonic group velocity (14) is υν ≈ 1 - χν ⩽ 1. We use a refractive photon index that is slightly larger than one, so that a rest frame exists for the photon. The causality conditions are Δυν × in > 0 and Δυout×ν > 0, cf. (16) and (18). The vacuum limit χν → 0 (photonic permeability tensor coinciding with Minkowski metric) is performed in the subsequent inequalities by putting δ nν ≈ 0 and δ n'ν ≈ 0 in the causality constraints and the refractive-index increment (9). Energy conservation means ωout = ωin - ων, with positive frequencies. The refractive indices of the in- and outgoing charges are δ nin,out ∼χin,out - min2 /(2ωin,out2 ), cf. (6), with derivatives δ n'in,out ∼χ 'in,out + min2 /ωin,out3 at ωin,out. The susceptibility functions χin,out (ω ) are identical, but taken at different energies ωin,out. Expanding χin (ω ) ≈χin + (ω - ωin )χ 'in in linear order at ωin, and making use of energy conservation, we can approximate χout (ωout ) ≈χin (ωin ) - ων χ 'in (ωin ) and χ 'out (ωout ) ≈χ 'in (ωin ). The refractive-index increment (19) reads in this case
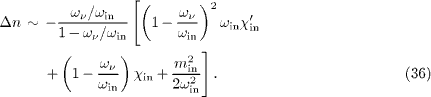
First, we show that one of the causality conditions Δυν × in > 0 and Δυout×ν > 0 is violated for negative χin. In fact, the velocity increment (20) reads
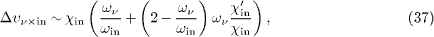
so that Δυν × in < 0 if both χin and χ 'in are negative. Increment (22) can be written as

so that Δυout×ν < 0 if χin is negative and χ 'in positive. Thus the emission π → π γ is causality violating if the susceptibility χin (ωin ) is negative.
This emission process is also forbidden in the case of a positive susceptibility χin (ωin ). If both χin and χ 'in are positive, this implies a negative refractive-index increment Δ n , cf. (36), so that momentum cannot be conserved. (In this case, the group velocity (27) of the incoming charge is subluminal.) If χin is positive and χ 'in negative, the conditions Δ n > 0 and Δυν × in > 0 cannot simultaneously be satisfied, cf. (36) and (37). In fact, we may drop the mass term in (36) and require (1 - ων /ωin )ωin χ 'in + χin < 0, which is necessary (but not sufficient) for Δ n > 0. The causality condition Δυν × in > 0 implies (ων /ωin - 2)ωin χ 'in - χin < 0, cf. (37). Adding these inequalities, we obtain - ωin χ 'in < 0, in contradiction to the assumed negative derivative χ 'in. We have thus demonstrated that photon emission by superluminal high-energy charges is forbidden since it is causality violating.
Conclusion
We have studied two-particle decay in a dispersive spacetime, deriving bounds on a superluminal group velocity of the decay products. The nonlinear causality and energy-momentum constraints can be linearized in the high-energy regime by introducing frequency-dependent susceptibility functions for the in- and outgoing particles which serve as expansion parameters. In this way, analytically tractable causality conditions are obtained even in multi-channel interactions. These constraints on the susceptibility functions in the isotropic aether frame (identified as CMB rest frame [22]) prevent time inversions in the rest frames of the subluminal particles and radiation modes (inertial in- and out-states) of the decay process [7].
Specifically, we discussed the dispersive kinematics of pion and kaon decay in the aether, and calculated the susceptibility functions with input parameters of the CNGS neutrino beam. The causality conditions are linear inequalities to be satisfied by the susceptibilities of the respective particles. We employed these constraints to obtain velocity estimates for the muon and muon neutrino generated by the decay. Finally we used causality conditions on susceptibility functions to demonstrate, without the use of specific input parameters, that photonic Cherenkov radiation by superluminal high-energy charges is causality violating.